直线与圆(切线三大定理)
圆和直线相切的公式
圆和直线相切的公式当直线与圆相切时，直线的方程和圆的方程存在以下几个关系：1.直线与圆的切点在直线上。
2.直线与圆的切点的切线与直线垂直。
3.直线与圆的切点的切线斜率等于直线的斜率。
现在，我们将分别介绍这些条件，并推导得出相切的公式。
1.直线与圆的切点在直线上：设直线的方程为 y = mx + c，圆的方程为 (x-a)² + (y-b)² = r²，其中(a, b)为圆的圆心坐标，r为半径长度。
为了找到直线与圆的切点，我们将方程代入圆的方程，得到：(x-a)² + (mx + c - b)² = r²将方程展开，得到:x² - 2ax + a² + m²x² + 2mcx + c² + b² - 2bmx = r²整理后，得到方程：(1 + m²)x² + 2(mc - am - bm)x + a² + c² + b² - 2ab - r² = 0如果直线与圆相切，方程只有一个根，也就是说，二次方程的判别式为零。
因此，判别式为：(2(mc - am - bm))² - 4(1 + m²)(a² + c² + b² - 2ab - r²) = 02.直线与圆的切点的切线与直线垂直：通过求得的切点，我们可以获得切线的斜率。
与直线垂直意味着切线的斜率的乘积与直线的斜率为-1、设直线的斜率为m，切线的斜率为k。
通过求导数得到切线的斜率k=-1/m。
3.直线与圆的切点的切线斜率等于直线的斜率：这个条件可以由上述条件推导得出。
当直线与圆相切时，直线的斜率等于切线的斜率。
现在，我们通过一个例子来解释这些公式的应用。
假设有一个以坐标原点为中心的圆，半径为r。
直线通过点(0,h)，与圆相切。
初中数学 文档：切线有关的定理
切线三大定理【知识要点】（按点列出）圆心角和圆周角、弦长、弧长的关系【教学过程】：【复习、新授、训练（例题与训练中的基础、拓展、综合、链接部分必与知识点紧密联系）、小结、作业）】知识点1.直线和圆的三种位置关系：知识点2.切线的判定和性质：判定：（1）当圆心到直线的距离d 等于半径r 时，直线是圆的切线；（2）经过半径外端垂直于的半径的直线，是圆的切线。
性质：如果一条直线与圆相切，另一条满足：（1）过圆心，（2）切点，（3）垂直于半径．其中任意两个条件，则必满足第三个条件。
知识点3、弦切角定理：弦切角等于所夹弧对的圆周角。
知识点4、切线长定理：从圆外一点向圆所引的两条切线段长相等；知识点5、圆幂定理：（1）PA ·PB=PC ·PD （2）PT 2=PA ·PB=PC ·PD知识点6、圆与三角形： d<r d=r d>r 关 系 相交 相切 相离 交点个数 两个交点 一个交点 没有交点 直线名称 割线 切线 不相交线 A PDC B A B T PD C Ac b A cADC B A B P1 2 +∠）12 r=（2）如图，是半圆的直径，EF BC ⊥于点，5BF FC=．已知点在的延长线上，与半圆 交于，且82AB AE ==，，则的长为多少．AB C DE F O考点3、圆和三角形(2011黑龙江省大庆)如图，△的两直角边边长为4，边长为3，它的内切圆为⊙0，⊙0与边、、分别相切于点、、，延长交斜边于点．(1)求⊙的半径长； (2)求线段的长．考点4、圆的综合题型已知：如图1，在直角梯形ABCD 中，AD ∥BC ，∠B=90°，AB=8厘米，AD=24厘米，BC=26厘米，AB 为圆O 的直径，动点P 从点A 开始沿AD 边向点D 以1厘米／秒的速度运动，动点Q 从点C 开始沿CB 边向点B 以3厘米／秒的速度运动，P 、Q 分别从A 、C 同时出发，当其中到达端点时，另一点也随之停止运动，设运动时间为t 秒．求(1)t 分别为何值时，四边形PQCD 为平行四边形、等腰梯形？(2)t 分别为何值时，直线PQ 与圆O 相切、相交、相离？(97年河北)【知识小结】（先由自己独立小结，最后由老师书面小结）直线与圆的关系：相交、相切、相离圆中切线三大定理：性质定理、判定定理、切线定理圆幂定理圆中内切三角形、四边形【作业】（精少，书面与识记部分均要求有）【教学后记】（对学生学习过程中的反应、吸收、优缺点与自己的教学方法进行反思）。
直线与圆的位置关系-切线长定理
O
P
A
B
切线与切线长是一回事吗？它们有什么区别与联系呢？
·
·
切线和切线长
切线和切线长是两个不同的概念： 1、切线是一条与圆相切的直线，不能度量； 2、切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。
O
P
A
B
比一比
O A B P 思考：已知⊙O切线PA、PB，A、B为切点，把圆沿着直线OP对折,你能发现什么? 折一折
130°
画一画
01
02
O
。
A
B
P
思考：已画出切线PA、PB，A、B为切点，则∠OAP= °,连接OP，可知A、B 除了在⊙O上，还在怎样的圆上?
90
如何用圆规和直尺作出这两条切线呢？
”
01
02
03
04
05
06
07
08
在经过圆外一点的切线上，这一点和切点之间的线段的长叫做这点到圆的切线长
（1）若PA=4、PM=2，求圆O的半径OA
OA=3
牛刀再试
已知：如图,PA、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA=12CM，求△PEF的周长。
E
A
Q
P
F
B
O
易证EQ=EA, FQ=FB,PA=PB
∴ PE+EQ=PA=12cm
24.2.2(3)直线与圆的位置关系(三) 切线长定理
202X
单击此处添加正文，文字是您思想的提炼， 请尽量言简意赅的阐述观点。
演讲人姓名
50°
1、如何过⊙O外一点P画出⊙O的切线？
切线的性质和判定定理
D
解：BD是⊙O的切线
连接OD
A
∵ OD=OA
O
C
B ∴∠ODA=∠BAD=∠B
=300
∴∠ BOD=600
∴∠ODB=900
即： OD⊥DB
∴BD是⊙O的切线
变式练习 练习3,△ABC中，以AB为直径的⊙O，
交边BC于P，BP=PC, PE⊥AC于E。
求证:PE是⊙O的切线。 证明：连结OP。
∵ AB为直径
思∵考直线L是
⊙如O图的：切如果线直，线L
是A⊙是O的切切点线。,切点为
AL是,∴ 点那不么L是⊥半一径O定AO垂于A与直A直呢线?
.O
一定垂直(可用反证法来证）
切线的性质定理:
L A
圆的切线垂直于过切点的半径
简记为：“知切线，连半径，得垂直”
切线的性质定理反证法
假设切线l不垂直于过切点的半 径OA，
想一想
过圆0内一点作直线，这条直线与圆有什么位置关系？过 半径OA上一点（A除外）能作圆O的切线吗？过点A呢？
O
r
A
l
圆的切线判定定理：
经过半径的外端且垂于这条半径
的直线是圆的切线。
条件：(1)经过半径的外端；(2)垂直于过该点半径；
符
号 语
∵l⊥OA，A点是⊙O上一点
言
表
达 ∴直线l是⊙O的切线
为什么?
解：AC与⊙O相切
连接OD,作OE⊥AC
E
∴∠OEC=900
∵ AB是⊙O的切线
∴OD⊥AB,
∴∠ODB=900=∠OEC
∵AB=AC
∴∠B=∠C
∵O是BC的中点
∴OB=OC
∴△OBD≌△OCE
直线和圆的位置关系
直线和圆的位置关系 【基础知识】1、直线和圆的位置关系：（1）相交：直线与圆有两个公共点时，叫做直线和圆相交，这时，直线叫做圆的割线，这两个公共点叫做交点。
（2）相切：直线与圆有一个公共点时，叫做直线与圆想切这时直线叫做圆的切线，唯一的（1） 切线的性质：定理：圆的切线垂直于经过切点的半径。
（2） 推论1：经过圆心且垂直于切线的直径必过切点。
（3） 推论2：经过切点且垂直于切线的直线必过圆心。
3、切线的判定定理及判定方法（1）切线判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线。
（2）切线的判定方法： ①与圆有唯一公共点的直线是圆的切线。
②到圆心的距离等于半径的直线是远的切线。
③经过半径外端并且垂直于这条半径的直线是圆的切线。
4、证明圆的切线的辅助线的方法：①连半径，证明垂直。
②做垂直，证半径。
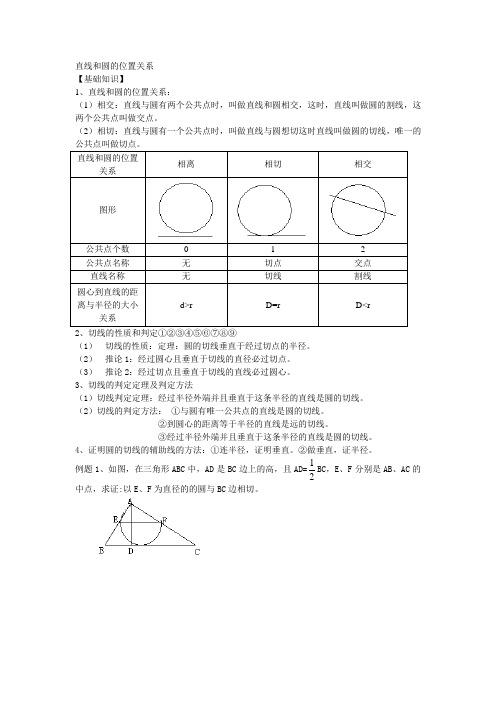
例题1、如图，在三角形ABC 中，AD 是BC 边上的高，且AD=21BC ，E 、F 分别是AB 、AC 的中点，求证:以E 、F 为直径的的圆与BC 边相切。
【跟踪练习】1、已知：如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE，求证：DE与半圆O相切．2、如图，已知CD是△ABC中AB边上的高，以CD为直径的⊙O交CA于点E，点G是AD的中点．求证：GE是⊙O的切线；5、三角形的内切圆（1）内切圆：和三角形三边都相切的圆叫做三角形的内切圆。
内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心，这个三角形叫做圆的外接三角形。
三角形的内心到三边的距离相等。
例题2．如图，在△ABC中，AB=AC，内切圆O与边BC，AC，AB分别切于D，E，F．（1）求证：BF=CE；（2）若∠C=30°，AC的长．例题3、如图，⊙I切△ABC的边分别为D，E，F，∠B=70°，∠C=60°，M是 DEF上的动点（与D，E不重合），∠DMF的大小一定吗？若一定，求出∠DMF的大小；若不一定，请说明理由．【跟踪练习】1．图1，⊙O内切于△ABC，切点为D，E，F．已知∠B=50°，∠C=60°，•连结OE，OF，DE，DF，那么∠EDF等于（）A．40°B．55°C．65°D．70°图1 图2 图32．如图2，⊙O是△ABC的内切圆，D，E，F是切点，∠A=50°，∠C=60°，•则∠DOE=（）A．70°B．110°C．120°D．130°3．如图3，△ABC中，∠A=45°，I是内心，则∠BIC=（）A．112.5°B．112°C．125°D．55°6、切线长定理及切线长概念（1）切线长的概念：在经过员外一点的圆的切线上，这点和切点之间的线段的长，叫做这点倒圆的切线长。
与圆有关的位置关系及切线定理
与圆有关的位置关系1、点与圆的位置关系如果圆的半径是r ，这个点到圆心的距离为d，那么：（1）点在圆外d>r ；（2）点在圆上d＝r；（3）点在圆内d<r；2、直线与圆位置关系的定义及有关概念（1）直线与圆有两个公共点，叫做直线与圆相交，这直线叫做圆的割线，公共点叫做交点（2）直线和圆有一公共点时，叫做直线和圆相切，这直线叫做圆的切线，公共点叫做切点（3）直线和圆没有公共点时，叫做直线和圆相离.3、直线和圆的位置关系如果⊙ O的半径为r ，圆心O到直线l 的距离为d，那么（1）直线l 和⊙ O相交d<r ；（2）直线l 和⊙ O相切d＝r；（3）直线l 和⊙ O相离d>r；典例精析例1：已知直线l ：y＝x－3 和点A（0，3），B（3，0），设P点为l 上一点，试判断P、A、B是否在同一个圆上？例2：下列说法正确的是（）A. 过圆内接三角形的顶点的直线是圆的切线B. 若直线与圆不相切，则它和圆相交C. 若直线和圆有公共点，直线和圆相交D. 若直线和圆有唯一公共点，则公共点是切点例3：设直线l到⊙ O的圆心的距离为d，⊙ O的半径为R，并使x2 2 dx R 0 ，试根据关于x 的一元二次方程根的情况讨论l 与⊙ O的位置关系.3、圆和圆的位置关系外离（没有公共点）外切（1）相离（2）相切（有一个公共点）（3）相交（有两个公共点）内含（包括同心圆）内切注：两圆同心是两圆内含的一种特例.2、两圆的位置与两圆的半径、圆心距之间的数量关系设两圆的半径分别为R 和r ，圆心距为d，那么（1）两圆外离d>R＋r （2）两圆外切d＝R＋r（3）两圆相交R－r <d<R+r（4）两圆内切d＝R－r （5）两圆内含d<R－r典例精析例1：已知两个圆的半径分别为2、3，圆心距是d，若两圆有公共点，则 d 的取值范围为例2：已知⊙ O1 和⊙ O2内切，圆心距为7cm，⊙ O1 的半径为8cm，求⊙ O2 的半径.例4：如图：⊙ M的半径为8cm，⊙ N的半径为6cm，MN＝10cm，两圆相交于A、B 两点，连接AB与MN交于点C，求AB的长为多少？与相切有关的性质定理1、切线的性质定理：定理：圆的切线垂直于过切点的半径. 推论1：经过圆心且垂直于切点的直线必经过切点.推论2：经过切点且垂直于切点的直线必经过圆心.2、切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.3、切线的判定方法（1）定义：和圆只有一个公共点的直线是圆的切线；（2）数量关系：和圆心的距离等于半径的直线是圆的切线；（证长度）（3）定理：过半径外端且与这条半径垂直的直线是圆的切线.（证角度）两圆相切与相交的性质：（1）如果两圆相切，那么两圆的连心线经过切点；（2）两圆相交，连心线垂直平分相交圆的公共弦。
九年级数学第三章直线与圆的位置关系
直线与圆的位置关系【学习目标】1.理解并掌握直线与圆的三种位置关系；2.理解切线的判定定理和性质定理.【要点梳理】要点一、直线与圆的位置关系1.切线的定义：直线与圆有唯一的公共点时，这条直线叫做圆的切线，这个唯一的公共点叫做切点.此时直线与圆的位置关系称为相切.2．直线和圆的三种位置关系：(1) 相交：当直线与圆有两个公共点时，叫做直线与圆相交．(2) 相切：当直线与圆有唯一公共点时，叫做直线与圆相切．这条直线叫做圆的切线，公共点叫做切点．(3) 相离：当直线与圆没有公共点时，叫做直线与圆相离．3．直线与圆的位置关系的判定和性质．直线与圆的位置关系能否像点与圆的位置关系一样通过一些条件来进行分析判断呢？由于圆心确定圆的位置，半径确定圆的大小，因此研究直线和圆的位置关系，就可以转化为直线和点(圆心)的位置关系．下面图(1)中直线与圆心的距离小于半径；图(2)中直线与圆心的距离等于半径；图(3)中直线与圆心的距离大于半径．一般地，直线与圆的位置关系有以下定理：如果⊙O的半径为r，圆心O到直线l的距离为d，那么，（1）d＜r直线l与⊙O相交；（2）d=r直线l与⊙O相切；（3）d＞r直线l与⊙O相离.要点进阶：这三个命题从左边到右边反映了直线与圆的位置关系所具有的性质；从右边到左边则是直线与圆的位置关系的判定．要点二、切线的性质定理和判定定理1．切线的性质定理：圆的切线垂直于过切点的半径.要点进阶：切线的性质定理中要注意：圆的切线是与过切点的半径垂直，不是与任意半径都垂直.2．切线的判定定理：过半径外端且垂直于半径的直线是圆的切线.要点进阶：切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可. 要点三、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心到三边的距离都相等.要点进阶：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).【典型例题】类型一、直线与圆的位置关系例1．在Rt△ABC中，∠C=90°，AC=3厘米，BC=4厘米，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？(1)r=2厘米； (2)r=2.4厘米； (3)r=3厘米举一反三：【变式】已知⊙O的半径为10cm，如果一条直线和圆心O的距离为10cm，那么这条直线和这个圆的位置关系为（）A. 相离B. 相切C. 相交D. 相交或相离类型二、切线的判定与性质例2．如图所示，在Rt△ABC中，∠B＝90°，∠A的平分线交BC于D，以D为圆心，DB长为半径作⊙D．求证：AC是⊙D的切线．例3.如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．（1）求BC的长；（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．例4．如图，AB为⊙O的直径，AC为⊙O的弦，AD平分∠BAC，交⊙O于点D，DE⊥AC，交AC的延长线于点E．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AE＝8，⊙O的半径为5，求DE的长．O C B A举一反三：【变式1】如图，在△ABC 中，∠CAB=90°，∠CBA=50°，以AB 为直径作⊙O 交BC 于点D ，点E 在边AC 上，且满足ED=EA ． （1）求∠DOA 的度数；（2）求证：直线ED 与⊙O 相切．举一反三：【变式2】如图所示，在△ABC 中，AB ＝BC ＝2，以AB 为直径的⊙O 与BC 相切于点B ，则AC 等于( )A ．2B ．3C ．22D ．23类型三、三角形的内切圆例5．如图，已知O 是△ABC 的内心，∠A=50°，求∠BOC 的度数.O C BA【变式】如图，△ABC 中，∠C=90°，BC=4，AC=3，⊙O 内切与△ABC ，则△ABC 去除⊙O 剩余阴影部分的面积为（ ）A.12-πB. 12-2πC. 14-4πD. 6-π【巩固练习】一、选择题1.已知：如图，PA ，PB 分别与⊙O 相切于A ，B 点，C 为⊙O 上一点，∠ACB=65°，则∠APB 等于( ) A ．65° B ．50° C ．45° D ．40°2．如图，AB 是⊙O 的直径，直线EC 切⊙O 于B 点，若∠DBC=α，则( ) A ．∠A=α B ．∠A=90°－α C ．∠ABD=α D ．∠α2190o-=ABD第1题图 第2题图3．设⊙O 的半径为3，点O 到直线l 的距离为d ，若直线l 与⊙O 至少有一个公共点，则d 应满足的条件是( )A.d=3B. d ＜3C. d≤3D.d＞34.如图，在⊙O 的内接四边形ABCD 中，AB 是直径，∠BCD=120°，过D 点的切线PD 与直线AB 交于点P ，则∠ADP 的度数为（ ）A ．40°B ． 35°C ． 30°D ． 45°5．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO ＝CD ，则∠PCA＝（ ） A.30° B.45° C.60° D.67.5°6．已知AB是⊙O的直径，点P是AB延长线上的一个动点，过P作⊙O的切线，切点为C，∠APC的平分线交AC于点D，则∠CDP等于（）A.30°B.60°C.45°D.50°二、填空题7．如图，AB是⊙O的直径，BC切⊙O于点B，AC交⊙O于点D.若AC=5，BC=3，则⊙O的半径为_______.8．如图，⊙O的切线PC交直径AB的延长线于点P，C为切点.若∠P=30°，⊙O的半径为1，则PB的长为______________.9．在△ABO中，OA=OB=2cm，⊙O的半径为1cm，当∠ABO=时，直线AB与⊙O相切．10.如图所示，已知直线AB是⊙O的切线，A为切点，OB交⊙O于点C，点D在⊙O上，且∠OBA＝40°，则∠ADC＝________．OCB A 11．如图所示，已知△ABC ，AC ＝BC ＝6，∠C ＝90°，O 是AB 的中点，⊙O 与AC 、BC 分别相切于点D 与点E ．点F 是⊙O 与AB 的一个交点，连DF 并延长交CB 的延长线于点G ，则CG ＝________．12．木工师傅可以用角尺测量并计算出圆的半径r .用角尺的较短边紧靠O ，并使较长边与O 相切于点C .假设角尺的较长边足够长，角尺的顶点为B ，较短边8cm AB .若读得BC 长为cm a ，则用含a 的代数式表示r 为 .三、解答题13. 如图，已知⊙O 是边长为2的等边△ABC 的内切圆，求⊙O 的面积.14． AB 是⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于D 点，过D 作⊙O 的切线DE 交BC 于E.求证：CE=BE.15.如图，AB是⊙O的弦，OC⊥OA，交AB与点P，且PC=BC，求证：BC是⊙O的切线．。
关于圆的切线的各种定理
切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线几何语言：∵l l ⊥⊥OA OA，，点A 在⊙O 上∴直线l 是⊙O 的切线（切线判定定理）切线的性质定理圆的切线垂直于经过切点的半径几何语言：∵OA 是⊙O 的半径，直线l 切⊙切⊙O O 于点A∴l l ⊥⊥OA OA（切线性质定理）（切线性质定理）推论1 1 经过圆心且垂直于切经过圆心且垂直于切线的直径必经过切点推论2 2 经过切点且垂经过切点且垂直于切线的直线必经过圆心切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角几何语言：∵直线PA PA、、PB 分别切⊙O 于A 、B 两点∴PA=PB PA=PB，∠，∠，∠APO=APO=APO=∠∠BPO BPO（切线长定理）（切线长定理）证明：连结OA OA、、OB∵直线PA PA、、PB 分别切⊙O 于A 、B 两点∴OA OA⊥⊥AP AP、、OB OB⊥⊥PB∴∠OAP=OAP=∠∠OBP=90OBP=90°°在△OPA和△OPB中：中：OAP=∠∠OBP∠OAP=OP=OPOA=OB=rHL））（HL∴△OPAOPB（OPA≌△≌△OPB∠BPOAPO=∠∴PA=PBPA=PB，∠，∠APO=弦切角概念顶点在圆上，一边和圆相交、另一边和圆相切的角叫做弦切角．它是继圆心角、圆周角之后第三种与圆有关的角．这种角必须满足三个条件：（1）顶点在圆上，即角的顶点是圆的一条切线的切点；所在的射线；（2）角的一边和圆相交，即角的一边是过切点的一条弦所在的射线；（3）角的另一边和圆相切，即角的另一边是切线上以切点为端点的一条射线。
它们是判断一个角是否为弦切角的标准，三者缺一不可准，三者缺一不可 （4）弦切角可以认为是圆周角的一个特例，即圆周角的一边绕顶点旋转到与圆相切时所成的角．正因为如此，弦切角具有与圆周角类似的性质．弦切角定理对的圆周角等于所夹的AC)对的圆周角等于所夹弦切角（即图中∠ACD)等于它所夹的弧(弧AC)所夹的弧的圆心角 [注，由于网上找得的图不是弧的读数的一半等于1/2所夹的弧的圆心角很完整，图中没有连结OC]几何语言：∵∠ACD所夹的是弧AC弦切角定理） ∴∠ACD=∠ABC=1/2∠COA=1/2弧AC的度数(弦切角定理）推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等，弧MN =MN =弧弧PQPQ ，弧，∠2所夹的是PQ几何语言：∵∠1所夹的是弧MNMN ，∠2∴∠1=∠2AD⊥EC证明：作AD⊥ECADC=90°∵∠ADC=90°ACD+∠CAD=90°∴∠ACD+∠CAD=90°∵ED与⊙O切于点CED∴OC⊥ED∴∠OCD=∠OCA+∠ACD=90°∴∠OCA=∠CAD OCA=∠CAD∵OC=OA=r OC=OA=r∴∠OCA=∠OAC OCA=∠OAC∴∠COA=180°COA=180°--∠OCA OCA--∠OAC=180°OAC=180°--2∠CAD 2∠CAD又∵∠ACD=90°ACD=90°--∠CAD ∠CAD∴∠ACDC=1/2∠COA ACDC=1/2∠COA∴∠ACD=∠ABC=1/2∠COA COA=1/2=1/2弧AC 的度数的度数切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。
25.5直线和圆的位置关系(第二课时)切线的性质定理
.
O
l
A
推理 过程
切线的性质定理:
圆的切线垂直于过切点的半径 l是⊙ O 的切线,
切点是A,连接OA。 这时，如在直线l上任取 一点不同于A的点P， 连接OP， 因为点P在⊙ O 外，则 OP ＞OA。 也就是说OA是点O到直 线l的最短距离，根据垂 线段最短，所以ＯＡ⊥ｌ
.O
l
A
例：在Rt⊿ABC中,∠ACB=90o,D是边AB上一 点，以BD为直径的⊙O与边AC相切于点E， 连结DE并延长,与BC的延长线交于点F． 求证：BD = BF
A
O
பைடு நூலகம்B D C
6、如图，⊙O的直径AB ＝4，C为圆周上一点， AC ＝2，过点C作⊙O的切线 l，过点B作l的 垂线BD，垂足为D，BD与⊙O 交于点E． ( 1) 求∠AEC的度数； （2）求证：四边形OBEC是菱形．
D C l A O B E
7、如图，⊙O的弦AD∥BC,过点D的切线交BC 的延长线于点E，AC∥DE交BD于点H，DO 及延长线分别交AC、BC于点 G、F. (1) 求证：DF垂直平分AC； （2）求证：FC＝CE； （3）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径.
直线与圆的位置关系量化
r O ┐d r
●
●
O
r
●
O
l
d ┐
l
d
┐
如果⊙O的半径为r,圆心O到直线l 的距离为d,那么 (1)d＜r 直线l 与⊙O相交
l
(2) d=r
(3) d ＞ r
直线l 与⊙O相切
直线l 与⊙O相离
将前面思考中的问题 反过来,如果l是⊙O 的切线,切点为A,那么 半径OA与直线l是不 是一定垂直呢?
55直线与圆的位置关系(切线长定理)
.A
o. F
.P
D
.B
1.切线长：在经过圆外一点的圆的切线上，这点和切点之间的 线段的长，叫做这点到圆的切线长。
2.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等， 圆心和这一点的连线平分两条切线的夹角。
几何语言表示为： ∵ PA,PB为⊙0的切线， ∴ PA=PB , OP平分∠APB。
3.由切线长可得到一个等腰三角形。这一点和圆心的连线不但 平分两切线的夹角，还垂直平分两切点间的线段。
5.5直线与圆的位置关 系(切线长定理)
1.什么是圆的切线.
答：直线和圆有 唯一公共点 时，这条直线叫做这个 圆的切线 2、切线的判定定理： 经过半径的外端且垂直于
这条半径的直线是圆的切线 3、切线的性质定理： 圆的切线垂直于经过切点
的半径
4、常见辅助线
想一想
过平面内一点作已知圆的切线，会有怎样的情形 呢？
圆心和这一点的连线平分两条切线的夹角。
几何语言表示为：∵ PA,PB为⊙0的切线 ，
∴ PA=PB , OP平分∠APB.
.A
E
o. F D
.P
.B
如图所示：P是⊙O外一点，PA 、PB为⊙O 的切线，A 和B是切点，
直线OP交AB于D，交⊙O于E、F则图中：
（1）共有 2 对相等线段（圆的半径除外）;
..O A
（1）过圆内 已知点不能 作圆的切线
.O
.A
（2）过圆上 已知点可作圆 的唯一一条切 线。
.O
.A
（3）过圆外一 已知点可作圆 的两条切线。
？情境问题
1.如图，点A在⊙O上，P是⊙O外一点， ∠OAP是直角，PA是⊙O的切线吗？为什么？
直线与圆 切线长定理 弦切角
直线与圆的位置关系一、直线与圆的位置关系1. 直线与圆的三种位置关系如果⊙O 的半径为r ，圆心O 到直线l 的距离为d ，那么 （1）直线l 和圆O 相交⇔d<r ：它们有2个公共点； （2）直线l 和圆O 相切r d =⇔：它们有1个公共点； （3）直线l 和圆O 相离r d >⇔：它们没有公共点.2. 切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。
要点：（1）经过半径外端；（2）垂直于这条半径。
3. 切线判定的三种方法（1）切线的定义：和圆只有一个公共点的直线是圆的切线 （2）圆心到直线的距离等于半径（3）切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线 4. 切线的性质定理：圆的切线垂直于过切点的半径由于过已知点有且只有一条直线与已知直线垂直，所以经过圆心垂直于切线的直线一定过切点；反过来，过切点垂直于切线的直线一定经过圆心，因此可以得到两个推论：推论1 经过圆心且垂直于切线的直线必经过切点 推论2 经过切点且垂直于切线的直线必经过圆心分析性质定理及两个推论的条件和结论间的关系，总结出如下结论： 如果一条直线具备下列三个条件中的任意两个，就可推出第三个 （1）垂直于切线 （2）过切点 （3）过圆心5. 关于切线的性质主要有五个①切线和圆只有一个公共点 ②切线和圆心的距离等于圆的半径 ③切线垂直于过切点的半径④经过圆心垂直于切线的直线必过切点⑤经过切点垂直于切线的直线必过圆心6.辅助线规律（1）直线与圆有公共点时，辅助线的作法是“连结圆心和公共点”，再证直线与半径垂直（2）当直线与圆并没明确有公共点时，辅助线的作法是“过圆心向直线作垂线”，再证圆心到直线的距离等于半径例题讲解例1：已知Rt△ABC的斜边AB＝6 cm，直角边AC＝3 cm.（1）若以C为圆心，2 cm长为半径的圆和AB的位置关系是_________；（2）若以C为圆心，4 cm长为半径的圆和AB的位置关系是_________；（3）若以C为圆心的圆和AB相切，则半径长为_________；（4）若以C为圆心的圆与边AB有一个交点，则圆的半径r的取值范围____________；（5）若以C为圆心的圆与边AB没有交点，则圆的半径r的取值范围______________. 变式练习：1.已知∠AOB＝30°，M为OA边上一点，以M为圆心、2 cm为半径作⊙M.若点M在OA边上运动，则当OM=_______________ cm时，⊙M与OB相切.第1题第2题第3题2.如图直线AB，CD相交于点O，∠AOC＝30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么秒种后⊙P与直线CD相切．3.如图，⊙O的半径为1，圆心O在正三角形的边AB上沿图示方向移动，当⊙O移动到与AC边相切时，OA的长为______．4.如图，直线y＝33x＋3与x轴、y分别相交与A、B两点，圆心P的坐标为(1，0)，圆P与y轴相切与点O.若将圆P沿x轴向左移动，当圆P与该直线相交时，横坐标为整数的点P′的个数是（ ） A ．2B ．3C ．4D ． 55. 在直角坐标系中，⊙M 的圆心坐标为(m ,0)，半径是2，如果⊙M 与y 轴相切，那么m =_____；如果⊙M 与y 轴相交，那么m 的取值范围是_____________．6. 在平面直角坐标系xOy 中，以点(－3，4)为圆心，4为半径的圆（ ）A ．与x 轴相交，与y 轴相切B ．与x 轴相离，与y 轴相交C ．与x 轴相切，与y 轴相交D ．与x 轴相切，与y 轴相离7. ⊙O 的半径r =5 cm ，点P 在直线l 上，若OP ＝5 cm ，则直线l 与⊙O 的位置关系是______. 8. 以三角形的一边长为直径的圆切三角形的另一边，则该三角形为_________. 9. 如图，P 为正比例函数x y 23上的一个动点，⊙P 的半径为3，设点P 的坐标为(x ，y ) (1)求⊙P 与直线x ＝2相切时点P 的坐标；(2)请直接写出⊙P 与直线x ＝2相交、相离时x 的取值范围.10. 如图，形如量角器的半圆O 的直径DE ＝12cm ，形如三角板的△ABC 中，∠ACB ＝90°，∠ABC ＝30°，BC =12cm.半圆O 以2cm/s 的速度从左向右运动，在运动过程中，点D 、E 始终在直线BC 上.设运动时间为t (s )，当t =0(s )时，半圆O 在△ABC 的左侧，OC ＝8cm.问：当t 为何值时，△ABC 的一边．．所在的直线与半圆O 所在的圆相切？11. 如图，在□ABCD 中，∠DAB ＝60°，AB ＝15㎝．已知⊙O 的半径等于3㎝，AB ，AD 分别与⊙O 相切于点E ，F ．⊙O 在□ABCD 内沿AB 方向滚动，与BC 边相切时运动停止．试求⊙O 滚过的路程．二、切线长定理：1. 切线长：在经过圆外一点的切线上，这点和切点之间的线段长，叫做这点到圆的切线长．2. 切线长和切线的区别切线是直线，不可度量；而切线长是切线上一条线段的长，而圆外一已知点到切点之间的距离，可以度量．3. 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角． 4. 两个结论：圆的外切四边形对边和相等； 圆的外切等腰梯形的中位线等于腰长．三、弦切角定理：1. 弦切角要注意两点：①角的顶点在圆上；②角的一边是过切点的弦，角的边一边是以切点为端点的一条射线．2. 弦切角定理：弦切角等于它所夹的弦对的圆周角，该定理也可以这样说：弦切角的度数等于它所夹弧的度数的一半． 3. 弦切角定理的推论：推论：如果两个弦切角所夹的弧相等，那么这两个弦切角相等．CABDO F E· AOCDBP例1： 已知PA 、PB 、DE 分别切⊙O 于A 、B 、C 三点，若PO=13cm ，PED ∆的周长为24cm ，40APB ∠=︒，求：（1）⊙O 的半径；（2）EOD ∠的度数．例2： 如图，⊙O 的直径AB=12cm ，AM 和BN 是⊙O 的两条切线，DC 切⊙O 于E ，交AM 于D ，交BN 于C ，设,AD x BC y ==．（1）求y 与x 的函数关系，并说明是什么函数？（2）若x 、y 是方程22300t t m -+=的两根，求x 、y 的值．（3）求COD ∆的面积．巩固练习1. 下列直线是圆的切线的是（ ）A ．与圆有公共点的直线B ．过圆直径外端点的直线C ．垂直于圆的半径的直线D ．到圆心的距离等于半径的直线2. 如图，在平面直角坐标系中，过格点A ，B ，C 作一圆弧，点B 与下列格点的连线中，能够与该圆弧相切的是（ ） A ．点(0，3)B ．点(2，3)C ．点(5，1)D．点(6，1)第2题 第3题 第4题· AOB F CNMED3. 如图，在ABC △中，10AB =，8AC =，6BC =，经过点C 且与边AB 相切的动圆与CA CB ，分别相交于点P Q ，，则线段PQ 长度的最小值是（ ） A ．4.75B ．4.8C ．5D ．424. 如图，PA 、PB 切⊙O 于点A 、B ，点C 是⊙O 上一点，且∠ACB =65°，则∠P = 度．5. 如图，M 与轴相交于点(20)A ，，(80)B ，，与轴相切于点C ，则圆心M 的坐标是 ．6. 木工师傅可以用角尺测量并计算出圆的半径r .用角尺的较短边紧靠⊙O ，并使较长边与⊙O 相切于点C .假设角尺的较长边足够长，角尺的顶点B ，较短边AB ＝8cm.若读得BC 长为a cm ，则用含a 的代数式表示r 为 .7. 如图，AB 为⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于P ，CE=BE ，E 在BC 上. 求证：PE 是⊙O 的切线．8. 已知：如图，是O 上一点，半径OC 的延长线与过点的直线交于点，OC BC =，12AC OB =．（1）求证：AB 是O 的切线；（2）若45ACD ∠=°，2OC =，求弦CD的长．OABPE C9. 如图，⊙O 直径AB=4，P 在AB 的延长线上，过P 作⊙O 切线，切点为C ，连接AC 。
圆和直线的位置关系
两圆位置关系的判定方法圆和圆的位置关系有五种：外离、外切、相交、内切、内含．如何判断两圆的位置关系呢？可试用以下三种方法：1、利用定义，即用两圆公共点（交点）的个数来判定两圆的位置关系．公共点的个数0 1 2两圆位置关系外离或内含外切或内切相交因为这个方法较易理解，所以不再举例．2、利用圆心距与两圆半径之间的关系来判断两圆的位置关系：d为圆心距，R与r 分别是两圆的半径，则有以下关系：两圆外切<=> d＝R+r；两圆外离<=>d＞R+r；两圆内含<=>d＜R-r(R＞r).两圆相交：<=>R-r＜d＜R+r两圆内切 <=>d＝R－r（R＞r）举两个例子帮助同学们理解一下：例题1：设⊙O1和⊙O2的半径分别为R、r，圆心距为d，当R=6cm，r=3cm，d=5cm时，⊙O1和⊙O2的位置关系是怎样的？当R=5cm，r=2cm，d=3cm时，⊙O1和⊙O2的位置关系是怎样的？例题2：已知两圆的半径分别为R和r（R>r），圆心距为 d ，若关于x的方程x2-2rx+(R-d)2=0有两个相等的实数根，那么两圆的位置关系为（）A、外切B、内切C、外离D、外切或内切3、根据公切线的条数来确定两圆的位置关系公切线条数 4 3 2 1 0两圆位置关系外离外切相交内切内含例题1：如果两圆的公切线有且只有一条，那么这两个圆的位置关系是（）A、相交B、外离C、内切D、外切一、填空：1、如果两个半径不相等的圆有两个公共点，那么这两个圆的位置关系是＿＿＿，且这两个圆的公切线有＿＿＿条．2、若两圆的公切线的条数是4条，则两圆的位置关系是＿＿＿＿．3、若两圆的半径分别为4cm和2cm，一条外公切线长为4cm，则两圆的位置关系是＿＿＿．4、在平面直角坐标系中，分别以点A（0，3）与B（4，0）为圆心，以8与3为半径作⊙A和⊙B，则这两个圆的位置关系为＿＿＿＿．二、选择：5、若两圆没有公共点，则两圆的位置关系是（）A、外离B、内含C、外切D、外离或内含6、已知⊙O1和⊙O2的半径分别为4cm和3cm，圆心距O1O2＝5cm，则⊙O1和⊙O2的公切线的条数为（）A、1条B、2条C、3条D、4条7、若两圆的直径分别是18+t，18－t（0＜t＜18），两圆的圆心距d=t，则两圆的位置关系为（）A、外切B、内切C、外离D、相交垂径定理及其推论垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。
平面直角坐标系中的直线与圆定理
平面直角坐标系中的直线与圆定理在平面直角坐标系中，直线和圆是常见的几何图形。
它们之间存在着一些重要的定理，需要我们深入了解和掌握。
本文将介绍平面直角坐标系中直线与圆的定理，并探讨它们的应用。
一、直线的方程在平面直角坐标系中，直线可以用方程表示。
一般来说，直线的方程有两种形式：一般方程和斜截式方程。
1. 一般方程直线的一般方程形式为Ax + By + C = 0，其中A、B、C为常数，且A和B不同时为0。
这种形式的方程被称为直线的一般方程，可以表示任意方向的直线。
例如，直线L的一般方程为2x + 3y - 6 = 0。
通过该方程，我们可以确定直线L在平面直角坐标系中的位置和性质。
2. 斜截式方程斜截式方程是直线方程的另一种常见形式。
斜截式方程的一般形式为y = kx + b，其中k为直线的斜率，b为直线在y轴上的截距。
例如，直线L的斜截式方程为y = 2x + 3。
通过该方程，我们可以知道直线L的斜率为2，截距为3，并且可以方便地绘制出该直线在平面直角坐标系中的形状。
二、圆的方程在平面直角坐标系中，圆也可以用方程进行表示。
圆的方程有两种形式：标准方程和一般方程。
1. 标准方程圆的标准方程形式为(x - a)² + (y - b)² = r²，其中(a, b)表示圆心的坐标，r表示圆的半径。
例如，圆C的标准方程为(x - 2)² + (y - 3)² = 4。
通过该方程，我们可以确定圆C的圆心坐标为(2, 3)，半径为2，并绘制出圆的形状。
2. 一般方程圆的一般方程形式为x² + y² + Dx + Ey + F = 0，其中D、E、F为常数。
例如，圆C的一般方程为x² + y² - 4x - 6y + 9 = 0。
通过该方程，我们可以判断圆C在平面直角坐标系中的位置和性质。
三、直线与圆的定理在平面直角坐标系中，直线与圆之间存在着一些重要的定理，下面将介绍其中的几个定理。
直线与圆的位置关系—知识讲解
直线与圆的位置关系—知识讲解【学习目标】1.理解并掌握直线与圆的三种位置关系；2.理解切线的判定定理和性质定理.【要点梳理】要点一、直线与圆的位置关系1.切线的定义：直线与圆有唯一的公共点时，这条直线叫做圆的切线，这个唯一的公共点叫做切点.此时直线与圆的位置关系称为相切.2．直线和圆的三种位置关系：(1) 相交：当直线与圆有两个公共点时，叫做直线与圆相交．(2) 相切：当直线与圆有唯一公共点时，叫做直线与圆相切．这条直线叫做圆的切线，公共点叫做切点．(3) 相离：当直线与圆没有公共点时，叫做直线与圆相离．3．直线与圆的位置关系的判定和性质．直线与圆的位置关系能否像点与圆的位置关系一样通过一些条件来进行分析判断呢？由于圆心确定圆的位置，半径确定圆的大小，因此研究直线和圆的位置关系，就可以转化为直线和点(圆心)的位置关系．下面图(1)中直线与圆心的距离小于半径；图(2)中直线与圆心的距离等于半径；图(3)中直线与圆心的距离大于半径．一般地，直线与圆的位置关系有以下定理：如果⊙O的半径为r，圆心O到直线l的距离为d，那么，（1）d＜r直线l与⊙O相交；（2）d=r直线l与⊙O相切；（3）d＞r直线l与⊙O相离.要点诠释：这三个命题从左边到右边反映了直线与圆的位置关系所具有的性质；从右边到左边则是直线与圆的位置关系的判定．要点二、切线的性质定理和判定定理1．切线的性质定理：圆的切线垂直于过切点的半径.要点诠释：切线的性质定理中要注意：圆的切线是与过切点的半径垂直，不是与任意半径都垂直.2．切线的判定定理：过半径外端且垂直于半径的直线是圆的切线.要点诠释：切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可. 要点三、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心到三边的距离都相等.要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).【典型例题】类型一、直线与圆的位置关系1．在Rt△ABC中，∠C=90°，AC=3厘米，BC=4厘米，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？(1)r=2厘米； (2)r=2.4厘米； (3)r=3厘米【答案与解析】解：过点C作CD⊥AB于D，在Rt△ABC中，∠C=90°， AC=3，BC=4，得AB=5，，∴AB·CD=AC·BC，∴AC BC34CD===2.4AB5∙⨯(cm)，（1）当r=2cm时，CD＞r，∴圆C与AB相离；（2）当r=2.4cm时，CD=r，∴圆C与AB相切；(3）当r=3cm时，CD＜r，∴圆C与AB相交．【总结升华】欲判定⊙C与直线AB的关系，只需先求出圆心C到直线AB的距离CD的长，然后再与r比较即可．举一反三：【变式】已知⊙O的半径为10cm，如果一条直线和圆心O的距离为10cm，那么这条直线和这个圆的位置关系为（）A. 相离B. 相切C. 相交D. 相交或相离【答案】B.类型二、切线的判定与性质2．如图所示，在Rt△ABC中，∠B＝90°，∠A的平分线交BC于D，以D为圆心，DB长为半径作⊙D．求证：AC是⊙D的切线．【思路点拨】作垂直，证半径．【答案与解析】证明：过D作DF⊥AC于F．∵∠B＝90°，∴DB⊥AB．又AD平分∠BAC，∴ DF＝BD＝半径．∴ AC与⊙D相切．【总结升华】如果已知条件中不知道直线与圆有公共点，其证法是过圆心作直线的垂线段，再证明垂线段的长等于半径的长即可．3.（2015•黄石）如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．（1）求BC的长；（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．【思路点拨】（1）根据圆周角定理求得∠ADB=90°，然后解直角三角形即可求得BD，进而求得BC即可；（2）要证明直线DE是⊙O的切线只要证明∠EDO=90°即可．【答案与解析】证明：（1）解：连接AD，∵AB是⊙O的直径，∴∠ADB=90°，又∵∠ABC=30°，AB=4，∴BD=2，∵D是BC的中点，∴BC=2BD=4；（2）证明：连接OD．∵D是BC的中点，O是AB的中点，∴DO是△ABC的中位线，∴OD∥AC，则∠EDO=∠CED又∵DE⊥AC，∴∠CED=90°，∠EDO=∠CED=90°∴DE是⊙O的切线．【总结升华】此题主要考查了切线的判定以及含30°角的直角三角形的性质．解题时要注意连接过切点的半径是圆中的常见辅助线．4．如图，AB为⊙O的直径，AC为⊙O的弦，AD平分∠BAC，交⊙O于点D，DE⊥AC，交AC的延长线于点E．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AE＝8，⊙O的半径为5，求DE的长．【思路点拨】（1）连接OD，证明OD∥AD即可；（2）作DF⊥AB于F，证明△EAD≌△FAD，将DE转化成DF来求.【答案与解析】解：（1）直线DE与⊙O相切．理由如下：连接OD．∵AD平分∠BAC，∴∠EAD＝∠OAD．∵OA＝OD，∴∠ODA＝∠OAD．∴∠ODA＝EAD．∴EA∥OD．∵DE⊥EA，∴DE⊥OD．又∵点D在⊙O上，∴直线DE与⊙O相切．（2）如上图，作DF⊥AB，垂足为F．∴∠DFA＝∠DEA＝90°．∵∠EAD＝∠FAD，AD＝AD，∴△EAD≌△FAD．∴AF＝AE＝8，DF＝DE.∵OA＝OD＝5，∴OF＝3．在Rt△DOF中，DF4．∴DE＝DF＝4．【总结升华】本题综合考察了平行线的判定，全等三角形的判定和勾股定理的应用，是一道很不错的中档题.举一反三：【变式1】（2015•盐城）如图，在△ABC中，∠CAB=90°，∠CBA=50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED=EA．（1）求∠DOA的度数；（2）求证：直线ED与⊙O相切．【答案与解析】（1）解；∵∠DBA=50°，∴∠DOA=2∠DBA=100°，（2）证明：连接OE．在△EAO与△EDO中，，∴△EAO≌△EDO，∴∠EDO=∠EAO，∵∠BAC=90°，∴∠EDO=90°，∴DE与⊙O相切．C B举一反三：【变式2】如图所示，在△ABC 中，AB ＝BC ＝2，以AB 为直径的⊙O 与BC 相切于点B，则AC 等于( )AC．．【答案】因为以AB 为直径的⊙O 与BC 相切于点B ，所以∠ABC ＝90°，在Rt△ABC中，AC==C ．类型三、三角形的内切圆5．如图，已知O 是△ABC 的内心，∠A=50°，求∠BOC 的度数.【思路点拨】O 是△ABC 的内心，∠A=50°，根据内切圆的性质可求∠OBC+∠OCB=11(180)=(18050)=6522A ︒-︒-︒︒∠ ，在△BOC 中，根据三角形内角和求出∠BOC 的度数. 【答案与解析】解：∵O 是△ABC 的内心，∠A=50°，∴∠OBC+∠OCB=11(180)=(18050)=6522A ︒-︒-︒︒∠， ∴∠BOC=180°-65°=115°.【变式】如图，△ABC中，∠C=90°，BC=4，AC=3，⊙O内切与△ABC，则△ABC去除⊙O剩余阴影部分的面积为（）A.12-πB. 12-2πC. 14-4πD. 6-π【答案】D.C B。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
日月桃李文化教育教案
学生： 郭曼 年级： 9 科目：数学 地点：中海 时间：2013 年 3 月 9 日 星期 日 形式：单独 老师： 王丽君 教学内容：直线与圆的位置关系（三大切线定理） 课时安排： 2 学时 【知识要点】（按点列出）
圆心角和圆周角、弦长、弧长的关系
【教学过程】：【复习、新授、训练（例题与训练中的基础、拓展、综合、链接部分必与知识点紧密联系）、小结、作业）】 知识点1、直线和圆的三种位置关系：
知识点2、切线的判定和性质：
1、 判定：（1）当圆心到直线的距离d 等于半径r 时，直线是圆的切线； （2）经过半径外端垂直于的半径的直线，是圆的切线。
2、性质：如果一条直线与圆相切，另一条满足：（1）过圆心，（2）切点，（3）垂直于半径．其中任意两个条件，则必满足第三个条件。
知识点3、弦切角定理：弦切角等于所夹弧对的圆周角。
知识点4、切线长定理：从圆外一点向圆所引的两条切线段长相等； 知识点5、圆幂定理： （1）PA ·PB=PC ·PD
（2）PT 2=PA ·PB=PC ·PD
知识点6、圆与三角形：
（1）1902BIC A ∠=+
∠o
，()1
2
S a b c r =++ （2） ()1
2
r a b c =+-
注意：(1)“连半径证垂直得切线”。
“作垂直证半径得切线”。
(2) 见切线要想到它垂直于过切点的半径；若过切点有垂线则必过圆心；过切点有弦，则想到弦切角定理，想到圆心角、圆周角性质，可再联想同圆或等圆弧弦弦心距等的性质应用。
（3）任意三角形有且只有一个内切圆，圆心为这个三角形内角平分线的交点。
知识点7:、圆与四边形 四边形对角互补
二、典例精讲
考点1、切线的性质和判定
例1、（1）如图，已知，△ABC 中，AB=AC ，以BC 的 中点O 为圆心的圆切AB 于D 。
求证：⊙O 与AC 也相切
d<r d=r d>r
关 系 相交 相切 相离
交点个数 两个交点 一个交点 没有交点
直线名称 割线 切线 不相交线
C
A O
B
D A P D C B A B T P D
C
A c b I a
C
B
A
c
b
B
C
a
r A
D C B A B P
（2）（2011广西梧州，25，10分）如图，AB 是⊙O 的直径，CD 是⊙O 的切线，切点为C ．延长AB 交CD 于点E ．连接AC ，作∠DAC =∠ACD ，作AF ⊥ED 于点F ，交⊙O 于点G ． （1） 求证：AD 是⊙O 的切线；
（2） 如果⊙O 的半径是6cm ，EC =8cm ，求GF 的长． 考点2、圆幂定理： 例2、（1）如图，已知PT 是⊙0的切线，PAB 、PCD 是⊙0的割线， BC ∥PT ，连接DA 并延长交PT 与Q
求证：PQ=TQ
（2）如图，BC 是半圆O ⊙的直径，EF BC ⊥于点F ，5BF
FC
=．已知点A 在CE 的延长线上，AB 与半圆交于D ，
且82AB AE ==，，则AD 的长为多少．
A B
C
D
E
F
O
考点3、圆和三角形 例3、(2011黑龙江省大庆) 如图，Rt △ABC 的两直角边AC 边长为4，BC 边长为3，它的内切圆为⊙0，⊙0与边AB 、BC 、AC 分别相切于点D 、E 、F ，延长CO 交斜边AB 于点G ． (1)求⊙O 的半径长； (2)求线段DG 的长．
考点4、圆的综合题型
例4、已知：如图1，在直角梯形ABCD 中，AD ∥BC ，∠B=90°，AB=8厘米，AD=24厘米，BC=26厘米，AB 为圆O 的直径，动点P 从点A 开始沿AD 边向点D 以1厘米／秒的速度运动，动点Q 从点C 开始沿CB 边向点B 以3厘米／秒的速度运动，P 、Q 分别从A 、C 同时出发，当其中到达端点时，另一点也随之停止运动，设运动时间为t 秒．
求(1)t 分别为何值时，四边形PQCD 为平行四边形、等腰梯形？ (2)t 分别为何值时，直线PQ 与圆O 相切、相交、相离？(97年河北)
A C
P T D
B Q B G O E
D A C
F
中考例题 1、（成都市2007B29）．如图，A 是以BC 为直径的⊙O 上一点，AD BC ⊥于点D ，过点B 作O 的切线，与CA 的延长线相交于点E G ，是AD 的中点，连结CG 并延长与BE 相交于点F ，延长AF 与CB 的延长线相交于点P ． （1）求证：BF EF =；
（2）求证：PA 是⊙O 的切线；
（3）若FG BF =，且⊙O 的半径长为32， 求BD 和FG 的长度．
2、（成都市2010B27）．已知：如图，ABC ∆内接于⊙O ，AB 为直径，弦CE AB ⊥于F ，C 是弧AD 的中点，连结BD 并延长交EC 的延长线于点G ，连结AD ，分别交CE 、BC 于点P 、Q ．（1）求证：P 是ACQ ∆的外心； （2）若3
tan ,84
ABC CF ∠=
=,求CQ 的长； （3）求证：(FP+PQ)2=FP ·FG
【知识小结】（先由自己独立小结，最后由老师书面小结） 直线与圆的关系：相交、相切、相离
圆中切线三大定理：性质定理、判定定理、切线定理 圆幂定理
圆中内切三角形、四边形
【作业】（精少，书面与识记部分均要求有）
（成都市2012B27）如图，AB 是⊙O 的直径，弦CD ⊥AB 于H ，过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ．切点为G ，连接AG 交CD 于K ．
（1）求证：KE =GE ；（2）若2
KG =KD ·GE ，试判断AC 与EF 的位置关系，并说明理由； （3） 在（2）的条件下，若sinE =
3
5
，AK =23，求FG 的长． O
D G C A
E
F
B P
【教学后记】（对学生学习过程中的反应、吸收、优缺点与自己的教学方法进行反思）
(1)∵AD∥BC，∴只要QC=PD，四边形PQCD就为平行四边形，此时，有3t=24-t，得t=6，即
当t=6秒时，四边形PQCD就是平行四边形．同理，只要PQ=CD，PD≠CQ时，四边形PQCD就是等腰梯形．
如图2，从P、D分别作BC的垂线交BC于E、F，则EF=PD，QE=FC=2．
∴当t=7时，四边形PQCD为等腰梯形．
(2)设运动t秒时，直线PQ与圆O相切于点M(如图3)，从P作PH⊥BC于H．则PH=AB，BH=AP．∴PH=8，HQ=26-3t-t=26-4t，
由切线长定理，得PQ=PA+QB=t+26-3t=26-2t，∵PQ2=PH2+HQ2，∴(26-2t)2=82+(26-4t)2，。