超市选址模型

合集下载

便利超市选址典型分析范例

12 X
解：从图中可以得出目的地的坐标
目的地
x, y
图书馆
6,7
东院食堂
2,5
C D座
10,5
E F座
10,3 28,20
x=∑x/n=28/4=7 y=∑y/n=20/4=5
因此,中心位置是(7,5),正好位于C座前的空地
假定下图描述的问题中运往各地商品数量不一样，而是如下所示，则重心位置：
公寓：k 公寓东侧门口; l 大学生公寓城11号楼管理室．
淘汰法
淘汰法：考察所有备选方案的各项指标，将不符合指标的方案排除，挑选出较优方案。主要考虑：人流量、可行性。资料来源：根据统计的人流量多少进行评分; 根据方案的可行性大小进行评分。如下表、图:
人流量—可行性比较表
地点
abcdef ghi j kl
2、经过小组讨论，制定出选址所适宜的方法及一些主考因素；
3、依次运用各类方法对挑选出的四个备选方案进行比较； 4、得出一个最佳方案； 5、项目总结。
若干地点：
西院：a 综合楼与天才小餐厅之间空地上; b 西院图书馆西侧5米处； c 西院食堂对过； d 体育馆内； e 原学工部；
东院：f 心园餐厅对过； g 东院食堂西侧； h 月牙报告厅附近； i D、E 座的北面教室 j 存车处到C座前空地；
四个备选方案人流量柱型图
3500
3000
2500
2000
1500
1000
500
0
1
2
3
4
析素经门选
选
注：以下是采用各种方法进
。营槛
时人
间口
、、
租学
金校、政面策积、等预一期系成

基于灰色预测法的超市选址模型研究

４５００５２，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：Ｓｕｐｅｒｍａｒｋｅｔｌｏｃａｔｉｏｎｉｓａｎｉｍｐｏｒｔａｎｔｐａｒｔｏｆｔｈｅｉｎｄｕｓｔｒｙｓｔｒａｔｅｇｉｃｄｅｃｉｓｉｏｎ－ｍａｋｉｎｇｂｅｃａｕｓｅｔｈｅｒｅｉｓａｖａｒｉｅｔｙｏｆｃｏｍｐｌｅｘｆａｃｔｏｒｓａｆｆｅｃｔｉｎｇｔｈｅｌｏｃａｔｉｏｎｏｆｔｈｅｓｕｐｅｒｍａｒｋｅｔｗｈｉｃｈｉｓｕｎａｂｌｅｔｏｃａｒｒｙｏｕｔａｃｃｕｒａｔｅｑｕａｎｔｉｔａｔｉｖｅａｎａｌｙｓｉｓ．Ａｓｅｃｏｎｄａｒｙｌｏｃａｔｉｏｎｉｎｄｉｃａｔｏｒｓｓｙｓｔｅｍｉｓｅｓｔａｂｌｉｓｈｅｄｔｏａｎａｌｙｚｅｔｈｅｗｅｉｇｈｔ，
ｃｏｍｂｉｎｅｄｗｉｔｈｔｈｅｌｏｃａｔｉｏｎｆａｃｔｏｒｓｔｒｕｃｔｕｒｅｏｆｔｈｅｒｅｌａｔｉｏｎｓｈｉｐｂｅｔｗｅｅｎｆｕｚｚｙｒａｎｄｏｍｄｙｎａｍｉｃｃｈａｎｇｅｓ，ｔｈｅ
ｂａｓｅｄｏｎＳｕｐｅｒｍａｐｏｂｊｅｃｔｓｃｏｍｐｏｎｅｎｔｓｄｅｖｅｌｏｐｅｄｓｅｃｏｎｄａｒｙｄｅｖｅｌｏｐｍｅｎｔｅｘｐｅｒｉｍｅｎｔ．

连锁复制秘笈之选址模型

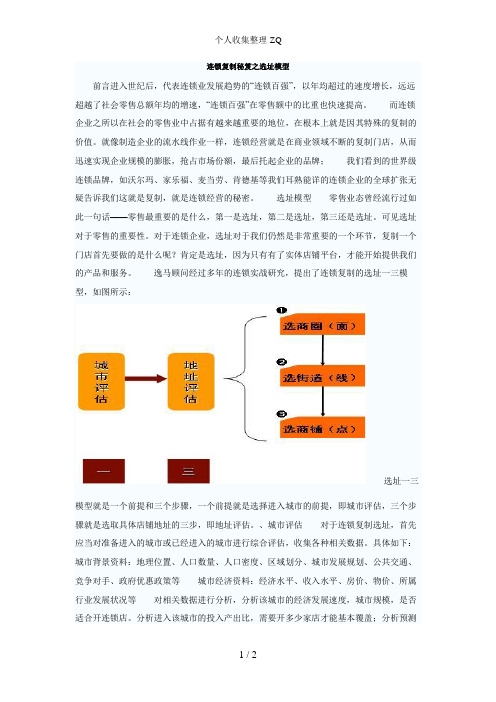
连锁复制秘笈之选址模型
前言进入世纪后，代表连锁业发展趋势的“连锁百强”，以年均超过的速度增长，远远超越了社会零售总额年均的增速，“连锁百强”在零售额中的比重也快速提高。而连锁企业之所以在社会的零售业中占据有越来越重要的地位，在根本上就是因其特殊的复制的价值。就像制造企业的流水线作业一样，连锁经营就是在商业领域不断的复制门店，从而迅速实现企业规模的膨胀，抢占市场份额，最后托起企业的品牌；我们看到的世界级连锁品牌，如沃尔玛、家乐福、麦当劳、肯德基等我们耳熟能详的连锁企业的全球扩张无疑告诉我们这就是复制，就是连锁经营的秘密。选址模型零售业态曾经流行过如此一句话——零售最重要的是什么，第一是选址，第二是选址，第三还是选址。可见选址对于零售的重要性。对于连锁企业，选址对于我们仍然是非常重要的一个环节，复制一个门店首先要做的是什么呢？肯定是选址，因为只有有了实体店铺平台，才能开始提供我们的产品和服务。逸马顾问经过多年的连锁实战研究，提出了连锁复制的选址一三模型，如图所示：选址一三模型就是一个前提和三个步骤，一个前提就是选择进入城市的前提，即城市评估，三个步骤就是选取具体店铺地址的三步，即地址评估。、城市评估对于连锁复制选址，首先应当对准备进入的城市或已经进入的城市进行综合评估，收集各种相关数据。具体如下：城市背景资料：地理位置、人口数量、人口密度、区域划分、城市发展规划、公共交通、竞争对手、政府优惠政策等城市经济资料：经济水平、收入水平、房价、物价、所属行业发展状况等对相关数据进行分析，分析该城市的经济发展速度，城市规模，是否适合开连锁店。分析进入该城市的投入产出比，需要开多少家店才能基本覆盖；分析预测第一年的营业额及各项费用支出预算，分析预测第二年的增长趋势；分析客流规律及；分析广告宣传成本；分析人文状况；分析其他影响经营的因素，如政府的工作效率等。在此基础上，形成该城市的评估报告，作为连锁企业进入该城市进行选址的前提依据。、地址评估）选商圈分析该城市各区域的商圈个数、商圈名称和类型，确定城市核心商圈、次级商圈与辅助商圈。对商圈的成熟度、发展规划、潜力、辐射范围、有无竞争对手等情况进行分析，以便选择符合定位，适合进入的商圈。）选街道分析对所选商圈的街道个数、名称和类型，对街道条件、人流车流、竞争情况等进行分析。街道条件：街道长度、街道宽度、店铺数量、人流出入口、街道成熟度人流车流：人流量、车流量（早、中、晚）竞争情况：典型竞争门店数吸引情况：有无与所属行业顾客群产生吸引力的设施或条件）选商铺选商铺主要分析两方面内容：外部评估和内部评估。外部评估：人流量、车流量、门店可视范围、门前空地、门前道路宽度、邻铺类型等。内部评估：面积、建筑结构、招牌长度、门面长度、配套水电条件、租金等。

离散数学超市选址

超市选址问题1 需求分析核心问题：求最短路径（选址的要求就是超市到各小区权值之和最少）；数据模型（逻辑结构）：带权有向图（权值计算：距离*频度）；核心算法：Floyd算法（佛洛依德算法：每一对顶点之间的最短路径）；总体思想：如果超市要选在某一个位置，那么先用Floyd算法得出个顶点之间的最短距离/最小权值。

2 运行环境Visual Stdio C++6.03 概要设计Floyd算法利用动态规划思想，通过把问题分解为子问题来解决任意两点之间的最短路径问题。

设G=（V,E,W）是一个带权有向图，其边V=[v1,v2,…,vn]。

对于k≤n,考虑其结点V的一个子集。

对于V中任何两个结点Vi,Vj,考虑从Vi到Vj的中间结点都在Vk中的所有路径，设是其中最短的。

如果结点Vk在从Vi到Vj的最短路径上，则分为两段，其中一段从Vi到Vk，另一断从Vk 到Vj，这样便得到表达式。

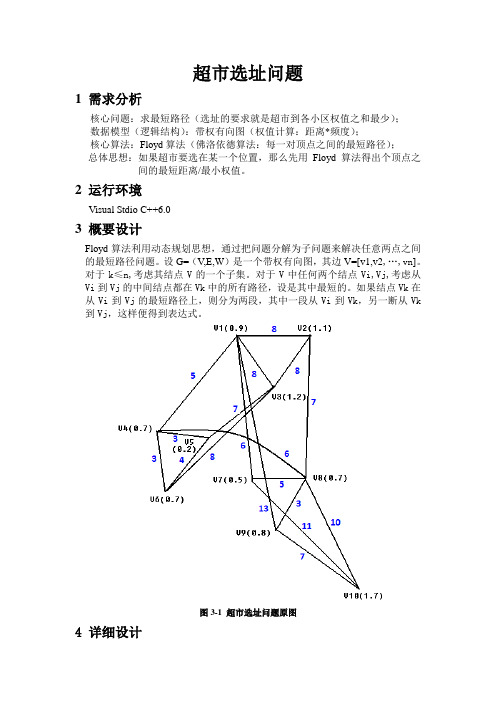
图3-1 超市选址问题原图4 详细设计让所有路径加上中间定点1，取A[i][j]与A[i][l] +A[l][j]中较小的值作A[i][j]的新值，完成后得到A（l），如此进行下去，当第k步完成后，A(k)[i][j]表示从i到且路径上的中间顶点的路径序号小于或等于k的最短路径长度。

当第n-1步完成后，得到A（n-1）, A（n-1）即所求结果。

A（n-1）[i][j]表示从i到j 且路径上的中点顶点的序号小于或等于n-1的最短路径长度，即A（n-1）[i][j]表示从i到j最短路径长度。

5调试分析有两个权值，各小区到超市的距离及小区的人数。

图的建立有很大的困难，经过分析这两个值可以合并为一个权值，从而便于分析和解决问题。

6 程序代码#include <string.h>#include <stdio.h>#include <time.h>#include "malloc.h"#include <iostream.h>#define TURE 1#define FALSE 0#define OK 1#define ERROR 0#define OVERFLOW -1#define INF 65535const int MAXVEX=100;typedef char Vextype;typedef struct{Vextype vexs[MAXVEX][MAXVEX];int adj[MAXVEX][MAXVEX];int dis[MAXVEX][MAXVEX];int f[MAXVEX];int n;int e;}Mgraph;void CreatMgraph(Mgraph *G){int i,j,k;printf("请输入小区个数:\n");scanf("%d",&(G->n));printf("请输入小区间的路径数:\n");scanf("%d",&(G->e));printf("请输入小区名称:\n");for(i=0;i<G->n;i++){printf("请输入第%d个小区名称:\n",i);scanf("%s",&G->vexs[i]);}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){G->adj[i][j]=0;G->dis[i][j]=0;G->f[i]=0;}for(k=0;k<G->e;k++){printf("请输入相通的两小区(输入格式:i,j):\n");scanf("%d,%d",&i,&j);printf("请输入相通两个小区间的距离(格式：dis)：\n");scanf("%d",&(G->dis[i][j]));G->adj[i][j]=1;G->adj[j][i]=1;G->dis[j][i]=G->dis[i][j];}for(k=0;k<G->n;k++){printf("请输入第%d个小区的人数:\n",k);scanf("%d",&(G->f[k]));}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){G->dis[i][j]*=G->f[i];if(G->adj[i][j]==0&&i!=j)G->dis[i][j]=INF;}}void Floyed(Mgraph *G){int A[MAXVEX][MAXVEX],path[MAXVEX][MAXVEX]; int i,j,k,pre;int count[MAXVEX];for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){A[i][j]=G->dis[i][j];path[i][j]=-1;count[i]=0;}for(k=0;k<G->n;k++){for(i=0;i<G->n;i++)for(j=0;j<G->n;j++)if(A[i][j]>(A[i][k]+A[k][j])){A[i][j]=A[i][k]+A[k][j];path[i][j]=k;}}cout<<endl<<"Floyed算法求解如下:"<<endl;for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){if(i!=j){cout<<" "<<i<<"->"<<j<<";";if(A[i][j]==INF){if(i!=j)cout<<"不存在路径"<<"\n"<<endl;}else{cout<<"路径长度为:"<<A[i][j]<<"\n";cout<<"路径为:"<<i<<" ";pre=path[i][j];while(pre!=-1){cout<<pre<<"\n";pre=path[pre][j];}cout<<j<<endl;}}}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){if(A[i][j]==INF)count[i]=0;elsecount[i]=1;}for(i=0;i<G->n;i++)if(count[i]){for(j=0;j<G->n;j++)A[i][0]+=A[i][j];}for(i=0;i<G->n;i++){k=0;if(count[i])if(A[k][0]>A[i][0])k=i;}cout<<"超市的最佳地址为:"<<G->vexs[k]<<endl; }void main(){Mgraph *Gh=NULL;Gh=(Mgraph *)malloc(sizeof(Mgraph)); CreatMgraph(Gh);Floyed(Gh);}7 测试结果7.1 输入7.2 输出8 参考文献：[1].谭浩强编著《C语言程序设计》,清华大学出版社 .[2].严蔚敏编著《数据结构与算法分析》，清华大学出版社.9 课程总结本次题目是设计一个超市选址的问题，在实际生活中，非常实际的一个题目，有着很大的实际用途。

设施选址模型

单设施选址模型设有n 个零售铺店，它们各自的坐标是j j x y （，）（j=1，2.。

n ）配送中心的坐标为00x y （，）.设配送中心到零售店j 的发送费用是j F ，总发送费用为T ，则有：nj j 1T F ==∑ （1）其中j F 可用下列的式子表示j j j k w d J F = （2）式中j k ——从配送中心到零售店j 的发送费率（单位吨公里的发送费）；j w ——向零售店j 的货物发送量；j d ——从配送中心到零售店之间的直线距离。

其中j d = （3）把式（2）代入（1）得nj j j j 1k w d T ==∑ （4）联立式（3）和（4）可求出使T 最小的0x ，0yn j j 0j j j 10k w (x x )/d 0x T=∂==∂∑- （5） nj j 0j j j 10k w (y y )/d 0y T=∂==∂∑- （6）联立（5）和（6）可求出最适合的*0x ，*0y ：njj jjj 1*0njjjj 1k w x /dx k w /d===∑∑ （7）njj jjj 1*0njjjj 1k w y /dy k w /d===∑∑ （8）由于式（7）和（8）右边含有j d ，即还有所求的0x ，0y ，可以采用迭代法莱进行计算。

迭代法计算步骤如下：（1）给出配送中心的出初始地点0000x y （，）。

（2）通过式（3）式（4）计算与0000x y （，）相对应的总发送费用0T 。

（3）把0000x y （，）代入（3）、（7）和（8）中，计算配送中心的改善地点1100x y （，）。

（4）通过式（3）、式（4）计算与1100x y （，）相对应的总发送费用1T 。

（5）把1T 和0T 进行比较，如果1T <T ,则返回（3）进行计算，再把1100x y （，）代入式（3）（7）（8）中，计算配送中心的再改善地点2200x y （，）。

生鲜门店选址分析模型——社区门店、市场门店和超市柜台店

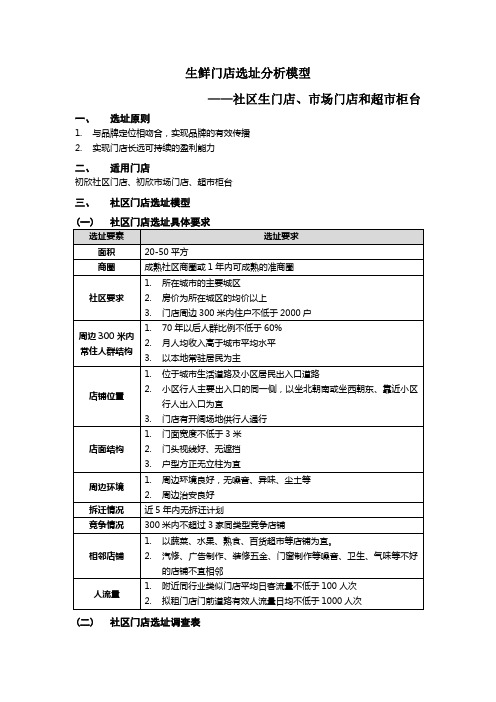
1. 所在城市的主要城区
社区要求 2. 房价为所在城区的均价以上
3. 门店周边 300 米内住户不低于 2000 户
1. 70 年以后人群比例不低于 60% 周边 300 米内
2. 月人均收入高于城市平均水平常住人群结构
3. 以本地常驻居民为主
1. 位于城市生活道路及小区居民出入口道路
店铺位置
2. 小区行人主要出入口的同一侧，以坐北朝南或坐西朝东、靠近小区行人出入口为宜
门店周边 500 米内同类型门店日均客流量
A 300 人以上 C 100-200 人
B 200-300 人 D 100 人以下
门店日均有效人流量（日平均人流量=选取各小时 A 3000 人以上
段人流量总和÷观察小时段次数×12 小时）
C 1000-2000 人
B 2000-3000 人 D 1000 人以下
2. 月人均收入高于城市平均水平常住人群结构
3. 以本地常驻居民为主
店铺位置
1. 位于农贸市场肉类售卖区 2. 有开阔场地供行人通行
1. 门面宽度不低于 2 米
店面结构 2. 门头视线好、无遮挡
3. 户型方正无立柱为宜
周边环境
1. 周边环境良好，无噪音、异味、尘土等 2. 周边治安良好
拆迁情况近 5 年内无拆迁计划
长度：宽度：
□有立柱 □无立柱
附图
附图
四、市场门店选址模型
(一) 市场门店选址具体要求
选址要素
选址要求
面积
10-30 平方
商圈
成熟农贸市场内
1. 所在城市的主要城区
社区要求 2. 房价为所在城区的均价以上
3. 门店周边 2 公里内住户不低于 5000 户

超市选址与设施规划

超市选址规划相关理论1.超市选址规划相关理论1.1 超市选址的意义对于大型综合超市而言，开设地点的重要性不可低估。

在西方国家，大型综合超市的开设地点被视为开业前所需的三大主要资源之一，因为特定开设地点决定了可以吸引有限距离或地区内的潜在客户的多少，这也就直接决定了销售收入的高低，从而直接反映出开设地点作为一种资源的价值大小。

具体来讲，大型综合超市选址策划的重要性主要表现在以下几个方面：1）店址选择是否得当，是影响经济效益的一个重要因素。

店址选择得当，就意味着其享有优越的“地利”优势，在同行业商店之间，如果在规模相当，商品构成、经营服务水平基本相同的情况下，必然享有较好的经济效益。

2）店址选择的资金投入大，且被长期占用。

店址一经确定，就需要大量的资金投入，即使为追求投资最小化选择租赁的方式，投入仍然很大，除了在合同期内需要支付租金以外，还需在照明、固定资产、门面等方面进行投入。

3）由于位置固定，合同期长，店址是零售商战略组合中灵活性最差的要素。

店址一旦选定，难以随意更改，一家大型综合超市不可能轻易搬迁，也不太可能轻易改变经营方式。

1.2 超市选址的指导原则1）方便顾客购物的原则。

满足顾客需求是超市经营的宗旨，因此超市位置的确定，必须首先考虑方便顾客购物，为此超市要符合以下条件：交通便利。

车站附近，是过往乘客的集中地段，人群流动性强，流动量大。

如果是几个车站交汇点，则该地段的商业价值更高。

超市开业之地如选择在这类地区就能给顾客提供便利购物的条件。

靠近人群聚集的场所，可方便顾客随机购物。

2）有利于超市的开拓发展的原则。

超市选址的最终目的是要保证超市的成功经营和长期的发展，超市选址时不仅要分析当前的市场形势，而且要从长远的角度去考虑是否有利于规模的扩大，以保证在有利于提高市场占有率和覆盖率，并在不断增强自身实力的基础上开拓市场。

3）有利于合理组织商品运送。

超市选址不仅要注意规模，而且要追求规模效益。

发展现代商业，要求集中进货、集中供货、统一运送，这有利于降低采购成本和运输成本，合理规划运输路线。

零售超市配送中心选址模型及其算法研究

：２，＝ｌ
为了便于建立数学模型，不失其实用性，设模型满足且假如下条件 ① 在选定范围内选出零售超市配送中心
，
ｊｉｓｅｃｄｆｆｉｌｔｉｓｅｅＩ，
ｏ０．Ｘ ≥ ０ｊｉ，
② 此系统运输包含由厂商到零售超市配送中心的运输，也包含配送中心到零售超市的运输； ⑧ 一个零售超市配送中心可供货给多个零售超市，可由也
中储网Ｈｐｗｗｃｎｈｕｃ１１国运ｔ：ｗｉｃｙｍ０ｔ／／ｈａｕｎｏ
Байду номын сангаас
Ｄ
零售超市配送中心ｉ的可变成本系数；
Ｕ：售超市配送中心的最大流量，零
没定实际问题参数集
Ｆ：售超市配送中心的固定费用；零
１模型的假设．１
∑ＺｉＤ，＝，…，ｉ ≥ ｚ１，，Ｘｊ ‘ ２，
ｌ
州
，
∑∑ｚ： ∑∑Ｚ，Ｉ，ｎｉ＝ｉ，…，＝２
ｋ＝１ｌｌ，＝ｌ
∑∑ｚｋＣｉ１，，㈣㈤㈣Ｘ『＝，… ＂，２
另外，目标函数式（），１中等式右边第一项是厂商到零售超市配送中心的运输费用，２项是配送中心到零售超市的配送第费用，３项是配送中心的管理费用，第它与配送中心的流量成正比，０∈（，］第四项是配送中心的固定投资费用。约束条件０１，

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

超市选址模型小组成员：高才萱：经济与工商管理学院国际经济与贸易专业彭爱军：经济与工商管理学院国际经济与贸易专业吴质：经济与工商管理学院电子商务专业摘要正确选址对于超市的成功运营至关重要，是运营决策中需要解决的首要问题。

作为一个最优化问题，选址问题的制约条件用分析的方法不易处理，用穷举的方法又因为潜在的选址点有无穷多个也不易实现。

本文引入图论将难以用分析的方法处理的制约条件加以简化处理，通过适当的假设规避大规模的潜在选址点，将复杂的问题简单化。

针对不同的假设，给出四种不同的超市选址模型，利用计算机编程给出令人满意的解。

关键词选址、最短路径、无向图、重心一．问题的背景及提出众所周知，选址是关系到零售门店成功关键的关键因素之一。

曾经有句名言叫做“连锁超市成功的关键有3个条件，那就是选址，选址，还是选址！”由此可见，选址在连锁商业的日常经营中的地位是多么的举足轻重。

因为选址是门店的重要工作，所以选址工作受到每个超市管理者的关注和重视。

好又多公司计划在四川省南充市城区修建一到两个大型超市，为了更好的实现最大化的收益，该集团委托本小组协助他们实现超市的最佳选址。

好又多公司希望我们的选址位置需要满足以下两点：1.给顾客提供充足的便利，便利程度主要指顾客到达超市的路途长短以及要尽可能的选在交通比较发达的干道旁。

2.顾客在按照便利原则（路径最短原则）选择超市时到达所选超市的客流量要尽量的大，因为到达超市的客流量直接影响到超市的赢利。

二．资料数据说明为完成此项选址工作我们找来了市区地图（见附图1），直接在图上进行选址是不现实的，所以我们根据好又多集团的要求1，仅保留了市区主干道，并且以干道交叉点为顶点，以干道长度（由南充市市政工程处提供）为边，把市区交通图简化为图1，同时要计算到达超市的客流量还需要知道南充市的人口分布情况，该资料由南充市公安局户籍科提供。

三、基本假设与符号说明3.1、基本假设（1）准备新建的超市可以容纳所有到来的顾客，可以满足所有人的需求；（2）超市选择的最佳地址只受路径长短的影响，与其他因素无关；（3）各个区居民平均分布于各区；（4）居民出行方式都选择公交汽车，而公交汽车站点设立在各个主干道的交叉处；居民在主干道交接点处换乘汽车的时间忽略不计；（5）所建立的任意两个超市没有任何区别，其选址也只受总路径长度的影响，与其他任何因素无关，人们只选择距离自己位置最近的超市进行购物消费；3.2、符号说明（1）为南充市各个区人口数；（2）为坐标系中各个乡镇中心点的坐标；（3）为第i点位置的标示;（4）为顶点、点之间的最短路径长度；（5）为通过顶点到达超市的人口数；（6）为分布在街道两旁的人口数；（7）为各区域所有顶点按照最短路径到达点的路径之和.（8）为各区域所有顶点按照最短路径到达或点的路径之和；（9）为各区域所有顶点按照最短路径到达点的人口数；四、模型的建立和求解实际上该问题是图论中的选址问题：给出一个无向赋权图，其中顶点集V代表所有的可能选址处，也就是所有的干道交叉点，E是每一条干道，为权重，其中，为赋权图中的标识长度，为各干道两旁居住的人口数。

我们需要作的任务是，找到一顶点子集，（其中k是商家拟建的超市个数，具体由商家决定）使得在此点集中每个点建立超市使目标值最优。

4.1模型一为了模型（一）的简单方便易操作，所以我们暂先不考虑道路、建筑物等其他因素的影响，任何两点之间可以直线行走。

另外暂考虑人口在各个区域内均匀分布，所以我们可以在城区各个区中分别找出几何中心位置集中代表该区人口的居住地点，进行建模。

以过一区几何中心（1）为x轴，过三区几何中心（3）为y轴，建立二维直角坐标系。

图中各区的几何中心坐标：——（1，0）、——（1.43，1.06）、——（0，1.631）、——（1.83，1.83）、——（0.77，2.8）、——（0.57，3.2）、——（2.28，3.25）、——（3.03，4.7）。

各区所居住人口数：=2.18 、 =3.4379 、 =3.5561 、 =6.24808=4.4873 、 =3.4252 、 =7.7711 、 =4.4282（6）（7）（5）（3）（4）（2）（1）4.1.1模型建立目标函数为：约束函数：4.1.2 模型的求解根据数学分析中关于多元函数最值的知识，最值只可能在边界和极值点处达到，而本问题的最优解显然不应在边界取到，另一方面我们可以看到函数的驻点是唯一的，而实际问题的最优解又是必然存在的，所以我们下面求得的驻点一定是最优值对应的最优值点：解得代入得：（x，y）={1.5499，2.5461 }从实际情况上看我们这个点是{1.5499，2.5461}，对应与地图上五星花园和仪凤街之间，而这一段恰恰是南充市最繁华的商业街区，可见我们的结果和现在的实际情况非常吻合。

从上面的公式和数学分析的关于重心坐标的计算的知识我们看出，在平面上选址实际上就是找出所谓的“重心”位置，那么当平面上各个点人口分布不均匀的时候，这个时候上面的公式将不适用，而且通过数学推导也很难得到一个通用的公式，但是我们可以根据物理学的知识采用的“悬挂法”来求重心位置。

具体方法如下：首先，根据实际的南充市地图作一个均匀的、轻质的摸板，然后根据人口分布的情况，在各个居民点放置对应成比例的砝码，最后通过悬挂法找到我们的实物模型的重心，再对应于实际地点，这就是我们需要找到的选址点。

模型的优点：思路比较简单、计算比较方便，有个计算器即可，推广之后的模型也不需要复杂的计算和计算机编程。

模型的缺点：首先地图上的任何两点之间不可能都能以直线的路径行走；而且如果得到的“最优解”不在要求的干道交叉点，虽然我们可以把离该“最优解”最近的路口作为一个近似解，但可信度并不十分理想。

为此我们建立模型二4.2模型二注意到问题本身兼有离散和连续的特征：可行点的选取是有限个的，只能选在干道的交叉处，这是离散的特征；人口均匀的分布在各个区，这又是连续的特征，所以这是一个既有离散又有连续的混合模型。

这方面的研究比较少，解决起来难度比较大。

所以我们需要对问题加以一定的简化。

首先我们考虑到“人口均匀的分布在各区内”这个条件直接处理起来比较麻烦，但是由于每个人选择乘公交车到达超市那么他们首先需要到达干道，然后按照到最近的路口乘公交车，那么我们可以把从顶点乘公交车的人口作为的一个权值，这样我们就把一个混合的规划问题转化成一个离散的规划问题。

的计算：由于我们只有南充各个区的人口情况，所以我们只能假设南充各个区的人口均匀分布在干道两旁，另外一方面每一个人按照最近路径选择乘车点，所以我们可以认为每条街道的人口数又平均分配在该干道的两个顶点。

所以其中为第j区的人口数。

由此问题简化为：给出一个无向赋权图。

我们需要作的任务是，找到一顶点集，（其中k 是商家拟建的超市个数，具体由商家决定）使得在此点集中每个点建立超市使目标值最优。

下面的模型取4.2.1 模型的建立选择下标，使得=minLP其中，；为顶点、点之间的最短路径长度；为通过顶点到达超市的人口数。

4.2.2 模型求解求解这个模型关键在于两个矩阵 L和P的求法，具体算法如下：（1）任意两点之间的最短通路构成的矩阵L首先，将赋权图中的长标志为矩阵L= ，如下：其次，令 =[ ]出发，依次构造出N个矩阵，，…，。

其中第k个矩阵 =[ ]的元素表示从到而中间点仅属于到的k个点的所有通路中的最短通路长。

已知 =[ ]，第k个矩阵 =[ ]定义如下：运算过程从k=1开始，让i、j分别取遍从1到N的所有值，然后k增加1，反复进行，直到k=N时终止。

这时 =[ ]的元素就是从到的最短通路长。

算法流程图如下：（2）各个端点所拥有的人口数构成的列矩阵P由公式我们可以得到矩阵求所有人到点最短路径之和的算法流程图是非是非结束（3）运用计算机,得到< < <……。

其中40是所有点中的最优解。

我们选择40点，实际上在我们选择的最优点就分布着四川万福来集团的南充总店，即使是次优点41、43点也已经有成百集团的超市建立，说明我们的结果和实际情况比较吻合。

模型的优点：模型中考虑了道路问题，取消了各个区域人口集中于一点的假设，将人口平均分布于各个区内无穷多个点转化为分布在有限的几个乘车点上。

模型的缺点：一个城市内不可能只开一家超市，存在一个公司开多家超市和多个公司开一家超市的问题。

现在我们考虑的情形。

模型三给出了一个集团公司作出决策开两家超市的情况；模型四考虑已经有若干家超市存在的前提下，新进超市应当如何选址。

4.3模型三假定两个超市分别选定在，点，据假设（11），则点处的人只选择，中较近的超市进行消费，则顶点的人到达超市所需要走的道路总长度为。

所以选址，，总的路径长度为4.3.1模型建立选择下标使得4.3.2、模型的求解为了简化计算，首先我们考虑到两个超市不可能建立在同一个点上，否则的话，可以将他们合并成一个超市，其次由于对称性，显然有。

由此我们只需计算矩阵的上三角部分。

求解算法流程图是非是非是非结束通过计算机运算得出如下几个可以选择的结果：（21，58）>（20，58）>（20，38）>（20，29）>……其中（21，58）是所有点中的最优解，“>”表示优先级数前者大于后者。

由此，我们认为其中（21，58）更具有合理性。

模型的优点：此模型考虑了建立多个超市情况，对于超市选址问题的解决。

模型的缺点：一个城市中的任何经济行为不可能没有竞争，而此模型中建立两个超市必然要有竞争，我们忽略竞争问题，是此模型的一大缺点。

实际生活中，在南充市城区市场领域进行经济行为的时候，市区内已经拥有一个或多个成熟经营的规模超市，在、、点已经存在这样的超市。

面对这样实际背景，我们给出模型四。

4.4模型四根据好又多公司的要求我们在、、点已经存在超市的情况下寻找建立“一个”超市的最优点，实际上使用我们下面的方法结合模型三，只需要对我们的模型稍加改动，我们就可以得到同时建立多个超市的最优点。

据假设（5），任何两个超市之间没有影响，也就是说在居民的眼里不存在区别。

假定超市建立在点：根据假设（5），对于点的人们来说，他们只会到决定的超市消费。

则点的居民到超市购物所走的路程为。

4.4.1 模型的建立选择下标，使得4.4.2、模型的求解求解的算法流程图，，是非是非结束通过计算机运算得出如下几个可以选择的结果：通过分析，最终我们选定41模型的优点：在这个模型中我们引入了竞争，更加符合实际。

模型的缺点：由于对超市的选址不仅仅依赖与路径长短，还和交通、选址地点周围人口的经济状况等有关，由于缺乏相关的数据，我们在这个模型中都没有涉及，相信如果有了相关的数据我们可以做的更好。