2020年江苏省中考数学复习无理数与实数第一轮重难点突破(解析版)
实数重难点突破

实数的重难点突破
一、实数与无理数的概念
1、无理数:无限不循环小数
2、实数:有理数与无理数的统称
注意:有理数与无理数是两个不同的概念,如果一个数是有理数,就不可能是无理数,反之亦然。
实数根据不同的分类标准,既可以分为有理数和无理数,也可以分为正实数、0、负实数。
0在实数中扮演者重要角色。
我们通常把正实数和0统称为非负数,把负实数和0统称为非正数。
例题:下列说法中正确的是()
A、有理数可分为正数和负数
B、实数可分为有理数、0和无理数
C、整数和小数统称为有理数
D、实数可分为负数和非负数
二、实数与数轴的关系
实数与数轴上的点是一一对应的,就是说所有的实数都可以用数轴上的点来表示;反之,数轴上的任何一个点都表示一个实数,不是有理数就是无理数。
例题:和数轴上的点一一对应的数是()
A、自然数
B、有理数
C、无理数
D、实数。
苏教版数学中考总复习(知识点考点梳理、重点题型分类巩固练习)(基础版)(家教、补习、复习用)
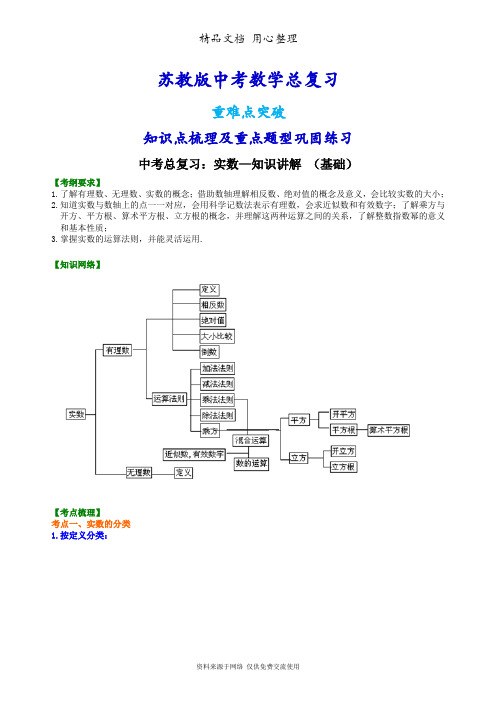
苏教版中考数学总复习重难点突破知识点梳理及重点题型巩固练习中考总复习:实数—知识讲解(基础)【考纲要求】1.了解有理数、无理数、实数的概念;借助数轴理解相反数、绝对值的概念及意义,会比较实数的大小;2.知道实数与数轴上的点一一对应,会用科学记数法表示有理数,会求近似数和有效数字;了解乘方与开方、平方根、算术平方根、立方根的概念,并理解这两种运算之间的关系,了解整数指数幂的意义和基本性质;3.掌握实数的运算法则,并能灵活运用.【知识网络】【考点梳理】考点一、实数的分类1.按定义分类:⎧⎧⎫⎧⎫⎪⎪⎪⎬⎪⎪⎨⎪⎭⎪⎪⎪⎪⎪⎨⎬⎩⎪⎪⎪⎪⎧⎨⎪⎪⎨⎪⎪⎪⎩⎭⎩⎪⎪⎫⎧⎪⎪⎨⎬⎪⎪⎩⎭⎩正整数自然数整数零有理数有限小数或无限循环小数负整数实数正分数分数负分数正无理数无理数无限不循环小数负无理数 2.按性质符号分类:⎧⎧⎧⎪⎨⎪⎨⎩⎪⎪⎪⎩⎪⎪⎨⎪⎧⎧⎪⎨⎪⎪⎨⎩⎪⎪⎪⎩⎩正整数正有理数正实数正分数正无理数实数零负整数负有理数负实数负分数负无理数 有理数:整数和分数统称为有理数或者“形如nm(m ,n 是整数n≠0)”的数叫有理数. 无理数:无限不循环小数叫无理数. 实数:有理数和无理数统称为实数. 要点诠释:常见的无理数有以下几种形式:(1)字母型:如π是无理数,24ππ、等都是无理数,而不是分数; (2)构造型:如2.10100100010000…(每两个1之间依次多一个0)就是一个无限不循环的小数;(3…都是一些开方开不尽的数;(4)三角函数型:sin35°、tan27°、cos29°等.考点二、实数的相关概念 1.相反数(1)代数意义:只有符号不同的两个数,我们说其中一个是另一个的相反数.0的相反数是0; (2)几何意义:在数轴上原点的两侧,与原点距离相等的两个点表示的两个数互为相反数; (3)互为相反数的两个数之和等于0.a 、b 互为相反数⇔a+b=0. 2.绝对值(1)代数意义:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.可用式子表示为:⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a (2)几何意义:一个数a 的绝对值就是数轴上表示数a 的点与原点的距离.距离是一个非负数,所以绝对值的几何意义本身就揭示了绝对值的本质,即绝对值是一个非负数.用式子表示:若a 是实数,则|a|≥0. 要点诠释:若,a a =则0a ≥;-,a a =则0a ≤;-a b 表示的几何意义就是在数轴上表示数a 与数b 的点之间的距离. 3.倒数(1)实数(0)a a ≠的倒数是a1;0没有倒数; (2)乘积是1的两个数互为倒数.a 、b 互为倒数1a b ⇔⋅=. 4.平方根(1)如果一个数的平方等于a ,这个数就叫做a 的平方根.一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身;负数没有平方根.a (a ≥0)的平方根记作a ±.(2)一个正数a 的正的平方根,叫做a 的算术平方根.a (a ≥0)的算术平方根记作a . 5.立方根如果x 3=a ,那么x 叫做a 的立方根.一个正数有一个正的立方根;一个负数有一个负的立方根;0的立方根仍是0.考点三、实数与数轴规定了原点、正方向和单位长度的直线叫做数轴,数轴的三要素缺一不可.每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数. 要点诠释:(1)数轴的三要素:原点、正方向和单位长度. (2)实数和数轴上的点是一一对应的.考点四、实数大小的比较1.对于数轴上的任意两个点,靠右边的点所表示的数较大.2.正数都大于0,负数都小于0,正数大于一切负数;两个负数;绝对值大的反而小.3.对于实数a 、b , 若a-b>0⇔a>b ;a-b=0⇔a=b ;a-b<0⇔a<b.4.对于实数a ,b ,c ,若a>b ,b>c ,则a>c.5.无理数的比较大小:利用平方转化为有理数:如果a>b>0, a 2>b 2⇔a>b b a >⇔;或利用倒数转化:如比较417-与154-.要点诠释:实数大小的比较方法:(1)直接比较法:正数都大于0,负数都小于0,正数大于一切负数;两个负数,绝对值大的反而小.(2)数轴法:在数轴上,右边的数总比左边的数大.考点五、实数的运算 1.加法同号两数相加,取相同的符号,并把绝对值相加;绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两个数相加得0;一个数同0相加,仍得这个数.满足运算律:加法的交换律a+b=b+a ,加法的结合律(a+b)+c=a+(b+c). 2.减法减去一个数等于加上这个数的相反数. 3.乘法两数相乘,同号得正,异号得负,并把绝对值相乘.几个非零实数相乘,积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数有奇数个时,积为负.几个数相乘,有一个因数为0,积就为0.乘法运算的运算律:(1)乘法交换律ab=ba ;(2)乘法结合律(ab)c=a(bc);(3)乘法对加法的分配律a(b+c)=ab+ac . 4.除法(1)除以一个数,等于乘上这个数的倒数.(2)两个数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数都得0. 5.乘方与开方(1)求n 个相同因数的积的运算叫做乘方,a n所表示的意义是n 个a 相乘.正数的任何次幂是正数,负数的偶次幂是正数,负数的奇次幂是负数. (2)正数和0可以开平方,负数不能开平方;正数、负数和0都可以开立方. (3)零指数与负指数011(0)(0).pp a a aa a-==≠,≠ 要点诠释:加和减是一级运算,乘和除是二级运算,乘方和开方是三级运算.这三级运算的顺序是三、二、一.如果有括号,先算括号内的;如果没有括号,同一级运算中要从左至右依次运算.考点六、有效数字和科学记数法一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.一个近似数,从左边第一个不是0的数字起,到精确到的数位为止,所有的数字,都叫做这个近似数的有效数字.精确度的形式有两种:(1)精确到哪一位;(2)保留几个有效数字.把一个数用±a ×10n (其中1≤<10,n 为整数)的形式记数的方法叫科学记数法.要点诠释:(1)当要表示的数的绝对值大于1时,用科学记数法写成a ×10n,其中1≤a <10,n 为正整数,其值等于原数中整数部分的数位减去1;(2)当要表示的数的绝对值小于1时,用科学记数法写成a ×10n,其中1≤a <10,n 为负整数,其值等于原数中第一个非零数字前面所用零的个数的相反数(包括小数点前面的零).【典型例题】类型一、实数的有关概念1.(1)a 的相反数是15-,则a 的倒数是_______.(2)实数a 、b 在数轴上对应点的位置如图所示: =______.0ab(3)(泉州市)去年泉州市林业用地面积约为10200000亩,用科学记数法表示为约____________.【答案】(1)5 ; (2)-a-b ; (3)1.02×107亩. 【解析】(1)注意相反数和倒数概念的区别,互为相反数的两个数只有性质符号不同,互为倒数的两个数要改变分子分母的位置;或者利用互为相反数的两个数之和等于0,互为倒数的两个数乘积等于1来计算.(2)此题考查绝对值的几何意义,绝对值和二次根式的化简.注意要去掉绝对值符号,要判别绝对值内的数的性质符号.由图知:0 0 |||| 0 ||().a b a b a b a b a b a b ><<∴+<=+=-+=--,,,,(3)考查科学记数法的概念.【点评】本大题旨在通过几个简单的填空,让学生加强对实数有关概念的理解. 举一反三:【变式】据市旅游局统计,今年“五·一”小长假期间,我市旅游市场走势良好,假期旅游总收入达到8.55亿元,用科学记数法可以表示为( )A .8.55×106B .8.55×107C .8.55×108D .8.55×109【答案】C.类型二、实数的分类与计算2.下列实数227、sin60°、3π、、3.14159、(2- )个A .1B .2C .3D .4【答案】C.【解析】无理数有sin60°、3π【点评】对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.举一反三:【课程名称: 实数 369214 :经典例题1】 【变式】在,30cos ,2π,)23(,4,8,14.30 --,45tan ,712,1010010001.0 ,51-13.0%,3 中,哪些是有理数? 哪些是无理数?【答案】03.14,2),-,45tan ,712,51-13.0%,3 都是有理数; π,cos30,2-0.1010010001,都是无理数.3.(2015•梅州)计算:+|2﹣3|﹣()﹣1﹣(2015+)0.【答案与解析】解:原式=2+3﹣2﹣3﹣1=﹣1.【点评】该题是实数的混合运算,包括绝对值,0指数幂、负整数指数幂等.只要准确把握各自的意义,就能正确的进行运算.举一反三:【课程名称:实数 369214 :经典例题8-9】【变式1】计算:(2015•甘南州)计算:|﹣1|+20120﹣(﹣)﹣1﹣3tan30°.【答案】解:原式=﹣1+1﹣(﹣3)﹣3×=+3﹣=3.【变式2】计算:12004200320022001+⨯⨯⨯ 【答案】设n=2001,则原式=1)3)(2)(1(++++n n n n1)23)(3(22++++=n n n n (把n 2+3n 看作一个整体)=1)3(2)3(222++++n n n n =n 2+3n+1=n(n+3)+1 =2001×2004+1 =4010005.类型三、实数大小的比较4.比较下列每组数的大小:(1)417-与154- (2)a 与a1(a ≠0) 【答案与解析】(140=>,40=>,4+与4+440>+>,44-<- (2)当a<-1或O<a<1时,a<a1;当-1<a<0或a>1时,a>a1; 当a=1±时,a=a1.【点评】(1)有时无理数比较大小,通过平方转化以后也无法进行比较,那么我们可以利用倒数关系比较;(2)这道题实际上是互为倒数的两个数之间的比较大小,我们可以利用数轴进行比较,我们知道,0没有倒数,±1的倒数等于它本身,这样数轴就被这3个数分成了4部分,下面就可以分类讨论每种情况.我们还可以利用函数图象来解决这个问题,把a1的值看成是关于a 的反比例函数,把a 的值看成是关于a 的正比例函数,在坐标系中画出它们的图象,可以很直观的比较出它们的大小.举一反三:【变式】比较下列每组数的大小: (1)817-和511- (2)52+和23+【答案】(1)将其通分,转化成同分母分数比较大小,1785840= ,1188540=, 171185<,所以171185->-.(2)277+=+=+)2277+=+=+<2+<+.类型四、平方根的应用5.已知:x ,y 2690y y +-+=,若axy-3x=y ,则实数a 的值是_______.【答案】14.2690y y -+=2(3)0y +-=两个非负数相加和为0,则这两个非负数必定同时为0,0=,(y-3)2=0, ∴ x=43-, y=3又∵axy-3x=y,∴ a=43()33134433x yxy⨯-++==-⨯.【点评】此题考查的是非负数的性质.类型五、实数运算中的规律探索6.细心观察图形,认真分析各式,然后解答问题21222312,213,214,2SSS+==+==+==1A2AA(1)请用含有n(n是正整数)的等式表示上述变化规律;(2)推算出OA10的长;(3)求出S12+ S22+ S32+…+ S102的值.【答案与解析】(1)由题意可知,图形满足勾股定理,()2,112nSnn n=+=+(2)因为OA1=1,OA2=2,OA3=3…,所以OA10=10(3)S12+ S22+ S32+…+ S102=2222)210()23()22()21(++++=)10321(41++++=455.【点评】近几年各地的中考题中越来越多的出现了一类探究问题规律的题目,这些问题素材的选择、文字的表述、题型的设计不仅考察了数学的基础知识,基本技能,更重点考察了创新意识和能力,还考察了认真观察、分析、归纳、由特殊到一般,由具体到抽象的能力.举一反三:【变式】图中是一幅“苹果图”,第一行有1个苹果,第二行有2个,第三行有4个,•第四行有8个,……你是否发现苹果的排列规律?猜猜看,第十行有______个苹果.【答案】29(512).苏教版中考数学总复习重难点突破知识点梳理及重点题型巩固练习中考总复习:实数—巩固练习 (基础)【巩固练习】 一、选择题1. 在实数-23,0,-3.1415,2-0.1010010001…(每两个1之间依次多1个0),sin30° 这8个实数中,无理数有( )A .1个B .2个C .3个D .4个2.我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665 575 306人.将665 575 306用科学记数法表示(保留三个有效数字)约为( ) A .66.6×107B .6.66×108C .0.666×108D .6.66×1073.(2015•杭州)若k <<k+1(k 是整数),则k=( ) A .6 B .7 C .8 D .94.在三个数0.5、、中,最大的数是( )A .0.5B .C .D .不能确定5.用四舍五入法按要求对0.05049分别取近似值,其中错误的是( ) A .0.1(精确到0.1)B .0.05(精确到百分位)C .0.050(精确到0.001)D .0.05(精确到千分位)6.我国古代的“河图”是由3×3的方格构成,每个方格内均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图中给出了“河图”的部分点图,请你推算出P 处所对应的点图是( )二、填空题7. ()0201112=-++y x 则x y= .8. (2014•辽阳)5﹣的小数部分是 .9.若22+-b a 与互为相反数,则a+b 的值为________. 10.已知a 与b 互为相反数,c 与d 互为倒数,m 的绝对值是1,则2m cd mba +-+的值为________.11.已知:22222233445522 33 44 55338815152424+=⨯+=⨯+=⨯+=⨯,,,,,若21010b ba a+=⨯符合前面式子的规律,则a+b=________.12.将正偶数按下表排列:第1列 第2列 第3列 第4列 第1行 2第2行 4 6第3行 8 10 12第4行 14 16 18 20 ……根据上面的规律,则2006所在行、列分别是________.三、解答题13. 计算:(1)2012201280.125⨯ (2)222121⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛+e e e e14.若333)43(,)43(,)43(--=-=-=c b a ,比较a 、b 、c 的大小。
2020年苏科版数学中考考点归纳整理(代数部分)超详细附典型例题与反馈练习

注:a-b 的相反数是 b-a;a+b 的相反数是-a-b.
(3)倒数:1 除以一个不等于零的实数所得的商,叫做这个数的倒数.若 a、b 互为倒数,则 ab=1.
(4)绝对值:在数轴上,一个数对应的点与原点的距离叫做这个数的绝对值.
a (a>0)
或
a (a≥0)
a
0 (a=0)
a=
-a (a<0)
-a (a≤0) 即:| a |是一个非负数,| a |≥0.
例:(a2)3=_________;2a2•a3=_________;(-3x2)3=_________;(-2a)2÷a=_________;(-a)3(-a)2=_________.
(a2b)3=(a2)3b3 运算过程中运用到的“幂的运算”的法则是________________.
7.(1)单项式:由数字与字母或字母与字母相乘组成的代数式叫做单项式,所有字母指数的和叫做次数,数字因数叫做系数.
(2)合并同类项的法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。
(3)合并同类项的步骤:①找出同类项;②运用加法交换律,把同类项交换位置后结合在一起;③利用法则,把同类项的系数
相加,字母和字母的指数不变.注:运用加法交换律时改变“项”的位置时,要注意连同符号一起移动.
(4)去(添)括号的法则: ①括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不变;
例:(1)注意配方问题中的分类思想: 若 4m2+1 加上一个单项式可以变成完全平方式,则这个单项式可以是_____________________________;
(2)若 a+b=3,ab=2,求(a-b)2 的值.(尝试自己编一些类似的问题并求解)
2020年江苏中考数学复习第1章第1课时 实数

解:原式 =3-1+4(5分) =6(6分)
27. [2018淮安17(1)题5分]计算:2sin45°+(π-1)0- 18 +|2 2 |. 解:原式 = 2 +1-3 2 +2 2
=1(5分)
返回目录
第1课时 实数
考点特训营
返回目录
【对接教材】苏科:七上第二章P12-P63,八上第四章P94-P113; 人教:七上第一章P2-P52,七下第六章P39-P62.
D. 2
2. (2017盐城7题3分)请写出一个无理数___3__(_答__案__不__唯__一__) .
返回目录
第1课时 实数
返回目录
江苏其他地市真题
3. (2015扬州1题3分)实数0是( A )
A. 有理数 B. 无理数 C. 正数
D. 负数
4. (2015泰州2题3分)下列4个数: 9,22,π,3 0 .其中无理数是( C )
温馨提示:常考的计数单位有:1千=103,1万=104,1亿=108,1万亿=1012; 常考的计量单位有:1mm=10-3m,1μm=10-6m,1nm=10-9m
返回思维导图
第1课时 实数
返回目录
负数<0<正数
返回思维导图
实
类别法 两个负数比较大小,绝对值大的数反而__小___
数
温馨提示:一组数里有正数、0、负数,求最大的数直接在正数里面
第1课时 实数
命题点 4 平方根、算术平方根和立方根 (宿迁2019.9)
18. (2019宿迁9题3分)实数4的算术平方根为___2____. 江苏其他地市真题 19. (2016徐州9题3分)9的平方根是___±__3___. 20. (2019连云港9题3分)64的立方根是___4_____.
2020年中考数学一轮专项复习——无理数与实数 中考真题汇编(含解析答案)

2020年中考数学一轮专项复习——无理数与实数中考真题汇编一.选择题1.(2019•济南)实数a、b在数轴上的对应点的位置如图所示,下列关系式不成立的是()A.a﹣5>b﹣5 B.6a>6b C.﹣a>﹣b D.a﹣b>0 2.(2019•南通)小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3(如图).以O为圆心,OB长为半径作弧,交数轴正半轴于点P,则点P所表示的数介于()A.1和2之间B.2和3之间C.3和4之间D.4和5之间3.(2019•莱芜区)在下列四个实数中,最大的数是()A.﹣1 B.﹣C.D.4.(2019•大庆)有理数﹣8的立方根为()A.﹣2 B.2 C.±2 D.±4 5.(2019•宁夏)下列各式中正确的是()A.=±2 B.=﹣3 C.=2 D.﹣=6.(2019•包头)计算|﹣|+()﹣1的结果是()A.0 B.C.D.6 7.(2019•吉林)若a为实数,则下列各式的运算结果比a小的是()A.a+1 B.a﹣1 C.a×1 D.a÷1 8.(2019•柳州)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=﹣1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i﹣9=﹣8+6i,因此,(1+3i)2的实部是﹣8,虚部是6.已知复数(3﹣mi)2的虚部是12,则实部是()A.﹣6 B.6 C.5 D.﹣5 9.(2019•邵阳)下列各数中,属于无理数的是()A.B.1.414 C.D.10.(2019•宜昌)如图,A,B,C,D是数轴上的四个点,其中最适合表示无理数π的点是()A.点A B.点B C.点C D.点D 11.(2019•咸宁)下列关于0的说法正确的是()A.0是正数B.0是负数C.0是有理数D.0是无理数12.(2019•荆门)﹣的倒数的平方是()A.2 B.C.﹣2 D.﹣13.(2019•广东)实数a、b在数轴上的对应点的位置如图所示,下列式子成立的是()A.a>b B.|a|<|b| C.a+b>0 D.<0 14.(2019•常德)下列各数中比3大比4小的无理数是()A.B.C.3.1 D.15.(2019•舟山)如图是一个2×2的方阵,其中每行、每列的两数和相等,则a可以是()A.tan60°B.﹣1 C.0 D.12019 16.(2019•南京)面积为4的正方形的边长是()A.4的平方根B.4的算术平方根C.4开平方的结果D.4的立方根17.(2019•白银)下列整数中,与最接近的整数是()A.3 B.4 C.5 D.618.(2019•重庆)估计(2+6)×的值应在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间二.填空题19.(2019•恩施州)0.01的平方根是.20.(2019•青海)根据如图所示的程序,计算y的值,若输入x的值是1时,则输出的y 值等于.21.(2019•青海)﹣5的绝对值是;的立方根是.22.(2019•莱芜区)计算:(﹣)﹣1++|1﹣π|=.23.(2019•上海)如果一个正方形的面积是3,那么它的边长是.24.(2019•陕西)已知实数﹣,0.16,,π,,,其中为无理数的是.25.(2019•辽阳)6﹣的整数部分是.26.(2019•遂宁)阅读材料:定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i 叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如计算:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;(4+i)(4﹣i)=16﹣i2=16﹣(﹣1)=17;(2+i)2=4+4i+i2=4+4i﹣1=3+4i根据以上信息,完成下面计算:(1+2i)(2﹣i)+(2﹣i)2=.27.(2019•台州)若一个数的平方等于5,则这个数等于.28.(2019•临沂)一般地,如果x4=a(a≥0),则称x为a的四次方根,一个正数a的四次方根有两个.它们互为相反数,记为±,若=10,则m=.29.(2019•舟山)数轴上有两个实数a,b,且a>0,b<0,a+b<0,则四个数a,b,﹣a,﹣b的大小关系为(用“<”号连接).30.(2019•成都)估算:≈(结果精确到1)三.解答题31.(2019•济南)计算:()﹣1+(π+1)0﹣2cos60°+32.(2019•青海)计算:(﹣1)0+(﹣)﹣1+|﹣1|﹣2cos45°33.(2019•大庆)计算:(2019﹣π)0+|1﹣|﹣sin60°.34.(2019•沈阳)计算:(﹣)﹣2+2cos30°﹣|1﹣|+(π﹣2019)0.35.(2019•陕西)计算:﹣2×+|1﹣|﹣()﹣236.(2019•永州)计算:(﹣1)2019+×sin60°﹣(﹣3).37.(2019•通辽)计算:﹣14﹣|﹣1|+(﹣1.414)0+2sin60°﹣(﹣)﹣138.(2019•上海)计算:|﹣1|﹣×+﹣8参考答案一.选择题1.解:由图可知,b <0<a ,且|b |<|a |, ∴a ﹣5>b ﹣5,6a >6b ,﹣a <﹣b ,a ﹣b >0, ∴关系式不成立的是选项C . 故选:C .2.解:由勾股定理得,OB ==,∵9<13<16, ∴3<<4,∴该点位置大致在数轴上3和4之间. 故选:C .3.解:∵﹣<﹣1<<,∴四个实数中,最大的数是. 故选:C .4.解:有理数﹣8的立方根为.故选:A . 5.解:A .,故选项A 不合题意;B .,故选项B 不合题意;C .,故选项C 不合题意;D .,故选项D 符合题意.故选:D .6.解:原式=3+3=6. 故选:D .7.解:A .a +1>a ,选项错误;B.a﹣1<a,选项正确;C.a×1=a,选项错误;D.a÷1=a,选项错误;故选:B.8.解:∵(3﹣mi)2=32﹣2×3×mi+(mi)2=9﹣6mi+m2i2=9+m2i2﹣6mi=9﹣m2﹣6mi,∴复数(3﹣mi)2的实部是9﹣m2,虚部是﹣6m,∴﹣6m=12,∴m=﹣2,∴9﹣m2=9﹣(﹣2)2=9﹣4=5.故选:C.9.解:=2是有理数;是无理数;故选:C.10.解:因为无理数π大于3,在数轴上表示大于3的点为点D;故选:D.11.解:0既不是正数也不是负数,0是有理数.故选:C.12.解:﹣的倒数的平方为:.故选:B.13.解:由图可得:﹣2<a<﹣1,0<b<1,∴a<b,故A错误;|a|>|b|,故B错误;a+b<0,故C错误;<0,故D正确;故选:D.14.解:∵四个选项中是无理数的只有和,而>4,3<<4∴选项中比3大比4小的无理数只有.故选:A.15.解:由题意可得:a+|﹣2|=+20,则a+2=3,解得:a=1,故a可以是12019.故选:D.16.解:面积为4的正方形的边长是,即为4的算术平方根;故选:B.17.解:∵32=9,42=16,∴3<<4,10与9的距离小于16与10的距离,∴与最接近的是3.故选:A.18.解:(2+6)×,=2+6,=2+,=2+,∵4<5,∴6<2+<7,故选:C.二.填空题(共12小题)19.解:0.01的平方根是±0.1,故答案为:±0.1;20.解:当x=1时,x2﹣=1﹣<0,∴y=(1﹣)(1+)=1﹣3=﹣2,故答案为:﹣2.21.解:﹣5的绝对值是5;的立方根是.故答案为:5,.22.解:原式=﹣3+4+π﹣1=π.故答案为:π.23.解:∵正方形的面积是3,∴它的边长是.故答案为:24.解:,、0.16是有理数;无理数有、π、.故答案为:、π、.25.解:∵1<<2,∴6﹣的整数部分是6﹣2=4.故答案为:4.26.解:(1+2i)(2﹣i)+(2﹣i)2=2﹣i+4i﹣2i2+4+i2﹣4i =6﹣i﹣i2=6﹣i+1=7﹣i.故答案为:7﹣i.27.解:若一个数的平方等于5,则这个数等于:±.故答案为:±.28.解:∵=10,∴m4=104,∴m=±10.故答案为:±1029.解:∵a>0,b<0,a+b<0,∴|b|>a,∴﹣b>a,b<﹣a,∴四个数a,b,﹣a,﹣b的大小关系为b<﹣a<a<﹣b.故答案为:b<﹣a<a<﹣b30.解:∵,∴,而37.7﹣36<49﹣37.7∴≈6.故答案为:6三.解答题(共8小题)31.解:()﹣1+(π+1)0﹣2cos60°+=2+1﹣2×+3=3﹣1+3=532.解:原式=1﹣3+﹣1﹣2×=1﹣3+﹣1﹣=﹣3.33.解:原式=1+﹣1﹣=.34.解:原式=4+2×﹣+1+1=6.35.解:原式=﹣2×(﹣3)+﹣1﹣4=1+.36.解:(﹣1)2019+×sin60°﹣(﹣3)=﹣1+2×+3=﹣1+3+3=537.解:原式=﹣1﹣(﹣1)+1+2×+2=﹣1﹣+1+1++2=3.38.解:|﹣1|﹣×+﹣8=﹣1﹣2+2+﹣4=﹣3。
2020年中考数学一轮复习基础考点及题型专题 实数(解析版)

专题实数考点总结【思维导图】【知识要点】知识点一平方根算术平方根概念:一般的如果一个正数x的平方等于a,即x2= a,那么这个正数x叫做a的算术平方根。
算术平方根的表示方法:非负数a的算术平方根记作√a,读作根号a,其中a是被开方数。
平方根概念:如果一个数的平方等于a,那么这个数就叫做a的平方根或二次方根,即如果x2=a,那么x叫做a 的平方根。
平方根的性质与表示:表示:正数a的平方根用±√a表示,√a叫做正平方根,也称为算术平方根,−√a叫做a的负平方根。
性质:一个正数有两个平方根:±√a(根指数2省略)且他们互为相反数。
0有一个平方根,为0,记作√0=0负数没有平方根平方根与算术平方根的区别与联系:1.(2017·甘肃中考模拟)正数9的平方根是( )A.3B.±3C D.±【答案】B【详解】因为±3的平方都等于9,所以答案为B2.(2016·山东中考模拟)81的算术平方根是()A.9 B.±9 C.3 D.±3【答案】A【解析】试题解析:∵92=81,∴81的算术平方根是9.故选A.3.(2018·江苏中考模拟)9的算术平方根是()A.﹣3B.±3C.3D 【答案】C【解析】试题分析:9的算术平方根是3.故选C.4.(2019·()A.﹣4B.±2C.±4D.4【答案】B【详解】∵42=16,4,±2,故选B.5.(2018·)A.B C.2±D.2【答案】B【解析】,而2,故选B.6.(2019·)A.4B.±4C.2D.±2【答案】C4,4的算术平方根是2,2,故选C.7.(2019·)A.9B.±9C.±3D.3【答案】D,又∵(±3)2=9,∴9的平方根是±3,∴9的算术平方根是3.3. 故选:D .8.(2019· ) A .32B .32-C .32±D .8116【答案】A 【解析】32, 故选:A.9.(2017·江苏中考真题)若方程的两根为和,且,则下列结论中正确的是 ( )A .是19的算术平方根B .是19的平方根C .是19的算术平方根D .是19的平方根【答案】C 【解析】试题分析:根据平方根的意义,可知x -5是19的一个平方根,由a >b ,可知a -5是19的算术平方根,b -5是其负的平方根. 故选:C考查题型一 利用算术平方根的非负性解题1.(2015·内蒙古中考真题)若30,a -+=则+a b 的值是( ) A .2 B 、1 C 、0 D 、1- 【答案】B 【解析】试题分析:由题意得,3﹣a=0,2+b=0,解得,a=3,b=﹣2,a+b=1,故选B .2.(2016·山西中考模拟)若(m -1)20,则m +n 的值是( ) A .-1 B .0C .1D .2【答案】A【详解】∵(m -1)20, ∴m−1=0,n+2=0; ∴m=1,n=−2, ∴m+n=1+(−2)=−1 故选:A.3.(2018·山东中考模拟)已知5a =7=,且a b a b +=+,则-a b 的值为( ) A .2或12 B .2或12-C .2-或12D .2-或12-【答案】A 【解析】根据a =5=7,得a 5,b 7=±=±,因为a b a b +=+,则a 5,b 7=±=,则a b -=5+7=12或-5+7=2. 故选A.考查题型二 利用平方根的性质解题1.(2019·南票区九龙街道初级中学中考模拟)若a 2=4,b 2=9,且ab <0,则a ﹣b 的值为( ) A .﹣2 B .±5C .5D .﹣5【答案】B 【解析】 ∵a 2=4,b 2=9, ∴a=±2,b=±3, ∵ab<0,∴a=2时,b=−3,a−b=2−(−3)=2+3=5, a=−2时,b=3,a−b=−2−3=−5, 所以,a−b 的值为5或−5. 故选:B.2.(2019·黑龙江中考模拟)对于实数a ,b 下列判断正确的是( ) A .若a b =,则 a b = B .若22a b >,则 a b >C b =,则a b =D =,则a b =【答案】D【详解】解:A 也可能是a=-b ,故A 错误;B ,22a b >只能说明|a|>b ,故B 错误; C ,a ,b 也可能互为相反数;D ,都表示算术平方根,故D 正确;3.(2018·江苏中考模拟)如果a ,b 分别是2016的两个平方根,那么a+b ﹣ab=___. 【答案】2016【详解】∵a ,b 分别是2016的两个平方根,∴a b == ∵a ,b 分别是2016的两个平方根, ∴a+b=0,∴ab=a×(﹣a )=﹣a 2=﹣2016, ∴a+b ﹣ab=0﹣(﹣2016)=2016, 故答案为:2016. 知识点二 立方根和开立方立方根概念:如果一个数的立方等于a ,即x 3=a ,那么x 叫做a 的立方根或三次方根, 表示方法:数a 的立方根记作√a 3,读作三次根号a立方根的性质:任何实数都有唯一确定的立方根。
2020版中考数学新素养突破大一复习徐州版(课件+课时训练):第01课时 实数及其运算

运算律
交换律 a+b=⑱ b+a ,ab=⑲ ba (a+b)+c=⑳ a+(b+c) ,
结合律 (ab)c=㉑ a(bc)
分配律 a(b+c)= ㉒ ab+ac
乘方 an=a·a·…·a(n个a相乘) 几种常见的运算
零次幂 任何非零实数的零次幂都为1,即a0=㉓ 1 (a≠0)
(续表)
负整数次幂
3.常考的计数单位和计量单位:1亿=⑨ 108 ,1万=⑩ 104 ;1 mm=10-3 m, 1 nm=10-9 m等. 4.科学记数法的还原 (1)绝对值大于10的数的还原:将数a的小数点向⑪ 右 移动n位; (2)绝对值大于0且小于1的数的还原:将数a的小数点向⑫ 左 移动|n|位. 5.近似数:一个近似数四舍五入到哪一位,那么就说这个近似数精确到哪一位.有 计数单位的近似数,由近似数的数位和后面的单位共同确定.如3.618万,数字8 实际上是十位上的数字,即精确到十位.
图1-2
题组二 易错题
【失分点】 忽略绝对值的分类讨论、数轴上的点对应数的符号.负数的乘方先定号再运算, 负整数指数幂是求幂后再求倒数,或者求倒数后再求幂.
5.实数0是 A.有理数 C.正数
(A )
B.无理数 D.负数
6. [2014·徐州8题]点A,B,C在同一 [答案] D
条数轴上,其中点A,B表示的数分别 [解析]此题画图时会出现两种情况,即点C
2.判断实数的正负,一定要先化简,再根据定义判断,如-(-2)=2是正数;注意-a不 一定是负数,要对a进行分类讨论.
考点二 实数的有关概念 1.数轴:规定了原点、④ 正方向 和⑤ 单位长度 的直线.数轴上的点与实数一 一对应.
中考数学 第1讲 实数复习讲义 苏科版

第1讲实数基础知识点:一、实数的分类:1、有理数:任何一个有理数总可以写成的形式,其中p、q是互质的整数,这是有理数的重要特征。
2、无理数:初中遇到的无理数有三种:开不尽的方根,如、;特定结构的不限环无限小数,如3、判断一个实数的数性不能仅凭表面上的感觉,往往要经过整理化简后才下结论。
二、实数中的几个概念1、相反数:只有符号不同的两个数叫做互为相反数。
(1)实数a的相反数是 -a;(2)a和b互为相反数a+b=02、倒数:(1)实数a(a≠0)的倒数是;(2)a和b 互为倒数;(3)注意0没有倒数3、绝对值:(1)一个数a 的绝对值有以下三种情况:(2)实数的绝对值是一个非负数,数轴上看,一个实数的绝对值,数轴上表示这个数的点到原点的距离。
(3)去掉绝对值符号必须要对绝对值符号里面的实数进行数性(正、负)确认,再去掉绝对值符号。
4、n次方根(1)平方根,算术平方根:设a≥0,称叫a的平方根,叫a的算术平方根。
(2)正数的平方根有两个,它们互为相反数;0的平方根是0;负数没有平方根。
(3)立方根:叫实数a的立方根。
(4)一个正数有一个正的立方根;0的立方根是0;一个负数有一个负的立方根。
三、实数与数轴1、数轴:规定了原点、正方向、单位长度的直线称为数轴。
原点、正方向、单位长度是数轴的三要素。
2、数轴上的点和实数的对应关系:数轴上的每一个点都表示一个实数,而每一个实数都可以用数轴上的唯一的点来表示。
实数和数轴上的点是一一对应的关系。
四、实数大小的比较1、在数轴上表示两个数,右边的数总比左边的数大。
2、正数大于0;负数小于0;正数大于一切负数;两个负数绝对值大的反而小。
3、作差法和作商法。
五、实数的运算1、加法:(1)同号两数相加,取原来的符号,并把它们的绝对值相加;(2)异号两数相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。
2、减法:减去一个数等于加上这个数的相反数。
3、乘法:(1)两数相乘,同号取正,异号取负,并把绝对值相乘。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
B . 3 4
7
7 5 3 5 习题精选 18 无理数与实数
一.选择题
(建议用时:60 分钟 满分:100 分)
1. 下列说法错误的是(
)
A .实数都可以表示在数轴上
B .数轴上的点不全是有理数
C. 坐标系中的点的坐标都是实数对
D . 是近似值,无法在数轴上表示准确
2.(当涂县期中)下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理
数;③负数没有立方根;④17 的平方根是﹣ ,其中正确的是(
)
A .0 个
B .1 个
C .2 个
D .3 个
3. 估计 的大小应在(
)
A .7~8 之间
B .8.0~8.5 之间
C .8.5~9.0 之间
D .9~10 之间
4. (烟台)下列实数中,有理数是(
)
π
A.
C .
2
D .0.101001001 5. 实数 2.6、 7 和2
的大小关系是(
)
A . 2.6 < 2 <
B . < 2.6 < 2
C . 2.6 < < 2 D.
2 < 2.6 <
6. 一个正方体水晶砖,体积为 100 cm 3 ,它的棱长大约在(
)
A .4~5 cm 之间
B .5~6 cm 之间
C .6~7 cm 之间
D .7~8 cm 之间
二.填空题
7.(南京)比较大小: ﹣3
5 - 2 .
2
8.在数轴上与 1 距离是 的点,表示的实数为 .
9.(南平模拟)计算: ﹣ 3 27 =
.
10. 5 - 的整数部分是
,小数部分是
.
2 17 76 2 2 7 2
2
2 7
9
23
11.已知x 为整数,且满足-≤x ≤,则x = .
12. (3 - 10) 的相反数是,绝对值是,平方等于.
三.解答题
13.(荣昌县校级期中)把下列各数填入相应的大括号内. ,﹣2,3 9 ,0,3 - 8 ,
16
,113
3.1415,π﹣3,144 ,3+ 29 ,3 2 ,0.2121121112…
整数集合:{
非负实数集合:{ 无理数集合:{ …};…};…}.
14.天安门广场的面积大约是440000 m2 ,若将其近似看作一个正方形,那么它的边长大约
是多少?(用计算器计算,精确到m )
15.已知x - 2+ | x2 - 3y -13 |= 0, 求x +y 的值.
【答案与解析】
一.选择题
1.【答案】D;
【解析】实数和数轴上的点一一对应,无理数也可以在数轴上表示.
3
64 76 76 8 2 3 100 3 100 5 5 5 5 2. 【答案】A ;
【解析】解:①实数与数轴上的点一一对应,故①错误;
②无理数是无限不循环小数,故②错误;
③负数的立方根是负数,故③错误;
④17 的平方根是± ,故④错误;
故选:A .
3. 【答案】C ;
【解析】 < <
81, 8 < < 9 ,因为 76 比较接近 81,所以
在 8.5~9.0
之间.
4. 【答案】D ;
【解析】解:A 、 不能正好开方,即为无理数,故本选项错误;
B 、3 4 不能正好开方,即为无理数,故本选项错误; π
C 、π为无理数,所以 为无理数,故本选项错误;
2
D 、小数为有理数,符合.
5. 【答案】C ;
【解析】
< = 2 .
6. 【答案】A ;
【解析】64 < 100 < 125,
< < 3 125, 4 < < 5 .
二.填空题
7. 【答案】<;
【解析】解:∵4<5<9,
∴2< <3,
∴ ﹣3<0, ﹣2>0,
∴ ﹣3<
5 - 2 . 2
8. 【答案】1± 3 ;
17 76 8 7 3 64
3 3 9 5 5 5 10 3
2 2 【解析】与 1 的距离是 的点在 1 的左右两边各有一个点,分别是1- 、1+ .
9. 【答案】0.
【解析】解: ﹣ =3﹣3=0.
10.【答案】2; 3 - ;
【解析】 2 < 5 - < 3 ,故整数部分为 2, 5 - -2 为小数部分.
11.【答案】 -1, 0, 1;
12. 【答案】 - 3, - 3, 19 - 6 【解析】( 三.解答题
- 3
)
2
= 10 - 6 10 + 9 = 19 - 6 .
13. 【解析】
解:整数集合:{﹣2,0,
,,…};
非负实数集合:
{ 0.2121121112…,…};
, 3
9 ,0, 16
,3.1415,π﹣3, 113
,3+
,3 ,
无理数集合:{ , 3 9
,π﹣3,3+ ,3 ,0.2121121112…,…}.
14.【解析】
解:设广场的边长为 x ,由题意,得
x 2 = 440000
x =
= 200
≈663( m ).
答:它的边长约为 663m. 15.【解析】
解:∵ x - 2+ | x 2 - 3y -13 |= 0,
∴ x -2=0 且 x 2 - 3y -13 =0 解得 x =2, y =-3,
∴
x + y =2-3=-1. 3 3 27 10 10 10 10 3 - 8 144 144 29 3 29 440000
11。
