材料力学作业与答案02(1)
材料力学课后习题答案详细

变形厚的壁厚:
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ,试求 C 与 D 两点间的距离改
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作
轴力图。若横截面面积 A1 200mm2 , A2 300mm2 , A3 400mm2 ,并求各横截 面上的应力。
A1 11.503cm2 1150.3mm2
AE
N EA A
366.86 103 N 2 1150.3mm2
159.5MPa
EG
N EG A
357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ,其横截面面尺寸如图所示。荷载
22
N 22 A2
10 103 N 300mm 2
33.3MPa
3
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
材料力学(金忠谋)第六版答案第02章

材料力学(金忠谋)第六版答案第02章习题2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其弹性模量E??105MPa.如不计柱自重,试求:作轴力图;各段柱横截面上的应力;各段柱的纵向线应变;柱的总变形.解:轴力图AC段应力???100??260????106?a????a CB 段应力?????106?a????a AC段线应变???4N- 图??????10??105CB段线应变????????10?4 5??10 总变形??????10?4???10?4???10?3m 2-2 图(a)所示铆接件,板件的受力情况如图所示.已知:P=7 kN,t=,b1=,b2=,b3=。
试绘板件的轴力图,并计算板内的最大拉应力。
解: 轴力图?1?1???22?73?2??107?1 0?6???a ??2?107?10?6???a ?3? 7?107?10?6???a ??2最大拉应力?max??3???a 2-3 直径为1cm 的圆杆,在拉力P=10 kN的作用下,试求杆内最大剪应力,以及与横截面夹角为?=30o的斜截面上的正应力与剪应力。
解: 最大剪应力?max??2?12?2?107?6??10?10???a 221?d??14 ??30?界面上的应力???????2?1?cos2????3???a 2?sin2???sin30????a ?22-4 图示结构中ABC与CD均为刚性梁,C与D均为铰接,铅垂力P=20kN作用在C铰,若杆的直径d1=1cm,杆的直径d2=2cm,两杆的材料相同,E=200Gpa,其他尺寸如图示,试求两杆的应力;C点的位移。
解1杆的应力?(1)??1?d1244?20??12?107?10?6???a 2杆的应力?(2)?2?1?d2422?20??22?107?10? 6???a ?l1? C点的位移?(1)?l1?200?103?2??10?3m? ?20 0?10?c?2?2??1? ?l2??(2)l2??2??10? 3m? 2-5 某铣床工作台进给油缸如图示,缸内工作油压p?2MPa,油缸内径D=,活塞杆直径d=,已知活塞杆材料的许用应力????50Mpa。
材料力学答案1精编版
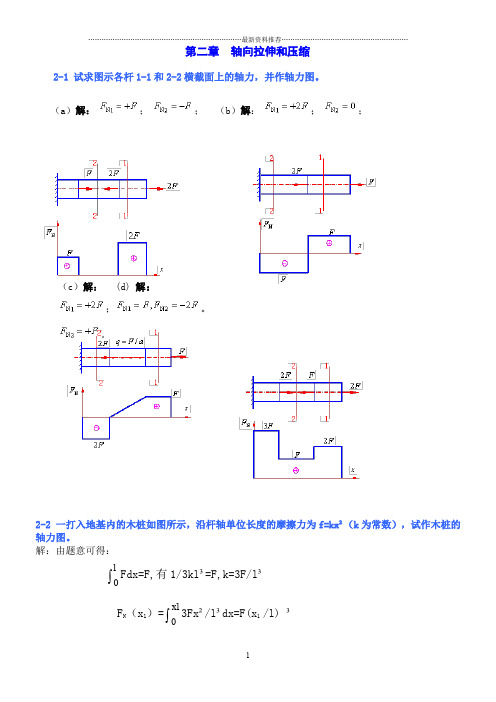
第二章 轴向拉伸和压缩2-1 试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a )解:;; (b )解:;;(c )解: ; 。
(d) 解:。
2-2 一打入地基内的木桩如图所示,沿杆轴单位长度的摩擦力为f=kx ²(k 为常数),试作木桩的轴力图。
解:由题意可得:⎰0lFdx=F,有1/3kl ³=F,k=3F/l ³F N (x 1)=⎰1x 3Fx ²/l ³dx=F(x 1 /l) ³2-3 石砌桥墩的墩身高l=10m ,其横截面面尺寸如图所示。
荷载F=1000KN ,材料的密度ρ=2.35×10³kg/m ³,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积:)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
MPa kPa mkN A N 34.071.33914.9942.31042-≈-=-==σ2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm ×8mm 的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE 和EG 横截面上的应力。
解:=1) 求内力 取I-I 分离体得 (拉)取节点E 为分离体,故(拉)2) 求应力75×8等边角钢的面积 A =11.5 cm 2(拉)(拉)2-5 图示拉杆承受轴向拉力 ,杆的横截面面积 。
如以 表示斜截面与横截面的夹角,试求当 ,30 ,45 ,60 ,90 时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6 一木桩柱受力如图所示。
材料力学题库(含答案)---2

材料力学-——2绪论一、是非题1。
1 材料力学主要研究杆件受力后变形与破坏的规律。
( ) 1。
2 内力只能是力。
( )1。
3 若物体各点均无位移,则该物体必定无变形. ( )1.4 截面法是分析应力的基本方法. ()二、选择题1。
5 构件的强度是指( ),刚度是指( ),稳定性是指(). A。
在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C。
在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设,可认为构件的( )在各点处相同。
A. 应力B。
应变C。
材料的弹性常数D. 位移1.7 下列结论中正确的是( )A。
内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D。
内力必大于应力参考答案:1.1 √ 1。
2 × 1.3 √ 1.4 × 1。
5 C,A,B 1。
6 C 1。
7 C轴向拉压一、选择题1.设杆CD面积为A(A) qρ=(B)(C)(D)2.(A)(C)3. 在A和B和点B(A)0;;(C)45; .4。
可在横梁(刚性杆)为A(拉和压相同)(A) [] 2A σ(C)[]Aσ5。
(A)(C)6. 一种措施?(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) (D ) 增大α角。
7。
图示超静定结构中,梁AB 示杆1的伸长和杆2的缩短,(A ) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C ) 12sin 2sin l l βα∆=∆; (D ) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆(A ) 两杆轴力均减小; (B ) 两杆轴力均增大;(C) 杆1轴力减小,杆2(D ) 杆1轴力增大,杆29. 结构由于温度变化,则:(A ) 静定结构中将引起应力,(B) 静定结构中将引起变形,(C ) (D ) 静定结构中将引起应力和变形10。
(完整版)材料力学试题及答案
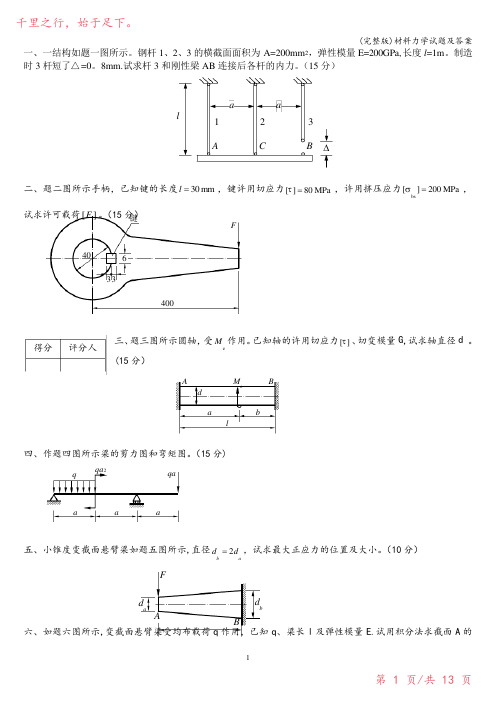
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。
材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩

习题2-1一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量MPa .如不计柱自重,试求:51010.0×=E (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形.解:(1)轴力图(2)AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=(3)AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε(4)总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为1cm 的圆杆,在拉力P =10kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为=30o 的斜截面上的正应力与剪应力。
α解:(1)最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−(2)界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
材料力学练习册答案

第二章 轴向拉伸和压缩2.1 求图示杆11-、22-、及33-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑x F ,得 01=N F22-截面,取右段如)(b由0=∑x F ,得 P F N -=233-截面,取右段如)(c由0=∑x F ,得 03=N F2.2 图示杆件截面为正方形,边长cm a 20=,杆长m l 4=,kN P 10=,比重3/2m kN =γ。
在考虑杆本身自重时,11-和22-截面上的轴力。
解:11-截面,取右段如)(a 由0=∑xF,得kN la F N 08.04/21==γ22-截面,取右段如)(b由0=∑xF,得kN P la F N 24.104/322=+=γ2.3 横截面为210cm 的钢杆如图所示,已知kN P 20=,kN Q 20=。
试作轴力图并求杆的总伸长及杆下端横截面上的正应力。
GPa E 200=钢。
解:轴力图如图。
杆的总伸长:m EA l F l N59102001.0102001.02000022-⨯-=⨯⨯⨯-⨯==∆ 杆下端横截面上的正应力:MPa A F N 20100020000-=-==σ 2.4 两种材料组成的圆杆如图所示,已知直径mm d 40=,杆的总伸长cm l 21026.1-⨯=∆。
试求荷载P 及在P 作用下杆内的最大正应力。
(GPa E 80=铜,GPa E 200=钢)。
解:由∑=∆EAl F l N ,得)104010806.0410********.04(1026.16296294---⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=⨯ππP4/4/4/4/)(a )(b )(c 2N1N )(a kNkN 图NF cm cmcm解得: kN P 7.16= 杆内的最大正应力:MPa A F N 3.13401670042=⨯⨯==πσ 2.5 在作轴向压缩试验时,在试件的某处分别安装两个杆件变形仪,其放大倍数各为1200=A k ,1000=B k ,标距长为cm s 20=,受压后变形仪的读数增量为mm n A 36-=∆,mm n B 10=∆,试求此材料的横向变形系数ν(即泊松比)。
材料力学内部习题集及答案

第二章 轴向拉伸和压缩2-1一圆截面直杆,其直径d =20mm,长L =40m ,材料的弹性模量E =200GPa ,容重γ=80kN/m 3,杆的上端固定,下端作用有拉力F =4KN ,试求此杆的:⑴最大正应力; ⑵最大线应变; ⑶最大切应力;⑷下端处横截面的位移∆。
解:首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 故最大正应力为:N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Addσππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α(α为杆内斜截面与横截面的夹角)为45︒时,maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点,2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为:240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。
已知杆横截面面积为A ,长度为L ,材料的容重为γ。
解:距离A 为x 处的轴力为 所以总伸长2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 2-3图示结构,已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作用,今通过试验测得两杆的纵向线应变分别为ε1=4×10-4,ε2=2×10-4,试确定荷载P 及其方位角θ的大小。
解:由胡克定律得 相应杆上的轴力为取A 节点为研究对象,由力的平衡方程得解上述方程组得2-4图示杆受轴向荷载F 1、F 2作用,且F 1=F 2=F ,已知杆的横截面面积为A ,材料的应力-应变关系为ε=c σn,其中c 、n 为由试验测定的常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、冲床的最大冲力为,被剪钢板的剪切极限应力,冲头材料的[]kN 400MPa 3600=τMPa 440=σ,试求在最大冲力作用下所能冲剪的圆孔的最小直径和板的最大厚度。
min d max
t 解:
[]mm 4.10cm 4.314
.341091.01091.010*********max
max
max 3363
=≤≥==××≥×=××=≥−−τπτπτσd F t dt
F d F
A
二、在厚度mm 5=t 的钢板上,冲出一个形状如图所示的孔,钢板剪切时的剪切极限应力,求冲床所需的冲力。
MPa 3000=τ
解:
kN 771105)
10025014.32(10300)22(6
600=×××+×××=+=≥−t l R A F πττ
三、图示螺钉在拉力作用下。
已知材料的剪切许用应力F []τ和拉伸许用应力[]σ之间的关系为:[][]στ6.0=,试求螺钉直径与钉头高度的合理比值。
d h 解:
[][][][][]
4.26.046.042=×====
σσσπτπσπh d dh dh d F
四、木榫接头如图所示。
mm 120==b a ,mm 350=h ,mm 45=c ,。
试求接头的剪切和挤压应力。
kN 40=F 解:
4MPa
.7MPa 45
0121040c 95MPa .0MPa 45
35010403
bs bs 3
=××====××===h F A F bh F A F στ
五、试作出图示各轴的扭矩图。
六、直径的圆轴,受到扭矩mm 50=D m kN 15.2⋅=T 的作用,试求在距离轴心处的切应力,并求该轴横截面上的最大切应力。
mm 10 解:MPa 6.87MPa 50161015.20MPa .35MPa 50
32101015.236max
46=×××===××××==πτπρτρt p W T I T
m KN ⋅单位:()a ()b m/m KN ⋅:沿轴长均匀分布,单位m
七、设圆轴横截面上的扭矩为T ,试求四分之一截面上内力系的合力的大小、方向及作用点。
解:
4
,159.032434cos 34
sin cos ,sin 2
22
0202020π
ααππρθρθτπρθρθτθ
ττθττπ
π
=====+==×==×=−==∫∫∫∫x y
y x d y d x y x F F tg d
T
d T F F F d T d d F d
T
d d F
d
d F T T F o o F 42.021634,4,00====×πρρρρ具体位置
线上,且垂直于的作用点在故合力
八、T 为圆杆横截面上的扭矩,试画出截面上与T 对应的切应力分布图。
九、阶梯圆轴如图所示。
已知:,mm 501=d mm 752=d ,m 5.01=l ,,,m 75.02=l kNm 2.1=C M kNm 8.1=B M ,。
求:(1)、该轴的扭转角;(2)、最大单位长度扭转角。
GPa 80=G 解: m
/1.40m
/1.40m /4rad 02.0m
/0.69m /rad 0121.022.1rad 02127.0m 0kN .3)(m
kN 2.1C max 1
BC
C 2
AB
1
BC 2AB BC AB B AB o o
o
o −==−=−==−=−==−=−=+=Φ+Φ=Φ⋅−=+−=⋅−=−=B p B p AB p BC
p AB C C BC GI T GI T GI l
T GI l T M M T M T ϕϕϕϕ
十、由厚度mm 8=t 的钢板卷制成的圆筒,平均直径为mm 200=D 。
接缝处用铆钉铆接。
若铆钉直径mm 20=d ,许用切应力[]MPa 60=τ,许用挤压应力[]MPa 160=σ,筒的两端受扭转力偶矩m kN 30⋅=e M 作用,试求铆钉的间距。
s 解:
[][][]挤压强度足够。
挤压强度校核:
160MPa MPa 5.117A 39mm s 39.3mm 0393m .06
.4778.18s 8kN
.18A m
/kN 6.477MPa 7.592max 2max =≤==≤===
==⋅===bs bs Q e dt
t F t
R M στσττπτ。
