材料力学讲解作业
材料力学作业参考题解(2)PPT学习教案

FN1 F gA1x
混凝土柱各段危险截面分别为柱中截 面和柱 底截面 ,其轴 力分别 为:
FN2 F gA1l1 gA2 (x l1)
FN1max F gA1l1
FN 2max F g( A1l1 A2l2 ) (受压)
由强度条件:
FN max [ ]
A
A1
F [ ] gl1
2.242m
m
第7页/共40页
2-12 图示接头,由两块钢板用四个直径相同 的钢铆 钉连接 而成。 已知载 荷F=80kN, 板宽b=80mm, 板厚δ =10mm,铆 钉直径 d =16mm,许 用切应 力[ τ ]=100MPa,许用挤压应力[σbs]=300MPa,许 用拉应 力[σ]=170MPa 。试校核接头的强度。(提示:设 每个铆 钉受力 相同)
FB
220 4 220 8
M B (F ) 0 FAy
12
220kN
M A(F) 0
FB
220 4 220 8 12
220kN
求杆AC和CD的轴力:
由A点的平衡条件:
FNAC
FAy cos45
2 220 311.13kN
(拉 )
由C点的平衡条件:
FNCD FNAC cos45 220kN
:bs : [ ]:[bs ]:[ ] 90: 240:120 3:8: 4
其中:
Fs F
A dh
bs
Fb Abs
(D2
F d2)/4
d 2 (D2
F /d2
1) / 4
FN A
F d 2
/
4
则有:
d3
d
h
4h 4
3
《材料力学》第2章 轴向拉(压)变形 习题解讲解

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
材料力学作业

材料力学作业 Prepared on 22 November 20202-4 木架受力如图所示,已知两立柱横截面均为100m m ×100mm 的正方形。
试求:(1)绘左、右立柱的轴力图;(2)求左、右立柱上、中、下三段内横截面上的正应力。
解:(1)求立柱各节点的受力为了求出ACEG 立柱(左立柱)和BDFH 立柱(右立柱)中的内力和应力,首先对各杆受力进行分析如下图2-4a 所示,并求出数值。
取AB 为研究对象,由平衡方程∑=0)(F m A,0211=⨯'-⨯BF F ①∑=0Y ,01=-'+'F F F B A②联合①和②解得,KN F F B A5='='。
又由牛顿第三定律得,KN F F AA 5='=,KN F FB B 5='=。
同理可得,KN F F CC 9='=,KN F FD D 3='=;KN F FE E 4='=,KNF F F F 12='=。
(2)绘左、右立柱的轴力图取左立柱(ACEG 立柱)为研究对象。
采用截面法,画受力图如图2-4b 所示,求得 )(5KN F N A AC -=-=;)(1495KN F F N C A CE -=--=--=;)(10495KN F F F N E C A EG -=+--=+--=。
同理又取右立柱(BDFH 立柱)为研究对象。
采用截面法求得)(5KN F N B BD -=-=;)(235KN F F N D B BD -=+-=+-=;)(141235KN F F F N F D B FH -=-+-=-+-=。
画轴力图如图左立柱所示和如图右立柱所示。
(3)求左、右立柱上、中、下三段内横截面上的正应力由轴向拉压正计算公式AN=σ应力得,左立柱上、中、下正应力:MPa mm N A N AC 5.010********3-=⨯⨯-==左上σ; MPa mm N A N CE 4.1100100101423-=⨯⨯-==左中σ; MPa mmN A N EG 1100100101023-=⨯⨯-==左下σ。
材料力学课后作业

和弯矩方程绘制剪力图和弯矩图。
32、如图示,设q、a均为己知。求:梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
33、如图示,设q、a均为己知。求:梁的剪力方程和弯矩方程并根据剪力方程
和弯矩方程绘制剪力图和弯矩图。
《材料力学》课后作业
1、试作图示各杆的轴力图。
2、求图示各杆 和 横截面上的轴力,并作轴力图。
答案:
3、 求图示阶梯状直杆横截面 、 和 上的轴力,并作轴力图。如横截面面积 , , ,求各横截面上的应力。
答案:
4、 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个 的等边角钢。已知屋面承受集度为 的竖直均布荷载。求拉杆 和 横截面上的应力。
40、割刀在切割工件时,受到F=1KN的切削力作用,割刀尺寸如图所示,若割刀的许用弯曲正应力〔σ〕=200MPa。试校核割刀的弯曲正应力强度。
答案:σmax=200MPa
41、图示为一承受纯弯曲的铸铁梁,其截面为⊥形,材料的拉伸和压缩许用应力之比
〔σ+〕/〔σ-〕=1/4。求水平翼板的合理宽度b。
答案:b=510mm
答案:σA=σD=-163.5MPaσB=38.8 MPaσC=58.8 MPa
38、矩形截面的悬臂梁受集中力和集中力偶作用,如图所示。试求Ⅰ-Ⅰ截面和固定端Ⅱ-Ⅱ截面上A、B、C、D四点处的正应力。
答案:I-I截面:σA=-7.41MPaσB=4.94MPaσC=0σD=7.41MPa
I-I截面:σA=9.26MPaσB=-6.18MPaσC=0σD=-9.26MPa
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
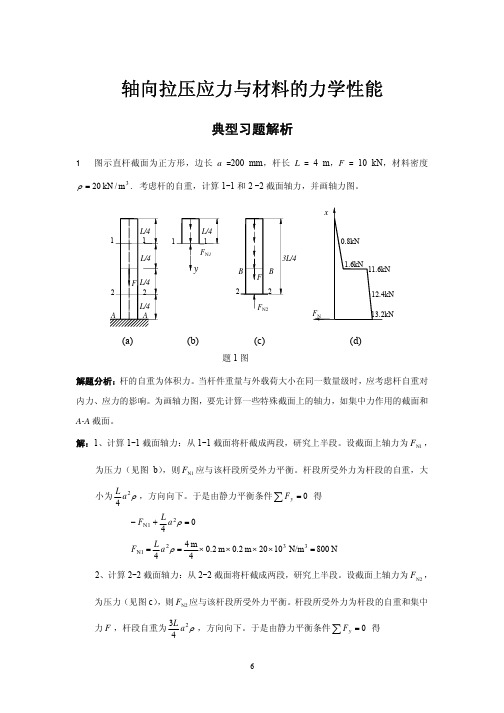
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
材料力学作业(8-11)

第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点,取截面的不同方位,各个面上的( )。
A 、正应力相同,切应力不同;B 、正应力不同,切应力相同;C 、正应力相同,切应力相同;D 、正应力不同,切应力不同。
2、在单元体的主平面上( )。
A 、正应力一定最大;B 、正应力一定为零;C 、切应力一定最小;D 、切应力一定为零。
3、图示矩形截面悬臂梁,A-A 为任意横截面,1点位于截面上边缘,3点位于中性层,则1、2、3点的应力状态单元体分别为( )。
A-AA B C4、图示单元体,其最大主应力为( )A 、σ;B 、2σ;C 、3σ;D 、4σ。
5、下面 单元体表示构件A 点的应力状态。
6、图示单元体,如果MPa 30=ασ,则βσ=( ) A 、100Mpa ; B 、50Mpa ; C 、20MPa ; D 、0MPa 。
(C)7、图示单元体应力状态,沿x 方向的线应变εx 可表示为( )A 、Eyσ; B 、)(1y x E μσσ−;C 、)(1x y E μσσ− ;D 、Gτ。
8、图示应力圆对应于单元体( )。
9、已知单元体及应力圆如图所示,σ1所在主平面的法线方向为( )。
A 、n 1;B 、 n 2;C 、n 3;D 、n4。
二、计算题1、已知应力状态如图所示,试用解析法计算图中指定截面上的正应力和切应力。
2、试画图示应力状态的三向应力圆,并求主应力、最大正应力和最大切应力。
3、边长为20mm的钢立方块置于刚性模中,在顶面受力F=14kN作用。
已知材料的泊松比为0.3,求立方体各个面上的正应力。
4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m,Q=120 kN。
试绘出截面上1、2、3、4各点的应力状态单元体,并求其主应力。
第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下,水管中的水会受冻而结冰。
根据低温下水管和冰所受力情况可知( )。
A 、冰先破裂而水管完好;B 、水管先破裂而冰完好;C 、冰与水管同时破裂;D 、不一定何者先破裂。
材料力学作业题解_第5-9章

1
ρ
于是,有
=
M EI EI
M=
代入弯曲正应力公式,得
ρ
σ max =
Mymax Eymax = I ρ
空心圆截面比实心圆截面最大正应力减少了
5.4 矩形截面悬臂梁如图所示,已知 l = 4 m , 确定此梁横截面的尺寸。 解:梁的最大弯矩发生在固定端处,其值为
b 3 = , q = 10 kN/m , [σ ] = 10 MPa 。试 h 5
q A
l
M max =
梁的强度条件
1 2 1 ql = ×10 × 42 =80 (kN ⋅ m) 2 2 M 80 ×106 = = ≤ [σ ] 1 2 W bh 6
m
n
8
m
22
n
13
发生,应加以比较,方可决定割刀内的最大正应力。 n-n 截面
2.5
4
1 WI = × 2.5 × 132 =70.4 (mm3 ) 6
M I = 1× 103 × 8=8 ×103 (N ⋅ mm)
σI =
n-n 截面
M I 8 ×103 = = 114 (MPa ) WI 70.4
− = σ max
C 截面
+ σ max =
10 × 106 ×158 = 26.3 (MPa)<[σ t ]=40 MPa 60.1× 106 10 × 106 × (230 − 158) = 12 (MPa)<[σ c ]=160 MPa 60.1×106
材料力学作业参考题解(1)

2F
q=F/a
F + FN :
2F
2-2 图示杆件由两根木杆粘接而成。欲使其在受拉时,粘接面上的正应力为其切应力的 倍, 图示杆件由两根木杆粘接而成。欲使其在受拉时,粘接面上的正应力为其切应力的2倍 试问粘接面的位置应如何确定? 试问粘接面的位置应如何确定?
解:本题实质上是要考察斜截面上的应力。由斜截面应力公式,有: 本题实质上是要考察斜截面上的应力。由斜截面应力公式,
2-4图示实心圆钢杆 和AC在A点作用有铅垂向下的力 图示实心圆钢杆AB和 在 点作用有铅垂向下的力 点作用有铅垂向下的力F=35kN。已知杆 和AC的直径分别 图示实心圆钢杆 。 已知杆AB和 的直径分别 点在铅垂方向的位移。 为d1=12mm和d2=15mm,钢的弹性模量 和 ,钢的弹性模量E=210GPa。试求 点在铅垂方向的位移。 。试求A点在铅垂方向的位移 解:求各杆内力,如图取A点为对象,由平衡条件,有: 求各杆内力,如图取 点为对象,由平衡条件, 点为对象
AAB =
F [σ ] sin θ
ABC =
F cosθ [σ ] sin θ
要求结构的总重量为最小即结构总体积最小,其体积为: 要求结构的总重量为最小即结构总体积最小,其体积为:
V = AAB ⋅ l AB + ABC ⋅ l BC =
令:
F l F cosθ Fl 1 cosθ ⋅ + ⋅l = + [σ ] sin θ cosθ [σ ] sin θ [σ ] sin θ cosθ sin θ
取A1=0.664m2 柱底固定,则柱顶位移值等于柱的伸缩量, 柱底固定,则柱顶位移值等于柱的伸缩量,可用叠加原理计算
2 FNi dx Fl1 ρgl12 ( F + ρgA1l1 )l2 ρgl2 ∆ A = ∆l = ∑ ∆li = ∑ ∫ = + + + li EA EA1 2 E EA2 2E i 1000 × 103 ×12 2.25 × 103 × 9.8 × 12 × 12 = + 9 20 × 10 × 0.576 2 × 20 ×109 (1000 + 2.25 × 9.8 × 0.576 × 12) ×103 × 12 2.25 ×103 × 9.8 × 12 ×12 + + = 2.242mm 20 ×109 × 0.664 2 × 20 × 109
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作下图所示梁的剪力图和弯矩图。
2m1m1mm1kN 2kN2kN 2kNA BCD梁分三段,AB 、BC 为空荷载段,CD 段为均布荷载段,均布荷载q=2kN/2m=1kN/m 。
A ,B ,D 三处剪力有突变,说明有集中力作用,在A 截面有向上集中力2kN ,在B 截面有向下集中力2kN ,在D 截面有向上集中力2kN 。
荷载图如图 (b)。
根据荷载图作弯矩图,如图 (c)所示。
如下图所示机构中,1,2两杆的横截面直径分别为cm d 101= ,cm d 202= ,P=10kN 。
横梁ABC ,CD 视为刚体。
求两杆内的应力。
p DCBA122m2m1.5m1m1mCD 杆的D 支座不受力,CD 杆内也不受力,所以p 可视为作用于ABC 杆的C 端。
取ABC 为受力体,受力图如图(b)所示。
MPaMPa A N MPaMPaA N kNN kN N 7.6310204103203.12710104101020210162222623111=⨯⨯⨯⨯===⨯⨯⨯⨯====--πσπσ,如图所示的阶梯形圆轴,直径分别为cm d 41=,cm d 72=。
轮上三个皮带轮,输入功率为kW N 171=,kW N 132=,kW N 303=。
轴的转速为n=200r/min ,材料的许用剪应力[τ]=60MPa 。
试校核其强度。
1计算各轮处的扭转外力偶矩。
mkN m kN m m kN m kN n N m m kN m kN n N m ⋅=⋅⨯=⋅=⋅⨯=⋅=⋅⨯==433.12003055.9621.02001355.9255.9812.02001755.9155.9321 (c)(b)kN m 31图3 传动轴可简化为图3(b),⑦扭矩图如图3(c)。
AD 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TAD 6.64104168126311max BC 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TBC 3.211071614326322max AD 段的单位长度扭转角为[]θπθ>=⨯⨯⨯⨯⨯⨯==-m m GI M p TAD /1.23/104108018032812842911οοBC 段的单位长度扭转角为[]θπθ<=⨯⨯⨯⨯⨯⨯==-m m GIp MINC/44.0/1074108018032143222829οο由此可知轴的强度与刚度都不够。
如图8所示的结构,由Q235刚制成,[σ] =160MPa ,斜撑杆外径D=45mm ,内径d=36mm ,3=st n ,斜撑杆的1001=λ,6.612=λ,中长柱的MPa cr )12.1304(λσ-=,试由压杆的稳定计算,确定结构的许用载荷[P]。
利用平衡关系,确定斜撑杆BD 的压力与P 的关系,即P N P N M BD o BD A 2202145sin 0==⨯-⨯=∑,,由于杆长m l 414.1=,惯性半径mm D d D i 41.14142=⎪⎭⎫⎝⎛+=,长度系数1=μ,所以 9801441.0414.11=⨯==ilμλ因为12λλλ≤≤,故BD 属于中长杆。
()()kNN d D A P MPaMPa b a cr cr cr cr 11110)3645(410619441949812.130462222=⨯-⨯⨯⨯=-===⨯-=-=-ππσσλσ 代入稳定安全系数计算式,有BDcrst N P n =即 []kN kN n P P stcr 1332211122=⨯==作图 6所示梁的剪力图和弯矩图。
图6求支反力:qa R qa R D A 4741==, qa R Q A A 41== AB 段内无荷载,为水平线,B 点集中力偶矩对剪力无影响,因此BC 段剪力都为水平,且4qaR Q BC BA ==。
CD 段内剪力为斜直线,截距为qa 2。
D 处剪力有突变,大小为D R 。
AB 段空载荷,弯矩图为斜直线。
但B 处有集中力偶作用,弯矩有突变,应分左、右两个截面计算。
在截面24a q a R M A BA ==,右截面2245qa qa a R M A Bc =+=。
图1BC 段,弯矩图应是斜直线。
CD CB M qa M ==223,即连接BC M 及CB M 。
CD 段为二次抛物线,但该段有0=Q 的点——E 点,离C 截面距离为a q Q CD 41/=,23249qa M E =。
连接C ,E ,D 的弯矩值(用下半圆曲线)。
可得弯矩图。
直径相同的铸铁圆截面直杆,可设计成图 7中(a )、(b )两种结构的形式,问哪种结构所承受的载荷P 大?大多少?pAA图7由于杆件材料、截面形状相同,并且为铸铁,属于脆性材料,抗压性能优于抗拉性能,因此比较两种结构的拉应力与P 的关系。
图2(a)中的AC 杆受拉,取A 点为受力体,受力图如图2(c)。
()t b σ为拉伸的强度极限。
令12)(P A N t b AC ==σ,则 ()21AP t b σ=图(b)中AB 杆受拉,取A 点为受力体,受力体如图2(d)。
令()32P A N t b AB ==σ,()A P t b σ32=,所以12P P 〉,即图(b)承受载荷P 大。
又()()323212==A AP P t b t b σσ所以图(b)承受的荷载P 是图(a)承受的荷载P 的32倍。
图23、简支梁承受均布载荷作用,如图8 所示。
若采用两种截面面积相等的实心和空心圆截面,D1=40mm, α=d2/D2=3/5。
试分别计算其最大的正应力,空心截面比实心截面的最大正应力减小了百分之几?图8图3 (1)几何尺寸。
依题意两种截面面积相等,即)1(4)(44222222221απππ-=-=D d D D所以 mm mm D D 505314012212=⎪⎭⎫ ⎝⎛-=-=αmm D d 305322==(2)最大正应力。
因简支梁受均布载荷作用,故最大弯矩: m kN m N ql M ⋅=⋅⨯⨯==182)102(8232max 实心截面3231D W z π= ()MPa Pa W M z 15904.01013233max max =⨯⨯==πσ 空心截面[]432'132απ-=D W z()MPa Pa W Mz6.93)531(05.010132433max 'max=⎥⎦⎤⎢⎣⎡-⨯⨯==πσ最大正应力发生在梁中间截面的上、下边缘。
(3)最大正应力的比较。
空心截面比实心截面的最大正应力减小了%1.411596.93159max 'max max =-=-σσσ图9所示结构,AB 为工字截面梁,其横梁面面积为22610mm A =,抗弯截面模量为3310141mm W z ⨯=。
已知AB 、CD 杆材料相同,其中E=160GPa ,稳定安全系数5.2=stn ,1001=λ,校核结构是否安全。
图9AB 、CD 杆的内力和变形形式:AB 杆承受拉弯变形,m kN M kN N AB ⋅==215210max , CD 杆位压杆,kN N CB 220=所以,结构的安全性包括AB 杆的强度问题和CD 杆压杆的稳定性。
(1) AB 梁的强度问题:[]σσ<=⎪⎪⎭⎫⎝⎛⨯⨯+⨯⨯=+=--MPa Pa W M A N 1561014110215101.2610210max 6343max 故AB 梁的强度足够。
(2) CD 杆压杆的稳定性113303.0411λμλ>=⨯⨯==il故CD 杆为细长杆。
()kN N l EI P cr 5.78)11(6403.010320024222=⨯⨯⨯⨯⨯⨯==ππμπ 工作安全系数5.277.23.285.78>===CD cr w N P n 故CD 杆的稳定性也满足要求。
所以,整个结构是安全的。
三根圆截面压杆,直径均为d=160mm ,材料为A3钢(E=206Gpa, 240s Mpa σ=,200p Mpa σ=,304, 1.12a Mpa b Mpa ==),三杆两端均为铰支,长度分别为123,,l l l ,且123245l l l m ===。
试求各杆的临界压力。
1μ=,三根杆的柔度分别为:可见:1杆适用欧拉公式,2杆适用经验公式,3杆适用强度公式。
1125l i μλ'==262.5l i μλ''==331.25li μλ'''==1100λ==257sa bσλ-==()2211225364cr cr E d F A KN ππσλ==='222()47104cr cr d F A a b KN πσλ''==-=一铸铁圆柱的直径为40mm ,其一端固定,另一端受到315 N.m 的力偶矩作用。
若该铸铁材料的许用拉应力为MPa t 30][=σ,试根据强度理论对圆柱进行强度校核。
解:圆柱表面的切应力最大,即:Mpa d T W T t 25)16//(/3max max max ===πτ圆柱表面首先破坏,其上任一点的应力状态为纯剪切,见图3。
进行应力分析可得:MPa 252520020022min max ±=+⎪⎭⎫ ⎝⎛-±+=⎭⎬⎫σσ∴ MPa 251=σ,02=σ, MPa 253-=σ由第一强度理论有:[]t MPa σσ≤=251, 满足强度条件。
悬背梁之某处收到支撑,如图(a )所示。
悬臂梁在集中载荷作用下的挠曲线方23348234cr cr sd F A KNπσσ===25MPa图3铸铁压力机框架,立柱横截面尺寸如图所示,材料的许用拉应力[σt ]=30MPa ,许用压应力[σc ]=120MPa 。
试按立柱的强度计算许可载荷F 。
已知, , 。
y ym m750=z 47mm 1031.5⨯=y I 33EIEI F F By 47=(1)立柱横截面的内力(2)立柱横截面的最大应力(3)求压力FF350NFM()Pa 66710151031.5075.0104253530max .F FF AF I Mz Ny t =⨯+⨯⨯⨯=+=---σFF N =()()N.m 10425107535033--⨯=⨯+=F F M ()Pa 93410151031.5125.0104253531max .F FF AF I Mz Ny c =⨯-⨯⨯⨯=-=---σ[]t t F σσ≤=667max .[]N4500066710306676=⨯=≤t F σ许可压力为:某传动轴设计要求转速n = 500 r / min,输入功率N1 = 500马力,输出功率分别N2 = 200马力及N3 = 300马力,已知:G=80GPa ,[τ]=70M Pa,[θ]=1º/m ,试确定:①AB 段直径d1和BC 段直径d2?②若全轴选同一直径,应为多少?③主动轮与从动轮如何安排合理?解:(1)计算外力偶矩据扭转强度条件:,,[]ccFσσ≤=934max.[]N128500934101209346=⨯=≤cFσ45000N45kNF≤=500400N1N3N2A CB7024(N m)Nmn=⋅max max[]tT Wττ=≤316tW dπ=T– 4.21(kNm)可得:由扭转刚度条件:可得:综上所述,可取:(2) 当全轴取同一直径时,(3) 轴上扭矩的绝对值的越小越合理,所以,1轮和2轮应该换位。
