【最新】KNN分类算法PPT 课件教案讲义(获奖作品) 图文
机器学习—分类3-1(KNN算法)

机器学习—分类3-1(KNN算法)基于KNN预测客户是否购买汽车新车型主要步骤流程:1. 导⼊包2. 导⼊数据集3. 数据预处理3.1 检测缺失值3.2 ⽣成⾃变量和因变量3.3 查看样本是否均衡3.4 将数据拆分成训练集和测试集3.5 特征缩放4. 使⽤不同的参数构建KNN模型4.1 模型1:构建KNN模型并训练模型4.1.1 构建KNN模型并训练4.1.2 预测测试集4.1.3 ⽣成混淆矩阵4.1.4 可视化测试集的预测结果4.1.5 评估模型性能4.2 模型2:构建KNN模型并训练模型数据集链接:1. 导⼊包In [2]:# 导⼊包import numpy as npimport pandas as pdimport matplotlib.pyplot as plt2. 导⼊数据集In [3]:# 导⼊数据集dataset = pd.read_csv('Social_Network_Ads.csv')datasetOut[3]:User ID Gender Age EstimatedSalary Purchased015624510Male19190000115810944Male35200000215668575Female26430000315603246Female27570000415804002Male19760000..................39515691863Female4641000139615706071Male5123000139715654296Female5020000139815755018Male3633000039915594041Female49360001400 rows × 5 columns3. 数据预处理3.1 检测缺失值In [4]:# 检测缺失值null_df = dataset.isnull().sum()null_dfOut[4]:User ID 0Gender 0Age 0EstimatedSalary 0Purchased 0dtype: int643.2 ⽣成⾃变量和因变量为了可视化分类效果,仅选取 Age 和 EstimatedSalary 这2个字段作为⾃变量In [5]:# ⽣成⾃变量和因变量X = dataset.iloc[:, [2, 3]].valuesX[:5, :]Out[5]:array([[ 19, 19000],[ 35, 20000],[ 26, 43000],[ 27, 57000],[ 19, 76000]], dtype=int64)In [6]:y = dataset.iloc[:, 4].valuesy[:5]Out[6]:array([0, 0, 0, 0, 0], dtype=int64)3.3 查看样本是否均衡In [7]:# 查看样本是否均衡sample_0 = sum(dataset['Purchased']==0)sample_1 = sum(dataset['Purchased']==1)print('不买车的样本占总样本的%.2f' %(sample_0/(sample_0 + sample_1)))不买车的样本占总样本的0.643.4 将数据拆分成训练集和测试集In [8]:# 将数据拆分成训练集和测试集from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0) print(X_train.shape)print(X_test.shape)print(y_train.shape)print(y_test.shape)(300, 2)(100, 2)(300,)(100,)3.5 特征缩放In [9]:# 特征缩放from sklearn.preprocessing import StandardScalersc = StandardScaler()X_train = sc.fit_transform(X_train)X_test = sc.transform(X_test)4. 使⽤不同的参数构建KNN模型4.1 模型1:构建KNN模型并训练模型4.1.1 构建KNN模型并训练In [10]:# 使⽤不同的参数构建KNN模型# 模型1:构建KNN模型并训练模型(n_neighbors = 5, weights='uniform', metric = 'minkowski', p = 2)from sklearn.neighbors import KNeighborsClassifierclassifier = KNeighborsClassifier(n_neighbors = 5, weights='uniform', metric = 'minkowski', p = 2) classifier.fit(X_train, y_train)Out[10]:KNeighborsClassifier()4.1.2 预测测试集In [11]:# 预测测试集y_pred = classifier.predict(X_test)y_pred[:5]Out[11]:array([0, 0, 0, 0, 0], dtype=int64)4.1.3 ⽣成混淆矩阵In [12]:# ⽣成混淆矩阵from sklearn.metrics import confusion_matrixcm = confusion_matrix(y_test, y_pred)print(cm)[[64 4][ 3 29]]4.1.4 可视化测试集的预测结果In [13]:# 可视化测试集的预测结果from matplotlib.colors import ListedColormapplt.figure()X_set, y_set = X_test, y_testX1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),alpha = 0.75, cmap = ListedColormap(('pink', 'limegreen')))plt.xlim(X1.min(), X1.max())plt.ylim(X2.min(), X2.max())for i, j in enumerate([0,1]):print(str(i)+"da"+str(j))plt.scatter(X_set[y_set == j, 0], X_set[y_set == j,1],color = ListedColormap(('red', 'green'))(i), label = j)plt.title('KNN (Test set)')plt.xlabel('Age')plt.ylabel('Estimated Salary')plt.legend()plt.show()0da01da1In [14]:X_set[y_set == 0,1]Out[14]:array([ 0.50496393, -0.5677824 , 0.1570462 , 0.27301877, -0.5677824 ,-1.43757673, -1.58254245, -0.04590581, -0.77073441, -0.59677555,-0.42281668, -0.42281668, 0.21503249, 0.47597078, 1.37475825,0.21503249, 0.44697764, -1.37959044, -0.65476184, -0.53878926,-1.20563157, 0.50496393, 0.30201192, -0.21986468, 0.47597078,0.53395707, -0.48080297, -0.33583725, -0.50979612, 0.33100506,-0.77073441, -1.03167271, 0.53395707, -0.50979612, 0.41798449,-1.43757673, -0.33583725, 0.30201192, -1.14764529, -1.29261101,-0.3648304 , 1.31677196, 0.38899135, 0.30201192, -1.43757673,-1.49556302, 0.18603934, -1.26361786, 0.56295021, -0.33583725,-0.65476184, 0.01208048, 0.21503249, -0.19087153, 0.56295021,0.35999821, 0.27301877, -0.27785096, 0.38899135, -0.42281668,-1.00267957, 0.1570462 , -0.27785096, -0.16187839, -0.62576869,-1.06066585, 0.41798449, -0.19087153])In [15]:np.unique(y_set)Out[15]:array([0, 1], dtype=int64)4.1.5 评估模型性能In [16]:# 评估模型性能from sklearn.metrics import accuracy_scoreprint(accuracy_score(y_test, y_pred))0.93In [17]:(cm[0][0]+cm[1][1])/(cm[0][0]+cm[0][1]+cm[1][0]+cm[1][1])Out[17]:0.934.2 模型2:构建KNN模型并训练模型In [1]:# 模型2:构建KNN模型并训练模型(n_neighbors = 3, weights='distance', metric = 'minkowski', p = 1)classifier = KNeighborsClassifier(n_neighbors = 100, weights='distance', metric = 'minkowski', p = 1) classifier.fit(X_train, y_train)In [19]:# 预测测试集y_pred = classifier.predict(X_test)y_pred[:5]Out[19]:array([0, 0, 0, 0, 0], dtype=int64)In [20]:# ⽣成混淆矩阵cm = confusion_matrix(y_test, y_pred)print(cm)[[63 5][ 4 28]]In [21]:# 可视化测试集的预测结果plt.figure()X_set, y_set = X_test, y_testX1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01), np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),alpha = 0.75, cmap = ListedColormap(('pink', 'limegreen')))plt.xlim(X1.min(), X1.max())plt.ylim(X2.min(), X2.max())for i, j in enumerate(np.unique(y_set)):plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],color = ListedColormap(('red', 'green'))(i), label = j)plt.title('KNN (Test set)')plt.xlabel('Age')plt.ylabel('Estimated Salary')plt.legend()plt.show()In [22]:# 评估模型性能print(accuracy_score(y_test, y_pred))0.91结论:1)由上⾯2个模型可见,不同超参数对KNN模型的性能影响不同。
knn 算法
一、介绍KNN(K- Nearest Neighbor)法即K最邻近法,最初由 Cover 和Hart于1968年提出,是最简单的机器学习算法之一,属于有监督学习中的分类算法。
算法思路简单直观:分类问题:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN是分类算法。
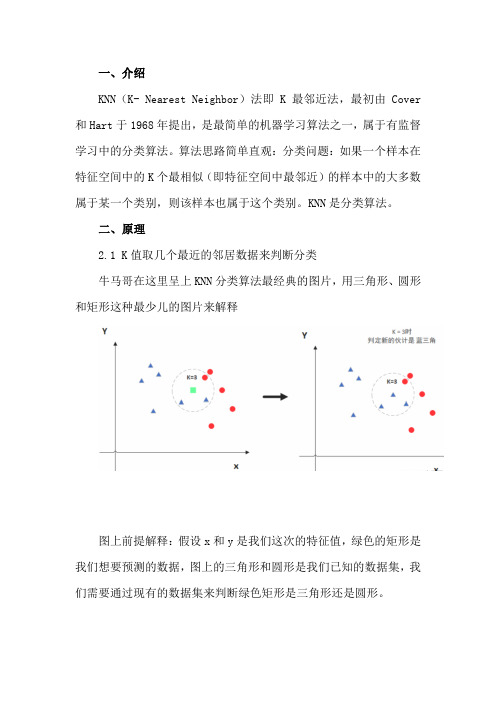
二、原理2.1 K值取几个最近的邻居数据来判断分类牛马哥在这里呈上KNN分类算法最经典的图片,用三角形、圆形和矩形这种最少儿的图片来解释图上前提解释:假设x和y是我们这次的特征值,绿色的矩形是我们想要预测的数据,图上的三角形和圆形是我们已知的数据集,我们需要通过现有的数据集来判断绿色矩形是三角形还是圆形。
当K = 3,代表选择离绿色矩形最近的三个数据,发现三个数据中三角形比较多,所以矩形被分类为三角形当K = 5,代表选择离绿色矩形最近的三个数据,发现五个数据中圆形最多,所以矩形被分类为圆形所以K值很关键,同时建议k值选取奇数。
2.2 距离问题在上面的原理中还有一个关键问题,就是怎么判断距离是否最近。
在这里采用的是欧式距离计算法:下图是在二维的平面来计算的,可以当作是有两个特征值那如果遇到多特征值的时候,KNN算法也是用欧式距离,公式如下:从这里就能看出KNN的问题了,需要大量的存储空间来存放数据,在高维度(很多特征值输入)使用距离的度量算法,电脑得炸哈哈,就是极其影响性能(维数灾难)。
而且如果要预测的样本数据偏离,会导致分类失败。
优点也是有的,如数据没有假设,准确度高,对异常点不敏感;理论成熟,思想简单。
三.KNN特点KNN是一种非参的,惰性的算法模型。
什么是非参,什么是惰性呢?非参的意思并不是说这个算法不需要参数,而是意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。
也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
K近邻算法PPT课件

• 包含目标点的叶结点对应包含目标点的最小超矩形区域。以此叶 结点的实例点作为当前最近点。目标点的最近邻一定在以目标点 为中心并通过当前最近点的超球体内部。然后返回当前结点的父 结点,如果父结点的另一子结点的超矩形区域与超球体相交,那 么在相交的区域内寻找与目标点更近的实例点。如果存在这样的 点,将此点作为新的当前最近点。
➢ 问题:给这个绿色的圆分类? ➢ 如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝
色小正方形,少数从属于多数,基于统计的方法,判定绿色的这 个待分类点属于红色的三角形一类。 ➢ 如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色 正方形,还是少数从属于多数,基于统计的方法,判定绿色的这 个待分类点属于蓝色的正方形一类。
区域内没有实例时终止。在此过程中,将实例保存在相应的结点
上。
2020/7/23
9
K近邻法的实现:kd树
2020/7/23
10
K近邻法的实现:kd树
2020/7/23
11
K近邻法的实现:kd树
➢ 搜索kd树
• 利用kd树可以省去大部分数据点的搜索,从而减少搜索的计算量 。这里以最近邻为例,同样的方法可以应用到K近邻。
2020/7/23
5
K近邻的三个基本要素
2020/7/23
6
K近邻的三个基本要素
➢ K值的选择
• 如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预 测, “学习”的近似误差会减小,只有与输入实例较近的训练实 例才会对预测结果起作用。但缺点是“学习”的估计误差会增大 ,预测结果会对近邻的实例点非常敏感。换句话说,k值的减小意 味着整体模型变得复杂,容易发生过拟合。
knn算法

KNN算法缺点
• 算法的复杂度高 • 该算法在分类时有个主要的不足是,当样本不平衡时,如 一个类的样本容量很大,而其他类样本容量很小时,有可 能导致当输入一个新样本时,该样本的K个邻居中大容量 类的样本占多数。
KNห้องสมุดไป่ตู้改进算法
应用场景
• 文本分类:文本分类主要应用于信息检索, 机器翻译,自动文摘,信息过滤,邮件分 类等任务。 • 回归:通过找出一个样本的k个最近邻居, 将这些邻居的属性的平均值赋给该样本, 就可以得到该样本的属性。 • 可以使用knn算法做到比较通用的现有用户 产品推荐,基于用户的最近邻(长得最像的 用户)买了什么产品来推荐是种介于电子商 务网站和sns网站之间的精确营销。
最近邻规则分类(K-Nearest Neighbor)KNN算法
孟凯 张鑫
简介与来历
• 邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分 类算法是数据挖掘分类技术中最简单的方法之一。所谓K 最近邻,就是k个最近的邻居的意思,说的是每个样本都 可以用它最接近的k个邻居来代表。 • KNN算法是对NN(nearest neighbor )算法即近邻算法 的 改 进 , 最 初 的 近 邻 算 法 是 由 T. M . C o v e r , 在 其 文 章” Rates of Convergence for Nearest Neighbor Procedures, ”中提出的,是以全部训练样本作为带标点, 计算测试样本与所有样本的距离并以最近邻者的类别作为 决策,后学者们对近邻算法进行了各方面的改进。
KNN距离函数
KNN算法步骤
• • • • 选择参数K 计算未知实例与已知实例的距离 选择最近K个实例 根据少数服从多数的投票法则,让位置实 例归类为K个最近邻样本中最多数的类别
第12.1章 k-Means聚类算法【本科研究生通用机器学习课程精品PPT系列】

4 小结 本章详细地介绍了K-means算法的基本概念、基本原理,并介绍了该算法的
特点和存在的缺陷,最后介绍了K-means算法的应用,从中可以看出K-means算法 的应用非常广泛。
k-均值算法 (k-Means)
其中p表示簇中的点,X是簇内点的集合,distance(p, centroid)即点p到簇质心的距离
聚类结果的SSE即各个簇的SSE之和,其值越小表示聚类 质量越好
主要内容
K-Means聚类算法 k-均值算法的改进 K-中心点聚类算法
考虑改对如进下学1生: 兴归趣数一据进化行聚类
学生编号 喜欢吃零食 喜欢看韩剧
A
8
B
7
C
8
D
8
E
0
F
0
G
1
H
2
喜欢打篮球 喜欢玩游戏 工资
8
0
0 5000
8
0
1 5100
7
0
1 5080
8
1
0 5030
0
10
8 5010
2
9
8 5090
2
9
9 5020
1
8
9 5040
结果被“工资”主导了!
改进1: 归一化
为什么结果被“工资”主导了?
解决方案: 归一化
例如x2,y2的差值很大, 而x1,y1等差异很小, 则计算得到的欧氏距离几乎
图: 4个簇及其质心
k-均值算法 (k-Means)
指定 k = 3 (即要将数据点分成3组)
1. 随机挑选3个点作为初始簇质心(centroid)
K-means算法讲解ppt课件

预测:预测是通过分类或估值起作用的,也就是说,通过 分类或估值得出模型,该模型用于对未知变量的预言。
聚类:在没有给定划分类的情况下,根据信息相似度将信 息分组。是一种无指导的学习。
关联规则:揭示数据之间的相互关系,而这种关系没有在 数据中直接表现出来。
偏差检测: 用于发现与正常情况不同的异常和变化。并分 析这种变化是有意的欺诈行为还是正常的变化。如果是异常 行为就采取预防措施。
完整最新ppt
13
决定性因素
Input & centroids
①数据的采集和抽象 ②初始的中心选择
Selected k
① k值的选定
MaxIterations & Convergence
①最大迭代次数 ②收敛值
factors?
Meassures
①度量距离的手段
完整最新ppt
14
主要因素
初始中 心点
Repeat 从簇表中取出一个簇
(对选定的簇进行多次二分实验) for i=1 to实验次数 do 试用基本K均值(k=2),二分选定的簇 end for 从实验中选取总SSE最小的两个簇添加到簇表中
Until 簇表中包含K个簇
17
谢谢!
完整最新ppt
18
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
6
什么是Kmeans算法?
Q1:K是什么?A1:k是聚类算法当中类的个数。 Q2:means是什么?A2:means是均值算法。
Summary:Kmeans是用均值算法把数 据分成K个类的算法!
完整最新ppt
7
Kmeans算法详解(1)
K-近邻算法PPT课件

.
19
示例:使用k-近邻算法
改进约会网站的配对结果
1.问题描述: 我都朋友佩琪一直使用在线约会网站寻找适 合自己的约会对象。尽管约会网站会推荐不 同的人选,但是她并不是喜欢每一个人。经 过一番总结,她发现曾交往过三种类型的人:
不喜欢的人 魅力一般的人 极具魅力的人
.
20
示例:使用k-近邻算法
改进约会网站的配对结果
(3)分析数据:可以使用任何方法。 (4)测试算法:计算错误率。 (5)使用算法:首先需要输入样本数据和结构化的输 出结果,然后运行k-近邻算法判定输入数据属于哪个分 类,最后应用对计算出的分类执行后续的处理。
.
10
准备:使用Python导入数据
1.创建名为kNN.py的Python模块
注:接下来所有的代码均保存于这个文件夹中,读者可以按照自己的习 惯在自己创建的文件夹中编写代码,也可以去网上查找源代码,但笔者 建议读者按照本PPT的顺序去创建模块并编写代码。
.
15
实施kNN分类算法
(2)以下为kNN近邻算法代码,将其保存于kNN.py中 def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0] diffMat = tile(inX, (dataSetSize,1)) - dataSet sqDiffMat = diffMat**2 sqDistances = sqDiffMat.sum(axis = 1) distances = sqDistances**0.5 sortedDistIndicies = distances.argsort() classCount = {} for i in range(k):
机器学习knn分类算法精品PPT课件

v 概述 v 算法流程 v K值选择 v 实例
Computer science and technology
10
实例
Example
约会网站信息查找
K
K-近邻 k-Nearest Neighbor classification
v 概述 v 算法流程 v K值选择 v 实例
Computer science and technology
Algorithm of ma1chi1n0e0l0e.a1rnin1g25.0 无 棕色 红尾鸳
2 3000.7 200.0 无 灰色 鹭鹰
v 关键术语 v 机器学习主要任务 3 3300.0 220.3 无 灰色 鹭鹰
v 十大算法
4 4100.0 136.0 有 黑色 普通潜鸟
训练集 训练样本 特征 目标变量 测试样本
02
M
机器学习十大算法
Algorithm of machine learning
K
S
v 关键术语 v 机器学习主要任务 v 十大算法
Computer science and technology
03
关键术语
Key Words
M
体重 翼展 脚 后背 种属 机器学习十大算法(g) (cm) 蹼 颜色
Computer science and technology
04
机器学习主要任务
Main Task
M
机器学习十大机算器法学习主要任务是如何解决分类问题——将数据划分
Algorithm of 到另m合外ac适还hi的有ne分项l类任ea中务rn。是in回g归——预测数值型数据,一个典型
常见的例子是数据拟合曲线:通过给定数据点最优拟合
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法基本介绍
• k近邻的非正式描述,就是给定一个样本集 exset,样本数为M,每个样本点是N维向量, 对于给定目标点d,d也为N维向量,要从 exset中找出与d距离最近的k个点(k<=N), 当k=1时,knn问题就变成了最近邻问题。 最原始的方法就是求出exset中所有样本与d 的距离,进行按出小到大排序,取前k个即 为所求,但这样的复杂度为O(N),当样本 数大时,效率非常低下.
算法描述
• 该算法的基本思路是:在给定新文本后,考虑在训练文本 集中与该新文本距离最近(最相似)的 K 篇文本,根据这 K 篇文本所属的类别判定新文本所属的类别 • 右图中,绿色圆要被决定赋予哪个类, 是红色三角形还是蓝色四方形?如果 K=3,由于红色三角形所占比例为2/3, 绿色圆将被赋予红色三角形那个类, 如果K=5,由于蓝色四方形比例为3/5, 因此绿色圆被赋予蓝色四方形类。
算法描述
• 算法分为以下几步:
一、:根据特征项集合重新描述训练文本向量 二、:在新文本到达后,根据特征词分词新文本, 确定新文本的向量表示 三、:在训练文本集中选出与新文本最相似的 K 个文本,计算公式为:
算法描述
• 其中,K 值的确定目前没有很好的方法,一般采用先定一 个初始值,然后根据实验测试的结果调整 K 值,一般初始 值定为几百到几千之间。(这里K采取随机取值) • 四、:在新文本的 K 个邻居中,依次计算每类的权重,计 算公式如下:
• 其中, x为新文本的特征向量, Sim(x,di)为相似度计算公 式,与上一步骤的计算公式相同,而y(di,Cj)为类别属性函 数,即如果di 属于类Cj ,那么函数值为 1,否则为 0。 • 五、:比较类的权重,将文本分到权重最大的那个类别中。
运行结果
• 训练及测试样例
【原创】定制代写 r/python/spss/matlab/WEKA/s as/sql/C++/stata/eviews 数据 挖掘和统计分析可视化调研报 告等服务(附代码数据),咨 询邮箱: glttom@ 有问题到 淘宝找“大数据部落”
