电工学C_唐介主编3版少学时_作业习题答案光信101-3
电工学试题(少学时)唐介
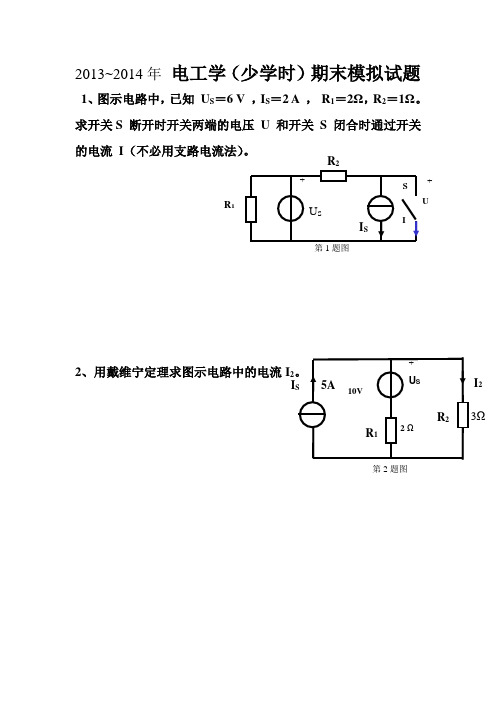
2013~2014年 电工学(少学时)期末模拟试题1、图示电路中,已知 U S =6 V ,I S =2 A , R 1=2Ω,R 2=1Ω。
求开关S 断开时开关两端的电压 U 和开关 S 闭合时通过开关的电流 I (不必用支路电流法)。
第1题图2、用戴维宁定理求图示电路中的电流I 2。
第2题图U S+ _I SR 1R 2U + _ISI S10V2 Ω5AR 2I 2R 1U S + _3Ω3、用叠加原理求图示电路中的电流 I 。
第3题图4、如图所示电路中,已知R=2Ω,Z 1=-j10Ω、Z 2=(40+j30)Ω,=∙I A 305∠。
求21∙∙I I 、和∙U 。
第4题图I S35 V2Ω7 AR 2 IR 1U S+ _1ΩR 3 3ΩR 4 4Ω5、在如图所示三相电路中,R=X C=X L=25Ω,接于线电压为220 V 的对称三相电源上,求各相线中的电流。
iL3第5题图6、图所示为一加减混合运算电路,已知R1= R2 = R3 = R4,R5 =R f。
求此电路的输出电压u o的表达式。
L1L2 L3IL1IL2IL3R-jX CjX i L1·i L2·I1·I2·I37、已知共集放大电路的R B = 75 kΩ,R E = 1 kΩ,R L = 1 k Ω,U CC = 12 V ,硅晶体管的β= 50 ,信号源的内阻R S可忽略不计,试对该电路进行静态和动态分析。
8、试用与非门实现一个三人表决机。
当两人或两人以上同意时方案通过,否则,不通过。
电工学少学时第三版_张南主编_课后练习答案_第一章(末)

电工学少学时第三版_张南主编_课后练习答案_第一章(末)上篇: 电工技术第一章: 电路分析基础1.1: 电路的基本概念、定律、分析方法(1) 正确理解电压、电流正方向的意义。
(2) 在正确理解电位意义的基础上,求解电路各点电位。
(3) 加强电压源的概念,建立电流源的概念。
(4) 了解电路有载工作、开路与短路的状态,强化额定值概念。
(5) 熟悉电路基本定律并能正确应用之。
(6) 学会分析、计算电路的基本方法基本内容1 电压、电流的正方向在分析计算电路之前,首先在电路图上标注各元件的未知电流和电压的正方向(这些假设的方向,又名参考方向),如图1-1-1所示。
图1-1-1根据这些正方向,应用电路的定理、定律列写方程(方程组),求解后若为正值..,说明假设的方向与实际的方向相同;求解后若为负值..,说明假设的方向与实际方向相反。
对于电路中的某个(些)已知的方向,有两种可能,其一是实际的方向,其二也是正方向,这要看题目本身的说明。
2 电路中的电位计算求解电路某点的电位,必须首先确定参考点,令该点电位为零,记为“⊥”,电路其余各点与之比较,高者为正(电位),低者为负(电位),如图1-1-2所示:图 1-1-2设C为参考点,则:c点的电位:V C=0(V)a点的电位:V a= +6 (V)b点的电位:V b =-9 (V)ab两点间的电压:U ab = V a- V b = (+6)-(-9) =15(V)注·电位具有单值性(参考点一旦设定,某点的电位是唯一的)。
·电位具有相对性(参考点选择不同,某点的电位也不同)。
·任意两点间的电位差叫电压,例如U ab = V a- V b,显然电压具有单值性和绝对性(与参考点选择无关)1 欧姆定律(1)一段无源支路(元件)的欧姆定律。
在图1-1-3中,U ab= R·I(取关联正方向)。
(2)一段有源支路(元件)的欧姆定律,实际上是电压降准则,如图1-1-4所示。
2013电工学(少学时)唐介主编第二章答案

三、练习题解答2.2.1 在图2.4所示稳态宜流屯路中•已知人=2A, (/s=2 V.加2(2, C= 2 pF. L=2 inH・求R. C和乙的电流和电压。
【解】木题U的是为了复习电容和电感在稳态直流电路屮的作用。
由『冇稳态fl流电路中.C柑为于开路•/•柑》干短路.因此fr图不参考方向下人=人=2 AU R=R*=*2 V = 4 Vl c - 0^c=^s=2V/£ = /s = 2 A以02.2.2 在图2.5所示稳态亢流电路中.已111 {/s=9 V.人=9A, /?= 9Q. C=9“F・L=9 mHo求a, b两点的电包及通过凡C. L的电流。
【解】本题目的与上题相同。
由于在稳态口流电路小,C相当于开路.厶相当十如路,所以求得匕=U§ =9 Vv b=0v -V 9-()I一_d_Lk 一 T U A -1 A /r=092.3.1在图2.6所示电路中,开关S冈合前电路己处丁稳态,试确定S闭合后电压々和电流b d,2的初始值和稳态值。
【解】(1)求初始值由于S闪A前,电路已稳定,C相为于开路,i产/戸1.5A"因此,根据换路定律,出换路前(S断丿「时)的电路,首先求得然后.根US «c(o)»u c (0) = =4x1.5 V = 6 V由換路后(S闭介时)的电路求得nJ0) = 6 A = 15A 1& 4w r(0) 6 «-<2 (0) = ------ = — A = 3 A2i c(0) “s7(°)-/2(0) = (1.5-1.5-3) A =-3 A(2) 求稳态值由丁•电路稳定后• C WI J TJT路.因此.首先求得i厂(m A然后.进一步求得R9人(8)= --- —人 =—=—x 1.5 A =0.5 A&+/L 5 4 + 2& ■<2(oo)= i c(oo) -(15 —0.5 -0) A = 1 Au c (<») = /?./)(°°) = 4x0.5 V = 2 V2.3.2在图2.7所示电路中,开关S闭介前屯路已处于稳态・认确'NSW 合麻电压“和电流…G,2的初始值和稳态值。
电工学 (少学时)第三版 唐介 课后答案 第3章习题

3.7.2 电路如图 3.22(教材图3.1 ,U=220 V, R 和 XL串联支路 )所示, 2)所示 的 P1 = 726 W, λ 1 = 0 . 6 。当开关S 闭合后,电路的总有功功率增加了 74 W, 无功功率减少了 168 var,试求总电流 I 及 Z2 的大小和性质。
ww
.k hd aw .c om
案 网
图3.21
课
后
图3.22
返 回
上一页
下一页
3.7.3 两台单相交流电动机并联在 220 V交流电源上工作, 取用的有功功率和功率因数分别为 P1 = 1 kW, λ 1 = 0 .8; P2 = =0.5 kW,λ2=0.707求总电流、总有功功率、无功功率、视 在功率和总功率因数。 3.7.4 图3.23(教材图3.13) 所示日光灯电路,接于 220 V、50 Hz交流电源上工作,测得灯管电 压为100 V、电流为0.4 A,镇流器 1)灯管的 的功率为7 W。求:( 求:(1 电阻 RL 及镇流器的电阻和电感; (2)灯管消耗的有功功率、电路 图3.23 消耗的总有功功率以及电路的功 3)欲使电路的功率因数提高到 0.9,需并联多大的 率因数;( 率因数;(3 4)画出完整的相量图。 电容?( 电容?(4
3.9.2 在图3.28(教材3.17)所
交流理想电压源的电压 ,交流理想电压源的电压 IS = 2 A ,
此频率时的 ,此频率时的 uS = 12 2 sin 314t V,
XC= 3 Ω, XL = 6 Ω, R = 4 Ω,求通 R中消耗的有功功率。
课
后
示电路中,直流理想电流源的电流
过电阻R的电流瞬时值、有效值和
3.2.1 已知某正弦电流当其相位角为 则该电流的有效值是多少?若此电流的周期为 10 ms,且在 t=0 时正处于正值过渡到负值时的零值,写出电流的瞬时 • 值表达式 I 和相量 I 。
电工学第三版习题答案

---------------------------------------------------------精品 文档第二章2-1 解:i=10sin(314t+60°) mAt =1ms,)31001.0100sin(10ππ+∙=s i 2-3解:(1)452003010021∠=-∠=∙∙U U(2)u 1滞后u 2 75°.2-4 解:)1.53sin(25)1.53sin(2521-=+=t i t i ωω2-5 解:)30sin 30(cos 50)150sin 150(cos 27.7021 j U j U +=+=∙∙2-6 解:)60sin 60(cos 210)30sin 30(cos 21021 -+-=+=∙∙j I j I2-8 解:电流与电压表的读数为有效值。
2-9 解:X L =ωL ∙∙=I jX UL---------------------------------------------------------精品 文档2-15 解:Z=R1+R2+j(X L -X C )CjI U L j I U RI U C L R ωω1∙∙∙∙∙∙-===2-28 解:220605.0220401cos 1cos 22111==⨯===U P I U P I UI P ϕϕ SP P P P UIS I I I I II I =+==+=∠=+=∙∙∙∙∙ϕϕϕcos 0)1sin 1(cos 212122112-30解:---------------------------------------------------------精品 文档22)sin (cos 31cos )1sin 1(cos 01211111∙∙∙∙∙∙∙∙=-=+==+=∠=I U Z I I I I I U P I I I U U ϕϕϕϕϕ2-32: 未接电容时接电容后:Ru Lu 1cos 1ϕUI P =---------------------------------------------------------精品 文档有功功率不变,电压不变,功率因数提高到0.9。
电工学 少学时 第3章改附习题解

交流:f
XL
电感L具有通直阻交的作用
第3章 交流电路
XL ω L2 π f L
感抗XL是频率的函数
根据: i 2I sinωt
I , XL
I U
2fL X L
O
f
u 2I ωLsin (ωt 90 )
可得相量式:
I U
I U
0 90 Iω L
90
则:
U I
U I
90 jL
U jI ω L I (jXL )
(2) 有功(平均)功率
1T
P
T
o
p dt
1T
T
o
UI si n (2ωt )dt 0
L是非耗
能元件
第3章 交流电路
分析:瞬时功率 :p i u UI si n2 ω t
u i
结论:
o
ωt 纯电感不消 耗能量,只和
i
+
u
i u
i u
i u+
- ++-
p
可逆的能量 转换过程
+ p <0 + p <0
返回
上一节
下一节
上一页 下一页
第3章 交流电路
▲复数的表示方法和计算方法:
+j
b
A
1. 复数的表示方法 模
A= a +j b
辐角
ψ
代数式 O
a +1
= c (cosψ +j sinψ ) 三角式
= c e jψ
指数式
图 3.2.1 复数
= c∠ψ
极坐标式
返回
上一节 下一节
电工学习题少学时答案
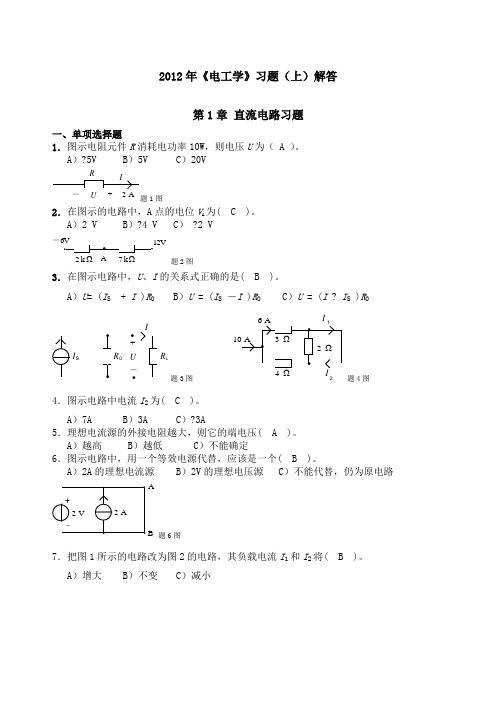
2012年《电工学》习题(上)解答第1章直流电路习题一、单项选择题1.图示电阻元件R消耗电功率10W,则电压U为( A )。
A)?5V B)5V C)20VU+题1图2.在图示的电路中,A点的电位V A为( C )。
A)2 V B)?4 V C)?2 V-2 k7 kΩΩ题2图3.在图示电路中,U、I的关系式正确的是( B )。
A)U= (I S+ I )R0 B)U = (I S-I )R0C)U = (I?I S)R0R L题3图I2题4图4.图示电路中电流I2为( C )。
A)7A B)3A C)?3A5.理想电流源的外接电阻越大,则它的端电压( A )。
A)越高 B)越低C)不能确定6.图示电路中,用一个等效电源代替,应该是一个( B )。
A)2A的理想电流源B)2V的理想电压源 C)不能代替,仍为原电路2 V题6图7.把图1所示的电路改为图2的电路,其负载电流I1和I2将( B )。
A)增大B)不变C)减小221Ω2V 2A图 1图2+题7图8.图示电路中,供出功率的电源是( A )。
A )理想电压源B )理想电流源C )理想电压源与理想电流源U 4VS 题8图S题9图9.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( B )。
A )4和3B )3和3C )3和410.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( B )。
A )可以用B )不可以用C )有条件地使用 11.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A )?18VB )18VC )?6VU I SS+题11图SA题12图12.在图示电路中,当开关S 闭合时A 点的电位V A ( C )。
A ) ?3VB )3VC )0V13.图示电路中,理想电流源I S1发出的电功率P 为( A )。
电工学少学时第三版 张南主编 课后练习答案 第二章(末)

电工学少学时第三版张南主编课后练习答案第二章(末)电工学少学时第三版张南主编课后练习答案第二章(末)第二章正弦交流电路2.1基本要求(1)深入了解正弦量的特性,尤其是RMS、初始相位和相位差。
(2)掌握正弦量的各种表示方法及其相互关系。
(3)掌握正弦交流电路的电压电流关系及复数形式。
(4)掌握三个单参数(R、l、c)的电压、电流和功率关系。
(5)能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6)深刻认识提高功率因数的重要性。
(7)了解交流电路的频率特性和谐振电路。
2.2基本内容2.2.1基本概念1.正弦量的三要素(1)振幅(um,EM,IM),瞬时值(U,e,I),有效值(U,e,I)。
注:有效值与振幅的关系为:有效值?振幅2。
(2)频率(f)、角频率(?)、周期(t)。
注:三者的关系是??2?f?2?。
t(3)相位(?t??)、初相角(?)、相位差(?1??2)。
注:相位差是同频率正弦量的相位之差。
2.正弦量的表示方法(1)函数式表示法:Uumsin(?t×u);Eemsin(?t??e);我波形表示法:例如,u的波形如图2-1-1(a)所示。
(3)相量(图)表示:使相量的长度等于正弦量的幅值(或有效值);使相量和横轴正方向的夹角等于正弦量的初相角;使相量旋转的角速度等于正弦量的角速度。
uuum?U我我0我?TU(b) ??u78。
78图2-1-1(a)图2-1-1(b)25.65?U注:① 绘制实际相量时,主要使用有效值,忽略水平轴,?11也节省了油漆,没有零参考相量(只有方向,.22没有尺寸)。
图2-1-1(b)是u和I的相量图。
64.36② 相同性质(相同频率)正弦量的加减可以用相量图来解决?UI2-1图2-6(b)示例u1?62sin(?t?30o)v,u2?42sin(?t?60o)v。
求u1?u2解:因为同频率同性质的正弦量相加后仍为正弦量,故u1?u2乐队?Uu2sin(?t??),只有你和我?一2问题解决了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R0 = R1 = 2 Ω I2 = U eS 20 = A=4A R0 + R2 2 + 3
1.9.4 用诺顿定理求图 1.10 所示电路中的电流 I2。 解: I eS =
US 10 + IS = + 5 A = 10 A R1 2 R0 = R1 = 2 Ω I2 = R0 2 I eS = × 10 A = 4 A 2+3 R0 + R2
τ = RC = 10 × 103 × 50 × 10−6 = 0.5 s uC = uC (∞) + [uC (0) − uC (∞)]e
− t τ
= [0 + (6 − 0) e
−
t 0.5
] V = 6e −2t V
u R = −uC = −6 e −2 t V −3 = −6e −2t t = 0.3465 s
− t τ − t − t 3
τ = R1C = 3 × 1 s = 3 s uC = uC (∞) + [uC (0) − uC (∞)]e iC = C
t − d uC = 2e 3 A dt
= [12 + (6 − 12) e 3ห้องสมุดไป่ตู้] V = 12 − 6e
V
2.6.2 在图 2.09 所示电路中,已知 US = 6 V,IS = 2 A,R1 = R2 = 6 Ω,L = 3 H。试用三要素法求开 关 S 闭合后的响应 iL 和 uL。 解:把开关闭合后的电路用戴维宁定理来等效
&。 3.5.1 R = 10 Ω,XC = 20 Ω,XL = 10 Ω,三者并联后接于 220 V 的交流电源上,求电路的总电流 I
解:
o o o & & & &= I & +I & +I & = U + U + U = 220∠0 + 220∠0 + 220∠0 A = 24.6∠ − 26.57 o A I R C L R − jX C jX L 10 − j20 j10
iC (0) = IS − i1 (0) − i2 (0) = (1.5 − 1.5 − 3) A = −3 A
(2)求稳态值
iC (∞) = 0 A i1 (∞) = R2 2 IS = ( × 1.5) A = 0.5 A R1 + R2 4+2
i2 (∞) = IS − i1 (∞) − iC (∞) = (1.5 − 0.5 − 0) A = 1 A uC (∞) = R1i1 (∞) = (4 × 0.5) V = 2 V
uL (0) = U S − R1i1 (0) = (12 − 4 × 1.8) V = 4.8 V
(2)求稳态值
u L (∞ ) = 0 i1 (∞) = i2 (∞) = U S − u L (∞) 12 − 0 = A=3 A R1 4 U S − uL (∞) 12 − 0 = A=2 A R2 6
U eS = −U S + R2 IS = ( −6 + 6 × 2 ) V = 6 V R0 = R2 = 6 Ω
共 12 页
第 3 页
iL (0) = iL (0−) = 0 A iL ( ∞ ) = τ= ueS 6 = A =1 A R0 6
L 3 = s = 0.5 s R0 6
− t τ
iL = iL (∞) + [iL (0) − iL (∞)]e uL = L d iL = 6e −2 t V dt
= [1 + (0 − 1) e
−
t 0.5
] A = 1 − e −2 t A
3.2.1 已知 i = 12 2 sin(ωt − 36o ) A ,试写出表示它的有效值相量的四种形式。
2.3.1 在图 2.03 所示电路中, 开关 S 闭合前电路已处于稳态, 试确定 S 闭合后电压 uC 和电流 iC、 i1、 i2 的初始值和稳态值。 解:(1)求初始值
uC (0) = R1 IS = (4 × 1.5) V = 6 V i1 (0) = i2 (0) = uC (0) 6 = A = 1.5 A R1 4 uC (0) 6 = A=3 A R2 2
U = U S − R2 I 2 = ( 6 − 1× 2 ) V = 4 V
S 闭合时,R2 两端电压等于 US,故:
I 2 = IS = 2 A
I2 =
I = I 2 − IS = ( 6 − 2 ) A = 4 A
1.7.1 用支路电流法求图 1.09 中各支路电流,并说明 US1 和 US2 是起电源作用还是起负载作用。图 中 US1 = 12 V,US2 = 15 V,R1 = 3 Ω,R2 = 1.5 Ω,R3 = 9 Ω。 解 : I1 + I 2 − I 3 = 0
o 解: ϕ1 = arccos λ1 = arccos 0.8 = 36.9
P = PR = RI 2 = 10 × 21.52 W = 4622.5 W
ϕ2 = arccos λ2 = arccos 0.707 = 45o P=P 1+P 2 = (1 + 0.5) kW = 1.5 kW Q = Q1 + Q2 = P 1 tan ϕ1 + P 2 tan ϕ 2 = (1× 0.75 + 0.5 × 1) kvar = 1.25 kvar S = P 2 + Q 2 = 1.52 + 1.252 k V⋅ A = 1.95 k V⋅ A S 1.95 × 103 = A = 8.86 A 220 U P 1.5 λ= = = 0.77 S 1.95 I=
IR =
U 100 = A =1 A R 100 Q = 0 var
P = UI = 100 × 1 W = 100 W ,
S 合向 b 时:
IL =
U U 100 = = A = 10 A X L 2 π fL 2 × 3.14 × 50 × 31.8 × 10−3 QL = UI L = 100 × 10 var = 1 000 var , P = 0 W
& = 12∠ − 36 A = 12 e 解: I
o
-j36o
o o A = 12 cos(−36 ) + jsin(−36 ) A = ( 9.71 − j7.05 ) A
3.3.1 在图 3.01 所示电路中,已知 R = 100 Ω,L = 31.8 mH,C = 318 μF。求电源的频率和电压为 50 Hz、100 V 时,开关 S 合向 a、b、c 位置时电流表的读数,并计算各元件中的有功功率和无功功率。 解:S 合向 a 时:
S 合向 c 时:
IC =
U = 2π fCU = 2 × 3.14 × 50 × 318 × 10−6 × 100 A = 10 A XC QC = UI C = 100 × 10 var = 1 000 var , P = 0 W
3.4.3 将一个电感线圈接到 20 V 直流电源时,通过的电流为 1 A,将此线圈改接于 2000 Hz、20 V 的电源时,电流为 0.8 A。求该线圈的电阻 R 和电感 L。 解:(1) 线圈接到 20 V 直流电源时
2.6.1 在图 2.08 所示电路中,已知 US = 6 V,IS = 2 A,R1 = R2 = 3 Ω,C = 1 F。开关闭合前 UC = 6 V。 试用三要素法求开关 S 闭合后的 uC 和 iC。 解: uC (0) = uC (0− ) = U C = 6 V
uC (∞) = U S + R1 IS = ( 6 + 3 × 2 ) V = 12 V
2.3.2 在图 2.04 所示电路中, 开关 S 闭合前电路已处于稳态, 试确定 S 闭合后电压 uL 和电流 iL、 i1、 i2 的初始值和稳态值。 解:(1)求初始值
共 12 页
第 2 页
iL (0) = i1 (0) = i2 (0) =
U S 12 = A =3 A R1 4 R2 6 iL (0) = × 3 A = 1.8 A R 1 + R2 4+6 R1 4 iL (0) = × 3 A = 1.2 A R1 + R2 4+6
R=
U 20 = Ω = 20 Ω I 1 U 20 = = 25 Ω I 0.8
(2) 线圈改接于 2000 Hz、20 V 的电源时
Z = XL = L=
2
Z − R 2 = 252 − 202 Ω = 15 Ω
XL 15 = H = 1.19 mH 2 π f 2 × 3.14 × 2000
共 12 页 第 4 页
iL (∞) = i1 (∞) + i2 (∞) = (3 + 2) A = 5 A
2.4.1 在图 2.4.1(a)所示的电路中,已知 U0 = 6 V,R = 10 kΩ,C = 50 μF。开关 S 合在 a 端时,电路 已处于稳态。求开关改合到 b 端后的响应 uR 以及 uR 降至 3 V(绝对值)时所需的时间。 解: uC (0) = U 0 = 6 V
恒压源单独作用时:
′′ = I1′′ = I 2
′′ = −1 A 恒流源与恒压源共同作用时: I1 = − I1′ + I1 ′ + I2 ′′ = 4 A I2 = I2
1.9.2 用戴维宁定理求图 1.10 所示电路中的电流 I2。 解: U eS = U S + I S R1 = (10 + 5 × 2 ) V = 20 V
US =6A R2
R2 I 2 + R3 I 3 − U S2 = 0 R1 I1 + R3 I 3 − U S1 = 0
