大学物理第11章光干涉
大学物理第十一章光学第2节 杨氏双缝干涉实验 劳埃德镜

2. 干涉条纹分析
ห้องสมุดไป่ตู้
s1
r1 r2
P
·
I
s
d
0
s2
d’
图中: 相邻实线与 虚线的相位差为
设01、02分别为s1、s2相干光的初相; A1、A2分别为 s1、s2 在P点的振幅。假设A0=A1=A2, 01=02 两光波在P点处的光强:
2 2 I=A2=2 A0 +2 A0 cos(Δ )
第 十一章 光学
13
物理学
第五版
11-2 杨氏双缝干涉实验 劳埃德镜
例2 以单色光照射到相距为0.2 mm的双缝 上,双缝与屏幕的垂直距离为1 m. (1)从第一级明纹到同侧的第四级明纹间的 距离为7.5 mm,求单色光的波长; (2)若入射光的波长为600 nm,中央明纹中 心距离最邻近的暗纹中心的距离是多少?
d'
B
p
x
o
s2
r
x r d d'
k 0,1,2, (2k 1) 减弱 2
第 十一章 光学
5
k
加强
物理学
第五版
11-2 杨氏双缝干涉实验 劳埃德镜
明、暗条纹的位置
d x= k d
k=0, 1, 2, ...明纹中心
d x= ( 2k- 1) d 2
r1
r2
d'
B
p
s
x
o
o
s2
r
d ' d
当 很小时(<5º )
波程差
sin tan x / d ' x r r2 r1 d sin d d'
大学-物理学-第五版-马文蔚-答案上下册第十一章

第十一章光学1、在双缝干涉实验中,两缝间距为mm 30.0,用单色光垂直照射双缝,在离缝m 20.1的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间的距离为mm 78.22,问所用光的波长为多少?解:双缝干涉暗纹条件'(21)2d x k d λ=±+ (0,1,2,)k =⋅⋅⋅中央明纹一侧第5条暗纹对应于4=k ,由于条纹对称,该暗纹到中央明纹中心的距离为mm 39.11278.22==x 那么由暗纹公式即可求得 337'2211.39100.3010 6.32810m 632.8nm (21) 1.20(241)xd d k λ---⨯⨯⨯⨯===⨯=+⨯⨯+2、用白光垂直入射到间距为mm 25.0=d的双缝上,距离缝m 0.1处放置屏幕,求零级明纹同侧第二级干涉条纹中紫光和红光中心的间距(白光的波长范围是nm 760~400)。
解:第k 级明纹位置应满足'd x k dλ= ),2,1,0(⋅⋅⋅±±=k 对紫光和红光分别取nm 4001=λ,nm 7602=λ;则同侧第二级条纹的间距'3621 1.010()2(760400)10 2.88mm 0.25d x k d λλ-⨯∆=-=⨯⨯-⨯=3、用58.1=n 的透明云母片覆盖杨氏双缝干涉装置的一条缝,若此时屏中心为第五级亮条纹中心,设光源波长为μm 55.0,(1)求云母片厚度。
(2)若双缝相距mm 60.0,屏与狭缝的距离为m 5.2,求0级亮纹中心所在的位置。
解:(1)由于云母片覆盖一缝,使得屏中心处的光程差变为λ5=∆,一条光路中插入厚度为e 的透明介质片光程变化e n )1(-。
所以λ5)1(=-=∆e n解得云母片厚度μm 74.4158.155.0515=-⨯=-=n e λ(2)因为mm 29.260.055.05.2=⨯==∆d D x λ, 又由于中心位置为5级明纹中心,故级条纹距中心为5倍条纹宽度,所以m m 45.1129.2555=⨯=∆=x x4、如图所示,在折射率为50.1的平板玻璃表面有一层厚度为nm 300,折射率为22.1的厚度均匀透明油膜,用白光垂直射向油膜,问:(1)哪些波长的可见光在反射光中干涉加强?(2)若要使透射光中nm 550=λ的光干涉加强,油膜的最小厚度为多少?由上式可得:k dn 22=λ , 1=k 时: nm 732130022.121=⨯⨯=λ 红光 2=k 时: nm 366230022.122=⨯⨯=λ 紫外, 故反射中波长为nm 732的红光产生干涉加强。
干涉

2π
其中λ为光在真空中的波长、δ 为光程差 为光在真空中的波长、 半波损失:光从光疏媒质射向光密媒质,在界面反射时, 半波损失:光从光疏媒质射向光密媒质,在界面反射时, 反射光发生π相位突变,这相当于减少或增加的λ/2光程。 λ/2光程 反射光发生π相位突变,这相当于减少或增加的λ/2光程。 薄膜干涉: 薄膜干涉: 入射光在薄膜上表面由于反射和折射而“分振幅”,在上、 入射光在薄膜上表面由于反射和折射而“分振幅” 在上、 下表面反射的光为相干光,他们相遇产生干涉。 下表面反射的光为相干光,他们相遇产生干涉。 等厚干涉:薄膜等厚处反射光的光程差相同,干涉情况一 等厚干涉:薄膜等厚处反射光的光程差相同, 形成等厚干涉条纹。 样,形成等厚干涉条纹。 劈尖:置于介质中的劈形介质薄膜,其上、下表面(不平 劈尖:置于介质中的劈形介质薄膜,其上、下表面( ),夹角很小 夹角很小。 行),夹角很小。
反射光增强: ne + 2
λ
= kλ
例题11 例题
11.一个玻璃劈尖,折射率1.52。波长为589.3nm 11.一个玻璃劈尖,折射率1.52。波长为589.3nm 一个玻璃劈尖 1.52 的钠光垂直入射,测得相邻条纹间距为5.0mm,则 的钠光垂直入射,测得相邻条纹间距为5.0mm, 5.0mm 劈尖的夹角为 。
例题2 例题
2.在双缝干涉实验中,用黄色自然光, 2.在双缝干涉实验中,用黄色自然光,在屏幕上形成 在双缝干涉实验中 干涉条纹,若在一缝后放绿色滤色片片, 干涉条纹,若在一缝后放绿色滤色片片,则 无干涉条纹. (A) 无干涉条纹. (B) 干涉条纹的间距不变, 但明纹的颜色变为黄绿 干涉条纹的间距不变, 相间. 相间. 干涉条纹的间距变窄, (C) 干涉条纹的间距变窄, 且明纹的颜色介于黄绿 之间. 之间. 干涉条纹的间距不变, 但明纹的颜色变成蓝色. (D) 干涉条纹的间距不变, 但明纹的颜色变成蓝色.
大学物理第五版薄膜干涉-劈尖

第十一章 光学
练习
10
物理学
第五版 例1 波长为680nm的平行光照射到
L=12cm长的两块玻璃片上,两玻璃片的左端
相互接触,右端被厚度D=0.048mm的纸片隔
试开问. 在这12 cm长度内会呈现多少条暗条纹 ?
解:根据薄膜干涉产生暗条纹条件
2d (2k 1)
2
2
k 0,1, 2, D
2f
b
单缝宽度变化,中央明纹宽度如何变化?
第十一章 光学
40
物理学
第五版
入射波长变化,衍射效应如何变化 ?
越大,1 越大,衍射效应越明显.
第十一章 光学
41
物理学
第五版
四.单缝衍射的动态变化
单缝上下移动,根据透镜成像原理衍射图 不变 .
R
单缝上移,零级
o 明纹仍在透镜光
f
轴上.
第十一章 光学
练习
实验装置
L1
K L2
S
*
f1
f2
E屏幕
2.单缝衍射图样的形成
第十一章 光学
28
物理学
第五版
定性分析:
设单缝宽为b ,波长为 的平行单色光垂直入射到单
缝上则:缝AB可视为波阵面的一部分,其上每一点为
子波源,向各方向发出子波,用衍射线表示。
定义:衍射线的方向与缝平
面法线的夹角称为衍射角
A
Q
方向相同的一组衍射线
d 2 2n
劈尖干涉
k 2n(暗纹)
第十一章 光学
8
物理学
第五版 (2)相邻明纹(暗纹)之间的厚度差:
dk 1
dk
2n
大学物理题库通用版-第11章-波动光学--光的干涉(含答案解析)
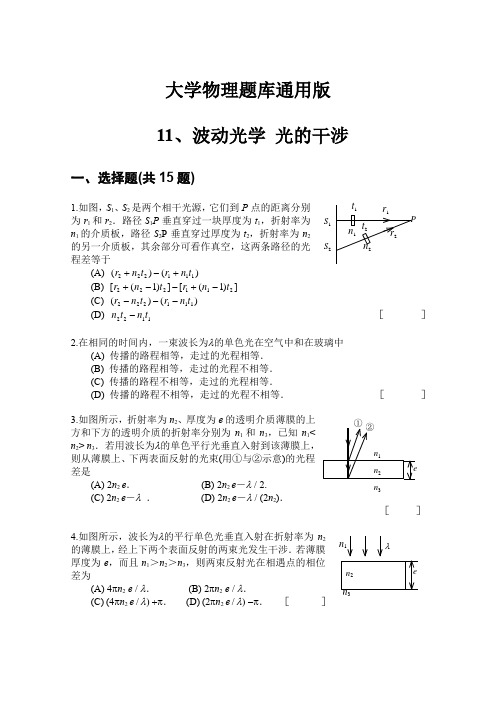
大学物理题库通用版11、波动光学 光的干涉一、选择题(共15题)1.如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2.路径S 1P 垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径的光程差等于 (A) )()(111222t n r t n r +-+(B) ])1([])1([211222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - [ ]2.在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等,走过的光程相等.(B) 传播的路程相等,走过的光程不相等.(C) 传播的路程不相等,走过的光程相等.(D) 传播的路程不相等,走过的光程不相等. [ ]3.如图所示,折射率为n 2、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3,已知n 1<n 2> n 3.若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束(用①与②示意)的光程差是(A) 2n 2 e . (B) 2n 2 e -λ / 2. (C) 2n 2 e -λ . (D) 2n 2 e -λ / (2n 2).[ ]4.如图所示,波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上,经上下两个表面反射的两束光发生干涉.若薄膜厚度为e ,而且n 1>n 2>n 3,则两束反射光在相遇点的相位差为(A) 4πn 2 e / λ. (B) 2πn 2 e / λ. (C) (4πn 2 e / λ) +π. (D) (2πn 2 e / λ) -π. [ ]P S 1S 2 r 1 n 1 n 2 t 2 r 2 t 1n 3n 1 λ5.如图所示,平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为 (A) 2πn 2e / ( n 1 λ1). (B)[4πn 1e / ( n 2 λ1)] + π. (C) [4πn 2e / (n 1 λ1) ]+ π. (D) 4πn 2e / ( n 1 λ1). [ ]6.一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜最小的厚度为(A) λ / 4 . (B) λ / (4n ).(C) λ / 2 . (D) λ / (2n ). [ ]7. 两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的(A) 间隔变小,并向棱边方向平移.(B) 间隔变大,并向远离棱边方向平移.(C) 间隔不变,向棱边方向平移.(D) 间隔变小,并向远离棱边方向平移. [ ]8.用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则(A) 干涉条纹的宽度将发生改变.(B) 产生红光和蓝光的两套彩色干涉条纹.(C) 干涉条纹的亮度将发生改变.(D) 不产生干涉条纹. [ ]9.把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为D (D >>d ),所用单色光在真空中的波长为λ,则屏上干涉条纹中相邻的明纹之间的距离是(A) λD / (nd ) (B) n λD /d .(C) λd / (nD ). (D) λD / (2nd ). [ ]10.在双缝干涉实验中,若单色光源S 到两缝S 1、S 2距离相等,则观察屏上中央明条纹位于图中O 处.现将光源S 向下移动到示意图中的S '位置,则 (A) 中央明条纹也向下移动,且条纹间距不变.(B) 中央明条纹向上移动,且条纹间距不变. (C) 中央明条纹向下移动,且条纹间距增大. (D) 中央明条纹向上移动,且条纹间距增大. [ ]11.在双缝干涉实验中,入射光的波长为λ,用玻璃纸遮住双缝中的一个缝,若玻璃n 1λ1 S S '纸中光程比相同厚度的空气的光程大2.5 λ,则屏上原来的明纹处(A) 仍为明条纹;(B) 变为暗条纹;(C) 既非明纹也非暗纹;(D) 无法确定是明纹,还是暗纹.[]12.在牛顿环实验装置中,曲率半径为R的平凸透镜与平玻璃扳在中心恰好接触,它们之间充满折射率为n的透明介质,垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ,则反射光形成的干涉条纹中暗环半径r k的表达式为(A) r k =Rkλ.(B) r k =nRk/λ.(C) r k =Rknλ.(D) r k =()nRk/λ.[]13.把一平凸透镜放在平玻璃上,构成牛顿环装置.当平凸透镜慢慢地向上平移时,由反射光形成的牛顿环(A)向中心收缩,条纹间隔变小.(B)向中心收缩,环心呈明暗交替变化.(C)向外扩张,环心呈明暗交替变化.(D)向外扩张,条纹间隔变大.[]14.如图a所示,一光学平板玻璃A与待测工件B之间形成空气劈尖,用波长λ=500 nm (1 nm=10-9 m)的单色光垂直照射.看到的反射光的干涉条纹如图b所示.有些条纹弯曲部分的顶点恰好与其右边条纹的直线部分的连线相切.则工件的上表面缺陷是(A) 不平处为凸起纹,最大高度为500 nm.(B) 不平处为凸起纹,最大高度为250 nm.(C) 不平处为凹槽,最大深度为500 nm.(D) 不平处为凹槽,最大深度为250 nm.[]15.在迈克耳孙干涉仪的一条光路中,放入一折射率为n,厚度为d的透明薄片,放入后,这条光路的光程改变了(A) 2 ( n-1 ) d.(B) 2nd.(C) 2 ( n-1 ) d+λ / 2.(D) nd.(E) ( n-1 ) d.[]二、填空题(共15题)1. 在双缝干涉实验中,两缝分别被折射率为n1和n2的透明薄膜遮盖,二者的厚度均为e.波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的相位差∆φ=________.图b2. 如图所示,假设有两个同相的相干点光源S 1和S 2,发出波长为λ的光.A 是它们连线的中垂线上的一点.若在S 1与A 之间插入厚度为e 、折射率为n 的薄玻璃片,则两光源发出的光在A 点的相位差∆φ=_2π (n -1) e / λ_.若已知λ=500 nm ,n =1.5,A 点恰为第四级明纹中心,则e =_____nm .(1 nm =10-9 m)3. 如图所示,两缝S 1和S 2之间的距离为d ,媒质的折射率为n =1,平行单色光斜入射到双缝上,入射角为θ,则屏幕上P 处,两相干光的光程差为___ ______.4.在双缝干涉实验中,所用光波波长λ=5.461×10–4 mm ,双缝与屏间的距离D =300 mm ,双缝间距为d =0.134 mm ,则中央明条纹两侧的两个第三级明条纹之间的距离为________ _______.5.用波长为λ的单色光垂直照射折射率为n 的劈形膜形成等厚干涉条纹,若测得相邻明条纹的间距为l ,则劈尖角θ=________.6.把双缝干涉实验装置放在折射率为n 的媒质中,双缝到观察屏的距离为D ,两缝之间的距离为d (d <<D ),入射光在真空中的波长为λ,则屏上干涉条纹中相 邻明纹的间距是_____________.7.用λ=600 nm 的单色光垂直照射牛顿环装置时,从中央向外数第4个(不计中 央暗斑)暗环对应的空气膜厚度为____________.(1 nm=10-9 m)8.用波长为λ的单色光垂直照射折射率为n 2的劈形膜(如图)图中各部分折射率的关系是n 1<n 2<n 3.观察反射光的干涉条纹,从劈形膜顶开始向右数第5条暗条纹中心所对应的厚度e =____________.9.波长为λ的平行单色光,垂直照射到劈形膜上,劈尖角为θ,劈形膜的折射率为n ,第三条暗纹与第六条暗之间的距离是______.10. 一束波长为λ=600 nm (1 nm=10-9 m)的平行单色光垂直入射到折射率为n =1.33的透明薄膜上,该薄膜是放在空气中的.要使反射光得到最大限度的加强,薄膜最小厚度应为________________nm .11.波长为λ的平行单色光垂直照射到劈形膜上,劈尖角为θ,劈形膜的折射率为n ,第k 级明条纹与第k +5级明纹的间距是__________.12.波长λ=600 nm 的单色光垂直照射到牛顿环装置上,第二个明环与第五个明环所对应的空气膜厚度之差为____nm .(1 nm=10-9 m)n 1n 2n 313.折射率分别为n 1和n 2的两块平板玻璃构成空气劈尖,用波长为λ的单色光垂直照射.如果将该劈尖装置浸入折射率为n 的透明液体中,且n 2>n >n 1,则劈尖厚度为e 的地方两反射光的光程差的改变量是_______.14.如图所示,在双缝干涉实验中SS 1=SS 2,用波长为λ的光照射双缝S 1和S 2,通过空气后在屏幕E 上形成干涉条纹.已知P 点处为第三级明条纹,则S 1和S 2到P 点的光程差为___3λ ____.若将整个装置放于某种透明液体中,P 点为第四级明条纹,则该液体的折射率n =________.15.已知在迈克耳孙干涉仪中使用波长为λ的单色光.在干涉仪的可动反射镜移动距离d 的过程中,干涉条纹将移动__________条. 三、计算题(共5题)1.白色平行光垂直入射到间距为a =0.25 mm 的双缝上,距D =50 cm 处放置屏幕,分别求第一级和第五级明纹彩色带的宽度.(设白光的波长范围是从400nm 到760nm .这里说的“彩色带宽度” 指两个极端波长的同级明纹中心之间的距离.) (1 nm=10-9 m)2.在双缝干涉实验中,波长λ=550 nm 的单色平行光垂直入射到缝间距a =2×10-4 m 的双缝上,屏到双缝的距离D =2 m .求:(1) 中央明纹两侧的两条第10级明纹中心的间距;(2) 用一厚度为e =6.6×10-5 m 、折射率为n =1.58的玻璃片覆盖一缝后,零级明纹将移到原来的第几级明纹处?(1 nm = 10-9 m)3.用波长为500 nm (1 nm=10-9 m)的单色光垂直照射到由两块光学平玻璃构成的空气劈形膜上.在观察反射光的干涉现象中,距劈形膜棱边l = 1.56 cm 的A 处是从棱边算起的第四条暗条纹中心.(1) 求此空气劈形膜的劈尖角θ;(2) 改用600 nm 的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹,A 处是明条纹还是暗条纹?(3) 在第(2)问的情形从棱边到A 处的范围内共有几条明纹?几条暗纹?2分4.图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm . (1) 求入射光的波长. (2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.5.用波长λ=500 nm 的平行光垂直照射折射率n =1.33的劈形膜,观察反射光的等厚干涉条纹.从劈形膜的棱算起,第5条明纹中心对应的膜厚度是多少? P E光的干涉习题答案一、选择题1、B ;2、C ;3、B ;4、A ;5、C ;6、B ;7、A ;8、D ;9、A ;10、B ;11、B ;12、B ;13、B ;14、B ;15、A二、填空题1、 2π(n 1 – n 2) e / λ2、4×103 nm3、d sin θ +(r 1-r 2)4、7.33 mm5、nl 2λ6、D λ / (dn )7、1.2=2λ μm8、249n λ9、3λ / (2n θ)10、113nm11、5λ / (2n θ)12、900 nm13、2 ( n – 1) e – λ /214、1.3315、2d /λ三、计算题1解:由公式x =kD λ / a 可知波长范围为∆λ时,明纹彩色宽度为∆x k =kD ∆λ / a2分 由 k =1可得,第一级明纹彩色带宽度为∆x 1=500×(760-400)×10-6 / 0.25=0.72 mm2分 k =5可得,第五级明纹彩色带的宽度为∆x 5=5·∆x 1=3.6 mm1分2解:(1) ∆x =20 D λ / a2分 =0.11 m2分 (2) 覆盖云玻璃后,零级明纹应满足(n -1)e +r 1=r 22分 设不盖玻璃片时,此点为第k 级明纹,则应有r 2-r 1=k λ 2分所以 (n -1)e = k λ k =(n -1) e / λ=6.96≈7 零级明纹移到原第7级明纹处 2分3解:(1) 棱边处是第一条暗纹中心,在膜厚度为e 2=21λ处是第二条暗纹中心,依此可知第四条暗纹中心处,即A 处膜厚度 e 4=λ23 ∴ ()l l e 2/3/4λθ===4.8×10-5 rad 5分(2) 由上问可知A 处膜厚为 e 4=3×500 / 2 nm =750 nm对于λ'=600 nm 的光,连同附加光程差,在A 处两反射光的光程差为λ'+2124e ,它与波长λ'之比为0.321/24=+'λe .所以A 处是明纹 3分 (3) 棱边处仍是暗纹,A 处是第三条明纹,所以共有三条明纹,三条暗纹.4解:(1) 明环半径 ()2/12λ⋅-=R k r 2分()Rk r 1222-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R λ) 对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5 3分 故在OA 范围内可观察到的明环数目为50个. 1分5解: 明纹, 2ne +λ21=k λ (k =1,2,…) 3分 第五条,k =5,ne 2215λ⎪⎭⎫ ⎝⎛-==8.46×10-4 mm 2分。
大学物理11-4 薄膜干涉(2)汇总

例 11-8 干涉膨胀仪如图所示,
干涉膨胀仪
一个石英圆柱环B放在平台上,
其热膨胀系数极小,可忽略不计。l
环上放一块平破璃板P,并在环
内放置一上表面磨成稍微倾斜的 柱形待测样品R,石英环和样品
l0
B
的上端面已事先精确磨平,于是
R的上表面与P的下表面之间形
成楔形空气膜,用波长为 的
单色光垂直照明,即可在垂直方 向上看到彼此平行等距的等厚条
dk
2n
n
2
b
n1 n
sin n 2
b
3)条纹间距(明纹或暗纹)
b 2n
tan D L
D n L L
2b 2nb
L
n n / 2 D
n1
b
劈尖干涉
11 - 4 薄膜干涉(2)
4 )干涉条纹的移动
每一条 纹对应劈尖 内的一个厚 度,当此厚 度位置改变 时,对应的 条纹随之移 动.
2
所以对于厚度均匀的平面薄膜来说,光程差是随光线的倾
角(入射角)的改变而改变,倾角相同,光程差相同,干
涉条纹的级数也相同。
11 - 4 薄膜干涉(2)
第十一章 波动光学
1 劈 尖干涉
n
T
L
n1
n1
d
S
劈尖角
M
2nd
D
2
n n1
k, k 1,2, 明纹
b
(2k 1) , k 0,1, 暗纹
B
膨胀值为 l N
2
根据热膨胀系数的定义
l
l0T
得样品的热膨胀系数
l N
l0T 2l0T
11 - 4 薄膜干涉(2) 劈尖干涉的应用
大学物理光的干涉详解

•
E1
完全一样(传播方向,频率, 相位,振动方向)
6
2. 光的单色性
例:普通单色光
: 10-2 10 0 Å 激光 :10-8 10-5 Å 可见光 103Å
7
3. 光的相干性
相干光:满足相干条件的几束光
相干条件:振动方向相同,频率相同,有恒定的相位差
相干光相遇时合成光的振动:
nd
k 0,1, 2L
19
注意:① k 等于几,代表第几级明纹。 ② 零级明纹(中央明纹)由光程差=0决定。
暗纹 (2k 1) , k 1,2, 3L
2
k级暗纹位置: x (2k 1) D
nd
k 1,2, 3
注意:k=1第一级暗纹, k=2第二级暗纹…. 无零级暗纹
Imin
-4 -2 0 2 4
-4 -2 0 2 4
衬比度差 (V < 1)
衬比度好 (V = 1)
▲ 决定衬比度的因素:
振幅比,光源的单色性,光源的宽度
干涉条纹可反映光的全部信息(强度,相位)。 15
8. 半波损失:
当光从光疏媒质(折射率较小)入射到光密媒质(折 射率较大)再反射回光疏媒质时,在反射点,反射光损失 半个波长。 (作光程差计算时,在原有光程差的基础上加或减半波长)
干涉结果
明纹: 2k k
2
k 0,1, 2
36
① n1 n n2 , n1 n n2
2e
n2
n12
sin2
i
2
k
k 1, 2, 3
注意:此处k等于几,代表第几级明纹,这
东北大学大学物理总结课件

3.会分析缝宽及波长对衍射条纹分布的影响。
4
11-8 圆孔衍射 光学仪器的分辨本领
1.了解夫琅和费圆孔衍射、艾里斑、瑞利判据、衍射对
光学仪器分辨本领的影响;
2.理解最小分辨角、光学仪器的分辨本领;
3.能够根据已知条件计算出光学仪器所能分辨的最小距
离。
11-9 衍射光栅
1.理解光栅、光栅常数、光栅衍射、缺级等概念;
17
5.理解可逆过程与不可逆过程的概念,能够使用公式:
dS dQ T
2 dQ
S2 S1 1 T
(对可逆过程)
计算基本的可逆与不可逆过程前后熵变。
6.理解玻尔兹曼关系式:
S k lnW
7.理解熵与热力学第二定律的统计意义。
8.了解信息熵。
18
CV
d e dT
V
iR 2
15
8.掌握p-V图中绝热线与等温线的区别及其形成的原因。
9.循环过程:
(1)掌握循环过程的特征;
(2)掌握正循环与热机(包括热机效率公式)间的关系;
(3)掌握逆循环与制冷机(包括制冷系数公式)间的关系。
10.掌握与理想气体循环过程有关的计算:
主要包括:吸热、作功、内能变化和效率、制冷系
明确作功和吸热是与过程有关的物理量。
4.热力学第一定律:掌握热力学第一定律的内容及其数
学表述: Q W E dQ dW d E
14
5.理解内能的概念: 明确内能是状态的单值函数,其增量只与始末状态
有关,而与系统所经历的具体过程无关的结论。 6.热力学第一定律的应用: (1)掌握理想气体等容、等温、等压和绝热过程的特征, 过程方程(其中绝热过程的过程方程要求会推导); (2)掌握上述过程中气体吸热、作功和内能变化的计算。 7.掌握理想气体热容量的计算方法和迈耶公式,能使用 能量均分定理计算各种刚性分子理想气体的热容量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/8/11
DUT 余 虹
3
11.1 干涉现象与 相干条件
一、基本概念
1、光矢量 E
光强 ——平均辐射强度
I S E2
E Eo cos( t )
1 2
E
2 o
2、光程 光程差
• r1
L1 n1r1
-) L2 n2r2
P
光程差 L1 L2
2020/8/11
DUT 余 虹
n1
r2 n2
n r1 • 直射光光程 nr1
•
2a•
r2
反射光光程 nr2 2
D
?
n(r
明
1) 暗
2
思考:与杨氏双缝实
验比干涉条纹有哪些相 同、不同之处?
2020/8/11
DUT 余 虹
15
11.3 光的时空相干性
一、准单色光的谱线宽度
I
Io Io 2
0 o
o
2
单色光 准单色光 光强降到一半时曲线的
I
s2
O
D
条件 : d D x D
ES1 ES 2 Eo cos t
2020/8/11
E1
Eo cos
E2 Eo
DUT
(t r1 )
cosu(t
余虹
r2 u
)
返回4
11
二、 光强分布
x
(r1 r2 )
u
s1
n r1
x•
2
u
(r1
r2 )
d
s2
r2 O0
DD
2 (r1 r2 ) n n
s1
d s2
h
n r1
x•
r2
0
D
明条纹中心:
m
( 2m
明
1) 暗
2
r2 r1 s2h d sin
d D sin tg x
x D
D
n(r2
r1 )
xnd D
暗条纹中心:
xmnd m
D
xm
(2m
1)
D
2nd
(m 1,2, )
xm
m
D
nd
2020/8/11
(m 0,1, ) 条纹宽度 x D
I12不处处为 0 的条件—— 相干条件
1) 相同
2)化E,1E且2 间的夹角 不随t变
2 3)相位差是常量
满足相干条件
I12 E10E20 cos
2 I1I2 cos
2020/8/11
DUT 余 虹
8
3、相干叠加光强分布
I I1 I2 2 I1I2 cos
只是空间的函
数,因此光强在空 间呈稳定分布。
在 = 2m 处 I M I1 I2 2 I1I2
=(2m+1) 处 I m I1 I2 2 I1I2
(m 0 , 1, )
I1 I2 Io
IM 4Io
Im 0
原子发光具有随机性、间断性,即使同一个原子
发出的前后两列波,也很难保证同时满足三个相干 条件。要获得相干光需要采取特殊的方法.
nd
DUT 余 虹
13
例题 杨氏双缝实验,=500nm ,在一光路中插入玻 璃片(n =1.5)后0点变为4级明纹中心。 求:玻璃片 厚度e。
解:光程差改变 ne e
(e, n)
s1 s2
2020/8/11
x
条纹移动 N = 4
N
0
e N
n1
4
n1
4000nm
DUT 余 虹
14
四、洛埃镜实验
m
(暗)2
2020/8/11
n1 n2 n3
DUT 余 虹
n1 n2 n3 To25
返回18 4
2、等倾干涉的特点
SL
i1 n1 n2 n3
•
1、倾角相同的光线形成的干涉光 光强相同。 2、所有的平行光汇聚在透镜焦平 面上的同一点。使条纹的对比度 更高。 3 、透镜正放,焦面上条纹是一组
返回4
s1 s2
4
例题
真空中波长为 的单色光,在折射率 n 的透 明介质中从 A 传播到 B ,两处相位差为 3 , 则沿此路径 AB 间的光程差为
(A)1.5 (C)3
(B) 1.5n (D) 1.5/n
分析:
A
B
n
介
相位差为 3 的两点几何距离为1.5 介,
光程差为1.5 介n = 1.5
2020/8/11
DUT 余 虹
5
3、单色光 复色光 准单色光
单色光的波列无头 无尾 无始无终。
E
Eo
cos[ (t
x) u
]
实际波列有限 长——复色光
o 108 s 1014 Hz c 3 108 ms1
间断振动
lo c o
波列越长 单色性越好
2020/8/11
DUT 余 虹
6
二、相干光和相干条件
2
= 2k
k
IM I1 I2 2 I1I2 cos
(明)
=(2k+1) (2k 1)
2
(k 0, 1,)
2020/8/11
Im I1 I2 2 I1I2 cos (暗)
当 I1 I2 Io DUT 余 虹
IM 4Io Im 0
12
三、 杨氏双缝实验条纹位置
x
1、 等倾干涉相长与相消的条件
AB cos i2 h
SL
i1
n1 n2
D
AC
n3 B
i2
2 ABn2 ADn1 AD AC sin i1
AC tg i2 2h
2hn2 cos i2
2hn1 ctg i2 sin i1
2hn2 cos i2
h
2h
n22
n12
sin2
i1(
2
)=
m( 明 )
2020/8/11
DUT 余 虹
9
4、 获得相干光的主要方法
• 分波阵面 法 具有确定相 • 分振幅干涉法 差的波阵面上的两个次 级子光源是相干的。
••
W入
W反
W透
• •
2020/8/11
W入 W反 W透
W
E
2 o
DUT 余 虹
10
11.2 杨氏双缝干涉 x
一、现象
s1
n r1
x ••
S
d
r2
宽度—— 谱线宽度
o
2
2020/8/11
DUT 余 虹
返回4
16
二、准单色光双缝干涉条纹
I x D
nd
2
o
2
1
o
2
不同波长的叠加 —— 非
相干叠加 —— 光强叠加
总光强曲线 条纹消失的级次?
01 2
x
0
2 ~ 3
1 ~ 4
2020/8/11
DUT 余 虹
17
11.4 分振幅干涉
一、 等倾干涉
1、波的独立性原理和叠加原理
S2 S1
2020/8/11
E E1 E2
1E1u1
2 E2u2
DUT 余 虹
7
2、相干条件
在交叠区 E E1 E2 I E 2 (E1 E2 )2 E12 E22 2E1 E2
I1 I2 I12 (干涉项)
当 I12 处处为0 时 I= I1 +I2 ——称作非相干叠加 —— 不相干。
2020/8/11
DUT 余 虹
1
第11章 光的干涉 第12章 光的衍射 第13章 光的偏振 第14章 光与物质相互作用
2020/8/11
DUT 余 虹
2
第11章 光的干涉
11.1 干涉现象与 相干条件 11.2 杨氏双缝干涉 11.3 光的时空相干性 11.4 分振幅干涉 11.5 迈克尔孙干涉仪
