基于实际信道的超混沌保密通信方案

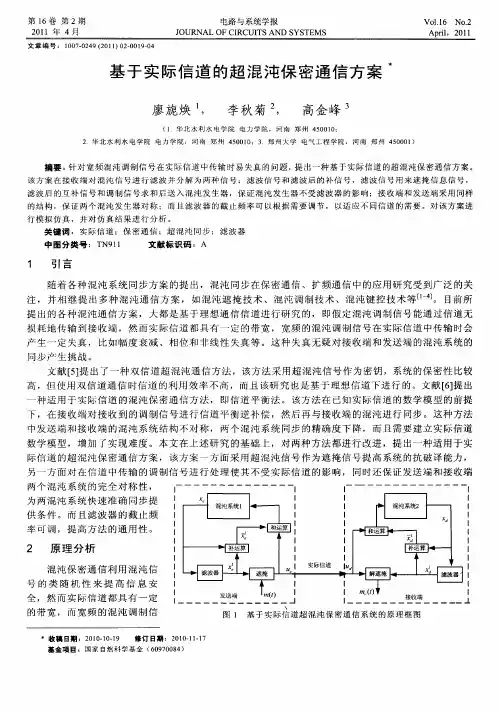
2011 年4月 JOURNAL OF CIRCUITS AND SYSTEMS April，2011 文章编号：1007-0249 (2011) 02-0019-04基于实际信道的超混沌保密通信方案*廖旎焕1，李秋菊2，高金峰3（1. 华北水利水电学院电力学院，河南郑州 450010；2. 华北水利水电学院电力学院，河南郑州 450010；3. 郑州大学电气工程学院，河南郑州 450001）摘要：针对宽频混沌调制信号在实际信道中传输时易失真的问题，提出一种基于实际信道的超混沌保密通信方案。

该方案在接收端对混沌信号进行滤波并分解为两种信号：滤波信号和滤波后的补信号，滤波信号用来遮掩信息信号，滤波后的互补信号和调制信号求和后送入混沌发生器，保证混沌发生器不受滤波器的影响；接收端和发送端采用同样的结构，保证两个混沌发生器对称；而且滤波器的截止频率可以根据需要调节，以适应不同信道的需要。

对该方案进行模拟仿真，并对仿真结果进行分析。

关键词：实际信道；保密通信；超混沌同步；滤波器中图分类号：TN911 文献标识码：A1 引言随着各种混沌系统同步方案的提出，混沌同步在保密通信、扩频通信中的应用研究受到广泛的关注，并相继提出多种混沌通信方案，如混沌遮掩技术、混沌调制技术、混沌键控技术等[1~4]。

目前所提出的各种混沌通信方案，大都是基于理想通信信道进行研究的，即假定混沌调制信号能通过信道无损耗地传输到接收端，然而实际信道都具有一定的带宽，宽频的混沌调制信号在实际信道中传输时会产生一定失真，比如幅度衰减、相位和非线性失真等。

这种失真无疑对接收端和发送端的混沌系统的同步产生挑战。

文献[5]提出了一种双信道超混沌通信方法，该方法采用超混沌信号作为密钥，系统的保密性比较高，但使用双信道通信时信道的利用效率不高，而且该研究也是基于理想信道下进行的。

文献[6]提出一种适用于实际信道的混沌保密通信方法，即信道平衡法。

该方法在已知实际信道的数学模型的前提下，在接收端对接收到的调制信号进行信道平衡逆补偿，然后再与接收端的混沌进行同步。

这种方法中发送端和接收端的混沌系统结构不对称，两个混沌系统同步的精确度下降，而且需要建立实际信道数学模型，增加了实现难度。

本文在上述研究的基础上，对两种方法都进行改进，提出一种适用于实际信道的超混沌保密通信方案，该方案一方面采用超混沌信号作为遮掩信号提高系统的抗破译能力，另一方面对在信道中传输的调制信号进行处理使其不受实际信道的影响，同时还保证发送端和接收端两个混沌系统的完全对称性，为两混沌系统快速准确同步提供条件。

而且滤波器的截止频率可调，提高方法的通用性。

2 原理分析混沌保密通信利用混沌信号的类随机性来提高信息安全，然而实际信道都具有一定的带宽，而宽频的混沌调制信* 收稿日期：2010-10-19 修订日期：2010-11-17基金项目：国家自然科学基金（60970084）图1 基于实际信道超混沌保密通信系统的原理框图号经过实际信道的传输后发生失真，导致接收端接收到的用于同步的信号发生改变，使接收端和发送端的同步精确度下降，甚至不能同步。

同步精确度下降的结果使解调出的信号和接收端传输的信息信号之间的误差增大，甚至解调不出有用信息信号。

为确保混沌调制信号不失真的通过实际信道，需要对发送端的宽频混沌调制信号进行处理，使其在实际信道中能够无失真的传输，而且还要保证对混沌调制信号的处理不能影响混沌系统的动力学特性。

为保证上述两点要求，本方案采用图1所示的结构，其工作原理分析如下：如图1所示，在发送端，混沌系统1产生的混沌信号并不直接用于遮掩，而是先对混沌信号e x 进行如式（1）、（2）的处理，分别被处理成滤波后的信号1e x 和滤波后信号的互补信号1e x ：即：e e x x ×=φ1（1）11e e e x x x −= （2）滤波后的混沌信号1e x 用于信息遮掩，如式（3）所示：)(1t m x u e e += （3）遮掩后的调制信号e u 在信道中进行传输。

由于经过滤波后的混沌遮掩信号1e x 为有限带宽信号，而信息信号本身是有限带宽信号，故在信道中传输的调制信号e u 也是有限带宽信号。

可以根据实际信道的特性选择滤波器的截止频率，来调节调制信号e u 的带宽。

只要保证调制信号的频带比实际信道的频带窄，就可以实现调制信号经过实际信道后不会发生失真。

但实际应用时如果滤波器的带宽选择过小，则混沌遮掩信号1e x 的类随机性受到严重影响，从而降低混沌保密通信的保密性。

在发送端，如果在发送端中没有引入反馈环，如图2所示，则接收端用于同步的信号为e u 而不是e x ，则两端的混沌系统不对称，难以实现精确同步。

如果在发送端把混沌调制信号e u 直接注入反馈环给混沌系统1，则滤波器的存在破坏了混沌系统的动力学特性。

故本方案中的反馈信号采用图1所示的滤波补信号1e x 和e u 的叠加信号，即：)(1t m x u x e e e +=+ （4） 由（4）式可知，对于发送端的混沌系统1而言，滤波器对其没有影响，这样就保证了在实际信道中传输有限带宽调制信号，而且滤波器的存在不破坏混沌系统1的动力学特性。

在接收端，为满足与发送端系统的结构对称性，混沌系统2产生的同步信号d x 被进行如式（5）和式（6）的处理，分别被处理成滤波后的信号1d x 和滤波后信号的补信号1d x ，即：d d x x ×=φ1（5）11d d d x x x −= （6）1d x 用于解调信息信号。

1d x 和接收到的信号d u 的叠加信号作为反馈信号注入混沌系统2，即式（7）表示的信号：)()(111t m x t m x x x u x x u x d e d d d d d d d +=++−=+−=+ （7）由式（7）可知，接收端的滤波器同样不会影响混沌系统2的动力学特性。

混沌系统1和混沌系统2采用完全对称的结构，只要采取合适的同步方案即可保证两个系统的精确同步。

如果滤波器的带宽比实际信道的带宽窄，则接收端接收到的信号不发生失真，即e d u u =。

在接收端和发送端混沌系统发生精确同步的情况下，即e d x x =，解调出来的信号)(t m r 为：)()()(1111t m x t m x x u x u t m d e d e d d r =−+=−=−= （8）由式（8）可知，信息信号从接收端精确地解调出来。

由上述分析可知，本方案中接收端和发送端采用同样的结构，保证了两端混沌系统的完全对称性，图2 无反馈环的原理框图第2期 廖旎焕等：基于实际信道的超混沌保密通信方案 21 为实现两端混沌发生器的准确同步提供条件。

由于滤波器对混沌发生器没有影响，无论滤波器的带宽参数如何选择，都不会影响混沌系统的动力学特性，可以根据需要实际信道的特点调整滤波器的带宽，故该方案适用范围比较广。

3 仿真分析为验证本方案的合理性，下面对方案进行Matlab 仿真。

为提高混沌保密系统的抗破译能力，发送端的混沌系统1选用高维混沌系统，在此采用Tamsevicious 提出的四阶超混沌系统，其状态方程为)]1()1([ ;)( ; ;4434413123211−−−=−==−−=x H x b x e dt dx x x c dtdx x dt dx x x ax dt dx （9） 式（9）中，)1(4−x H 为阶跃函数，当3,10,7.0====e c b a 时，式（9）表示的混沌系统具有两个正的李雅普诺夫指数。

构造接收端的混沌系统2的状态方程为：)]1()1([ ;)( ; );(443441312113211−−−=−==−+−−=y H y b y e dtdu y y c dt dy y dt dy y x k y y ay dt dy （10） 式（9）中，1x 为同步耦合变量。

由文献[7]可知，采用单变量单向耦合的方法可以实现两个系统的精确同步。

1x 一方面用于对信息信号进行遮掩，另一方面用于和接收端的混沌系统2系统进行耦合同步。

发送端和接收端的滤波器采用四阶巴特沃斯低通滤波器，信息信号为选用低频正弦信号。

用Matlab 进行仿真结果如图3所示。

图3(a)为待传输的信息信号波形。

图3(b)为经滤波后的混沌遮掩信号，由图3(b)可知，经过滤波后的遮掩信号仍然保持混沌特性.图3(c)为未经滤波的混沌信号的幅频图的一部分，图3(d)经滤波后的混沌遮掩信号的幅频图，比较图3(c)和图3(d)可知，没有经过滤波的混沌遮掩信号为宽频信号，而经过低阶滤波器的混沌调制信号的高频成分被虑除掉。

单从信号经过信道不发生畸变的角度出发，滤波器的截至频率越低越好，但滤波器的截至频率过低，有可能使遮掩信号的混沌特性丧失，从而使系统的保密性下降。

所以滤波器的截至频率应根据所选用的混沌系统的特性及信道特性进行综合选择。

图3(e)为解调出的信息信号，图3(f)为解调误差信号。

由图3(e)和图3(f)可知，经过短暂的时间延迟后，信息信号可以准确的从发送端解调出来。

解调开始时段的误差是由于两个混沌系统的同步误差 (d) 滤波后混沌遮掩信号u e 的频谱 (e) 解调出的信息信号m r (t ) (f) 信息信号m (t )的解调误差图3对基于实际信道超混沌保密通信系统的仿真结果(a) 信息信号m (t ) (b) 混沌调制信号u e (c) 未滤波的混沌信号x 1的频谱22 电路与系统学报第16卷所引起。

两个混沌系统的同步需要一定的时间，为避免这种解调误差出现，可以在接收端和发送端的混沌系统精确同步后再进行遮掩传输。

4 结论本文提出一种适用于实际信道的超混沌保密通信方案。

该方案在接收端对混沌信号首先进行滤波并分解为两种信号：滤波信号用来遮掩信息信号，滤波的互补信号和信息信号的和送入混沌发生器，保证混沌发生器不受滤波器的影响。

接收端和发送端采用同样的结构，保证两个混沌发生器的对称性。

滤波器的截止频率可以根据需要调节，以适应不同信道的需要。

用超混沌系统进行仿真，仿真结果表明该方案的有效性。

下一步对该方案的研究重点在于如何选择一种既是高维混沌系统来提高系统的抗破译能力，而且混沌信号的频谱又具有一定的带宽，从而使滤波器的截至频率可以选取的比较小，从而把其受信道的影响降低到最小。

参考文献：[1] Pecora LM, Carroll T L. Synchronization in chaotic system [J]. Phys. Rev.Lett, 1990,64(8):821-824.[2] K Murali, Haiyang Yu. Secure Communication using a chaos based signal encryption scheme [J]. IEEE Transactions on consumer Electronic,2001, 47(4): 709-714.[3] H Dedicu, M P Kennedy. Chaos shift keying Modulation and demodulation of a chaotic character using self –synchronizing Chua’s circuits [J].IEEE Transaction Circuits and system-II, 1993, 40: 634-642.[4] 关新平, 范正平, 等. 混沌控制及其在保密通信中的应用[M]. 国防工业出版社, 2002.[5] 高金峰, 廖旎焕. 一种超混沌混合保密通信方案[J]. 电路与系统学报, 2005, 10(4): 128-130.[6] Carroll T L. Communicating with use of filtered synchronized chaotic signals [J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications, 1995, 42: 105-110.[7] 蒋品群, 罗晓署, 等. 超混沌振荡器的单变量单向耦合同步及其电路实验仿真[J]. 物理学报, 2002, 51(9): 1937-1941.作者简介：廖旎焕（1975-），女，硕士，讲师，研究方向为非线性控制及应用；李秋菊（1977-），女，河南驻马店人，讲师，硕士，2005年毕业于北京航天航空大学，主要从事计算机控制和仿真研究，电子技术教学与应用；高金峰（1963-），工学博士，教授，研究生导师，长期从事非线性系统理论及控制等方面的研究。