有关三角形的角
初中数学几何专题-与三角形有关的角(优质讲义)

第二讲 与三角形相关的角【知识归类】1、三角形内角和定理;2、三角形内角和定理的推论(外角定理);3、直角三角形的性质及判定.【典例讲练】一、基础过关 【例1】(1)如图1,在△ABC 中,∠A =70°,∠B =50°,则∠C =__________°.(2)如图2,在△ABC 中,点D 在CA 的延长线上,∠B =35°,∠C =52°,则∠BAD =__________° (3)如图3,在△ABC 中,AC ⊥BC ,∠B =36°,则∠A =__________°.【练】(1)在△ABC 中,∠A =30°,则∠B +∠C =__________°.(2)在△ABC 中,∠ABC 的外角为55°,∠A =35°,则∠C =__________°.(3)在△ABC 中,∠A =37°,∠C =53°,则AB 与BC 的位置关系为__________.【拓】小明把一副含45°,30°的直角三角板如图摆放,其中∠C =∠F =90°,∠A =45°,∠D =30°,则∠1+∠2等于__________°.二、内角和、方程、不等式【例2】在△ABC 中,80C ∠=︒,20A B ∠-∠=︒,则B ∠的度数是( )A .60︒B .30︒C .20︒D .40︒【变1】在△ABC 中,若∠A ﹣2∠B +∠C =0,则∠B 的度数是( )A .30°B .45°C .60°D .75°【变2】适合条件∠A =∠B =12∠C 的三角形是( )A .锐角三角形B .等边三角形C .钝角三角形D .直角三角形图3图2图1CBADC BAC BAF EDCBA21【变3】在锐角△ABC 中,∠B =3∠C ,则∠C 的取值范围是___________.【拓】在三角形中,最大角α的取值范围是___________.〖总结〗三、简单应用【例3】如图,△ABC 中,80A ∠=︒,剪去A ∠后,得到四边形BCED ,则12∠+∠= .【变1】如图,将ABC △沿着DE 翻折,若1280∠+∠=︒,则B ∠= .【变2】如图,由图1的ABC △沿DE 折叠得到图2;图3;图4.(1)如图2,猜想BDA CEA ∠+∠与A ∠的关系,并说明理由; (2)如图3,猜想BDA ∠和CEA ∠与A ∠的关系,并说明理由; (3)如图4,猜想BDA ∠和CEA ∠与A ∠的关系,并说明理由.21ED B CA A BCDE 12图112ABCD E 图212ED CBA 图321ABCD E图421ED CBA四、高、双直角、双高【例4】如图,CD ⊥AB ,∠1=∠2,∠A =55°,求∠BCA 的度数.【变1】如图,已知在△ABC 中,∠C =∠ABC =2∠A ,BD 是AC 边上的高,求∠DBC 的度数.【变2】如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D .(1)若∠B =35°,求∠ACD 的度数; (2)求证:∠ACD =∠B .【变3】在△ABC 中,(1)如图一,AB 、AC 边上的高CE 、BD 交于点O ,若∠A =60°,则∠BOC = _________ °. (2)如图二,若∠A 为钝角,请画出AB 、AC 边上的高CE 、BD ,CE 、BD 所在直线交于点O ,则∠BAC +∠BOC = _________ °,再用你已学过的数学知识加以说明. (3)由(1)(2)可以得到,无论∠A 为锐角还是钝角,总有∠BAC +∠BOC = _________ °.〖总结〗DCBA五、高线+角平分线【例5】如图,在△ABC 中,AD 是BC 边上的高,BE 平分∠ABC 交AC 边于E ,∠BAC =60°,∠ABE =25°.求∠DAC 的度数.【变1】已知△ABC 中,∠ACB =90°,CD 为AB 边上的高,BE 平分∠ABC ,分别交CD 、AC 于点F 、E ,求证:∠CFE =∠CEF .【变2】在△ABC 中,∠C >∠B ,AE 是△ABC 中∠BAC 的平分线;(1)若AD 是△ABC 的BC 边上的高,且∠B =30°,∠C =70°(如图1),求∠EAD 的度数;(2)若F 是AE 上一点,且FG ⊥BC ,垂足为G (如图2),求证:∠EFG =12(∠C -∠B );(3)若F 是AE 延长线上一点,且FG ⊥BC ,G 为垂足(如图3),②中结论是否依然成立?请给出你的结论,并说明理由.【变3】如图,已知AD 是△ABC 的角平分线(∠ACB >∠B ),EF ⊥AD 于P ,交BC 延长线于M ,(1)如果∠ACB =90°,求证:∠M =∠1;(2)求证:∠M =12(∠ACB ﹣∠B ).〖总结〗【例6】如图,求α∠的度数.【变1】如图,P 是△ABC 内一点,试比较∠BPC 与∠A 的大小.【变2】如图,127.5∠=︒,295∠=︒,338.5∠=︒,则4∠的度数为_________°.【变3】如图,CGE α∠=,则A B C D E F ∠+∠+∠+∠+∠+∠= .【变4】如图,点E 在AC 的延长线上,∠BAC 与∠DCE 的平分线交于点F ,∠B =60°,∠F =56°,则∠BDC的度数为__________°.〖总结〗αD CB A73︒30︒37︒PCBA4321ABDECαGFEDCBAFEDBA【例7】如图,求C D ∠+∠的度数.【变1】如图,线段AD 与BC 交于点O ,连接AB ,CD ,求证:∠A +∠B =∠C +∠D .【变2】(1)如图,求A B C D E ∠+∠+∠+∠+∠的度数.(2)如下图,已知133α∠=︒,83β∠=︒,求A B C D ∠+∠+∠+∠= .【拓1】(三叶草模型)如图所示,点E 和D 分别在ABC ∆的边BA 和CA 的延长线上,CF 、EF 分别平分ACB ∠和AED ∠,试探索F ∠与B ∠,D ∠的关系: .【拓2】如图,∠ABC +∠ADC =180°,OE 、OF 分别是角平分线,则判断OE 、OF 的位置关系__________.〖总结〗 70︒30︒E DCBA O DCBAABC D EFDCBAβαO F E D C BA【例8】在△ABC中.(1)如图①,点P在AC上(不同于A,C两点),∠BPC与∠A的大小关系是;(2)如图②,点P在△ABC内部,∠BPC与∠A的大小关系是;(3)如图③,点P是∠ABC,∠ACB平分线的交点,此时,∠BPC与∠A的等量关系是:;(4)如图④,点P是∠ABC的平分线与∠ACE的平分线交点时,∠BPC与∠A的等量关系是:;(5)如图⑤,点P是∠DBC与∠BCE的平分线交点,∠BPC与∠A的等量关系是:.【变】(1)在△ABC中,BD是ABC∠的角平分线,CD是∠ACB的外角平分线,BD、CD交于点D,若70∠=︒,则DA∠=__________.(2)在△ABC中,BI平分∠ABC,CI平分∠ACB,∠BIC=130°,则∠A=__________.(3)在△ABC中,点P是△ABC的∠A和∠C的外角平分线的交点,∠B=40°,则∠BPC=__________.【拓1】如图,已知BF、CE交于点D,BE、CF交于点A,∠AEC与∠ABF的平分线交于点M,∠ACE与∠AFB的平分线交于点N,试探究∠M与∠N的大小关系,并说明理由.【拓2】阅读下面的材料,并解决问题:已知在△ABC 中,∠A =60°. (1)如图(1),∠ABC 、∠ACB 的角平分线交于点O ,则∠BOC = ;(2)如图(2),∠ABC 、∠ACB 的三等分线交于点O 1、O 2,则∠BO 1C = ;∠BO 2C = ; (3)如图(3),∠ABC 、∠ACB 的n 等分线交于点O 1、O 2、……、O n -1,则∠BO 1C = ;∠BO n -1C = .(用含n 的代数式)图(1) 图(2) 图(3)〖总结〗【家庭作业】1、若△ABC 中,2(∠A +∠C )=3∠B ,则∠B 的外角度数为__________..2、如图,∠A =20°,∠C =90°,则∠B +∠D =__________.3、如图,已知70A ∠=︒,40B ∠=︒,20C ∠=︒,则BOC ∠度数为__________.4、如图,将纸片△ABC 沿着DE 折叠压平,则( ).A .12A ∠=∠+∠B .1(12)2A ∠=∠+∠C .1(12)3A ∠=∠+∠D .1(12)4A ∠=∠+∠5、如图,∠AEB ,∠AFD 的平分线相交于点O ,∠DAB +∠BCD =200°,则∠EOF 的度数为 .第2题图 第3题图 第4题图 第5题图 OB A CO 2O 1BA CCDA B CABCDE 12DCO FBPAE6、已知:在△ABC中,(1)如图(1),BD平分∠ABC,CD平分∠AC B.试判断∠A和∠BDC的关系.(2)如图(2),BE平分∠ABC,CE平分外角∠ACM.试判断∠A和∠BEC的关系.(3)如图(3),BF平分外角∠CBP,CF平分外角∠BCQ.试判断∠A和∠BFC的关系.7、如图,AD,AE分别是△ABC的高和角平分线.(1)已知∠B=40°,∠C=60°,求∠DAE的度数;(2)设∠B=α,∠C=β(α<β).请直接写出用α、β表示∠DAE的关系式____________.8、在△ABC 中,BO 平分∠ABC ,点P 为直线AC 上一动点,PO ⊥BO 于点O . (1)如图1,当∠ABC =40°,∠BAC =60°,点P 与点C 重合时,∠APO = _________ ; (2)如图2,当点P 在AC 延长线时,求证:∠APO =12(∠ACB ﹣∠BAC );(3)如图3,当点P 在边AC 所示位置时,请直接写出∠APO 与∠ACB ,∠BAC 等量关系式 _________ .9、如图,△ABC 三条角平分线AD 、BE ,CF 交于点G ,GH ⊥BC 于H ,求证:∠BGD =∠CGH .10、如图,在三角形ABC 中,42A ∠=︒,ABC ∠和ACB ∠的三等分线分别交于D 、E ,求B D C ∠的度数.11、如图,已知∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的角平分线与∠ABO的外角平分线交于点C.①当∠OAB=60°时,求∠ACB的度数;②试猜想,随着点A,B的移动,∠ACB的度数是否变化?说明理由.12、如图(1),AD,BC交于O点,根据“三角形内角和是180°”,不难得出两个三角形中的角存在以下关系:①∠DOC=∠AOB;②∠D+∠C=∠A+∠B.【提出问题】分别作出∠BAD和∠BCD的平分线,两条角平分线交于点E,如图(2),∠E与∠D、∠B之间是否存在某种数量关系呢?【解决问题】为了解决上面的问题,我们先从几个特殊情况开始探究.已知∠BAD的平分线与∠BCD的平分线交于点E.(1)如图(3),若AB∥CD,∠D=30°,∠B=40°,则∠E=.(2)如图(4),若AB不平行CD,∠D=30°,∠B=50°,则∠E的度数是多少呢?小明是这样思考的,请你帮他完成推理过程:易证∠D+∠1=∠E+∠3,∠B+∠4=∠E+∠2,∴∠D+∠1+∠B+∠4=,∵CE、AE分别是∠BCD、∠BAD的平分线,∴∠1=∠2,∠3=∠4.∴2∠E=,又∵∠D=30°,∠B=50°,∴∠E=度.(3)在总结前两问的基础上,借助图(2),直接写出∠E与∠D、∠B之间的数量关系是:.【类比应用】如图(5),∠BAD的平分线AE与∠BCD的平分线CE交于点E.已知:∠D=m°、∠B=n°,(m<n)求:∠E的度数.。
与三角形有关的角(提高) 知识讲解(82)

与三角形有关的角(提高)知识讲解【要点梳理】要点一、三角形的内角1. 三角形内角和定理:三角形的内角和为180°.要点诠释:应用三角形内角和定理可以解决以下三类问题:①在三角形中已知任意两个角的度数可以求出第三个角的度数;②已知三角形三个内角的关系,可以求出其内角的度数;③求一个三角形中各角之间的关系.2. 直角三角形:如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形.要点诠释:如果直角三角形中有一个锐角为45°,那么这个直角三角形的另一个锐角也是45°,且此直角三角形是等腰直角三角形.要点二、三角形的外角1.定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角.如图,∠ACD是△ABC的一个外角.要点诠释:(1)外角的特征:①顶点在三角形的一个顶点上;②一条边是三角形的一边;③另一条边是三角形某条边的延长线.(2)三角形每个顶点处有两个外角,它们是对顶角.所以三角形共有六个外角,通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.2.性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任意一个与它不相邻的内角.要点诠释:三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据.另外,在证角的不等关系时也常想到外角的性质.3.三角形的外角和:三角形的外角和等于360°.要点诠释:因为三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180°,可推出三角形的三个外角和是360°.知识点三、多边形的概念1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.2.相关概念:边:组成多边形的各条线段叫做多边形的边.顶点:每相邻两条边的公共端点叫做多边形的顶点.内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角。
专题02 与三角形相关的角(知识点串讲)(解析版)
专题02 与三角形有关的角知识网络重难突破一、三角形的内角和等于180°1. 三角形三个内角和等于180°.2.几种常见的证明三角形内角和为180 的方法:①添加平行线: 22112211 ②折叠:332211③把三角形的三个内角剪下来能拼成一个平角.典例1.(2021·山西九年级二模)在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A .B .C .D .【答案】C【分析】根据“直角三角形两锐角互余”是由三角形内角和定理推导的判断即可.【解析】解:∵“直角三角形两锐角互余” 是由三角形内角和定理推导的即,作CD AB ⊥后,利用直角三角形两锐角互余得到三角形内角和是180°的证明方法不正确, 故选:C .【点睛】本题主要考查三角形内角和定理,要证明三角形的内角和等于180°即三角形三个内角的和是平角,就要作辅助线,使得三角形的三个内角的和转化成组成平角的三个角之和.典例2.(2021·全国)直角三角形的两个锐角的度数比为1:3,则较小的锐角是__.【答案】22.5°.【分析】设两个锐角度数为x °,3x °,根据直角三角形中两个锐角互余列方程求解即可.【解析】设两个锐角度数为x °,3x °,由题意得:x +3x =90,解得:x =22.5,∴较小的锐角是22.5°.故答案为:22.5°.【点睛】本题考查了直角三角形两个锐角互余,以及一元一次方程的应用,根据性质列出方程是解答本题的关键.典例3.如图,ABC 中,50A ∠=︒,点E ,F 在,AB AC 上,沿EF 向内折叠AEF ,得DEF ,则图中12∠+∠等于( )A .130︒B .120︒C .65︒D .100︒【答案】D【分析】根据三角形的内角和等于180°求出∠AEF +∠AFE 的度数,再根据折叠的性质求出∠AED +∠AFD 的度数,然后根据平角等于180°解答.【解析】解:∵∠A =50°,∴∠AEF +∠AFE =180°-50°=130°,∵沿EF 向内折叠△AEF ,得△DEF ,∴∠AED +∠AFD =2(∠AEF +∠AFE )=2×130°=260°,∴∠1+∠2=180°×2-260°=360°-260°=100°.故选:D .【点睛】本题考查了三角形的内角和定理,翻转变换的性质,整体思想的利用是解题的关键.二. 直角三角形 ↔ 2个锐角互余直角三角形:如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形.常考知识点:如果直角三角形中有一个锐角为45°,那么这个直角三角形的另一个锐角也是45°,且该三角形是等腰直角三角形.典例1.(2020·利辛县启明中学八年级月考)在下列条件中,能确定ABC 是直角三角形的条件有( ) ①A B C ∠+∠=∠,②::1:2:3A B C ∠∠∠=,③90A B ∠=︒-∠,④A B C ∠=∠=∠A .1个B .2个C .3个D .4个【答案】C【分析】结合三角形的内角和为180°逐个分析4个条件,可得出①②③中∠C=90°,④能确定ABC 为等边三角形,从而得出结论.【解析】解:①∵∠A+∠B=∠C,且∠A+∠B+∠C=180°,∴∠C+∠C=180°,即∠C=90°,此时ABC 为直角三角形,①符合题意;②∵∠A:∠B:∠C=1:2:3,∴∠A+∠B=∠C,同①,此时ABC 为直角三角形,②符合题意;③∵∠A=90°-∠B,∴∠A+∠B=90°,∴∠C=90°,③符合题意;④∵∠A=∠B=∠C,且∠A+∠B+∠C=180°,∴∠A=∠B=∠C=60°,∴ABC为等边三角形,④不符合题意;综上可知:①②③能确定ABC为直角三角形.故选:C.【点睛】本题考查了直角三角形的定义以及三角形内角和定理,解题的关键是结合三角形的内角和定理逐个分析4个条件.三、三角形的外角的性质1.三角形的外角:三角形的一边与另一边的延长线组成的角叫做三角形的外角.注意:三角形每个顶点处有两个外角,它们是对顶角.所以三角形共有六个外角,通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.2.三角形外角的性质:①三角形的一个外角等于与它不相邻的两个内角的和.②三角形的一个外角大于任意一个与它不相邻的内角.③三角形的外角和等于360°.等于()典例1.(2021·湖南八年级期末)将一副三角板按如图所示的方式放置,则DACA.75°B.90°C.105°D.120°【答案】C【分析】根据三角板的每个角度及三角形的有关性质求解.【解析】解:在△AFC中,由三角形外角性质可得:∠DAC=∠DFC+∠C=60°+45°=105°,故选C.【点睛】本题考查三角形的综合应用,熟练掌握三角板的构成及三角形的外角性质是解题关键.典例2.(2021·辽宁八年级期中)如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD =30°,则∠DCE的度数为_____.【答案】70°.【分析】由三角形的外角的性质定理得到∠ACE=∠A+∠ABC,∠DCE=∠CBD+∠D,再由已知∠ABD=∠CBD,∠A=∠D=40°,∠ACD=30°解方程组可求得结果.【解析】∵BD平分∠ABC,∴∠ABD=∠CBD,∵∠ACE=∠A+∠ABC=40°+2∠CBD,∴∠DCE+∠ACD=∠A+2∠CBD,∵∠DCE=∠CBD+∠D,∠A=∠D=40°,∠ACD=30°,∴∠DCE+30°=40°+2∠CBD,即∠DCE=2∠CBD+10°①,∠DCE=40°+∠CBD②,由①②得∠DCE=70°,故答案为:70°.【点睛】本题主要考查了三角形的外角的性质定理,角平分线的定义,熟练应用三角形的外角的性质定理是解决问题的关键.典例3.(2020·山东八年级期中)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为___________.【答案】360°【分析】根据三角形的外角等于不相邻的两个内角的和,以及多边形的内角和即可求解.【解析】解:∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,∠4=∠G+∠H,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=∠1+∠2+∠3+∠4,又∵∠1+∠2+∠3+∠4=360°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.故选:D..【点睛】本题考查了三角形的外角的性质以及多边形的外角和定理,正确转化为多边形的外角和是关键.四. 多边形的对角线1. 多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.如果多边形的任何一边所在直线都使余下的边都在这条直线的同一侧,这样的多边形叫做凸多边形.①多边形的边:组成多边形的各条线段叫做多边形的边.②多边形的顶点:每相邻两边的公共端点叫做多边形的顶点.③正多边形:各个角相等,且各条边都相等的多边形叫做正多边形.(两个条件缺一不可)④多边形的对角线:在多边形中,连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.n边形的对角线:一个顶点有(3)n-条对角线,共有(3)2n n-条对角线.典例1.观察下面图形,并回答问题.(1)四边形有_______条对角线;五边形有_______条对角线:六边形有_______条对角线.n 边形有______条对角线;(无需证明)(2)若一个多边形有35条对角线,这个多边形的边数是?【答案】见解析【分析】(1)根据图形求出多边形的对角线条数;(2)设这个多边形的边数是n ,由题意得:()3352n n -=,解方程即可得出答案.【解析】解:()1观察图形可得:四边形的对角线的条数为:()43414222-⨯⨯==; 五边形的对角线的条数为:()53525522-⨯⨯==; 六边形的对角线的条数为:()63636922-⨯⨯==; ⋅⋅⋅依次类推:n 边形的对角线的条数为:()32n n -. ()2设这个多边形的边数是n ,由题意得:()3352n n -=, 解得:110n =,27n =-(不合题意,舍去).答:这个多边形的边数是10.【点睛】本题主要考查了多边形对角线的条数的公式总结,熟记公式对今后的解题大有帮助.五. 多边形的内角和1. 多边形的内角:多边形相邻两边组成的角叫做它的内角.2. n 边形的内角和为(n-2)·180°(n ≥3).证明方法:分割成(n-2)个三角形求内角和3.正多边形的每个内角都相等,都等于n-°;(2)180n典例1.(2021·内蒙古包头市·八年级期末)若多边形的边数由n增加到n+1(n为大于3的正整数),则其内角和的度数()A.增加180°B.减少180°C.不变D.不能确定【答案】A【分析】根据多边形的内角和定理即可求出答案.【解析】解:n边形的内角和是(n−2)•180°,n+1边形的内角和是(n+1−2)•180°=(n−1)•180°,则(n−1)•180°−(n−2)•180°=180°,故选:A.【点睛】此题考查了多边形的内角与外角,正确理解多边形的内角和定理是解决的关键.典例2.(2021·浙江八年级期末)如果一个多边形的内角和等于540°,则它的边数为()A.3 B.4 C.5 D.6【答案】C【分析】根据n边形的内角和为(n-2)•180°得到(n-2)•180=540,然后解方程即可.【解析】解:设这个多边形的边数为n,∴(n-2)•180=540,∴n=5.故选:C.【点睛】本题考查了多边行的内角和定理:n边形的内角和为(n-2)•180°.典例3.若一个正多边形的每个内角为144︒,则这个正多边形的边数是()A.7 B.10 C.12 D.14【答案】B【分析】根据多边形的内角和公式,可得答案.【解析】解:设正多边形是n边形,由内角和公式得(n-2)180°=144°×n,解得n=10,故选:B.【点睛】本题考查了多边形内角与外角,由内角和得出方程是解题关键.典例4.一张四边形纸片剪去一个角后,内角和将()A.减少180°B.不变C.增加180°D.以上都有可能【答案】D【分析】若剪掉四边形相邻两条边的一部分,则剩下的部分是五边形.若从四边形一个角的顶点,沿直线向对角的邻边剪,且只剪掉一条邻边的一部分,则剩下的部分为四边形.若沿着四边形的对角线剪,则剩余部分为三边形(三角形).即可求得内角和的度数.【解析】解:如下图所示:观察图形可知,四边形剪掉一个角后,剩下的图形可能是五边形,也可能是四边形,还可能是三角形.则剩下的纸片图形是三角形或四边形或五边形.内角和是:180°或360°或540°.故选:D.【点睛】本题考查了多边形的内角和,解题的关键是能理解一个四角形截取一个角后得到的图形的形状.典例5.在计算一个多边形内角和时,多加了一个角,得到的内角和为1500°,那么原多边形的边数为()A.9 B.10 C.11 D.10或11【答案】B【分析】设多加上的一个角的度数为x,原多边形的边数为n,根据多边形内角和定理,列出等式,进而即可求解.【解析】设多加上的一个角的度数为x,原多边形的边数为n,则(n-2)×180+x=1500,(n-2)×180=8×180+60-x,∵n-2为正整数,∴60-x能被180整除,又∵x>0,∴60-x=0,∴(n-2)×180=8×180,∴n=10,故选B【点睛】本题主要考查多边形的内角和定理,根据定理,列出方程,是解题的关键.六. 多边形的外角和1. 多边形的外角和为360°.注意:在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n边形的外角和恒等于360°,它与边数的多少无关;2. 正n边形的每个内角都相等,所以它的每个外角都相等,都等于360n°;典例1.(2021·山东青岛市·八年级期末)如图,小明从A点出发,沿直线前进16米后向左转45°,又向左转45°,…,照这样走下去,共走路程为()A.96米B.128米C.160米D.192米【答案】B【分析】根据多边形的外角和即可求出答案.【解析】解:根据题意可知,他需要转360÷45=8次才会回到原点,所以一共走了8×16=128(米).故选:B.【点睛】本题主要考查了利用多边形的外角和定理求多边形的边数.任何一个多边形的外角和都是360°.典例2.(2021·山东八年级期末)如图,1234∠+∠+∠+∠的度数为__________.【答案】360︒【分析】根据多边形的外角和定理即可求解.【解析】解:由多边形的外角和定理知,∠1+∠2+∠3+∠4=360°,故答案是:360°.【点睛】本题考查了多边形的外角和定理,理解定理是关键.典例3.(2021·河北八年级期末)如图,在正八边形ABCDEFGH 中,对角线BF 的延长线与边DE 的延长线交于点M ,则M ∠的大小为__________.【答案】22.5︒【分析】利用正多边形的内角和公式与外角和公式结合题意即可求出45FEM ∠=︒,67.5EFB ∠=︒,再利用三角形外角性质即可求出M ∠. 【解析】解:根据正八边形的性质可知360458FEM ︒∠==︒,180(82)1358EFG ︒⨯-∠==︒, 由图可知1113567.522EFB EFG ∠=∠=⨯︒=︒, ∴67.54522.5M EFB FEM ∠=∠-∠=︒-︒=︒.故答案为:22.5︒.【点睛】本题考查正多边形的内角和与外角和公式以及三角形外角的性质.掌握正多边形的内角和与外角和公式是解答本题的关键.巩固训练一、单选题1.(2021·四川九年级一模)如图,//AB CD ,80C ∠=︒,∠CAD =60°,BAD ∠的度数等于( )A .60°B .50°C .45°D .40°【答案】D 【分析】根据三角形的内角和为180°,即可求出∠D 的度数,再根据两直线平行,内错角相等即可知道∠BAD 的度数.【解析】解:∵∠C =80°,∠CAD =60°,∴∠D =180°-80°-60°=40°,∵AB ∥CD ,∴∠BAD =∠D =40°.故选:D .【点睛】本题考查了三角形的内角和为180°,以及两直线平行,内错角相等的性质,难度适中.2.(2021·全国九年级专题练习)如图,ABC 中,65A ∠=︒,直线DE 交AB 于点D ,交AC 于点E ,则BDE CED ∠+∠=( ).A .180︒B .215︒C .235︒D .245︒【答案】D 【分析】根据三角形内角和定理求出ADE AED ∠+∠,根据平角的概念计算即可.【解析】解:65A ∠=︒,18065115ADE AED ∴∠+∠=︒-︒=︒,360115245BDE CED ∴∠+∠=︒-︒=︒,【点睛】本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180︒是解题的关键.3.(2020·涿州市实验中学八年级期中)下列说法中错误的是( )A .在△ABC 中,若∠A :∠B :∠C =2:2:4,则△ABC 为直角三角形B .在△ABC 中,若∠A =∠B ﹣∠C ,则△ABC 为直角三角形C .在△ABC 中,若∠A =12∠B =13∠C ,则△ABC 为直角三角形 D .在△ABC 中,∠A =∠B =2∠C ,则△ABC 为直角三角形【答案】D【分析】根据三角形内角和定理求出三角形的三个内角即可判断.【解析】解:A 、在△ABC 中,因为∠A :∠B :∠C =2:2:4,所以∠C =90°,∠A =∠B =45°,△ABC 为直角三角形,本选项不符合题意.B 、在△ABC 中,因为∠A =∠B ﹣∠C ,所以∠B =90°,△ABC 为直角三角形,本选项不符合题意. C 、在△ABC 中,因为∠A =12∠B =13∠C ,所以∠C =90°,∠B =60°,∠A =30°,△ABC 为直角三角形,本选项不符合题意. D 、在△ABC 中,因为∠A =∠B =2∠C ,所以∠A =∠B =72°,∠C =36°,△ABC 不是直角三角形,本选项符合题意,故选:D .【点睛】本题考查三角形内角和定理,直角三角形的判定和性质等知识,解题的关键是熟练掌握三角形内角和定理,属于中考常考题型.4.(2021·陕西八年级期末)如图,已知12//l l ,45A ∠=︒, 2100∠=︒,则1∠的度数为( )A .50°B .55°C .45°D .60°【分析】依据12//l l ,得到1ABC ∠=∠,再根据45A ∠=︒,2100A ABC ,即可得到55ABC ∠=︒,可得出155ABC .【解析】解:12//l l ,1ABC ∴∠=∠,又45A ∠=︒,2100A ABC , 21004555ABC A ,155ABC故选:B .【点睛】本题考查了平行线的性质,三角形的内角和定理,外角的性质,熟悉相关性质是解题的关键.5.如图,1∠,2∠,3∠,4∠一定满足的关系式是( )A .1234∠+∠=∠+∠B .1243∠+∠=∠-∠C .1423∠+∠=∠+∠D .1423∠+∠=∠-∠【答案】D 【分析】根据外角的性质分别得到∠AEF =∠4+∠3,∠2=∠1+∠AEF ,从而推断出∠2–∠3=∠1+∠4.【解析】解:如图,在△BED 中,∠AEF =∠4+∠3,在△AEF 中,∠2=∠1+∠AEF ,∴∠2=∠1+∠4+∠3,即∠2–∠3=∠1+∠4,故选:D .【点睛】本题考查了三角形外角的性质,解题的关键是根据外角的性质得到∠AEF=∠4+∠3,∠2=∠1+∠AEF.6.(2021·浙江八年级期末)从六边形的一个顶点出发最多能画对角线的条数为()A.5条B.4条C.3条D.2条【答案】C【分析】根据由n边形的一个顶点可以引(n-3)条对角线解答即可.【解析】解:由n边形的一个顶点可以引(n-3)条对角线,故过六边形的一个顶点可以画对角线的条数是3,故选:C.【点睛】本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.掌握n 边形从一个顶点出发可引出(n-3)条对角线是解题的关键.7.一个正多边形的一个内角是150 ,则这个正多边形的边数为()A.2 B.3 C.9 D.12【答案】D【分析】一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.【解析】解:外角是:180°-150°=30°,360°÷30°=12.则这个正多边形是正十二边形.故选:D.【点睛】本题考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数是解题关键.8.(2021·陕西八年级期末)若一个正多边形的一个外角是45°,则这个正多边形的边数是()A.7 B.8 C.9 D.10【答案】B【分析】根据正多边形每个外角都相等且外角和为360°列式解答即可.【解析】解:∵正多边形每个外角都相等且外角和为360°∴正多边形的边数是360°÷45°=8.故选B.【点睛】本题主要考查了正多边形的外角的性质和外角和,灵活运用正多边形每个外角都相等且外角和为360°成为解答本题的关键.二、填空题9.(2020·辽宁七年级期中)“生活中处处有数学”,请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,我们就可以得到一个著名的常用的几何结论,这一结论是____.【答案】三角形的内角和是180°【分析】根据折叠前后的两个角相等,把三角形的三个角转化为一个平角,可以得到三角形内角和定理.【解析】解:根据折叠的性质,∠A=∠3,∠B=∠1,∠C=∠2,∵∠1+∠2+∠3=180°,∴∠B+∠C+∠A=180°,∴定理为:三角形的内角和是180°.故答案为:三角形的内角和是180°.【点睛】本题主要考查了三角形的内角和定理的证明,熟练掌握翻折变换的性质是解题的关键.10.(第十三章相交线平行线(基础卷)-2020-2021学年七年级数学下学期期末专项复习(沪教版))如图,AB∥MN,点C在直线MN上,CB平分∠ACN,∠A=40°,则∠B的度数为__.【答案】70°【分析】先由AB ∥MN 知∠A +∠ACN =180°,结合∠A 度数得出∠ACN 的度数,再由CB 平分∠ACN 知∠ACB =12∠ACN =70°,最后根据三角形内角和定理可得答案.【解析】解:∵AB ∥MN ,∴∠A +∠ACN =180°,又∵∠A =40°,∴∠ACN =180°﹣∠A =140°,∵CB 平分∠ACN ,∴∠ACB =12∠ACN =70°,∴∠B =180°﹣∠A ﹣∠ACB =70°,故答案为:70°.【点睛】本题主要考查了与平行线有关的三角形内角和问题,结合角平分线的性质求解是解题的关键.11.(2020·山西八年级期末)边长相等的正方边形ABFG 和正五边形BCDEF 如图所示拼接在一起,则∠FGE =____°.【答案】9【分析】根据多边形的内角和定理计算即可;【解析】∵四边形ABFG 是正方形,∴90BFG ∠=︒,又∵五边形BCDEF 是正五边形,∴正五边形的内角和为()52180540-⨯︒=︒,∴5405108BFE ∠=︒÷=︒,∴36010890162GFE ∠=︒-︒-︒=︒,∵FG FE =,∴FGE FEG ∠=∠,∴180FGE FEG EFG ∠+∠+∠=︒,即1602180FGE ︒+∠=︒,∴9FGE ∠=︒;故答案是9.【点睛】本题主要考查了多边形内角和定理,准确分析计算是解题的关键.12.(2020·贵州黔西南布依族苗族自治州·八年级期末)一个多边形,除了一个内角外,其余各角的和为3000°,则内角和是______.【答案】3060【分析】设这个多边形是n 边形,剩余的内角度数为x ,根据题意得(2)1803000n x -⨯=+变形 为18016(120)2180x n ⨯++-=,由n 是正整数,0180x <<求出x 的值即可得到答案. 【解析】设这个多边形是n 边形,剩余的内角度数为x ,由题意得(2)1803000n x -⨯=+∴18016(120)2180x n ⨯++-=, ∵n 是正整数,0180x <<, ∴x=60,∴这个多边形的内角和为3060,故答案为:3060.【点睛】此题考查多边形的内角和公式,多边形内角大于0度小于180度的性质,熟记多边形的内角和公式是解题的关键.13.(2021·甘肃酒泉市·八年级期末)一个多边形的每一个内角都是144︒,那么这个多边形是_____边形.【答案】10.【分析】根据题意,利用多边形的外角和为360度,即可求得.【解析】一个多边形的每一个内角都是144︒ ∴它的每一个外角都是18014436︒-︒=︒.多边形的外角和为360︒∴边数等于角的个数3603610=︒÷︒=.故答案为:10.【点睛】本题考查了多边形外角和定理,正多边形的特点,通过外角解决问题是解题的关键.14.(2021·上海奉贤区·八年级期中)一个多边形的内角和是它的外角和的3倍,则这个多边形是_____边形.【答案】八【分析】多边形的内角和为()2180,n -︒外角和为360,︒ 再列方程()21803360,n -︒=⨯︒解方程可得答案.【解析】解:设这个多边形为n 边形,则()21803360,n -︒=⨯︒26,n ∴-=8,n ∴=故答案为:八【点睛】本题考查的是多边形的内角和与外角和,掌握多边形的内角和定理与外角和定理是解题的关键.15.若正多边形的一个外角为40︒,则从此多边形的一个顶点出发可作的对角线共有________条.【答案】6【分析】根据多边形的外角和定理可求解多边形的边数,再根据从多边形的一个顶点出发可作的对角线为(n -3)条可求解.【解析】解:∵多边形的外角和为360︒,∴360409︒÷︒=;从它的一个顶点出发,可以引出936-=条对角线.【点睛】本题主要考查多边形的外角和对角线,掌握定理是解题的关键.16.(2020·北京师范大学三帆中学朝阳学校八年级月考)如图,小张从P 点向西直走10米后,向左转,转动的角度为α,再走10米,如此重复,小林共走了100米回到点P ,则α的值是___________.【答案】36°【分析】根据题意可先确定出该多边形的边数,再利用外角和求解即可. 【解析】由题可知,小张全程下来走了一个正多边形,且边数1001010n ==, ∴根据多边形的外角和定理可求得:3603610α︒==︒,故答案为:36°.【点睛】本题考查多边形的外角和定理,根据题意准确判断多边形的边数是解题关键.三、解答题17.在一个直角三角形中,如果两个锐角度数之比为2:3,那么这两个锐角为多少度?【答案】见解析【分析】根据比例设两个锐角度数分别为2k ,3k ,然后根据直角三角形两锐角互余列出方程求解即可.【解析】解:设两个锐角度数分别为2k ,3k ,由题意得,2390k k +=,解得18k =,所以,236k =,354k =,故这两个锐角分别为36°,54°【点睛】本题考查了直角三角形两锐角互余的性质,利用“设k 法”表示出这两个锐角求解更简便.18.四边形ABCD 中,四个内角度数之比是1:2:3:4,求出四个内角的度数.【答案】见解析【分析】设四个内角度数分别是x °,2x °,3x °,4x °,由多边形内角和公式可得:x +2x +3x +4x =180(4-2),再解方程即可得到答案.【解析】解:设四个内角度数分别是,2,3,x x x 4x ,根据题意得:()23442180x x x x +++=-⨯,解得:36x =,272,3108,4144x x x === .答:四边形的四个内角的度数分别为:36,72,108,144 .【点睛】此题主要考查了多边形内角公式,解题的关键是掌握内角和公式:()2180n -⨯︒(3n ≥,且n 为整数) .。
有关三角形的角PPT课件

直角三角形中特殊角度关系
互余关系
在直角三角形中,两个锐角互余,即 它们的角度和为90度。
勾股定理
在直角三角形中,直角边的平方和等 于斜边的平方。
特殊角度
如30度、45度、60度等。在含有这些 特殊角度的直角三角形中,边与边之 间存在一定的比例关系。
相似三角形角度关系
相似三角形的定义
两个三角形的对应角相等,则这 两个三角形相似。
电磁学中的角度
在电磁学中,角度影响电场和磁场的分布和强度,如电磁波的传 播方向与电场、磁场之间的夹角。
05
三角形角度相关数学竞赛题解 析
Chapter
数学竞赛中常见题型介绍
角度计算题
通过已知条件,求解三角形内角或外角的度数。
角度关系证明题
证明三角形中某些角之间的特定关系,如相等、 互补等。
角度与边长关系题
探究三角形角度与边长之间的内在联系,如正弦 定理、余弦定理的应用。
经典数学竞赛题解析与讨论
经典题目一
已知三角形ABC中,角 A=60度,角B和角C的 度数比是2:3,求角B和 角C的度数。
经典题目二
在三角形ABC中, AB=AC,D是BC上一点 ,且BD=AD,求角 BAC的度数。
经典题目三
三角形ABC中,角A、B 、C的对边分别为a、b 、c,且满足 a^2+b^2+c^2+338= 10a+24b+26c,试判 断三角形ABC的形状。
有关三角形的角PPT课件
目录
• 三角形基本概念及性质 • 三角形角度关系探究 • 三角形角度计算方法 • 三角形角度在实际问题中应用 • 三角形角度相关数学竞赛题解析
01
三角形基本概念及性质
三角形有关的角度计算
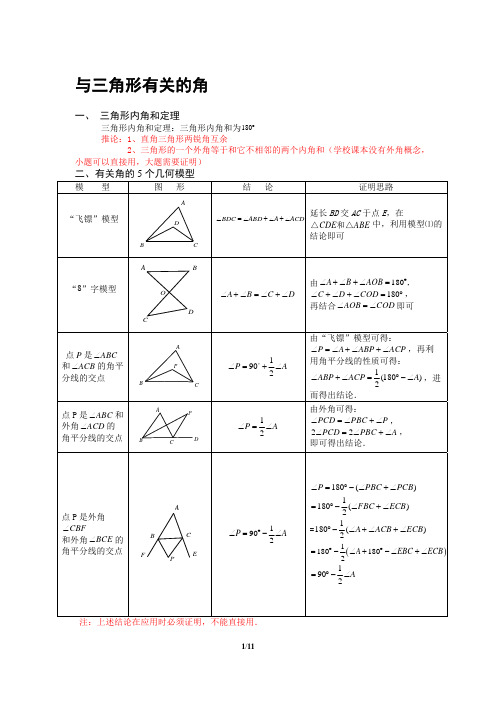
与三角形有关的角一、三角形内角和定理三角形内角和定理:三角形内角和为180︒推论:1、直角三角形两锐角互余2、三角形的一个外角等于和它不相邻的两个内角和(学校课本没有外角概念,小题可以直接用,大题需要证明)1. 【易】(2010年重庆巴蜀中学初一下期中)如图所示,已知,OB OA OD OC ==,且65,20O C ∠=︒∠=︒,则AEB ∠的度数为( )A .90︒B . 115︒C . 95︒D . 105︒2. 【易】(2010湖北武汉二中初一下期中)如图,在直角三角形中,,是斜边上的高,,,垂足分别为、,则图中与(除之外)相等的角的个数是( )A .B .C .D .3. 【易】(北京汇文中学2013年初一数学第二学期期中考试试卷)适合条件1123∠=∠=∠A B C 的ABC △是( )A .锐角三角形B .直角三角形C .钝角三角形D .等边三角形4. 【易】(2009年大兴一模)把两块含有的相同的直角三角尺按如图所示摆放,使点、、在同一直线上,连结,则等于( )A .B .C .D .5. 【中】(2009年武珞路中学七年级下期中)如图,已知140A BCD ∠+∠=︒,BO 平分ABC ∠,DO 平分ADC ∠,则BOD ∠=( )A .40︒B .60︒C .70︒D .80︒6. 【中】(2012年昌平二中初一第二学期期中)如下几个图形是五角星和它的变形.DOEC BAABC AC AB ≠AD BC DE AC ⊥DF AB ⊥E F C ∠C FEDCBA234530︒C B E CD BCD ∠15︒30︒35︒45︒OFEDCBAAC B DE7. 8. 3.内9. ⑴ 图①中是⑵ 如果把图(即CAD ∠⑶如果把图(即CAD ∠【易】(中的延长线上D ∠的度数【中】(北小学已学习的度数和为结合上述知已知如图1之为“字问题一:⑴ 在图1中⑵ 如图2,别相交于⑶ 在⑵的条之间的数量问题二:如图3,的平内外角角分线【易】(20角平分线A 8AD ABC ∠AC是一个五角星图①中的点D B C +∠+∠图②中的点C D B AC +∠+∠中关村中学20上,过D 作D 数__________北京十二2013习:三角形的为180︒,上述知识,完成如,线段字形”. 中,请直接写和M 、N ,若条件下,若图量关系. ,且平分线线模型012年杭州市AD ,BE所在AB DAB ∠D BC ∥DQ 图1 OD星,求A ∠+∠A 向下移到B D E +∠+∠)向上移动到CE D +∠+∠014届初一第DE AB ⊥于E ___. 3学初一数学内角和为述结论不受三下问题: 、相交子写出、的平,图2中的且和和相交于市坎山镇中初在直线所成的18CD A ∠BCD ∠40D =︒∠∠DAB ∠BQACBB C +∠+BE 上,形成)有无变化?BD 上,形成E )有无变化第二学期期中,交AC 学第二学期期,即对于三角形的形状子点,连接、、平分线和,和为任的平分点,判断初一第二学期的角的度数是80︒O B ∠C ∠AP 36B =︒∠D B ∠BCD ∠Q 图2 4321MNO D E ∠+∠.成如图②的图?说明你的结成如图③的图化?说明你的中考试)如图于F .已知期末考试试题于任意三角形状与大小的影接、之间的相交于点请直接写出任意角,请直分线和断与期期中)在△是( )AD CB D ∠CP AP C P ∠Q ∠ PBD形,则图②中结论的正确性图形,则此时的结论的正确图,ABC △中30A ∠=︒,∠题)ABC △,∠响. ,我们把形的数量关系;点,并且与出的度数直接写出相交于点的大小关系ABC 中,∠P P ∠∠CP QAC中五个角的和性.时五个角的和确性.中,点D 在B 80FCD =︒,A 、B ∠、如图1的图形 与、数; 与、点,,并说明理60C =︒.两CD AB P D ∠P ADC∠ 图3O和和BC则C∠形称分和由.两条B ∠C P BD10.11.12. 13.14. 则A .60︒ 【易】如图40D ∠=︒.A .50︒【易】(北分线的交点CAB ∠的度A .36︒ 【中】(武ABC ∠的平平分ACB ∠④BOC ∠= A .①③④ 【中】(20若50A ∠=A .15︒ 【易】(204∠=____1BA图,在ABC ∆则A ∠等于 北达资源中学点,点N 是度数为( 武汉二中广雅平分线与AB △B ,以下结论2COP ∠+∠011年北京八︒,10D ∠= 012年成都金___度.AMCBB .120︒ 中,B ∠的平于( )B .60︒ 学初一下学期数ABC △两个外)B .42︒ 雅中学七年级BC 的外角∠论: ①OCP ∠P .B .②③④八十中初一下︒,则P ∠的度B .20︒ 金牛初一下期2EDC 平分线与∠数学期中测试外角平分线的 (下)数学月ACD 的平分90CP =︒;②下期中)如图度数为( 期末)如图,C .150︒ C 的外角平分C .70︒ 试)如图:点的交点,如果C .54︒ 月考(四))分线相交于点②90BOC ∠=C .①②③图,ABD ∠,)C .25︒ 若130∠=︒D 分线相交于D D 点M 是AB △果:CMB C∠∠ D )如图,在△点P ,O 是B 12A ︒+∠;③ D ACD ∠的角 D ,295∠=︒,.60︒或12,.80︒ BC 两个内角3:2CNB =,.60︒ABC 中,BP 上一点,③12P A ∠=∠.①②③④角平分线交于.30︒335∠=︒,0︒角平则CO;④点P ,15.16.17.18.19.【易】(2050ACB∠=【易】(20ACB∠与∠A∠的度数【中】(清线,可知∠CP仍然是【中】(20ACD∠的平2A∠;……__________【中】如右BE、CE交1BA012年昌平二︒,BP平分011年天津红ABC的角平为_______.清华附初一下90BPC=︒B∠、C∠的010年昌平五平分线交于点…,2008A BC∠__.右图所示,在交于E,BD423AC二中初一第二分ABC∠,CP红桥区七年级平分线的交点期中)如图⑴12A+∠,把图的平分线,猜五中七下期中点1A,得1A∠与2008A CD∠在ABC∆中,D、CD交于A21D二学期期中)P平分ACB∠级第二学期期.BD的延长⑴,BP、C图⑴中的A△猜想BPC∠与中试卷)如图;1A BC∠D的平分线相CD、BE是D,试探索如图,AB△B.则BPC∠中考试数学长线交ACCP是任意ABC变成⑵中A∠、D∠的图,在ABC△与1A CD∠的平相交于点2009A是外角平分线D∠与E∠的BC中,AB∠C的度数____)如图在A△于E,且ED∠ABC△中B∠中的四边形A的数量关系是C中,A a∠=平分线相交于,得2009A∠.线,BD、C的关系:____80BC=︒,____________ABC中,D50DC=︒,则、C∠的角平ABCD,BP是__________,ABC∠于点2A,得.则2009A∠CE是内角平_______._.是则平分、_.与=分线,20.21.22.23.【易】(20个相等的角⑴求P∠的度⑵若MON∠⑶经过⑴,【中】如图E,求BD∠【中】(20⑴如图1,⑵如图2,动,探究:⑶如图3,EP交于点探究:P∠【中】(20⑴如图1,系是______⑵如图2,A∠的关系是⑶如图3,关系是____010年初一下角.即MAP∠度数;80N=︒,其余⑵的计算,图,在三角形DC的度数.012年北京八两条斜边所当DEF△中在DEF△转当DEF△转P.的度数是否发012年江苏省BO、CO分___________BO、CO分是_________BO、CO分___________下期中)计算PPAB=∠,余条件不变,猜想并证明形ABC中,∠八十中初一下所形成的钝角中的直角边E转动过程,∠转动到如图所发生变化?并省苏州市相城分别是ABC△_____(直接分别是ABC△___________分别是ABC△_______,请证算题:如图,BP把ABN∠,求P∠的度MON∠与42A= ,下期中)将一角α的度数是EF绕点C转αβ+∠的大所示的位置时并说明理由;城区第二学期C中ABC∠写出结论);C两个外角__,请证明你C一个内角和证明你的结论90MON∠=N平分成两个度数;P∠的关系.ABC∠和A∠一副三角板按是______.转动时(0︒<大小是否发生时,作FCB∠期期中考试初和ACB∠的平;CBD∠和B∠你的结论.和一个外角的论.0︒,AP把∠个相等角,即ACB的三等分如图方式放置45β<︒),生变化?并说B、FEB∠的一数学试卷)平分线,则∠CE的平分线的平分线,则MAB平分成即ABP N∠=∠分线分别交于置.ACB△保持说明理由.的平分线CP)BOC与A∠线,则BOC∠则BOC∠与成两NBP.于D、持不、的关C与A∠的24.25.26.⑷利用以上OF、OD上P,猜想【易】(20分线,交点(过程不写【中】(20试判断AE∠【中】(20高,AE、度数.B上结论完成以上的动点,P∠的大小是否010年深圳外点为点O,O写理由)012年北京ED与ACB∠011年河南省BF是角平分OA图1下问题:如ABO△的外角否变化?请证外国语初一下H BC⊥于点101初一第的大小关系省实验中学内分线相交于点C D图4FOA图4,已知:角OBE∠的平证明你的猜想下测试)已知点H,请写出二学期期中系,并对结论内部中考数学点O,BAC∠图2BOAPB9DOF∠=平分线与内角想.知:AD、BE出BOD∠与)如图,已知进行证明.学第一轮复习50,C C=︒∠=CEDE0︒,点A、角OAB∠的平E、CF是△COH∠的关系知12∠+∠=资料3)A△70︒,求D∠BA图3B分别是射线平分线相交于ABC三条角系,并说明理180︒,3∠ABC中,ADDAC,BOA∠CO线于点角平理由B=∠,D是A的D27.28.29.【中】(20ABC∠,且【中】(20从点出发利用上述知如下图,若反射:在若⑴写出⑵若第次【中】(清点在⑴ 作⑵ 如图2,动的时候⑶ 当的化,如果2PECAA01OA A∠A∠n1n n nA A A-+∠C AQACB∠A∠011年育才中且12∠=∠,012年十一中发经过镜面反知识以及你所若、是处进行第一,_____次反射后,反射________清华附中初一上,连接和的作候,的大小在大于果变化请写出1FDBAOB OC1102OA A=∠12A A=1=CBB ABD∠PBC∠M∠+中学初一下期DC与BE交中学第二学期反射后(是所学过的数学是两个平面镜一次反射,在____;射光线能与平__;(是大一下期中)如并延长.的平分线交于和的平的度数和于小于出ODOθ∠=1A A∠nBBCQ∠N∠0︒90︒M N∠+∠期末)已知:交于点F.期七年级数学是反射光线知识,解决下镜,一束光线在处进行第______平面镜相交,大于等于1的图1,两条射于点,探平分线交于点会如何变化间变化时,的变化范围2A23A=M如图所示,在学期中练习试),有性质下列问题:线从出发,第二次反射…___;根据上面所的整数)射线、探索与点,问当?并给出理由请直接回答.A23A A∠AP AM∠∠N在ABC△中卷)材料:如.在这两个平……_______所求的结果,交于点的关系;点和点在由.:12∠=∠4A=AQ AAB CM N∠+∠中,BE平分如图,一束光平面镜之间来__;猜测,点在在和的度数是否B AAP AQ光线来回上,上运否变AP30.31.32.【中】(201⑴判断⑵若将直线判断图)【中】如图.⑴求⑵在⑴中,与⑶如图乙、、之【中】(20直角三角形BDC A∠=∠F∠ADH∠BAC∠EAD∠BEAD∠B∠C∠B1年三帆初一,过点与线绕这点、、图甲,在.若将、之间图丙,平之间又有什么010年武汉市形,ACBFDA BCD∠DFH AHD∠AB△D甲E DA7C∠=B∠C∠AE乙FADE9AOB∠=一下期中)如图作直线之间存在的点旋转(不之间中,间的数量关系平分,么数量关系?市新洲区初一,斜边DDFDDBCD∠BC∠C70,50B︒∠=BAC∠BC90︒A图,已知,使的数量关系,不含与、间存在的数量,,改为“系吗?为上?请你任意选一下期末)如与轴交A△F DFAB70C=︒∠︒∠F AE丙FADEAB y,,并证明;重合的量关系并证明,”,而上一点,选择其中一种如图,在平面于点.ABC DAC∥CD50B=︒ADC B>∠FDCC为边上一点情况),交明.(如有需垂直于而其它条件不于,种情况证明.直角坐标系中ABD BCBC⊥D点,交射线于点需要,请自己,平分不变,你能求,这时中,CAD AEEFD∠AOB△点,己画分求出与是HD33.34.35.⑴若⑵延长求度数⑶如图,点旋转时(是否发生【中】(20,点⑴如图1⑵如图2,⑶如图3,系式______【中】(杭点的直线⑴如图1,⑵如图2,【中】(20纸片之间有一种⑴若折成图间的关系;⑵若折成图⑶若折成图A∠=ABA∠OAABC∠BABC△,求证交轴于点;平分(斜边与生改变?若不011年武汉二点为直线上当当点在点在边_______ .杭州七年级下线交于若若010年武汉市片沿折叠种数量关系保图2或图3,即(不必证明图4,写出图5,写出AOC∠xOF AO∠AB图1P40ABC∠=PACPACAD EABE∠=BAD∠+DE∠∠证:,过作,轴正半轴始不变,请求其度二中广雅中学上上一动,延长线上时所示位置时期末复习)在,交于,市洪山区数学叠成图1,此保持不变,请找即点落在)与、与、B B∠=∠E OOM BCO∠yAC︒BAC∠CCAC30︒EBD∠90EBD∠=AA1∠∠A1∠∠;,的平分线交始终相交于点度数;若改变学下学期期末点,PO B⊥,点与时,求证:时,请直接写在中,,求,学七年级(下时点落在找出这种数量或上之间的关系之间的关系BOCOD AB⊥O图260=︒PABC△F AEF∠20D=︒︒BM AD⊥ABE CD22且交的延长线点),在⑵变,请说明理末七年级数学BO于点,与点重合时写出中,.求的度于,求下)期末数学四边形量关系并说明上时,分别写系式;(不必系式.(不必DOB∠=FOCOC(12APO∠=APO∠ABC∠=AFE=∠BAD∠DMBCD,线于点,当⑵的条件下,理由.)在时,与,,是度数.求模拟试卷)如内部,则明理由.出与必证明)必证明)EOB∠O∠PAABC△APO∠=ACB BA∠-∠ACB∠C∠D BADB E∠-∠DEA∠∠当试问的中,平分..的等量上一点,的度数如图:将与、;与OAE OEA=∠ABO△P∠图3BO)CBAC∠BCEBMA∠1∠2A∠∠,绕度数分量关过.之AO2∠111/1136. 【中】(2012年江苏省苏州市相城区第二学期期中考试初一数学试卷)现有两块大小相同的直角三角板和,,30A D ∠=∠=︒.⑴ 将这两块三角板摆成如图①的形式,使、、、在同一条直线上,点在边上,与相交于点,试求的度数;⑵ 将图①中的固定,把绕着点逆时针旋转如图②的形式,当旋转的角度等于多少度时,?并说明理由.37. 【难】(2010年湖北省武汉市洪山区七年级(下)期末数学模拟试卷)把一付学生用三角板(和)如图⑴放置在平面直角坐标系中,点在轴正半轴上,直角边与轴重合,斜边与轴重合,直角边交轴于,斜边交轴于,是中点,.⑴ 把图1中的绕点顺时针旋转度()得图2,此时的面积是,的面积是,分别求、、三点的坐标; ⑵ 如图3,设的平分线和的平分线交于点,的平分线和的平分线交于点,当改变的大小时,的值是否会改变,若改变,请说明理由,若不改变,请求出其值.图5图4图3图2图112121221A B CD EABCDEA B CDE A BCD EEDCB A ABC DEF 90ACB DFE ∠=∠=︒B F E A C DF DE AC G AGD ∠ABC △DEF △F DF AC ∥图2图1ABCDEF GF ED CBA30,60,90︒︒︒45,45,90︒︒︒A y AC y AD y AE x F AB x G O AC 8AC =Rt AED △A α090︒α<︒≤AGH △10AHF △8F H B AHF ∠AGH ∠M EFH ∠FOC ∠N αN M ∠+∠图3图2图1。
三角形有关的角度计算

三角形有关的角度计算三角形是最简单的多边形之一,它由三条边和三个角组成。
在三角形中,角度的求解是一个重要的问题。
本文将探讨有关三角形角度的计算方法和相关公式。
一、三角形角度的基本概念在三角形ABC中,我们可以定义以下几个基本概念:1.内角:指位于三角形内部的角。
在三角形ABC中,角A、角B和角C都是内角。
2.外角:指位于三角形外部的角。
在三角形ABC中,角D、角E和角F都是外角。
3.锐角:指小于90度的角。
在三角形ABC中,如果角A、角B和角C 都小于90度,则它是一个锐角三角形。
4.直角:指等于90度的角。
在三角形ABC中,如果角A、角B或角C 等于90度,则它是一个直角三角形。
5.钝角:指大于90度但小于180度的角。
在三角形ABC中,如果角A、角B或角C有一个大于90度,则它是一个钝角三角形。
6.外角和内角的关系:任意一个外角等于其对应的两个内角之和。
在三角形ABC中,对于外角D来说,有D=A+B。
二、角度计算的基本原理要计算三角形的角度,我们需要使用一些基本原理和公式:1.三角形的内角和为180度:在三角形ABC中,角A+角B+角C=180度。
2.外角和内角的关系:在三角形ABC中,任意一个外角等于其对应的两个内角之和。
如D=A+B。
3.相似三角形的角度关系:如果两个三角形相似,他们的内角分别相等。
如在相似三角形ABC和DEF中,角A=角D、角B=角E、角C=角F。
1.等边三角形:一个等边三角形的三个角度都是60度。
因为等边三角形的三条边都相等,所以三个内角也相等。
2.直角三角形:一个直角三角形的一个角度是90度。
因为直角三角形的其中一个角是直角(90度)。
3.等腰三角形:一个等腰三角形的两个底角(底边两边对应的内角)是相等的。
因为等腰三角形的两条底边是相等的,根据相似三角形的性质,两个底角也是相等的。
对于普通三角形ABC,如果已知其中两个角,我们可以用180度减去这两个角的和,得到第三个角的度数。
人教版八年级上册11.2三角形有关的角(教案)

一、教学内容
人教版八年级上册11.2三角形有关的角:本节课我们将学习三角形的内角和定理,掌握三角形的内角和为180°,并能运用这一性质解决相关问题。具体内容包括:
1.三角形的内角和定理:了解三角形的内角和为180°,并掌握其证明方法。
2.三角形内角的性质:探讨三角形内角的大小关系,了解等腰三角形、等边三角形内角的特点。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了三角形的内角和定理、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对内角和定理的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
2.教学难点
-难点理解:学生对于三角形的内角和定理的理解,特别是为什么三角形的内角和是固定的180°。
-逻辑推理:在证明内角和定理的过程中,学生可能会对几何逻辑推理感到困惑。
-实际应用:将内角和定理应用到解决具体问题时,学生可能会在选择和使用定理上遇到困难。
-操作技巧:在测量和计算过程中,学生可能对角度的精确计算和测量方法掌握不熟练。
3.运用内角和定理解决实际问题:通过具体实例,学会运用三角形的内角和定理解决生活中的问题。
本节课将结合实际案例,让学生在实际操作中掌握三角形内角和的性质,提高解决问题的能力。
二、核心素养目标
1.培养学生的空间观念:通过探究三角形的内角和定理,使学生能够形成对几何图形的直观认识,提高空间想象力。
2.发展学生的逻辑推理能力:在学习三角形的内角和定理证明过程中,引导学生运用演绎推理,培养严谨的逻辑思维。
三角形的角的特点

三角形的角的特点三角形是几何学中一个非常重要的概念,它具有一些独特的角度特点。
本文将详细解释三角形的角的特点,并以标题中心扩展的方式进行描述。
一、三角形的角的特点三角形是由三条线段组成的图形,其中的角是三角形的基本组成部分。
三角形的角有以下几个重要特点:1. 内角和定理:三角形的内角和等于180度。
无论三角形的形状如何,其内角和总是保持不变。
这个定理可以用一个简单的公式表示:A + B + C = 180°,其中A、B、C分别表示三角形的三个内角。
2. 外角和定理:三角形的外角和等于360度。
三角形的外角是指从一个内角的补角延长出来的角,外角和定理表示了三角形内、外角之间的关系。
3. 直角三角形:直角三角形是指其中一个内角为90度的三角形。
直角三角形的两个边长满足勾股定理:斜边的平方等于两个直角边的平方之和。
4. 锐角三角形:锐角三角形是指其中所有内角都小于90度的三角形。
锐角三角形的特点是三个内角都是锐角。
5. 钝角三角形:钝角三角形是指其中有一个内角大于90度的三角形。
钝角三角形的特点是有一个内角是钝角。
6. 等腰三角形:等腰三角形是指其中两边的长度相等的三角形。
等腰三角形的特点是两个底角(底边对应的内角)相等。
7. 等边三角形:等边三角形是指其中三条边的长度都相等的三角形。
等边三角形的特点是三个内角都是60度。
8. 顶角和底角:在一个三角形中,顶角是指顶点所对的内角,底角是指两条边所对的内角。
9. 相似三角形:相似三角形是指具有相同形状但大小不同的三角形。
相似三角形的对应角度相等。
二、三角形角的特点的中心扩展除了以上提到的基本特点,三角形的角还有一些与三角形的中心相关的特点。
三角形的中心是指可以通过三角形的某些特殊点来确定的点。
1. 重心:三角形的重心是指三条中线的交点,它同时也是三条高线的交点。
重心将三角形分成六个小三角形,其中每个小三角形的重心都是大三角形重心的三分之一。
2. 重心角:重心角是指从重心到三个顶点的连线所形成的角。
