理论力学第七版答案第九章
理论力学习题解答(8-13章)

对于一个物体,如果受到的合力为零,则该物体处于力的平衡状态。
力的平衡与运动状态
力的平衡状态下,物体的运动状态保持不变,即速度和方向都不发生变化。
力矩是力和力臂的乘积,表示力对物体转动作用的物理量。
力矩概念
力矩的方向
力矩的几何意义
力矩的方向按照右手定则确定,即右手四指从转动轴指向力的方向,大拇指指向转动方向。
动量定理,描述了物体加速度与其所受合外力之间的线性关系。
详细描述
牛顿第二定律,也被称为动量定理,表述为F=ma,其中F代表合外力,m代表质量,a代表加速度。该定律揭示了物体的加速度与作用在物体上的力成正比,与物体的质量成反比。
牛顿第二定律
作用与反作用定律,描述了作用力和反作用力大小相等、方向相反的特性。
伯努利方程
层流与湍流,定常流动与非定常流动,一维、二维、三维流动。
流体流动的分类
流体质量守恒,流量连续,无质量亏损或增加。
连续性方程
流体动力学基础
03
拉格朗日法
追踪流体质点运动的方法,描述流场中质点位置随时间变化。
01
微元体分析法
对流场中微小体积元进行分析,列出流体运动和力的平衡方程。
02
欧拉法
描述流体运动随时间变化的方法,基于流体质点运动观点。
天体运动的计算方法
天体运动的计算方法通常涉及到对万有引力定律的应用,以及运用运动学和动力学原理。
总结词
在计算天体运动时,首先需要确定天体的质量、位置和速度等参数,然后根据万有引力定律计算出天体之间的相互作用力。接着,运用牛顿第二定律和运动学原理,可以求解出天体的加速度、速度和位移等参数。最后,通过比较理论计算结果和观测数据,可以对天体运动的规律进行验证和预测。
理论力学第七版答案解析第九章

9-10 在瓦特行星传动机构中,平衡杆O 1A 绕O 1轴转动,并借连杆AB 带动曲柄OB ;而曲柄OB 活动地装置在O 轴上,如图所示。
在O 轴上装有齿轮Ⅰ,齿轮Ⅱ与连杆AB 固连于一体。
已知:r 1=r 2=0.33m ,O 1A =0.75m ,AB =1.5m ;又平衡杆的角速度O 1=6rad/s 。
求当=60°且=90°时,曲柄OB 和齿轮Ⅰ的角速度。
题9-10图【知识要点】 Ⅰ、Ⅱ两轮运动相关性。
【解题分析】 本题已知平衡杆的角速度,利用两轮边缘切向线速度相等,找出ωAB ,ωOB 之间的关系,从而得到Ⅰ轮运动的相关参数。
【解答】 A 、B 、M 三点的速度分析如图所示,点C 为AB 杆的瞬心,故有 ABA O CA v A AB ⋅⋅==21ωω ωω⋅=⋅=A O CD v AB B 123所以 s rad r r v BOB /75.321=+=ωs rad r v CM v MAB M /6,1==⋅=I ωω 9-12 图示小型精压机的传动机构,OA =O 1B =r =0.1m ,EB =BD =AD =l =0.4m 。
在图示瞬时,OA ⊥AD ,O 1B ⊥ED ,O 1D 在水平位置,OD 和EF 在铅直位置。
已知曲柄OA 的转速n =120r/min ,求此时压头F 的速度。
题9-12图【知识要点】 速度投影定理。
【解题分析】 由速度投影定理找到A 、D 两点速度的关系。
再由D 、E 、F 三者关系,求F 速度。
【解答】 速度分析如图,杆ED 与AD 均为平面运动,点P 为杆ED 的速度瞬心,故 v F = v E = v D由速度投影定理,有A D v v =⋅θcos可得 s ll r n r v v A F /30.1602cos 22m =+⋅⋅==πθ 9-16 曲柄OA 以恒定的角速度=2rad/s 绕轴O 转动,并借助连杆AB 驱动半径为r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。
理论力学 陈立群 第9章习题解答

第九章平衡问题——能量方法 习题解答9-1质量为3 kg 的质点以5 m/s 的速度沿水平直线向左运动。
今对其施以水平向右的的常力,此力的作用经30 s 而停止,这时质点的速度水平向右,大小为55 m/s 。
求此力的大小及其所做的功。
解:取质点m 为研究对象。
由质点动量定理;()12v v F -=m t :()12v v m Ft +=,解得:()())N (630555312=+=+=t v v m F .由质点动能定理; ()())J (450055532121222122=-⨯⨯=-==v v m Fs W .9-2如图所示,一弹簧振子沿倾角为ϑ的斜面滑动,已知物块重G ,弹簧刚度系数为k ,动摩擦因数为f ;求从弹簧原长压缩s 的路程中所有力的功及从压缩s 再回弹λ的过程中所有力的功。
解:取物块为研究对象。
物块受到重力G ,弹簧力F ,斜面摩擦力m ax F 和法向反力N F 作用,其中仅法向反力N F 不作功。
在弹簧压缩过程中,所有力的功为 ()221cos sin ks s f G W --=ϑϑ 在弹簧压缩s 再回弹λ的过程中,所有力的功为 ()()[]2221cos sin λλϑϑ--+--=s s k f G W 。
9-3弹簧原长l ,刚度系数为k ,一端固定在O 点,此点在半径为r = l 的圆周上。
如弹簧的另一端由图示的B 点拉至A 点,求弹簧力所做的功。
AC ⊥BC ,OA 为直径。
解:在B 点弹簧的变形为()l 121-=λ,在A 点弹簧的变形为l =2λ。
弹簧力所做的功为()()222211221kl k W --=-=λλ。
9-4图示机构在力F 1和F 2作用下在图示位置平衡,不计各构件自重和各处摩擦,OD=BD=l 1,AD=l 2。
求F 1/F 2的值。
解:用解析法解题。
()j i F ϑϑcos sin 11-=F , i F 22F = 点A 和B 的坐标及其变分为()()j i r ϑϑsin cos 2121l l l l A ++--= ,i r ϑcos 21l B -=题9-2图题9-3图质点的受力图()()j i r δϑϑδϑϑ⋅++⋅-=cos sin δ2121l l l l A ,i r δϑϑ⋅=sin 2δ1l B 。
理论力学(第七版)课后题答案哈工大

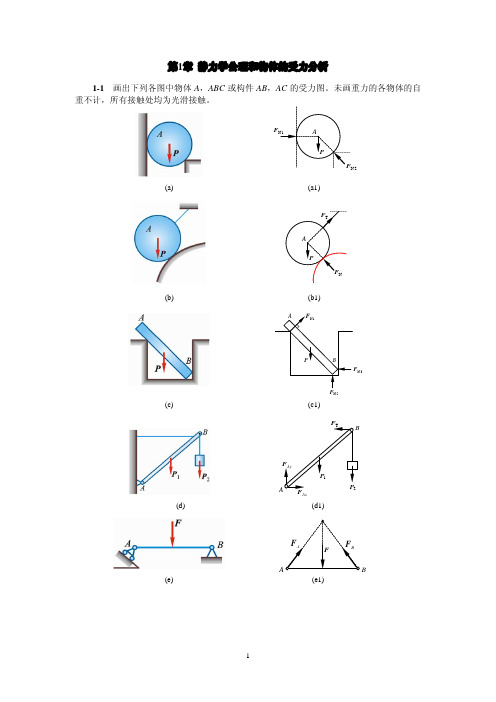
第1章 静力学公理和物体的受力分析
1-1 画出下列各图中物体 A,ABC 或构件 AB,AC 的受力图。未画重力的各物体的自 重不计,所有接触处均为光滑接触。
FN 1
A
P FN 2
(a)
(a1)
FT A P FN
(b)
A
(b1)
FN1
P
B FN 3
FR = (80i + 140 j ) N
FR = (80 N) 2 + (140 N) 2 = 161 N
2-2 如图 2-2a 所示,固定在墙壁上的圆环受 3 条绳索的拉力作用,力 F1 沿水平方向, 力 F3 沿铅直方向,力 F2 与水平线成 40°角。3 个力的大小分别为 F1=2 000 N,F2=2 500 N, F3=1 500 N。求 3 个力的合力。
C
FN 2
′ FN
B
P2
(a1)
FN1
(a) FN 1
B
C P2 FAy A
FN 2
FN
P1
P1
FAy
A F Ax
FAx
(a2)
(a3)
FN1
A P1 B P2
FN 3
FN 2
(b)
(b1)
′ FN
FN 1
A
B P2
FN 3
P1
FN
FN 2
(b3)
(b2)
3
理论力学(第七版)课后题答案 哈工大.高等教育出版社
F2 = 173 kN
如图 2-5a 所示,刚架的点 B 作用 1 水平力 F,刚架重量不计。求支座 A,D 的约
y F B C x
理论力学第七版答案、高等教育出版社出版

仅供个人学习参考哈工大理论力学(I )第7版部分习题答案1-2两个老师都有布置的题目2-3?2-6?2-14?2-?20?2-30?6-2?6-4?7-9??7-10?7-17?7-21?8-5?8-8?8-16?8-24?10-4?10-6?11-5?11-15?10-3以下题为老师布置必做题目1-1(i,j ),1-2(e,k)2-3,2-6,2-14,2-20,2-306-2,6-47-9,7-10,7-17,7-21,7-268-5,8-8(瞬心后留),8-16,8-2410-3,10-410-611-5,11-1512-10,12-15,综4,15,16,1813-11,13-15,13-166-2图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5m 在铅垂面内转动,杆AB=0.8m ,A 端为铰链,B 端有放置工件的框架。
在机构运动时,工件的速度恒为0.05m/s ,杆AB 始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B 的轨迹方程。
10-3如图所示水平面上放1均质三棱柱A ,在其斜面上又放1均质三棱柱B 。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA 三棱柱B 质量mB 的3倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A 、B 两三棱柱组成1质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统 质心位置在水平方向守恒。
设A 、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c 所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4如图所示,均质杆AB ,长l ,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A 相对图b 所示坐标系的轨迹。
理论力学(I)第九章课件(第7版哈尔滨工业大学)详解

x A f1 (t ) y A f 2 (t ) f 3 (t )
对于每一瞬时 t ,都可以求出对应的 x A , y A , , 图形S 在该瞬时的位置也就确定了。 二.平面运动分解为平动和转动
当图形S上A点不动时,则刚体作定轴转动。
当图形S上 角不变时,则刚体作平动。
故刚体平面运动可以看成是平动和转动的合成运动。
选取运动情况已知的点作为基点)
12
曲柄连杆机构
AB杆作平面运动 平面运动的分解
(请看动画)
13
§9-3
平面图形内各点的速度
一.基点法(合成法) 已知:图形S内一点A的速度 v A ,
vB 图形角速度 求:
取A为基点, 将动系固结于A点, 动系作平动。
取B为动点, 则B点的运动可视为牵连运动为平动和相对运动
8
例如
车轮的运动。
车轮的平面运动可以看成
是车轮随同车厢的平动和相对
车厢的转动的合成。
车轮对于静系的平面运动 车厢(动系Ax y ) 相对静系的平动
(绝对运动) (牵连运动)
车轮相对车厢(动系Ax y)的转动
(相对运动)
9
我们称动系上的原点A为基点,于是 刚体的平面运动可以 分解为随基点的平动 和绕基点的转动。
1
第九章 刚体的平面运动
§9–1 刚体平面运动的概述
§9–2 平面运动分解为平动和转动 ·
刚体的平面运动方程 §9–3 平面图形内各点的速度 §9–4 平面图形内各点的加速度 习题课
2
§9-1 刚体平面运动的概述
刚体的平面运动是工程上常见的一种运动,这是一种较为 复杂的运动.对它的研究可以在研究刚体的平动和定轴转动的 基础上,通过运动合成和分解的方法,将平面运动分解为上述
哈工大理论力学第七版课后习题答案(高清无水印版)
如图 2-5a 所示,刚架的点 B 作用 1 水平力 F,刚架重量不计。求支座 A,D 的约
y F B C x
FA
(a) 图 2-5
A
(b)
D
FD
解 研究对象:刚架。由三力平衡汇交定理,支座 A 的约束力 FA 必通过点 C,方向如 图 2-5b 所示。取坐标系 Cxy ,由平衡理论得
FT A
y
10 m
10 m P/2 O
θ
(a) 图 2-6
D
C
FT C x
(b)
解 本题为悬索问题,这里采用近似解法,假定绳索荷重均匀分布。取 AC 段绳索为研 究对象,坐标及受力如图 2-6b 所示。图中:
W1 =
由平衡理论得
P = 200 N 2
(1)
∑ Fx = 0, FT C − FT A cosθ = 0
B
A FA
C
E
C
E FEy
FEx
FC
(l2)’
FC
(l4)’
(l3)’
′ FAD
A
FCy FCx F1 BCFra bibliotek(m)
(m1)
FAD
D E
H
F2
FAD
A
FE
(m2)
FH
(m3) 7
D
′ FAD
A
FN A
Fk
FOy FOx O
B
FN B
(n)
(n1)
FN1
B ′ FB
D
q
FN 2 FN 3
(n2)
F
B
D
FAx
(a2)
(a3)
FN1
理论力学第七版课后习题答案

理论力学第七版课后习题答案第一章: 引言习题1-11.问题描述:给定物体的质量m=2kg,加速度a=3m/s^2,求引力F。
2.解答:根据牛顿第二定律F=ma,其中m表示物体的质量,a表示物体的加速度。
代入已知值,可求得F=6N。
习题1-21.问题描述:给定物体的质量m=5kg,引力F=20N,求加速度a。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=4m/s^2。
第二章: 运动的描述习题2-11.问题描述:一个物体以恒定速度v=10m/s匀速直线运动,经过t=5s,求物体的位移。
2.解答:位移等于速度乘以时间,即s=vt。
代入已知值,可得s=50m。
习题2-21.问题描述:一个物体以初始速度v0=5m/s匀加速直线运动,加速度a=2m/s^2,经过t=3s,求物体的位移。
2.解答:由于物体是匀加速直线运动,位移可以通过公式s=v0t+0.5at^2计算。
代入已知值,可得s=(53)+(0.52*3^2)=45m。
第三章: 动力学基础习题3-11.问题描述:一个物体质量为m=4kg,受到的力F=10N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2.5m/s^2。
习题3-21.问题描述:一个物体质量为m=3kg,受到的力F=6N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
第四章: 动力学基本定理习题4-11.问题描述:一个物体质量为m=8kg,受到的力F=16N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
习题4-21.问题描述:一个物体质量为m=6kg,受到的力F=12N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
以上是理论力学第七版课后习题的答案。
希望能对你的学习有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9-10 在瓦特行星传动机构中,平衡杆O 1A 绕O 1轴转动,并借连杆AB 带动曲柄OB ;而曲柄OB 活动地装置在O 轴上,如图所示。
在O 轴上装有齿轮Ⅰ,齿轮Ⅱ与连杆AB 固连于一体。
已知:r 1=r 2=0.33m ,O 1A =0.75m ,AB =1.5m ;又平衡杆的角速度ωO 1=6rad/s 。
求当γ=60°且β=90°时,曲柄OB 和齿轮Ⅰ的角速度。
题9-10图【知识要点】 Ⅰ、Ⅱ两轮运动相关性。
【解题分析】 本题已知平衡杆的角速度,利用两轮边缘切向线速度相等,找出ωAB ,ωOB 之间的关系,从而得到Ⅰ轮运动的相关参数。
【解答】 A 、B 、M 三点的速度分析如图所示,点C 为AB 杆的瞬心,故有 ABA O CA v A AB ⋅⋅==21ωω ωω⋅=⋅=A O CD v AB B 123所以 s rad r r v BOB /75.321=+=ωs rad r v CM v MAB M /6,1==⋅=I ωω 9-12 图示小型精压机的传动机构,OA =O 1B =r =0.1m ,EB =BD =AD =l =0.4m 。
在图示瞬时,OA ⊥AD ,O 1B ⊥ED ,O 1D 在水平位置,OD 和EF 在铅直位置。
已知曲柄OA 的转速n =120r/min ,求此时压头F 的速度。
题9-12图【知识要点】 速度投影定理。
【解题分析】 由速度投影定理找到A 、D 两点速度的关系。
再由D 、E 、F 三者关系,求F 速度。
【解答】 速度分析如图,杆ED 与AD 均为平面运动,点P 为杆ED 的速度瞬心,故 v F = v E = v D由速度投影定理,有A D v v =⋅θcos可得 s ll r n r v v A F /30.1602cos 22m =+⋅⋅==πθ 9-16 曲柄OA 以恒定的角速度ω=2rad/s 绕轴O 转动,并借助连杆AB 驱动半径为r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。
设OA =AB =R =2r =1m ,求图示瞬时点B 和点C 的速度与加速度。
题9-16图【知识要点】 基点法求速度和加速度。
【解题速度】 分别对A 、B 运动分析,列出关于B 点和C 点的基点法加速度合成方程,代入已知数据库联立求解。
【解答】 轮子速度瞬心为P, AB 杆为瞬时平动,有smrPCvs radrvsmRvvBCBBAB/828.222/42,/2==⋅=======ωωωωω取A为基点,对B点作加速度分析,有nBAtBAnAnBtBaaaaa++=+由已知条件0,,22===nBAABnBaRarvaω解得22/8,0smrvaa BnBtB===取B为基点,由C点加速度的叠加原理,tCBnCBBCaaaa++=由已知条件0,,2=⋅==tCBBnCBnBBaraaaω故C点加速度222/3.11smaaaCBnBC=+=9-19在图示机构中,曲柄OA长为r,绕O轴以等角速度ω转动,AB=6r,BC=r33。
求图示位置时,滑块C的速度和加速度。
题9-19图【知识要点】刚体的平面运动。
【解题分析】分别对系统中B点的速度和加速度进行分析,再利用矢量投影,列出方程,由几何关系代入数据即可求解。
【解答】由速度分析图,有CBBCBAABvvvvvv+=+=,由题设中已知数据得6,30sin 23,3,30sin 0200010ωωωωω=======BC v v v r v AB v v v CB B CBCBA A BA由加速度分析图,对AB 杆, nBA t BA n A B a a a a ++=由已知条件 AB a r a n BA n A ⋅=⋅=2120,ωω向AB 轴投影,得nBAn A B a a a -=2121 对BC 杆,nCB t CB B a a a a ++=C由已知条件 2220,31ωω⋅=⋅-=BC n CB B a r a 向BC 轴投影,得 2012323ωr a a a n CB B C =--= 9-24 如图所示,轮O 在水平面上滚动而不滑动,轮心以匀速υO =0.2m/s 运动。
轮缘上固连销钉B ,此销钉在摇杆O 1A 的槽内滑动,并带动摇杆绕O 1轴转动。
已知:轮的半径R =0.5m ,在图示位置时,A O 1是轮的切线,摇杆与水平面间的交角为60°。
求摇杆在该瞬时的角速度和角加速度。
【知识要点】 平面运动,点的合成运动。
【解题分析】 本题先研究轮子的整体运动,再以销钉B 为动点。
选定不同的基点,最终得到不同的解答方程,联立方程,代入已知数据求解。
【解答】 对轮进行加速度与速度的分析,得到,0,0000===ωαωRv 以销钉B 为动点,摇杆为动系。
r e a v v v +=题9-24图得到 s radBO v v v v e e r /2.0,23,2310100====ωω 销钉B 的加速度为tBO n BO B a a a a ++=0 (1) c r n e t e B a a a a a +++= (2)联立(1)(2),得到c r n e t e n BO a a a a a +++=由已知题设条件r e n e te n BO v a B O a a B O a R a ⋅=⋅=⋅==012011011202,,ωωω由BO 1 轴上的投影可得 e nBO t e a a a -=解得21/046.01s rad BO a t e AO -==α 9-25 平面机构的曲柄OA 长为2l ,以匀角速度ωO 绕O 轴转动。
在图示位置时,AB =BO ,并且∠OAD =90°。
求此时套筒D 相对于杆BC 的速度和加速度。
【知识要点】 刚体的平面运动。
题9-25图【解题分析】 本题先对整个杆以及杆中D 、A 两点进行速度与加速度的分析,利用速度和加速度的合成公式求解。
【解答】 选BC 杆为动点,OA 杆为动系。
Br Be Ba v v v +=得到 l v l v Br Ba 0033,332ωω=⋅=AD 杆作平面运动,则DA A D v v v +=可得0032332334ωωωω==⋅=⋅=AD DA AD DA D v l v l v又有 B De Dr De D v v v v v =+=,得到D 的相对速度 l l v v v B D Dr 0016.1332ωω=⋅=-= 加速度分析。
c Br nBe Ba a a a a ++=由题设所给的已知条件Br e n Be v a l a ⋅=⋅=0202,ωω由加速度投影,可得 l a Ba ⋅=2034ωADa l a ADt DAA nDAt DA A D ⋅=⋅=++=220,2ωωa a a a再一次投影,得到 l a D ⋅=2098ω Dr De Da a a a += 得到 l l a Dr 202022.2910ωω==9-29 图示平面机构中,杆AB 以不变的速度υ沿水平方向运动,套筒B 与杆AB 的端点铰接,并套在绕O 轴转动的杆OC 上,可沿该杆滑动。
已知AB 和OE 两平行线间的垂直距离为b 。
求在图示位置(γ=60°,β=30°,OD =BD )时杆OC 的角速度和角加速度、滑块正的速度和加速度。
题9-29图【知识要点】 刚体的平面运动,点的运动合成。
【解题分析】 本题取B 为动点,再以OC 杆为动系,DE 、OE 杆作平面运动。
【解答】 由加速度c r ne t e B a a a a a +++=由已知条件r e c e n e v a OB a ⋅=⋅=ωω2,2由et a 方向的投影,得到 0=+c et a a得到 2202833,43b v a a b v a et et ⋅-==⋅-=OB 又选OC 为动系 v B =v e + v r 代入已知数据,得到 v v v v v v B r B e 2121,2323====v v v b v OB v e D e 432,430==⋅==ω DE 杆作平面运动,由 ED D e v v v +=得到 4,21332vv v v v ED D E ===nED t ED n D t D E a a a a a +++=由已知条件 EDva a a a a ED nED n e n D t e t D2,21,21===由向DE 轴的投影,得到 b v a E 2387-=9-31 图示行星齿轮传动机构中,曲柄OA 以匀角速度ωO 绕O 轴转动,使与齿轮A 固结在一起的杆BD 运动。
杆BE 与BD 在点B 铰接,并且杆BE 在运动时始终通过固定铰支的套筒C 。
如定齿轮的半径为2r ,动齿轮半径为r ,且AB =5r 。
图示瞬时,曲柄OA 在铅直位置,BD 在水平位置,杆BE 与水平线间成角ϕ=45°。
求此时杆BE 上与C 相重合一点的速度和加速度。
题9-31图【知识要点】 刚体平面运动和点的运动的合成。
【解题分析】 本题先取出C 为动系,列出速度迭加方程求解;再取C '点,结合B 点,列出加速度叠加方程,联立求解。
【解答】 选套筒C 为动系,选BE 杆上的点B 和C '为动点,作速度分析,有 r e B v v v += 又由轮边缘线速度相同,有PB ⋅=rv v AB 解得 ()()()()0000062.021562.221523cos 87.625123sin ωωωωωϕθωωϕθ=-===-=+==+=+=BC v r r v ve r r v v e e B B r 由刚体性质,得到关联速度公式r v cr r c r 087.6,ω='==''v v v 又由加速度分析,有 0,=++=tBA tBA nBA A B a a a a a若选B 为动点,套筒为动系,有c r n e te B a a a a a +++=将上两式相加c r ne t e n BA A a a a a a a +++=+代入已知条件有上式在BC 上投影()r r a r 202073.135123ωω=+=再选C '点为动点,套筒为动系,得到加速度关系式 c c r c e c e ''''++=a a a a 由已知条件 r e c c r c a ar a ωω2,==''得到杆上C '点加速度为 r a a a c c r c202214.16ω=+=''。
