拓扑优化学习报告_北理工_王路
拓扑优化zuoye

关于拓扑优化1. 基本概念拓扑优化是结构优化的一种,结构优化可分为尺寸优化、形状优化、形貌优化和拓扑优化。
拓扑优化以材料分布为优化对象,通过拓扑优化,可以在均匀分布材料的设计空间中找到最佳的分布方案。
拓扑优化相对于尺寸优化和形状优化,具有更多的设计自由度,能够获得更大的设计空间,是结构优化最具发展前景的一个方面。
2. 发展起源拓扑优化的研究历史是从桁架结构开始的。
Maxwell 在1854年首次进行了应力约束下最小桁架的基本拓扑分析。
1904年Michell用解析分析的方法研究了应力约束、一个载荷作用下的结构,得到最优桁架缩影满足的条件,后称为Michell准则,并将符合Michell 准则的桁架称为Michell桁架,也称最小重量桁架,这是结构拓扑优化设计理论研究的一个里程碑。
但是,Michell提出的桁架理论只能用于单工况并依赖于选择适当的应变场,并不能用于工程实际。
直到1964年,Dom、Gomory、Greenberg等人提出基结构法,进一步将数值理论引入该领域,此后拓扑优化的研究重新活跃起来了。
所谓的基结构就是一个由众多构件联结而成的、包括所有载荷作用点、支撑点在内的结构。
Michell桁架理论在近几十年得到了重要的进展。
Cox证明了Michell的桁架同时也是最小柔度设计。
Hegemier等将Michell准则推广到刚度、动力参数约束,以及非线性弹性等情况。
Hemp纠正了其中的一些错误。
Rozvany对MIchell桁架的唯一性和杆件的正交性进行了讨论,对Michell准则做了进一步的修正。
现在,已经建立了多工况以及应力和位移组合约束情况的优化准则。
Dobbs和Fetton使用最速下降法求解多工况应力约束下桁架结构的拓扑优化。
Shen和Schmidt采用分枝定界法求解在应力和位移两类约束下桁架结构在多工况作用下的最优拓扑。
王光远等提出了结构拓扑优化的两相法。
Kirsch针对离散结构的拓扑优化问题提出了一种两阶段算法。
焊点拓扑优化提高车身性能研究

焊点拓扑优化提高车身性能研究随着汽车工业的不断发展,汽车性能的要求也不断提高。
为了提高车身的性能,焊点拓扑优化成为了重要的研究方向。
在现有车身的焊接设计中,焊缝存在于许多位置,这些焊缝不仅增加了车身的重量,而且还会对汽车的性能产生重大的影响。
为了进一步提高车身的刚度和强度,实现轻量化,需要对焊点拓扑进行研究和优化。
一般来说,优化焊点拓扑和焊接顺序可以达到减少焊缝数量、焊接点数量和焊接时间的效果,从而减少了车身的重量和成本,并提高了汽车的性能。
首先,通过建立数学模型,研究焊点的拓扑结构,可以比较容易地发现焊点的弱点以及潜在的优化空间,对焊接结构进行优化设计,并借助仿真分析工具进行验证和优化。
在优化设计中,可以采用结构拓扑优化的思想,通过减少焊缝的数量和面积来优化焊接结构,从而达到提高车身刚度和强度、减少车身压缩和扭曲等目的。
另外,合理的焊接顺序和焊接参数也是优化车身性能的重要因素。
焊点拓扑结构的优化需要考虑到焊缝长度、焊缝分布和焊接方向等参数,通过优化这些参数可以减少焊接过程中的应力和变形,保证焊接品质。
实际生产中,焊接工艺的优化可以减少焊接时间、提高焊接质量和减少成本,因此,在选择焊接方案时需要综合考虑这些因素。
总之,焊点拓扑优化提高车身性能是汽车工业中的一项重要研究领域。
通过对焊点拓扑的优化,可以减少焊缝的数量和面积,从而达到减轻车身重量、提高车身性能和降低生产成本的目的。
除了优化焊点拓扑外,也需要考虑焊接顺序和焊接参数的影响,从而保证焊接质量。
最终,通过理论研究和实验验证,可以获得优化的焊接方案,为汽车工业的持续发展做出贡献。
焊点拓扑优化不仅可以降低车身重量和成本,也可以提高车身的稳定性和安全性能。
在传统设计中,焊缝数量较多且分布不均匀,会导致变形和应力集中。
在紧急情况下,车身可能会出现裂纹或者破裂,严重的情况下,会危及驾驶员的生命安全。
而通过焊点拓扑优化,可以减少焊缝数量,提高焊接质量,进而提高车身的稳定性和安全性能。
光纤通信网络中的拓扑结构设计优化

光纤通信网络中的拓扑结构设计优化在现代社会,光纤通信网络已经成为信息传输的主要手段,其高速、大容量的传输能力使其在各个领域发挥着重要作用。
而光纤通信网络的拓扑结构设计优化,对于提高网络的性能和可靠性起着至关重要的作用。
本文将针对光纤通信网络中的拓扑结构设计优化进行详细探讨。
首先,光纤通信网络的拓扑结构。
拓扑结构是指网络中节点和链接的组织方式。
常见的拓扑结构包括星型、环形、总线型、网状等。
在设计光纤通信网络拓扑结构时,需考虑网络的传输延迟、网络容量、可扩展性、鲁棒性等因素。
其次,针对拓扑结构设计的优化方法。
为了提高光纤通信网络的性能和可靠性,需要对拓扑结构进行优化。
优化的目标是减少传输延迟,提高网络的容量和可扩展性。
常见的优化方法包括节点位置优化、链接选择优化、链路带宽分配优化等。
首先,节点位置优化。
节点的位置对于网络的性能有着重要影响。
通过合理地选择节点的位置,可以减少网络的传输延迟。
一种常见的节点位置优化方法是基于地理位置信息的优化。
通过考虑节点之间的地理距离,可以有效地选择节点的位置,使得网络的传输延迟最小化。
其次,链接选择优化。
链接的选择也对网络的性能有着重要影响。
传输延迟较小的链接将有助于提高网络的性能。
为了选择传输延迟较小的链接,可以使用一些算法进行优化。
例如,最小生成树算法可以找到一组传输延迟较小的链接,从而提高网络的性能。
最后,链路带宽分配优化。
链路带宽的分配也是网络性能有限的关键。
通过合理地分配链路的带宽,可以最大化网络的容量和可扩展性。
为了实现链路带宽的优化,可以采用一些优化算法,例如最大流最小割算法。
在实际应用中,还可以针对特定的应用场景进行拓扑结构设计优化。
例如,对于大规模数据中心网络,可以采用多级结构的拓扑结构。
这种结构可以通过合理地分配链路的带宽和节点的位置,提供更高的可用性和可扩展性。
此外,在进行拓扑结构设计优化时,还需要考虑网络的可靠性。
网络的可靠性是指网络在面对节点或链接故障时仍能正常工作的能力。
北航拓扑优化程序学习报告

拓扑优化的99行程序学习报告4月19日2011《结构优化设计》课程学习报告任课教师:李书一、 前言:在最近的结构优化设计课程上学习了O.Sigmund 的《A 99 line topology optimization code written in Matlab 》一文,对拓扑优化的理论原理与实际的计算机程序实现都有了一定的理解,文章主要是通过拓扑优化的原理来实现对简单结构的静力学问题的优化求解,而编写的代码仅有99行,包括36行的主程序,12行的OC 优化准则代码,16行的网格过滤代码和35行的有限元分析代码。
自1988 年丹麦学者Bendsoe 与美国学者Kikuchi 提出基于均匀化方法的结构拓扑优化设计基本理论以来,均匀化方法应用到具有周期性结构的材料分析中,近几年该方法已经成为分析夹杂、纤维增强复合材料、混凝土材料等效模量,以及材料的细观结构拓扑优化常用的手段之一。
其基本思想是在组成拓扑结构的材料中引入微结构,优化过程中以微结构的几何尺寸作为设计变量,以微结构的消长实现其增删,并产生介于由中间尺寸微结构组成的复合材料,从而实现了结构拓扑优化模型与尺寸优化模型的统一。
文章就是通过均匀化的基础,结合拓扑结构优化的工程实际,以计算机模拟的方法将拓扑优化的一般过程呈现出来,有助于初涉拓扑优化的读者对拓扑优化有个基础的认识。
二、 拓扑优化问题描述为了简化问题的描述,文中假设设计域是简单的矩形形式,且在进行有限元离散的时候采用正方形单元对其进行离散。
这样不仅便于进行单元离散和单元编号,也利于对结构进行几何外形的描述。
一般说来,基于指数逼近法的拓扑优化最小化的问题可作如下描述:01min :()()():0min 1NT p Te e e Xe c X U KU x u k u V X subjecttof V KU FX x =⎫==⎪⎪⎪=⎬⎪⎪=⎪<≤≤⎭∑文中采用的对结构材料属性的描述是所谓的“指数逼近法”或者称为SIMP逼近法,即(Solid Isotropic Material with Penalization 带惩罚因子的各项同性材料模型法),该方法是拓扑优化中常用的变密度材料插值模型中最具代表性的一种。
连续体结构拓扑优化理论与应用研究

连续体结构拓扑优化理论与应用研究前言近年来,随着三维打印、计算机辅助设计等技术的发展,连续体结构拓扑优化逐渐被广泛应用于工程设计中。
连续体结构拓扑优化指的是基于一定的约束条件下,通过优化连续体结构的材料分布和形状来实现结构尽可能轻量化、刚度尽可能大的目的。
本文将从理论、方法和应用三个方面,对连续体结构拓扑优化进行全面阐述。
第一章连续体结构拓扑优化理论1.1 拓扑优化的概念拓扑优化是指利用数学方法优化结构的材料分布和形状以达到某种性能目标的一种方法。
与传统的结构优化相比,拓扑优化不仅考虑结构的大小和形状,还考虑结构的材料分布。
这就要求将结构的材料分布看作设计变量,并且采用合适的材料性质描述模型来描述材料在不同条件下的特性。
1.2 拓扑优化的方法拓扑优化的方法主要可分为两类:自适应法和演化法。
自适应法主要是一种灵活的算法,通过规定合适的自适应方法进行优化;演化法则主要依靠基因或者其它进化原理来进行结构的筛选。
1.3 拓扑优化的应用拓扑优化的应用非常广泛,例如在航空航天、汽车制造、建筑设计等领域都有广泛的应用。
在航空航天领域,拓扑优化可以减轻飞机自重,提高飞机的飞行性能和使用寿命。
在汽车制造领域,拓扑优化可以降低车辆的重量,提高车辆的燃油效率和安全性能。
在建筑设计领域,拓扑优化可以使建筑结构尽可能的轻量化,增加建筑设计的美感和实用性。
第二章连续体结构拓扑优化方法2.1 拓扑敏感度分析法拓扑敏感度分析法是一种基于有限元方法的拓扑优化方法。
该方法通过对应力场的敏感度进行迭代求解,实现了结构的材料优化分布和形状。
该方法的优点是计算速度快、收敛速度快,但其缺点是对初始设计要求较高。
2.2 拓扑优化基尔霍夫法拓扑优化基尔霍夫法也是一种基于有限元方法的拓扑优化方法。
该方法将结构划分为若干个有限元单元,在设计变量的控制下分别分配材料,使得结构满足一定的约束条件。
该方法的优点是便于求解、可以同时考虑结构的刚度和稳定性等多个目标。
学习拓扑学的心得体会

学习拓扑学的心得体会第一篇:学习拓扑学的心得体会学习《拓扑学》的心得体会摘要:拓扑学是一门综合性比较强的数学学科,是我们大学生学习必不可少的学科。
我们之前学习了的物理学、高等代数、数学分析、初等几何等多门学科都有关联,是我们之前学习的延伸,接触了比之前更高深的问题,同时加深了与其他学科的联系。
在学习集合相关概念时,引发了我对于现实生活中的一些思考,进一步感受到了数学的严谨性。
在学习拓扑中的基,由此想到了之前在初等数论中学习的鸽巢原理。
在学习连续函数的不同定义时,与之前学习的数学分析中的相关类容作出了比较,并进一步理解了函数的连续性。
关键词:数学学科;延伸;联系;严谨性一、什么是拓扑学?我们所谓的拓扑学,是在数学学科当中比较抽象的一门学科。
它的英文名是T opology,直译是地质学,也就是和研究地形、地貌相类似的有关的学科。
我国早期有人曾经把它翻译成为“形势几何学”、“连续几何学”、“一对一的连续变换群下的几何学”,但是,这几种译名无论对于老师还是学生来说都不大好理解,于是在1956年最终用统一的《数学名词》把它确定为拓扑学,这是按音译过来的。
拓扑学是数学当中一个重要的、基础性的学科分支。
它最初是几何学的一个分支,主要研究几何图形在连续变形下保持不变的性质,现在已成为研究连续性现象的重要的数学分支。
然而,这种几何学又和通常的平面几何、立体几何又有所不同。
通常的平面几何或立体几何所研究的对象是点、线、面之间的位置关系以及它们的度量性质,而拓扑学对于研究对象的长短、大小、面积、体积等度量性质和数量关系都无关。
举例来说,在通常的平面几何里,把平面上的一个图形搬到另一个图形上,如果它们能够完全重合,那么这两个图形叫做全等图形。
但是,在拓扑学里所研究的图形,在运动中无论它的大小或者形状都发生变化。
在拓扑学里没有不能弯曲的元素,每一个图形的大小、形状都可以改变。
例如,前面讲的欧拉在解决哥尼斯堡七桥问题的时候,他画的图形就不考虑它的大小、形状,仅考虑点和线的个数,这些就是拓扑学思考问题的出发点。
拓扑优化
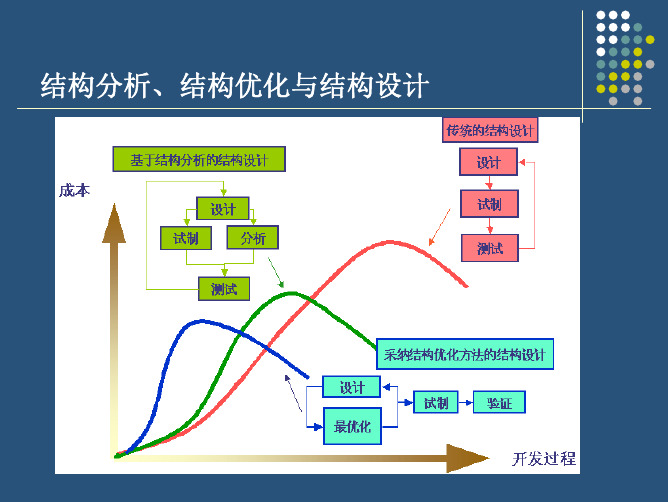
¾ ¾
¾ ¾
TOSCA应用的常见问题
¾
¾
¾
TOSCA是否支持组合件结构拓扑优化? TOSCA通过提取结构分析结果进行优化求解,从原则上说,任何支持的结 构分析类型结构形式下的拓扑优化功能均能完成。对于软件系统来说,组 合件和单个零部件结构表现为刚度阵规模大小不同,故而TOSCA支持组合 件结构拓扑优化。 TOSCA软件的学习方式? TOSCA.help是最好的学习教程,帮助内容包括安装方式和支持的求解器, 命令行解释,算法适用范围,学习算例等。 TOSCA优化结果能否导入到CAD软件中? TOSCA.Smooth模块对结果进行平滑处理并可生成igs,stl等几何格式,可 导入到CAD软件模型中进行处理。
TOSCA应用的常见问题
¾
TOSCA是否支持强度优化? 应力具有局部性特点,即在强度较弱的结构部位进行加强即可满足工程要 求,通常工程优化流程为在得到刚度最大化结构的基础上进一步进行优化 设计以满足应力约束要求。同时刚度最大化结果可理解为“全局应力”最小 化结构,强度拓扑优化结果通常与刚度拓扑优化结果较大的相似性。 TOSCA 拓扑优化模块不具备强度优化功能,而在形状优化中设置应力约束 条件。
( SIMP − model)
连续体结构拓扑优化建模方式
体积比约束: 建模方式对应的工程含义为“结构体积一定的情况下,目标函数如柔顺 度、固有频率值最小或最大”。 建模方法的好处在于:由于体积敏度值保持恒正(或恒负),有利于 优化求解,通常情况下优化迭代收敛性好。 体积最小化目标: 建模方式对应的工程含义为“在满足结构响应量如节点位移、固有频率 值不大于(或不小于)许用值的情况下,结构体积最小化”。 建模方法的好处在于:具有处理多种不同性质约束的能力。
拓扑优化_精品文档

们可以通过限制子集的等级或是扩展设计集来获得一个适当的模式。对于柔度,均
匀的多尺度层状微结构组成了一个扩展的设计空间,同时也意味着整数约束 松弛
为连续约束。
2.2 解决灰色尺度:差值模式
由于整数模型的计算求解非常困难,通常采用变量连续化方法,将0
将p取的足够大(根据经验可取p≥3),这将会导致黑白(即0-1)设计问题。
式(9)优化设计问题是一种标准的连续变量的尺寸优化问题,并且 是在一个固定域定义的。所以前一节提到的方法也可以应用到该问题上。
人们也提出了多种以上问题的替代形式,都是基于同样的原来,即可
以在0-1之间差值或是根据材料特性,在弱材料 0 和强材料 1
这不仅意味着需要处理大量的设计变量,而且也影响到有限元分析的计算成本。 些为了得到高精度的设计,运用模拟退火法、遗传算法、或是确定性方法计算成本 都是很高的,而且这些方法只适用于相对较小的规模,或是些特定的设计问题,如 最小柔顺性问题。
在式(2)的连续性问题假设中可以看出,寻求结构拓扑的基本思想是通过寻找
该问题可以表示为在输入端有一个外力作用下输出端的最大位移。为了满足 几何最优和结构最优的假定,输出端用到了弹簧刚度系数为kout的线性弹簧。刚 度越大,则输出位移越小,输出载荷越大;相反,弹簧刚度越小,则输出位移越 大,输出载荷越小。同时为了模拟输入端的激励,我们基于弹簧刚度系数为kin的 线性弹簧,输入载荷为fin来建立线性应变模式,
水平集方法
基本思路是引入一个水平集函数 x,t,然后采用如下的方式对
结构的拓扑形式加以描述:
x,t 0 x,t 0 x,t 0
x
x t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s.t
KU F
V fV0 xi , j i , j
i 1 j 1 m n
0 xmin xi , j xmax 1
其中:
X ——单元相对密度矢量
C ——结构的柔度
F ——载荷矢量
U ——位移矢量
北京理工大学 车辆工程 王路
FILTER %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%% function [dcn]=check(nelx,nely,rmin,x,dc) dcn=zeros(nely,nelx); for i = 1:nelx for j = 1:nely sum=0.0; for k = max(i-floor(rmin),1):min(i+floor(rmin),nelx) for l = max(j-floor(rmin),1):min(j+floor(rmin),nely) fac = rmin-sqrt((i-k)^2+(j-l)^2); sum = sum+max(0,fac); dcn(j,i) = dcn(j,i) + max(0,fac)*x(l,k)*dc(l,k); end end
E( xi ) Emin ( xi ) p ( E0 Emin ), xi 0,1
其中:
E(xi ) ——插值以后的弹性模量 E0 ——实体部分材料的弹性模量 Emin ——孔洞部分材料的弹性模量
(1)
xi ——单元相对密度,取值为
1 时表示有材料,为 0 时表示无材料即孔洞
p ——惩罚因子
(二)拓扑优化问题的描述
(1)材料插值模型
变密度理论的材料插值模型通过引入中间密度单元, 将离散型问题转化成连续型优化问 题,而实际上,中间密度单元是无法存在和制造,因此要尽量避免中间密度单元的产生,减 少中间密度单元的数目,此时就需要对设计变量中出现的中间密度值进行惩罚。
北京理工大学 车辆工程 王路 目前材料插值模型主要分为两类,SIMP 法和 RAMP 法,基于 SIMP 格式的 材料插值模型为:
k ——结构刚度矩阵
u i , j ——单元位移矢量 k i , j ——单元刚度矩阵
k 0 ——初始段元刚度矩阵
i , j ——单元体积
V ——优化后的体积
f ——保留的体积分数
V0 ——初始体积
xmin ——设计变量的取值下限
xmax ——设计变量的取值上限
n ——子域内单元的个数
(三)程序解读
是否满足精度要求
是 结束循环
图 1. 99 行程序的流程图 具体程序分析: 总体程序为: %%%% A 99 LINE TOPOLOGY OPTIMIZATION CODE BY OLE SIGMUND, JANUARY 2000 %%% %%%% CODE MODIFIED FOR INCREASED SPEED, September 2002, BY OLE SIGMUND %%% function top(nelx,nely,volfrac,penal,rmin); nelx=80; nely=20; volfrac=0.4; penal=3; rmin=2; % INITIALIZE
北京理工大学 车辆工程 王路 dcn(j,i) = dcn(j,i)/(x(j,i)*sum); end end %%%%%%%%%% FE-
ANALYSIS %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%% function [U]=FE(nelx,nely,x,penal) [KE] = lk; K = sparse(2*(nelx+1)*(nely+1), 2*(nelx+1)*(nely+1)); F = sparse(2*(nely+1)*(nelx+1),1); U = zeros(2*(nely+1)*(nelx+1),1); for elx = 1:nelx for ely = 1:nely n1 = (nely+1)*(elx-1)+ely; n2 = (nely+1)* elx +ely; edof = [2*n1-1; 2*n1; 2*n2-1; 2*n2; 2*n2+1; 2*n2+2; 2*n1+1; 2*n1+2]; K(edof,edof) = K(edof,edof) + x(ely,elx)^penal*KE; end end % DEFINE LOADS AND SUPPORTS (HALF MBB-BEAM) F(2*(nelx/2+1)*(nely+1),1) = 1; fixeddofs alldofs freedofs = [2*(nely/2+1),2*nelx*(nely+1)+2*(nely/2+1)]; = [1:2*(nely+1)*(nelx+1)]; = setdiff(alldofs,fixeddofs);
北京理工大学 车辆工程 王路 x(1:nely,1:nelx) = volfrac; loop = 0; change = 1.; % START ITERATION while change > 0.01 loop = loop + 1; xold = x; % FE-ANALYSIS [U]=FE(nelx,nely,x,penal); % OBJECTIVE FUNCTION AND SENSITIVITY ANALYSIS [KE] = lk; c = 0.; for ely = 1:nely for elx = 1:nelx n1 = (nely+1)*(elx-1)+ely; n2 = (nely+1)* elx +ely; Ue = U([2*n1-1;2*n1; 2*n2-1;2*n2; 2*n2+1;2*n2+2; 2*n1+1;2*n1+2],1); c = c + x(ely,elx)^penal*Ue'*KE*Ue; dc(ely,elx) = -penal*x(ely,elx)^(penal-1)*Ue'*KE*Ue; end end % FILTERING OF SENSITIVITIES [dc] = check(nelx,nely,rmin,x,dc); % DESIGN UPDATE BY THE OPTIMALITY CRITERIA METHOD [x] = OC(nelx,nely,x,volfrac,dc);
% SOLVING U(freedofs, : )= K(freedofs,freedofs) \ F(freedofs,: ); U(fixeddofs,: )= 0; %%%%%%%%%% ELEMENT STIFFNESS
MATRIX %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%% function [KE]=lk E = 1.;
find
X ( x1,1 , x1,2 , x1,3 , , xi , j )T R
i 1,2, , m j U U T KU uiT, j ki , j ui , j ( xi , j ) p uiT, j k0ui , j
北京理工大学 车辆工程 王路 colormap(gray); imagesc(-x); axis equal; axis tight; axis off;pause(1e-6); end %%%%%%%%%% OPTIMALITY CRITERIA
UPDATE %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% function [xnew]=OC(nelx,nely,x,volfrac,dc) l1 = 0; l2 = 100000; move = 0.2; while (l2-l1 > 1e-4) lmid = 0.5*(l2+l1); xnew = max(0.001,max(x-move,min(1.,min(x+move,x.*sqrt(-dc./lmid))))); if sum(sum(xnew)) - volfrac*nelx*nely > 0; l1 = lmid; else l2 = lmid; end end %%%%%%%%%% MESH-INDEPENDENCY
在本文中,在本篇文章中,讨论的 SIMP 的表达为:
E ( xi,j ) ( xi,j ) p E0
其中: xi,j 为第 i 个子域内第 j 个单元的相对密度。 (2)数学模型
(2)
根据在体积或质量约束下求最小柔度,即最大刚度来建立优化模型,基于 变密度理论的 SIMP 法的周期性拓扑优化问题的数学模型可以表达为:
北京理工大学 车辆工程 王路 nu = 0.3; k=[ 1/2-nu/6 1/8+nu/8 -1/4-nu/12 -1/8+3*nu/8 ... -1/4+nu/12 -1/8-nu/8 nu/6 1/8-3*nu/8];
北京理工大学 车辆工程 王路
基于 99 行程序的拓扑优化学习报告
(一)背景和前言
随着汽车工业的飞速发展以及日益突出的能源问题, 汽车工业面临的挑战以 及竞争环境也越来越激烈, 对汽车产品提出了降低其制造成本及燃油经济性的新 要求。在提高汽车安全性、减少汽车排放和解决能源消耗的背景下,提出了汽车 轻量化技术。实现汽车轻量化的途径包括三个方面:结构优化技术、新型材料和 先进性制造工艺。其中,我们所讨论的是结构优化技术,其中结构优化设计分为 三个层次:尺寸优化(Size Optimization) 、形状优化(Shape Optimization)和拓 扑优化(Topology Optimization) 。本文我们基于 99 行 matlab 程序初步学习拓扑 优化技术中的理论和优化方法。 拓扑优化技术指的是在给定的设计空间内寻求最佳的材料布局, 同时在满足 平衡方程、物理关系、几何关系和边界约束条件下使得结构达到某种性能最优的 应用技术。 拓扑优化的理论研究最早可以追溯到 Michel 提出的桁架理论,连续体结构 的拓扑优化由于描述和数值计算得困难,发展一直相对缓慢,直到 Bendsoe 和 Kikuchi 在 1988 年提出的均匀化方法之后才得到迅速的发展, 其基本思想是在组 成拓扑结构中引入微结构,通过微结构的几何参数作为设计变量,通过微结构的 增加和删减实现结构的拓扑形状的改变,实现拓扑优化和尺寸优化的统一。 在微结构的基础上,我们介绍变密度法的应用,变密度法是在均匀化方法的 基础上产生的, 把材料引入微结构代之以密度在 0~1 之间变化的假想材料, 把密 度作为设计变量,从而实现材料的删减,因其模型简单、计算变量相对较少成为 目前广泛采用的方法。根据不同的插值模式,变密度法又有不同的插值模型: SIMP 法(Solid Isotropic Material with Penalization) 、Hashin-Shtrikman 法,以及 RAMP 法(Rational Approximation of Material Properties) 。
