第二章 几何光学成像
合集下载
例题

1 1 1 ( nL1 1 )( ) f1 r 1
1 1 1 ( nL 2 1 )( ) f2 r r2 1
1 1 1 f f1 f2
其它求法?
光
学
第二章 几何光学成像例题 例题5
置于空气中两薄透镜,焦距分别为12cm和-8cm,相距16cm。一 物体高3cm,位于第一个透镜前30cm处,求像。 F1 F2’ F1’ F2
1
n n 1 1.5 1 nr 1 ( 50 ) 100
1 1 ? ? f 22 f 22
光
学
第二章 几何光学成像例题 例题6
一胶合厚透镜由一个凸透镜和一个平凸透镜组成,曲率半径分 别为50cm、-50cm,中心厚度分别2cm、3cm,折射率分别为1.5 和1.6。求系统焦距
光
学
第二章 几何光学成像例题
例题1:
在圆柱形木塞的圆心,垂直于 圆平面插入一根大头针,然后把木 塞倒放浮在水面上,观察者在水面 上方不论在什么位置都刚好看不到 水下的大头针,设大头针露出的长 度为h,木塞直径为d,求水的折 射率。 解决本问题的关键是利用全反射现象
d
h
1 sin i n
1 n sin i
1 d1 1 1 1 f1 f11 f12 f11 f12 f11 f12
光
学பைடு நூலகம்
第二章 几何光学成像例题 例题6 一胶合厚透镜由一个凸透镜和一个平凸透镜组成,曲率半径分
别为50cm、-50cm,中心厚度分别2cm、3cm,折射率分别为1.5 和1.6。求系统焦距
H2 H ‘2
光
学
第二章 几何光学成像例题 例题5
置于空气中两薄透镜,焦距分别为12cm和-8cm,相距16cm。一 物体高3cm,位于第一个透镜前30cm处,求像。 F1 F2’ F1’ F2
1 1 1 ( nL 2 1 )( ) f2 r r2 1
1 1 1 f f1 f2
其它求法?
光
学
第二章 几何光学成像例题 例题5
置于空气中两薄透镜,焦距分别为12cm和-8cm,相距16cm。一 物体高3cm,位于第一个透镜前30cm处,求像。 F1 F2’ F1’ F2
1
n n 1 1.5 1 nr 1 ( 50 ) 100
1 1 ? ? f 22 f 22
光
学
第二章 几何光学成像例题 例题6
一胶合厚透镜由一个凸透镜和一个平凸透镜组成,曲率半径分 别为50cm、-50cm,中心厚度分别2cm、3cm,折射率分别为1.5 和1.6。求系统焦距
光
学
第二章 几何光学成像例题
例题1:
在圆柱形木塞的圆心,垂直于 圆平面插入一根大头针,然后把木 塞倒放浮在水面上,观察者在水面 上方不论在什么位置都刚好看不到 水下的大头针,设大头针露出的长 度为h,木塞直径为d,求水的折 射率。 解决本问题的关键是利用全反射现象
d
h
1 sin i n
1 n sin i
1 d1 1 1 1 f1 f11 f12 f11 f12 f11 f12
光
学பைடு நூலகம்
第二章 几何光学成像例题 例题6 一胶合厚透镜由一个凸透镜和一个平凸透镜组成,曲率半径分
别为50cm、-50cm,中心厚度分别2cm、3cm,折射率分别为1.5 和1.6。求系统焦距
H2 H ‘2
光
学
第二章 几何光学成像例题 例题5
置于空气中两薄透镜,焦距分别为12cm和-8cm,相距16cm。一 物体高3cm,位于第一个透镜前30cm处,求像。 F1 F2’ F1’ F2
第二章 几何光学成像

nL r2 n nL
f 2
nr2 n nL
将上式代入(2.37)式
f
s
f1 f2 f1 f2
n nL n n nL
r1
r2
f s
f1f 2 f1 f2
n nL n n nL
r1
r2
可见 f n 当n n 1 f n
f f
1
(nL
1)(
1 r1
1 r2
)
——磨镜者公式
第二章 几何光学
成像
• §2-1 • §2-2 • §2-3 • §2-4
成像 共轴球面组傍轴成像 薄透镜
理想光具组理论
几何光学
用几何学方法来研究光的直线传播、反射、折射、 成像等问题的学科称为几何光学。
波动光学揭示了光的本质,所有的光学现象都可 以用波动的概念来解释,但是在实际应用中,用几何 学方法来研究将更为方便,这不必涉及光的本质,从 几个简单的基本实验定律出发,就可以解决许多光学 技术及照明工程等问题。
s2 n2 (s r)2
s2
n2 (s r)2
4r
sin
2
(
/
2)[ n 2
1 (s
r)
n2
1 (s
] r)
(书上错误)
2r(1 cos)[ 1 Fra bibliotek ]n2 (s r) n2 (s r)
给定s和 角可以求出s,
发现也s与 的大小有关,
单心性被破坏, 因此,
单个球面折射不能成像!
3、球面反射对光束单心性的破坏
焦距 f f r 2
三、傍(近)轴物点成像与横向放大率
1、共轭点 2、共轭平面 3、物平面∏ 4、像平面∏′ 5、符号约定 在轴线上方 y ( y′) >0 6、横向放大率 V y
第二章几何光学
三、傍轴物点成像与横向放大率
第
二 章
PΠ
n
n’
Q
几
i
C
A
i’
Q’
-y’ P’
何
s
Σ
s’
Π’
光
学
傍轴条件:y 2 , y2 s 2 ,s2 ,r 2
成
像
对于折射球面: V y ns y ns
讨论放大率的正负 与像的虚实
对于反射球面: V y s ys
四、逐次成像
第 二
n1
n3 n2
章
二
折射面的曲 5.7mm 网膜的曲率 9.8mm
率半径R
半径R’
章
物方焦距f -17.1mm 像方焦距f ’ 22.8mm
几
何
人眼的调节功能
光
1、改变眼睛的焦距使距离不同的物体都能在视网
学
膜上形成清晰的像,这个过程称为眼睛的调节。
成
像
眼睛能看清的最远点称为远点(无穷远);
眼睛能看清的最近点称为近点(25cm)。
之,高度y(y’)<0。
(5)图示中的各个量均为正值。
第
第二节 共轴球面组傍轴成像
二
一、光在单个球面上的折射
章 几 何
nl A
P
Oφ
s
r
B
l’ C s’
P’ n’
光 学
1
l r 2 r s2 2rr scos 2
成
1
l r 2 s r 2 2rs r cos 2
像
由费马原理可得:
像
和像方主点重合的。
四、惠更斯目镜与冉斯登目镜
第 二
1、惠更斯目镜
第2章 光学成像的几何学原理

(2.2-16)
傍轴光线在平面上的反射成像公式: (2.2-17)
像似深度:傍轴光线在平面上折射成像时的像距s'。
说明:平面镜是唯一能够理想成像的光学系统,而球面折射、反射以及平 面折射系统则只有在近轴近似条件下才能准确成像。
2 光学成像的几何学原理
2.2 光在单个球面上的折射与成像
2.2.4 离轴物点的傍轴光线成像
物(像)方焦距f ( f ' ) :F (F ' )到球面顶点O之距离
(2.2-9)
2 光学成像的几何学原理
2.2 光在单个球面上的折射与成像
说明:
2.2.3 轴上物点的傍轴光线成像
① 焦点是特殊的轴上物点和像点。因此,物
方焦距与物距、像方焦距与像距遵守相同 的符号规则。
F n
n'
O
f>0(f '>0):F(F')为实焦点,且位于O点
1. 物空间与像空间的基本概念 2. 光学系统理想成像的条件
2 光学成像的几何学原理
§2. 2 光在单个球面上的折射 与成像
2 光学成像的几何学原理
2.2 光在单个球面上的折射与成像
主要内容
1. 基本概念和符号规则 2. 光在单个球面上的折射,同心性的破坏
3. 轴上物点的傍轴光线成像 4. 高斯物像公式与牛顿物像公式 5. 光在单个球面上的反射成像
2 光学成像的几何学原理
2.2 光在单个球面上的折射与成像
2.2.2 光在单个球面上的折射,同心性的破坏
(1) 像距与物距的关系
M n
i h
i'
n' Q'
Q
u O
-u'
第二章几何光学成像

光轴--各折反射球面的球心所在的一条直线上
光线与光轴的夹角小于 5 0 时,有sin ≈tan ≈ ,
光学系统满足这样条件的区域,轴上发出的同心光束, 经系统变换后,仍为同心光束,近轴条件限制了光线与光轴 的夹角。
在近轴条件下,单球面折射系统可视为理想光学系统, 同心光束经其变换后,可认为仍具有单心性。
像空间--- 经光学系统变换后的光束所在的几何空间。 它包括所有的实像点.虚像点所在的几何空间。
说明:
① 对于给定的光学系统,无论物与像是实是虚,均具有共轭特点, 这是光路可逆性原理的必然结果。
② 实物、实像的意义在于有光线实际发自或通过该点,而虚物、 虚像仅仅是由光的直线传播性质给人眼造成的一种错觉,实际上 并没有光线经过该点。
上页 下页
2.光在单个球面上的折射 --光在两介质分界面发生折射,界面是球面的一部分。
y
•
n p
u
i M i
h AH
n n
p’ C
u
Q'
y•
s
r
s
Q
n:物方介质的折射率
Q:物点
n':物方介质的折射率
Q':像点
C:球心
顶点:球面在光具组中的对称点A
光轴:使光线不发生偏折的方向,如过球心并垂直于球面的方向
s
s
在上图折射系统中, A和A是一对共轭物像点, u
和 u 是一对共轭角. 我们定义角放大率为
u,
u
(1-4-9)
上页 下页
由上图可得
u s ,
u
s
因为 y ns , y n s
因此有
所以 s ny . s n y
nu ynuy.
光线与光轴的夹角小于 5 0 时,有sin ≈tan ≈ ,
光学系统满足这样条件的区域,轴上发出的同心光束, 经系统变换后,仍为同心光束,近轴条件限制了光线与光轴 的夹角。
在近轴条件下,单球面折射系统可视为理想光学系统, 同心光束经其变换后,可认为仍具有单心性。
像空间--- 经光学系统变换后的光束所在的几何空间。 它包括所有的实像点.虚像点所在的几何空间。
说明:
① 对于给定的光学系统,无论物与像是实是虚,均具有共轭特点, 这是光路可逆性原理的必然结果。
② 实物、实像的意义在于有光线实际发自或通过该点,而虚物、 虚像仅仅是由光的直线传播性质给人眼造成的一种错觉,实际上 并没有光线经过该点。
上页 下页
2.光在单个球面上的折射 --光在两介质分界面发生折射,界面是球面的一部分。
y
•
n p
u
i M i
h AH
n n
p’ C
u
Q'
y•
s
r
s
Q
n:物方介质的折射率
Q:物点
n':物方介质的折射率
Q':像点
C:球心
顶点:球面在光具组中的对称点A
光轴:使光线不发生偏折的方向,如过球心并垂直于球面的方向
s
s
在上图折射系统中, A和A是一对共轭物像点, u
和 u 是一对共轭角. 我们定义角放大率为
u,
u
(1-4-9)
上页 下页
由上图可得
u s ,
u
s
因为 y ns , y n s
因此有
所以 s ny . s n y
nu ynuy.
第二章 几何光学成像-复习

QM MQ' 2a
旋转双曲面:两焦点共轭,一实一虚。
QM MQ' 2a
旋转抛物面:焦点和轴上无限远点共轭,可实可虚。 广泛使用(发射或接收)。
2019/2/9 6
(3)折射等光程面和齐明点 笛卡尔卵形面:四次曲面,给定后只有一对共轭点。
折射球面,有一对共轭点,称为 齐明点(不晕点) .M 。 n
符号规则,修改一条: 像距 s 及焦距 f 也以在A 之左为正(实为正)。 P 在折射的公式中,将s y 和 f 分别换成-s 和 - P Q f 即得现在的公式。 也可仅让 n = -n 即可。
此时 F 和
M
C
h O
n
s
P s ' r
d
F 两个焦点重合
1 1 2 s' s r 2019/2/9
sin 2 ( / 2) ( / 2) 2 1 s s' 则有 n( s r ) n' ( s'r )
可得:
2019/2/9
n' n n'n s' s r
(2.19) 高斯公式
11
2.2 轴上物点成像焦距、物像距公式
1.平行于主轴的入射光线折射后与主轴相交的位置称为球
入射光从左向右传播时 1)若 Q 和 F 点在A点的左方,则 s 0 , f 0 若 Q 和 F 点在A点的右方,则 s 0 , f 0 F 和 C点在A点的左方, 则 s ' 0 f ' 0 r 0 2)若Q、 , , F 和 C点在A点的右方, 则 s ' 0 f ' 0 r 0 若Q、 , , 3)若入射光由右向左传播时,符号法则与上述规定相反 4)各个量在绘图中均用绝对值标示,实物(像)距均 大于零,虚物(像)距均小于零。
旋转双曲面:两焦点共轭,一实一虚。
QM MQ' 2a
旋转抛物面:焦点和轴上无限远点共轭,可实可虚。 广泛使用(发射或接收)。
2019/2/9 6
(3)折射等光程面和齐明点 笛卡尔卵形面:四次曲面,给定后只有一对共轭点。
折射球面,有一对共轭点,称为 齐明点(不晕点) .M 。 n
符号规则,修改一条: 像距 s 及焦距 f 也以在A 之左为正(实为正)。 P 在折射的公式中,将s y 和 f 分别换成-s 和 - P Q f 即得现在的公式。 也可仅让 n = -n 即可。
此时 F 和
M
C
h O
n
s
P s ' r
d
F 两个焦点重合
1 1 2 s' s r 2019/2/9
sin 2 ( / 2) ( / 2) 2 1 s s' 则有 n( s r ) n' ( s'r )
可得:
2019/2/9
n' n n'n s' s r
(2.19) 高斯公式
11
2.2 轴上物点成像焦距、物像距公式
1.平行于主轴的入射光线折射后与主轴相交的位置称为球
入射光从左向右传播时 1)若 Q 和 F 点在A点的左方,则 s 0 , f 0 若 Q 和 F 点在A点的右方,则 s 0 , f 0 F 和 C点在A点的左方, 则 s ' 0 f ' 0 r 0 2)若Q、 , , F 和 C点在A点的右方, 则 s ' 0 f ' 0 r 0 若Q、 , , 3)若入射光由右向左传播时,符号法则与上述规定相反 4)各个量在绘图中均用绝对值标示,实物(像)距均 大于零,虚物(像)距均小于零。
《几何光学成像》课件 (2)

《几何光学成像》PPT课 件 (2)
深入浅出地介绍几何光学成像原理,并通过丰富的图例和实例,帮助大家更 好地理解。
第一部分:凸透镜的成像原理
1
凸透镜的定义和性质
了解凸透镜的基本概念和特性。
物距、像距和焦距的概念
2
掌握物距、像距和焦距的定义和关系。
3
成像公式的推导和应用
学习利用成像公式计算物体和图像的位
鼓励学生们制定接下来的 学习计划和目标。
光线追迹法求像的位置和大小
4
置关系。
通过光线追迹法确定像的位置和大小。
第二部分:平面镜的成像原理
平面镜的定义和性质
了解平面镜的基本概念和特性。
光线反射定律和反射规律
掌握光线反射的规律和特点。
成像特点和成像实例
分析平面镜成像的特点,并通过实例进行说明。
第三部分:透镜成像的常见问题与解答题目,进行详细的解析和
常见问题答疑
2
解题策略。
回答学生们在透镜成像理论中常遇到的
问题和疑惑。
3
实践案例与练习
提供一些实际案例和练习题,帮助学生 巩固所学知识。
结束语
1 总结回顾
对全文内容进行简要总结 和回顾,强调知识要点。
2 学习感悟
分享学习这门课程的心得 和感悟。
3 接下来的学习计划
深入浅出地介绍几何光学成像原理,并通过丰富的图例和实例,帮助大家更 好地理解。
第一部分:凸透镜的成像原理
1
凸透镜的定义和性质
了解凸透镜的基本概念和特性。
物距、像距和焦距的概念
2
掌握物距、像距和焦距的定义和关系。
3
成像公式的推导和应用
学习利用成像公式计算物体和图像的位
鼓励学生们制定接下来的 学习计划和目标。
光线追迹法求像的位置和大小
4
置关系。
通过光线追迹法确定像的位置和大小。
第二部分:平面镜的成像原理
平面镜的定义和性质
了解平面镜的基本概念和特性。
光线反射定律和反射规律
掌握光线反射的规律和特点。
成像特点和成像实例
分析平面镜成像的特点,并通过实例进行说明。
第三部分:透镜成像的常见问题与解答题目,进行详细的解析和
常见问题答疑
2
解题策略。
回答学生们在透镜成像理论中常遇到的
问题和疑惑。
3
实践案例与练习
提供一些实际案例和练习题,帮助学生 巩固所学知识。
结束语
1 总结回顾
对全文内容进行简要总结 和回顾,强调知识要点。
2 学习感悟
分享学习这门课程的心得 和感悟。
3 接下来的学习计划
第二章几何光学成像

上页 下页
2.光在单个球面上的折射 光在单个球面上的折射 --光在两介质分界面发生折射,界面是球面的一部分. --光在两介质分界面发生折射,界面是球面的一部分. 光在两介质分界面发生折射
n
y
u
s
p
i
A
h
M
φ
i ′ p'
C
s′
n′
n′ u′
Q'
H
r
y′
n:物方介质的折射率 : n':物方介质的折射率 : C:球心 :
Q
理 想 光 具 组
Q'
理想光具组
3.物 像的定义 物
实物 虚物 实像 虚像
发散同 心光束
未经光学系统变换的发散同心光束的心,称为实物. 未经光学系统变换的发散同心光束的心,称为实物. 未经光学系统变换的会聚同心光束的心,称为虚物. 未经光学系统变换的会聚同心光束的心,称为虚物. 经光学系统变换后的会聚同心光束的心,称为实像. 经光学系统变换后的会聚同心光束的心,称为实像. 经光学系统变换后的发散同心光束的心,称为虚像. 经光学系统变换后的发散同心光束的心,称为虚像.
n′ n n′ n + = s′ s r
n r, 得物方焦距 f = s = n′ n
的点为物方焦点 F , 它与无穷远处的像点关于
系统共轭. 过 F 点垂直于光轴的平面, 叫作物方焦平面. 系统共轭 点垂直于光轴的平面 叫作物方焦平面 (2) 像方焦点 ) 将
s = ∞ 代入
像距为
n′ n n′ n n′ ' + = 得像方焦距 f ′ = s = r, s′ s r n′ n
n
以光具组的顶点和主光轴为基准,规定光路图中各几何量的符号如下: 以光具组的顶点和主光轴为基准,规定光路图中各几何量的符号如下: A H C
2.光在单个球面上的折射 光在单个球面上的折射 --光在两介质分界面发生折射,界面是球面的一部分. --光在两介质分界面发生折射,界面是球面的一部分. 光在两介质分界面发生折射
n
y
u
s
p
i
A
h
M
φ
i ′ p'
C
s′
n′
n′ u′
Q'
H
r
y′
n:物方介质的折射率 : n':物方介质的折射率 : C:球心 :
Q
理 想 光 具 组
Q'
理想光具组
3.物 像的定义 物
实物 虚物 实像 虚像
发散同 心光束
未经光学系统变换的发散同心光束的心,称为实物. 未经光学系统变换的发散同心光束的心,称为实物. 未经光学系统变换的会聚同心光束的心,称为虚物. 未经光学系统变换的会聚同心光束的心,称为虚物. 经光学系统变换后的会聚同心光束的心,称为实像. 经光学系统变换后的会聚同心光束的心,称为实像. 经光学系统变换后的发散同心光束的心,称为虚像. 经光学系统变换后的发散同心光束的心,称为虚像.
n′ n n′ n + = s′ s r
n r, 得物方焦距 f = s = n′ n
的点为物方焦点 F , 它与无穷远处的像点关于
系统共轭. 过 F 点垂直于光轴的平面, 叫作物方焦平面. 系统共轭 点垂直于光轴的平面 叫作物方焦平面 (2) 像方焦点 ) 将
s = ∞ 代入
像距为
n′ n n′ n n′ ' + = 得像方焦距 f ′ = s = r, s′ s r n′ n
n
以光具组的顶点和主光轴为基准,规定光路图中各几何量的符号如下: 以光具组的顶点和主光轴为基准,规定光路图中各几何量的符号如下: A H C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 几何光学系统中,唯一能够完善成像的是 平面反射成像。
• 1. 一个尺寸不足5m的验光室,想用平面反射镜来 满足5m检查距离,人与视力表在同一位置时,他 们与反射镜之间的距离多大。为2.5m
眼
视力表 2.5m
2.5m 视力表的像
反射镜
• 2. 平面反射镜所成像的特点为(
)。
• A.实像 B.虚像 C.倒立
例
• 1.一个物体经小孔所成的“像”为( • A.实像 B.虚像 C.倒立 • D.正立 E.镜像
)。
• 2. 小孔直径要小于入射光波长是小孔成像需满足 的条件之一。
• ( × ),应为大于
第三节 单平面光学系统成像
• 一、平面反射成像 • 成像特点: • 正像 • 虚像 • 像距等于物距:-l = l • 横向放大率为+1 • 镜像:左右颠倒的成像性质称为镜像
h 202
h 10
• 3.一个物体位于球面镜顶点左侧10cm处,其像落在顶点 右侧20cm处。则该球面镜的曲率半径为( )。
• A.40cm B.-40cm C.20cm D.-20cm
1 1 2 20 10 r
• 4.曲率半径为40cm的球面反射镜,3mm高的物在球面镜
顶点前40处时,所成像的特点为(
l (1 1)6mm 1.5
第四节 薄三棱镜的成像
• 三、薄三棱镜偏向角计算公式
•
δ =(n-1)α
(例)计算折射率为1.5、顶角为10°的薄三棱 镜,出射光线的最小偏向角。
δ =(n-1)α =(1.5-1)×10° = 5°
薄三棱镜成像
• 特点:出射光偏向棱镜底,像偏向顶部。
• 1. 折射率为n、顶角为 α的薄三棱镜,出射光线 的最小偏向角 为( )。 δ =(n-1)α
第二章 几何光学成像
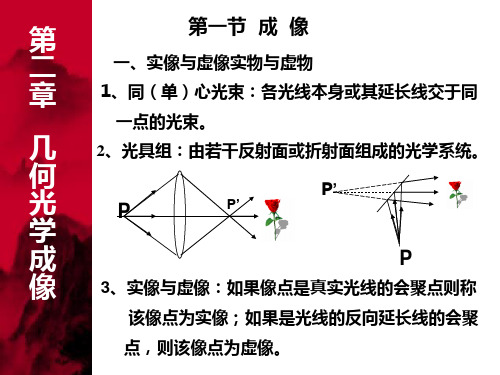
• 第一节 成像的基本条件 • 一、实像与虚像
• 真实光线通过光束的“心”所成的像为实像。
保持光束的单心性是成像的基本条件。
例
• 1. 成像光学系统保持光束的 本条件。单心性
是成像的基
• 2. 实像可以在像的位置被屏幕接收到。(√)
三、物空间与像空间
• 物点所在的空间叫做物空间,也称为物方。 • 像点所在的空间叫做像空间,也称为像方。记!
l (11)t n
• 1.通过一个厚玻璃板观察一个发光点,看到发光 点的位置( )。
• A.移近了 B.移远了 C.不变 D.不能确定
• 2. 人眼透过厚度为6mm,折射率为1.5的平板玻 璃看物体,物体的像( )。
• A.比物体离玻璃板近2mm
• B.比物体离玻璃板远2mm
• C.与物体位置相同 • D.在玻璃后无限远处
l 1.332m 1
• 3.人眼看水下的鱼,所看的像特点为(
• A.实像
B.虚像
• C.像比鱼的实际位置更靠近水面
• D.像比鱼的实际位置更远离水面
• E.像的位置会随眼的位置而变化
)。
• 4. 人眼看水下的鱼时,所看到鱼的像不随眼位置 的改变而改变。( ) ד不随”改为“随”
平板玻璃
• 人眼透过折射率为n,厚度为t的玻璃板看 物体,物体像的位置为:
• 水下鱼看水面上物体成像位置:l 1.33 l 1
例
• 1. 试计算人看水下80cm处的鱼时像的深度。
l80cm60cm 1.33
60cm 80cm
• 2. 水(n=1.33)下的鱼垂直水面看距水面2m高树 上的鸟,像离水面的高度为( )。
• A.2.66m B.3mm C.1.50mm D.2mm
)。
• A.像在顶点前40cm处 • B.像的大小为3mm • C.像的大小为1.5mm • D.像在顶点前20cm处 • E.像是倒立的源自1 1 2 l 40 40
h 401
h 40
• 5. 物点位于球面反射镜焦点与顶点之间的某点时,所成像
的特点为(
)。
• A.倒立像
B.正立像
C.实像
• D.虚像
六、符号规则
1. 距离
• ⑴ 沿轴距离 • 以基准面或基准点为初始点测量,逆入射光线方
向的距离取负号,顺光线方向的距离取正号。
• 以透镜的基点为初始点测量,逆着入射光线方向 的距离取正号。()×,应为:取负号
第二节 小孔成像
小孔成像需要满足以下条件: ⑴ 小孔的直径比物体小 ⑵ 小孔的直径要大于入射光的波长 ⑶ 一定要有成像的屏幕
物
像
• f':焦距
• r:球面半径
例
• 1. 一个半径为8cm的凹球面反射镜,其焦距多大?
解:
1 2 2 f r 8cm
f ' = -4cm
2. 半径为40cm的凸球面镜,焦距多大?
解:
1 2 2 f r 40cm
f ' = 20cm
4. 横向放大率
• 像的横向大小h′与物的横向大小h的比值称为像的 横向放大率,用β表示。记!
h l
hl
例
• 1.汽车的后视镜为
面镜,其焦点位于镜面
。
凸,后面
• 2.一个物体位于半径为40cm的凹面镜顶点前10cm处,其 像为( )。
• A.顶点后20cm的正立实像 • B.顶点后20cm的正立虚像 • C.顶点前20cm的倒立实像
1 1 2 l 10 40
• D.顶点后20cm的倒立实像
E.放大的像
• 6.下列选项中,关于球面反射成像系统正确的说法包括
•(
)。
• A.焦距等于球面半径的一半;
• B.像方焦点与物方焦点在同一位置;
• C.横向放大率大于0时,表明像放大;
• D.横向放大率大于1时,表明像放大;
• E.横向放大率大于0时,表明像倒立。
二、球面折射成像
• 1. 近轴成像公式
• D.正立 E.镜像
• 3. 平面镜成像的横向放大率为( )。
• A.+1 B.-1 C.0
D.∞
• 4. 我们常将
的成像性质称为镜像。
• 答:左右颠倒
• 5. 几何光学系统中,唯一能够完善成像的是平面
折射成像。( )√
二、平面折射成像
• 成像特点:近轴光线成虚像,正立,横向 放大率为1。
• 人看水下物体成像位置: l l 1 .33
n n(nn) l l r
2. 焦距与焦度
• 2.人眼通过薄三棱镜观察物体,所看到的像靠棱 镜底一侧。( ) ד底”改为“顶”
• 3. 人眼通过薄三棱镜所看到的是物体的
该像比物体偏向棱镜
。虚像,顶
像,
第五节 单球面光学系统的近轴成像
• 一、球面反射成像 • 1. 近轴成像公式
1 1 1 2 l l f r
• l: 物距
• l':像距
