初三中考压轴题专题——y与x的函数关系式1-3
2021年中考数学压轴题提升训练实际问题中的方程组与函数题型含解析

实际问题中的方程(组)与函数题型【例1】俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%,在试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售,设每天销售量为y本,销售单价为x元.(1)请直接写出y与x直接的函数关系式及x的取值范围;(2)当每本足球纪念册的销售单价是多少元时,商店每天获利2400元?(3)当每本足球纪念册的销售单价是多少元时,商店每天的利润w最大?最大利润是多少元?【答案】见解析.【解析】解:(1)y=300-10(x-44),整理得:y=-10x+740,(44≤x≤52);(2)由题意得:(x-40)(-10x+740)=2400,解得:x=50,x=64(舍),即当每本足球纪念册的销售单价是50元时,商店每天获利2400元.(3)由题意得:w=(x-40)(-10x+740)=-10(x-57)2+2890∵-10<0,对称轴为x=57,∴当x<57时,w随x增大而增大,∵44≤x≤52,∴当x=52时,w取最大值,最大为2640元,即当每本足球纪念册的销售单价是52元时,商店每天的利润最大,最大利润是2640元.【例2】某养殖专业户计划购买甲、乙两种牲畜,已知乙种牲畜的单价是甲种牲畜单价的2倍多200元,买3头甲种牲畜和1头乙种牲畜共需5700元.(1)甲、乙两种牲畜的单价各是多少元?(2)相关资料表明:甲、乙两种牲畜的成活率分别为95%和99%,若购买以上两种牲畜共50头,并使这50头的成活率不低于97%,且要使购买的总费用最低,应如何购买?【答案】见解析.【解析】解:(1)设甲种牲畜的单价为x元,由题意得:3x+2x+3000=7500,解得:x=1100,2×1100+200=2400,即甲种牲畜的单价为1100元,乙种牲畜的单价为2400元.(2)设购买甲种牲畜m头时,总购买费用为w元,则w=1100m+2400(50-m)=-1300m+120000,由题意知:95%m+99%(50-m)≥97%×50,解得:m≤25,即0≤m≤25,∵-1300<0,∴w随m的增大而减小,当m=25时,w取最小值,即费用最低,∴购买两种牛各25头时,费用最低.【变式2-1】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.(1)现在实际购进这种水果每千克多少元?(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系.①求y与x之间的函数关系式;②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)【答案】见解析.【解析】解:(1)设现在实际购进这种水果价格为每千克a元,则原来价格为每千克(a+2)元,由题意,得:80(a+2)=88a,解得:a =20.即现在实际购进这种水果每千克20元;(2)①设y 与x 之间的函数关系式为:y =kx +b ,将(25,165),(35,55)代入y =kx +b 得,251653555k b k b +=⎧⎨+=⎩, 解得:11440k b =-⎧⎨=⎩, 即y 与x 之间的函数关系式为:y =﹣11x +440;②设这种水果的销售价格为x 元/千克时,利润为w 元,则w =(x ﹣20)y=(x ﹣20)(﹣11x +440)=﹣11(x ﹣30)2+1100,∵﹣11<0,∴当x =30时,w 有最大值,最大值为1100.即这种水果的销售单价定为30元时,能获得最大利润,最大利润是1100元.【例3】在江苏卫视《最强大脑》节目中,搭载百度大脑的机器人小度以3:1的总成绩,,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.(1)求该商家第一次购进机器人多少个?(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?【答案】见解析.【解析】解:(1)设该商家第一次购进机器人x 个, 由题意得:1100024000102x x+=, 解得:x =100.经检验,x =100是所列方程的解,且符合题意.答:该商家第一次购进机器人100个.(2)设每个机器人的标价是a 元.由题意得:a ﹣11000﹣24000≥×20%,解得:a ≥140.答:每个机器人的标价至少是140元.【变式3-1】由于技术更新,智能电视的功能越来越强大,价格也逐渐下降,某电器商行经营的A 款40英寸智能电视去年销售总额为5万元,今年每台销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.(1)今年A 款40英寸智能电视每台售价多少元?(用列方程的方法解答)(2)该电器商行计划新进一批A 款40英寸智能电视和新款B 款40英寸智能电视共60台,且B 款40英寸智能电视的进货数量不超过A 款40英寸智能电视数量的两倍,应如何进货才能使这批智能电视获利最多?A ,B 两款40英寸智能电视的进货和销售价格如下表:【答案】见解析.【解析】解:设今年A 款40英寸智能电视每台售价为x 元,则去年每台售价为(x +400)元,由题意得: ()50000120%50000400x x⨯-=+, 解得:x =1600,经检验,x =1600是原方程的解,符合题意,∴今年A 款40英寸智能电视每台售价为1600元.(2)设购进A 款电视a 台,则购进B 款(60-a )台,此时获利y 元,y =(1600-1100)a +(2000-1400)(60-a )=-100a +36000,其中:60-a ≤2a ,0≤a ≤60,即20≤a ≤60,且a 为整数;∵-100<0,∴y 随a 的增大而减小,当a =20时,y 取最大值,即当进A 款电视20台,B 款电视40台时,获利最大.【例4】紫石中学为了给同学们提供更好的学习环境,计划购买一批桂花树和香樟树来绿化校园,经市场调查发现购买2棵桂花树3棵香樟树共需360元,购买3棵桂花树2棵香樟树共需340元.(1)桂花树香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于桂花树的1.5倍,请你算算,该校本次购买桂花树和香樟树共有哪几种方案.【答案】见解析.【解析】解:(1)设桂花每棵x 元,香樟树每棵y 元,由题意得:2336032340x y x y +=⎧⎨+=⎩, 解得:x =60,y =80,答:桂花树每棵60元,香樟树每棵80元.(2)设桂花树购买x 棵,则香樟树购买(150-a )棵,由题意得:()608015010840150 1.5x x x a ⎧+-≤⎨-≥⎩, 解得:58≤x ≤60,∴有三种购买方案:桂花树58棵,香樟树92棵;桂花树59棵,香樟树91棵;桂花树60棵,香樟树90棵.【变式4-1】冬季来临,某网店准备在厂家购进 A ,B 两种暖手宝共 100 个用于销售,若购买 A 种暖手宝 8 个,B 种暖手宝 3 个,需要 950 元;若购买 A 种暖手宝 5 个,B 种暖手宝 6 个,则需要 800 元.(1)购买 A ,B 两种暖手宝每个各需多少元?(2)①由于资金限制,用于购买这两种暖手宝的资金不能超过 7 650 元,设购买 A 种暖手宝 m 个,求②在①的条件下,购进A种暖手宝不能少于 50 个,则有哪几种购买方案?(3)购买后,若一个A种暖手宝运费为 5 元,一个B种暖手宝运费为 4 元, 在第(2)问的各种购买方案中,购买 100 个暖手宝,哪一种购买方案所付的运费最少?最少运费是多少元?【答案】见解析.【解析】解:(1)设A、B两种暖手宝的价格分别为x元/个、y元/个,由题意得:83950 56800x yx y+=⎧⎨+=⎩,解得:x=100,y=50,即A、B两种暖手宝的价格分别为100元/个,50元/个.(2)①由题意得:100m+50(100-m)≤7650,解得:m≤53,∴m的取值范围是:0≤m≤53,且m为整数;②∵50≤m≤53,∴共有以下四种购买方案,A种50个,B种50个;A种51个,B种49个;A种52个,B种48个;A种53个,B种47个;(3)设总运费为w元,则:w=5m+4(100-m)=m+400,∵1>0,∴w随m的增大而增大,当m=50时,运费最少,最少为450元,∴当购买A种产品50个,B种产品50个时,总运费最少,最少为450元 .1.为支持国家南水北调工程建设,小王家由原来养殖户变为种植户, 经市场调查得知,种植草莓不超过20 亩时,所得利润y(元)与种植面积m(亩)满足关系式y=1 500 m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过 15 亩时,每亩可获得利润 1800 元;超过 15 亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系式为z=-20x+2 100.(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量(2)如果小王家计划承包40 亩荒山种植草莓和樱桃,当种植樱桃面积(x 亩)满足0<x <20时,求小王家总共获得的利润w (元)的最大值.【答案】见解析.【解析】解:(1)由题意得:()()2180001520210015x x p x x x ⎧<≤⎪=⎨-+>⎪⎩(2)种植樱桃面积x 亩,则种植草莓面积(40-x )亩,由题意知,①当0<x ≤15时,w =1800x +1380(40-x )+2400=420x +57600,∵420>0,∴w 随x 的增大而增大,当x =15时,w 最大,最大值为63900,②当15<x ≤20时,w =-20x 2+2100x +1380(40-x )+2400=-20(x -18)2+64080,∵-20<0,∴当x =18时,w 取最大值,最大值为64080,∵64080>63900,∴当x =18时,小王家总共获得的利润w 取最大值,最大值为64080元.2.某游乐园的门票销售分两类:一类个人门票,分为成人票,儿童票;一类为团体门票(一次购买门票 10 张及以上),每张门票在成人票价格基础上打 6 折.已知一个成人带两个儿童购门票需 80 元;两个成人带一个儿童购门票需 100 元.(1)每张成人票和儿童票的价格分别是多少元?(2)光明小学 4 名老师带领 x 名儿童到该游乐园,设购买门票需 y 元.①若每人分别购票,求 y 与 x 之间的函数关系式;②若购买团体票,求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围;③请根据儿童人数变化设计一种比较省钱的购票方案.【答案】见解析.【解析】解:设成人票每张a元,儿童票每张b元,由题意得:a+2b=80,2a+b=100,解得:a=40,b=20,即成人票每张40元,儿童票每张20元;(2)①y=4×40+20x=160+20x②y=40×0.6(x+4)=24x+96,由x+4≥10,得x≥6,且x为整数.③(i)当160+20x>24x+96,即x<16,∴当6≤x<16且x为整数时,应全部购买团体票较为优惠;(ii)当160+20x=24x+96,即x=16,∴当x=16时,购买团体票或分别购买均可以;(iii)当160+20x<24x+96,即x>16,∴当x>16且x为整数时,应分别购买较为优惠.3..近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加,某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?(2)该公司计划一次购进两种型号的空气净化器共 80 台,其中B型空气净化器的进货量不多于A 型空气净化器的 2 倍,为使该公司销售完这 80 台空气净化器后的总利润最大,请你设计相应的进货方案;(3)已知A型空气净化器的净化能力为 200 m3/小时,B型空气净化器的净化能力为 300 m3/小时,某长方体室内活动场地的总面积为 200 m2,室内墙高 3 m,该场地负责人计划购买 5 台空气净化器每天花费30 分钟将室内空气净化一新,若不考虑空气对流等因素,至多要购买A型空气净化器多少台?【答案】见解析.【解析】解:(1)设每台A型空气净化器和B型空气净化器的销售利润分别是x元,y元,由题意得:5395034900x yx y+=⎧⎨+=⎩,解得:x=100,y=150,∴每台A型空气净化器和B型空气净化器的销售利润分别是100元,150元. (2)设购买A型m台,则购进B型(80-x)台,利此时润为w元,由题意知:80-m≤2m,0≤m≤80,m为整数可得:803≤m≤80,m为整数,W=100m+150(80-m)=-50m+12000,∵-50<0,∴w随m的增大而减小,当m=27时,w取最大值,80-27=53,即购进A型27台,B型53台时,售完后获利最大. (3)设购买A型a台,则够买B型(5-a)台,∴12×200a+12×300(5-a)≥200×3,解得:a≤3,∵0≤a≤5,∴0≤a≤3,且a为整数,即至多要购买A型空气净化器3台.4.某水果店购买一批时令水果,在20天内销售完毕,店主将本次此销售数据绘制成函数图象,如图①,日销售量y(千克)与销售时间x(天)之间的函数关系;如图②,销售单价p(元/千克)与销售时间x(天)之间的函数关系式.(1)求y关于x和p关于x的函数关系式;(2)若日销售量不低于36千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售金额最高是第几天?【答案】见解析.【解析】解:(1)分两种情况:①当0≤x≤15时,设日销售量y与销售时间x的函数解析式为y=k1x,∵直线y=k1x过点(15,45),∴15k1=45,解得k1=3,∴y=3x(0≤x≤15);②当15<x≤20时,设日销售量y与销售时间x的函数解析式为y=k2x+b, ∵点(15,45),(20,0)在y=k2x+b的图象上,∴15k2+b=45, 20k2+b=0解得:k2=-9,b=180∴y=﹣9x+180(15<x≤20);∴y与x之间的函数关系式为:y=3015 91801520x xx x≤≤⎧⎨-+<≤⎩.①当0≤x<10时,p=25,当10≤x≤20时,设销售单价p与销售时间x之间的函数解析式为:p=mx+n, ∵点(10,25),(20,15)在p=mx+n的图象上,∴10m+n=25,20m+n=15,解得:m=-1,n=35,∴p=﹣x+35(10≤x≤20),∴p=25010351020xx x≤<⎧⎨-+≤≤⎩;(2)若日销售量不低于36千克,即y≥36.当0≤x≤15时,y=3x,3x≥36,解得:x≥12;当15<x≤20时,y=﹣9x+180,﹣9x+180≥36,解得:x≤16,∴12≤x≤16,∴“最佳销售期”共有:16﹣12+1=5(天);∵p=﹣x+35(10≤x≤20),k=﹣1<0,∴p随x的增大而减小,∴当12≤x≤16时,x取12时,p有最大值,此时p=﹣12+35=23.∴此次销售过程中“最佳销售期”共有5天,在此期间销售金额最高是第12天.5..某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.(1)求这两种品牌计算器的单价;(2)学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B 品牌计算器超出10个以上超出的部分按原价的八折销售.①设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;②小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由.【答案】见解析.【解析】解:(1)设A品牌计算器的单价为m元,B品牌计算器的单价为n元,由题意得:2m+n=122,m+2n=124,解得:m=40,n=42,即A品牌计算器的单价为40元,B品牌计算器的单价为42元.(2)①由题意:y1=0.9×40x=36x,当0<x≤10时,y2=42x;当x>10时,y2=42×10+42(x﹣10)×0.8=33.6x+84.∴y2=42010 33.68410x xx x≤≤⎧⎨+>⎩.②当购买数量超过10个时,y2=33.6x+84.(i)当y1<y2时,36x<33.6x+84,即x<35,当10<x<35时,购买A品牌的计算器更合算;(ii)当y1=y2时,36x=33.6x+84,即x=35,∴当x=35时,购买两种品牌的计算器花费一样多;(iii)当y1>y2时,36x>33.6x+84,即x>35.∴当x>35时,购买B品牌的计算器更合算.6..某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由.【答案】见解析.【解析】解:(1)设一根A型跳绳售价是x元,一根B型跳绳的售价是y元,根据题意,得:2x+y=56,x+2y=82,解得:x=10,y=36,即一根A型跳绳售价是10元,一根B型跳绳的售价是36元;(2)由m≤3(50﹣m),得:m≤37.5,∴0≤m≤37,且m为整数,设购进A型跳绳m根,总费用为W元,根据题意,得:W=10m+36(50﹣m)=﹣26m+1800,∵﹣26<0,∴W随m的增大而减小,∴当m=37时,W最小=838,即当购买A型跳绳37根,B型跳绳13根时,最省钱.7..为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?(2)若购进A种树苗a棵,所需费用为W,求W与x的函数关系式;(3)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.【答案】见解析.【解析】解:(1)设购进A种树苗x棵,则购进B种树苗(17﹣x)棵,由题意得:80x+60(17﹣x)=1220,解得:x=10,即购进A种树苗10棵,B种树苗7棵;(2)W与a的函数关系式:W=80a+60(17﹣a)=20a+1020;(3)由题意得:17-a<a,即a>8.5,∴8.5<a≤17,且a为整数,由(2)知,W=20a+1020,W随a的增大而增大,∴a=9时,即购买9棵A种树苗,8棵B种树苗时,费用最少,W=80×9+60×8=1200,即购买9棵A种树苗,8棵B种树苗时,费用最少,需要1200元.8..孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.(1)求A种,B种树木每棵各多少元?(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.【答案】见解析.【解析】解:(1)设A种树每棵x元,B种树每棵y元,依题意得:25600 3380x yx y+=⎧⎨+=⎩,解得:10080xy=⎧⎨=⎩,答:A种树每棵100元,B种树每棵80元;(2)设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,有a≥3(100﹣a),解得:a≥75.设实际花费金额是y元,则:y=0.9[100a+80(100﹣a)]=18a+7200.∵18>0,∴y随a的增大而增大,∴当a=75时,y取最小值,即当a=75时,y最小值=18×75+7200=8550(元).答:当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为8550元.9..某校计划购进甲、乙两种规格的书架,经市场调查发现有线上和线下两种购买方式,具体情况如下表:(1)如果在线下购买甲、乙两种书架共30个,花费8 280元,求甲、乙两种书架各购买了多少个?(2)如果在线上购买甲、乙两种书架共30个,且购买乙种书架的数量不少于甲种书架的3倍,请求出花费最少的购买方案及花费.【答案】见解析.【解析】解:(1)设线下购买甲种书架x个,乙种书架y个,由题意得:30 2403008280x yx y+=⎧⎨+=⎩,解得:1218 xy=⎧⎨=⎩,即线下购买甲种书架12个,乙种书架18个.(2)设购买甲种书架a个,则购买乙种书架(30-a)个,总花费为w元, ∵30-a≥3a,即a≤7.5(其中a为正整数),W=(210+20)a+(250+30)(30-a)=-50a+8400,∵-50<0,∴w随a的增大而减小,当a=7时,w最小,最小值为8050元,即当购买7个甲种书架,23个乙种书架时,总费用最低,最低为8050元.10..某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)50 60 70销售量y(千克)100 80 60(1)求y与x之间的函数表达式;(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?【答案】见解析.【解析】解:(1)设y与x之间的函数解析式为y=kx+b,由题意得:50100 6080k bk b+=⎧⎨+=⎩,解得:2200kb=-⎧⎨=⎩,y与x之间的函数表达式是:y=﹣2x+200;(2)由题意得,W=(x﹣40)(﹣2x+200)=﹣2(x﹣70)2+1800,(3)∵W=﹣2(x﹣70)2+1800,40≤x≤80,∵﹣2<0,∴当40≤x≤70时,W随x的增大而增大,当70≤x≤80时,W随x的增大而减小, 且当x=70时,W取得最大值,此时W=1800.11..小王是“新星厂”的一名工人,请你阅读下列信息:信息一:工人工作时间:每天上午8:00﹣12:00,下午14:00﹣18:00,每月工作25天; 信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表: 生产甲产品数(件) 生产乙产品数(件) 所用时间(分钟) 10 10 350 3020850信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元.信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元,请根据以上信息,解答下列问题:(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?【答案】见解析.【解析】解:(1)设生产一件甲种产品需x 分钟,生产一件乙种产品需y 分钟. 由题意得:10103503020850x y x y +=⎧⎨+=⎩,解得:x =15,y =20,即生产一件甲产品需要15分钟,生产一件乙产品需要20分钟.(2)设生产甲种产品共用x 分钟,则生产乙种产品用(25×8×60﹣x )=(12000-x )分钟,收入为w 元,则生产甲种产品15x 件,生产乙种产品1200020x-件. ∴w =1.5×15x +2.8×1200020x-=﹣0.04x +1680, ∵15x≥60,即:x ≥900, w =﹣0.04x +1680中,∵﹣0.04<0,∴w 随x 的增大而减小,∴当x =900时,w 取得最大值,最大值为:1644元, 则小王该月收入最多是1644+1900=3544元, 此时生产甲60件,乙555件,∴小王该月最多能得3544元,此时生产甲、乙两种产品分别60件,555件.12..“京东电器”准备购进A、B两种品牌台灯,其中A每盏进价比B每盏进价贵30元,A售价120元,B 售价80元已知用1040元购进的A数量与用650元购进B的数量相同.(1)求A、B的进价;(2)超市打算购进A、B台灯共100盏,要求A、B的总利润不得少于3400元,不得多于3550元,问有多少种进货方案?(3)在(2)的条件下,该超市决定对A台灯进行降价促销,A台灯每盏降价m(8<m<15),B的售价不变,超市如何进货获利最大?【答案】见解析.【解析】解:(1)设A品牌台灯进价为x元/盏,则B品牌台灯进价为(x﹣30)元/盏,由题意得:104065030x x=-,解得:x=80,经检验x=80是原分式方程的解,80﹣30=50(元/盏),答:A、B两种品牌台灯的进价分别是 80 元/盏,50 元/盏(2)设超市购进A品牌台灯a盏,则购进B品牌台灯有(100﹣a)盏, 根据题意得:3400≤(120﹣80)a+(80﹣50)(100﹣a)≤3550解得:40≤a≤55.∵a为整数,55-40+1=16,∴该超市有 16 种进货方案(3)设超市销售台灯所获总利润为w元,w=(120﹣m﹣80)a+(80﹣50)(100﹣a)=(10﹣m)a+3000∵8<m<15①当 8<m<10 时,即 10﹣m>0,w随a的增大而增大,当a=55 时,所获总利润w最大,此时进货方案为:A品牌台灯 55 盏、B品牌台灯 45 盏;②当m=10 时,w=3000;当A品牌台灯数量满足 40≤a≤55时,利润均为 3000元;③当 10<m<15 时,即 10﹣m<0,w随a的增大而减小,当a=40 时,所获总利润w最大,此时进货方案为:A品牌台灯 40 盏、B品牌台灯 60 盏.13..为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.(1)种植A,B两种蔬菜,每亩各需投入多少万元?(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.【答案】见解析.【解析】解:(1)设种植A,B两种蔬菜,每亩各需分别投入x万元,y万元,由题意得:203036 302034 x yx y+=⎧⎨+=⎩解得:0.60.8xy=⎧⎨=⎩,即种植A,B两种蔬菜,每亩各需分别投入0.6万元,0.8万元. (2)由题意得:w=0.8m+1.2×1000.60.8m-=﹣0.1m+150 ∵1000.6m-≥0,∴0≤m≤5003,(3)∵m≥2×1000.60.8m-解得:m≥100在w=﹣0.1m+150中,∵﹣0.1<0,∴w随m的增大而减小,∴当m=100时,w取最大值为:140万元,∴1000.60.8m-=50即当种A蔬菜100亩,B种蔬菜50亩时,获得最大利润为140万元.14..2018年4月8日﹣11日,博鳌亚洲论坛2018年年会在海南省博鳌镇召开.本届博鳌亚洲论坛的主题为“开放创新的亚洲,繁荣发展的世界”.围绕这一主题,年会设置了“全球化与一带一路”“开放的亚洲”“创新”“改革再出发”四大板块,展开60多场正式讨论.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.(1)甲种商品与乙种商品的销售单价各多少元?(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?【答案】见解析.【解析】解:(1)设甲种、乙种商品的销售单价分别是x元,y元,由题意,得:23 321500x yx y=⎧⎨-=⎩解得:x=900,y=600,.答:甲种商品的销售单价是900元,乙种商品的单价为600元(2)设销售甲种商品a万件,则销售乙种商品(8﹣a)万件,由题意,得:900a+600(8﹣a)≥5400解得:a≥2,即至少销售甲种商品2万件.15..某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B 型手机获得的利润分别为3000元和2000元.(1)求每部A型手机和B型手机的销售利润分别为多少元?(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.①求y关于n的函数关系式;②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.【答案】见解析.【解析】解:(1)设每部A型手机的销售利润为x元,则每部B型手机的销售利润为(x-50)元,根据题意,得:3000200050x x=-,解得:x=150,经检验:x=50是原方程的解,150-50=100,答:每部A型手机的销售利润为150元,每部B型手机的销售利润为100元;(2)①设购进B型手机n部,则购进A型手机(110﹣n)部,则y=150(110﹣n)+100n=﹣50n+16500,∵110﹣n≤2n,∴3623≤n≤110且n为整数,∴y关于n的函数关系式为y=﹣50n+16500 (3623≤n≤110且n为整数);②∵﹣50<0,∴y随n的增大而减小,∴当n=37时,y取得最大值,最大值为14650元,答:购进A型手机73部、B型手机37部时,销售总利润最大;(3)y=150(110﹣n)+(100+m)n=(m﹣50)n+16500,其中,3623≤n≤80,且n为整数),①当30<m<50时,y随n的增大而减小,当n=37时,y取得最大值,即购进A型手机73部、B型手机37部时销售总利润最大;②当m=50时,m﹣50=0,y=16500,n取3623≤n≤80的整数时,获得最大利润;③当50<m<100时,y随n的增大而增大, ∴当n=80时,y取得最大值,即购进A型手机30部、B型手机80部时销售总利润最大.16..某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.(1)求两种球拍每副各多少元?(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.【答案】见解析.【解析】解:(1)设直拍球拍每副x元,横拍球每副y元,由题意得,201520359000 10201052051600x yy x++⨯=⎧⎨+⨯=+⨯+⎩,解得:220260xy=⎧⎨=⎩,答:直拍球拍每副220元,横拍球每副260元;(2)设购买直拍球拍m副,则购买横拍球(40﹣m)副,所需的费用为w元,由题意得:m≤3(40﹣m),即m≤30,则w=(220+20)m+(260+20)(40﹣m)=﹣40m+11200,∵﹣40<0,∴w随m的增大而减小,∴当m=30时,w取最小值,最小值为10000(元).答:购买直拍球拍30副,则购买横拍球10副时,费用最少为10000元.17..某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.(1)求购买1个排球、1个篮球的费用分别是多少元?(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?【答案】见解析.。
初三中考压轴题专题——y与x的函数关系式

5.(2011普陀区模拟考压轴题)直角三角板ABC 中,∠A =30°,BC =1.将其绕直角顶点C 逆时针旋转一个角α(0120α︒<<︒且α≠ 90°),得到Rt△''A B C , (1)如图9,当''A B 边经过点B 时,求旋转角α的度数;(2)在三角板旋转的过程中,边'A C 与AB 所在直线交于点D ,过点 D 作DE ∥''A B 交'CB 边于点E ,联结BE .①当090α︒<<︒时,设AD x =,BE y =,求y 与x 之间的函数解析式及定义域; ②当ABC BDE S S ∆∆=31时,求AD 的长.CBACBA图9备用图备用图6.(2011年上海市中考)在Rt △ABC 中,∠ACB =90°,BC =30,AB =50.点P 是AB 边上任意一点,直线PE ⊥AB ,与边AC 或BC 相交于E .点M 在线段AP 上,点N 在线段BP 上,EM =EN ,12sin 13EMP ∠=. (1)如图1,当点E 与点C 重合时,求CM 的长;(2)如图2,当点E 在边AC 上时,点E 不与点A 、C 重合,设AP =x ,BN =y ,求y 关于x 的函数关系式,并写出函数的定义域;(3)若△AME ∽△ENB (△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应),求AP 的长.8.(2010年上海市中考压轴题)如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;(2)若CE=2,BD=BC,求∠BPD的正切值;(3)若1tan3BPD∠=,设CE=x,△ABC的周长为y,求y关于x的函数关系式.图9 图10(备用) 图。
2022-23学年人教版九年级数学上学期压轴题汇编专题08 二次函数的实际应用—销售问题(含详解)

2022-2023学年人教版数学九年级上册压轴题专题精选汇编专题08 二次函数的实际应用—销售问题考试时间:120分钟 试卷满分:100分姓名:__________ 班级:__________考号:__________题号一 二 三 总分得分评卷人得 分 一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2022九下·嘉祥开学考)某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )A .55B .56C .57D .582.(2分)(2021九上·北京月考)商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x 元(x 正整数),每星期销售的利润为y 元,则y 与x 的函数关系式为( )A .y =10(200﹣10x )B .y =200(10+x )C .y =10(200﹣10x )2D .y =(10+x )(200﹣10x )3.(2分)(2021九上·淮北月考)某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量 y (件)与销售单价 x (元)之间满足函数关系式 5550y x =-+ ,若要求销售单价不得低于成本,为每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )A .90元,4500元B .80元,4500元C .90元,4000元D .80元,4000元4.(2分)(2021九上·江干月考)某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )元。
中考数学【压轴题全揭秘(河南专版)】专题01_动点与函数图象(原卷版)_

专题01 动点与函数图象【例1】(2019·郑州外国语测试)如图所示,在矩形ABCD中,AB=8,AD=4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N的速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图象为()A B C D【变式1-1】(2019·洛阳二模)如图,点P是边长为2 cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设DP=x cm,则△POD的面积y(cm2)随x(cm)变化的关系图象为()A B C D【变式1-2】(2019·叶县一模)如图,在△ABC中,△ABC=60°,△C=45°,点D,E分别为边AB,AC上的点,且DE△BC,BD=DE=2,CE=52,BC=245.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ△BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为()A.B.C.D.【例2】(2019·省实验一模)如图,正方形ABCD,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是()A.B.C.D.【变式2-1】(2019·名校模考)如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF△BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的()A.线段BE B.线段EF C.线段CE D.线段DE【变式2-2】(2018·洛宁县模拟)如图1,正△ABC 的边长为4,点P 为BC 边上的任意一点,且△APD =60°,PD 交AC 于点D ,设线段PB 的长度为x ,图1中某线段的长度为y ,y 与x 的函数关系的大致图象如图2,则这条线段可能是图1中的( )图1 图2 A .线段ADB .线段APC .线段PDD .线段CD【例3】(2019·周口二模)如图1,E 为矩形ABCD 边AD 上的一点,点P 从点B 沿折线BE -ED -DC 运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止,它们运动的速度都是2 cm /s .若P ,Q 同时开始运动,设运动时间为t (s ),△BPQ 的面积为y (cm 2),已知y 与t 的函数关系图象如图2,则CDBE的值为( ) ABCD图1 图2【变式3-1】(2019·枫杨外国语三模)如图 1,动点 K 从△ABC 的顶点 A 出发,沿 AB ﹣BC 匀速运动到点 C 停止.在动点 K 运动过程中,线段 AK 的长度 y 与运动时间 x 的函数关系如图 2 所示,其中点 Q 为曲线部分的最低点,若△ABC的面积是,则 a 的值为图1 图2图1图2【变式3-2】(2019·中原名校大联考)如图1,在矩形ABCD中,动点M从点A出发,沿A→B→C方向运动,当点M到达点C时停止运动,过点M作MN△AM交CD于点N,设点M的运动路程为x,CN=y,图2表示的是y与x的函数关系的大致图象,则矩形ABCD的面积是()A.20B.18C.10D.91. (2019·濮阳二模)如图,点A在x轴上,点B,C在反比例函数y=kx(k>0,x>0)的图象上.有一个动点P从点A出发,沿A→B→C→O的路线(图中“→”所示路线)匀速运动,过点P作PM△x轴,垂足为M,设△POM的面积为S,点P的运动时间为t,则S关于t的函数图象大致为()A.B.C.D.2.(2019·南阳模拟)如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE△AC,交BC于E点;过E点作EF△DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y 与x函数关系的图象是()A.B.C.D.3.(2019·平顶山三模)如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是()A.B.C.D.4.(2017·预测卷)如图甲,点E为矩形ABCD边AD上一点,点P,Q同时从B点出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ 的面积为y(cm2),已知y与t的函数关系的图象如图乙(曲线OM为抛物线的一部分),则下列结论:△当0<t≤5时,y=25t2 △tan△ABE=34△点H的坐标为(11,0)△△ABE与△QBP不可能相似.其中正确的是(把你认为正确结论的序号都填上)5.(2019·焦作二模)如图1,在等边△ABC中,点D是BC边的中点,点P为AB边上的一个动点,设xAP ,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则等边△ABC的面积为.6.(2019·三门峡一模)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x ,两个三角形重叠面积为y ,则y 关于x 的函数图象是( )ABCD7.(2019·许昌月考)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P 从点A 出发,沿A →D →E →F →G →B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( )A .B .C .D .8.(2019·信阳模拟)如图1,在△ABC 中,△C =90°,动点P 从点C 出发,以1cm /s 的速度沿折线CA →AB 匀速运动,到达点B 时停止运动,点P 出发一段时间后动点Q 从点B 出发,以相同的速度沿BC 匀速运动,当点P 到达点B 时,点Q 恰好到达点C ,并停止运动,设点P 的运动时间为t s ,△PQC 的面积为S cm 2,S 关于t 的函数图象如图2所示(其中0<t ≤3,3≤t ≤4时,函数图象均为线段(不含点O ),4<t <8时,函数图象为抛物线的一部分)给出下列结论:△AC =3cm ;△当S =65时,t =35或6.下结论正确的是( )A .△△都对B .△△都错C .△对△错D .△错△对9.(2018·新乡一模)如图,平行四边形ABCD 中,ABcm ,BC =2cm ,△ABC =45°,点P 从点B 出发,以1cm /s 的速度沿折线BC →CD →DA 运动,到达点A 为止,设运动时间为t (s ),△ABP 的面积为S (cm 2),则S 与t 的函数表达式为.10.(2019·郑州外国语模拟)如图,在等腰△ABC 中,AB =AC =4cm ,△B =30°,点P 从点Bcm /s 的速度沿BC 方向运动到点C 停止,同时点Q 从点B 出发以2cm /s 的速度沿B →A →C 运动到点C 停止,若△BPQ 的面积为y ,运动时间为t (s ),则y 与t 的函数关系式为:.11.(2019·安阳一模)如图,在四边形ABCD 中,AD △BC ,DC △BC ,DC =4 cm ,BC =6 cm ,AD =3 cm ,动点P ,Q 同时从点B 出发,点P 以2 cm /s 的速度沿折线BA -AD -DC 运动到点C ,点Q 以1 cm /s 的速度沿BC 运动到点C ,设P ,Q 同时出发t s 时,△BPQ 的面积为y cm 2,则y 与t 的函数图象大致是( )ABCDBBC12.(2019·开封模拟)如图,菱形ABCD 的边长是4 cm ,△B =60°,动点P 以1 cm /s 的速度从点A 出发沿AB 方向运动至点B 停止,动点Q 以2 cm /s 的速度从点B 出发沿折线BCD 运动至点D 停止.若点P ,Q 同时出发,运动了t s ,记△BPQ 的面积为S cm 2,则下面图象中能表示S 与t 之间的函数关系的是( )A .B .C .D .13. 如图,矩形ABCD 中,AB =2AD =4cm ,动点P 从点A 出发,以lcm /s 的速度沿线段AB 向点B 运动,动点Q 同时从点A 出发,以2cm /s 的速度沿折线AD →DC →CB 向点B 运动,当一个点停止时另一个点也随之停止.设点P 的运动时间是x (s )时,△APQ 的面积是y (cm 2),则能够反映y 与x 之间函数关系的图象大致是()14.(2019·信阳一模)如图,锐角三角形ABC 中,BC =6,BC 边上的高为4,直线MN 交边AB 于点M ,交AC 于点N ,且MN △BC ,以MN 为边作正方形MNPQ ,设其边长为x (x >0),正方形MNPQ 与△ABC 公共部分的面积为y ,则y 与x 的函数图象大致是( )A B C D15.(2018·开封二模)如图,在平面直角坐标系中,已知A(0,1),B0),以线段AB为边向上作菱形ABCD,且点D在y轴上. 若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行,直至顶点D落在x轴上时停止.设菱形落在x轴下方部分的面积为S,则表示S与滑行时间t的函数关系的图象为()图1 图2A B C D。
九年级数学中考专题:动点问题综合压轴题

2023年九年级数学中考专题:动点问题综合压轴题1.如图,在ABC 中,4AB =,6BC =,P 是BC 边上一动点,60APN B ∠=∠=︒,过A 点作射线AM BC ∥,交射线PN 于点D .(1)求AC 的长; (2)求证:2=?AP BP AD ;(3)连接CD ,若ACD 为直角三角形,求BP 的长.2.如图1,,=90DC AB D ∠︒,,10cm,6cm AC BC AB BC ⊥==.点P 以1cm/s 的速度从点A 出发,沿AB 方向向点B 运动,同时点Q 以2cm/s 的速度从点B 出发,沿B →C →A 方向向点A 运动,当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t (s ).(1)AD 的长为 ;(2)求t 为何值时,PQ 平行于ABC ∆的一边;(3)当点Q 在边BC 上运动,求t 为何值时,PBQ ∆的面积为264cm 53.如图1,正方形ABCD 中,点P 为对角线BD 上一动点,点E 在AD 的延长线上,且62AP PE AB DE ===,,.(1)填空:PE 的长为______;(2)如图2,过点P 作PF EC ⊥于点F ,交DC 于点H ,延长FP 交AB 于点G ,求证:BG CH DE =+;(3)若点E 在直线AD 上运动,直线PE 与直线CD 交于点M ,其他条件不变,则PM 的长为______;(4)若点P 为正方形ABCD 对角线BD 上的动点,则22PD BP +的最小值为______.4.如图1,在Rt ABC △中,=90=6cm =8cm ACB AC BC ∠︒,,,动点P 从点B 出发,在BA 边上以每秒5cm 的速度向点A 匀速运动,同时动点Q 从点C 出发,在CB 边上以每秒4cm 的速度向点B 匀速运动,运动时间为t 秒()02t <<,连接PQ .(1)若BPQ 与ABC △相似,求t 的值; (2)直接写出BPQ 是等腰三角形时t 的值; (3)如图2,连接AQ 、CP ,若AQ CP ⊥,求t 的值.5.如图,在平面直角坐标系xOy 中,已知点A(0)2,,点C 是x 轴上的动点,线段CA 绕着点C 逆时针旋转90°至线段CB ,连接BO ,设点C 的横坐标为m .(1)BC 的长度是________(用含m 的式子表示); (2)求点B 的坐标(用含m 的式子表示); (3)求线段BO 长度的最小值.6.如图,Rt ACB △中,90,ACB AC BC ∠=︒=,E 点为射线CB 上一动点,连接AE ,作AF AE ⊥且AF AE =.(1)如图1,过F 点作FD AC ⊥交AC 于D 点,求证:EC CD DF +=; (2)如图2,连接BF 交AC 于G 点,若3AGCG=,求证:E 点为BC 中点; (3)当E 点在射线CB 上,连接BF 与直线AC 交于G 点,若52BC BE =,则AGCG= (直接写出结果).7.如图,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的动点,连接AC ,BC ,过点C 作ACB ∠的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)当CA CD =时,求E ∠的大小;(2)若⊙O 的半径为5,8AC =,求CD 的长;(3)如图2,当CD 不过点O 时,过点O 作OM CD ⊥交CD 于点M ,试判断AC BCOM-是否为定值,若是,求出该值;若不是,请说明理由.8.已知:AB 为O 的直径,BC AC =,D 为弦AC 上一动点(不与A 、C 重合).(1)如图1,若BD 平分CBA ∠,连接OC 交BD 于点E . ⊙求证:CE CD =; ⊙若2OE =,求AD 的长.(2)如图2,若BD 绕点D 顺时针旋转90︒得DF ,连接AF .求证:AF 为O 的切线.9.如图,在锐角ABC ∆中,60A ∠=︒,点D ,E 分别是边,AB AC 上一动点,连接BE 交直线CD 于点F .(1)如图1,若AB AC >,且,BD CE BCD CBE =∠=∠,求CFE ∠的度数;(2)如图2,若=AB AC ,且=BD AE ,在平面内将线段AC 绕点C 顺时针方向旋转60°得到线段CM ,连接MF ,点N 是MF 的中点,连接CN .在点D ,E 运动过程中,猜想线段,,BF CF CN 之间存在的数量关系,并证明你的猜想.10.如图,正方形ABCD 中,=4AB ,点M 是射线BA 上的一动点,BP CM ⊥,垂足为P ,PD PN ⊥,与射线BC 交于点N ,连接DN .(1)若点M 在边AB 上(与点B 、A 不重合). ⊙求证:BP BNCP BC=; ⊙连接DN ,设BM x =,DPNBPCS y S ∆∆=,求y 与x 的函数关系式,并写出函数定义域; (2)若3DPNCPNS S=,求出BM 的长.11.如图⊙,在矩形ABCD 中,AB <AD ,对角线AC ,BD 相交于点O ,动点P 由点A 出发,沿AB →BC →CD 向点D 运动.设点P 运动的路程为x ,设AOP 的面积为y ,y 与x 的函数关系图象如图⊙所示.(1)AB=cm,AD=cm;(2)若点P运动的速度为1cm/s,另一点Q同时以23cm/s的速度从A出发沿AD运动,点P运动的时间为t.当P、Q中有一点到达点D时,另一点随之停止.如图⊙,连接OQ、BQ、DP,设⊙BOQ面积为S 1,DOP面积为S2,当点P在BC上时,若S1与S2的乘积为S,求S与t的函数关系式.(3)点P运动的时间为t,连接DP,将点A沿直线DP翻折到点E,连接PE、DE,DE 交射线AC于点F,当t为何值时,DAF为等腰三角形.12.如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与A、C重合),连接PB,过点P作PE⊙PB,交射线DC于点E,已知AD=3,AC=5.设AP的长为x.(1)AB=_______;当x=1时,PEPB=______;(2)试探究:PEPB是否是定值?若是,请求出这个值;若不是,请说明理由;(3)连接BE,设⊙PBE的面积为S,求S的最小值.13.如图,在矩形ABCD 中,设=AB a ,AD b =,且>a b .(1)若a b ,为方程240x kx k -++=的两根,且BD =k 的值.(2)在(1)的条件下,P 为CD 上一点(异于C D 、两点),P 在什么位置时,APB △为直角三角形?(3)P 为CD 上一动点(异于C D 、两点),当a b ,满足什么条件时,使APB △为直角三角形的P 点有且只有一个?请直接写出a b ,满足的数量关系.14.如图1,在矩形ABCD 中,8AB =,10AD =,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G .(1)求线段CE 的长;(2)如图2,M ,N 分别是线段AG DG ,上的动点(与端点不重合),且DMN DAM ∠=∠,设DN x =.⊙求证四边形AFGD 为菱形;⊙是否存在这样的点N ,使DMN 是直角三角形?若存在,请求出x 的值;若不存在,请说明理由.15.如图,矩形ABCO 中,点C 在x 轴上,点A 在y 轴上,点B 的坐标是(-6,8),矩形ABCO 沿直线BD 折叠,使得点A 落在对角线OB 上的点E 处,折痕与0A 、x 轴分别交于点D 、F .(1)求证:⊙BOF 是等腰三角形; (2)求直线BD 的解析式;(3)若点P 是平面内任意一点,点M 是线段BD 上的一个动点,过点M 作MN ⊙x 轴,垂足为点N 在点M 的运动过程中是否存在以P 、N 、E 、O 为顶点的四边形是菱形?若存在,直接写出点M 的坐标:若不存在,请说明理由16.如图,在Rt ABC △中,⊙ACB =90°,AC =3,BC =4,过点B 作射线1BB AC ∥.动点D 从点A 出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E 从点C 出发沿射线AC 方向以每秒3个单位的速度运动.过点D 作DH ⊙AB 于H ,过点E 作EF ⊙AC 交射线BB ′于F ,G 是EF 中点,连接DG .设点D 运动的时间为t 秒.(1)当t 为何值时,AD =AB ,并求出此时DE 的长度; (2)当DEG △与ACB △相似时,求t 的值;(3)以DH 所在直线为对称轴,线段AC 经轴对称变换后的图形为A C ''.当线段A C ''与射线BB ',有公共点时,求t 的取值范围.17.在菱形ABCD 中,6AB =,=60A ∠︒,点E 在AD 边上,4AE =,点P 是边AB 上△沿EP翻折得到FEP.一个动点,连结EP,将AEP(1)当EF AB∥时,求AEP的度数;(2)若点F落在对角线BD上,求证:DEF BFP;(3)若点P在射线BA上运动,设直线PF与直线BD交于点H,问当AP为何值时,BHP 为直角三角形.18.已知ABC为等边三角形,其边长为4.点P是AB边上一动点,连接CP.(1)如图1,点E在AC边上且AE=BP,连接BE交CP于点F.⊙求证:BE=CP;⊙求⊙BFC的度数.(2)如图2,将线段CP绕点C顺时针旋转120°得线段CQ,连接BQ交AC于点D.设BP=x,CD=y,求y与x的函数关系式.19.在平面直角坐标系中,已知点A的坐标为(0,2),△ABO为等边三角形,P是x轴上的一个动点(不与O点重合),将线段AP绕A点按逆时针旋转60°,P点的对应点为点Q,连接OQ,BQ(1)点B 的坐标为 ;(2)⊙如图⊙,当点P 在x 轴负半轴运动时,求证:⊙ABQ =90°;⊙当点P 在x 轴正半轴运动时,⊙中的结论是否仍然成立?请补全图⊙,并作出判断(不需要说明理由);(3)在点P 运动的过程中,若△OBQ 是直角三角形,直接..写出点P 的坐标.20.如图1,在平面直角坐标系中,一次函数2y =+的图像经过点A (m ),与y 轴交于点B ,与x 轴交于点C .抛物线213y x bx c =-++经过点A 交y 轴于点D (0,6).(1)求m 的值及抛物线的表达式;(2)如图2,点E 为抛物线上一点且在直线AC 上方,若EAC 的面积为E 的坐标;(3)坐标轴上有一动点F ,连接AF ,当⊙BAF =60°时,直接写出点F 的坐标.参考答案:1.(1)AC =(3)满足条件的PB 的长为42.(1)4.8cm (2)3013t =或t =5 (3)23.(1)(4)364.(1)t 的值为1或4132(2)BPQ 是等腰三角形时t 的值为:23或89或6457(3)78t =5.(2)(2,)m m --(3)当1m =时OB 最小,最小值为2OB =6. (3)67.(1)67.5E ∠=︒(2)CD =(3)AC BC OM-=8.(1);⊙49.(1)60︒(2)2BF CF CN +=,10.(1)⊙2832(04)16x x y x -+=<<(2)BM 的长为2或10±11.(1)3;4 (2)()23272706884S t t t =-+-≤<(3)4312.(1)4,34(2)是定值,34(3)542513.(1)k=8(2)P 在(3或(3位置时,APB △为直角三角形(3)2a b =14.(1)3(2)⊙见解析;⊙5=2x 或215.(1)见解析(2)y =12-x +5 (3)存在,M 点的坐标为(245-,375)、(4,7)-或(103-,203)16.(1)当t =1时,AD =AB ,此时DE 的长度为1(2)t =34或16或94或176 (3)56≤t ≤433017.(1)60°;(3)4或2+2或4+18.(1)⊙120︒ (2)12(04)2y x x =-≤≤19.1)(2)成立(3)(0)或0)20.(1)m 的值为4,2163y x x =-+;(2)E (0,6)或(0);(3)F (0)或(0,203).。
中考数学压轴题提升训练一次函数与反比例函数综合题含解析

一次函数与反比例函数综合题【例1】。
如图,直线l:y=ax+b交x轴于点A(3,0),交y于第一象限的点P,点P的轴于点B(0,-3),交反比例函数y kx横坐标为4.的解析式;(1)求反比例函数y kx(2)过点P作直线l的垂线l1,交反比例函数y k的图象于x点C,求△OPC的面积.【答案】见解析。
【解析】解:(1)∵y=ax+b交x轴于点A(3,0),交y轴于点B(0,-3),∴3a+b=0,b=-3,解得:a=1,即l1的解析式为:y=x-3,当x=4时,y=1,即P(4,1),将P点坐标代入y k得:k=4,x;即反比函数的解析式为:y4x(2)设直线l1与x轴、y轴分别交于点E,D,∵OA=OB=3,∴∠OAB=∠OBA=45°,∵l⊥l1,∴∠DPB=90°,∴∠ODP=45°,设直线l1的解析式为:y=-x+b,将点P(4,1)代入得:b=5,联立:y=-x+5,y4x,解得:x=1,y=4或x=4,y=1,即C(1,4),∴S△OPC=S△ODE-S△OCD-S△OPE=12×5×5-12×5×1-12×5×1=152.【变式1—1】.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–12x+3交AB,BC于点M,N,反比例函数kyx的图象经过点M,N.(1)求反比例函数的解析式;(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.【答案】见解析.【解析】解:(1)∵B(4,2),四边形OABC为矩形,∴OA=BC=2,在y=–12x+3中,y=2时,x=2,即M(2,2),将M(2,2)代入kyx=得:k=4,∴反比例函数的解析式为:4yx=.(2)在4yx=中,当x=4时,y=1,即CN=1,∵S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-12×2×2-12×4×1=4,∴S△OPM=4,即12·OP·OA=4,∵OA=2,∴OP=4,∴点P 的坐标为(4,0)或(-4,0)。
中考压轴题-二次函数综合(八大题型+解题方法)——冲刺2024年中考数学考点押题(全国通用)(解析)

中考压轴题-二次函数综合 (八大题型+解题方法)1、求证“两线段相等”的问题:借助于函数解析式,先把动点坐标用一个字母表示出来;然后看两线段的长度是什么距离即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴y 轴的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等;2、“平行于y 轴的动线段长度的最大值”的问题:由于平行于y 轴的线段上各个点的横坐标相等常设为t,借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标;3、求一个已知点关于一条已知直线的对称点的坐标问题:先用点斜式或称K ,且与已知直线垂直的直线解析式,再求出两直线的交点坐标,最后用中点坐标公式即可;4、“抛物线上是否存在一点,使之到定直线的距离最大”的问题:方法1先求出定直线的斜率,由此可设出与定直线平行且与抛物线相切的直线的解析式注意该直线与定直线的斜率相等,因为平行直线斜率k 相等,再由该直线与抛物线的解析式组成方程组,用代入法把字母y 消掉,得到一个关于x 的的一元二次方程,由题有△=2b -4ac=0因为该直线与抛物线相切,只有一个交点,所以2b -4ac=0从而就可求出该切线的解析式,再把该切线解析式与抛物线的解析式组成方程组,求出x 、y 的值,即为切点坐标,然后再利用点到直线的距离公式,计算该切点到定直线的距离,即为最大距离; 方法2该问题等价于相应动三角形的面积最大问题,从而可先求出该三角形取得最大面积时,动点的坐标,再用点到直线的距离公式,求出其最大距离;方法3先把抛物线的方程对自变量求导,运用导数的几何意义,当该导数等于定直线的斜率时,求出的点的坐标即为符合题意的点,其最大距离运用点到直线的距离公式可以轻松求出;5、常数问题:1点到直线的距离中的常数问题:“抛物线上是否存在一点,使之到定直线的距离等于一个 固定常数”的问题:先借助于抛物线的解析式,把动点坐标用一个字母表示出来,再利用点到直线的距离公式建立一个方程,解此方程,即可求出动点的横坐标,进而利用抛物线解析式,求出动点的纵坐标,从而抛物线上的动点坐标就求出来了;2三角形面积中的常数问题:“抛物线上是否存在一点,使之与定线段构成的动三角形的面积等于一个定常数”的问题:先求出定线段的长度,再表示出动点其坐标需用一个字母表示到定直线的距离,再运用三角形的面积公式建立方程,解此方程,即可求出动点的横坐标,再利用抛物线的解析式,可求出动点纵坐标,从而抛物线上的动点坐标就求出来了;3几条线段的齐次幂的商为常数的问题:用K 点法设出直线方程,求出与抛物线或其它直线的交点坐标,再运用两点间的距离公式和根与系数的关系,把问题中的所有线段表示出来,并化解即可;6、“在定直线常为抛物线的对称轴,或x 轴或y 轴或其它的定直线上是否存在一点,使之到两定点的距离之和最小”的问题:先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出利用求交点坐标的方法;7、三角形周长的“最值最大值或最小值”问题:① “在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题简称“一边固定两边动的问题:由于有两个定点,所以该三角形有一定边其长度可利用两点间距离公式计算,只需另两边的和最小即可;② “在抛物线上是否存在一点,使之到定直线的垂线,与y 轴的平行线和定直线,这三线构成的动直角三角形的周长最大”的问题简称“三边均动的问题:在图中寻找一个和动直角三角形相似的定直角三角形,在动点坐标一母示后,运用=C C 动动定定斜边斜边,把动三角形的周长转化为一个开口向下的抛物线来破解;8、三角形面积的最大值问题:① “抛物线上是否存在一点,使之和一条定线段构成的三角形面积最大”的问题简称“一边固定两边动的问题”:方法1:先利用两点间的距离公式求出定线段的长度;然后再利用上面3的方法,求出抛物线上的动点到该定直线的最大距离;最后利用三角形的面积公式= 12底×高;即可求出该三角形面积的最大值,同时在求解过程中,切点即为符合题意要求的点;方法2:过动点向y 轴作平行线找到与定线段或所在直线的交点,从而把动三角形分割成两个基本模型的三角形,动点坐标一母示后,进一步可得到)()(左(定)右(定)下(动)上(动)动三角形x x y y 21−⋅−=S ,转化为一个开口向下的二次函数问题来求出最大值;②“三边均动的动三角形面积最大”的问题简称“三边均动”的问题:先把动三角形分割成两个基本模型的三角形有一边在x 轴或y 轴上的三角形,或者有一边平行于x 轴或y 轴的三角形,称为基本模型的三角形面积之差,设出动点在x 轴或y 轴上的点的坐标,而此类题型,题中一定含有一组平行线,从而可以得出分割后的一个三角形与图中另一个三角形相似常为图中最大的那一个三角形;利用相似三角形的性质对应边的比等于对应高的比可表示出分割后的一个三角形的高;从而可以表示出动三角形的面积的一个开口向下的二次函数关系式,相应问题也就轻松解决了;9、“一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”:由于该四边形有三个定点,,即可得到一个定三角形的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与7相同;10、“定四边形面积的求解”问题: 有两种常见解决的方案:方案一:连接一条对角线,分成两个三角形面积之和;方案二:过不在x 轴或y 轴上的四边形的一个顶点,向x 轴或y 轴作垂线,或者把该点与原点连结起来,分割成一个梯形常为直角梯形和一些三角形的面积之和或差,或几个基本模型的三角形面积的和差11、“两个三角形相似”的问题: 两个定三角形是否相似:(1)已知有一个角相等的情形:运用两点间的距离公式求出已知角的两条夹边,看看是否成比例 若成比例,则相似;否则不相似;(2)不知道是否有一个角相等的情形:运用两点间的距离公式求出两个三角形各边的长,看看是否成比例若成比例,则相似;否则不相似;一个定三角形和动三角形相似:(1)已知有一个角相等的情形:先借助于相应的函数关系式,把动点坐标表示出来一母示,然后把两个目标三角形题中要相似的那两个三角形中相等的那个已知角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那两边对应成比例要注意是否有两种情况,列出方程,解此方程即可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点;2不知道是否有一个角相等的情形:这种情形在相似性中属于高端问题,破解方法是,在定三角形中,由各个顶点坐标求出定三角形三边的长度,用观察法得出某一个角可能是特殊角,再为该角寻找一个直角三角形,用三角函数的方法得出特殊角的度数,在动点坐标“一母示”后,分析在动三角形中哪个角可以和定三角形中的那个特殊角相等,借助于特殊角,为动点寻找一个直角三角形,求出动点坐标,从而转化为已知有一个角相等的两个定三角形是否相似的问题了,只需再验证已知角的两边是否成比例若成比例,则所求动点坐标符合题意,否则这样的点不存在;简称“找特角,求动点标,再验证”;或称为“一找角,二求标,三验证”;12、“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题:首先弄清题中是否规定了哪个点为等腰三角形的顶点;若某边底,则只有一种情况;若某边为腰,有两种情况;若只说该三点构成等腰三角形则有三种情况;先借助于动点所在图象的解析式,表示出动点的坐标一母示,按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程;解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点就是不能构成三角形这个题意;13、“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题:这类问题,在题中的四个点中,至少有两个定点,用动点坐标“一母示”分别设出余下所有动点的坐标若有两个动点,显然每个动点应各选用一个参数字母来“一母示”出动点坐标,任选一个已知点作为对角线的起点,列出所有可能的对角线显然最多有3条,此时与之对应的另一条对角线也就确定了,然后运用中点坐标公式,求出每一种情况两条对角线的中点坐标,由平行四边形的判定定理可知,两中点重合,其坐标对应相等,列出两个方程,求解即可;进一步有:①若是否存在这样的动点构成矩形呢先让动点构成平行四边形,再验证两条对角线相等否若相等,则所求动点能构成矩形,否则这样的动点不存在;②若是否存在这样的动点构成棱形呢先让动点构成平行四边形,再验证任意一组邻边相等否若相等,则所求动点能构成棱形,否则这样的动点不存在;③若是否存在这样的动点构成正方形呢先让动点构成平行四边形,再验证任意一组邻边是否相等和两条对角线是否相等若都相等,则所求动点能构成正方形,否则这样的动点不存在;14、“抛物线上是否存在一点,使两个图形的面积之间存在和差倍分关系”的问题:此为“单动问题”〈即定解析式和动图形相结合的问题〉,后面的19实为本类型的特殊情形;先用动点坐标“一母示”的方法设出直接动点坐标,分别表示如果图形是动图形就只能表示出其面积或计算如果图形是定图形就计算出它的具体面积,然后由题意建立两个图形面积关系的一个方程,解之即可;注意去掉不合题意的点,如果问题中求的是间接动点坐标,那么在求出直接动点坐标后,再往下继续求解即可;15、“某图形〈直线或抛物线〉上是否存在一点,使之与另两定点构成直角三角形”的问题:若夹直角的两边与y轴都不平行:先设出动点坐标一母示,视题目分类的情况,分别用斜率公式算出夹直角的两边的斜率,再运用两直线没有与y轴平行的直线垂直的斜率结论两直线的斜率相乘等于-1,得到一个方程,解之即可;若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式;补救措施是:过余下的那一个点没在平行于y轴的那条直线上的点直接向平行于y的直线作垂线或过直角点作平行于y轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定;16、“某图象上是否存在一点,使之与另两定点构成等腰直角三角形”的问题;①若定点为直角顶点,先用k点法求出另一直角边所在直线的解析式如斜率不存在,根据定直角点,可以直接写出另一直角边所在直线的方程,利用该解析式与所求点所在的图象的解析式组成方程组,求出交点坐标,再用两点间的距离公式计算出两条直角边等否若等,该交点合题,反之不合题,舍去;②若动点为直角顶点:先利用k点法求出定线段的中垂线的解析式,再把该解析式与所求点所在图象的解析式组成方程组,求出交点坐标,再分别计算出该点与两定点所在的两条直线的斜率,把这两个斜率相乘,看其结果是否为-1 若为-1,则就说明所求交点合题;反之,舍去;17、“题中含有两角相等,求相关点的坐标或线段长度”等的问题:题中含有两角相等,则意味着应该运用三角形相似来解决,此时寻找三角形相似中的基本模型“A”或“X”是关键和突破口;18、“在相关函数的解析式已知或易求出的情况下,题中又含有某动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或线段长”的问题:此为“单动问题”〈即定解析式和动图形相结合的问题〉,本类型实际上是前面14的特殊情形;先把动图形化为一些直角梯形或基本模型的三角形有一边在x 轴或y轴上,或者有一边平行于x 轴或y 轴面积的和或差,设出相关点的坐标一母示,按化分后的图形建立一个面积关系的方程,解之即可;一句话,该问题简称“单动问题”,解题方法是“设点动点标,图形转化分割,列出面积方程”;19、“在相关函数解析式不确定系数中还含有某一个参数字母的情况下,题中又含有动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或参数的值”的问题:此为“双动问题”即动解析式和动图形相结合的问题;如果动图形不是基本模型,就先把动图形的面积进行转化或分割转化或分割后的图形须为基本模型,设出动点坐标一母示,利用转化或分割后的图形建立面积关系的方程或方程组;解此方程,求出相应点的横坐标,再利用该点所在函数图象的解析式,表示出该点的纵坐标注意,此时,一定不能把该点坐标再代入对应函数图象的解析式,这样会把所有字母消掉;再注意图中另一个点与该点的位置关系或其它关系,方法是常由已知或利用2问的结论,从几何知识的角度进行判断,表示出另一个点的坐标,最后把刚表示出来的这个点的坐标再代入相应解析式,得到仅含一个字母的方程,解之即可;如果动图形是基本模型,就无须分割或转化了,直接先设出动点坐标一母式,然后列出面积方程,往下操作方式就与不是基本模型的情况完全相同;一句话,该问题简称“双动问题”,解题方法是“转化分割,设点标,建方程,再代入,得结论”;常用公式或结论:1横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长=纵标之差的绝对值=-y y 大小=-y y 下上 2点轴距离:点P 0x ,0y 到X 轴的距离为0y ,到Y 轴的距离为o x ; 3两点间的距离公式:若A 11,x y ,B 2,2x y , 则AB=目录:题型1:存在性问题 题型2:最值问题 题型3:定值问题 题型4:定点问题题型5:动点问题综合 题型6:对称问题 题型7:新定义题 题型8:二次函数与圆题型1:存在性问题1.(2024·四川广安·二模)如图,抛物线2y x bx c =−++交x 轴于()4,0A −,B 两点,交y 轴于点()0,4C .(1)求抛物线的函数解析式.(2)点D 在线段OA 上运动,过点D 作x 轴的垂线,与AC 交于点Q ,与抛物线交于点P ,连接AP 、CP ,求四边形AOCP 的面积的最大值.(3)在抛物线的对称轴上是否存在点M ,使得以点A 、C 、M 为顶点的三角形是直角三角形?若存在,请求出点M【答案】(1)234y x x =−−+;(2)四边形AOCP 的面积最大为16;(3)点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭.【分析】本题主要考查了二次函数综合,熟练掌握用待定系数法求解函数解析式的方法和步骤,以及二次函数的图象和性质,是解题的关键. (1)把()4,0A −,()0,4C 代入2y x bx c =−++,求出b 和c 的值,即可得出函数解析式; (2)易得182AOCSOA OC =⋅=,设()2,34P t t t −−+,则(),4Q t t +,求出24PQ t t =−−,则()()212282ACP C A S PQ x x t =⋅−=−++,根据四边形AOCP 的面积()22216ACP AOCS St =+=−++,结合二次函数的增减性,即可解答;(3)设3,2M m ⎛⎫− ⎪⎝⎭,根据两点之间距离公式得出232AC =,22254AM m =+,229(4)4CM m =+−,然后分情况根据勾股定理列出方程求解即可.【解析】(1)解:把()4,0A −,()0,4C 代入2y x bx c =−++得:01644b c c =−−+⎧⎨=⎩,解得:34b c =−⎧⎨=⎩,∴该二次函数的解析式234y x x =−−+;(2)解:∵()4,0A −,()0,4C ,∴4,4OA OC ==,∴1144822AOC S OA OC =⋅=⨯⨯=△,设直线AC 的解析式为4y kx =+, 代入()4,0A −得,044k =−+,解得1k =,∴直线AC 的解析式为4y x =+, 设()2,34P t t t −−+,则(),4Q t t +,∴()223444PQ t t t t t=−−+−+=−−∴()()()22114422822ACPC A SPQ x x t t t =⋅−=−−⨯=−++,∴四边形AOCP 的面积()22216ACP AOCSSt =+=−++,∵20−<,∴当2t =−时,四边形AOCP 的面积最大为16; (3)解:设3,2M m ⎛⎫− ⎪⎝⎭,∵()4,0A −,()0,4C ,∴2224432AC =+=,2222325424AM m m ⎛⎫=−++=+ ⎪⎝⎭,()()2222394424CM m m ⎛⎫=−+−=+− ⎪⎝⎭,当斜边为AC 时,AM CM AC 222+=,即()2225943244m m +++−=,整理得:24150m m ++=,无解;当斜边为AM 时,222AC CM AM +=,即2292532(4)44m m ++−=+,解得:112m =;∴311,22M ⎛⎫− ⎪⎝⎭当斜边为CM 时,222AC AM CM +=,即2225932(4)44m m ++=+−, 解得:52m =−;∴35,22M ⎛⎫−− ⎪⎝⎭综上:点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭.2.(2024·内蒙古乌海·模拟预测)如图(1),在平面直角坐标系中,抛物线()240y ax bx a =+−≠与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为()1,0−,且OC OB =,点D 和点C 关于抛物线的对称轴对称.(1)分别求出a ,b 的值和直线AD 的解析式;(2)直线AD 下方的抛物线上有一点P ,过点P 作PH AD ⊥于点H ,作PM 平行于y 轴交直线AD 于点M ,交x 轴于点E ,求PHM 的周长的最大值;(3)在(2)的条件下,如图2,在直线EP 的右侧、x 轴下方的抛物线上是否存在点N ,过点N 作NG x ⊥轴交x 轴于点G ,使得以点E 、N 、G 为顶点的三角形与AOC 相似?如果存在,请直接写出点G 的坐标;如果不存在,请说明理由.【答案】(1)1a =,3b =−,=1y x −−(2)4+(3)存在,点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】本题主要考查的是二次函数的综合应用,掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式,列出PM 的长与a 的函数关系式是解题的关键.(1)先求得C 的坐标,从而得到点B 的坐标,设抛物线的解析式为()()14y a x x =+−,将点C 的坐标代入求解即可;先求得抛物线的对称轴,从而得到点()3,4D −,然后可求得直线AD 的解析式=1y x −−;(2)求得45BAD ∠=︒,接下来证明PMD △为等腰直角三角形,所当PM 有最大值时三角形的周长最大,设()2,34P a a a −−,()1M a −−,则223PM aa =−++,然后利用配方可求得PM 的最大值,最后根据MPH△的周长(1PM=求解即可;(3)当90EGN ∠=︒时,如果OA EG OC GN = 或OA GNOC EN =时,则AOC ∽EGN △,设点G 的坐标为(),0a ,则()2,34N a a a −−,则1EG a =−,234NG aa =−++,然后根据题意列方程求解即可.【解析】(1)点A 的坐标为()1,0−,1OA ∴=.令0x =,则4y =−,()0,4C ∴−,4OC =,OC OB =Q , 4OB ∴=,()4,0B ∴,设抛物线的解析式为()()14y a x x =+−,将0x =,4y =−代入得:44a −=−,解得1a =,∴抛物线的解析式为234y x x =−−;1a ∴=,3b =−; 抛物线的对称轴为33212x −=−=⨯,()0,4C −,点D 和点C 关于抛物线的对称轴对称,()3,4D ∴−;设直线AD 的解析式为y kx b =+.将()1,0A −、()3,4D −代入得:034k b k b −+=⎧⎨+=−⎩,解得1k =−,1b =-,∴直线AD 的解析式=1y x −−;(2)直线AD 的解析式=1y x −−,∴直线AD 的一次项系数1k =−,45BAD ∴∠=︒. PM 平行于y 轴,90AEP ∴∠=︒,45PMH AME ∴∠=∠=︒.MPH ∴的周长(122PM MH PH PM MP PM PM =++=++=. 设()2,34P a a a −−,则(),1M a a −−, 则()22213423(1)4PM a a a a a a =−−−−−=−++=−−+.∴当1a =时,PM 有最大值,最大值为4.MPH ∴的周长的最大值(414=⨯=+(3)在直线EP 的右侧、x 轴下方的抛物线上存在点N ,过点N 作NG x ⊥轴交x 轴于点G ,使得以点E 、N 、G 为顶点的三角形与AOC 相似;理由如下:设点G 的坐标为(),0a ,则()2,34N a a a −−①如图2.1,若OA EG OC GN = 时,AOC ∽EGN △. 则 211344a a a −=−++,整理得:280a a +−=.得:a =负值舍去),∴点G为⎫⎪⎪⎝⎭; ②如图2.2,若OA GN OC EN =时,AOC ∽NGE ,则21434a a a −=−++,整理得:2411170a a −−=,得:a =负值舍去),∴点G为⎫⎪⎪⎝⎭, 综上所述,点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭. 3.(2024·重庆·一模)如图,在平面直角坐标系中,抛物线2y ax bx =+x 轴交于点()1,0A −,()5,0B ,与y 轴交于点C ,连接BC ,AC .(1)求抛物线的表达式;(2)P 为直线BC 上方抛物线上一点,过点P 作PD BC ⊥于点D ,过点P 作PE x 轴交抛物线于点E,求4+PD PE 的最大值及此时点P 的坐标; (3)点C 关于抛物线对称轴对称的点为Q ,将抛物线沿射线CAy ',新抛物线y '与y 轴交于点M ,新抛物线y '的对称轴与x 轴交于点N ,连接AM ,MN ,点R 在直线BC 上,连接QR .当QR 与AMN 一边平行时,直接写出点R 的坐标,并写出其中一种符合条件的解答过程.【答案】(1)2y x x =++(2)当154t =时,PE的最大值,15,416P ⎛ ⎝⎭, (3)R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(.【分析】(1)利用待定系数法求抛物线解析式即可;(2)先求得2y x =2x =,过点P 作PG x ⊥轴交BC 于点F ,利用勾股定理求得BC ==DPF OBC ∽,得PF DP BC OB =即PF PD=,从而得PF =,求出设直线BC的解析式后,设2,P t ⎛+ ⎝,则,F t ⎛+ ⎝,从而2PF =+,当点P在E 点右侧时()424PE t t t =−−=−,从而得2154t ⎫=−⎪⎝⎭,利用二次函数的性质即可求解;当点P 在E 点左侧时:442PE t t t =−−=−时,同理可求.然后比较4+PE 的最大值即可得出答案. (3)先求得1OA=,OC AC =设抛物线2y =H ⎛ ⎝⎭平移后为P ,过点P 作PW ⊥直线2x =,则AOC PWH ∽,得1OA OC AC WP HW PH ====,进而得平移后的抛物线2y x +'=,从而求得()1,0N,M ⎛ ⎝⎭,然后分QR AM ∥,QR MN ∥,QR AN ∥三种情况,利用二次函数的性质及一次函数的与二元一次方程的关系求解即可得解.【解析】(1)解:∵抛物线2y ax bx =+x 轴交于点()1,0A −,()5,0B 两点,代入坐标得:02550a b a b ⎧−=⎪⎨+=⎪⎩,解得:a b ⎧=⎪⎪⎨⎪=⎪⎩,∴抛物线的函数表达式为255y x x =−++(2)解:∵)2225555y x x x =−+=−−+,∴2y x =2x=,顶点为⎛ ⎝⎭ 过点P 作PG x ⊥轴交BC 于点F ,当0x =时,200y =∴(C ∵()5,0B ∴BC ==∵PG x ⊥轴,PD BC ⊥,x 轴y ⊥轴,∴909090CBO BFG DPF PFD PDF BOC ∠∠∠∠∠∠+=︒+=︒==︒,,∵PFD BFG ∠∠=∴DPF CBO ∠∠=∴DPF OBC ∽,∴PF DP BC OB =即PF PD =,∴PF PD =∴44+PD PE =PF +PE ,设直线BC :y kx b =+,把(C ,()5,0B 代入得:05k b b =+⎧⎪=,解得5k b ⎧=−⎪⎨⎪=⎩, ∴直线BC:y =设2,P t ⎛ ⎝,则,F t ⎛+ ⎝,∴22PF ⎛⎛=−+=+ ⎝⎝,∵2y x =2x =,PE x 轴,∴24,E t ⎛−+ ⎝当点P 在E 点右侧时:()424PE t t t =−−=−,当24PE t =−时:∴+PD PE =PF +()221524545416t t ⎛⎫=−+−=−−+ ⎪⎝⎭ ∴当154t =时,的最大值∴2151544⎛⎫= ⎪⎝⎭,∴154P ⎛ ⎝⎭; 当点P 在E 点左侧时:442PE t t t =−−=−时,∴+PD PE =PF +()225424t t ⎫=−=−⎪⎝⎭, ∴当54t =时,的最大值.2,55P t ⎛−+ ⎝∴25544⎛⎫ ⎪⎝⎭∴5,416P ⎛ ⎝⎭,∵> 综上所诉,当点P 在E 点右侧时:即154t =时,的最大值,154P ⎛ ⎝⎭, (3)解:设直线AC :y mx n =+,把()1,0A −,(C , ∴1OA =,OC =∴AC ==设抛物线2y x =H ⎛ ⎝⎭平移后为P , 过点P 作PW ⊥直线2x =,则AOC PWH ∽,∴1OA OC AC WP HW PH ====∴1PW =,HW=∴21,5P ⎛−⎝即1,5P ⎛ ⎝⎭,∴平移后的抛物线)22155555y x x x =−−+=−++', ∴()1,0N令0x =,y '=,∴M ⎛ ⎝⎭ 如图,当QR AM ∥时,设直线AM 的解析式为:y px q =+,把M ⎛ ⎝⎭,()1,0A −代入得:0p q q =−+⎧=解得p q ⎧=⎪⎪⎨⎪=⎪⎩, ∴直线AM的解析式为:y =, ∴设直线QR的解析式为:y x n =∵(C ,Q 和C 关于2x =对称,∴(Q把(Q代入5y x n =+45n +,解得n =,∴直线QR的解析式为:y = 联立直线QR的解析式y =与直线BC:y x =+55y x y x ⎧=−⎪⎪⎨⎪=⎪⎩,解得3x y =⎧⎪⎨=⎪⎩,∴R ⎛ ⎝⎭ 同理可得:当QR MN ∥时,6,5R ⎛− ⎝⎭ 当QR AN ∥时,(R所有符合条件的R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(. 【点睛】本题考查待定系数法求抛物线解析式,勾股定理,抛物线的性质,抛物线平移,一次函数的平移,相似三角形的判定及性质,图形与坐标,掌握待定系数法求抛物线解析式,抛物线的性质,抛物线平移,相似三角形的判定及性质,图形与坐标,利用辅助线画出准确图形是解题关键.题型2:最值问题4.(2024·安徽合肥·二模)在平面直角坐标系中,O 为坐标原点,抛物线23y ax bx =+−与x 轴交于()1,0A −,()3,0B 两点,与y 轴交于点C ,连接BC .(1)求a ,b 的值;(2)点M 为线段BC 上一动点(不与B ,C 重合),过点M 作MP x ⊥轴于点P ,交抛物线于点N . (ⅰ)如图1,当3PA PB=时,求线段MN 的长; (ⅱ)如图2,在抛物线上找一点Q ,连接AM ,QN ,QP ,使得PQN V 与APM △的面积相等,当线段NQ 的长度最小时,求点M 的横坐标m 的值.【答案】(1)1a =,2b =−(2)(ⅰ)2MN =;(ⅱ)m 的值为32或12【分析】本题考查诶粗函数的图象和性质,掌握待定系数法和利用函数性质求面积是解题的关键.(1)运用待定系数法求函数解析式即可;(2)(ⅰ)先计算BC 的解析式,然后设(),3M m m −,则3PM PB m ==−,1PA m =+,根据题意得到方程133m m +=−求出m 值,即可求出MN 的长;(ⅱ)作QR PN ⊥于点R ,由(ⅰ)可得1PA m =+,3PB PM m =−−,223PN m m =−++,然后分为点Q 在PN 的左侧和点Q 在PN 的右侧两种情况,根据勾股定理解题即可.【解析】(1)由题意得309330a b a b −−=⎧⎨+−=⎩,解得12a b =⎧⎨=−⎩;(2)(ⅰ)当0x =时,3y =−,∴()0,3C −,设直线BC 为3y kx =−,∵点()3,0B ,∴330k −=,解得1k =,∴直线BC 为3y x =−,设(),3M m m −,则3PM PB m ==−,1PA m =+, ∵3PA PB =, ∴133m m +=−,解得2m =,经检验2m =符合题意,当2m =时,222233y =−⨯−=−, ∴3PN =,31PM PB m ==−=,∴2MN =;(ⅱ)作QR PN ⊥于点R ,由(ⅰ)可得1PA m =+,3PB PM m =−−,223PN m m =−++,PQN V 的面积为()21232m m QR −++⋅,APM △的面积为()()1312m m −+,∴()()()211233122m m QR m m −++⋅=−+,解得1QR =;当点Q 在PN 的左侧时,如图1,Q 点的横坐标为1m QR m −=−,纵坐标为()()2212134m m m m −−⨯−−=−,∴R 点的坐标为()2,4m mm−,∵N 点坐标为()2,23m mm −−,∴32RN m =−,∴()22231NQ m =−+,∴当32m =时,NQ 取最小值;当点Q 在PN 的右侧时,如图2,Q 点的横坐标为1m QR m +=+,纵坐标为()()2212134m m m +−⨯+−=−,∴R 点的坐标为()2,4m m−,∵N 点的坐标为()2,23m mm −−,∴21RN m =−, ∴()222211NQ m =−+,∴当12m =时,NQ 取最小值.综上,m 的值为32或12.。
初三专题构建y与x的函数关系式——圆
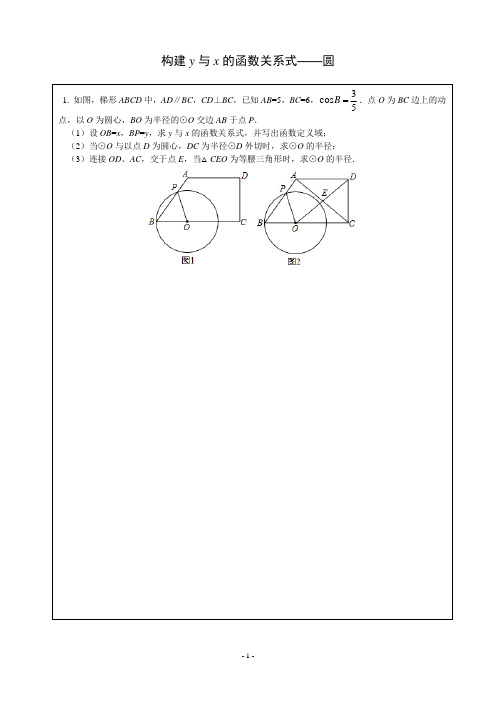
构建y 与x 的函数关系式——圆1. 如图,梯形ABCD 中,AD ∥BC ,CD ⊥BC ,已知AB =5,BC =6,53cosB .点O 为BC 边上的动点,以O 为圆心,BO 为半径的⊙O 交边AB 于点P .(1)设OB =x ,BP =y ,求y 与x 的函数关系式,并写出函数定义域; (2)当⊙O 与以点D 为圆心,DC 为半径⊙D 外切时,求⊙O 的半径;(3)连接OD 、AC ,交于点E ,当△CEO 为等腰三角形时,求⊙O 的半径.2如图,在半径为5的⊙O 中,点A 、B 在⊙O 上,∠AOB =90°,点C 是弧AB 上的一个动点,AC 与OB 的延长线相交于点D ,设AC =x ,BD =y .(2011•静安区二模) (1)求y 关于x 的函数解析式,并写出它的定义域;(2)如果⊙O 1与⊙O 相交于点A 、C ,且⊙O 1与⊙O 的圆心距为2,当OB BD 31时,求⊙O 1的半径;(3)是否存在点C ,使得△DCB ∽△DOC ?如果存在,请证明;如果不存在,请简要说明理由.3 在梯形ABCD中,AD∥BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心,BE为半径画⊙E交线段DE于点F.(1)如图,当点F在线段DE上时,设BE=x,DF=y,试建立y关于x的函数关系式,并写出自变量x的取值范围;(2)当以CD为直径的⊙O与⊙E相切时,求x的值;(3)连接AF、BF,当△ABF是以AF为腰的等腰三角形时,求x的值.(2011•徐汇区二模)4.如图1,已知⊙O的半径长为1,PQ是⊙O的直径,点M是PQ延长线上一点,以点M为圆心作圆,与⊙O交于A、B两点,连接P A并延长,交⊙M于另外一点C.(1)若AB恰好是⊙O的直径,设OM=x,AC=y,试在图2中画出符合要求的大致图形,并求y关于x的函数解析式;(2)连接OA、MA、MC,若OA⊥MA,且△OMA与△PMC相似,求OM的长度和⊙M的半径长;(3)是否存在⊙M,使得AB、AC恰好是一个正五边形的两条边?若存在,试求OM的长度和⊙M的半径长;若不存在,试说明理由.(2011•嘉定区二模)5如图,在Rt △ABC 中,∠ACB =90°.半径为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,连接DE 并延长,与线段BC 的延长线交于点P . (1)当∠B =30°时,连接AP ,若△AEP 与△BDP 相似,求CE 的长; (2)若CE =2,BD =BC ,求∠BPD 的正切值; (3)若31tan =∠BPD ,设CE =x ,△ABC 的周长为y ,求y 关于x 的函数关系式.(2010•上海)6.已知:⊙O的直径AB=8,⊙B与⊙O相交于点C、D,⊙O的直径CF与⊙B相交于点E,设⊙B 的半径为x,OE的长为y.(1)如图,当点E在线段OC上时,求y关于x的函数解析式,并写出定义域;(2)当点E在直径CF上时,如果OE的长为3,求公共弦CD的长;(3)设⊙B与AB相交于G,试问△OEG能否为等腰三角形?如果能够,请直接写出BC的长度(不必写过程);如果不能,请简要说明理由.(2009•静安区二模)二、巩固训练:1、在半径为4的⊙O 中,点C 是以AB 为直径的半圆的中点,OD ⊥AC ,垂足为D ,点E 是射线AB 上的任意一点,DF //AB ,DF 与CE 相交于点F ,设EF =x ,DF =y .(1)如图1,当点E 在射线OB 上时,求y 关于x 的函数解析式,并写出函数定义域; (2)如图2,当点F 在⊙O 上时,求线段DF 的长.(2013•宁波模拟)2、已知:如图,△ABC 为等边三角形,43AB =,AH ⊥BC ,垂足为点H , 点D 在线段HC 上,且HD = 2,点P 为射线AH 上任意一点,以点P 为圆心,线段PD 的长为半径作⊙P ,设AP = x . (1)当x = 3时,求⊙P 的半径长;(2)如图2,如果⊙P 与线段AB 相交于E 、F 两点,且EF = y ,求y 关于x 的函数解析式,并写出它的定义域.(2010•闵行区三模)3、如图,已知在△ABC 中,AB =15,AC =20,2cot =A ,P 是边AB 上的一个动点,⊙P 的半径为定长.当点P 与点B 重合时,⊙P 恰好与边AC 相切;当点P 与点B 不重合,且⊙P 与边AC 相交于点M 和点N时,设AP =x ,MN =y . (1)求⊙P 的半径;(2)求y 关于x 的函数解析式,并写出它的定义域.4、如图,已知△ABC 中,AB =AC =5,BC =4,点O 在BC 边上运动,以O 为圆心,OA 为半径的圆与边AB 交于点D (点A 除外),设OB x =,AD y =.(1)求ABC ∠sin 的值;(2)求y 关于x 的函数解析式,并写出函数的定义域.(2010•青浦区二模)5、如图,已知线段AB =10,点C 在线段AB 上,⊙A 、⊙B 的半径分别为AC 、BC ,D 是⊙B 上一点,AD 交⊙A 于E ,EC 的延长线交⊙B 于F . (1)求证:BF //AD ;(2)若BD ⊥AD ,AC =x ,DF =y ,求y 与x 的函数关系式,写出定义域.(2008•奉贤区模拟)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.(2011普陀区模拟考压轴题)
直角三角板ABC 中,∠A =30°,BC =1.将其绕直角顶点C 逆时针旋转一个角α(0120α︒<<︒且α≠ 90°),得到Rt △''A B C ,
(1)如图9,当''A B 边经过点B 时,求旋转角α的度数;
(2)在三角板旋转的过程中,边'A C 与AB 所在直线交于点D ,过点 D 作DE ∥''A B 交'CB 边于点E ,联结BE .
①当090α︒<<︒时,设AD x =,BE y =,求y 与x 之间的函数解析式及定义域; ②当ABC BDE S S ∆∆=3
1
时,求AD 的长.
C
B
A
C
B
A
图9
备用图
备用图
6.(2011年上海市中考)
在Rt △ABC 中,∠ACB =90°,BC =30,AB =50.点P 是AB 边上任意一点,直线PE ⊥AB ,与边AC 或BC 相交于E .点M 在线段AP 上,点N 在线段BP 上,EM =EN ,
12sin 13
EMP ∠=
. (1)如图1,当点E 与点C 重合时,求CM 的长;
(2)如图2,当点E 在边AC 上时,点E 不与点A 、C 重合,设AP =x ,BN =y ,求y 关于x 的函数关系式,并写出函数的定义域;
(3)若△AME ∽△ENB (△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应),求AP 的长.
8.(2010年上海市中考压轴题)
如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.
(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;
(2)若CE=2,BD=BC,求∠BPD的正切值;
(3)若
1
tan
3
BPD
∠=,设CE=x,△ABC的周长为y,求y关于x的函数关系式.
图9 图10(备用)
图。
