数学文卷·2016届江苏省扬州中学高二质量检测(5月)(2015.05)
2015-2016年江苏省扬州中学高二(下)期中数学试卷(文科)和答案

2015-2016学年江苏省扬州中学高二(下)期中数学试卷(文科)一、填空题:每题5分,14小题,满分70分1.(5分)已知x2∈{0,1,x},则实数x的值是.2.(5分)已知复数z=(1+i)(2﹣i),则|z|=.3.(5分)若函数f(2x+1)=x2﹣2x,则f(3)=.4.(5分)函数f(x)=+的定义域是.5.(5分)命题“∀x∈[1,2],使x2﹣a≥0”是真命题,则a的范围是.6.(5分)执行如图所示的流程图,则输出的k的值为.7.(5分)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:(1)f(x1+x2)=f(x1)f(x2)(2)f(x1x2)=f(x1)+f(x2)(3)当f(x)=e x时,上述结论中正确结论的序号是.8.(5分)已知函数y=f(x)是定义在R上的偶函数,当x≤0时,f(x)=x+2,那么不等式2f(x)﹣1>0的解集是.9.(5分)若f(x)=﹣x2+2ax与在区间[1,2]上都是减函数,则a的值范围是.10.(5分)定义在R上的函数f(x)满足,则f(2016)=.11.(5分)当x∈(﹣∞,1],不等式1+2x+4x•a>0恒成立,则实数a的取值范围为.12.(5分)若关于x的函数f(x)=(t>0)的最大值为M,最小值为N,且M+N=6,则实数t的值为.13.(5分)如图.小正六边形沿着大正六边形的边按顺时针方向滚动,小正六边形的边长是大正六边形的边长的一半.如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中,向量围绕着点O旋转了θ角,其中O为小正六边形的中心,则sin+cos=.14.(5分)设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=a f(x)﹣1(a>0且a≠1).当a=时,g(x)=t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,则实数t的取值范围.二、解答题:6小题,满分90分.15.(14分)已知复数,z2=2+(3a+1)i(a∈R,i是虚数单位).(1)若z1∈R,求a的值;(2)若复数z1﹣z2在复平面上对应点落在第一象限,求实数a的取值范围.16.(14分)已知p:x2﹣7x+10<0,q:x2﹣4mx+3m2<0,其中m>0.(1)若m=4,且p∧q为真,求x的取值范围;(2)若¬q是¬p的充分不必要条件,求实数m的取值范围.17.(14分)已知定义域为R的函数f(x)=是奇函数.(1)求a,b的值;(2)解不等式f(x)<;(3)求f(x)的值域.18.(16分)已知函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:①当x∈R时,f(x)的最小值为0,且f(x﹣1)=f(﹣x﹣1)成立②当x∈(0,5)时,x≤f(x)≤2|x﹣1|+1 恒成立(1)求f(1)的值.(2)求f(x)的解析式(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f (x+t)≤x.19.(16分)某油库的设计容量是30万吨,年初储量为10万吨,从年初起计划每月购进石油m万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前x个月的需求量y(万吨)与x的函数关系为y=(p>0,1≤x≤16,x∈N*),并且前4个月,区域外的需求量为20万吨.(1)试写出第x个月石油调出后,油库内储油量M(万吨)与x的函数关系式;(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定m 的取值范围.20.(16分)设函数f(x)=a x﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.(1)求k值;(2)若f(1)<0,试判断函数单调性并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;(3)若f(1)=,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.2015-2016学年江苏省扬州中学高二(下)期中数学试卷(文科)参考答案与试题解析一、填空题:每题5分,14小题,满分70分1.(5分)已知x2∈{0,1,x},则实数x的值是﹣1.【考点】12:元素与集合关系的判断.【解答】解:∵x2∈{1,0,x},∴x2=1,x2=0,x2=x,由x2=1得x=±1,由x2=0,得x=0,由x2=x得x=0或x=1.综上x=±1,或x=0.当x=0时,集合为{1,0,0}不成立.当x=1时,集合为{1,0,1}不成立.当x=﹣1时,集合为{1,0,﹣1},满足条件.故答案是:﹣1.2.(5分)已知复数z=(1+i)(2﹣i),则|z|=.【考点】A8:复数的模.【解答】解:复数z=(1+i)(2﹣i)=3+i,则|z|==,故答案为:.3.(5分)若函数f(2x+1)=x2﹣2x,则f(3)=﹣1.【考点】36:函数解析式的求解及常用方法.【解答】解法一:(换元法求解析式)令t=2x+1,则x=则f(t)=﹣2=∴∴f(3)=﹣1解法二:(凑配法求解析式)∵f(2x+1)=x2﹣2x=∴∴f(3)=﹣1解法三:(凑配法求解析式)∵f(2x+1)=x2﹣2x令2x+1=3则x=1此时x2﹣2x=﹣1∴f(3)=﹣1故答案为:﹣14.(5分)函数f(x)=+的定义域是{2}.【考点】33:函数的定义域及其求法.【解答】解:要使函数有意义,则,解得:x=2.函数的定义域为:{2}.故答案为:{2}.5.(5分)命题“∀x∈[1,2],使x2﹣a≥0”是真命题,则a的范围是(﹣∞,1].【考点】2H:全称量词和全称命题.【解答】解:命题p:a≤x2在[1,2]上恒成立,y=x2在[1,2]上的最小值为1;∴a≤1;故答案为:(﹣∞,1].6.(5分)执行如图所示的流程图,则输出的k的值为4.【考点】EF:程序框图.【解答】解:当k=1,S=1时,进入循环,S=1,不满足退出循环的条件,k=2,S=2,不满足退出循环的条件,k=3,S=6,不满足退出循环的条件,k=4,S=15,满足退出循环的条件,故输出的k的值为4.故答案为:47.(5分)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:(1)f(x1+x2)=f(x1)f(x2)(2)f(x1x2)=f(x1)+f(x2)(3)当f(x)=e x时,上述结论中正确结论的序号是(1)、(3).【考点】2K:命题的真假判断与应用.【解答】解:∵f(x)=e x时,f(x)定义域中任意的x1,x2(x1≠x2),∴f(x1+x2)===f(x1)f(x2),故(1)正确;f(x1x2)=≠+=f(x1)+f(x2),故(2)不正确;∵f(x)=e x是增函数,∴,故(3)正确.故答案为:(1)、(3).8.(5分)已知函数y=f(x)是定义在R上的偶函数,当x≤0时,f(x)=x+2,那么不等式2f(x)﹣1>0的解集是(﹣,).【考点】3K:函数奇偶性的性质与判断.【解答】解:当x≤0时,∵2f(x)﹣1>0,即2x+4﹣1>0,解得x>﹣,∴﹣<x≤0.∵f(x)是定义在R上的偶函数,∴当0时,2f(x)﹣1>0仍成立.∴2f(x)﹣1>0的解集为(﹣,).故答案为:.9.(5分)若f(x)=﹣x2+2ax与在区间[1,2]上都是减函数,则a的值范围是(0,1].【考点】3E:函数单调性的性质与判断;3V:二次函数的性质与图象.【解答】解:∵函数f(x)=﹣x2+2ax的对称轴为x=a,开口向下,∴单调减区间为[a,+∞)又∵f(x)在区间[1,2]上是减函数,∴a≤1∵在区间[1,2]上是减函数,∴a>0综上得0<a≤1故答案为(0,1]10.(5分)定义在R上的函数f(x)满足,则f(2016)=.【考点】3T:函数的值.【解答】解:∵定义在R上的函数f(x)满足,∴f(2016)=f(﹣2016+3×672)=f(0)=30﹣1=.故答案为:.11.(5分)当x∈(﹣∞,1],不等式1+2x+4x•a>0恒成立,则实数a的取值范围为(,+∞).【考点】3R:函数恒成立问题.【解答】解:由题意:设2x=t,则不等式1+2x+4x•a>0转化为1+t+at2>0恒成立,∵x∈(﹣∞,1],∴0<t≤2,令函数f(t)=a•t2+t+1,当a=0时,函数f(t)=t+1在(0,2]恒大于0.当a≠0时,要使函数f(t)在(0,2]大于0恒成立,则:,解得:,∴实数a的取值范围为(+∞).故答案为(,+∞).12.(5分)若关于x的函数f(x)=(t>0)的最大值为M,最小值为N,且M+N=6,则实数t的值为3.【考点】3H:函数的最值及其几何意义.【解答】解:由题意,f(x)==t+,函数y=是奇函数,函数f(x)最大值为M,最小值为N,且M+N=6,∴2t=6,∴t=3,故答案为:3.13.(5分)如图.小正六边形沿着大正六边形的边按顺时针方向滚动,小正六边形的边长是大正六边形的边长的一半.如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中,向量围绕着点O旋转了θ角,其中O为小正六边形的中心,则sin+cos=﹣1.【考点】F1:归纳推理.【解答】解:从图中得出:第一个到第二个OA转过了60度,第二个到第三个转过了120度,依此类推每一次边上是60度,转角是120度,共有6个转角一共就是1080度,所以x sin180°+cos180°=﹣1.故答案为:﹣114.(5分)设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=a f(x)﹣1(a>0且a≠1).当a=时,g(x)=t2﹣2mt+1对所有的x∈[﹣1,1]及m∈[﹣1,1]恒成立,则实数t的取值范围(﹣∞,﹣2]∪{0}∪[2,+∞)..【考点】3R:函数恒成立问题.【解答】解:由f(﹣x)=﹣f(x)得kx2﹣2x=﹣kx2﹣2x,∴k=0,∵g(x)=a f(x)﹣1=(a2)x﹣1,①当a2>1,即a>1时,g(x)=(a2)x﹣1在[﹣1,2]上为增函数,∴g(x)最大值为g(2)=a4﹣1;②当a2<1,即0<a<1时,∴g(x)=(a2)x在[﹣1,2]上为减函数,∴g(x)最大值为g(﹣1)=﹣1,∴g(x)max=;由②得g(x)在x∈[﹣1,1]上的最大值为g(1)=﹣1=1,∴1≤t2﹣2mt+1即t2﹣2mt≥0在[﹣1,1]上恒成立,令h(m)=﹣2mt+t2,∴即,∴t∈(﹣∞,﹣2]∪{0}∪[2,+∞).二、解答题:6小题,满分90分.15.(14分)已知复数,z2=2+(3a+1)i(a∈R,i是虚数单位).(1)若z1∈R,求a的值;(2)若复数z1﹣z2在复平面上对应点落在第一象限,求实数a的取值范围.【考点】A1:虚数单位i、复数;A4:复数的代数表示法及其几何意义.【解答】解:(1)复数,z1∈R,可得a2﹣3=0,解得:;(2)由条件复数,z2=2+(3a+1)i得,因为z1﹣z2在复平面上对应点落在第一象限,故有,∴,解得﹣2<a<﹣1.16.(14分)已知p:x2﹣7x+10<0,q:x2﹣4mx+3m2<0,其中m>0.(1)若m=4,且p∧q为真,求x的取值范围;(2)若¬q是¬p的充分不必要条件,求实数m的取值范围.【考点】29:充分条件、必要条件、充要条件;2E:复合命题及其真假.【解答】解(1)由x2﹣7x+10<0,解得2<x<5,所以p:2<x<5;又x2﹣4mx+3m2<0,因为m>0,解得m<x<3m,所以q:m<x<3m.当m=4时,q:4<x<12,又p∧q为真,p,q都为真,所以4<x<5.(2)由¬q是¬p的充分不必要条件,即¬q⇒¬p,¬p≠>¬q,其逆否命题为p⇒q,q≠>p,由(1)p:2<x<5,q:m<x<3m,所以,即:.17.(14分)已知定义域为R的函数f(x)=是奇函数.(1)求a,b的值;(2)解不等式f(x)<;(3)求f(x)的值域.【考点】3K:函数奇偶性的性质与判断.【解答】解:(1)因为f(x)是奇函数,所以f(0)=0⇒﹣1+b=0,解得b=1,又由f(1)=﹣f(﹣1)⇒,解得a=2.(2)不等式f(x)<,即不等式<,化简可得2x>,∴x>,∴不等式的解集为{x|x>};(3)f(x)=﹣+,∵2x+1>1,∴﹣<f(x)<,∴f(x)的值域是(﹣,).18.(16分)已知函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:①当x∈R时,f(x)的最小值为0,且f(x﹣1)=f(﹣x﹣1)成立②当x∈(0,5)时,x≤f(x)≤2|x﹣1|+1 恒成立(1)求f(1)的值.(2)求f(x)的解析式(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f (x+t)≤x.【考点】3H:函数的最值及其几何意义.【解答】解:(1)∵当x∈(0,5)时,x≤f(x)≤2|x﹣1|+1 恒成立,∴当x=1时,1≤f(1)≤2|1﹣1|+1;∴f(1)=1;(2)∵f(x﹣1)=f(﹣x﹣1),∴函数f(x)=ax2+bx+c的图象关于x=﹣1对称,又∵当x∈R时,f(x)的最小值为0,∴f(x)=a(x+1)2,a>0;又∵f(1)=4a=1;∴a=;故f(x)=(x+1)2;(3)∵f(x+t)=(x+t+1)2≤x,∴x2+(2t﹣2)x+t2+2t+1≤0;设g(x)=x2+(2t﹣2)x+t2+2t+1,则g(1)=t2+4t≤0,g(m)=m2+(2t﹣2)m+t2+2t+1≤0;则﹣4≤t≤0,1﹣t﹣2≤m≤1﹣t+2,所以m≤1+4+2•=9,故m的最大值为9.19.(16分)某油库的设计容量是30万吨,年初储量为10万吨,从年初起计划每月购进石油m万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前x个月的需求量y(万吨)与x的函数关系为y=(p>0,1≤x≤16,x∈N*),并且前4个月,区域外的需求量为20万吨.(1)试写出第x个月石油调出后,油库内储油量M(万吨)与x的函数关系式;(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定m的取值范围.【考点】5C:根据实际问题选择函数类型.【解答】解:(1)由题意,20=,∴2p=100,∴y=10(1≤x≤16,x∈N*),∴油库内储油量M=mx﹣x﹣10+10(1≤x≤16,x∈N*);(2)∴0≤M≤30,∴0≤mx﹣x﹣10+10≤30(1≤x≤16,x∈N*),∴(1≤x≤16,x∈N*)恒成立.;设=t,则≤t≤1,.由≤(x=4时取等号),可得m≥,由20t2+10t+1=≥(x﹣16时取等号),可得m≤,∴≤m≤.20.(16分)设函数f(x)=a x﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数.(1)求k值;(2)若f(1)<0,试判断函数单调性并求使不等式f(x2+tx)+f(4﹣x)<0恒成立的t的取值范围;(3)若f(1)=,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.【考点】3K:函数奇偶性的性质与判断;4E:指数函数综合题.【解答】解:(1)∵f(x)是定义域为R的奇函数,∴f(0)=0,…(2分)∴1﹣(k﹣1)=0,∴k=2.…(4分)(2)∵函数f(x)=a x﹣a﹣x(a>0且a≠1),∵f(1)<0,∴a﹣<0,又a>0,∴1>a>0.…(6分)由于y=a x单调递减,y=a﹣x单调递增,故f(x)在R上单调递减.不等式化为f(x2+tx)<f(x﹣4).∴x2+tx>x﹣4,即x2+(t﹣1)x+4>0 恒成立,…(8分)∴△=(t﹣1)2﹣16<0,解得﹣3<t<5.…(10分)(3)∵f(1)=,a﹣=,即2a2﹣3a﹣2=0,∴a=2,或a=﹣(舍去).…(12分)∴g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x,由(1)可知k=2,故f(x)=2x﹣2﹣x,显然是增函数.∵x≥1,∴t≥f(1)=,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2(t≥)…(15分)若m≥,当t=m时,h(t)min=2﹣m2=﹣2,∴m=2…(16分)若m<,当t=时,h(t)min=﹣3m=﹣2,解得m=>,舍去…(17分)综上可知m=2.…(18分)。
2015-2016年江苏省扬州中学高二(下)期中数学试卷(理科)和答案

2015-2016学年江苏省扬州中学高二(下)期中数学试卷(理科)一、填空题(本大题共14小题,每小题5分,共70分)1.(5分)复数z=的共轭复数为.2.(5分)命题“x=π”是“sin x=0”的条件.3.(5分)设异面直线l1,l2的方向向量分别为=(1,1,0),=(1,0,﹣1),则异面直线l1,l2所成角的大小为.4.(5分)的二项展开式中,x3的系数是.(用数字作答)5.(5分)某团队有6人入住宾馆中的6个房间,其中的房号301与302对门,303与304对门,305与306对门,若每人随机地拿了这6个房间中的一把钥匙,则其中的甲、乙两人恰好对门的概率为.6.(5分)已知可导函数f(x)的导函数f′(x)满足f′(x)>f(x),则不等式的解集是.7.(5分)设f(k)=+++…+(k∈N*),那么f(k+1)﹣f(k)=.8.(5分)若数列{a n}的通项公式,记f(n)=(1﹣a1)(1﹣a2)…(1﹣a n),试通过计算f(1),f(2),f(3)的值,推测出f(n)=.9.(5分)甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数是.10.(5分)已知:(x+2)8=a0+a1(x+1)+a2(x+1)2+…+a8(x+1)8,其中a i=(i=0,1,2…8)为实常数,则a1+2a2+…+7a7+8a8=.11.(5分)某班某天要安排语文、数学、政治、英语、体育、艺术6节课,要(以求数学课排在前3节,体育课不排在第1节,则不同的排法种数为.数字作答).12.(5分)如图,四棱锥P﹣ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.则二面角B﹣DE﹣C的平面角的余弦值是.13.(5分)已知函数f(x)=x3+ax2+bx在区间[﹣1,1)、(1,3]内各有一个极值点,则a﹣4b的取值范围是.14.(5分)我们在学习立体几何推导球的体积公式时,用到了祖日恒原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线(a>0,b>0),与x 轴,直线y=h(h>0)及渐近线所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积.二.解答题(本大题共6题,共90分)15.(14分)已知命题:“∃x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题,(1)求实数m的取值集合M;(2)设不等式(x﹣a)(x+a﹣2)<0的解集为N,若x∈N是x∈M的必要条件,求a的取值范围.16.(14分)已知复数w满足w﹣4=(3﹣2w)i(i为虚数单位).(1)求w;(2)设z∈C,在复平面内求满足不等式1≤|z﹣w|≤2的点Z构成的图形面积.17.(14分)已知的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的.(1)求展开后所有项的系数之和及所有项的二项式系数之和;(2)求展开式中的有理项.18.(16分)如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).(Ⅰ)求证:PB⊥DE;(Ⅱ)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长.19.(16分)某班级共派出n+1个男生和n个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有E n种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有F n种选法.(1)试求E n和F n;(2)判断lnE n和F n的大小(n∈N+),并用数学归纳法证明.20.(16分)已知函数f(x)(x∈R),f′(x)存在,记g(x)=f′(x),且g′(x)也存在,g′(x)<0.(1)求证:f(x)≤f(x0)+f′(x0)(x﹣x0);(x0∈R)(2)设n),且λ1+λ2+…+λn=1,x i∈R(i=1,…,n)(n∈N+)求证:λ1f(x1)+λ2f(x2)+…+λn f(x n)≤f(λ1x1+λ2x2+…+λn x n)(3)已知a,f(a),f[f(a)],f{f[(f(a)]}是正项的等比数列,求证:f(a)=a.2015-2016学年江苏省扬州中学高二(下)期中数学试卷(理科)参考答案与试题解析一、填空题(本大题共14小题,每小题5分,共70分)1.(5分)复数z=的共轭复数为.【考点】A5:复数的运算.【解答】解:∵z==,∴.故答案为:.2.(5分)命题“x=π”是“sin x=0”的充分不必要条件.【考点】29:充分条件、必要条件、充要条件.【解答】解:x=π⇒sin x=0,反之不成立,例如取x=0,满足sin x=0.∴“x=π”是“sin x=0”的充分不必要条件.故答案为:充分不必要.3.(5分)设异面直线l1,l2的方向向量分别为=(1,1,0),=(1,0,﹣1),则异面直线l1,l2所成角的大小为.【考点】LM:异面直线及其所成的角.【解答】解:∵异面直线l 1,l2的方向向量分别为,∴cos<>===,∴<>=.∴异面直线l1,l2所成角的大小为.故答案为:.4.(5分)的二项展开式中,x3的系数是﹣10.(用数字作答)【考点】DA:二项式定理.【解答】解:T r+1=,令5﹣2r=3得r=1,所以x3的系数为(﹣2)1•C51=﹣10.故答案为﹣105.(5分)某团队有6人入住宾馆中的6个房间,其中的房号301与302对门,303与304对门,305与306对门,若每人随机地拿了这6个房间中的一把钥匙,则其中的甲、乙两人恰好对门的概率为.【考点】CB:古典概型及其概率计算公式.【解答】解:法一、6个人拿6把钥匙共有种不同的拿法,记甲、乙恰好对门为事件A,则事件A包括甲、乙拿了301与302,其余4人随意拿.共种;甲、乙拿了303与304,其余4人随意拿.共种;甲、乙拿了305与306,其余4人随意拿.共种;所以甲、乙两人恰好对门的拿法共有种.则甲、乙两人恰好对门的概率为p(A)=.故答案为.法二、仅思考甲乙2人那钥匙的情况,甲可以拿走6个房间中的任意一把钥匙,有6种拿法,乙则从剩余的5把钥匙中那走一把,共有6×5=30种不同的拿法,而甲乙对门的拿法仅有种,所以甲乙恰好对门的概率为.故答案为.6.(5分)已知可导函数f(x)的导函数f′(x)满足f′(x)>f(x),则不等式的解集是(1,+∞).【考点】63:导数的运算.【解答】解:令g(x)=,则g′(x)=,因为f'(x)>f(x),所以g′(x)>0,所以,函数g(x)为(﹣∞,+∞)上的增函数,由ef(x)>f(1)e x,得:,即g(x)>g(1),因为函数不等式,所以g(x)>g(1),所以,x>1.故答案为(1,+∞).7.(5分)设f(k)=+++…+(k∈N*),那么f(k+1)﹣f(k)=.【考点】3T:函数的值.【解答】解:∵f(k)=+++…+(k∈N*),∴f(k+1)=++…++;(k∈N*),则f(k+1)﹣f(k)=++…++﹣(+++…+)=;故答案为:8.(5分)若数列{a n}的通项公式,记f(n)=(1﹣a1)(1﹣a2)…(1﹣a n),试通过计算f(1),f(2),f(3)的值,推测出f(n)=.【考点】8B:数列的应用;8H:数列递推式;F1:归纳推理.【解答】解:∵∴又∵f(n)=(1﹣a1)(1﹣a2)…(1﹣a n)∴,…由此归纳推理:∴===故答案为:9.(5分)甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数是336.【考点】D9:排列、组合及简单计数问题.【解答】解:由题意知本题需要分组解决,∵对于7个台阶上每一个只站一人有A73种;若有一个台阶有2人另一个是1人共有C31A72种,∴根据分类计数原理知共有不同的站法种数是A73+C31A72=336种.故答案为:336.10.(5分)已知:(x+2)8=a0+a1(x+1)+a2(x+1)2+…+a8(x+1)8,其中a i=(i=0,1,2…8)为实常数,则a1+2a2+…+7a7+8a8=1024.【考点】DA:二项式定理.【解答】解:∵[1+(x+1)]8=a0+a1(x+1)+…+a8(x+1)8,其中a i=(i=0,1,2…8)为实常数,两边分别对x求导数,可得8(x+2)7=a1+2a2(x+1)+…+7a7(x+1)6+8a8(x+1)7,再令x=0,可得则a1+2a2+…+7a7+8a8=8•27=1024,故答案为:1024.11.(5分)某班某天要安排语文、数学、政治、英语、体育、艺术6节课,要(以求数学课排在前3节,体育课不排在第1节,则不同的排法种数为312.数字作答).【考点】D3:计数原理的应用.【解答】解:分两类,数学科排在第一节,或不排在第一节,第一类,当数学课排在第一节时,其它课任意排有种,第一类,当数学课排在第二或第三节课时,第一节从语文、政治、英语、艺术四门科种任排一节,再排数学,然后排其它节次,共有=192种,根据分类计数原理得不同的排法种数为120+192=312种.故答案为:312.12.(5分)如图,四棱锥P﹣ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.则二面角B﹣DE﹣C的平面角的余弦值是.【考点】MJ:二面角的平面角及求法.【解答】解:以D为原点,DA为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,设PD=DC=2,则B(2,2,0),D(0,0,0),C(0,2,0),P(0,0,2),E(0,1,1),=(2,2,0),=(0,1,1),设平面BDE的法向量=(x,y,z),则,取x=1,得=(1,﹣1,1),平面DEC的法向量=(0,0,1),设二面角B﹣DE﹣C的平面角为θ,则cosθ==.∴二面角B﹣DE﹣C的平面角的余弦值是.故答案为:.13.(5分)已知函数f(x)=x3+ax2+bx在区间[﹣1,1)、(1,3]内各有一个极值点,则a﹣4b的取值范围是(﹣16,10].【考点】6D:利用导数研究函数的极值.【解答】解:由题意,f′(x)=x2+ax+b,∵f(x)的两个极值点分别是x1,x2,x1∈(﹣1,1),x2∈(1,3),∴,对应的平面区域如图所示:令z=a﹣4b,得:b=a﹣z,平移直线b=b=a﹣z,显然直线过A(﹣4,3)时,z最小,最小值是﹣16,过B(﹣2,﹣3)时,z最大,最大值是10,故答案为:(﹣16,10].14.(5分)我们在学习立体几何推导球的体积公式时,用到了祖日恒原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线(a>0,b>0),与x 轴,直线y=h(h>0)及渐近线所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.【考点】F3:类比推理.【解答】解:由题意,图形是一个圆环,圆环的半径为AC,BC,其面积S=π(AC2﹣BC2)∵⇒,同理∴AC2﹣BC2=a2,由祖暅原理知,此旋转体的体积,等价于一个半径为a,高为h的柱体的体积为a2hπ.故答案为:a2hπ.二.解答题(本大题共6题,共90分)15.(14分)已知命题:“∃x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题,(1)求实数m的取值集合M;(2)设不等式(x﹣a)(x+a﹣2)<0的解集为N,若x∈N是x∈M的必要条件,求a的取值范围.【考点】29:充分条件、必要条件、充要条件;2K:命题的真假判断与应用;73:一元二次不等式及其应用.【解答】解:(1)由x2﹣x﹣m=0可得m=x2﹣x=∵﹣1<x<1∴M={m|}(2)若x∈N是x∈M的必要条件,则M⊆N①当a>2﹣a即a>1时,N={x|2﹣a<x<a},则即②当a<2﹣a即a<1时,N={x|a<x<2﹣a},则即③当a=2﹣a即a=1时,N=φ,此时不满足条件综上可得16.(14分)已知复数w满足w﹣4=(3﹣2w)i(i为虚数单位).(1)求w;(2)设z∈C,在复平面内求满足不等式1≤|z﹣w|≤2的点Z构成的图形面积.【考点】A4:复数的代数表示法及其几何意义.【解答】解:(1)∵w(1+2i)=4+3i,∴;(2)在复平面内求满足不等式1≤|z﹣w|≤2的点Z构成的图形为一个圆环,其中大圆为:以(2,﹣1)为圆心,2为半径的圆;小圆是:以(2,﹣1)为圆心,1为半径的圆.∴在复平面内求满足不等式1≤|z﹣w|≤2的点Z构成的图形面积=22π﹣12×π=3π.17.(14分)已知的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的.(1)求展开后所有项的系数之和及所有项的二项式系数之和;(2)求展开式中的有理项.【考点】DA:二项式定理.【解答】解:的展开式的通项,由已知,得出化简,解得(1)在展开式两端令x=1,得展开后所有项的系数之和为37=2187.所有项的二项式系数之和27=128.(2)当为整数时,项为有理项.所以r=0,2,4,6.有理项分别为1,22C72x=84x,24C74x2=560x2,26C76x3=448x3.18.(16分)如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).(Ⅰ)求证:PB⊥DE;(Ⅱ)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长.【考点】LW:直线与平面垂直;MI:直线与平面所成的角.【解答】解:(Ⅰ)∵DE⊥AB,∴DE⊥BE,DE⊥PE,….(2分)∵BE∩PE=E,∴DE⊥平面PEB,又∵PB⊂平面PEB,∴BP⊥DE;….(4分)(Ⅱ)∵PE⊥BE,PE⊥DE,DE⊥BE,∴分别以DE、BE、PE所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),…(5分)设PE=a,则B(0,4﹣a,0),D(a,0,0),C(2,2﹣a,0),P(0,0,a),…(7分)可得,,…(8分)设面PBC的法向量,∴令y=1,可得x=1,z=因此是面PBC的一个法向量,…(10分)∵,PD与平面PBC所成角为30°,…(12分)∴,即,…(11分)解之得:a=,或a=4(舍),因此可得PE的长为.…(13分)19.(16分)某班级共派出n+1个男生和n个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有E n种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有F n种选法.(1)试求E n和F n;(2)判断lnE n和F n的大小(n∈N+),并用数学归纳法证明.【考点】RG:数学归纳法.【解答】解:(1)根据领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,可得;根据从男生(含男生甲)和女生中各选一名代表到主席台服务,可得…4分(2)因为lnE n=2lnn!,F n=n(n+1),所以lnE1=0<F1=2,lnE2=ln4<F2=6,lnE3=ln36<F3=12,…,由此猜想:当n∈N*时,都有lnE n<F n,即2lnn!<n(n+1)…6分下用数学归纳法证明2lnn!<n(n+1)(n∈N*).①当n=1时,该不等式显然成立.②假设当n=k(k∈N*)时,不等式成立,即2lnk!<k(k+1),则当n=k+1时,2ln(k+1)!=2ln(k+1)+2lnk!<2ln(k+1)+k(k+1),要证当n=k+1时不等式成立,只要证:2ln(k+1)+k(k+1)≤(k+1)(k+2),只要证:ln(k+1)≤k+1…8分令f(x)=lnx﹣x,x∈(1,+∞),因为,所以f(x)在(1,+∞)上单调递减,从而f(x)<f(1)=﹣1<0,而k+1∈(1,+∞),所以ln (k+1)≤k+1成立,则当n=k+1时,不等式也成立.综合①②,得原不等式对任意的n∈N*均成立…10分20.(16分)已知函数f(x)(x∈R),f′(x)存在,记g(x)=f′(x),且g′(x)也存在,g′(x)<0.(1)求证:f(x)≤f(x0)+f′(x0)(x﹣x0);(x0∈R)(2)设n),且λ1+λ2+…+λn=1,x i∈R(i=1,…,n)(n∈N+)求证:λ1f(x1)+λ2f(x2)+…+λn f(x n)≤f(λ1x1+λ2x2+…+λn x n)(3)已知a,f(a),f[f(a)],f{f[(f(a)]}是正项的等比数列,求证:f(a)=a.【考点】63:导数的运算;8B:数列的应用.【解答】解:(1)证明:设ϕ(x)=f(x)﹣f(x0)﹣f'(x0)(x﹣x0),则ϕ'(x)=f'(x)﹣f'(x0)∵g'(x)<0故g(x)=f'(x)为减函数,则x=x0为ϕ(x)的极大值点.∵ϕ(x)≤ϕ(x0)=0,即f(x)≤f(x0)+f'(x0)(x﹣x0)(当且仅当在x=x0取到)(2)证明:由(1)可知:f(x1)≤f(x0)+f'(x0)(x1﹣x0),两边同乘以λ1得λ1f(x1)≤λ1f(x0)+λ1f'(x0)(x1﹣x0),λ2f(x2)≤λ2f(x0)+λ2f'(x0)(x2﹣x0),…λn f(x n)≤λn f(x0)+λn f'(x0)(x n﹣x0),上式各式相加,得λ1f(x1)+λ2f(x2)+…+λn f(x n)≤(λ1+λ2+…+λn)f (x0)+f'(x0)•[λ1(x1﹣x0)+λ2(x2﹣x0)+…+λn(x n﹣x0)],因为λ1+λ2+…+λn=1,设x0=λ1x1+λ2x2+…+λn x n,则λ1(x1﹣x0)+λ2(x2﹣x0)+…+λn(x n﹣x0)=0,由此,λ1f(x1)+λ2f(x2)+…+λn f(x n)≤f(λ1x1+λ2x2+…+λn x n))等号当且仅当在x1=x2=…=x n时成立,(3)证明:记公比为q,q>0,则f(a)=aq,f[f(a)]=aq2,f{f[f[f(a}}=aq3,取x1′=a,,λ=∈(0,1),则λx1+(1﹣λ)x2=aq,f[λx1+(1﹣λ)x2]=f(aq)=f[f(a)]=aq2,又∵λf(x1)+(1﹣λ)f(x2)=λf(a)+(1﹣λ)f(aq2),=λf(a)+(1﹣λ)f{f[f(a)]},=λaq+(1﹣λ)aq3,=aq3+λaq﹣λaq3,=aq3+λaq(1﹣q2),=aq3+aq(1﹣q2),=aq2,即aq3+λaq(1﹣q2)=aq2=f[λx1+(1﹣λ)x2],在(2)中取n=2,λ1=λ,λ2=1﹣λ,即λf(x1)+(1﹣λ)f(x2)≤f[λx1+(1﹣λ)x2],当且仅当x1=x2时成立,即a=aq2⇒q=1,∴f(a)=a.。
【百强校】2015-2016学年江苏省扬州中学高二上学期开学考数学试卷(带解析)

绝密★启用前【百强校】2015-2016学年江苏省扬州中学高二上学期开学考数学试卷(带解析)试卷副标题考试范围:xxx ;考试时间:149分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)第II 卷(非选择题)一、填空题(题型注释)1、若实数满足,则的最小值是 .2、若是函数的两个不同的零点,且这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则的值等于 .3、设,则的最大值为________.4、设数列的前项和,且成等差数列,则.5、在空间四边形所成的角为 .6、一条光线从点射出,经轴反射后与圆相切,则反射光线所在直线的斜率为 .7、若圆x 2+y 2=1与圆x 2+y 2-6x+8y+25-m 2=0相外离,则实数m 的取值范围是________.8、下列命题:①分别在两个平面内的两条直线是异面直线; ②和两条异面直线都垂直的直线有且仅有一条; ③和两条异面直线都相交的两条直线异面或相交; ④若则.其中真命题的个数是 .9、若直线.10、经过两点M (-2,m ),N (1,4)的直线MN 的倾斜角等于45°,则m= .11、在等差数列中,若,则= .12、.13、不等式的解集为________.14、设集合.二、解答题(题型注释)15、已知数列{}满足是数列{}的前n 项和.(1)若数列{}为等差数列:①求数列{}的通项公式; ②若数列满足,数列满足,试比较数列的前n 项和与的前n 项和的大小;(2)若对任意的恒成立,求实数x 的取值范围.16、已知以点为圆心的圆经过点和,线段的垂直平分线交圆于点和,且.(1)求直线的方程; (2)求圆的方程; (3)设点在圆上,试问使△的面积等于8的点共有几个?证明你的结论.17、如图,四边形为矩形,,,.(1);(2).18、和的中点,求:(1)(2)19、在中,角的对边分别为,且.(1)求的值;(2)若求的面积.20、已知两直线l 1:ax -by +4=0,l 2:(a -1)x +y +b =0.()求分别满足下列条件的a ,b 的值.(1)直线l 1过点(-3,-1),并且直线l 1与l 2垂直; (2)直线l 1与直线l 2平行,并且坐标原点到l 1,l 2的距离相等.参考答案1、.2、93、4、5、45°6、或7、8、19、10、111、812、13、14、15、(1)①;②当时,;当时,;当时,(2).16、(1);(2)或;(3)两个.17、证明见解析.18、(1);(2).19、(1);(2)2.20、(1);(2)或.【解析】1、试题分析:表示圆及其内部,易得直线与圆相离,且,当时,,如下图所示,可行域为小的弓形内部,目标函数为,则可知当,时,,当时,,可行域为大的弓形内部,目标函数为,同理可知当,时,,综上所述,的最小值为3.考点:1.线性规划的运用;2.分类讨论的数学思想;3.直线与圆的位置关系【名师点睛】本题主要考查了以线性规划为背景的运用,属于中档题根据可行域是圆及其内部的特点,结合直线与圆的位置关系的判定,首先可以将目标函数的两个绝对值号中去掉一个,再利用分类讨论的数学思想去掉其中一个绝对值号,利用线性规划知识求解,理科试卷的线性规划问题基本考查含参的线性规划问题或者是利用线性规划的知识解决一些非线性的目标函数或可行域的问题,常需考查目标函数或可行域的几何意义求解,在复习时应予以关注.2、试题分析:由题意,又,所以,不妨设,则成等差数列,成等比数列,所以,解得,所以.考点:等差数列与等比数列的性质.【名师点睛】本题通过一元二次方程根与系数的关系把等差数列与等比数列联系起来,由等差数列的性质知三个数(不相等)成等差数列,这三个一定是按从小到大(或从小到大)的顺序排列的,由等比数列的性质知,等比数列中奇数项一定同号,偶数项也一定同号.由此我们把适当排列可得等差数列,也可得等比数列,从而得的值.3、试题分析:,当且仅当,即时等号成立,故最大值为.考点:基本不等式.【名师点睛】条件最值的求解通常有两种方法:一是消元法,即根据条件建立两个量之间的函数关系,然后代入代数式转化为函数的最值求解;二是将条件灵活变形,利用常数代换的方法构造和或积为常数的式子,然后利用基本不等式求解最值.三是运用公式解题时,既要掌握公式的正用,也要注意公式的逆用,例如a2+b2≥2ab逆用就是ab≤,≥(a,b>0)逆用就是ab≤2(a,b>0)等.还要注意“添、拆项”技巧和公式等号成立的条件等.4、试题分析:因为,所以,所以,所以,因为成等差数列,则,即,,所以是等比数列,.考点:等比数列的通项公式.5、试题分析:如图,取中点,连接,则,,是与所成的,因为所以,,所以,即与所成的角为.考点:异面直线所成的角.6、试题分析:根据反射定律,反射光线就是过点所作圆的切线,设其斜率为,反射光线所在直线方程为,即,所以,解得.考点:直线与圆的位置关系.7、试题分析:的标准方程为,圆心为,半径为,由题意,又,所以.考点:两圆位置关系.8、试题分析:分别在两个平面内的两条直线也可能相交或平行,①错;和两条异面直线都垂直的直线有无数条,②错;和两条异面直线都相交的两条直线异面或相交,不可能平行,③正确;若与是异面直线,gn 也是异面直线,则与可能相交,可能平行,可能异面④错.正确的命题只有1个.考点:两条直线的位置关系.9、试题分析:当直线不在平面时,,也可能有直线在平面上,不可能相交.考点:直线与平面的位置关系.10、试题分析:由题意,解得.考点:直线的斜率.11、试题分析:由题意,,所以.考点:等差数列的性质.12、试题分析:.考点:两角和与差的正弦(余弦)公式.13、试题分析:由得,,所以.考点:解指数不等式.14、试题分析:由已知,所以.考点:集合的运算.15、试题分析:(1)①只要由成等差数列,求出,公差即可;②由①,这样,,因此,要比较大小,只要作差,有,其中,讨论的正负即得结论;(2),已知的等式,一般处理方法是,由知,两式作差,得,所以,再作差得,这说明数列中,,,分别成等差数列,故要使数列递增,则要求且,由此可得的范围.试题解析:(1)①因为,所以,即,又,所以,因为数列是等差数列,所以,即,解得,则.所以.②因为,所以,其前项和.又因为,所以其前项和,所以.当时,;当时,;当时,.(2)由知,两式作差,得,所以,再作差得.所以当时,,当时,,当时,,当时,.因为对任意的恒成立,所以且.所以解得.故实数的取值范围是.考点:等差数列的通项公式,数列的和,数列的单调性.16、试题分析:(1)求出中点坐标,且的斜率与的斜率互为负倒数,可得方程;(2)要求圆的方程,关键是求出圆心坐标,(半径已知是),可设圆心为,由圆心在直线上,且半径为联立方程组可解得;(3)由三角形面积为8,可得边上的高为,即到的距离,下面只要判断圆上有几个点到直线的距离为,也即判断到直线距离为的两条平行线与圆的位置关系.试题解析:⑴直线的斜率,中点坐标为,∴直线方程为⑵设圆心,则由在上得:①又直径,, ②由①②解得或∴圆心或.∴圆的方程为或.(3),∴当面积为8时,点到直线的距离为.又圆心到直线的距离为,圆的半径,且,∴圆上共有两个点使面积为8.考点:圆的标准方程,圆的性质,直线与圆的位置关系.17、试题分析:(1)立体几何中要证线线垂直,一般先证线面垂直,考虑到平面(因为),故的,又有平面,从而有,于是有平面;(2)要证线面平行,只要证线线平行,由于是中点,因此我们取中点,可证是平行四边形,从而有,由此可得线面平行.试题解析:(1)证明:,∴,则又∵,则∴又∴(2)取DE中点N,连结AN,FN,FM,∵由N、F为ED、CE的中点,又NFMA是平行四边形考点:线面垂直与线面平行.【名师点睛】1.判断或证明线面平行的常用方法:(1)利用线面平行的定义(无公共点);(2)利用线面平行的判定定理(a⊂α,b⊂α,a∥b⇒a∥α);(3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β);(4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).2.证明直线和平面垂直的常用方法:(1)利用判定定理;(2)利用面面垂直的性质定理;(3)利用结论:直线a∥直线b,a⊥平面α⇒b⊥α;(4)利用结论:直线a⊥直线α,α∥平面β⇒a⊥β.18、试题分析:(1)求异面直线所成的角,关键是要作出这个角,(1)由,,知就是要求的角;(2),作交延长线于,则,就是所求的角(或补角).试题解析:AD1==a=BC1A1B== aA1C1==2 a∴cos∠A1BC1==∴sin∠A1BC1=(2)延长D1A1到F使A1F=D1A1,则AF∥DA1∥CB1.所求角为AF与AC1的夹角.AF=B1C= aAC1==3aFC1= acos∠FAC1=∴AC1与B1C所成角的余弦值为.考点:异面直线所成的角.19、试题分析:(1)观察已知式,应用三角形的性质知,这样,条件就变为两角和的余弦公式形式,从而求得,再同角关系式得;(2)只要用余弦定理求得边,就可得三角形的面积.试题解析:(1)由cos(A-B)cosB-sin(A-B)sin(A+C)=,得cos(A-B)cosB-sin(A-B)sinB=.则cos(A-B+B)=,即cosA=,又0<A<π,则sinA=.(2)根据余弦定理,有,解得c=1或c=-7(负值舍去).∴考点:两角和的余弦公式,余弦定理,三角形的面积.20、试题分析:直线与直线垂直的充要条件是,直线与直线平行的充要条件是且(或).试题解析:(1)∵,∴,①又点(-3,-1)在上,∴-3a+b+4=0.②由①②得a=2,b=2.(2)∵,∴a+b(a-1)=0,∴b=,故的方程可分别表示为:(a-1)x+y+=0,(a-1)x+y+=0,又原点到的距离相等.∴4=,∴a=2或a=,∴a=2,b=-2或a=,b=2.考点:两条直线的垂直与平行,点到直线的距离.【名师点睛】(1)利用两直线的斜率判定两直线的平行、垂直关系,注意斜率不存在的情况不能忽略.(2)利用两直线一般式方程的系数判定平行或垂直,可有效避免分类讨论.。
江苏省扬州中学高二数学下学期5月月考试卷

扬州中学08-09学年高二下学期5月月考高二数学试卷一、填空题(145'⨯)1.已知全集U Z =,2{1,0,1,2},{|}A B x x x =-==,则U AC B 为_____________2.函数212log (56)y x x =-+的单调增区间为____________3.若0.52a =,πlog 3b =,22πlog sin 5c =,则,,a b c 从大到小排序为__________ 4.直线2+=kx y 与曲线3y x mx n =++相切于点)4,1(,则n =_____________5.已知()f x 和()g x 为奇函数,若()()()1H x af x bg x =++在区间(0,)+∞有最大值5,则()H x 在区间(,0)-∞上的最小值为________6.函数3||22)21(-+=x x y 的值域为_____________ 7.已知2|log |y x =的定义域为[, ]a b , 值域为[0, 2],则区间[, ]a b 的长度b a -的最小值为_________8.函数()x f y =是R 上的奇函数,满足()()x f x f -=+33,当(0,3)x ∈时,()x x f 2=,则当(6,3)x ∈--时,()x f =_____________9.已知函数3()12f x x x a =-+在区间[3,3]-上的最大值与最小值分别为,M m ,则M m -=____________10.若21()ln(2)2f x x b x =-++∞在(-1,+)上是减函数,则b 的取值范围是________ 11.若不等式012421≥-+-+a a x x 在[]1,2上恒成立,则实数a 的取值范围为__________12.已知命题21:[1,2],02x p x e x a ∀∈--≥是真命题,命题2:,2860q x R x ax a ∃∈+--≤ 是假命题,则实数a 的取值范围是 13.已知1()sin x f x e x =,1()(),2n n f x f x n -'=≥,则20091(0)ii f ==∑14.已知2()(0)f x ax bx c a =++≠,且方程()f x x =无实数根,下列命题:①方程[()]f f x x =也一定没有实数根;②若0a >,则不等式[()]f f x x >对一切实数x 都成立;③若0a <,则必存在实数0x ,使00[()]f f x x >;④若0a b c ++=,则不等式[()]f f x x <对一切实数x 都成立。
江苏省扬州中学2015-2016学年高二上学期期末调研测试数学试卷【范本模板】
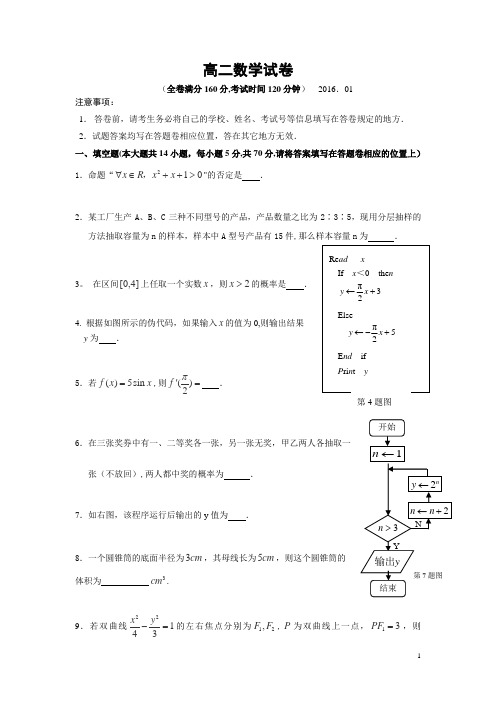
高二数学试卷(全卷满分160分,考试时间120分钟) 2016.01注意事项:1. 答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方. 2.试题答案均写在答题卷相应位置,答在其它地方无效.一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上) 1.命题“210x R x x ∀∈++>,"的否定是 .2.某工厂生产A 、B 、C 三种不同型号的产品,产品数量之比为2∶3∶5,现用分层抽样的方法抽取容量为n 的样本,样本中A 型号产品有15件,那么样本容量n 为 .3。
在区间]4,0[上任取一个实数x ,则2x >的概率是 .4. 根据如图所示的伪代码,如果输入x 的值为0,则输出结果 y 为 .5.若()5sin f x x =,则()2f π'= .6.在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为 .7.如右图,该程序运行后输出的y 值为 .8.一个圆锥筒的底面半径为3cm ,其母线长为5cm ,则这个圆锥筒的 体积为 3cm .9.若双曲线22143x y -=的左右焦点分别为12,F F ,P 为双曲线上一点,13PF =,则2PF = .10.设l ,m 是两条不同的直线,α,β是两个不重合的平面,给出下列四个命题: ①若α∥β,l α⊥,则l β⊥; ②若l ∥m ,l α⊂,m β⊂,则α∥β; ③若m α⊥,l m ⊥,则l ∥α; ④若l ∥α,l β⊥,则αβ⊥.其中真命题的序号..有 .(写出所有正确命题的序号..)11.已知抛物线2y =的准线恰好是双曲线22214x y a -=的左准线,则双曲线的渐近线方程为 .12.已知可导函数)(x f )(R x ∈的导函数)(x f '满足()f x <)(x f ',则不等式2016()(2016)x f x f e -≥的解集是 .13.若椭圆的中心为坐标原点,长轴长为4,一条准线方程为4x =-,则该椭圆被直线1y x =+截得的弦长为 .14.若0,0a b >>,且函数2()(3)xf x ae b x =+-在0x =处取得极值,则ab 的最大值等于 .二、解答题:(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)CMDBNQA15.(本小题满分14分)某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[]50,100之间)(1)求频率分布直方图中a 的值;(2)估算该班级的平均分;(3)若规定成绩达到80分及以上为优秀等级,从该班级40名学生中任选一人,求此人成绩为优秀等级的概率.16.(本小题满分14分)如图,在四面体ABCD 中,AB CD ⊥,AB AD ⊥.M ,N ,Q 分别为棱AD ,BD ,AC 的中点.(1)求证://CD 平面MNQ ;(2)求证:平面MNQ ⊥平面ACD .17.(本小题满分15分)已知命题:p “存在2,20x R x x m ∈-+≤”,命题q :“曲线22151x y m m+=-+表示焦点在x 轴上的椭圆”,命题:r 1t m t <<+ (1)若“p 且q ”是真命题,求m 的取值范围;(2)若q 是r 的必要不充分条件,求t 的取值范围.18.(本小题满分15分)已知函数32()39f x x x x a =-+++.(1)当2a =-时,求()f x 在2x =处的切线方程;(2)若()f x 在区间[]2,2-上的最大值为22,求它在该区间上的最小值. 19.(本小题满分16分)椭圆2222:b y a x E +)0(1>>=b a 经过点,且离心率为22,过点P 的动直线l 与椭圆相交于B A ,两点.(1)求椭圆E 的方程;(2)若椭圆E 的右焦点是P ,其右准线与x 轴交于点Q ,直线AQ 的斜率为1k ,直线BQ 的斜率为2k ,求证:120k k +=;(3) 设点(),0P t 是椭圆E 的长轴上某一点(不为长轴顶点及坐标原点),是否存在与点P 不同的定点Q ,使得QA PAQB PB=恒成立?若存在,求出点Q 的坐标;若不存在,说明理由.20.(本小题满分16分)已知函数2(1)()ln 2x f x x -=-,1)(-=x x g(1)求函数()f x 的单调递减区间;(2)若关于x 的方程()()0f x g x a -+=在区间1(,)e e上有两个不等的根,求实数a 的取值范围;(3)若存在01x >,当0(1,)x x ∈时,恒有)()(x kg x f >,求实数k 的取值范围.2016年1月高二数 学 试 题 参 考 答 案一、填空题:1.210x R x x ∃∈++≤, 2.75 3.12 4.5 5. 0 6.137. 32 8。
江苏省扬州中学高二数学下学期质量检测试卷(5月)文

扬州中学高二(文科)数学试卷一、填空题:本大题共14小题,每小题5分,共70分.1.若集合{1,2,3,4,5},{1,2},{2,3}U A B ===,则()U C A B U = ▲ . 2.已知命题:,cos 1p x R x ∀∈≤, 则p ⌝: ▲ . 3.函数()()lg 12f x x x =--的定义域为 ▲ . 4.“函数()sin()f x x ϕ=+为奇函数” 是“0ϕ=”的 ▲ 条件.5.在复平面内,复数21iz i+=-对应的点位于第 ▲ 象限. 6.函数3y x =在点(1,1)处的切线方程为 ▲ .7.如果函数()ln 3f x x x =+-的零点所在的区间是(,1)n n +,则正整数n = ▲ .8.若0.4444,0.4,log 0.4a b c ===,则,,a b c 的大小关系为 ▲ .(从大到小)9.在ABC ∆中,已知sin :sin :sin 5:7:8A B C =,则角B = ▲ . 10.如图所示的是函数sin(),(0,0,||)y A x A ωϕωϕπ=+>>< 图象的一部分,则其解析式y = ▲ . 11.若1sin()64απ-=,则sin(2)6a π+的值为 ▲ .12.已知2228x y x +=+(,x y R ∈),则2245x y +的最大值为 ▲ .13.已知定义在R 上的偶函数()f x 满足对任意x R ∈都有(4)()f x f x +=,且当[]2,0x ∈-时,1()()12x f x =-.若在区间(2,6)x ∈-内函数()()log (2)a g x f x x =-+有3个不同的零点,则实数a 的取值范围为 ▲ .14. 设函数()f x 的定义域为D ,若存在定义域[,]a b D ⊆,使得函数()f x 在[,]a b 上的值域也为[,]a b ,则称()f x 为“等域函数”。
2015-2016学年江苏省扬州中学高二期末调研测试
2015-2016学年江苏省扬州中学高二期末调研测试(考试时间:120分钟,满分:120分)第I卷(三部分,共100分)第二部分英语知识运用(共两节,满分50分)第一节单项填空(共15小题;每小题1分,满分30分)请认真阅读下面各题, 从题中所给的A、B、C、D 四个选项中, 选出最佳选项, 并在答题卡上将该项涂黑。
21. In rap music, the singer, or rapper, will speak or rap the words ______ thebeat.A. apart fromB. along withC. all throughD. up to22. Who did the teacher have ______ an article for the wall newspaper justnow?A. writingB. writeC. to writeD. written23. - Do you think attending training courses is a great help when you look fora new job?- Well, it all depends. ______, it gives me a chance to try.A. SomehowB. BesidesC. AnywayD. Therefore24. With everything he had missing, he was ______ hopeless and killed himself.A. hardlyB. luckilyC. totallyD. sincerely25. In this school, students ______ the teachers fail may have to take theclasses again.A. whichB. whenC. whoseD. /26. It took ______ building materials to construct the energy-saving houses.It took brains, too.A. less thanB. more thanC. for freeD. after all27. - I failed the driving test a third time.- ______!You had spent so much time.A. Shame on youB. No wayC. Take careD. Never mind28. Although it had been ______ struggle for him to finish ______ experiment, he enjoyed the result with______ satisfaction.A. the; an; /B. a; the ; /C. a; an; aD. /; the; a29. Most of us thought ______ there was no hard evidence, Peter hadsomething to do with the crime.A. whileB. asC. whenD. if30. Hearing my advice, she just laughed and ______ it as impractical.A. convincedB. preferredC. balancedD. dismissed31. With all teeth ______, the old man had a limited variety of choices on hisdiet.A. giving upB. showing upC. falling outD. carrying out32. It’s well known th at the Diaoyu Islands belong to China, which is ______an island but the Chinese people’s dignity (尊严)as well.A. no more thanB. not more thanC. more thanD. less than33. I ______ all the cooking for my family, but recently I've been too busy to doit.A. will doB. doC. am doingD. had done34. The host was quite annoyed when he found that his things on the desk hadbeen ______.A. troubledB. interruptedC. upsetD. disturbed35. There was more rainfall than ______ this summer in the mountain areas.A. usualB. commonC. ordinaryD. normally第二节:完形填空(共20小题;每小题1分,满分20分)请认真阅读下面短文,从短文后各题所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
江苏省扬州中学高二数学5月月考试题文
江苏省扬州中学高二数学5月月考试题文(本试卷满分160分,时间120分钟,请将答案写在答题纸上)一、填空题:本大题共14小题,每小题5分,共70分. 1.已知全集为R ,集合{}{}20,1,0A x x x B =-==-,则A B =. 2.直线3x -y +a =0(a 为常数)的倾斜角为________. 3.sin(1740)-︒=.4.已知角θ的终边经过点P (4,m ),且sin θ=35,则m =________.5.设(1)1i x yi +=+,其中,x y 都是实数,则x yi +=________.6. 已知函数32,0()tan ,02x x f x x x π⎧≤⎪=⎨-<≤⎪⎩,则(())4f f π=________.7. 观察下列各式:223344551,3,4,7,11a b a b a b a b a b +=+=+=+=+=,……则1010a b +=.8.已知1a b >>,若5log log 2a b b a +=,b a a b =,则ab =. 9.已知1cos sin 21cos sin x xx x-+=-++,则tan x =.10.在△ABC 中,角A ,B 均为锐角,则“cosA>sinB”是“△ABC 是钝角三角形”的条件.(填“充分不必要”,“必要不充分”,“充要”,“既不充分又不必要”) 11.在ABC ∆中,角,,A B C 的对边分别是,,a b c ,8,10a b ==,ABC ∆的面积为203,则ABC ∆的最大角的正切值是.12.已知32()f x x ax bx =++满足(1)(1)220f x f x ++-+=,则()f x 的单调递减区间是. 13.已知函数222()224,()1()(,)f x ax b b g x x a a b R =--++=---∈,若存在0x 满足0()f x 是()f x 的最大值,0()g x 是()g x 的最小值,则所有满足条件的整数对(,)a b是 .14.已知方程2()()10f x kf x -+=恰有四个不同的实数根,当函数2()x f x x e =时,实数k 的取值范围是.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15.(本题满分14分)已知复数12z z 、在复平面内对应的点分别为(2,1),(,3),A B a a R -∈(1)若12z z -=求a 的值;(2)若复数12z z z =⨯对应的点在二、四象限的角平分线上,求a 的值.16.(本题满分14分)已知命题:p 函数2()2f x x mx m =-+的图象与x 轴至多有一个交点,命题2:log 11q m -≤. (1)若⌝q 为真命题,求实数m 的取值范围; (2)若p ∨q 为假命题,求实数m 的取值范围.17.(本题满分15分)将函数()sin()(0,)22f x x ππωϕωϕ=+>-<<图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移6π个单位长度得到sin y x =的图象. (1)求函数()f x 的解析式;(2)当[]0,3x π∈时,方程()f x m =有唯一实数根,求m 的取值范围.18.(本小题满分15分)某度假山庄拟对一半径为1百米的圆形地块(如图)进行改造,在该地块上修建一个等腰梯形的游泳池ABCD(A 、B 、C 、D 在圆周上),其中AB DC ,DAB=3π∠,圆心O 在梯形内部。
高二数学月考试题及答案-扬州中学2014-2015学年高二下学期质量检测试卷(5月)(理)
江苏省扬州中学2014-2015学年高二下学期质量检测试卷(5月)(理)一.填空题(每题5分,合计70分)1. 已知复数z =(1i)(12i)+-(i 为虚数单位),则z 的实部为 .2. 设全集{}I 1,2,3,4=,集合{}S 1,3=,{}4T =,则()I S T =ð .3. 已知,,,a b c R ∈命题“若3,a b c ++=则2223a b c ++≥”的否命题是 .4. 函数12y x -=的定义域为 .5. “1x >”是“2x x >”的 条件(在“充分不必要、必要不充分、充要、既不充分又不必要”中选择作答)。
6. 若ABC ∆内切圆半径为r ,三边长为,,a b c ,则ABC ∆的面积1()2S r a b c =++. 类比到空间,若四面体内切球半径为R ,四个面的面积为1234,,,S S S S ,则四面体的体积V = .7. 函数1()1(0,1)x f x a a a -=->≠的图象恒过定点 .8. 函数2y x =的值域为 .9. 设{}1,2,3,...,10,,A B A B =⊆含有3个元素,且其中至少有2个偶数,则满足条件的集合B 的个数为 .10.设函数()f x 是定义在R 的偶函数,当0x ≥时,()2 1.x f x =+若()3,f a =则实数a 的值为 .11.设函数()()(,f x x a x a b a b =--+都是实数),则下列叙述中,正确的是 .(1)对任意实数,,a b 函数()y f x =在R 上是单调函数;(2)存在实数,,a b 函数()y f x =在R 上不是单调函数;(3)对任意实数,,a b 函数()y f x =的图象都是中心对称图形;(4)存在实数,,a b 函数()y f x =的图象不是中心对称图形;12.已知集合{}{}2(,)20,(,)10,02,A x y x mx y B x y x y x =+-+==-+=≤≤如果,A B ≠∅则实数m 的取值范围是 .13. 设函数()sin cos .f x ax x x =++若函数()f x 的图象上存在不同的两点,,A B 使得曲线()y f x =在点,A B 处的切线互相垂直,则实数a 的取值范围为 .14.已知函数,0,()ln ,0,kx k x f x x x +≤⎧=⎨>⎩(其中0)k ≥,若函数(())1y f f x =+有四个零点,则实数k 的最小值是 .二.解答题(14+14+15+15+16+16=90)15.设全集是实数集R ,{}{}222730,0.A x x x B x x a =-+≤=+<(1) 当4a =-时,求;A B (2) 若()B B,R A =ð求实数a 的取值范围.16. 已知命题:p 指数函数()(26)x f x a =-在R 上单调递减,命题:q 关于x 的方程2x -3ax 2210a ++=的两个实根均大于3.若p 或q 为真,p 且q 为假,求实数a 的取值范围.17. 已知n 的展开式中前三项的系数成等差数列.(1) 求展开式中二项式系数最大的项;(2) 求展开式中所有的有理项.18. 某市环保研究所对市中心每天环境污染情况进行调查研究后,发现一天中环境综合污染指数()f x 与时间x(小时)的关系为()[]212,0,2413x f x a a x x =+-+∈+,其中a 是与气象有关的参数,且30,4a ⎡⎤∈⎢⎥⎣⎦,若用每天()f x 的最大值为当天的综合污染指数,并记作()M a .(1)令[]2,0,241x t x x =∈+,求t 的取值范围; (2)求函数()M a ;。
2015~2016学年扬州市第一中学高二理科期末调研测试数学试题
2015~2016学年扬州市第一中学高二期末调研测试数学(理科)2016.06第I卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上..1.已知函数f(x)=|x﹣2|,g(x)=﹣|x+3|+m,若函数f(x)的图象恒在函数g(x)图象上,则实数m的取值范围是.2.命题“∀x∈R,x2+x+1>0”的否定是.3.已知集合A={0,a},B={3a,1},若A∩B={1},则A∪B=.4.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<)的部分图象如图所示,则f(π)的值为.5.3<m<9是方程+=1表示的椭圆的条件.(从“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个正确的填写)6.设,则中最大的数是.7.已知定义在R上的奇函数y=f(x)满足:①当x∈(0,1]时,f(x)=()x;②f(x)的图象关于直线x=1对称,则f(﹣log224)=.8.设函数f(x)=x2﹣2ax+3﹣2a的两个零点x1,x2,且在区间(x1,x2)上恰有两个正整数,则实数a的取值范围为.9.已知函数f(x)=3sin(ωx+φ)(ω>0,0≤φ<π)的部分图象如图所示,则该函数的解析式为f(x)=.10.若复数z满足,则的最小值为.11.设函数f(x)=的值域为R,则实数a的取值范围为.12.定义在上的函数满足:,,是的导函数,则不等式(其中为自然对数的底数)的解集为.13.若函数(a为常数,是自然对数的底)恰有两个极值点,则实数的取值范围为.14.如图,矩形ABCD的三个顶点A、B、C分别在函数的图象上,且矩形的边分别平行于两坐标轴. 若点A的纵坐标为2,则点D的坐标为__________二、解答题:本大题共6小题,共90分,解答时应写出文字说明、证明过程或演算步骤15.已知A={x|﹣x2+3x﹣2>0},B={x|x2﹣(a+1)x﹣a≤0}.(1)化简集合B;(2)若A⊆B,求实数a的取值范围.16.已知虚数满足.(1)求;(2)是否存在实数,是为实数,若存在,求出值;若不存在,说明理由;(3)若在复平面内对应的点在第一、三象限的角平分线上,求复数.17.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)的图象经过点(0,1),且其相邻两对称轴之间的距离为π.(1)求函数f(x)的解析式;(2)设若sinα+f(α)=,α∈(0,π),求的值.18.现代人对食品安全的要求越来越高,无污染,无化肥农药等残留的有机蔬菜更受市民喜爱,为了适应市场需求,我市决定对有机蔬菜实行政府补贴,规定每种植一亩有机蔬菜性补贴农民x元,经调查,种植亩数与补贴金额x之间的函数关系式为f(x)=8x+800(x≥0),每亩有机蔬菜的收益(元)与补贴金额x之间的函数关系式为g(x)=.(1)在政府未出台补贴措施时,我市种植这种蔬菜的总收益为多少元?(2)求出政府补贴政策实施后,我市有机蔬菜的总收益W(元)与政府补贴数额x之间的函数关系式;(3)要使我市有机蔬菜的总收益W(元)最大,政府应将每亩补贴金额x定为多少元?19.对于函数y=f(x),若x0满足f(x0)=x0,则称x0位函数f(x)的一阶不动点,若x0满足f(f(x0))=x0,则称x0位函数f(x)的二阶不动点,若x0满足f(f(x0))=x0,且f (x0)≠x0,则称x0为函数f(x)的二阶周期点.(1)设f(x)=kx+1.①当k=2时,求函数f(x)的二阶不动点,并判断它是否是函数f(x)的二阶周期点;②已知函数f(x)存在二阶周期点,求k的值;(2)若对任意实数b,函数g(x)=x2+bx+c都存在二阶周期点,求实数c的取值范围.20.己知函数(1)若,求函数的单调递减区间;(2)若关于x的不等式恒成立,求整数 a的最小值:(3)若,正实数满足,证明:第II卷(附加题)21.已知直线l的参数方程:(t为参数)和圆C的极坐标方程:.(1)将直线l的参数方程化为普通方程,圆C的极坐标方程化为直角坐标方程;(2)判断直线l和圆C的位置关系.22.已知矩阵(Ⅰ)求实数a,b,c,d的值;(Ⅱ)求直线y=3x在矩阵M所对应的线性变换下的像的方程.23.如图,AB为圆O的直径,BC与圆O相切于点B,D为圆O上的一点,AD∥OC,连接CD.求证:CD为圆O的切线.24.某校开设8门校本课程,其中4门课程为人文科学,4门为自然科学,学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.(1)求某同学至少选修1门自然科学课程的概率;(2)已知某同学所选修的3门课程中有1门人文科学,2门自然科学,若该同学通过人文科学课程的概率都是,自然科学课程的概率都是,且各门课程通过与否相互独立.用表示该同学所选的3门课程通过的门数,求随机变量的概率分布列和数学期望。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扬州中学高二(文科)数学试卷2015.5.29一、填空题:本大题共14小题,每小题5分,共70分. 1.若集合{1,2,3,4,5},{1,2},{2,3}U A B ===,则()U C A B = ▲ .2.已知命题:,cos 1p x R x ∀∈≤, 则p ⌝: ▲ .3.函数()()lg 1f x x =-的定义域为 ▲ . 4.“函数()sin()f x x ϕ=+为奇函数” 是“0ϕ=”的 ▲ 条件.5.在复平面内,复数21iz i+=-对应的点位于第 ▲ 象限. 6.函数3y x =在点(1,1)处的切线方程为 ▲ .7.如果函数()ln 3f x x x =+-的零点所在的区间是(,1)n n +,则正整数n = ▲ . 8.若0.4444,0.4,log 0.4a b c ===,则,,a b c 的大小关系为 ▲ .(从大到小)9.在ABC ∆中,已知sin :sin :sin 5:7:8A B C =,则角B = ▲ . 10.如图所示的是函数sin(),(0,0,||)y A x A ωϕωϕπ=+>>< 图象的一部分,则其解析式y = ▲ . 11.若1sin()64απ-=,则sin(2)6a π+的值为 ▲ .12.已知2228x y x +=+(,x y R ∈),则2245x y +的最大值为 ▲ .13.已知定义在R 上的偶函数()f x 满足对任意x R ∈都有(4)()f x f x +=,且当[]2,0x ∈-时,1()()12x f x =-.若在区间(2,6)x ∈-内函数()()log (2)a g x f x x =-+有3个不同的零点,则实数a 的取值范围为 ▲ .14. 设函数()f x 的定义域为D ,若存在定义域[,]a b D ⊆,使得函数()f x 在[,]a b 上的值域也为[,]a b ,则称()f x 为“等域函数”。
已知函数()xf x a =,(1a >)为“等域函数”,则实数a 的取值范围为 ▲ .二、解答题:本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分14分)已知函数22()cos cos sin f x x x x x =+-(1)求()f x 的最小正周期 及 单调增区间; (2)当[,]63x ππ∈-时,求函数)(x f 的值域.16.(本小题满分14分)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,已知4cos 5B =,6=b , (1)当5=a 时,求角A ;(2)当ABC ∆的面积为27时,求c a +的值.17.(本小题满分14分)已知1tan(),cos 2αβα-==,其中(0,),(0,)2παβπ∈∈. (1)求tan β的值; (2)求2αβ-的值.18.(本小题满分16分)已知函数12()2x x m f x n+-+=+,(其中m 、n 为参数)(1)当1m n ==时,证明:)(x f 不是奇函数; (2)如果)(x f 是奇函数,求实数m 、n 的值;(3)已知0,0m n >>,在(2)的条件下,求不等式1(())()04f f x f +<的解集.19.(本小题满分16分)已知函数()cos f x a x =,,22x ππ⎡⎤∈-⎢⎥⎣⎦,其中a 为参数.(1)设t t 的取值范围,并把()f x 表示为t 的函数()g t ; (2)求函数()f x 的最大值(结果用a 表示); (3)若对任意12,,22x x ππ⎡⎤∈-⎢⎥⎣⎦,都有()()121f x f x -≤,求实数a 的取值范围. (不需要过程,直接写出a 的范围即可)20.(本小题满分16分) 已知函数()ln 1a f x x x =+-,其中a 为参数,2221()ln 2x g x e x e x e x =⋅+-, (1)若1a =,求函数()f x 的单调区间; (2)当[]1,x e ∈时,求函数()f x 的最小值;(3)函数()g x 是否存在垂直于y 轴的切线? 请证明你的结论论。
扬州中学高二(文科)数学答案2015.5.291. {}4,5 2.,cos 1x R x ∃∈> 3.(1,2] 4. 必要不充分 5.一 6.32y x =- 7. 2 8.a b c >> 9.3π 10.2sin(2)3x π+11.1718- 12. 64 13.)2 14.1(1,)ee15.解:⑴()2cos 22sin(2)6f x x x x π=+=+ --------------4分∴()f x 的最小正周期为22T ππ==, --------------6分令222,()262k x k k Z πππππ-≤+≤+∈,可得,()36k x k k Z ππππ-≤≤+∈,∴函数()f x 的单调增区间为[,],()36k k k Z ππππ-+∈;------------8分 ⑵∵[,]63x ππ∈-∴52666x πππ-≤+≤ ∴1sin(2)126x π-≤+≤ ∴函数)(x f 的值域为[]1,2- ------------14分 16..解:(1)∵54cos =B ,∴ 53sin =B 由正弦定理B b A a sin sin =可得1sin 2=A ……………………3分 又∵ 56=<=a b∴<A B ∴ o30=A ……………………7分(2)∵ 1sin 2S ac B =,53sin =B ,∴ 32710=ac ,即90=ac .由余弦定理B ac c a b cos 2222-+= 得22228361445=+-=+-a c ac a c ,即22180+=a c . ……………………11分 所以222()2180180360+=++=+=a c a c ac ,所以,+=a c . ……………………14分17. 解:(1) ∵cos α=(0,)2πα∈∴1tan 3α= ∵tan tan 1tan()1tan tan 2αβαβαβ--==+⋅,而1tan 3α=∴解得1tan 7β=-……6分 (2) tan()tan tan(2)tan()11tan()tan αβααβαβααβα-+-=-+==-- ……9分∵1tan 07β=-<,(0,)βπ∈∴(,)2πβπ∈ 又∵1tan 13α=<,(0,)2πα∈∴(0,)4πα∈∴2(,0)αβπ-∈- ∴324παβ-=-……14分注:多一解扣2分18.解:(1)1212)(1++-=+x x x f , ∴511212)1(2-=++-=f ,412121)1(=+-=-f ,∵)1()1(f f -≠-,∴)(x f 不是奇函数; ……4分(2)∵)(x f 是奇函数时 ∴)()(x f x f -=-,即112222x x x x m mn n--++-+-+=-++对定义域内任意实数x 成立.化简整理得关于x 的恒等式2(2)2(24)2(2)0x x m n mn m n -⋅+-⋅+-=, ∴20,240m n mn -=⎧⎨-=⎩ 即12m n =-⎧⎨=-⎩或12m n =⎧⎨=⎩. ……10分(注:少一解扣2分)(3)由题意得1,2m n ==∴12112()(1)22221x x x f x +-+==-+++ ,易判断()f x 在R 上递减,∵1(())()04f f x f +< ∴11(())()()44f f x f f <-=-1()4f x ∴>-23x ∴< 2log 3x ∴<,即0)(>x f 的解集为2(,log 3)-∞ ……16分19.解:(1)22222cos t x ==+=+,又∵,22x ππ⎡⎤∈-⎢⎥⎣⎦,∴cos 0,x ≥ ∴[]222cos 2,4t x =+∈, 又∵0t >,∴2t ⎤∈⎦, -------3分 ∵21cos 12x t =-,∴()212g t at t a =+-,2t ⎤∈⎦. -------5分 (2)即求()212g t at t a =+-,2t ⎤∈⎦的最大值. 当0a =时,()g t t =在2t ⎤∈⎦上递增,∴()()max 22g t g == ;当0a >时,()221211222a g t a t t a t a a a a⎛⎫⎛⎫=+-=+-- ⎪ ⎪⎝⎭⎝⎭,对称轴为1t a =-.()g t在2t ⎤∈⎦上递增,∴()()max 22g t g a ==+ ; -------7分当0a <时,()221211222a g t a t t a t a a a a⎛⎫⎛⎫=+-=+-- ⎪ ⎪⎝⎭⎝⎭,对称轴为1t a =-.若1a -≤2a ≤-时,()max g t g ==;12a <-<,即122a -<<-时,()max 112g t g a a a ⎛⎫=-=-- ⎪⎝⎭; 若12a -≥,即102a -≤<时,()()max 22g t g a ==+; -------10分 综上得,当2a ≤-时,()max f x g ==;当122a -<<-时,()max 112f x g a a a ⎛⎫=-=-- ⎪⎝⎭; 当12a ≥-时,()()max 22f x g a ==+. ------ 11分 (3)要使得()()121f x f x -≤对区间,22ππ⎡⎤-⎢⎥⎣⎦内的任意12,x x 恒成立,只需()()max min 1f x f x -≤.也就是要求()()max min 1g t g t -≤对2t ⎤∈⎦成立因为当1a -≤,即当2a ≤时,()()min 22g t g a ==+;当122a +->20a <<时, ()min g t g ==结合问题(2)需分四种情况讨论:①12a ≥-时,()()max min 21g t g t a -=+成立,所以112a -≤<;122a <<-时()()max min 112g t g t a a -=---,即1102a a ++≥,注意到函数()12p a a a =+122a <<-上单调递减,故()11312 2 2p a p ⎛⎫>-=--=- ⎪⎝⎭,于是1311022a a +>-+>成立,所以122a <<-③22a -<≤时()()max min 1212g t g t a a a -=----≤,即12302a a ++≥,注意到函数()122q a a a =+在22a -<≤上单调递增,故()22q a q ⎛>-=- ⎝⎭,∴1623022a a -++>>成立,∴22a -<≤;④a ≤时,()()max min 21g t g t a -=-≤,即3a ≥,3a ≤≤;综上得,实数a 的取值范围是1⎤⎦. ………………16分 20. 解:(1)1a =时,22111'()x f x x x x-=-= ,定义域为(0,)+∞, 令'()0f x =,得 1x =,()f x ',()f x 随x 的变化情况如下表:f 的单调递增区间为,单调递减区间为;4分(2)221'()a x af x x x x-=-= ,[]1,x e ∈ 当0a ≤时,'()0f x >,所以()f x 在区间[]1,e 上单调递增,所以,()f x 在区间[]1,e 上的最小值为(1)1f a =-,当0a >时,令'()0f x =,则x a = ,① 若a e >,则'()0f x <对[]1,x e ∈成立,则()f x 在区间[]1,e 上单调递减, 所以,()f x 在区间[]1,e 上的最小值为()af e e=, ② 若1a e ≤≤,则有所以在区间上的最小值为,③若1a <,则'()0f x >对[]1,x e ∈成立,所以()f x 在区间[]1,e 上单调递增, 所以,()f x 在区间[]1,e 上的最小值为(1)1f a =-,综上得: min(1)1,(1)()()ln ,(1)(),()f a a f x f a a a e af e a e e ⎧⎪=-<⎪==≤≤⎨⎪⎪=>⎩…………………10分 (3)即考虑方程()0g x '=有没有解,求导得21()(ln )(1)xg x x e e x x'=++-,令()0g x '=,则21(ln )(1)0x x e e x x ++-=,即21(1)ln xe x x x e -+=下面分别研究左右两个函数的值域,∵由(1)得1a =时()f x 的最小值为(1)0f = ∴1()ln 1(1)0f x x f x =+-≥=,即1ln 1x x+≥, 令2(1)()x e x h x e -=,则2(2)()xe x h x e -'=,∴()h x 在(,2)-∞上递增,在(2,)+∞上递减,∴max ()(2)1h x h ==又∵等号不能同时取到,∴方程21(1)ln xe x x x e-+=无解, 即函数()g x 不存在垂直于y 轴的切线。
