1数学模型引言(2014-2-24) (1)
2014年数学建模国家一等奖优秀论文

2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的报名参赛队号为(8位数字组成的编号):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2014 年 9 月 15日赛区评阅编号(由赛区组委会评阅前进行编号):2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):小区开放对道路通行的影响摘要2016年2月21日,国务院发布《关于进一步加强城市规划建设管理工作的若干意见》,其中第十六条关于推广街区制,原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步开放等意见,引起了广泛的关注和讨论。
条件分布在生活中的应用1

学士学位论文题目学生姓名指导教师年级系别专业学院学校2014年4月目录摘要 (1)关键词................................ 错误!未定义书签。
引言.................................. 错误!未定义书签。
一、条件分布 (2)(一)条件分布的定义 .................. 错误!未定义书签。
(二)二维离散型随机变量的条件分布 (3)(三)二维连续型随机变量的条件分布 (4)二、条件分布在生活中的应用 (5)(一)条件分布在经济预算中的应用 (5)(二)条件分布在刑侦破案中的应用 (7)(三)条件分布在劳动生产中的应用 (8)总结 (10)英文摘要 (11)浅谈条件分布在生活中的应用摘要:随着时代的进步以及科学的发展,数学在生活中的应用越来越广泛,而概率论作为数学的一个重要组成部分,也逐渐发展起来并广泛应用于各个领域.条件分布研究了不同随机变量的关系,本课题中先说明了条件分布的基础概念,然后就二维随机变量中的离散型随机变量及连续型随机变量的条件分布分别作了简单的介绍,最后从经济预算,刑侦破案,劳动最优化来体现条件分布在生活中的应用。
关键词:条件分布;随机变量;应用引言概率是一门与生活联系紧密的学科同时也是一门相当有趣的数学分支学科,数学家们冲破了古希腊的演绎框架,向自然界和社会生活的多方面汲取灵感,而后发展成完整的数学分支。
除了分析学这一大系统之外,概率论就是这一时期使"欧几里得几何相形见绌"的几个重大成就之一。
在概率论的基本概念中,我们学习了条件概率,它是对随机事件而言,所谓随机事件就是试验中的样本空间的特定子集。
当这一子集中的一个样本点出现时,称为这一事件发生。
而我们探讨的条件分布是对于随机变量而言的。
设随机试验的样本空间为Ω,对于,Ω∈ω有唯一的实数)(ωX 与之对应,这样就得得到一个实值单值函数)(ωX ,若R B ∈,B}X |{∈)(ωω是事件,)(ωX 就为随机变量。
一元二次方程的应用(1)
解:
规律总结:增长率(或降低率)问题的规律
(1)增长率问题:设基数为a,平均增长率为x,则一次增长后的值为a(1+x),两次增长后的值为a(1+x)2,依次类推,n次增长后的值为a(1+x)n
(2)降低率问题:设基数为a,平均降低率为x,则则一次降低后的值为a(1-x),两次降低后的值为a(1-x)2,依次类推,n次降低后的值为a(1-x)n
跟踪训练:
1、小明家承包的土地前年的粮食产量是50吨,前年、去年、今年的总产量是175吨,小明家去年、今年平均每年的粮食产量增长率是多少?
2、某企业向银行贷款200万元用于生产某种新产品,约定两年到期时一次性还本付息,两年总利息为本金的8%,由于产销对路,两年到期时,该企业除还清贷款的本金和利息外,还盈余72万元。假定该企业在生产这种新产品期间,每年比上一年资金增长的百分率相同,则这个百分率是多少?
里辛一中“分层互助”导学案
初三数学 课题:一元二次方程的应用(1)备课时间:2014-03-24
课堂寄语:自觉是进步之母,自贱是堕落之源,故自觉不可无,自贱不可有。人应该支配习惯,而绝不能让习惯支配人;一个人若不能去掉它的坏习惯,那简直一文不值。
学习
目标
1、掌握列一元二次方程解应用题的一般步骤
2、能够熟练应用常见基本图形的面积公式、体积公式,会利用一元二次方程解决几何中一些与面积有关的问题
2、列一元二次方程解应用题的一般步骤
①审②设③列④解⑤验⑥答
二、【自主学习】
自学课本62页,并写出小明和小亮设计方案的一元二次方程
小明:
小亮:
三、【探究新知】
探究一:面积问题
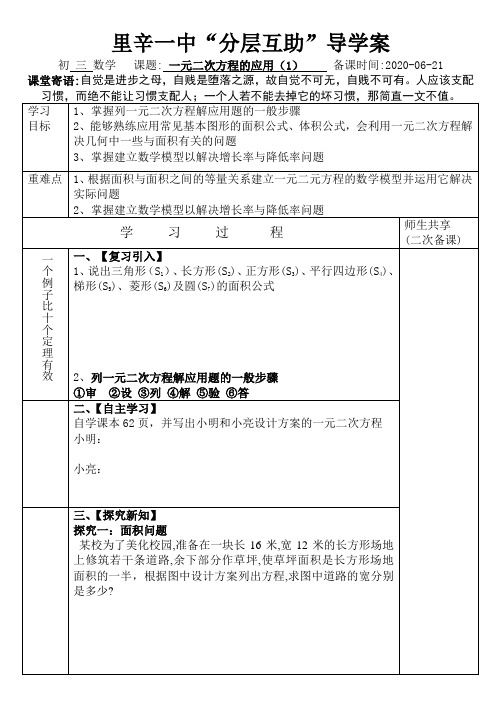
某校为了美化校园,准备在一块长16米,宽12米的长方形场地上修筑若干条道路,余下部分作草坪,使草坪面积是长方形场地面积的一半,根据图中设计方案列出方程,求图中道路的宽分别是多少?
数学建模-猎狗追兔子问题

数学建模论文《数学建模》(2014春)课程期末论文摘要(一)对于问题一:自然科学中存在许多变量,也有许多常量,而我们要善于通过建立合适的模型找到这些变量之中的不变量。
猎狗追赶兔子的问题是我们在生活中常见的实例,而题目把我们生活中的普通的例子抽象成为高等数学中微分方程的例子,通过对高阶微分方程的分析,建立微分方程模型,并用数学软件编写程序求解,得出结论,解决生活中常见的实际问题。
(二)对于问题二:学习使用matlab进行数学模型的求解,掌握常用计算机软件的使用方法。
关键词微分方程导数的几何意义猎狗追兔子数学建模数学软件一、问题重述如图1所示,有一只猎狗在B 点位置,发现了一只兔子在正东北方距离它250m 的地方O 处,此时兔子开始以8m/s 的速度正向正西北方向,距离为150m 的洞口A 全速跑去. 假设猎狗在追赶兔子的时候,始终朝着兔子的方向全速奔跑。
请回答下面的问题:⑴ 猎狗能追上兔子的最小速度是多少? ⑵ 在猎狗能追上兔子的情况下,猎狗跑过的路程 是少?⑶ 假设猎狗在追赶过程中,当猎狗与兔子之间的距离为30m 时,兔子由于害怕导致奔跑速度每秒减半, 而狗却由于兴奋奔跑速度每秒增加0.1倍,在这种情 况下回答前面两个问题。
二、问题分析与假设在猎狗追赶兔子的时候猎狗一直朝着兔子的方向追赶,所以可以建立平面直角坐标系,通过导数联立起猎狗运动位移,速度和兔子的运动状态。
1.假设兔子的运动是匀速的。
2.假设猎狗的运动轨迹是一条光滑并且一阶导数存在的曲线。
3.猎狗的运动时匀速或者匀变速的。
4.猎狗运动时总是朝向兔子。
三、模型的建立及求解3.1 符号规定1.(x ,y ):猎狗或者兔子所在位置的坐标。
2. t :从开始到问题结束经过的时间。
3. a:猎狗奔跑的路程。
4. v:猎狗的奔跑速度。
3.2 模型一的建立与求解猎狗能够抓到兔子的必要条件:猎狗的运动轨迹在OA 要有交点以OA 为y 轴,以OB 为x 轴建立坐标系,则由图有O(0,0),A(0,150),B(250,0),兔子的初始位置0点,而猎狗初始位置是B 点,t (s )后猎狗到达了C (x ,y ),而兔子到达了D (0,8t ),则有CD 的连线是猎狗运动轨迹的一条切线,由导数的几何意义有:NW8dy y tdx x-=dav dt =da =三式联立消去t ,得到;设:若猎狗可以追上兔子则有当兔子在OA,猎狗在OB 之间运动时此方程有解,设:得到:得到:两式联立相加得到:1.如果q=1即v=8 m/s 得到所以此情况无交点,所以v=8m/s 猎狗无法追上兔子; 2.如果q<1即v>8m/s 得到此情况有交点,所以有可能能够追上兔子,如果要追上兔子需要y<=150; 解得到: 即所以这种情况下能够追上的最小速度是 .3.如果q>1 利用上式得到,所以这种情况不能追上兔子。
数学建模论文写作注意及技巧

体现摘要中“三要素”的关键词组( 体现摘要中“三要素”的关键词组(一 般是名词) 般是名词)
4.问题重述 问题重述 对问题充分分析的基础上, 对问题充分分析的基础上,写出自己 对问题的理解,不是复制拷贝. 对问题的理解,不是复制拷贝 5.问题分析 问题分析 为建模和求解做必要的铺垫,有承上启 为建模和求解做必要的铺垫 有承上启 下的作用. 下的作用 整篇论文的引论部分, 整篇论文的引论部分,起到吸引读者和 继续阅读的铺垫作用. 继续阅读的铺垫作用
关于铁路大提速下京沪线列车的最优调度模型铁路大提速下的京沪线列车调度京沪线客货列车提速调度优化模型摘要abstract对论文内容不加注释和评论的简短陈述作用不阅读论文全文即能获得必要的信息并吸引读者产生浓厚的兴趣和肯定
论文写作
全国评阅时将首先根据摘要和论 文整体结构及概貌对论文优劣进行 初步筛选。 初步筛选。 一、写作要点 1.充分体谅读者,为读者着想; 充分体谅读者,为读者着想; 充分体谅读者 2.体现三要素:解决什么问题、 体现三要素:解决什么问题、 体现三要素 用到什么方法、得到什么结果; 用到什么方法、得到什么结果; 3. 论文整体结构清晰,文章前后 论文整体结构清晰, 呼应,一气呵成; 呼应,一气呵成;
6.模型假设 模型假设 为明确问题、简化问题、自设条件、 为明确问题、简化问题、自设条件、限 制模型的适用范围等的必要说明 部分假设需写出合理性解释,或必要的检验 部分假设需写出合理性解释,或必要的检验. 合理性解释 7. 变量说明 为便于读者阅读和理解, 为便于读者阅读和理解,在论文前置部 分给出贯穿文章的主要变量. 分给出贯穿文章的主要变量 整体变量整体说明, 原则 整体变量整体说明,局部变量局 部说明,重复变量反复说明. 部说明,重复变量反复说明 电力市场输电阻塞管理模型
数学模型教案

数学模型教案引言:数学模型是数学与实际问题相结合的产物,是解决实际问题的有力工具。
在数学教学中,引入数学模型可以增强学生对数学的兴趣,提高解决问题的能力。
本教案旨在通过引导学生建立数学模型,培养他们的逻辑思维和问题解决能力,使数学变得更加有趣和实用。
一、教学目标1.了解数学模型的概念和基本原理;2.掌握建立数学模型的方法和步骤;3.培养学生运用数学模型解决实际问题的能力;4.促进学生的逻辑思维和抽象思维的发展。
二、教学内容1.数学模型的概念和分类;2.建立数学模型的方法和步骤;3.应用数学模型解决实际问题。
三、教学过程1.引入在现实生活中,我们经常遇到各种各样的问题,例如交通拥堵、疾病传播等。
这些问题是很复杂的,我们是否可以运用数学来解决呢?请思考一下。
2.概念讲解数学模型是对实际问题进行抽象和描述的数学表达式或方程组。
数学模型可以分为确定性模型和随机性模型。
确定性模型可以精确描述实际问题,而随机性模型则考虑了随机因素。
3.案例分析以交通拥堵问题为例,引导学生思考如何建立数学模型。
首先,我们需要确定影响交通流量的主要因素,例如道路长度、车流量、车速等。
然后,我们可以根据这些因素建立一个数学方程,来描述道路流量和速度之间的关系。
4.模型建立在教师的引导下,学生分组进行数学模型的建立。
教师可以提供不同的实际问题,例如疾病传播、环境污染等,让学生自行分析问题,找出关键因素,并建立相应的数学模型。
5.模型求解学生通过对建立的数学模型进行求解,得出相应的结果。
教师可以引导学生运用数学知识,例如代数方程、概率统计等,来解决实际问题。
6.模型评价学生对建立的数学模型进行评价,并讨论模型的准确性和适用性。
教师引导学生思考模型存在的局限性,并提出改进的意见。
四、教学评价通过教师的指导和学生的积极参与,预期达到以下评价标准:1.学生对数学模型的概念和基本原理有一定的了解;2.学生能够独立建立数学模型,并进行求解;3.学生运用数学模型解决实际问题的能力有所提高;4.学生具备一定的逻辑思维和问题解决能力。
2014考研数学一真题及答案解析(完整版)

2
2014 年全国硕士研究生入学统一考试
数学一试题答案
一、选择题:1~8 小题,每小题 4 分,共 32 分,下列每小题给出的四个选项中,只有一项 符合题目要求的,请将所选项前的字母填在答题纸 指定位置上. ... (1)B (2)D (3)D (4)B (5)B (6)A (7) (B) (8) (D)
π
2
,根据单调有界必有极限定理,得 lim an 存在,
n →∞
设 lim an = a ,由
n →∞
∑b
n =1
∞
n
收敛,得 lim bn = 0 ,
n →∞
,得 cos a − a = cos 0 = 1 。 故由 cos a n − a n = cosb n ,两边取极限(令 n → ∞ ) 解得 a = 0 ,故 lim an = 0 。
n →∞
(20) 【答案】① ( −1, 2,3,1)
T
− k1 + 2 − k2 + 6 − k3 − 1 2k1 − 1 2k2 − 3 2k3 + 1 ②B= (k , k , k ∈ R) 3k1 − 1 3k2 − 4 3k3 + 1 1 2 3 k2 k3 k1
(21) 【答案】利用相似对角化的充要条件证明。
0, y < 0, 3 y, 0 ≤ y < 1, 4 (22) 【答案】 (1) FY ( y ) = 1 1 1 + y ,1 ≤ y < 2, 2 2 1, y ≥ 2.
(2)
3 4 1 πθ , EX 2 θ = 2
的下侧使之与围成闭合的区域?4?7327663dddd221113131131310231222010122010222211?????????????ddzsincosdzsincosdxdydzyx619答案1证an单调由20na根据单调有界必有极限定理得nnlima存在设aalimnn由1nnb收敛得0nnlimb故由nnnbcosaacos?两边取极限令n得10?cosaacos
让学生经历“数学模型”的建构过程——听特级教师钱守旺“路程、时间与速度”一课有感

让学生经历“数学模型”的建构过程——听特级教师钱守旺
“路程、时间与速度”一课有感
姜秀英
【期刊名称】《小学教学》
【年(卷),期】2014(000)002
【摘要】前段时间,我有幸现场观摩了特级教师钱守旺执教的“路程、时间与速度”一课。
一上课,教师和学生就谈奥运比赛,主题是每种比赛比什么。
【总页数】2页(P25-26)
【作者】姜秀英
【作者单位】辽宁喀左县第五小学
【正文语种】中文
【相关文献】
1.让学生经历“数学模型”的建构过程——听特级教师钱守旺“路程、时间与速度”一课有感
2.将抽象概念置于真实的生活情境中——观钱守旺老师"比的意义"一课
有感3.让学生"经历,体验,探索"学习数学的过程--听《质数和合数》一课有感4.挖
掘教学素材渗透情感教育——特级教师钱守旺《认识时间》教学片段赏析5.用活
教材,教活学生——听特级教师钱守旺教学“年、月、日”有感
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开普勒三定律
1. 开普勒第一定律:
所有的行星围绕太 阳运动的轨道都是 椭圆,太阳处在所 有椭圆的一个焦点 上。
行星
太阳
F
F
椭圆有两个焦点
39
2.开普勒第二定律:
太阳和行星的连线在相等的时间内扫过的面积相等。
S1
S2
S1=S2
近日点速度快,远日点速度慢
40
3. 开普勒第三定律:
所有行星的轨道半长轴的三次方跟公转周期的 二次方的比值都相等。
1
W c1 ( I1 3) c2 ( I 2 3) D1[exp( D2 ( I1 3)) 1]
这是一个偏微分方程组的初边值问题, 可以用数值方法中的有限元法进行求解。
35
四个不同时期的流体速度图像
36
应力/应变分布图
同样可以发现,最大主应力和主应变均在右心 室曲率最大的地方出现,而疤痕和补丁附近的 应变值较小(原因是疤痕和补丁的材料较硬).
44
1973年,Freddy机器人通过视觉感知来定位和组装 了模型。 1974年,随着政府资助机构减少了对于人工智能研 究的拨款预算,人工智能寒冬到来。 1975年,斯坦福大学的Meta-DENDRAL程序发现关 于分子的新规律,成果被发表在了美国化学学会的 期刊上。 1980年,自动行驶的汽车在慕尼黑大学里以90公里/ 小时的速度行驶。 1988年,人工智能的主要形式变为基于不确定数据 的概率推理,而不再是以往那样侧重于逻辑。 1989年,美国航天局(NASA)利用自动聚类的电 脑程序发现以往未知的几类恒星。
31
32
虚拟外科手术
上图为一位患有右心室机能障碍的患者,术 前、术后的心脏图像。
33
流体模型:
流体运动方程
流体连续性方程 速度边界条件 压力边界条件 右心室外壁面为 自由面 不同材料接触面 为相互作用界 面
u ( ((u u g ) )u ) p 2u t u 0 v u u | , |inlet ,outlet 0 t n P |inlet pin (t )(inlet _ open) v |inlet 0(inlet _ closed ) P |outlet pout (t )(outlet _ open ) v |outlet 0(outlet _ closed ) p |LV pLV (t )
4
4、模型的建立
5、模型的计算
5
6
7
8
6 模型验证
某日,和丹佛、Spring 一同去安贞华联的 PizzaHut 饕餮,要了一份自助沙拉。测量了一下各参数, 数值如下: R = 16.8 cm÷2 = 8.4 cm L = 5.5 cm d = 0.8 cm 取 k = 1/3,计算得到 N = 37 根,实际上也正好是 37 根,如图 6-1 完全吻合! 接着,按照前述方法,层层摆放, 因为只有 3 人,不想浪费,所以只摆了 6 层的圆台体, 便收工开吃了。最后 3 人吃到半 S,沙拉堆到了嗓子 眼儿,差点 P 掉⋯⋯
高技术的出现把我们的社会推进到数学 技术的新时代
49
高技术本质上是数学技术。
核磁共振成像技术:积分方程、几何学
期权定价:随机微分方程(Black-Scholes公式) 复合材料设计:控制论、偏微分方程及其计算 地震分析和预测:统计学、湍流动力系统 药物设计:统计学、组合学、拓扑学
9
一、首先准备一个碟子,里面放准备堆上去的 材料和用于粘贴的沙拉酱
10
二、在碗里面结实地填上许多材料,碗沿上合理 的贴上整齐结实的胡萝卜条。
11
12
三、在已经填整齐的碗的内圈整齐地放上形状合适(能摆 一个圆)的大菠萝块。
13
四、再在菠萝圈中间填上你喜欢的小东西
14
五、内圈抹平摆整齐以后再在外圈(胡萝卜条上)再整齐地摆上一圈 菠萝。
2
必胜客(PizzaHut)沙拉塔的堆叠方案分析
【摘要】本文通过分析必胜客沙拉塔的堆叠问题,提出一种能够使堆叠 的沙拉塔体积最大化的方 案,即将胡萝卜条呈放射状铺在盘子的外缘, 并探出接近一半的长度,以此为底,再使用菠萝块摆 在外围作为承重墙, 中间摆放喜爱的内容,如此逐层提高,便可达到理想高度,从而得到理想 体 积。最后,本文给出了堆叠沙拉塔的图文攻略。 【关键字】必胜客,沙拉塔
37
太阳系模型
《数学百科全书》1977-1986 吉夫诺夫
利用第谷近30年详细的天文观测资料,开
普勒发现行星运动三定律; 牛顿建立行星运动学方程从理论上证明开普 勒三定律; 亚当斯和勒威耶分别运用天文观测资料和牛 顿模型计算出海王星的轨道和位臵; 柏林天文台台长伽勒根据勒威耶的报告观测 到海王星.
K(m³ /s ² )
3.36×10^18 3.36×10^18 3.36×10^18
3.36×10^18
3.36×10^18 3.36×10^18 3.37×10^18 3.37×10^18 1.03×10^13 1.03×10^13
所有行星的半长轴的三次方与周期的平方的比值都相等, 月球、卫星的比值也相等。
3
3 模型假设
3.1 忽略各种材料的密度差异; 胡萝卜和黄桃不是一种东西,密度自然也不相同,但是为了便于 分析,将其视为同密度物质; 3.2 忽略材料之间的缝隙; 各种材料之间不可避免的会有很多 空洞,虽然可以用葡萄干、玉米粒等小颗粒来填补,但是仍然会 有不少空洞;这里将其忽略之; 3.3 认为沙拉塔的外形是圆台体; 因为盘子内部——即盘子边 缘所在平面到盘子底部这部分容积——无论何种码放方法,都 是填满内 容的,所以这部分体积对不同的方法贡献相同,故不予考虑; 圆台体的形状,用通俗的话说,就是圆锥体平行于底面切去上方 尖部后所剩形状。 3.4 认为萝卜条是横截面为正方形的立方柱; 横截面为正方形 的立方柱,举例来说,如 0.5 cm ×0.5 cm ×10cm 即是。
45
1997年,IBM"更深的蓝"超级电脑击败了国际象棋冠军卡斯帕 罗夫。 1998年,由Hasbro生产的第一个人工智能的宠物Furby开始在 美国出售;美国航天局(NASA)第一次有了完全由电脑程序 自动控制的飞行器。 2000年,Nomad机器人探索南极洲的偏远地区,采集气象观 测样本。 2004年,一个电脑程序可以比一个专业级真人飞行员更快地 学会操纵遥控直升机。 2007年,美国艾尔伯特大学的人工智能程序完全破解了西洋 跳棋游戏。 2011年,苹果的语音识别软件Siri可以让用户和iPhone对话; iRobot公司出售出了第600万个Roomba吸尘器机器人。 2012年,Google翻译做的翻译总量已经超过了所有人类翻译 者所做的总合。 2012年,通过10亿个连接,Google的人工智能神经网络可以 46 去识别一些常见的物体,像人脸和猫
w=u+,
30
min F(u)
u
F(u) u u w
2
2
dxdy
这是一个泛函极值点问题,也称为变分问题,它 可以转化为一个偏微分方程的初边值问题。 图像去噪的偏微分方程模型:
ut u xx u yy (u w) u 0 n u |t 0 w
15
六、在黄桃的外面,外层菠萝的上面堆上黄瓜。为下一 层菠萝做准备
16
七、黄瓜放好后在表层撒点玉米粒火腿肠之类的小东西以 使表面平一
就这样一层一层往上堆
19
初步的成果
20
21
22
23
24
25
26
这也能用数学? 定位系统(GPS)
行星
太阳
R3 =K T2
O F R
F
R:半长轴 T:公转周期
41
行星/卫星
水星 金星 地球 火星 木星 土星 天王星 海王星 月球 同步卫星
半长轴(km)
57 108 149 228 778 1426 2870 4498 0.3844 0.0424
周期(天)
87.97 225 365 687 4333 10759 30660 60148 27.3 1
ij n j |out _ wall 0 r ij n j |int erface s ij n j |int erface
34
固流模型(FSI)
vi ,tt ij , j ,
j 1 3 3
i 1,2,3 i, j 1,2,3
ij vi , j v j ,i v ,i v , j / 2,
1 问题提出
必胜客(PizzaHut)内有 28 元的自助沙拉,方法是向一只空碗内放入喜爱 的各色沙拉原料。据说, 国外必胜客的自助沙拉吃完是可以续添的,可 是国内似乎无此规定。当然,追求尽可能多的码放是 几乎每个消费者的 目标。本文目的就是讨论如何才能达到这一目标,并给出一种合理可行 的方法。 2 问题分析 追求码放质量的极大化,属于极值问题。 码放出来的沙拉塔形状近似是一个圆台体,在认为各材料密度近似的假 设下,只需使圆台体的体积 极大即可。
机械制造:几何学、控制论
地质勘测:信号(图象)处理、 文本信息处理:代数、几何、数据结构 地理信息系统:计算几何、优化算法
50
物理学与数学 生物学与数学 经济学与数学 政治学与数学 语言,文学与数学 军事国防与数学 心理学与数学 教育学与数学
42
人工智能
机器翻译、拼写纠错、汉字输入、文献查 询、手写体识别——用计算机处理人类语 言问题
计算机复杂的语音识别问题——
43
人工智能的时间线
1950年,图灵提出,经过编程的电子计算机可以像真人一 样回答问题。 1956年,在美国达特茅斯学院的一个暑期工作坊上,这个 领域的早期创始者们正式提出了"人工智能"这个词汇。 1958年 Allen Newell和Herbert Simon预测在十年内,电脑 可以击败国际象棋世界冠军,不过在现实中这整整花了四十 年。 1961年,电脑解决了大学一年级程度的微积分题目。 1965年,世界上第一个用于心理治疗的聊天机器人ELIZA, 尝试着和人进行对话。 1967年,STUDENT程序成功地解决了用文字描述的一道大 学程度的代数题目。
