汇交力系习题解答
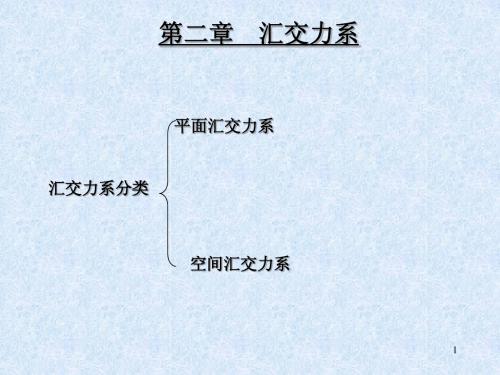
汇交力系
§ 2-2 平面汇交力系合成与平衡的解析法
例题2-2. 如图所示的平面刚架ABCD,自重不计.在
B点作用一水平力 P ,设P = 20kN.求支座A和D的约
束反力。
B P
2m
C
A
4m
D
8
§ 2-2 平面汇交力系合成与平衡的解析法
解: ①平面钢架ABCD为研究对象 P
②画受力图 ③列平衡方程 B RA C
5
§ 2-3 平面汇交力系合成与平衡的几何法
[例2-1] 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm 的障碍物。求:在中心作用的水平力F的大小和碾子对障 碍物的压力。 解: ①选碾子为研究对象 ②几何法
F Ptga
NB P cos a
r 2 (r h) 2 tga 0.577 r h
2m
A
D
4m
Fix = 0 P +RA cos = 0 Fiy = 0 RA sin +RD = 0
④求解方程
RD
RD
C P
RA = - 22.36 kN RD =10 kN
RA
9
§ 2-2
平面汇交力系合成与平衡的解析法 求SCD , RA
[例2-3] 已知 P=2kN
解: ①研究AB杆 ②画出受力图
2
§ 2-1
力在空间直角坐标轴上的投影
Rx X 1 X 2 X 4 X
二、合力投影定理
Ry Y1 Y2 Y3 Y4 Y
简写为:
Rx X
Ry Y
结论:平面汇交力系合力在任一轴上的投影,等于
各分力在同一轴上投影的代数和。
平面汇交力系习题知识分享
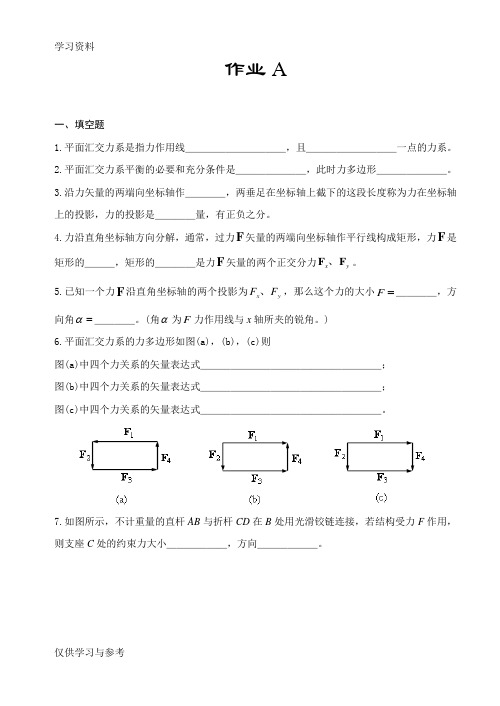
作业A一、填空题1.平面汇交力系是指力作用线__________,且_________一点的力系。
2.平面汇交力系平衡的必要和充分条件是_______,此时力多边形_______。
3.沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影是____量,有正负之分。
4.力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 是矩形的___,矩形的____是力F 矢量的两个正交分力y x F F 、。
5.已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)6.平面汇交力系的力多边形如图(a),(b),(c)则图(a)中四个力关系的矢量表达式__________________; 图(b)中四个力关系的矢量表达式__________________; 图(c)中四个力关系的矢量表达式__________________。
7.如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8.如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9.平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力和约束力)构成的力系属_____力系 (3)列出刚架的平衡方程(坐标如图)∑=0xF :_____________________; ∑=0yF:_____________________。
(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
平面汇交力系习题
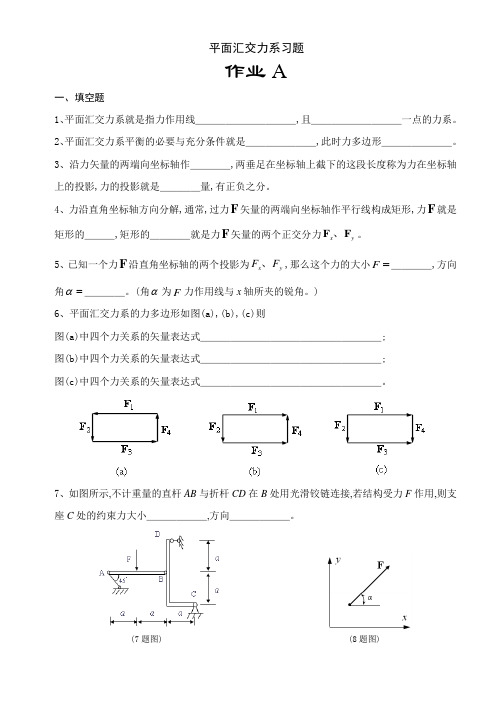
作业A一、填空题1、平面汇交力系就是指力作用线__________,且_________一点的力系。
2、平面汇交力系平衡的必要与充分条件就是_______,此时力多边形_______。
3、沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影就是____量,有正负之分。
4、力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 就是矩形的___,矩形的____就是力F 矢量的两个正交分力y x F F 、。
5、已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)6、平面汇交力系的力多边形如图(a),(b),(c)则图(a)中四个力关系的矢量表达式__________________;图(b)中四个力关系的矢量表达式__________________;图(c)中四个力关系的矢量表达式__________________。
7、如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8、如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9、平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力与约束力)构成的力系属_____力系(3)列出刚架的平衡方程(坐标如图)∑=0x F:_____________________; ∑=0yF :_____________________。
(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
汇交力系例题
C
Y P TBD cos cos TBC cos cos 0
Z RA TBD sin TBC sin 0
联立解得
TBC 735 N
TBD 1094 N
RA 1500 N
p.4
例题
例题
例4.已知四根绳索AB、BC、BD、DE相互联接如图所示, DB保持水平,DE和BC分别与水平和铅垂线的夹角均
A
45o
0.8m
CB
0.4m
y
SC
A
45o C
RA
B x
E
P
EB BC 0.4m tg EB 0.4 1
AB 1.2 3 (2) 列出平衡方程;
X 0, RA cos Sc cos 45 0
Y 0,RA sin Sc sin 45 P 0
(3) 求未知力;
P
2
Sc sin 45 cos45tg
C EA
D
B -
y TDB D + x
y
TBE
TBC
B
TBD
x
P
TDA
P
SAB
解: (1) 研究D点,画受力图;
(2) 列出平衡方程并求解;
X 0,TDB cos( ) TDA cos( ) 0
Y 0,TDB sin( ) TDA sin( ) P 0
TDB
NA
O
O’与 O为矩形OAO’B的两个顶点,
O’ B
力的作用线既通过O’点也通过O点。
NB
由几何关系得
P A
90 2
NA
O
OA Lsin
p.6
例题
例题
例6. 铰接四连杆机构CABD的CD边固定。在铰链A上作用一 力Q,BAQ=45。在铰链B上作用一力R,ABR=30,
平面汇交力系答案

平面汇交力系答案【篇一:工程力学答案】1.作用在刚体上两个不在一直线上的汇交力f1和f2 ,可求得其合力r = f1 + f2 ,则其合力的大小 ( b;d )(a) 必有r = f1 + f2 ; (b) 不可能有r = f1 + f2 ; (c) 必有r f1、r f2 ;(d) 可能有r f1、r f2。
2. 以下四个图所示的力三角形,哪一个图表示力矢r是f1和f2两力矢的合力矢量 ( b )r f1 (a)f2r f1 (b)f2r f1 (c)f2r f1 (d)f23. 以下四个图所示的是一由f1 、f2 、f3 三个力所组成的平面汇交力系的力三角形,哪一个图表示此汇交力系是平衡的( a )f3 f1 (a)f2f3 f1 (b)f2f3 f1 (c)f2f3 f1 (d)f24.以下四种说法,哪一种是正确的( a) (a)力在平面内的投影是个矢量;(b)力对轴之矩等于力对任一点之矩的矢量在该轴上的投影;(c)力在平面内的投影是个代数量;(d)力偶对任一点o 之矩与该点在空间的位置有关。
5. 以下四种说法,哪些是正确的?( b ) (a) 力对点之矩的值与矩心的位置无关。
(b) 力偶对某点之矩的值与该点的位置无关。
(c) 力偶对物体的作用可以用一个力的作用来与它等效替换。
(d) 一个力偶不能与一个力相互平衡。
四、作图题(每图15分,共60分)画出下图中每个标注字符的物体的受力图和整体受力图。
题中未画重力的各物体的自重不计。
所有接触处均为光滑接触。
1213、平面力偶系合成的结果为一合力偶,此合力偶与各分力偶的代数和相等。
(√ ) 14、一个力和一个力偶可以合成一个力,反之,一个力也可分解为一个力和一个力偶。
(√ ) 15、力的平移定理只适用于刚体,而且也只能在同一个刚体上应用。
(√ )16、平面任意力系向作用面内任一点(简化中心)简化后,所得到的作用于简化中心的那一个力,一般说来不是原力系的合力。
汇交力系习题解答

第二章习题解答2—1如图所示,固定在墙壁上的圆环首三条绳索的拉力作用,力F1沿水平方向,力F3沿铅直方向,力F2与水平线成40度角。
三力的大小分别为F1=2000N,F2=2500N,F3=1500N.求三力的合力。
解:图解法解题时,首先要确定比例尺,即每单位长度代表多大的力,这里我们用单位代表500N,三力在圆环的圆心处相交。
如图(b),力系的力多边形如图(c)。
在图上量出OC的长度和L和与水平之间的夹角有。
Fr=L×500=5000Nφ=38°26'由(c)图的几何关系可见OB=BC,∠BOC=∠BCO=(40°-36°52')=1°34'故合力F r的大小约为Fr=2F2cos1°34'=2×2500×0.99963=4998N与水平方向之间的夹角为φ=38°26'例:用解析法求圆环受三个力的合力。
解:如图建立坐标,则NF F F F NF F F F y R y x xR 310764279.025********cos 391576604.025********cos 2321=⨯+=︒+===⨯+=︒+==∑∑ 合力的大小NF F F yR xR r 5000310739152222=+=+=合力与X 轴之间的夹角为 '283850003915cos arccos1︒===-R Rx F F α2—2 物体重P=20 kN ,用绳子挂在子架的滑轮B 上,绳子的另一端杰在绞车D 上,如图所示。
转动绞车,物体便能升起。
,A 、B 、C 处均为光滑铰链连接。
钢丝绳、杆和滑轮的自重不计,并忽略摩擦和滑轮的大小。
试求平衡时杆AB 和BC 所受得力。
解:该题与例题基本相同1、确定研究对象。
系统中AB,BC 为二力杆,设AB 受拉力,BC 受压力,以各力汇交的滑轮为研究对象。
2、画滑轮的受力图如图(C )建立坐标,列平衡方程(坐标轴要尽量和未知的约束力的方向一致或垂直)030cos 60cos 0030cos 60cos ,0=+︒+︒-==︒-︒+=∑∑P P F F F P F F BC y BC AB x4、解方程,得kN F kNF BC BA 64.747.54==1、 答2—3 火箭沿与水平面成θ=25°角的方向作匀速直线运动,如图所示。
平面汇交力系习题知识分享

作业A一、填空题1.平面汇交力系是指力作用线__________,且_________一点的力系。
2.平面汇交力系平衡的必要和充分条件是_______,此时力多边形_______。
3.沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影是____量,有正负之分。
4.力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 是矩形的___,矩形的____是力F 矢量的两个正交分力y x F F 、。
5.已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)6.平面汇交力系的力多边形如图(a),(b),(c)则图(a)中四个力关系的矢量表达式__________________; 图(b)中四个力关系的矢量表达式__________________; 图(c)中四个力关系的矢量表达式__________________。
7.如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8.如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9.平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力和约束力)构成的力系属_____力系 (3)列出刚架的平衡方程(坐标如图)∑=0xF :_____________________; ∑=0yF:_____________________。
(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
工程力学三力汇交原理经典例题

工程力学三力汇交原理经典例题1、下列估测最接近实际情况的是()[单选题]A.一个鸡蛋的质量约为500gB.教室里课桌的高度约为8m(正确答案)C.一支普通牙刷的长度约为40cmD.做一遍眼保健操的时间约为20min2、人耳听不到次声波,是因为响度太小[判断题] *对错(正确答案)答案解析:次声波和超声波的频率超过了人耳的听觉范围3、90.某工厂要制造一种特殊用途的钢铝罐,钢罐内表面要压接一层25mm厚的铝膜,一时难住了焊接和锻压专家,后经技术人员的联合攻关解决了这一难题:他们先把铝膜紧贴到钢罐内表面,再往钢罐内灌水,插入冷冻管使水结冰,然后铝膜与钢罐就压接在一起了,其原因是()[单选题] *A.铝膜与钢罐间的水把它们冻牢了B.水结冰时膨胀产生的巨大压力把它们压牢了(正确答案)C.结冰时铝膜与钢罐间的冰把它们粘牢了D.水结冰时放出的热量把它们焊牢了4、23.口罩成为常态防疫“神器”,戴眼镜的人们常因口罩佩戴出现镜片模糊的情况,这是液化现象。
下列实例中与它物态变化相同的是()[单选题] *A.初春,冰雪消融B.夏天,清晨草叶或树叶上形成露珠(正确答案)C.深秋,屋顶的瓦上结了一层霜D.冬天,室外冰冻的衣服变干了5、仅受地磁场作用,可自由转动的小磁针静止时,N极指向地理北极附近[判断题] *对(正确答案)错答案解析:受地磁场作用,小磁针N极指北方,S极指南方6、3.空间站以恒定的速率绕地球转动:因为空间站速度大小不变,所以加速度为零.[判断题] *对错(正确答案)7、在图65的四种情境中,人对物体做功的是()[单选题]A.提着桶在水平地面上匀速前进B.举着杠铃保持杠铃静止C.用力搬石头但没有搬动D.推着小车前进(正确答案)8、4.电火花计时器接学生电源直流输出端.[判断题] *对错(正确答案)9、家庭电路中与灯泡串联的开关可以接在火线上,也可以接在零线上[判断题] *对错(正确答案)答案解析:开关接火线10、43.在试管中放少量碘,塞紧盖子放入热水中,当固态碘变为紫色的碘蒸气并充满试管后,将试管从热水中取出,放入凉水中,碘蒸气又会变为固态碘附在试管内壁上,关于碘的物态变化过程,下列说法正确的是()[单选题] *A.先升华后凝华(正确答案)B.先汽化后凝固C.先升华后凝固D.先汽化后凝华11、探究物体受到的浮力与液体密度的关系时,需要控制物体体积相同[判断题] *对错(正确答案)答案解析:需要控制物体排开液体的体积相同12、探究物体所受重力大小与物体的体积的关系时,物体密度是需要控制的变量[判断题] *对错(正确答案)答案解析:需要控制质量相同13、2.两物体的速度分别是v1=2 m/s,v2=-3 m/s,则它们的大小关系为v1>v [判断题] *对错(正确答案)14、水的温度没有达到沸点时,水是不能变为水蒸气的[判断题] *对错(正确答案)答案解析:水在任何温度下都可以蒸发变成水蒸气15、1.将石块竖直上抛至最高点时v=0,是平衡状态.[判断题] *对错(正确答案)16、我们知道X射线是一种高频率的电磁波,所以X射线的波长短[判断题] *对(正确答案)错答案解析:波速等于波长乘以频率,真空中波速一定,频率高,波长短17、【多选题】下列有尖物体内能的说法正确的是( AB)A.橡皮筋被拉伸时,分子间势能增加(正确答案)B.1kg0℃的水内能比l kg0℃的冰内能大(正确答案)C.静止的物体其分子的平均动能为零D.物体被举得越高,其分子势能越大18、2.在探索微小粒子的历程中,科学家们用一系列高能物理实验证实了大量微小粒子的存在,下列微粒按空间尺度从大到小的顺序排列的是()[单选题] *A.质子、夸克、原子核、电子B.原子、原子核、电子、质子C.原子、原子核、质子、电子(正确答案)D.夸克、质子、原子核、原子19、用天平测小石块质量的实验中,有如下实验计划,正确的操作顺序是()①将游码移至标尺左端的“0”刻度线处;②将托盘天平放置在水平工作台面上;③在天平的左盘放入小石块;④调节平衡螺母,使天平横梁平衡;⑤用镊子在右盘中加减砝码,移动游码,使天平平衡;⑥正确读出砝码和游码的示数. [单选题] *A. ①②③④⑤⑥B. ②①④③⑤⑥(正确答案)C. ②③①④⑤⑥D. ③②①④⑤⑥20、51.下列不是光源的是()[单选题] *A.萤火虫B.太阳C.月亮(正确答案)D.燃烧的火把21、27.下列物态变化属于液化的是()[单选题] *A.夏天,挂在衣架上的湿衣服晾干了B.北方的冬天,水蒸气在树上形成了雾凇C.春天到来,江河中的冰化成水D.初秋的清晨,树叶上的露珠(正确答案)22、小刚是一名初中生,他从一楼跑到三楼的过程中,克服自己重力所做的功最接近下面哪个值()[单选题]A.3JB.30JC.300JD.3000J(正确答案)23、36.城市环保建设——洒水车给街道洒水是环保工人的必修内容,是净化空气的主要举措。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题解答2—1如图所示,固定在墙壁上的圆环首三条绳索的拉力作用,力F1沿水平方向,力F3沿铅直方向,力F2与水平线成40度角。
三力的大小分别为F1=2000N,F2=2500N,F3=1500N.求三力的合力。
解:图解法解题时,首先要确定比例尺,即每单位长度代表多大的力,这里我们用单位代表500N,三力在圆环的圆心处相交。
如图(b),力系的力多边形如图(c)。
在图上量出OC的长度和L和与水平之间的夹角有。
Fr=L×500=5000Nφ=38°26'由(c)图的几何关系可见OB=BC,∠BOC=∠BCO=(40°-36°52')=1°34'故合力F r的大小约为Fr=2F2cos1°34'=2×2500×0.99963=4998N与水平方向之间的夹角为φ=38°26'例:用解析法求圆环受三个力的合力。
解:如图建立坐标,则NF F F F NF F F F y R y x xR 310764279.025********cos 391576604.025********cos 2321=⨯+=︒+===⨯+=︒+==∑合力的大小NF F F yR xR r 5000310739152222=+=+=合力与X 轴之间的夹角为 '283850003915cos arccos1︒===-R Rx F F α2—2 物体重P=20 kN ,用绳子挂在子架的滑轮B 上,绳子的另一端杰在绞车D 上,如图所示。
转动绞车,物体便能升起。
,A 、B 、C 处均为光滑铰链连接。
钢丝绳、杆和滑轮的自重不计,并忽略摩擦和滑轮的大小。
试求平衡时杆AB 和BC 所受得力。
解:该题与例题基本相同1、确定研究对象。
系统中AB,BC 为二力杆,设AB 受拉力,BC受压力,以各力汇交的滑轮为研究对象。
2、画滑轮的受力图如图(C )建立坐标,列平衡方程(坐标轴要尽量和未知的约束力的方向一致或垂直)030cos 60cos 0030cos 60cos ,0=+︒+︒-==︒-︒+=∑∑P P F F F P F F BC y BC AB x4、解方程,得kN F kNF BC BA 64.747.54==1、 答2—3 火箭沿与水平面成θ=25°角的方向作匀速直线运动,如图所示。
火箭的推力F 1=100 kN 与运动方向成θ=5°角。
如火箭重P=200 kN ,求空气动力F 2和他与飞行方向之间的夹角γ。
解:火箭匀速直线运动,受平衡力作用,即在重力P ,推力F 1和空气动力F 2的共同作用下平衡。
则三力必汇交与一点C 。
1、 选火箭为研究对象。
2、 作受力图,建立坐标。
如图。
3、 列平衡方程0cos )sin(,00sin )cos(,02121=-++==-+=∑∑P F F FF F Fy x φθβφθβ4、 解上述方程。
方程移项整理得: )2()sin(cos )1()cos(sin 1212 θβφθβφ+-=+=F P F F F将上述(1)菏(2)分别平方后相加,整理有: kN F 173)30sin 1020()30cos 100(222=︒-+︒= 由(1)和(2)之比有'582930sin 102030cos 10︒=︒-︒=φφtg故 '58942590︒=︒-︒+=φγ此题也可以用图解法,如图,用单位长度代表100KN,平衡,力多边形自行封闭。
由图可见,其力多边形为一直角三角形。
所以有空气动力F 2的大小为173 kN,与运动方向之间的夹角为95度。
2—4 在图示钢架的点B 作用一水平力F ,钢架重量不计。
求支座A 和D 约束力F A 和F D .。
解:以钢架为研究对象,受力如图(b )和(c )1、 用图解法,力多边形如图(d )可得:F F F F A D 25,2== 力的方向如地图所示。
2、 解析法:由(c )图可见,三力汇交与(c )点,故图建立坐标有:sin ,00cos ,0=+==+=∑∑ααA D y A x F F F F F F由几何关系可知: 51sin ,52cos ==αα 所以有 F F F F A D 25,2-== FA 为负,说明其实际方向和假设方向相反。
2—5 如图所示,输电线ABC 架在两电线杆之间,形成一下垂曲线,下垂距离CD=f=1m,两电线杆间距离AB=40 m 。
癫痫ABC 段重P=400N,可近似认为沿AB 直线均匀分布。
求电线的中点和两端的拉力。
解:选取BC 段位研究对象。
AC 与BC 对称,BC 断受力有Tb 、Tc 及P/2,此三力构成一平面力系。
它可以用图解法,也可以用几何法,还可以用解析法。
用解析法,如图建立坐标,列平衡方程。
02sin ,00cos ,0=-==-=∑∑P F FF F FB yC B x ϑϑ 又:05.1011101sin ,05.101011010cos 222=+==+=αα 得: NF NF C B 20002010== 答:对称FA=FB 为2010N ,FC 为2000N.。
2—6、图示为一拔桩机,在桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的另一点B系另一绳BE,将它的另一端固定在点E 。
然后,在绳的点D 用力向下拉,并使绳的BD 段水平,AB 段铅直。
DE 段与水平线、CB 段与铅直线间成等角θ=0.1 rad (当θ很小时,tan θ=θ)如向下的拉力F=800N ,求绳AB 作用与桩上的拉力。
解:选B 、C 两点为研究对象,受力如图(C )和(b ),建立坐标。
对B 点列平衡方程。
(B 点要求的是FA ,FC 是未知的约束力如此建立坐标,就不必求FC ,仅列出X 轴上的平衡方程即可。
))1(0cos sin 0 =-=∑θθD A x F F F 列B 点的平衡方程有: )2(0cos sin 0' =-=∑θθF F F D Y又B 、D 之间为钢化的绳子FD 与FD ’为一对作用与反作用力即:)3(' D D F F =代入数据解得:kN Fctg ctg F F D A 8010810800422=⨯=⨯===θθ绳对桩的拉力与F 方向相反,大小相等。
2—7图示液压夹紧机构中,D 为固定铰链,B ,C ,E 为活动铰链。
已知力F ,机构平衡时角度如图所示,各构件自重不计,各接触处光滑。
求此时工件H 所受的压紧力。
1、 对B 列平衡方程0sin 0=-=∑F F FBC Y θ (1) 2、 对C 列平衡方程 0sin sin cos 00cos sin cos 0=--==--=∑∑θθθθθθDC EC BC X DC BC EC Y F F F FF F F F 3、 对E 列平衡方程 0cos 0=-=∑θEC H Y F F F又:CE EC CBBC F F F F == 解上述方程得:θ2sin 2F F H =2—8铰链四杆机构CABD 的CD 边固定,在铰链A,B 处有力F 1,F 2作用,如图所示。
该铰链机构在图示位置平衡,杆重略去不计。
求力F 1与F 2的关系。
解:选A ,B 。
两点为研究对象。
受力如图,建立坐标。
对A 点列平衡方程有0=∑X F015cos 30cos 1=︒-︒AB F F对B 点列平衡方程有0=∑X F060cos 30cos 2'=︒-︒F F AB又: 'AB AB F F = 解得:2396593.030cos 15cos 30cos 15cos 60cos 30cos '21=︒︒=︒︒=︒︒AB AB F F F F 644.023396593.021==F F 2-9如图所示,刚架上作用力F 。
分别计算力F 对点A 和B 的力矩。
解:(1)求力到点的距离d 来计算其力矩。
如图(b )F 到A 点的距离θcos b AC d A ==θcos )(Fb Fd F M A A ==F 到B 点的距离d B =BD=AE-AC=asin θ-bcos θM B (F )=Fd B =F (asin θ-bcos θ)(2)用合力矩定理计算。
此时将力F 分解为F x 和F yθθsin cos F F F F Y x -==力作用点对距心A 的坐标F A (0,b )。
M A (F )=xF y -yF x =-Fbcos θ力的作用点对距心B 的坐标F B (-a,b))cos sin (cos )sin ()(θθθθb a F bF F a yF xF F M X Y B -=---=-=两种方法结论相同。
2-10在图示结构中,各构件的自重略去不计。
在构件AB 上作用一力偶矩为M 的力偶,求支座A 和C 的约束力。
解:如图B ,BC 杆为二里杆,设受力如图,则。
F C =F BAB 杆受平面力偶系作用平衡。
F A 和F C ’组成力偶与M 平衡。
列力偶平衡方程有:2200a M AB M F M AB F M A A ===-=∑ 答:FA 和FB 大小相等,方向如图所示。
2-11已知梁AB 上作用一力偶,力偶矩为M ,梁长为L,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力。
解:选AB 梁为研究对象。
因为力偶是滑动矢量,所以(a )、(b )两情况下力偶的作用相同。
AB 梁受平面力偶作用下平衡,F A 和F B 组成力偶,如图(d )。
列平衡方程00=-=∑M L F M AL M F F B A == 方向如(d )图所示(c )图情况下,B 点作用力的方向如图(e )所示,此时的力偶臂d=ABcos θ。
列(c )的平衡方程为:00=-=∑M d F M Aθcos L M d M F F B A === 方向如(e )图所示2—12两齿轮的半径分别为r1、r2,作用于轮Ⅰ上的主动力偶的力偶矩为M1,齿轮的压力角为θ,不计两齿轮的重量。
求使二轮维持匀速转动时齿轮Ⅱ的主力偶之矩M2及轴承O1,O2的约束力的大小和方向。
解:二齿轮的压力角为θ,也就是说两齿轮的作用力沿mn 。
两齿轮匀速转动,则受平衡力偶作用。
设两轮的相互作用力为F ,F 与轴心约束力组成力偶。
以齿轮为研究对象对Ⅰ轮列平衡方程∑=0M0cos 11=-θFr Mθcos 11r M F = 所以,O 1,O 2的约束力大小为θcos 11r M ,方向沿mn ,齿轮Ⅰ受O1轴的力向下,O 1轴受齿轮的力向上。
O 2轴受齿轮的力向下。
对Ⅱ轮列平衡方程1122222cos 0cos 0M r r Fr M Fr M M ===-=∑θθ2—13在图示机构中,曲柄OA 上作用一力偶,其矩为M ;另在滑块D 上作用水平力F 。
