平面简单力系习题
平面任意力系习题及答案

平面任意力系习题及答案平面任意力系习题及答案力学是物理学的一个重要分支,研究物体受力的作用和运动规律。
平面任意力系是力学中的一个重要概念,它涉及到多个力在平面内的作用和平衡问题。
在本文中,我们将探讨一些关于平面任意力系的习题,并提供相应的答案。
1. 问题描述:一个物体受到三个力的作用,力的大小和方向分别为F1=10N,θ1=30°;F2=15N,θ2=120°;F3=8N,θ3=210°。
求物体所受合力的大小和方向。
解答:首先,我们需要将力的分量计算出来。
根据三角函数的定义,我们可以得到F1x=F1*cosθ1=10*cos30°=8.66N,F1y=F1*sinθ1=10*sin30°=5N;F2x=F2*cosθ2=15*cos120°=-7.5N,F2y=F2*sinθ2=15*sin120°=12.99N;F3x=F3*cosθ3=8*cos210°=-6.93N,F3y=F3*sinθ3=8*sin210°=-4N。
然后,我们将分量相加,得到合力的分量。
Fx=F1x+F2x+F3x=8.66N-7.5N-6.93N=-5.77N,Fy=F1y+F2y+F3y=5N+12.99N-4N=13.99N。
最后,我们可以利用勾股定理计算合力的大小和方向。
合力的大小为F=sqrt(Fx^2+Fy^2)=sqrt((-5.77N)^2+(13.99N)^2)=15.16N,合力的方向为θ=arctan(Fy/Fx)=arctan(13.99N/-5.77N)=-68.6°。
因此,物体所受合力的大小为15.16N,方向为-68.6°。
2. 问题描述:一个物体受到四个力的作用,力的大小和方向分别为F1=8N,θ1=30°;F2=12N,θ2=120°;F3=10N,θ3=210°;F4=6N,θ4=300°。
平面任意力系习题

A
a
D
E
F
a
4m
B
1E
B
C
A
F
G
D
ll
6
6
a
a
题 3-28图
题3-29图
3-30.构架由杆 ACE 、DEF 、BCD 铰接而成的, 所受的力及几何尺寸如图所示,各杆的
自重不计,试求杆 BCD 在铰链 C 处给杆 ACE 的力。
D
A b
E a
C a
B
b
b
题 3-30图
3-31.如图所示的构架,起吊重物的重为 滑轮和杆的自重,几何尺寸如图,试求支座
B1
2
A
α
题 3-37图
4F 4F
F
3
a
1
F
2
a
a
a
a
a
题 3-36 图
()
3-9.桁架中的杆是二力杆。 ( )
3-10.静滑动摩擦力 F 应是一个范围值。 ( )
2. 填空题(把正确的答案写在横线上)
3-11.平面平行力系的平衡方程
n
n
M A (Fi ) 0
M B(Fi ) 0 ,
i1
i1
其限制条件
。
3-12. 题 3-12 图平面力系,已知: F1=F 2=F 3=F 4=F , M=Fa , a 为三角形边长,如以 A
C
A
l /2
l /2
l/6 B
题3-26图
3-27.均质杆 AB 重为 P1,一端用铰链 A
支与墙面上,并用滚动支座 C 维持平衡,另一端又与重为 P2 的均质杆 BD 铰接,杆 BD 靠
与光滑的台阶 E 上,且倾角为 α ,设 AC 2 AB , BE 2 BD 。试求 A 、 C 和 E 三处的约
3 平面任意力系习题一
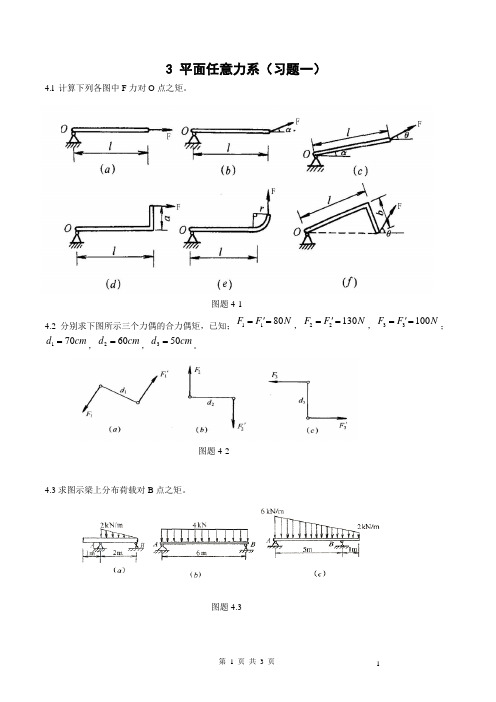
3 平面任意力系(习题一)4.l 计算下列各图中F 力对O 点之矩。
图题4-14.2 分别求下图所示三个力偶的合力偶矩,已知;1180F F N '==,22130F F N '==,33100F F N '==;170d cm =,260d cm =,350d cm =。
图题4-24.3求图示梁上分布荷载对B 点之矩。
图题4.34.4各梁受荷载情况如图题2.3所示,试求(1)各力偶分别对A 、B 点的矩。
(2)各力偶中二个力在x 、y 轴上的投影。
图题4.44.5 求图题4.5示各梁的支座反力图题4.5 图题4.64.6 如图题4.6所示,已知皮带轮上作用力偶矩80m N m =⋅,皮带轮的半径0.2d m =,皮带紧拉边力N F T 5001=,求平衡时皮带松边的拉力2T F 。
4.7 如图所示,四个力作用于O 点,设F 1=50N ,F 2=30N ,F 3=60N ,F 4=100N 。
试分别用几何法和解析法求其合力。
题4.7 (a)图 题4.7 (b)图4.8 拖动汽车需要用力F=5kN ,若现在改用两个力F1和F2,已知F1与汽车前进方向的夹角20=α,分别用几何法和解析法求解:(1)若已知另外一个作用力F2与汽车前进方向的夹角 30=β,试确定F1和F2的大小; (2)欲使F2为最小,试确定夹角β及力F1、F2的大小。
图题4.84.9 支架由杆AB 、AC 构成,A 、B 、C 三处都是铰链约束。
在A 点作用有铅垂力F ,用两种方法求在图示两种情况下杆AB 、AC 所受的力,并说明所受的力是拉还是压。
题4.9图 题4.10图4.10 简易起重机如图所示,重物W=100N ,设各杆、滑轮、钢丝绳自重不计,摩擦不计,A 、B 、C 三处均为铰链连接。
求杆件AB 、AC 受到的力。
平面任意力系习题答案

平面任意力系习题答案平面任意力系是指作用在物体上的力不满足平面力偶系或平面共面力系的条件,即力的作用线不在同一平面上,也不互相平行。
解决这类问题通常需要应用静力学的基本原理,如力的平衡条件、力矩平衡等。
习题1:已知一平面任意力系作用在刚体上,力F1=50N,方向为水平向右;力F2=30N,方向为竖直向上;力F3=40N,方向为与水平面成30度角斜向上。
求力系的合力。
答案:首先,将力F3分解为水平分量和竖直分量:- 水平分量:F3x = F3 * cos(30°) = 40 * (√3/2) = 20√3 N- 竖直分量:F3y = F3 * sin(30°) = 40 * (1/2) = 20 N然后,计算合力的水平分量和竖直分量:- 水平合力:Fx = F1 + F3x = 50 + 20√3 N- 竖直合力:Fy = F2 + F3y = 30 + 20 N最后,计算合力的大小和方向:- 合力大小:F = √(Fx^2 + Fy^2) = √((50 + 20√3)^2 + (30 + 20)^2) N- 方向:与水平面夹角θ满足tan(θ) = Fy / Fx习题2:一个平面任意力系作用在刚体上,已知力F1=60N,作用点A;力F2=40N,作用点B;力F3=50N,作用点C。
A、B、C三点不共线。
求力系的合力矩。
答案:首先,计算各力对任意一点(如A点)的力矩:- 力矩M1 = 0(因为力F1作用在A点,力矩为0)- 力矩M2 = F2 * (B到A的距离)- 力矩M3 = F3 * (C到A的距离)然后,计算合力矩:- 合力矩M = M1 + M2 + M3由于题目没有给出具体的距离,我们无法计算出具体的数值。
但是,上述步骤提供了计算合力矩的方法。
习题3:已知一平面任意力系作用在刚体上,力F1和F2的合力为100N,方向与F1相反,求F1和F2的大小。
答案:设F1的大小为xN,F2的大小为yN。
第二章平面力系习题解答

习 题2-1 试计算图2-55中力F 对点O 之矩。
图2-55(a) 0)(=F O M (b) Fl M O =)(F (c) Fb M O -=)(F (d) θsin )(Fl M O =F(e) βsin )(22b l F M O +=F(f) )()(r l F M O +=F2-2 一大小为50N 的力作用在圆盘边缘的C 点上,如图2-56所示。
试分别计算此力对O 、A 、B 三点之矩。
图2-56mN 25.6m m N 625030sin 2505060cos 30sin 5060sin 30cos 50⋅=⋅=︒⨯⨯=︒⨯︒-︒⨯︒=R R M Om N 075.17825.1025.630cos 50⋅=+=⨯︒+=R M M O A m N 485.9235.325.615sin 50⋅=+=⨯︒+=R M M O B2-3 一大小为80N 的力作用于板手柄端,如图2-57所示。
(1)当︒=75θ时,求此力对螺钉中心之矩;(2)当θ为何值时,该力矩为最小值;(3) 当θ为何值时,该力矩为最大值。
图2-57(1)当︒=75θ时,(用两次简化方法)m N 21.20mm N 485.59.202128945.193183087.21sin 8025075sin 80⋅=⋅=+=⨯︒⨯+⨯︒⨯=O M (2) 力过螺钉中心 由正弦定理)13.53sin(250sin 30θθ-︒= 08955.03/2513.53cos 13.53sin tan =+︒︒=θ ︒=117.5θ(3) ︒=︒+︒=117.95117.590θ2-4 如图2-58所示,已知N 200N,300N,200N,150321='====F F F F F 。
试求力系向O 点的简化结果,并求力系合力的大小及其与原点O 的距离d 。
图2-58kN 64.1615110345cos kN 64.4375210145cos 321R321R-=+-︒-=∑='-=--︒-=∑='F F F F F F F F F F y y x x主矢RF '的大小 kN 54.466)()(22R =∑+∑='y x F F F 而 3693.064.43764.161tan RR ==''=x y F F α ︒=27.20α m N 44.21162.0511.045cos )(31⋅=-⨯+⨯︒=∑=F F M M O O Fmm 96.45m 04596.054.466/44.21/R==='=F M d O2-5 平面力系中各力大小分别为kN 60kN,260321===F F F ,作用位置如图2-59所示,图中尺寸的单位为mm 。
平面力系平衡问题课堂练习题

例2-19 已知: PE 10kN, PG 7kN, 各杆长度均为1m;
求: 1,2,3杆受力.
解: 取整体,求支座约束力.
Fx 0
FAx 0
M B 0 2PE PG 3FAy 0
Fy 0 FAy FBy PE PG 0
FAy 9kN
FBy 8kN
38
用截面法,取桁架左边部分.
2m
2m
解方程可得 F4 10kN
节点C在y方向的平衡方程可用来校核
C
F1
F4
F’3
当计算出杆的受力的代数值为正时,表明 该杆受力的方向符合假设的方向,即该杆受拉。 反之,当计算出该杆受力的代数值为负时,表 明该杆受压。
34
平面桁架如图所示。设两主动力大小F =10 kN , 作用在节点A和节点B上,a =1.5 m,h =3 m。求1, 2,3和4各杆受的内力。
19
例2- 已知:P , a ,各杆重不计; 24求:B 铰处约束力.
解:取整体,画受力图
MC 0 FBy 2a 0
FBy 0
取DEF杆,画受力图
M D 0 FE sin 45 a F 2a 0
Fx 0 FE cos 45 FD' x 0 ME 0 FDy 'a F 2a 0
取AB杆(不含销钉B),画受力图.
Fx 0
FAx
1 2
q
3a
FABx
0
FAx qa
Fy 0 FAy FABy 0
MA 0
FAy P qa
1 M A 2 q 3a a FABx 3a FABy a 0
M A (P qa)a
26
组合梁AC和CE用铰链C相连,A端为固定端,E端为活动 铰链支座。受力如图所示。已知: l =8 m,F=5 kN,均布载 荷集度q=2.5 kN/m,力偶矩的大小M= 5 kN•m,试求固端A, 铰链C和支座E的约束力。
工程力学-平面任意力系习题
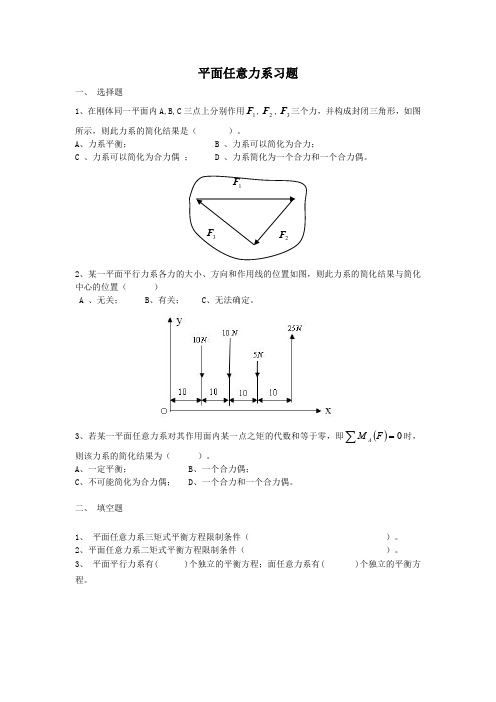
平面任意力系习题
一、选择题
1、在刚体同一平面内A,B,C 三点上分别作用1F ,2F ,3F 三个力,并构成封闭三角形,如图所示,则此力系的简化结果是(
)。
A、力系平衡;
B 、力系可以简化为合力;
C 、力系可以简化为合力偶;
D 、力系简化为一个合力和一个合力偶。
1
F 2
F 3F 2、某一平面平行力系各力的大小、方向和作用线的位置如图,则此力系的简化结果与简化中心的位置()
A 、无关;B、有关;C、无法确定。
3、若某一平面任意力系对其作用面内某一点之矩的代数和等于零,即
()∑=0F M A 时,则该力系的简化结果为(
)。
A、一定平衡;
B、一个合力偶;
C、不可能简化为合力偶;
D、一个合力和一个合力偶。
二、填空题
1、平面任意力系三矩式平衡方程限制条件(
)。
2、平面任意力系二矩式平衡方程限制条件(
)。
3、平面平行力系有(
)个独立的平衡方程;面任意力系有()个独立的平衡方
程。
三、计算题
1、已知:F、M、q、L,各杆自重不计,试求A、C处约束反力。
2、求图示组合梁支座的约束反力。
3-习题平面任意力系

FAx A
FAy y
F
B
C
FB
解得
NB 2.5KN () FAX 1.4KN () FAY 1.1KN ()
x
(b)
4KN/m
5KN
B
C
3
4
A
解:
FAX 0 FAY 12 5 0
M ( A) M A 121.5 5 3 0
FG
50 510 2
50(kN)
② 再研究梁CD 由 MC 0
FD 6 FG' 1 0
FD
50 6
8.33(kN)
③
再
研
究
整
体
MA 0, FB 3 FD 12 P10Q6 0 FB 100(kN) Y 0, FAy FB FD Q P 0 FAy 48.33(kN)
M (O) FBA cos l1 NCl2 = 0
NC 3562N
杠杆作用在工件上的夹紧力为3562N
3 10曲柄滑道机构如图所示,已知M 600N.m,OA 0.6m,BC 0.75m,
机构在图示位置处于平衡。滑道和连杆位置角 30, 60,不计摩擦。
铅垂线的夹角 10,各构件自重和各处摩擦都不计。试求杠杆作用于
工件上的夹紧力。
解:作用在活塞上的力 F PS P (D2 d 2 ) 120
4 F 0 120
FAB sin10
以COB杆为研究对象
3 7如图所示,组合梁两杆由AC和DC铰接所构成,起重机置于梁上。 已知起重机重P1 50kN,其重心在铅垂线EC上,起重荷载P2 10kN,今 不计梁重,梁结构尺寸如图,试求当起重机的外伸臂和梁AB在同一铅垂 面内时,支座A、B、D的约束力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 平面简单力系习题
1.是非题(对画√,错画×)
2-1.汇交力系平衡的几何条件是力的多边形自行封闭。
( )
2-2.两个力F 1、F 2在同一轴上的投影相等,则这两个力大小一定相等。
( ) 2-3.力F 在某一轴上的投影等于零,则该力一定为零。
( )
2-4.合力总是大于分力。
( )
2-5.平面汇交力系求合力时,作图的力序可以不同,其合力不变。
( ) 2-6.力偶使刚体只能转动,而不能移动。
( )
2-7.任意两个力都可以合成为一个合力。
( )
2-8.力偶中的两个力在其作用面内任意直线段上的投影的代数和恒为零。
( ) 2-9.平面力偶矩的大小与矩心点的位置有关。
( )
2-10.力沿其作用线任意滑动不改变它对同一点的矩。
( )
2.填空题(把正确的答案写在横线上)
2-11.作用在刚体上的三个力使刚体处于平衡状态,其中两个力汇交于一点,则第三个力的作用线 。
2-12.力的多边形自行封闭是平面汇交力系平衡的 。
2-13.不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接如图所示,若结构受力F 作用,则支座C 处的约束力大小 ,方向 。
2-14.不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接如图所示,若结构受力F 作用,则支座C 处的约束力大小 ,方向 。
2-15.用解析法求汇交力系合力时,若采用的坐标系不同,则所求的合力 。
( )
2-16.力偶是由 、 、 的两个力组成。
2-17.同平面的两个力偶,只要 相同,则这两个力偶等效。
2-18.平面系统受力偶矩M =的作用,如图所示,杆AC 、B C 自重不计,A 支座约束力大
题2-13图
题2-14图
小 ,支座约束力大小 。
2-19.如图所示,梁A 支座约束力大小 ,B 支座约束力的大小 。
2-20.平面力偶系的平衡条件 。
3.简答题
2-21用解析法求平面汇交力系的平衡问题时,x 和y 轴是否一定相互垂直?当x 和y 轴不垂直时,对平衡方程0011=F =F n i yi n i xi ∑∑
==有何限制条件?为什么?
2-22.在刚体的A 、B 、C 、D 四点作用有四个大小相等、两两平行的力,如图所示,这四个力组成封闭的力的多边形,试问此刚体平衡吗?若使刚体平衡,应如何改变力系中力的方向?
2-23.力偶不能单独与一个力相平衡,为什么如图所示的轮子又能平衡呢?
2-24.在保持力偶矩大小、转向不变的情况下,如图所示,可否将力偶矩M 移动到AC 上?移动后A 、B 支座的约束力又如何?
2-25.
4.2-26.如图所示,固定在墙壁上的圆环受三个绳子的拉力作用,力F 1沿水平方向,F 3沿铅直方向,F 2与水平成40°角,三个力的大小分别F 1=2kN ,F 2=,F 3=,求力系的合力。
2-27.如图所示简易起重机用钢丝绳吊起重量P =2kN 的重物,不计各杆的自重,摩擦及滑轮的大小不计,A 、B 、C 三处均为铰链连接。
试求杆AB 、AC
所受的力。
2-28.均质杆AB 重P 、长为l ,两端放置在相互垂直的光滑斜面上。
已知一斜面与水平
题2-24图
题2-19图
F 1 F 2 F 3 F 4 A 题2-22图
B C D 题2-23F 题2-18图
面的夹角α,求平衡时杆与水平所成的夹角 及OA的距离。
2-29.在图示刚架的点B作用一水平力F,刚架自重不计,求支座A、D的约束力。
2-30.如图所示的机构中,在铰链A、B作用有力F1、F2处于平衡,不计各杆自重,求力F1与F2的关系。
2-31.直角杆CDA和BDE在D处铰接,如图所示,系统受力偶M作用,各杆自重不计,试求支座A、B处的约束力。
2-32.由
F,如图所示,各
2-33.AB和冲头B组成。
A、B两处为铰链连接,OA=R、AB=l,忽略摩擦和物体的自重,当OA在水平位置时,冲头的压力为F时,求:(1)作用在轮Ⅰ上的力偶矩M的大小;(2)轴承O处的约束力;(3)连杆AB所受的力;(4)冲头给导轨的侧压力。
题2-31图
2-34.铰链四连杆机构ABCD受两个力偶作用处于平衡状态,,已知力偶矩M1=,CD=,AB=,各杆自重不计,试求力偶矩M2及BC杆所受的力。
2-35.如图所示的构架中,在杆BE上作用一力偶,其矩为M,C、D在AE、BE杆的中点,各杆的自重不计,试求支座A和铰链E处的约束力。
