第二章平面力系习题解答
第二章平面力系习题解答
习 题2-1 试计算图2-55中力F 对点O 之矩。
图2-55(a) 0)(=F O M (b) Fl M O =)(F (c) Fb M O -=)(F (d) θsin )(Fl M O =F(e) βsin )(22b l F M O +=F(f) )()(r l F M O +=F2-2 一大小为50N 的力作用在圆盘边缘的C 点上，如图2-56所示。
试分别计算此力对O 、A 、B 三点之矩。
图2-56mN 25.6m m N 625030sin 2505060cos 30sin 5060sin 30cos 50⋅=⋅=︒⨯⨯=︒⨯︒-︒⨯︒=R R M Om N 075.17825.1025.630cos 50⋅=+=⨯︒+=R M M O A m N 485.9235.325.615sin 50⋅=+=⨯︒+=R M M O B2-3 一大小为80N 的力作用于板手柄端，如图2-57所示。
(1)当︒=75θ时，求此力对螺钉中心之矩；(2)当θ为何值时，该力矩为最小值；(3) 当θ为何值时，该力矩为最大值。
图2-57(1)当︒=75θ时，（用两次简化方法）m N 21.20mm N 485.59.202128945.193183087.21sin 8025075sin 80⋅=⋅=+=⨯︒⨯+⨯︒⨯=O M (2) 力过螺钉中心 由正弦定理)13.53sin(250sin 30θθ-︒= 08955.03/2513.53cos 13.53sin tan =+︒︒=θ ︒=117.5θ(3) ︒=︒+︒=117.95117.590θ2-4 如图2-58所示，已知N 200N,300N,200N,150321='====F F F F F 。
试求力系向O 点的简化结果，并求力系合力的大小及其与原点O 的距离d 。
图2-58kN 64.1615110345cos kN 64.4375210145cos 321R321R-=+-︒-=∑='-=--︒-=∑='F F F F F F F F F F y y x x主矢RF '的大小 kN 54.466)()(22R =∑+∑='y x F F F 而 3693.064.43764.161tan RR ==''=x y F F α ︒=27.20α m N 44.21162.0511.045cos )(31⋅=-⨯+⨯︒=∑=F F M M O O Fmm 96.45m 04596.054.466/44.21/R==='=F M d O2-5 平面力系中各力大小分别为kN 60kN,260321===F F F ，作用位置如图2-59所示，图中尺寸的单位为mm 。
工程力学__习题详解_第二章
解： ①选碾子为研究对象
②取分离体画受力图 ∵当碾子刚离地面时NA=0,拉力F最大,这时 由平衡的几何条件，力多边形封闭，故
拉力F和自重及支反力NB构成一平衡力系。
NB P cos r 2 (r h) 2 又由几何关系：tg 0.577 r h
F Ptg
10
所以
F=11.5kN , NB=23.1kN
为该力系的汇交点
三、平面汇交力系合成与平衡的解析法
从前述可知：平面汇交力系平衡的必要与充分条件是该力系 的合力为零。 即：
Rx X 0 R y Y 0
为平衡的充要条件，也叫平衡方程
14
静力学
例题 3
平面汇交力系与平面力偶系
利用铰车绕过定滑轮B的 绳子吊起一货物重P = 20 kN，
由力的平行四边形法则作， 也可用力的三角形来作。 由余弦定理：
R F1 F2 2 F1 F2 cos
2 2
为力多边形
R 1 合力方向由正弦定理： sin sin(180 )
F
4
力三角形规则
F F1 F2 F2 F1
力多边形规则
5
FR1 F1 F2
30
P C
不计并忽略摩擦和滑轮的大小， 试求平衡时杆AB和BC所受的力。
27
静力学
平面汇交力系与平面力偶系
解：
A
60
取滑轮B为研究对象，忽略滑轮的 大小，画受力图。 列写平衡方程
D
B
Fx 0,
30
FAB F1 cos 60 F2 cos 30 0 FBC F1 cos 30 F2 cos 60 0
第2章平面简单力系习题
第2章 平面简单力系习题1.是非题（对画√，错画×）2-1.汇交力系平衡的几何条件是力的多边形自行封闭。
（ ）2-2.两个力F 1、F 2在同一轴上的投影相等，则这两个力大小一定相等。
（ ） 2-3.力F 在某一轴上的投影等于零，则该力一定为零。
（ ） 2-4.合力总是大于分力。
（ ）2-5.平面汇交力系求合力时，作图的力序能够不同，其合力不变。
（ ） 2-6.力偶使刚体只能转动，而不能移动。
（ ） 2-7.任意两个力都能够合成为一个合力。
（ ）2-8.力偶中的两个力在其作用面内任意直线段上的投影的代数和恒为零。
（ ） 2-9.平面力偶矩的大小与矩心点的位置相关。
（ ） 2-10.力沿其作用线任意滑动不改变它对同一点的矩。
（ ） 2.填空题（把准确的答案写在横线上）2-11.作用在刚体上的三个力使刚体处于平衡状态，其中两个力汇交于一点，则第三个力的作用线 。
2-12.力的多边形自行封闭是平面汇交力系平衡的 。
2-13.不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接如下图，若结构受力F 作用，则支座C 处的约束力大小 ，方向 。
2-14.不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接如下图，若结构受力F 作用，则支座C 处的约束力大小 ，方向 。
2-15.用解析法求汇交力系合力时，若采用的坐标系不同，则所求的合力 。
（ ）2-16.力偶是由 、 、 的两个力组成。
2-17.同平面的两个力偶，只要 相同，则这两个力偶等效。
2-18.平面系统受力偶矩M =10kN.m 的作用，如下图，杆AC 、B C 自重不计，A 支座约题2-13图题2-14图束力大小 ，支座约束力大小 。
2-19.如下图，梁A 支座约束力大小 ，B 支座约束力的大小 。
2-20.平面力偶系的平衡条件 。
3.简答题2-21用解析法求平面汇交力系的平衡问题时，x 和y 轴是否一定相互垂直？当x 和y 轴不垂直时，对平衡方程0011=F=F ni yini xi ∑∑==有何限制条件？为什么？2-22.在刚体的A 、B 、C 、D 四点作用有四个大小相等、两两平行的力，如下图，这四个力组成封闭的力的多边形，试问此刚体平衡吗？若使刚体平衡，应如何改变力系中力的方向？2-23.力偶不能单独与一个力相平衡，为什么如下图的轮子又能平衡呢？ 2-24.在保持力偶矩大小、转向不变的情况下，如下图，可否将力偶矩M 移动到AC 上？移动后A 、B 支座的约束力又如何？x 图 2-6题2-24图题2-19图 F 1F 2 F 3F 4A题2-22图 B C D 题2-23图 F 题2-18图2-25.如何准确理解投影和分力、力对点的矩和力偶矩的概念？ 4.计算题2-26.如下图，固定在墙壁上的圆环受三个绳子的拉力作用，力F 1沿水平方向，F 3沿铅直方向，F 2与水平成40°角，三个力的大小分别F 1=2kN ，F 2=2.5kN ，F 3=1.5KN ，求力系的合力。
《理论力学》第二章力系的简化习题解
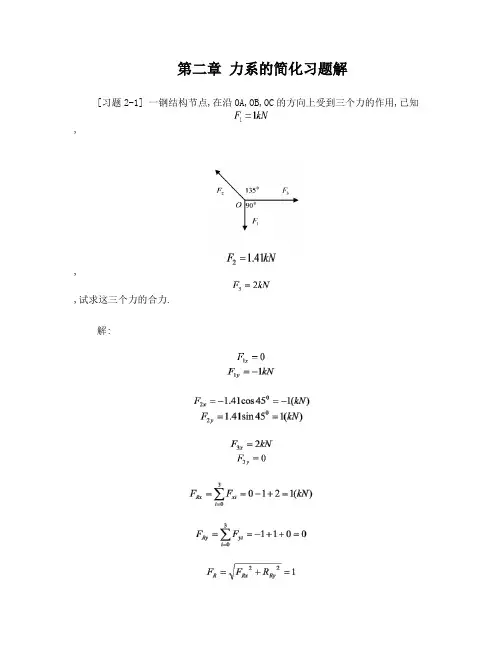
第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。
已知F1＝60Ｎ，F2＝400Ｎ，F3＝500Ｎ，F4＝200Ｎ，试将该力系向Ａ点简化(图中长度单位为mm)。
解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成，各力大小、作用线位置和方向见图。
(完整版)工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）2 第一章静力学基础（d）（e）（f）（g）第一章静力学基础 3 1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f）（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如第二章 平面力系 9图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
第二章力系的简化和平衡方程习题答案
第二章力系的简化和平衡方程一、填空题1、在平面力系中，若各力的作用线全部，则称为平面汇交力系。
2、求多个汇交力的合力的几何法通常要采取连续运用力法则来求得。
3、求合力的力多边形法则是：将各分力矢首尾相接，形成一折线，连接其封闭边，这一从最先画的分力矢的始端指向最后面画的分力矢的的矢量，即为所求的合力矢。
4、平面汇交力系的合力作用线过力系的。
5、平面汇交力系平衡的几何条件为：力系中各力组成的力多边形。
6、平面汇交力系合成的结果是一个合力，这一个合力的作用线通过力系的汇交点，而合力的大小和方向等于力系各力的。
7、若平面汇交力系的力矢所构成的力多边形自行封闭，则表示该力系的等于零。
8、如果共面而不平行的三个力成平衡，则这三力必然要。
9、在平面直角坐标系内，将一个力可分解成为同一平面内的两个力，可见力的分力是量，而力在坐标轴上的投影是量。
10、合力在任一轴上的投影，等于各分力在轴上投影的代数和，这就是合力投影定理。
11、已知平面汇交力系合力R在直角坐标X、Y轴上的投影，利用合力R与轴所夹锐角a的正切来确定合力的方向，比用方向余弦更为简便，也即tg a= | Ry / Rx | 。
12、用解析法求解平衡问题时，只有当采用坐标系时，力沿某一坐标的分力的大小加上适当的正负号，才会等于该力在该轴上的投影。
13、当力与坐标轴垂直时，力在该坐标轴上的投影会值为；当力与坐标轴平行时，力在该坐标轴上的投影的值等于力的大小。
14、平面汇交力系的平衡方程是两个的方程，因此可以求解两个未知量。
15、一对等值、反向、不共线的平行力所组成的力系称为_____。
16、力偶中二力所在的平面称为______。
17、在力偶的作用面内，力偶对物体的作用效果应取决于组成力偶的反向平行力的大小、力偶臂的大小及力偶的______。
18、力偶无合力，力偶不能与一个_____等效，也不能用一个______来平衡.19、多轴钻床在水平工件上钻孔时，工件水平面上受到的是_____系的作用。
02 平面力系题解
且：
FT1 FT2 P 20 (kN)
FAB 54.64 (kN) FCB 74.64 (kN)
联立上述方程，解得： 即：AB 杆受 54.64kN 的拉力；支杆 CB 受 74.64kN 的压力。 四连杆机构 OABO1，在图示位置平衡。已知 OA= 40cm，O1B = 60cm，作用 在曲柄 OA 上的力偶矩大小为 m2 1Nm ,不计杆重，求作用在 O1B 上的力偶矩 m1 的大小 及连杆 AB 所受的力。
2.5
P
(a)
(b)
(c)
P
3
F
班级
F
学号
姓名
F
日期
A
B
A
B
A
B
(d) (e) (f) 答：未知量数等于独立的平衡方程数，能用静力平衡方程求解的问题称为静定问题； 未知量数大于独立的平衡方程数，不能用静力平衡方程求解的问题称为静不定问题。 图示的六种情况中，(c)、(e)两种情况为静定问题，其余为静不定问题。 图(a)：平面汇交力系，有 2 个方程，未知量有 3 个，1 次静不定问题； 图(b)：平面平行力系，有 2 个方程，未知量有 3 个，1 次静不定问题； 图(c)：平面一般力系，有 3 个方程，未知量有 3 个，静定问题； 图(d)：平面一般力系，有 3 个方程，未知量有 4 个，1 次静不定问题； 图(e)：平面一般力系，有 6 个方程，未知量有 6 个，静定问题； 图(f)：平面一般力系，有 6 个方程，未知量有 7 个，1 次静不定问题。
2
班级
学号
姓名
日期
D
M C l A l l (a) l B
D
FC
45 C
工程力学课后习题答案
2-7已知梁AB上作用一力偶，力偶矩为M，梁长为l，梁重不计。求在图a,b,两三种情况下，支座A和B的约束反力。
（a）（b）
题2-7图
（a） (注意，这里，A与B处约束力为负，表示实际方向与假定方向相反，结果应与你的受力图一致，不同的受力图其结果的表现形式也不同)
(b)
2-8在题图所示结构中二曲杆自重不计，曲杆AB上作用有主动力偶，其力偶矩为M，试求A和C点处的约束反力。
题3-1图
3-2图示力系中，F1=100N，F2=300N，F3=200N，各力作用线的位置如图所示。将力向原点O简化
题3-2图
3-3边长为a的等边三角形板，用六根杆支持在水平面位置如图所示。若在板面内作用一力偶，其矩为M，不计板重，试求各杆的内力。
题3-3图
3-4如图所示的空间构架由三根杆件组成，在D端用球铰链连接，A、B和C端也用球铰链固定在水平地板上。今在D端挂一重物P=10kN，若各杆自重不计，求各杆的内力。
以BC杆为研究对象
2-27尖劈顶重装置如图所示。在B块上受力P的作用。A与B块间的摩擦因数为fs（其他有滚珠处表示光滑）。如不计A和B块的重量，求使系统保持平衡的力F的值。
题2-27图
以整体为研究对象，显然水平和铅直方向约束力分别为
以A滑块为研究对象，分别作出两临界状态的力三角形
2-28砖夹的宽度为25cm，曲杆AGB与GCED在G点铰接。砖的重量为W，提砖的合力F作用在砖夹的对称中心线上，尺寸如图所示。如砖夹与砖之间的摩擦因数fs=0.5，试问b应为多大才能把砖夹起（b是G点到砖块上所受正压力作用线的垂直距离）
题2-8图
作两曲杆的受力图，BC是二力杆，AB只受力偶作用，因此A、B构成一对力偶。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2-1试计算图2-55中力F对点O之矩。
图2-55
(a)
(b)
(c)
(d)
(e)
(f)
2-2一大小为50N的力作用在圆盘边缘的C点上，如图2-56所示。试分别计算此力对O、A、B三点之矩。
图2-56
2-3一大小为80N的力作用于板手柄端，如图2-57所示。(1)当 时，求此力对螺钉中心之矩；(2)当 为何值时，该力矩为最小值；(3)当 为何值时，该力矩为最大值。
(1)当W3＝25kN时
(2)空载时，载荷W3=0。在起重机即将绕E点翻倒的临界情况，
满载时，载荷W2=30kN。在起重机即将绕D点翻倒的临界情况，
2-13梁AB用三根支杆支承，如图2-67所示。已知F1＝30kN，F2＝40kN，M＝30kN·m，q＝20kN/m，试求三根支杆的约束反力。
图2-67
2-18四连杆机构如图2-72所示，已知OA＝0.4m，O1B＝0.6m，M1＝1N·m。各杆重量不计。机构在图示位置处于平衡，试求力偶矩M2的大小和杆AB所受的力。
图2-72
杆OA
杆O1B
2-19曲柄滑块机构在图2-73所示位置平衡，已知滑块上所受的力F=400N，如不计所有构件的重量，试求作用在曲柄OA上的力偶的力偶矩M。
(a)假设三杆都受压
(b)假设三杆都受压
2-14水平梁AB由铰链A和杆BC所支持，如图2-68所示。在梁上D处用销子安装一半径为r＝0.1m的滑轮。跨过滑轮的绳子一端水平地系于墙上，另一端悬挂有重W＝1800N的重物。如AD＝0.2m，BD＝0.4m，a＝45º，且不计梁、杆、滑轮和绳子的重量。试求铰链A和杆BC对梁的反力。
图2-63
2-10外伸梁的支承和载荷如图2-64所示。已知F=2kN，M=2.5 kN·m，q＝1kN/m。不计梁重，试求梁的支座反力。
图2-64
(a)
(b)
2-11如图2-65所示，铁路式起重机重W=500kN，其重心在离右轨1.5m处。起重机的起重量为W1=250kN，突臂伸出离右轨10m。跑车本身重量忽略不计，欲使跑车满载或空载时起重机均不致翻倒，试求平衡锤的最小重量W2以及平衡锤到左轨的最大距离x。
图2-70
(a)
CD段
AC段
(b)
CD段
AC段
(c)
CD段
AC段
(d)
CD段
AC段
2-17四连杆机构如图2-71所示，今在铰链A上作用一力F1，铰链B上作用一力F2，方向如图所示。机构在图示位置处于平衡。不计杆重，试求F1与F2的关系。
图2-71
B点
向x轴(AB方向)投影
A点
向y轴(力F1方向)投影
图2-65
满载时，临界状态
(1)
空载时，临界状态
(2)
联立(1)、(2)求得
2-12汽车起重机如图2-66所示，汽车自重W1＝60kN，平衡配重W2＝30kN，各部分尺寸如图所示。试求：(1)当起吊重量W3＝25kN，两轮距离为4m时，地面对车轮的反力；(2)最大起吊重量及两轮间的最小距离。
图2-6所示的颚式破碎机机构，已知工作阻力FR=3kN，OE=100mm，BC=CD=AB=600mm，在图示位置时 ， ，试求在此位置时能克服工作阻力所需的力偶矩M。
图2-74
杆AB
点C
轮O
2-21三铰拱如图2-75所示，跨度l=8m，h=4m。试求支座A、B的反力。(1)在图2-75a中，拱顶部受均布载荷q＝20kN/m作用，拱的自重忽略不计；(2)在图2-75b中，拱顶部受集中力F＝20kN作用，拱每一部分的重量W＝40kN。
图2-77
整体
杆AC
向垂直于BE的方向轴投影
整体
2-24在图2-78所示的构架中，BD杆上的销钉B置于AC杆的光滑槽内，力F=200N，力偶矩 ，不计各构件重量，试求A、B、C处的约束力。
图2-78
整体
杆BD
杆AC
2-25图2-79所示的构架中，AC、BD两杆铰接，在E、D两处各铰接一半径为r的滑轮，连于H点的绳索绕过滑轮E、D、K后连于D点，直径为r的动滑轮K下悬挂一重为W的重物，不计滑轮和杆的重量。试求A、B处的约束反力。
图2-79
整体
杆AC
整体
2-26如图2-80所示，构架在AE杆的中点作用一大小为20kN水平力，各杆自重不计，试求铰链E所受的力。
图2-75
(a)
对称性
CB部分
(b)整体
CB部分
2-22在图2-76所示的构架中，物体重W＝1200N，由细绳跨过滑轮E而水平系于墙上，尺寸如图。不计杆和滑轮的重量，试求支座A、B处的反力和杆BC的内力。
图2-76
整体
杆AB
2-23如图2-77所示的构架，已知F＝1kN，不计各杆重量，杆ABC与杆DEF平行，尺寸如图，试求铰支座A、D处的约束反力。
图2-68
2-15组合梁由AC和DC两段铰接构成，起重机放在梁上，如图2-69所示。已知起重机重W1=50kN，重心在铅直线EC上，起重载荷W2=10kN。不计梁重，试求支座A、B和D三处的约束力。
图2-69
起重机
CD段
AC段
2-16组合梁如图2-70所示，已知集中力F、分布载荷集度q和力偶矩M，试求梁的支座反力和铰C处所受的力。
图2-57
(1)当 时，（用两次简化方法）
(2)力过螺钉中心
由正弦定理
(3)
2-4如图2-58所示，已知 。试求力系向O点的简化结果，并求力系合力的大小及其与原点O的距离d。
图2-58
主矢 的大小
而
2-5平面力系中各力大小分别为 ，作用位置如图2-59所示，图中尺寸的单位为mm。试求力系向O点和O1点简化的结果。
图2-61
2-8在图2-62所示的刚架中，已知F＝10kN，q＝3kN/m，M＝8kN·m，不计刚架自重。试求固定端A处的反力。
图2-62
2-9如图2-63所示，对称屋架ABC的A处用铰链固定，B处为可动铰支座。屋架重100kN，AC边承受垂直于AC的风压，风力平均分布，其合力等于8kN。试求支座A、B处的反力。
图2-59
2-6电动机重W＝5kN，放在水平梁AC的中央，如图2-60所示。忽略梁和撑杆的重量，试求铰支座A处的反力和撑杆BC所受压力。
图2-60
汇交力系方法
2-7起重机的铅直支柱AB由A处的径向轴承和B处的止推轴承支持。起重机重W＝3.5kN，在C处吊有重W1＝10kN的物体，结构尺寸如图2-61所示。试求轴承A、B两处的支座反力。