平面一般力系习题
(完整版)平面一般力系习题答案
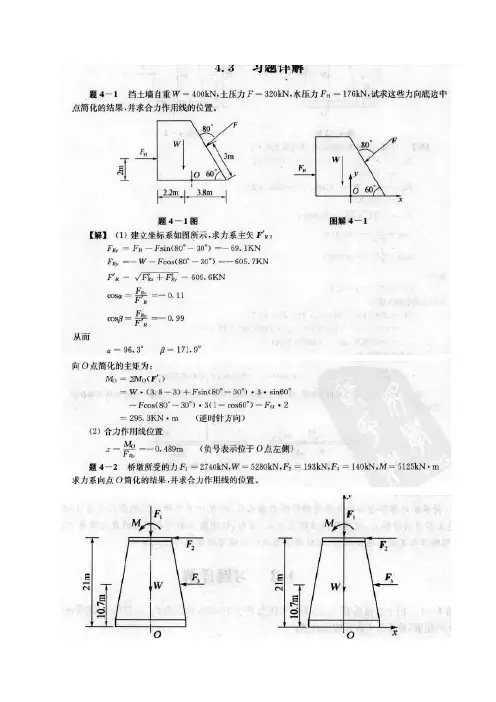
题4-5已知F1=150N,F2=200N,F3=300N,F=F’=200N.求力系向O点简化的结果；并求力系合力的大小及与原点O的距离d。
题4-6 如图所示刚架中，q = 3 kN/m，F = 6 √2kN，M = 10 kN⋅m，不计刚架的自重。
求固定端A 的约束力。
题4-7 无重水平梁的支承和载荷如所示。
已知力F，力偶矩为M 的力偶和强度为q 的均匀载荷。
求支座A 和B 处的约束力。
题4-9 如图所示，各连续梁中，已知q，M，a 及θ，不计梁的自重，求各连续梁在A，B，C 三处的约束力。
题4-10 由AC 和CD 构成的组合梁通过铰链C 连接。
它的支承和受力如图所示。
已知q = 10 kN/m，M = 40 kN⋅m，不计梁的自重。
求支座A，B，D 的约束力和铰链C受力。
题4-11 求图示混合结构在荷载F的作用下，杆件1、2所受的力。
平面任意力系习题
A
a
D
E
F
a
4m
B
1E
B
C
A
F
G
D
ll
6
6
a
a
题 3-28图
题3-29图
3-30.构架由杆 ACE 、DEF 、BCD 铰接而成的， 所受的力及几何尺寸如图所示，各杆的
自重不计，试求杆 BCD 在铰链 C 处给杆 ACE 的力。
D
A b
E a
C a
B
b
b
题 3-30图
3-31.如图所示的构架，起吊重物的重为 滑轮和杆的自重，几何尺寸如图，试求支座
B1
2
A
α
题 3-37图
4F 4F
F
3
a
1
F
2
a
a
a
a
a
题 3-36 图
（）
3-9.桁架中的杆是二力杆。 （ ）
3-10.静滑动摩擦力 F 应是一个范围值。 （ ）
2. 填空题（把正确的答案写在横线上）
3-11.平面平行力系的平衡方程
n
n
M A (Fi ) 0
M B(Fi ) 0 ，
i1
i1
其限制条件
。
3-12. 题 3-12 图平面力系，已知： F1=F 2=F 3=F 4=F , M=Fa ， a 为三角形边长，如以 A
C
A
l /2
l /2
l/6 B
题3-26图
3-27.均质杆 AB 重为 P1，一端用铰链 A
支与墙面上，并用滚动支座 C 维持平衡，另一端又与重为 P2 的均质杆 BD 铰接，杆 BD 靠
与光滑的台阶 E 上，且倾角为 α ，设 AC 2 AB , BE 2 BD 。试求 A 、 C 和 E 三处的约
工程力学 习题详解 第四章
n
mO ( R ) Rd M O (主矩)
———合力矩定理
M O ( R ) mO ( Fi )
n i 1
由于简化中心是任意选取的，故此式有普遍意义。 即：平面任意力系的合力对作用面内任一点之矩等于力系 中各力对于同一点之矩的代数和。
12
静力学
例题4-1
第4章 平面任意力系
F
A C B
Fx 0,
FAx FC cos 45 0 FAy FC sin 45 F 0 FC cos 45 l F 2l 0
Fy 0,
M A F 0,
解平衡方程可得
FC 2 F
D
cos 45 FAx FC cos 45 2 F 20 kN
组合梁AC和CE用铰链C相连，A端为固定端，E端 为活动铰链支座。受力如图所示。已知： l =8 m， F=5 kN，均布载荷集度q=2.5 kN/m，力偶矩的大小 M= 5 kN•m，试求固端A，铰链C和支座E的约束力。 F q B l/4
M E
A
H
C
l/4
D l/4
l/8 l/8
30
解： 1.取CE段为研究对象。受力分析如图。
例题4-5
如图所示为一悬臂梁，A为固定端，设梁上受强度
为q的均布载荷作用，在自由端B受一集中力F和一力偶
M作用，梁的跨度为l，求固定端的约束力。
q
A l
M
F
45
B
24
解：
取梁为研究对象，受力分析如图 由平衡方程
M F
45
q
A
Fx 0,
Fy 0,
FAx F cos 45 0
3 平面任意力系习题一
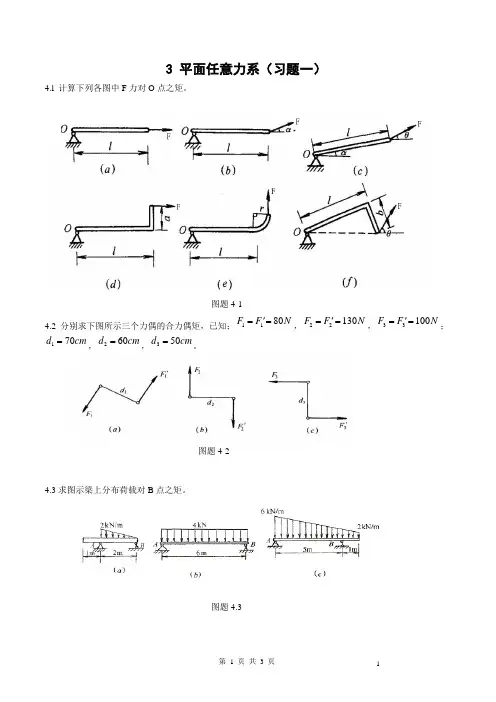
3 平面任意力系（习题一）4.l 计算下列各图中F 力对O 点之矩。
图题4-14.2 分别求下图所示三个力偶的合力偶矩，已知；1180F F N '==，22130F F N '==，33100F F N '==；170d cm =，260d cm =，350d cm =。
图题4-24.3求图示梁上分布荷载对B 点之矩。
图题4.34.4各梁受荷载情况如图题2.3所示，试求(1)各力偶分别对A 、B 点的矩。
(2)各力偶中二个力在x 、y 轴上的投影。
图题4.44.5 求图题4.5示各梁的支座反力图题4.5 图题4.64.6 如图题4.6所示，已知皮带轮上作用力偶矩80m N m =⋅，皮带轮的半径0.2d m =，皮带紧拉边力N F T 5001=，求平衡时皮带松边的拉力2T F 。
4.7 如图所示，四个力作用于O 点，设F 1=50N ，F 2=30N ，F 3=60N ，F 4=100N 。
试分别用几何法和解析法求其合力。
题4.7 (a)图 题4.7 (b)图4.8 拖动汽车需要用力F=5kN ，若现在改用两个力F1和F2，已知F1与汽车前进方向的夹角20=α，分别用几何法和解析法求解：（1）若已知另外一个作用力F2与汽车前进方向的夹角 30=β，试确定F1和F2的大小； （2）欲使F2为最小，试确定夹角β及力F1、F2的大小。
图题4.84.9 支架由杆AB 、AC 构成，A 、B 、C 三处都是铰链约束。
在A 点作用有铅垂力F ，用两种方法求在图示两种情况下杆AB 、AC 所受的力，并说明所受的力是拉还是压。
题4.9图 题4.10图4.10 简易起重机如图所示，重物W=100N ，设各杆、滑轮、钢丝绳自重不计，摩擦不计，A 、B 、C 三处均为铰链连接。
求杆件AB 、AC 受到的力。
工程力学-平面任意力系习题
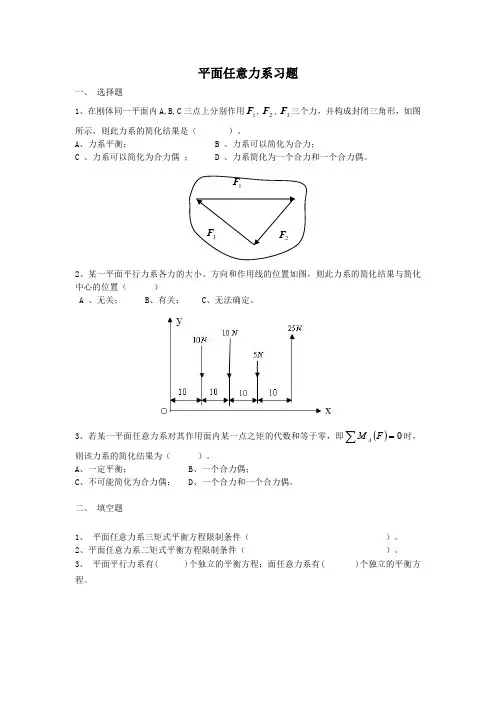
平面任意力系习题
一、选择题
1、在刚体同一平面内A,B,C 三点上分别作用1F ,2F ,3F 三个力，并构成封闭三角形，如图所示，则此力系的简化结果是（
）。
A、力系平衡；
B 、力系可以简化为合力；
C 、力系可以简化为合力偶；
D 、力系简化为一个合力和一个合力偶。
1
F 2
F 3F 2、某一平面平行力系各力的大小、方向和作用线的位置如图，则此力系的简化结果与简化中心的位置（）
A 、无关；B、有关；C、无法确定。
3、若某一平面任意力系对其作用面内某一点之矩的代数和等于零，即
()∑=0F M A 时，则该力系的简化结果为（
）。
A、一定平衡；
B、一个合力偶；
C、不可能简化为合力偶；
D、一个合力和一个合力偶。
二、填空题
1、平面任意力系三矩式平衡方程限制条件（
）。
2、平面任意力系二矩式平衡方程限制条件（
）。
3、平面平行力系有(
)个独立的平衡方程；面任意力系有()个独立的平衡方
程。
三、计算题
1、已知：F、M、q、L，各杆自重不计，试求A、C处约束反力。
2、求图示组合梁支座的约束反力。
大工16秋《工程力学(一)》期末考试复习题
来的
，最大弯曲剪应力为原来的
。
3
答案：1/8, 1/4
知识点解析：本题考查简支梁受弯截面弯曲正应力和弯曲剪应力与截面尺寸的关系，弯曲
正应力与正方形截面边长的三次方成反比，弯曲剪应力与正方形截面边长的平方成反比，
因此当截面边长变为原来的 2 倍，弯曲正应力变为原来的 1/8，弯曲剪应力变为原来的 1/4。
为
，
，
。
答案：连续性，均匀性，各向同性
2. 图中分布力的合力的大小为
，对点 A 之矩大小为
。
答案： ql / 2() ， ql 2 / 3 (顺时针)
知识点解析：本题考查分布力大小及合力作用点的计算，三角形分布力合理大小为三角形
的面积，合力作用点为形心处。
3.将圆截面压杆改为面积相等的圆环截面压杆，其他条件不变，则其柔度将
24. 一点的应力状态如图所示，则其主应力1、 2、 3 分别为（ ）。
10
A． 30MPa、100MPa、50MPa B． 50MPa、30MPa、 50MPa C． 50MPa、0MPa、 50MPa D． 50MPa、30MPa、50MPa
答案：B 知识点解析：本题考查单元体主应力计算。 25. 轴向拉伸杆，正应力最大的截面和剪应力最大的截面（ ）。
5
3、平面汇交力系平衡的（ ）是力系的合力为零。 A．充分条件 B．必要条件 C．充要条件 D．以上选项均不对
答案：C 知识点解析：本题考查平面汇交力系的平衡条件，平面汇交力系平衡的充要条件为力系的 合力为零。
4、弯曲梁，当某截面的剪力 Q 0 时，（ ）。
A．此截面上弯矩有突变 B．此截面上弯矩有极值 C．此截面上弯矩一定为该梁的最大值 D．此截面上的弯矩一定为零 答案：B 5、认为材料发生脆断破坏的主要因素是最大拉应力的强度理论是（ ）。 A．第一强度理论 B．第二强度理论 C．第三强度理论 D．第四强度理论 答案：A 知识点解析：本题考查各强度理论的基本概念。 6、下列关于轴向拉压杆的说法正确的是（ ）。 A．杆内各点位移均为零则杆无变形 B．杆的总伸长量为零则各截面无位移 C．某一段杆内变形为零则该段内各截面无位移 D．某一截面位移为零则该截面上各点无应力 答案：A 知识点解析：本题考查轴向拉压杆内力、各点位移和变形之间的关系。 7、矩形截面梁发生横力弯曲时，在横截面的中性轴处（ ）。 A．正应力最大，剪应力为零 B．正应力和剪应力均为零 C．正应力和剪应力均最大
理论力学习题集
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图，各接触面均为光滑面。
1-2 画出下列指定物体的受力图，各接触面均为光滑，未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图，除注明者外，各物体自重不计，所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在铰车D 上，如图所示。
转动铰车，物体便能升起，设滑轮的大小及滑轮转轴处的摩擦忽略不计，A、B、C三处均为铰链连接。
当物体处于平衡状态时，试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体，求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN，P2=800kN及制动力T=193kN，桥墩自重W=5280kN，风力Q=140kN。
各力作用线位置如图所示，求将这些力向基底截面中心O简化的结果，如能简化为一合力，试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示，试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中，已知q=15kN/m，求A、B、C处的约束力。
2-6 图示平面结构，自重不计，由AB、BD、DFE三杆铰接组成，已知：P=50kN，M=40kN·m，q=20kN/m，L=2m，试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计，D、E处为铰链，B、C为链杆约束，A为固定端，已知：q G=1kN/m，q=1kN/m，M=2kN·m，L1=3m，L2=2m，试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成，O、B处为铰链，A、E是固定铰支座，尺寸如图，已知：r=20cm，在滑轮上吊有重Q=1000N的物体，杆及轮重均不计，试求支座A和E以及AO杆上的O处约束反力。
平面任意力系习题汇总
习题3-1．求图示平面力系的合成结果，长度单位为m。
解：(1)取O点为简化中心，求平面力系的主矢：
求平面力系对O点的主矩：
(2)合成结果：平面力系的主矢为零，主矩不为零，力针。
习题3－2．求下列各图中平行分布力的合力和对于A点之矩。
解：(1)平行力系对A点的矩是：
解：(1)研究AB杆，受力分析（注意BC是二力杆），画受力图：
列平衡方程：
(2)研究铰C，受力分析（注意BC、CD、CE均是二力杆），画受力图：
由力三角形：
其中：
(3)研究OE，受力分析，画受力图：
列平衡方程：
习题3－10．图示液压升降装置，由平台和两个联动机构所组成，联动机构上的液压缸承受相等的力（图中只画了一副联动机构和一个液压缸）。连杆EDB和CG长均为2a，杆端装有滚轮B和C，杆AD铰结于EDB的中点。举起重量W的一半由图示机构承受。设W=9800N，a=0.7m，l=3.2m，求当θ=60o时保持平衡所需的液压缸的推力，并说明所得的结果与距离d无关。
解：(1)研究整体，受力分析（注意1杆是二力杆），画受力图：
列平衡方程：
解方程组：
(2)研究1杆（二力杆），受力分析，画受力图：
由图得：
(3)研究铰C，受力分析，画受力图：
由力三角形得：
杆1和杆3受压，杆2受拉。
习题3－9．图示破碎机传动机构，活动颚板AB=60cm，设破碎时对颚板作用力垂直于AB方向的分力P=1kN，AH=40cm，BC=CD=60cm，OE=10cm；求图示位置时电机对杆OE作用的转矩M。
图中的几何关系是：
(3)列平衡方程
(4)解方程组：
反力实际方向如图示；
(5)研究BC杆，是二力杆，画受力图：
工程力学习题册第三章 答案
第三章平面一般力系答案一、填空(将正确的答案填写在横线上)1、作用在物体上的各力的作用线都在同一平面内 ,并呈任意分布的力系,称为平面一般力系。
2、平面一般力系的两个基本问题是平面力系的简化 ,其平面条件的的应用。
3、力的平移定理表明,若将作用在物体某点的力平移到物体上的另一点,而不改变原力对物体的作用效果,则必须附加一力偶,其力偶距等于原来的力对新作用点的距。
4、平面一般力系向已知中心点简化后得到一力和一力偶距。
5平面一般力系的平衡条件为;各力在任意两个相互垂直的坐标轴上的分量的代数和均为零力系中所有的力对平面内任意点的力距的代数和也等零。
6.平面一般力系平衡方程中,两个投影式ΣFix=0 和ΣFiy=0 保证物体不发生移动 ;一个力矩式ΣMo(Fi)=0 保证物体不发生转动。
三个独立的方程,可以求解三个未知量。
7.平面一般力系平衡问题的求解中,固定铰链的约束反力可以分解为相互垂直的两个分力固定端约束反力可以简化为相互垂直的两个分力和一个附加力偶矩。
8.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣFiX=0适用于平面一般力系,使其用限制条件为AB连线与X轴不垂直。
9.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣMc(Fi)=0的使用限制条约为ABC不在同一直线上。
10.若力系中的各力作用现在同一平面内且相互平行,称为平面平行力系。
它是平面一般力系的特殊情况。
11.平面平行力系有两个独立方程,可以解出两个未知量。
12.平面平行力系的基本平衡方程是：ΣFi X=0，ΣM O(Fi)=0二、判断题（正确的打“√”，错误的打“×”）1.作用于物体上的力,其作用线可在物体上任意平行移动,其作用效果不变。
(×)2.平面一般力系的平衡方程可用于求解各种平面力系的平衡问题。
(√)3.若用平衡方程解出未知力为负值,则表明：(1)该力的真实方向与受力图上假设的方向相反。
(√)(2)该力在坐标轴上的投影一定为负值。
工程力学(高教第3版 陈位宫主编)习题解答：第4章 平面一般力系
第4章 平面一般力系题4-1 解：kN 73230cos 32R .F F F 'x =+=kN 230sin 31R -=--=F F F'ykN 393)()(2R 2R R .F F F 'y 'x '=+=230sin 31)(321⨯-⨯-⨯-==∑ F F F M F m M i O Om kN 2⋅-= m 590R.F M d 'O==题4-2 解：以A 为原点，在x 处取微段d x 。
1）合力：作用在此段上分布集度载荷为x lq q x =， d x 上分布的力为x q d x则：⎰⎰===llx Q qlx x l q x q F 002d d2）合力对A 点之矩： 2031d )(ql x x q F m lxQ A ==⎰题4-3 解（a ）：取AB 梁为研究对象，画受力图∑=0xF ，045cos 2=+Ax F ∑=0yF，045sin 2=-+B Ay F F∑=0)(F mA，0645sin 2451=⨯-⨯+-B F .得：kN 41.F Ax -= kN 11.F Ay -= kN 52.F =解（b ）：取AC 刚架为研究对象∑=0yF，0534=-⨯-A F∑=0)(F m A ，0355.134=⨯-⨯⨯-A m得：kN 17=A F m kN 33⋅=A m解（c ）：取AB 刚架为研究对象∑=0x F ，0535=⨯-Ax F ∑=0yF ，0545=⨯-+B Ay F F ∑=0)(F m A，05.2535254525.2=⨯⨯+⨯⨯-⨯+B F 得：kN 3=Ax F kN 5=Ay F kN 1-=B F题4-4解：取均质杆AB 为研究对象，画受力图∑=0xF ，015cos =-T Ax F F ∑=0yF，015sin =-- T Ay F W F∑=0)(F m A ，sin 45cos 2⨯+- AB F ABWT 得：kN 6830.F Ax = kN 1831.F Ay = kN 7070.F T =题4-5解：取立柱为研究对象∑=0xF ，0=⨯+h q F Ax ∑=0yF，0=--G P F Ay∑=0)(F m A ，02=⨯-⨯⨯-a P hh q m A 得：kN 20-=Ax F kN 100=Ay F m kN 130⋅=A m题4-6 解：1）取整体为研究对象∑=0xF，0=-T Ax F F∑=0y F ，0=-+W F F B Ay ∑=0)(F mA，0)5.1()2(4=--+-⨯r F r W F T B得：N 1200=Ax F N 150=Ay F N 1050=B F 2）取AB 杆为研究对象∑=0)(F mD，0sin 222=+⨯+⨯-θBC B Ay F F FN 1500-=BC FAyBBB题4-7解：取整体为研究对象∑=0xF ，0cos =--βW F F BD Ax∑=0y F ，0sin =---βW W P F Ay∑=0)(F m B ，045sin 45cos 45cos 2=⨯+⨯- AB F AB F ABPAx Ay 得：kN 74.F Ax = kN 94.F Ay = kN 1022.F BD =题4-8解：取汽车为研究对象∑=0)(F mD0)2(5.14213=+-⨯+⨯-⨯x P x F P P ExP P x P F E 31245.1)2(-++=∑=0)(F mE0)4()5.1(2312=+-⨯+--⨯x P x F x P P DxP x P x P F D 2)4()5.1(231⨯-++-=当空载时（P 3=0）： 0≥D F 得 m 53.x ≥当满载时： 0≥E F 得 kN 353≤PF BD W βαPABCWF AxF Ay 1.5mxE F EF D题4-9 解：1）取整体为研究对象∑=0)(F mA03N =⨯-⨯a F a F DF F D 31N =2）取AB 杆为研究对象∑=0)(F mB023=⨯-⨯-a F a F AyF F Ay32=3）取AD 杆为研究对象∑=0yF，0N =++-D Ey Ay F F FF F Ey 31=∑=0)(F m A 032323N =⨯++-a F a F a F D Ey ExF F Ex =题4-10 解：1）取整体为研究对象∑=0)(F mE01612520=⨯-⨯⨯A FkN 75=A F2）取BD 杆为研究对象∑=0)(F mD0105.7520=⨯-⨯⨯By FkN 75=By F3）取AC 杆为研究对象∑=0)(F mC043255.2=⨯-+⨯A BxBy F F F kN 26=Bx F题4-11 解：1）取整体为研究对象∑=0)(F mA0)(=+-⨯bll W l F CxkN 7=Cx F∑=0xF0=+Ax Cx F F kN 7-=Ax F∑=0yF0=-+W F F Ay Cy （1）2）取CEB 杆为研究对象∑=0)(F mB032=⨯+⨯-⨯-l F l F l F Cx Cy TkN 3=FDyA代入（1）得：kN 3=Ay F题4-12 解a ）：1）取BC 梁为研究对象∑=0)(F m B0630cos 3120=⨯+⨯-C FkN 369.F C =∑=0xF030sin =- C Bx F FkN 634.F Bx =∑=0y F 030cos 620=+⨯-CBy F F kN 60=By F2）取AB 梁为研究对象∑=0)(F mA0340=⨯--By A F mm kN 220⋅=A m∑=0x F 0=-Bx Ax F FkN 634.F Ax =∑=0yF0=-By Ay F FkN 60=Ay F解b ）：1）取CD 梁为研究对象∑=0)(F m C04515=⨯+-⨯-D FkN 52.F D =∑=0xF 0=Cx F ∑=0yF05=+-D Cy F FkN 52.F =D2）取AB 梁为研究对象∑=0)(F m A0435215=⨯-⨯-⨯+⨯-Cy B F FkN 15=B F∑=0xF 0=Ax F∑=0yF05.255=--+-B Ay F FkN 52.F Ay -=解c ）：1）取BC 梁为研究对象∑=0)(F mB046=⨯+-C FkN 51.F C =∑=0y F 041=-+C B F FkN 521.F B =2）取铰链B 为研究对象∑=0yF012=-B B F FkN 522.F B =3）取AB 梁为研究对象因其受二力和一力偶平衡，则其二力必等值反向构成一力偶。
习题解答(平面力系)
② 受力如图 ③ 选坐标、取矩点B点 ④ 列方程为:
X 0 X B 0; Y 0 YB P 0; YB P
M B 0 M B P DE 0
解方程得
M B 100011000( Nm 7 )
① 再研究CD杆 ② 受力如图
o M 0 , S sin 45 CE P ED 0 E CA ③ 取E为矩心，列方程
FB
FAx 0 FAy FB F 0 FB 2a M F 3a 0
17
习题2-14
解答要点:
q
D A
M
B
F
C
F
1.取整体为研究对象
q
FAX
2.受力分析如图
FAY
D 3.列平衡方程如下:
A
M
B
C
F F
FB
x y
0, 0,
FAx 0 FAy FB F qa 0
M A
FA
B
FB
对于c图
M M 0, FBl cos M 0 FB l cos
16
习题2-14
解答要点: 1.取整体为研究对象 2.受力分析如图 3.列平衡方程如下:
A
M
B
F
FAX
A
FAY
M
B
F
F 0, F 0, M ( F ) 0,
x y A
19
习题2-20
解答要点一: 1.先取BC为研究对象
A
B
FBY
M
y C
x
M
FC
2.受力分析如图
3.列平衡方程如下:
力学平面力系习题
1.(10分)已知P＝40kN，A、B、C三处都是铰接，杆的自重不计。求图示三角支架A、C铰的约束反力。
第1题图
2.(10分)图示各梁，不计梁的自重和摩擦。求各梁在荷载P作用下支座B的约束反力。
第2题图
3.(13分)结构如图所示，已知P＝80kN,M＝120kN·m,L＝4m。求A、B支座的约束反力。
二、判断题(每题1分，共10分)
1.物体的平衡状态是指物体相对于地球保持静止的状态。()
2.作用力与反作用力总是一对等值、反向、共线的力。()
3.因作用力与反作用力大小相等，方向相反，且沿着同一直线，所以作用力与反作用力是一对平衡力。()
4.在同一平面内的两个力偶，只要力偶矩大小相是从第一个分力的________点，指向最后一个分力的________点。
5.平面一般力系向作用面内的任一点O简化，就分解成了________和________两个力系。
6.使物体产生运动或产生运动趋势的力称________________。
7.力垂直于某轴，则力在该轴上投影为________________。
A.充分条件B.必要条件C.充分必要条件D.无关系
3.只限制物体任何方向移动，不限制物体转动的支座称________支座。()
A.固定铰B.可动铰C.固定端D.光滑面
4.只限制物体垂直于支承面方向的移动，不限制物体向其他方向运动的支座称________支座。()
A.固定铰B.可动铰C.固定端D.光滑面
5.既限制物体任何方向运动，又限制物体转动的支座称________支座。()
A.固定铰B.可动铰C.固定端D.光滑面
6.平面汇交力系平衡的必要和充分条件是该力系的________为零。()
平面力系习题及答案
平面力系习题及答案平面力系习题及答案引言：在物理学中，平面力系是一个重要的概念。
它描述了在一个平面内作用的多个力的相互作用和平衡状态。
理解平面力系的性质和解决与之相关的习题是物理学学习的重要内容。
本文将介绍一些常见的平面力系习题，并提供详细的解答。
一、斜面上的物体考虑一个斜面上的物体，如何确定物体在斜面上的受力情况和平衡状态呢？解答：首先，我们需要将斜面上的力分解为垂直于斜面的分力和平行于斜面的分力。
根据牛顿第二定律，物体在垂直方向上的受力和平行方向上的受力应该平衡。
因此，可以根据斜面的倾角和物体的质量来确定这两个方向上的受力情况。
二、悬挂物体考虑一个悬挂在绳子上的物体，如何确定绳子和物体之间的受力情况和平衡状态呢？解答：首先，我们需要将绳子的拉力分解为垂直于绳子的分力和平行于绳子的分力。
根据牛顿第二定律，物体在垂直方向上的受力应该等于物体的重力，而在平行方向上的受力应该为零。
因此，可以根据物体的质量和绳子的角度来确定这两个方向上的受力情况。
三、平衡力系考虑一个平衡力系，如何确定各个力的大小和方向呢？解答：对于一个平衡力系，各个力的大小和方向应该满足力的平衡条件。
即，合力为零。
我们可以通过分析各个力的向量和方向，利用几何关系和三角函数来求解各个力的大小和方向。
四、平面力系的应用平面力系的概念和解题方法在实际生活中有很多应用。
例如，我们可以利用平面力系的原理来解决物体在斜坡上滑动的问题，或者解决悬挂物体的平衡问题。
此外，平面力系的概念也可以应用于机械设计和结构分析等领域。
结论：平面力系是物理学中一个重要的概念，理解和掌握平面力系的性质和解题方法对于物理学学习和实际应用都具有重要意义。
通过解决平面力系的习题，我们可以加深对物理学原理的理解，并提高解决实际问题的能力。
希望本文提供的平面力系习题及答案能对读者有所帮助。
平面一般力系习题
平面一般力系习题在力学中，平面一般力系是指力作用在一个平面内的力的集合。
解决平面一般力系的习题，需要熟悉平面力的相关概念和定律，并能够应用力的平衡条件进行分析和计算。
下面将介绍一些关于平面一般力系的习题，并给出解答过程。
习题一：有两个力F1和F2作用在一个物体上，力F1的大小为10N，方向与x轴正方向夹角为30°；力F2的大小为8N，方向与y 轴正方向夹角为60°。
求合力的大小和方向。
解答：将力F1分解为x轴和y轴上的分力F1x和F1y，由三角函数可知F1x=F1*cos30°=10N*cos30°=10N*0.866≈8.66N，F1y=F1*sin30°=10N*sin30°=10N*0.5=5N。
将力F2分解为x轴和y轴上的分力F2x和F2y，由三角函数可知F2x=F2*sin60°=8N*sin60°=8N*0.866≈6.93N，F2y=F2*cos60°=8N*cos60°=8N*0.5=4N。
合力的分量为Fx=F1x+F2x=8.66N+6.93N≈15.59N，Fy=F1y+F2y=5N+4N=9N。
合力的大小为F=√(Fx²+Fy²)=√(15.59N²+9N²)≈18.07N。
合力的方向与x轴的夹角θ为tanθ=Fy/Fx=9N/15.59N≈0.577。
因此，合力的大小为约18.07N，方向与x轴的夹角约为0.577弧度。
习题二：一个物体受到三个力F1、F2和F3的作用，力F1的大小为8N，方向与x轴正方向夹角为60°；力F2的大小为6N，方向与y轴正方向夹角为45°；力F3的大小为10N，方向与x轴正方向夹角为120°。
求合力的大小和方向。
解答：将力F1分解为x轴和y轴上的分力F1x和F1y，由三角函数可知F1x=F1*cos60°=8N*cos60°=8N*0.5=4N，F1y=F1*sin60°=8N*sin60°=8N*0.866≈6.93N。
工程力学习题册第二章 - 答案供参习
第二章平面基本力系答案一、填空题(将正确答案填写在横线上)1.平面力系分为平面汇交力系、平面平行力系和平面一般力系。
2.共线力系是平面汇交力系的特例。
3.作用于物体上的各力作用线都在同一平面内 ,而且都汇交于一点的力系,称为平面汇交力系。
4.若力FR对某刚体的作用效果与一个力系的对该刚体的作用效果相同,则称FR为该力系的合力,力系中的每个力都是FR的分力。
5.在力的投影中,若力平行于x轴,则F X＝ F或-F ;若力平行于Y轴,则Fy＝F或-F :若力垂直于x轴,则Fx=0;若力垂直于Y轴,则Fy＝ 0 。
6.合力在任意坐标轴上的投影，等于各分力在同一轴上投影的代数和。
7.平面汇交力系平衡的解析条件为：力系中所有力在任意两坐标轴上投影的代数和均为零。
其表达式为∑Fx＝0 和∑Fy＝0 ，此表达式有称为平面汇交力系的平均方程。
8.利用平面汇交力系平衡方程式解题的步骤是：（1）选定研究对象，并画出受力图。
（2）选定适当的坐标轴，画在受力图上；并作出各个力的投影。
（3）列平衡方程，求解未知量。
9.平面汇交力系的两个平衡方程式可解两个未知量。
若求得未知力为负值，表示该力的实际指向与受力图所示方向相反。
10.在符合三力平衡条件的平衡刚体上，三力一定构成平面汇交力系。
11.用力拧紧螺丝母，其拎紧的程度不仅与力的大小有关，而且与螺丝母中心到力的作用线的距离有关。
12.力矩的大小等于力和力臂的乘积，通常规定力使物体绕矩心逆时针转动时力矩为正，反之为负。
力矩以符号Mo(F) 表示，O点称为距心，力矩的单位是N.M 。
13.由合力矩定力可知，平面汇交力系的合力对平面内任一点的力矩，等于力系中的各分力对于同一点力矩的代数和。
14.绕定点转动物体的平衡条件是：各力对转动中心O点的矩的代数和等于零。
用公式表示为∑Mo(Fi) ＝0 。
15.大小相等、方向相反、作用线平行的二力组成的力系，称为力偶。
力偶中二力之间的距离称为力偶臂。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单体
[例] 图示力系，已知：P1=100N, P2=50N, P3=200N,图中距离
单位cm。
求：1、力系主矢及对A、B、C
三点之矩？ 2、力系简化最后结果。
y
P1
A
P2
R
4
B
6 3C
解： 1、建立坐标系
P3 x
2、X=∑Fx=P3 =200N
Y=∑Fy=P1+ P2 =100+50 =150N
Q2
q
l 4
联立求解：可得
mA= 30 kN·m NA= -12.5 kN
求图示机构平衡时，力偶m, F2K 0 N
B
C
B
SBC
SB C C
2m 2m
m
F
m
A
D
列平衡方程求解：
A RAX R AY
D
RD
m AF0: SBC 4F 20 SBC240210KN
m0:
SB C 4m0 m 1 4 0 4 K 0 .m N
P2
R
P1
B
4
A 6 3C
P3
m A30 N0 cm
P2
P1
B
4
R
m B20 N0 cm
A 6 3C
P3
P2
P1
B
4
R
m C10N 5 c0mA 6 3 C
P3
3、简化最终结果 选简化中心：A点 主矢Fra bibliotekR 2N 50
方向： =36.9°
y
P2
P1
mA
B
A
R R C
P3 x
n
mO(R)mO(Fi)
i1
三、平面一般力系的平衡方程
一矩式
二矩式
三矩式
X 0 Y 0 mO (F )0
X 0 mA(F )0 mB(F )0
mA(F )0 mB(F )0 mC (F )0
A,B连线不 x轴
平面平行力系的平衡方程
X0 成为恒等式
A,B,C不共线
一矩式
二矩式
Y 0
mA(F)0 A B 连线不平行于力线
mA(F)0 mB(F)0
平面汇交力系的平衡方程 m A(F)0成为恒等式
平面力偶系的平衡方程
X 0
Y 0
m i 0
四、静定与静不定
独立方程数 大于或等于未知力数目—为静定
独立方程数 小于 未知力数目—为静不定
五、物系平衡 物系平衡时，物系中每个构件都平衡， 解物系问题的方法常是：由整体 局部
主矩 M Om A30 N c 0m
最终结果 合力
大小： R R 2N 5方0 向: =36.9° 在A点左还是右？
位置图示： hmA3001.2cm R 250
练习：简化中心可任选，试以C点为简化中心，求简化最终结果。 思考：两次简化合力位置是否相同？
选简化中心：C点 主矢 R 2N 50
P
Q2
mA
NE=2.5 kN （向上） NC=2.5 kN （向上）
AH
NA l/8 l/4
C
l/8
N
C
2、取AC 段为研究对象，受力分析如图。
l Q2 q 4
列平衡方程：
P
Q2
mA
F0: y
NANC Pq4l 0
m F 0 : A
AH
NA l/8 l/4
C
l/8
N
C
L AP8 lq4 l3 8 lN C 2 l0
例题分析 [例] 已知各杆均铰接，B端插入地内，P=1000N， AE=BE=CE=DE=1m，杆重不计。 求AC 杆内力？B点的反力？
解：① 选整体研究
② 受力如图 ③ 选坐标、取矩点、Bxy,B点 ④ 列方程为:
X0 XB0; Y0 YBP0; Y BP m B0M B P D 0 E
P
q
m
E AHB C D
l/8 l/8 l/4 l/4 l/4
Q1
m
CH
E
NC l/8 3l/8
NE
解：
Q1
q
l 4
1、取CE 段为研究对象，受力分析如图。
列平衡方程：
Q1
m
Fy0: NCq4l NE 0
m C F 0 :q4 l8 lmNE2 l 0
NC
CH
l/8
3l/8
E
NE
联立求解：可得
∴主矢 R X 2 Y 2 2 2 1 0 2 2 5 0 N 5 00
co c so R ,x s ) (X 2 0 0 .8 0 ∴ =36.9° R 250 m A m A ( F i ) P 2 6 5 6 3 N 0 c 0 m 0 m B m B ( F i ) P 3 4 P 1 6 2 4 1 6 0 2 N c 0 0 m C m C ( F i ) P 1 9 P 2 3 1 9 5 3 0 1 N 0 c 0
a(63)sin 915 5 0 .4 cm
250
结论：不论简化中心取何处，最终简化结果应一致。
例： 简支梁受力如图，已知F＝300N, q=100N/m,
求A ,B处的约束反力。
解：简支梁受力如图所示：
F x 0 F A x0
F q
F Ax A
CD
F Ay 2m 2m
4m
Fy0
F A F y B F q 4 0 1
B
M A0
FB
F B 8 4 q 6 F 2 0
代入（1）式
FB37N5 FAy32N5
例 求图示结构中A、B处的约束反力。P=10kN F=20kN， 解：1、取AD为研究对象，受力分析如图。
2、列平衡方程求解
F
P
3m
2m
A
60 C D
F
P
RAY
RAX A
CD
S
B
m A(F )0 F 3 P 5 S s 6 i 3 n 0
FX0 FY0
R A XSco 6s 0 0 R A Y S s6 i n 0 F P 0
RAX 2.1K 7N RAY6.6KN S4.3 2KN
物体系的平衡问题
例 组合梁AC 和CE 用铰链C 相连，A端为固定端，E
端为活动铰链支座。受力如图所示。已知： l =8 m，
P=5 kN，均布载荷集度q=2.5 kN/m，力偶矩的大小m= 5kN·m，试求固端A、铰链C 和支座E 的反力。
y
P2
B
方向： =36.9°
P1
h
主矩 M0=m C 10 N c 5m 0 A 6 3
4
a
C
最终结果 合力
R
R mC
P3 x
大小： R R 2N 5方0 向: =36.9°
位置图示： hM 010 54.0 2cm 思考：两次简化合
R 250
力位置是否相同？
h 1 .2 cm
平面一般力系习题分析
（ 适用于建筑专业）
《平面一般力系习题课》
本章小结： 一、力线平移定理是力系简化的理论基础
力 力+力偶
二、平面一般力系的合成结果
① 合力（主矢） R ' 0 ,M O 0 ;或 R ' 0 ,M O 0 ;
② 合力偶（主矩） R'0,MO0;
③ 平衡 R'0,MO0;
合力矩定理