集合的运算 交集并集 补集
第6课时 集合的并集、交集、补集的综合运算
课时目标
1.深刻理解交集、并集、补集的含义及运算.
2.能进行集合的并交补运算.
识记强化
1.集合的运算性质
(1)A∪B=B∪A,A∪A=A,A∪∅=A,A∩B=B∩A,A∩A=A,A∩∅=∅.
(2)A⊆(A∪B),B⊆(A∪B),(A∩B)⊆A,(A∩B)⊆B.
2.下列各式中,表达错误的是()
A.∅⊆{x|x<4} B.2 ∈{x|x<4}
C.∅∈{∅,{0},{1}} D.{2 }∈{x|x<4}
答案:D
解析:对于B,C,元素与集合之间用“∈”或“∉”符号,且2 是集合{x|x<4}中的元素,所以B表达正确,∅是集合{∅,{0},{1}}中的一个元素,所以C表达正确;对于A,D,集合与集合之间用“⊆”或“ ”符号,且∅是任何集合的子集,所以A表达正确,D表达错误.
(3)A⊆B⇔A∪B=B⇔A∩B=A.
(4)A∪( A)=U,A∩( A)=∅.
(5) ( A)=A, U=∅, ∅=U.
2.全集具有相对性,即对于研究某个问题时的全集可能在研究另一个问题时就不是全集;补集是相对于全集而言的,由于全集具有相对性,那么补集也具有相对性,在不同的全集下,一个集合的补集可能不相同.
课时作业
(时间:45分钟,满分:90分)
一、选择题(本大题共6小题,每小题5分,共30分)
1.设全集U={1,3,5,7},若集合M满足 M={5,7},则集合M为()
A.{1,3} B.{1}或{3}
C.{1,3,5,7} D.{1}或{3}或{1,3}
答案:A
解析:由U={1,3,5,7}及 M={5,7},得M={1,3},故选A.
数学中的集合运算法则

数学中的集合运算法则数学作为一门精确而又抽象的学科,涉及到众多的概念和运算法则。
其中,集合运算法则是数学中一个重要的分支,它研究的是集合之间的关系和运算规律。
本文将探讨数学中的集合运算法则,以及它们的应用。
一、交集运算法则交集运算是指将两个集合中所有共有的元素组成一个新的集合。
在数学中,交集运算有以下几个法则:1. 交换律:对于任意两个集合A和B,A∩B=B∩A。
这意味着,交集运算的结果与操作数的顺序无关。
2. 结合律:对于任意三个集合A、B和C,(A∩B)∩C=A∩(B∩C)。
这意味着,交集运算可以连续进行,结果不会受到括号的影响。
3. 吸收律:对于任意两个集合A和B,如果A是B的子集,则A∩B=A。
这意味着,如果一个集合是另一个集合的子集,它们的交集就是自身。
交集运算法则在实际应用中有着广泛的应用。
例如,在数据库查询中,可以使用交集运算来找出同时满足多个条件的数据。
二、并集运算法则并集运算是指将两个集合中的所有元素组成一个新的集合。
在数学中,并集运算有以下几个法则:1. 交换律:对于任意两个集合A和B,A∪B=B∪A。
这意味着,并集运算的结果与操作数的顺序无关。
2. 结合律:对于任意三个集合A、B和C,(A∪B)∪C=A∪(B∪C)。
这意味着,并集运算可以连续进行,结果不会受到括号的影响。
3. 吸收律:对于任意两个集合A和B,如果A是B的子集,则A∪B=B。
这意味着,如果一个集合是另一个集合的子集,它们的并集就是另一个集合。
并集运算法则在实际应用中也有着广泛的应用。
例如,在概率论中,可以使用并集运算来计算两个事件同时发生的概率。
三、差集运算法则差集运算是指从一个集合中去除另一个集合中的元素,得到一个新的集合。
在数学中,差集运算有以下几个法则:1. 差运算:对于任意两个集合A和B,A-B表示从A中去除B中的元素得到的新集合。
2. 吸收律:对于任意两个集合A和B,如果A是B的子集,则A-B=∅。
交集并集补集相关概念符号

交集并集补集相关概念符号交集并集补集相关概念符号一、交集的概念和符号交集是集合论中的一个重要概念,表示两个或多个集合共有的元素组成的集合。
在数学中,我们用符号“∩”来表示交集。
例如,对于集合A 和集合B,它们的交集可以表示为A∩B。
二、并集的概念和符号并集也是集合论中的一个重要概念,表示两个或多个集合所有元素的总和。
在数学中,我们用符号“∪”来表示并集。
例如,对于集合A和集合B,它们的并集可以表示为A∪B。
三、补集的概念和符号补集是集合论中的另一个重要概念,表示在一个全集合中减去某个给定集合后所得到的剩余元素集合。
在数学中,我们用符号“¯”或“-”来表示补集。
例如,对于集合A在全集合U中的补集,可以表示为A¯或A-。
交集、并集和补集是集合论中常用的运算符号,它们可以帮助我们更好地处理集合之间的关系。
四、交集、并集和补集的运算规律1. 交换律:对于任意两个集合A和B,有A∩B = B∩A和A∪B =B∪A。
换句话说,交集和并集的顺序不影响最终的结果。
2. 结合律:对于任意三个集合A、B和C,有(A∩B)∩C = A∩(B∩C)和(A∪B)∪C = A∪(B∪C)。
换句话说,无论交集还是并集,我们可以先进行任意两个集合的运算,然后再与第三个集合进行运算,最终得到的结果是一样的。
3. 分配律:对于任意三个集合A、B和C,有A∩(B∪C) =(A∩B)∪(A∩C)和A∪(B∩C) = (A∪B)∩(A∪C)。
换句话说,交集和并集之间满足分配律。
4. 对偶律:对于任意两个集合A和B,有(A∩B)¯ = A¯∪B¯和(A∪B)¯= A¯∩B¯。
换句话说,交集和并集的补集等于补集的并集和交集。
五、总结交集、并集和补集是集合论中非常重要的概念符号,通过它们我们可以更好地处理集合之间的关系。
交集表示两个或多个集合共有的元素,用符号“∩”表示;并集表示两个或多个集合所有元素的总和,用符号“∪”表示;补集表示在全集合中减去某个给定集合后所得到的剩余元素集合,用符号“¯”或“-”表示。
并集交集补集
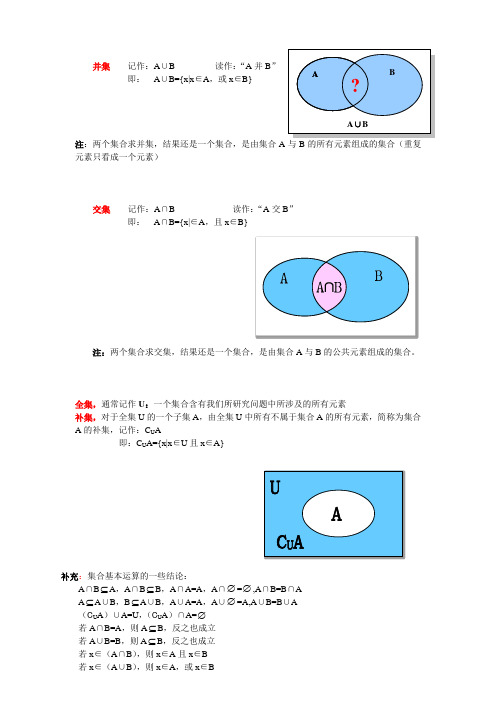
并集 记作:A ∪B 读作:“A 并B ”
即: A ∪B={x|x ∈A ,或x ∈B}
注:两个集合求并集,结果还是一个集合,是由集合A
与B 的所有元素组成的集合(重复元素只看成一个元素)
交集 记作:A ∩B 读作:“A 交B ”
即: A ∩B={x|∈A ,且x ∈B} 注:两个集合求交集,结果还是一个集合,是由集合A 与B 的公共元素组成的集合。
全集,通常记作U :一个集合含有我们所研究问题中所涉及的所有元素
补集,对于全集U 的一个子集A ,由全集U 中所有不属于集合A 的所有元素,简称为集合A 的补集,记作:C U A
即:C U A={x|x ∈U 且x ∈A}
A
U
C U A
A ∪
B B
A ? 补充:集合基本运算的一些结论:
A ∩
B ⊆A ,A ∩B ⊆B ,A ∩A=A ,A ∩∅=∅,A ∩B=B ∩A
A ⊆A ∪
B ,B ⊆A ∪B ,A ∪A=A ,A ∪∅=A,A ∪B=B ∪A
(C U A )∪A=U ,(C U A )∩A=∅
若A ∩B=A ,则A ⊆B ,反之也成立
若A ∪B=B ,则A ⊆B ,反之也成立
若x ∈(A ∩B ),则x ∈A 且x ∈B
若x ∈(A ∪B ),则x ∈A ,或x ∈B。
三集合标准公式

三集合标准公式
在集合论中,三个重要的集合标准公式是交集、并集和补集。
这些公式可以用来描述集合之间的关系,以及对集合进行操作。
1. 交集
交集是指两个或多个集合中共同存在的元素的集合。
交集的符号为“∩”,表示为A∩B。
例如,如果集合A包含元素{1,2,3},集合B包含元素{2,3,4},则A∩B={2,3}。
交集的公式为:
A∩B={x|x∈A且x∈B}
其中,符号“|”表示“满足”,符号“∈”表示“属于”。
2. 并集
并集是指两个或多个集合中所有元素的集合。
并集的符号为“∪”,表示为A∪B。
例如,如果集合A包含元素{1,2,3},集合B包含元素{2,3,4},则A∪B={1,2,3,4}。
并集的公式为:
A∪B={x|x∈A或x∈B}
其中,符号“或”表示“至少满足一个”。
3. 补集
补集是指一个集合中不属于另一个集合的元素的集合。
补集的符号为“-”,表示为A-B。
例如,如果集合A包含元素{1,2,3},集合B包含元素{2,3,4},则A-B={1}。
补集的公式为:
A-B={x|x∈A且x∉B}
其中,符号“不属于”表示“不满足”。
这三个集合标准公式在集合论中非常重要,它们可以用来描述集合之间的关系,进行集合运算,以及解决各种集合问题。
交集并集补集差集

交集并集补集差集交集、并集、补集和差集是集合论中的重要概念。
它们是用来描述集合之间的关系和操作的。
本文将对这些概念进行详细介绍,并阐明它们在数学中的应用。
首先,我们来了解一下集合。
在数学中,集合是由一些确定的元素组成的整体。
这些元素可以是任何事物,可以是数字、字母、词语等。
例如,集合A可以包含元素1、2、3,记作A={1, 2, 3}。
交集是指两个集合中共同存在的元素组成的集合。
记作A∩B。
例如,如果集合A={1, 2, 3},集合B={2, 3, 4},那么A和B的交集为{2, 3}。
交集可以理解为两个集合中的共同点。
并集是指两个集合中所有元素组成的集合。
记作A∪B。
例如,如果集合A={1, 2, 3},集合B={2, 3, 4},那么A和B的并集为{1, 2, 3, 4}。
并集可以理解为两个集合的总体。
补集是指一个集合相对于全集中不属于该集合的元素组成的集合。
通常,全集是指研究对象所属的领域的范围。
记作A'或A^c。
例如,如果全集为{1, 2, 3, 4, 5},集合A={2, 3},那么A的补集为{1, 4, 5}。
补集可以理解为除了该集合中的元素以外的所有元素。
差集是指一个集合相对于另一个集合的补集的元素组成的集合。
记作A-B。
例如,如果集合A={1, 2, 3},集合B={2, 3, 4},那么A和B的差集为{1}。
差集可以理解为属于一个集合但不属于另一个集合的元素。
交集、并集、补集和差集在数学中广泛应用。
它们是数学推理和证明的基础工具。
在集合论证明中,我们经常使用这些操作来判断两个集合是否相等或确定集合之间的包含关系。
此外,交集、并集、补集和差集也常用于概率、统计学和计算机科学中的问题。
在概率中,我们可以通过交集和并集来计算事件的概率。
例如,A和B是两个事件,我们可以通过计算A∩B和A∪B来确定事件A和事件B发生的可能性。
在统计学中,交集和并集可以用来描述样本空间和事件之间的关系。
专题02集合的交、并、补运算

专题02集合的交、并、补运算(总4页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第02讲集合的交、并、补运算考纲要求:1、理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.2、理解在给定集合中一个子集的补集的含义,会求给定子集的补集.3、能使用韦恩(Venn)图表达集合的关系及运算.基础知识回顾:1、集合的基本运算集合的并集集合的交集集合的补集符号表示 A∪B A∩B 若全集为U,则集合A的补集为U A图形表示意义{x|x∈A,或x∈B} {x|x∈A,且x∈B} {x|x∈U,且xA}2、集合的运算性质①A∪B=ABA,A∩B=A AB;②A∩A=A,A∩=;③A∪A=A,A∪=A;④A∩U A=,A∪U A=U,U(U A)=A,U(A∪B)=U A∩U B, U(A∩B)=U A∪U B应用举例:类型一:已知集合中的元素,求其交集、并集或补集【例1】【2017河南省洛阳市一中高三入学考试】若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( )A.{-1} B.{1} C.{1,-1} D.【例2】【2017湖南省长沙市长郡中学高三摸底】已知集合2{|230}A x x x =--≤,{|ln(2)}B x y x ==-,则A B =( )A .(1,3)B .(1,3]C .[1,2)-D .(1,2)-【例3】【2017东北四市高三联考】设集合M ={x|-2<x<3},N ={x|2x +1≤1},则M ∩(R N)= 类型二:已知集合交集、并集或补集中的元素,求其集合中的元素【例4】【2017浙江省温州市高三月考试题】设全集{}()1,2,3,4,5,U U C AB =={}(){}1,A 3UC B =,则集合B =( ) A .{}1,2,4,5 B .{}2,4,5 C .{}2,3,4 D .{}3,4,5【例5】【2017河北省温邯郸市高三月考试题】已知全集{1,2,3,4,5}U =,集合{1,2,3}A =,{3,4,5}B =,则U A C B ( )A .{3}B .{1,2,4,5}C .{1,2}D .{1,3,5}类型三:已知集合关系求参数的值或范围【例6】【2017年长郡中学高三入学考试】已知集合2{|4}A x y x ==-,{|1}B x a x a =≤≤+,若A B A =,则实数a 的取值范围为( )A .(,3][2,)-∞-+∞B .[1,2]-C .[2,1]-D .[2,)+∞【例7】【2017江苏省南通市如东县一中高三月考】【已知A ={x |x 2-3x +2=0},B ={x |ax -2=0},若A ∩B =B ,则实数a 的值为( )A .0或1或2B .1或2C .0D .0或1【例8】【2017西藏林芝市高三月考】已知集合A ={x |x 2-2x -3≤0},B ={x |x 2-2mx +m 2-4≤0,x ∈R ,m ∈R}.(1)若A ∩B =[0,3],求实数m 的值;(2)若A R B ,求实数m 的取值范围.类型四:新定义集合运算问题【例9】【2017江西省新余市第一中学高三开学考试】设,A B 是非空集合, 定义{}|,A B x x A x B =∈∉且,已知{}{}2|20,|2x A x x x B y y =--≤==,则AB =( )A .∅B .[]1,0-C .[)1,0-D .(]1,2【例10】【浙江省温州市2017届高三8月模拟考试数学(理)试题】设集合0123{,,,}S A A A A =,在S 上定义运算⊕为:i j k A A A ⊕=,其中k 为i j +被4除的余数,i ,j =0,1,2,3.若230()m A A A A ⊕⊕=,则m 的值为( )A .0B .1C .2D .3方法、规律归纳:1、一个性质:要注意应用AB 、A ∩B =A 、A ∪B =B 、U A U B 、A ∩(U B )=这五个关系式的等价性.两种方法2、两种方法:韦恩图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用数轴图示法要特别注意端点是实心还是空心.实战演练:1.【2017河南省天一大联考高三阶段性考试】已知集合{1,2,3,4}A =,2{|log (31),}B n n k k A ==-∈,则A B =( )A .{3}B .{1}C .{1,3}D .{1,2,3}2.【2017广东省珠海市高三摸底考试】设集合{}{}11,3<<-=∈==x x B R x y y A x , ,则A B =A. ()11-,B. ()10,C. ()∞+,1-D. ()+∞0, 3.【2017青岛一中高三质检】2.已知数集A ={a 1,a 2,…,a n }(1≤a 1<a 2<…<a n ,n ≥2)具有性质P :对任意的i ,j (1≤i ≤j ≤n ),a i a j 与a j a i两数中至少有一个属于A ,则称集合A 为“权集”,则( ) A .{1,3,4}为“权集” B .{1,2,3,6}为“权集”C .“权集”中元素可以有0D .“权集”中一定有元素14.【2017北京市高三入学定位考试】已知集合{|11}A x R x =∈-<<,{|03}B x R x =∈≤≤,则A B =( )A .{|01}x x ≤<B .{|13}x x <≤C .{|13}x x -<≤D .{|1,}x x x <-≥或05.【2017广东省惠州市高三第一次调研考试】已知{1,2,4,8,16}A =,2{|log ,}B y y x x A ==∈,则A B =( )A .{1,2}B .{2,4,8}C .{1,2,4}D .{1,2,4,8}6.【2017新疆兵团农二师华山中学2高三试题】已知集合{|21}A x x =-<<,2{|20}B x x x =-≤,则A B =( )A .{|01}x x <<B .{|01}x x ≤<C .{|11}x x -<≤D .{|21}x x -<≤7.【2017湖北省襄阳市第四中学高三月考试题】已知集合1|,,11M y y x x R x x ⎧⎫==+∈≠⎨⎬-⎩⎭,集合{}2|230N x x x =--≤,则( ) A .M N =∅ B .R M C N ⊆ C .R M C M ⊆ D .M N R ⋃=8.【2017江西吉安一中高三月考】已知集合M ={x |x +2x -8≤0},N ={x |y =-x 2+3x -2},在集合M 中任取一个元素x ,则“x ∈M ∩N ”的概率是 .9.【2017湖北省襄阳市第四中学高三周考】已知集合A ={-1,1},B ={x |x 2-2ax +b =0},若∅≠B 且A ∪B =A ,求a ,b 的值.10.【2017江苏省南通市如东县一中高三月考】设A={x|x 2+4x=0},B={x|x 2+2(a+1)x+a 2-1=0},其中x ∈R,如果A ∩B=B,求实数a 的取值范围.。
集合间的基本运算(交集,并集,补集)非常全面的题型分类

集合间的基本运算一、并集(1)文字语言:由所有属于集合A或属于集合B的元素组成的集合,称为集合A 与B的并集.(2)符号语言:A∪B={x|x∈A,或x∈B}.(3)图形语言;如图所示.二、交集交集的三种语言表示:(1)文字语言:由属于集合A且属于集合B的所有元素组成的集合,称为A与B 的交集.(2)符号语言:A∩B={x|x∈A,且x∈B}.(3)图形语言:如图所示.三、并集与交集的运算性质题型一 并集及其运算例1 (1)设集合M ={4,5,6,8},集合N ={3,5,7,8},那么M ∪N 等于( ) A.{3,4,5,6,7,8} B.{5,8} C.{3,5,7,8} D.{4,5,6,8}(2)已知集合P ={x |x <3},Q ={x |-1≤x ≤4},那么P ∪Q 等于( ) A.{x |-1≤x <3} B.{x |-1≤x ≤4} C.{x |x ≤4}D.{x |x ≥-1} (3).已知集合=A {}31<≤-x x ,=B {}52≤<x x ,则B A ⋃=( )A .{}32<<x xB .{}51≤≤-x xC .{}51<<-x xD .{}51≤<-x x变式练习1 已知集合A ={x |(x -1)(x +2)=0};B ={x |(x +2)(x -3)=0},则集合A ∪B 是( ) A.{-1,2,3}B.{-1,-2,3}C.{1,-2,3}D.{1,-2,-3}2.若集合=A {}x ,3,1,=B {}2,1x ,B A ⋃={}x ,3,1,则满足条件的实数x 有( )A .1个B .2个C .3个D .4个题型二 交集及其运算例2 (1)设集合M ={m ∈Z |-3<m <2},N ={n ∈Z |-1≤n ≤3},则M ∩N 等于( ) A.{0,1} B.{-1,0,1} C.{0,1,2}D.{-1,0,1,2}(2)若集合A ={x |1≤x ≤3},B ={x |x >2},则A ∩B 等于( ) A.{x |2<x ≤3} B.{x |x ≥1} C.{x |2≤x <3} D.{x |x >2}变式练习2(1)设集合A ={x |x ∈N ,x ≤4},B ={x |x ∈N ,x >1},则A ∩B =________. (2)集合A ={x |x ≥2或-2<x ≤0},B ={x |0<x ≤2或x ≥5},则A ∩B =________.(3).设集合=M {}23<<-∈m Z m ,{}31≤≤-∈=n Z n N ,则N M ⋂=( ) A .{}1,0 B .{}1,0,1- C .{}2,1,0 D .{}2,1,0,1-(4).集合=A {}121+<<-a x a x ,=B {}10<<x x ,若=⋂B A ∅,求实数a 的取值范围.题型三已知集合的交集、并集求参数例3已知集合A={x|2a≤x≤a+3},B={x|x<-1,或x>5},若A∩B=∅,求实数a的取值范围变式练习3设集合M={x|-3≤x<7},N={x|2x+k≤0},若M∩N≠∅,则实数k的取值范围为________.例4设集合A={x|x2-x-2=0},B={x|x2+x+a=0},若A∪B=A,求实数a 的取值范围.变式练习4设集合A={x|x2-3x+2=0},集合B={x|2x2-ax+2=0},若A∪B =A,求实数a的取值范围.例5 (1)设集合A={(x,y)|x-2y=1},集合B={(x,y)|x+y=2},则A∩B 等于( )A.∅B.{53,13}C.{(53,13)} D.{x=53,y=13}(2)已知集合A={y|y=x2-2x-3,x∈R},B={y|y=-x2+2x+13,x∈R},求A∩B.变式练习5(1)设集合A={y|y=x2-2x+3,x∈R},B={y|y=-x2+2x+10,x∈R},求A∪B;(2)设集合A ={(x ,y )|y =x +1,x ∈R },集合B ={(x ,y )|y =-x 2+2x +34,x ∈R },求A ∩B .6.设集合A ={x |x 2=4x },B ={x |x 2+2(a -1)x +a 2-1=0}. (1)若A ∩B =B ,求a 的取值范围; (2)若A ∪B =B ,求a 的值.课后练习 一、选择题1.设集合A ={-1,0,-2},B ={x |x 2-x -6=0},则A ∪B 等于( ) A.{-2} B.{-2,3} C.{-1,0,-2}D.{-1,0,-2,3}2.已知集合M ={x |-1≤x ≤1,x ∈Z },N ={x |x 2=x },则M ∩N 等于( ) A.{1} B.{-1,1} C.{0,1}D.{-1,0,1}3.已知集合M ={0,1,2,3,4},N ={1,3,5},P =M ∩N ,则P 的子集共有( )A.2个B.4个C.6个D.8个4.已知集合M={x|-3<x≤5},N={x|x<-5或x>5},则M∪N等于( )A.{x|x<-5或x>-3}B.{x|-5<x<5}C.{x|-3<x<5}D.{x|x<-3或x>5}三、解答题5.已知集合A={x|-2≤x≤5},B={x|2a≤x≤a+3},若A∪B=A,求实数a的取值范围.6.已知集合A={x|x2-px+15=0}和B={x|x2-ax-b=0},若A∪B={2,3,5},A∩B={3},分别求实数p,a,b的值.7.(1)已知集合A={-4,2a-1,a2},B={a-5,1-a,9},若A∩B={9},求a的值;(2)若P={1,2,3,m},Q={m2,3},且满足P∩Q=Q,求m的值.四、全集(1)定义:如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集.(2)记法:全集通常记作U.五、补集对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作∁U A符号语言为∁U A={x|x∈U,且x∉A}图形语言为六、补集的性质①A∪(∁U A)=U;②A∩(∁U A)=∅;③∁U U=∅,∁U∅=U,∁U(∁U A)=A;④(∁U A)∩(∁U B)=∁U(A∪B);⑤(∁U A )∪(∁U B )=∁U (A ∩B ).题型一 补集运算例1 (1)设全集U ={1,2,3,4,5},集合A ={1,2},则∁U A 等于( ) A.{1,2} B.{3,4,5} C.{1,2,3,4,5}D.∅(2)若全集U =R ,集合A ={x |x ≥1},则∁U A =________.变式练习 1 已知全集U ={x |x ≥-3},集合A ={x |-3<x ≤4},则A C U =________.2.已知全集U ={x |1≤x ≤5},A ={x |1≤x <a },若∁U A ={x |2≤x ≤5},则a =________.题型二 补集的应用例2 设全集U ={2,3,a 2+2a -3},A ={|2a -1|,2},∁U A ={5},求实数a 的值.变式练习2若全集U={2,4,a2-a+1},A={a+4,4},∁U A={7},则实数a=________.题型三并集、交集、补集的综合运算例3 已知全集U={x|-5≤x≤3},A={x|-5≤x<-1},B={x|-1≤x<1},求∁U A,∁U B,(∁U A)∩(∁U B).变式练习3设全集为R,A={x|3≤x<7},B={x|2<x<10},求∁R(A∪B)及(∁R A)∩B.题型四利用Venn图解题例4 设全集U={不大于20的质数},A∩∁U B={3,5},(∁U A)∩B={7,11},(∁U A)∩(∁UB)={2,17},求集合A,B.变式练习4全集U={x|x<10,x∈N*},A⊆U,B⊆U,(∁U B)∩A={1,9},A∩B={3},(∁U A)∩(∁U B)={4,6,7},求集合A,B.变式练习5已知集合A={x|x2-4ax+2a+6=0},B={x|x<0},若A∩B≠∅,求a的取值范围.课后作业一、选择题1.已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁U(A∪B)等于( )A.{1,3,4}B.{3,4}C.{3}D.{4}2.已知全集U={1,2,3,4,5,6,7},A={3,4,5},B={1,3,6},则A∩(∁U B)等于( )A.{4,5}B.{2,4,5,7}C.{1,6}D.{3}3.设全集U={a,b,c,d,e},集合M={a,c,d},N={b,d,e},那么(∁U M)∩(∁N)等于( )UA.∅B.{d }C.{a ,c }D.{b ,e }4.已知集合A ={x |x <a },B ={x |1<x <2},且A ∪(∁R B )=R ,则实数a 的取值范围是( )A.{a |a ≤1}B.{a |a <1}C.{a |a ≥2}D.{a |a >2}5.设全集是实数集R ,M ={x |-2≤x ≤2},N ={x |x <1},则(∁R M )∩N 等于( )A.{x |x <-2}B.{x |-2<x <1}C.{x |x <1}D.{x |-2≤x <1}6.已知集合A ={x |-4≤x ≤-2},集合B ={x |x -a ≥0},若全集U =R ,且A ⊆∁U B ,则a 的取值范围为________.7.设U ={1,2,3,4,5,6,7,8,9},(∁U A )∩B ={3,7},(∁U B )∩A ={2,8},(∁U A )∩(∁U B )={1,5,6},则集合A =________,B =________.8.已知全集U =R ,A ={x ||3x -1|≤3},B ={x |⎩⎨⎧ 3x +2>0,x -2<0},求∁U (A ∩B ).9.已知集合A ={x |3≤x <6},B ={x |2<x <9}.(1)分别求∁R (A ∩B ),(∁R B )∪A ;(2)已知C ={x |a <x <a +1},若C ⊆B ,求实数a 的取值范围.10.已知A ={x |-1<x ≤3},B ={x |m ≤x <1+3m }.(1)当m =1时,求A ∪B ;(2)若B ⊆∁R A ,求实数m 的取值范围.11.已知集合{}31<≤-=x x A ;{}242-≥-=x x x B .(1)求B A ⋂;(2)若集合{}02>+=a x x C ,满足C C B =⋃,求实数a 的取值范围.12.设集合A ={x |x 2=4x },B ={x |x 2+2(a -1)x +a 2-1=0}.(1)若A ∩B =B ,求a 的取值范围;(2)若A ∪B =B ,求a 的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创设情景 兴趣导入
问题1 某小区共有150户居民,其中有110户订阅了报纸,问该 小区内有多少户居民没有订阅报纸?
问题2 某学习小组学生的集合为U={王明,曹勇,王亮,李冰, 张军,赵云,冯佳,薛香芹,钱忠良,何晓慧},其中在 学校应用文写作比赛与技能大赛中获得过金奖的学生集合 为P={王明,曹勇,王亮,李冰,张军},没有获得金奖的 学生有哪些?
.
67
89
A 13
45
U
01 2 B
46 3 5 78
9
U
巩固知识 典型例题
例 2 设 U=R, A x | 1 x 2 ,求 A .
通过观察数轴得到所求集合的补集,注意端点的处理.
演示说明
创 新培养 自我归纳Байду номын сангаас
对于非空集合 A:
A∩( U A )=
,
A∪( U A )=
,
UU =
,
U =
,
U ( U A )=
.
运用知识 强化练习
教材练习 1.3.3
1.设U 小于10的正整数 , A 1,4,7 ,求 U A .
2.设U = R , A x | 2 x 4 ,求 A .
理论升华 整体建构
集合 运算
什么是集合的交运算?如何用符号表示?如何用图形表示? 什么是集合的并运算?如何用符号表示?如何用图形表示? 什么是集合的补运算?如何用符号表示?如何用图形表示?
补集
如果集合A是全集U子集,那么,由U中不属于A的所有元 素组成的集合叫做集合A在全集U中的补集.
U A x x U 且 x A
.
演示说明
巩固知识 典型例题
例 1 设U 0,1, 2,3, 4,5,6,7,8,9 , A 1,3, 4,5 , B 3,5,7,8 .
求 UA及 UB.
02
动脑思考 探索新知
全集
如果一个集合含有我们所研究的各个集合的全部元素, 在研究过程中,可以将这个集合叫做全集,一般用U来表示, 所研究的各个集合都是这个集合的子集.
问题1中小区所有150户居民和问题2中学习小组的所有10名学生 就是所研究问题的全集 .
在研究数集时,常把实数集R作为全集.
动脑思考 探索新知
阅读 教材章节1.3 书写 学习与训练 1.3训练题 实践 了解全集和补集的生活应用
再见
运用
在进行集合的交运算、并运算和补运算时各自的特点是什么? .
.
用列举法和描述法表示集合时运算需要注意的问题是什么? .
交集
并集
补集
巩固知识 典型例题
例 3 设全集U 0,1,2,3,4,5,6,7,8,9 ,集合 A 1,3, 4,5 ,
B 3,5,7,8 .求 U A , U B , U A U B , U A U B , U A B , U A B .
.
1
7
43
58
A
B
02 6 9 U
巩固知识 典型例题 例 4 设全集 U =R,集合 A={x|x≤2},B={x|x>-4},
求 UA , UB, A B, A B.
在理解集合运算的含义基础上,充分运用数轴的表示来
.
进行求解.
作图解决
运用知识 强化练习
完成练习
1.设U 1,2,3,4,5,6,7,8 , A 2,4,6 , B 3,4,5 , 求 A B , A B , U A , U B , U A U B , U A U B .
第一章 集 合
1.3 集合的运算
高教社
复习知识 揭示课题
1 交集和并集的概念是什么?(含义和符号 ) 2 集合交运算和并运算各自的特点是什么? 3 用列举法和描述法表示的集合在运算时需要注意什么?
复习知识 揭示课题
完成练习
1.A={-1,0,1,2}, B={0,2,4,6},求A∩B , A∪B. 2. A={x|-2<x ≤ 2},B ={x|0 ≤ x≤4},求A∩B , A∪B.
2.设U | 0 180 , A | 0 90 , B | 90 180 ,
求 U A, U B , U A U B , U A U B .
归纳小结 强化思想
集合运算
运算特点
概念记法
高教社
综合应用
自我反思 目标检测
学习方法
学习行为
学习效果
作 业
高教社
