建筑结构荷载规范风振系数
风振系数及其计算取值

风振系数及其计算取值 Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT风振系数及其计算取值科技名词定义中文名称:风振系数英文名称:wind vibration coefficient 定义:脉动风压引起高耸建筑物的动力作用。
此时风压应再乘以风振系数βz。
风振系数βz与风速、脉动结构的尺度、结构固有频率、振型、结构组织以及地面粗糙度等有关。
应用学科:资源科技(一级学科);气候资源学(二级学科)风振系数是指风对建筑物的作用是不规则的,风压随风速、风向的紊乱变化而不停地改变。
通常把风作用的平均值看成稳定风压或平均风压,实际风压是在平均风压上下波动的。
平均风压使建筑物产生一定的侧移,而波动风压使建筑物在该侧移附近左右振动。
对于高度较大,刚度较小的高层建筑,波动风压会产生不可忽略的动力效应,在设计中必须考虑。
目前采用加大风荷载的办法来考虑这个动力效应,在风压值上乘以风振系数。
当房屋高度大于30m、高宽比大于时,以及对于构架、塔架、烟囱等高耸结构,均考虑风振。
( PS:对于30m以下且高宽比小于的房屋建筑,可以不考虑脉动风压影响,此时风振系数取β(z)=。
对于低矮、刚度比较大的结构,脉动风压引起的结构振动效应比较小,一般不需要考虑脉动风振作用,而仅考虑平均风压作用。
但是为了考虑脉动风压的影响,还是引入一个与风振系数不同的参数:阵风系数。
阵风系数考虑的是脉动风压的瞬间增大系数,即脉动风压的变异效应。
门式钢架也只需要考虑阵风系数。
但是门式钢架规程中没有采用阵风系数。
而参照美国的规范弄的,这个规范里的体型系数也是参考美国的,规程中解释已经考虑了阵风系数。
这与荷载规范GB5009中的体型系数不一样。
)《建筑结构荷载规范》(GB5009-2001)在计算风荷载时提到了这两个系数,但是在结合实际工程使用中,结构上的风荷载可分为两种成分:平均风和脉动风。
对应地,风对结构的作用也有静力的平均风作用和动力的脉动风作用。
通用规范风荷放大系数

通用规范风荷放大系数
《建筑结构荷载规范》中的风振系数和阵风系数都是在平均风压基础上的放大系数。
它们都是因为要考虑风压随时间的上下波动(风荷载脉动)而引入的,只不过阵风系数用于围护结构,只取决于风场特性;而风振系数用于主要受力结构,除了风场特性之外还和结构的动力特性相关。
规范的“风荷载放大系数”是这两个系数的统称,第4.6.5条的第1款和第2款分别规定了主要受力结构和围护结构风荷载放大系数的取值要求。
主要受力结构的放大系数不能小于1.2,是对所有工程结构都适用吗?和原来荷载规范的风振系数适用范围似乎不同?
是的。
和原来荷载规范的规定有所不同,主要受力结构风荷载放大系数的规定,适用于所有工程结构。
作用于结构表面的风压时时刻刻都在发生变化,即使不考虑动力放大效应、将结构作为准静态结构(即根据Kx(t)=P(t)计算结构的响应),风荷载引起的响应也是围绕均值波动的(见下图)。
只用平均风荷载进行设计,将会低估结构的响应。
因此,所有工程结构
在进行主要受力结构设计时,都应当考虑风荷载脉动的增大效应,在平均风荷载基础上乘以放大系数。
而且根据通用规范,主要受力结构的放大系数不应小于1.2。
关于构架风振系数的探讨

关于构架风振系数的探讨摘要:随着生产装置的大型化,装置中的构筑物尺寸也随之增大、增高。
风荷载作为水平荷载的重要性尤为突出。
风荷载中的风振系数对风荷载大小的影响相对较大,从风振系数的计算公式中可以分析出,结构的基本自振周期影响风振系数。
本文通过不同的结构模型,探讨风振系数与结构基本自振周期的关系。
关键词:风荷载;风振系数;基本自振周期1引言随着经济的发展,石油化工行业也随之发展迅速。
为满足生产需要,装置构筑物的尺寸也随之增大、增高。
而石化行业的构筑物作为生产装置建设的重要组成部分,其具有鲜明的行业特点。
不同于一般的民用建筑,石化行业的构筑物外形设计出于工艺布置的要求,其体型往往较一般民用建筑复杂,且其使用功能明确,服务于单台或多台石化设备,多数为敞开式无围护结构。
因此在构筑物的设计中,风荷载与地震作用作为重要的水平荷载需重点考虑。
风荷载是空气流动形成的,对构筑物的作用时不规则的,风荷载实际上是一种随机时变活荷载,但不同于一般活荷载(楼面和屋面活荷载、吊车荷载、雪荷载)为了结构设计方便,基本上都是将风荷载转为确定性的静力等效风。
因此,风引起对结构作用的风荷载是石化行业各类构筑物的重要设计荷载。
在高耸结构中,竖向荷载对结构设计产生重要影响,但水平荷载却起着决定性作用,是结构计算中必不可少的组成部分。
风荷载计算中风振系数比较复杂,与之影响的因素较多,因此风振系数的计算相当重要。
风振系数是指风对建筑物的作用是不规则的,风压随风速、风向的紊乱变化而不停地改变。
通常把风作用的平均值看成稳定风压或平均风压,实际风压是在平均风压上下波动的。
平均风压使建筑物产生一定的侧移,而波动风压使建筑物在该侧移附近左右振动。
对于高度较大,刚度较小的高层建筑,波动风压会产生不可忽略的动力效应,在设计中必须考虑。
2风荷载计算中风振系数的分析2.1风荷载的计算目前石化行业构筑物抗风设计中对于风荷载的取值主要依据SH/T 3077-2012《石油化工钢结构冷换框架设计规范》(本文简称《冷换规范》)附录A[1]计算。
风荷载计算算例

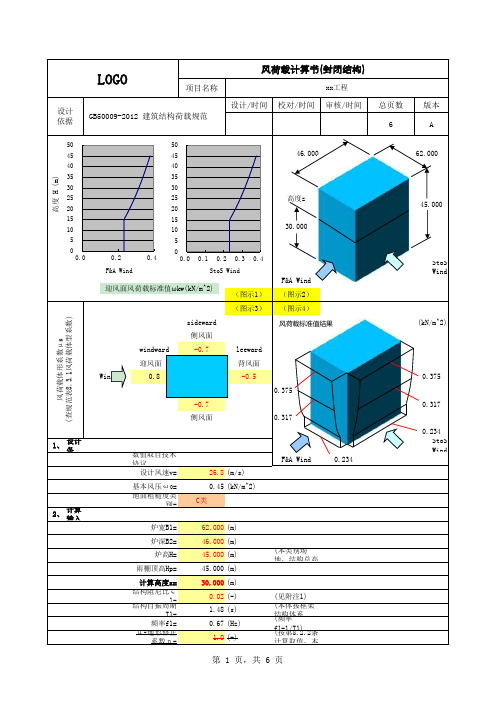
.风荷载计算 根据《建筑结构荷载规范》(GB50009-2012)规范,风荷载的计算公式为:0k z s z w u u βω= ()s u ——体型系数z u ——风压高度变化系数z β——风振系数0ω——基本风压k w ——风荷载标准值体型系数s u 根据建筑平面形状由《建筑结构荷载规范》项次30,迎风面体型系数(压风指向建筑物内侧),背风面(吸风指向建筑外侧面),侧风面(吸风指向建筑外侧面)。
风压高度变化系数z u 根据建筑物计算点离地面高度和地面粗糙度类别,按照规范表确定。
本工程结构顶端高度为+=米,建筑位于北京市郊区房屋较稀疏,由规范条地面粗糙度为B 类。
由表高度90米和100米处的B 类地面粗糙度的风压高度变化系数分别为和。
则米高度处的风压高度变化系数通过线性插值为:对于高度大于30m 且高宽比大于的房屋,以及基本自振周期T1大于的各种高耸结构,应考虑风压脉动对结构产生顺风向风振的影响。
本工程30层钢结构建筑。
基本周期估算为()1T =0.10~0.15n=3.0~4.5s ,应考虑脉动风对结构顺风向风振的影响,并由下式计算:1012Z z gI B β=+ ()式中:g ——峰值因子,可取10I ——10m 高度名义湍流强度,对应ABC 和D 类地面粗糙,可分别取、、和;R ——脉动风荷载的共振分量因子z B ——脉动风荷载的背景分量因子脉动风荷载的共振分量因子可按下列公式计算:式中:1f ——结构第1阶自振频率(Hz )w k ——地面粗糙度修正系数,对应A 、B 、C 和D 类地面粗糙,可分别取、、和; 1ζ——结构阻尼比,对钢结构可取,对有填充墙的钢结构房屋可取,对钢筋混凝土及砌体结构可取,对其他结构可根据工程经验确定。
经过etabs 软件分析,结构自振周期1 4.67f s =脉动风荷载的背景分量因子可按下列规定确定:式中:1()z φ——结构第1阶振型系数H ——结构总高度(m ),对应A 、B 、C 和D 类地面粗糙度,H 的取值分别不能大于300m 、350m 、450m 和550m ;x ρ——脉动风荷载水平方向相关系数;z ρ——脉动风荷载竖向方向相关系数;k 、1α——脉动风荷载的空间相关系数可按下列规定确定:(1)竖直方向的相关系数可按下式计算:式中:H ——结构总高度(m );对应A 、B 、C 和D 类地面粗糙度,H 的取值分别不应大于300m 、350m 、450m 和550m ;(2) 水平方向相关系数可按下式计算:式中:B ——结构迎风面宽度(m ),2B H ≤。
建筑结构荷载规范风振系数

建筑结构荷载规范·风荷载·顺风向风振和风振系数编制日期:2002-3-1 点击:344 人次如果公式不能正确显示,您需要安装IE6和MathPlayer7.4.1对于基本自振周期T1 大于0.25s 的工程结构,如房屋、屋盖及各种高耸结构,以及对于高度大于30m 且高宽比大于1.5 的高柔房屋,均应考虑风压脉动对结构发生顺风向风振的影响。
风振计算应按随机振动理论进行,结构的自振周期应按结构动力学计算。
注:近似的基本自振周期T1 可按附录E 计算。
7.4.2对于一般悬臂型结构,例如构架、塔架、烟囱等高耸结构,以及高度大于30m,高宽比大于1.5 且可忽略扭转影响的高层建筑,均可仅考虑第一振型的影响,结构的风荷载可按公式(7.1.1-1)通过风振系数来计算,结构在z 高度处的风振系数βz可按下式计算:`β_z=1+(ξv varphi_z)/μ_z`(7.4.2)式中`ξ`—脉动增大系数;`v`—脉动影响系数;`v varphi_z`—振型系数;`μ_z`—风压高度变化系数。
7.4.3脉动增大系数,可按表7.4.3 确定。
注:计算`ω_0T_1^2`时,对地面粗糙度B 类地区可直接代入基本风压,而对A 类、C 类和D 类地区应按当地的基本风压分别乘以1.38、0.62 和0.32 后代入。
7.4.4脉动影响系数,可按下列情况分别确定。
1结构迎风面宽度远小于其高度的情况(如高耸结构等):1) 若外形、质量沿高度比较均匀,脉动系数可按表7.4.4-1 确定。
2) 当结构迎风面和侧风面的宽度沿高度按直线或接近直线变化,而质量沿高度按连续规律变化时,表7.4.4-1 中的脉动影响系数应再乘以修正系数`θ_B`和`θ_voθ_B`应为构筑物迎风面在z 高度处的宽度Bz 与底部宽度`B_o` 的比值;`θ_ν`可按表7.4.4-2 确定。
注:`B_H、B_o` 分别为构筑物迎风面在顶部和底部的宽度。
建筑结构荷载规范

设 甲类 防 乙类 分 丙类 类 丁类
重大建筑工程和地震时可能发生严重次生灾害的建筑 地震时使用功能不能中断需尽快恢复的建筑 除甲乙丁类以外的一般建筑 抗震次要建筑
2023/12/5
35
2.抗震设防措施
抗震措施:除结构地震作用计算和抗力计算以外的抗震设计内容, 包括抗震构造措施。
2023/12/5
9
2023/12/5
10
2023/12/5
11
2)群体风压体型系数
对建筑群,尤其是高层建筑群,当房屋 相互间距较近时,由于漩涡的相互干扰, 房屋某些部位的局部风压会显著增大。为 此,《高层规程》规定,当多栋或群集的 高层建筑相互间距较近时,宜考虑风力相 互干扰的群体效应。一般可将单体建筑的
措
构改用抗震性能较好的结构类型时,应允许仍按本地区抗震设防烈度的要求采取
施
抗震措施。
丙类 应符合本地区抗震设防烈度度的要求
丁类 应允许比本地区抗震设防烈度的要求适当降低,但抗震设防烈度为6度时 不应降低
较小乙类建筑:工矿企业的变电所、空压站以及城市供水水源的泵房等。
抗震性能较好的结构类型指钢筋混凝土结构或钢结构。
坏,经一般修理或不需修理仍可继续使用。
当遭受高于本地区抗震设防烈度的预估的罕遇地震影响时,
不致倒塌或发生危及生命的严重破坏。
2023/12/5
32
3.“两阶段”抗震设计方法
第一阶段: 对绝大多数结构进行小震作用下的结构和构件承载力验
算;在此基础上对各类结构按规定要求采取抗震措施。
第二阶段: 对一些规范规定的结构进行大震作用下的弹塑性变形验
地震时,由于地震波的作用产生地面运 动,并通过房屋基础影响上部结构,使结 构产生的动态作用,这就是地震作用。地 震波会使房屋产生竖向振动和水平振动, 一般对房屋的破坏主要是由水平振动造成 的,因此设计中主要考虑水平地震作用, 只有震中附近的高烈度区或竖向振动会产 生严重后果时,才同时考虑竖向地震作用。
风振系数及其计算取值

风振系数及其计算取值公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]风振系数及其计算取值科技名词定义中文名称:风振系数英文名称:wind vibration coefficient 定义:脉动风压引起高耸建筑物的动力作用。
此时风压应再乘以风振系数βz。
风振系数βz与风速、脉动结构的尺度、结构固有频率、振型、结构组织以及地面粗糙度等有关。
应用学科:资源科技(一级学科);气候资源学(二级学科)风振系数是指风对建筑物的作用是不规则的,风压随风速、风向的紊乱变化而不停地改变。
通常把风作用的平均值看成稳定风压或平均风压,实际风压是在平均风压上下波动的。
平均风压使建筑物产生一定的侧移,而波动风压使建筑物在该侧移附近左右振动。
对于高度较大,刚度较小的高层建筑,波动风压会产生不可忽略的动力效应,在设计中必须考虑。
目前采用加大风荷载的办法来考虑这个动力效应,在风压值上乘以风振系数。
当房屋高度大于30m、高宽比大于时,以及对于构架、塔架、烟囱等高耸结构,均考虑风振。
( PS:对于30m以下且高宽比小于的房屋建筑,可以不考虑脉动风压影响,此时风振系数取β(z)=。
对于低矮、刚度比较大的结构,脉动风压引起的结构振动效应比较小,一般不需要考虑脉动风振作用,而仅考虑平均风压作用。
但是为了考虑脉动风压的影响,还是引入一个与风振系数不同的参数:阵风系数。
阵风系数考虑的是脉动风压的瞬间增大系数,即脉动风压的变异效应。
门式钢架也只需要考虑阵风系数。
但是门式钢架规程中没有采用阵风系数。
而参照美国的规范弄的,这个规范里的体型系数也是参考美国的,规程中解释已经考虑了阵风系数。
这与荷载规范GB5009中的体型系数不一样。
)《建筑结构荷载规范》(GB5009-2001)在计算风荷载时提到了这两个系数,但是在结合实际工程使用中,结构上的风荷载可分为两种成分:平均风和脉动风。
对应地,风对结构的作用也有静力的平均风作用和动力的脉动风作用。
风荷载计算(GB50009-2012)
1.04 1.03 1.01 1.00 0.98 0.97 0.95 0.94 0.92 0.90 0.89 0.87 0.85 0.83 0.81 0.79 0.77 0.75 0.73 0.71 0.69 0.66 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65 0.65
风荷载计算书(封闭结构)
xx工程
F&A Wind
βz
合计ωk
(-)
(kN/m^2)
StoS Wind
βz
合计ωk
(-)
(kN/m^2)
1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
0.609 0.600 0.592 0.583 0.575 0.566 0.557 0.547 0.538 0.528 0.518 0.508 0.498 0.487 0.476 0.465 0.453 0.441 0.428 0.415 0.402 0.388 0.380 0.380 0.380 0.380 0.380 0.380 0.380 0.380 0.380
第 4 页,共 6 页
LOGO
项目名称
风荷载计算书(封闭结构)
xx工程
表3--
序号
(-) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建筑结构荷载规范·风荷载·顺风向风振和风振系数
编制日期:2002-3-1 点击:344 人次如果公式不能正确显示,您需要安装IE6和MathPlayer
7.4.1对于基本自振周期T1 大于0.25s 的工程结构,如房屋、屋盖及各种高耸结构,以及对于高度大于30m 且高宽比大于1.5 的高柔房屋,均应考虑风压脉动对结构发生顺风向风振的影响。
风振计算应按随机振动理论进行,结构的自振周期应按结构动力学计算。
注:近似的基本自振周期T1 可按附录E 计算。
7.4.2对于一般悬臂型结构,例如构架、塔架、烟囱等高耸结构,以及高度大于30m,高宽比大于1.5 且可忽略扭转影响的高层建筑,均可仅考虑第一振型的影响,结构的风荷载可按公式(7.1.1-1)通过风振系数来计算,结构在z 高度处的风振系数βz可按下式计算:
`β_z=1+(ξv varphi_z)/μ_z`(7.4.2)
式中`ξ`—脉动增大系数;
`v`—脉动影响系数;
`v varphi_z`—振型系数;
`μ_z`—风压高度变化系数。
7.4.3脉动增大系数,可按表7.4.3 确定。
注:计算`ω_0T_1^2`时,对地面粗糙度B 类地区可直接代入基本风压,而对A 类、C 类和D 类地区应按当地的基本风压分别乘以1.38、0.62 和0.32 后代入。
7.4.4脉动影响系数,可按下列情况分别确定。
1结构迎风面宽度远小于其高度的情况(如高耸结构等):
1) 若外形、质量沿高度比较均匀,脉动系数可按表7.4.4-1 确定。
2) 当结构迎风面和侧风面的宽度沿高度按直线或接近直线变化,而质量沿高度按连续规律变化时,表7.4.4-1 中的脉动影响系数应再乘以修正系数`θ_B`和`θ_voθ_B`应为构筑物迎风面在z 高度处的宽度Bz 与底部宽度`B_o` 的比值;`θ_ν`可按表7.4.4-2 确定。
注:`B_H、B_o` 分别为构筑物迎风面在顶部和底部的宽度。
2结构迎风面宽度较大时,应考虑宽度方向风压空间相关性的情况(如高层建筑等):若外形、质量沿高度比较均匀,脉动影响系数可根据总高度H 及其与迎风面宽度B 的比值,按表7.4.4-3 确定。
7.4.5振型系数应根据结构动力计算确定。
对外形、质量、刚度沿高度按连续规律变化的悬臂型高耸结构及沿高度比较均匀的高层建筑,振型系数也可根据相对高度z/H 按附录F 确定。
7.5.1计算围护结构风荷载时的阵风系数应按表7.5.1 确定。
资料来源:《建筑结构荷载规范》GB 50009—2001
7.6.1对圆形截面的结构,应根据雷诺数Re 的不同情况按下述规定进行横风向风振(旋涡脱落)的校核:
1当Re<3×105时(亚临界的微风共振),应按下式控制结构顶部风速υH不超过临界风速υcr,υcr和υH可按下列公式确定:
`v_(cr)=D/(T_1S_t)`(7.6.1-1)
`v_H=sqrt((2000γWμHω_0)/ρ)`(7.6.1-2)
式中`T_1`—结构基本自振周期;
`S_t`—斯脱罗哈数,对圆截面结构取0.2;
`γ_W`—风荷载分项系数,取1.4;
`μ_H`—结构顶部风压高度变化系数;
`ω_0`—基本风压(`kN//m^2`);
`ρ`—空气密度(`kg//m^3`)。
当结构顶部风速超过`υ_(cr)`时,可在构造上采取防振措施,或控制结构的临界风速`υ_(cr)` 不小于15m/s。
2Re≥3.5×106且结构顶部风速大于`υ_(cr)`时(跨临界的强风共振),应按第7.6.2条考虑横风向风荷载引起的荷载效应。
3雷诺数Re 可按下列公式确定:
`R_e=69000vD`(7.6.1-3)
式中υ—计算高度处的风速(m/s);
D—结构截面的直径(m)。
4当结构沿高度截面缩小时(倾斜度不大于0.02),可近似取
2/3 结构高度处的风速和直径。
7.6.2跨临界强风共振引起在z 高处振型j 的等效风荷载可由下列公式确定:
`ω_(czj)=│λ_j│v_(cr)^2varphi_(zj)//12800ζ_j(kN//m^2)`(7.6.2-1)
式中`λ_j`—计算系数,按表7.6.2 确定;
`varphi_(zj)` —在z 高处结构的j 振型系数,由计算确定或参考附录F;
`ζ_j`—第j 振型的阻尼比;对第1 振型,钢结构取0.01,房屋钢结构取0.02,混凝土结构取0.05;对高振型的阻尼比,若无实测资料,可近似按第1 振型的值取用。
表7.6.2 中的`H_1` 为临界风速起始点高度,可按下式确定:
`H_1=H×(v_(cr)/v_H)^(1/a)`(7.6.2-2)
式中`α`—地面粗糙度指数,对A、B、C 和D 四类分别取0.12、0.16、0.22 和0.30;
`υ_H`—结构顶部风速(m/s)。
注: 校核横风向风振时所考虑的高振型序号不大于4,对一般悬臂型结构,可只取第1 或第2 个振型。
7.6.3校核横风向风振时,风的荷载总效应可将横风向风荷载效应`S_c` 与顺风向风荷载效应`S_A` 按下式组合后确定:
`S=sqrt(S_c^2+S_A^2)`(7.6.3)
7.6.4对非圆形截面的结构,横风向风振的等效风荷载宜通过空气弹性模型的风洞试验确定;也可参考有关资料确定。
. .。
