圆波导与矩形波导比较
微波技术__期末考试试卷

微波技术 期末考试试卷(A )标准答案及评分标准一、简答题(每小题3分) 1、 如何判断长线和短线?答:长线是传输线几何长度l 与工作波长λ可以相比拟的传输线(1.5分),(必须考虑波在传输中的相位变化效应),短线是几何长度l 与工作波长λ相比可以忽略不计的传输线(1.5分)。
(界限可以认为是/0.05l λ≥)。
2、 何谓分布参数电路?何谓集总参数电路? 答:集总参数电路由集总参数元件组成,连接元件的导线没有分布参数效应,导线沿线电压、电流的大小与相位与空间位置无关(1.5分)。
分布参数电路中,沿传输线电压、电流的大小与相位随空间位置变化,传输线存在分布参数效应(1.5分)。
3、 何谓色散传输线?对色散传输线和非色散传输线各举一个例子。
答:支持色散模式传输的传输线,(0.5分)色散模式是传输速度(相速与群速)随频率不同而不同的模式(0.5分)。
支持非色散模式传输的传输线(0.5分),非色散模式是传输速度(相速与群速)不随频率而改变的模式。
(0.5分) 色散模式传输线:波导(0.5分)非色散模式传输线:同轴,平行双导体,微带。
(0.5分) 4、 均匀无耗长线有几种工作状态?条件是什么?答:均匀无耗长线有三种工作状态,分别是驻波、行波与行驻波。
(1.5分) 驻波:传输线终端开路、短路或接纯电抗;(0.5分) 行波:半无限长传输线或终端接负载等于长线特性阻抗;(0.5分) 行驻波:传输线终端接除上述负载外的任意负载阻抗;(0.5分)5、 什么是波导中的模式简并?矩形波导和圆波导中的简并有什么异同? 答:不同模式具有相同的特性(传输)参量叫做模式简并。
(1分) 矩形波导中,TE mn 与TM mn (m 、n 均不为零)互为模式简并。
(1分) 圆波导的简并有两种,一种是极化简并。
其二是模式简并,(1分)6、 空气填充的矩形波导(宽边尺寸为a ,窄边尺寸为b )中,要求只传输10H 波型,其条件是什么?答:由于10H 的截止波长2c a λ=,而20H 的截止波长为a ,01H 的截止波长为2b ,若保证10H 单模传输,因此传输条件max (,2)2a b a λ<<(3分)。
微波技术第3章1矩形波导

可见前五个导模是 TE10、TE20、TE01、 TE11、TM11。
35
则TE10模 TE20模 TE01模 TE11和TM11模 TE21和TM21模 TE12和TM12模
• 当f0 = 10GHz时,λc=3cm
fcTE10=6.562GHz fcTE20=13.123GHz fcTE01=14.764GHz fcTE11=16.156GHz fcTE21=19.753GHz fcTE12=30.248GHz
传播。
编辑ppt
13
TE20模场结构
TE10 TE20
编辑ppt
14
(2)TE01模与TE0n模
其场分量为
Ex
j n
b H mn sin n b y e
jz
Hy
j n
b
ny
H mn sin b e
jz
Hz
ny H mn cos b e
jz
Ey Ez H x 0
TE01模只有Ex、Hy和Hz三个场分量,它们与x无关,故 沿a边场无变化;
波分布或TM11模场;如 图。
注:TE11与TM11是简并模,这种简并称为模式简并; 同理,TEmn与TMmn (m>0, n>0) 是简并模。
编辑ppt
19
3.管壁电流 Js nˆHtan
主模:TE10模工作下
波导底面 y = 0 ; nˆ yˆ
JSy 0 y ˆ [x ˆHx zˆHz] x ˆHz zˆHx
ZTM
Eu Hv
2
1
k
c
编辑ppt
31
(5)TE10模矩形波导的传输功 率
P Re 1 E H * ds 2S
圆波导与矩形波导比较
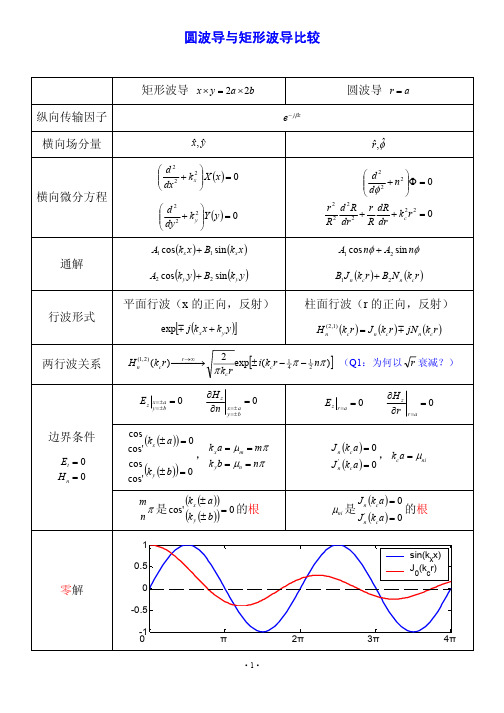
B1 J n (kc r ) + B2 N n (kc r )
平面行波(x 的正向,反射) 行波形式
exp m j (k x x + k y y )
→∞ (1, 2 ) Hn (kc r ) r →
柱面行波(r 的正向,反射)
( 2 ,1) (kc r ) = J n (kc r ) m jN n (kc r ) Hn
驻波波节数: 从中心到边界 的半驻波数
0 0 π 2π 3π 0.5
|sin(kxx)| |J0(kcr)|
4π
相邻波节反相,柱面波周向周期变化 各自周期相等 边界处的函数值取其中一零解上,不同的零点,包含波节数不同 驻波异同 零解从 = 0 开始 等幅驻波 两驻波关系 坐标系/驻波函数的不同仅方便满足边界条件时,函数形式简单 *柱面波的求解方法 3 级数、积分、插值,高阶递推
[
]
两行波关系
2 1 ] (Q1:为何以 r 衰减?) exp[± i(kc r − 1 4 π − 2 nπ ) π kc r
Ez
x=± a y =±b
=0
∂H z ∂n
x=± a y =±b
=0
Ez
r =a
=0
∂H z ∂r
=0
r =a
边界条件
Et = 0 Hn = 0
cos (k x (± a )) = 0 k a = µ m = mπ cos' , x k y b = µ n = nπ cos ( k y (± b )) = 0 cos'
0 -0.5 -1 0 π
·1·
2π
3π
4π
满足边界条件 后的驻波解
cos mπ A cos' a
微波技术基础试题三

一.简答:(50分)1.什么是色散波和非色散波?(5分)答:有的波型如TE波和TM波,当波导的形状、尺寸和所填充的介质给定时,对于传输某一波形的电磁波而言,其相速v p和群速v g都随频率而变化的,把具有这种特性的波型称为色散波。
而TEM波的相速v p和群速v g 与频率无关,把具有这种特性的波型称为非色散波。
2.矩形波导、圆波导和同轴线分别传输的是什么类型的波?(5分)答:(1)矩形波导为单导体的金属管,根据边界条件波导中不可能传输TEM 波,只能传输TE波和TM波。
(2)圆波导是横截面为圆形的空心金属管,其电磁波传输特性类似于矩形波导不可能传输TEM波,只能传输TE波和TM波。
(3)同轴线是一种双导体传输线。
它既可传输TEM波,也可传输TE 波和TM波。
3.什么是TE波、TM波和TEM波?(5分)答:根据导波系统中电磁波按纵向场分量的有无,可分为三种波型: (1)横磁波(TM 波),又称电波(E 波):0=H Z ,0≠E Z ; (2)横电波(TE 波),又称磁波(H 波):0=E Z ,0≠H Z ;(3)横电磁波(TEM ):0=E Z ,0=H Z 。
4.导波系统中的相速和相波长的含义是什么?(5分)答:相速v p 是指导波系统中传输电磁波的等相位面沿轴向移动的速度。
相波长λp 是指等相位面在一个周期T 移动的距离。
5.为什么多节阶梯阻抗变换器比单节阻抗变换器的工作频带要宽?(5分) 答:以两节阶梯阻抗变换器为例,设每节4λ阻抗变换器长度为θ,三个阶梯突变的电压反射系数分别为ΓΓΓ21,,则点反射系数为eeUU j j ir θθ42210--ΓΓΓ++==Γ,式中说明,当采用单节变换器时只有两个阶梯突变面,反射系数Γ的表达式中只有前两项,若取ΓΓ=10,在中心频率处,2/πθ=这两项的和为零,即两突变面处的反射波在输入端相互抵消,从而获得匹配;但偏离中心频率时,因2/πθ≠,则两个反射波不能完全抵消。
第四章2 波导和空腔(矩、圆形波导、谐振腔)

3) k 0
X "( x) 0 Y "( y ) 0
X ( x) A0 B0 x Y ( y) C0 D0 y
u( x, y) ( A0 B0 x)(C0 D0 y)
m n x)sin( y )exp(ik z z ) a b
横纵向场关系式
H TM波, z 0
Ez H z 1 Ex 2 ik z i 2 k z x y 1 Ey 2 k z2 Ez H z ik z i y x
则te10cte106562ghzte20cte2013123ghzte30cte3019685ghzte01cte0114764ghzte02cte0229528ghzte11和tm11cte1116156ghzte21和tm21cte2119753ghzte12和tm12cte1230248ghzte10te20te01te11tm1120944m1此时该波导只能传输te1015ghz时此时该波导能传输te10te20te01三个导模则te10cte106562ghzte20cte2013123ghzte30cte3019685ghzte01cte0114764ghzte02cte0229528ghzte11和tm11cte1116156ghzte21和tm21cte2119753ghzte12和tm12cte1230248ghz第四章波导和空腔第四章波导和空腔4646圆形波导圆形波导纵向分量均满足的helmholtz方程谐振动方程bessel方程tm模式1基本方程和分离变量解谐振动方程m阶实宗量bessel方程sincossincos第二种表示形式是考虑到圆波导结构具有轴对称性场的极化方向具有不确定性使导波场在方向存在cosm和sinm两种可能的分布
(完整版)微波课后作业题(部分)

习题课1.1 设一特性阻抗为50Ω的均匀传输线终端接负载R l =100Ω,求负载反射系数Γl ,在离负载0.2λ、0.25λ及0.5λ处的输入阻抗及反射系数分别为多少?解:根据终端反射系数与终端阻抗的关系10l 10100501100503Z Z Z Z --Γ===++根据传输线上任一点的反射系数与输入阻抗的关系2()j zlz ein 01()1()z Z Z z 得到离负载0.2λ、0.25λ及0.5λ处的输入阻抗及反射系数分别为2πj20.2λj0.8πλ1(0.2λ)3l eeZ (0.2λ)29.4323.79Ωin2πj20.25λλ1(0.25λ)3l e Z (0.25)25Ωin2πj20.5λλ1(0.5λ)3l e(反射系数具有λ/2周期性) Z (0.5)100Ωin (输入阻抗具有λ/2周期性)1.2 求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗;若在两导体间填充介电常数εr=2.25的介质,求其特性阻抗及300MHz 时的波长。
解:空气同轴线的特性阻抗为0.7560ln60ln65.9Ω0.25b Z a填充相对介电常数εr=2.25的介质后,其特性阻抗为60600.75lnln 43.9Ω0.252.25rb Z af =300Mhz 时的波长/=0.67m rc f1.4 有一特性阻抗Z 0=50Ω的无耗均匀传输线,导体间的媒质参数εr=2.25,μr=1,终端接有R l =1Ω的负载。
当f =100MHz 时,其线长度为λ/4。
试求:① 传输线实际长度; ② 负载终端反射系数; ③ 输入端反射系数; ④ 输入端阻抗。
解:①传输线上的波长为/=2m g rc f所以,传输线的实际长度为=0.5m 4gl②根据终端反射系数与终端阻抗的关系10l 101504915051Z Z Z Z --Γ===-++③根据传输线上任一点的反射系数与终端反射系数的关系220.2524949()5151j j zl z ee ④传输线上任一点的反射系数与输入阻抗的关系in 04911()51502500Ω491()151z Z Z z1.10 特性阻抗为Z 0=150Ω的均匀无耗传输线, 终端接有负载Z l =250+j100Ω,用λ/4阻抗变换器实现阻抗匹配(如图所示),试求λ/4阻抗变换器的特性阻抗Z 01及离终端距离。
圆形波导的理论分析和特性
传播常数: mn k k 截至波长: cmn 截至频率 2 a u 'mn v
u 'mn k a
2
2
3.2 18
3.2 19 3.2 20
f cmn
cmn
u 'mn 2 a
其中贝塞尔函数最小根u11'=1.841对应TE11模。 c=3.41a;次低模为根u01=3.832, c=1.64a
圆形波导分析 – TM modes.(续四)
波导阻抗: Z TM Ef Er Hf H r w k
2 2 cmn 2
3.2 25
2
传播常数: mn k k 截至波长: cmn 截至频率 2 a u mn v
u mn k a
m 0 n 1
u m n co s m f j ( w t z ) jw m a 2 E mn J m ( r) e 2 si n m f u mn r a co s m f j ( w t z ) jw a ' u mn E mn J m ( r) e sin m f u mn a
3.2 26
3.2 27 3.2 28
f cmn
cmn
u mn 2 a
其中贝塞尔函数最小根 u01=2.405对应TM01模。 c=2.62a
圆形波导的特性
圆形波导模的传输条件是c> 或fc<f;传输特性 与矩形波导类似,为高通器件。 圆形波导存在两种模式简并现象: TE0n与TMm0的模兼并; 另一种是m非零的TEmn与TMmn模的极化简并。 圆形波导的基模—— 主模为TE11,其截止波长最长(TE11=3.41a) 次模为TM01,其截止波长最长(TM01=2.62a)
射频技术基础:第2章 规则金属波导

Z (z) Aerz
(2- 1- 9)
A+为待定常数, 对无耗波导γ =jβ, 而β为相移常数。
现设Eoz(x, y) = A+Ez(x, y), Ez(x, y, z)=Eoz(x, y)e-jβz
(2- 1- 10a)
同理, 纵向磁场也可表达为: Hz(x, y, z)=Hoz(x, y)e -jβz
多工器
双工器
引言
规则金属波导 Regular Waveguide 无限长笔直金属管组成 纵向均匀(尺寸、填充) 封闭 ----- 能量局限在波导之中
规则金属波导管壁材料:铜、铝,有时其壁上镀金或银。
金属波导优点:导体损耗和介质损耗小、功率容量大、 没有辐射损耗、结构简单、易于制造。
形状:横截面有矩形、圆形、脊形、椭圆形、三角形等。
H z
x H z
y
|x0 |y0
H z
x H z
y
|
xa
0
|
y
b
0
(2- 2- 6)
将式(2 -2 -5)代入式(2 -2 -6)可得
A2 0 B2 0
kx
m
a
ky
n
b
m 0、1、2、
n=0、1、2、
(2- 2- 7)
第2章 规则金属波导
于是矩形波导TE波纵向磁场的基本解为
Hz
3) kc2 0
这时 k 2 kc2 k 而相速vp / c / rr , 即相速
比无界媒质空间中的速度要慢, 故又称之为慢波。
金属波导的处理方法和特点:
小结:
(1)maxwell方程+边界条件,属于本征值问题 (2)认为管内填充的介质为理想介质 (3)由于管壁为金属,导电率高,认为是理想的导体 (4)边界条件:认为波导管壁处的切向电场分量和法向磁场分量为0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
驻波波节数: 从中心到边界 的半驻波数
0 0 π 2π 3π 0.5
|sin(kxx)| |J0(kcr)|
4π
相邻波节反相,柱面波周向周期变化 各自周期相等 边界处的函数值取其中一零解上,不同的零点,包含波节数不同 驻波异同 零解从 = 0 开始 等幅驻波 两驻波关系 坐标系/驻波函数的不同仅方便满足边界条件时,函数形式简单 *柱面波的求解方法 3 级数、积分、插值,高阶递推
ˆ ˆ, φ r
d2 2 dφ 2 + n Φ = 0 2 2 r d R r dR + + k c2 r 2 = 0 2 2 R dr R dr
A1 cos nφ + A2 sin nφ
横向微分方程
A1 cos(k x x ) + B1 sin (k x x )
通解
A2 cos(k y y ) + B2 sin (k y y )
B1 J n (kc r ) + B2 N n (kc r )
平面行波(x 的正向,反射) 行波形式
exp m j (k x x + k y y )
→∞ (1, 2 ) Hn (kc r ) r →
柱面行波(r 的正向,反射)
( 2 ,1) (kc r ) = J n (kc r ) m jN n (kc r ) Hn
圆波导与矩形波导比较
矩形波导 x × y = 2a × 2b 纵向传输因子 横向场分量
ˆ, y ˆ x
d2 2 dx 2 + k x X (x ) = 0 d2 2 + k y 2 Y ( y ) = 0 dy
圆波导 r = a
e − jβ z
J n (k c a ) = 0
' (k c a ) = 0 Jn
, kc a = µ ni
m n
π 是 cos'
(k x (± a )) (k y (± b)) = 0 的根
µ ni 是
J n (kc a ) = 0
' (kc a ) = 0 Jn
的根
1 0.5
sin(kxx) J0(kcr)
零解
0 -0.5 -1 0 π
·1·
2π
3π
4π
满足边界条件 后的驻波解
cos mπ A cos' a
1
cos nπ x y cos' b
J µ ni cos nφ A n r ' J n a cos' nφ
[
]
两行波关系
2 1 ] (Q1:为何以 r 衰减?) exp[± i(kc r − 1 4 π − 2 nπ ) π kc r
Ez
x=± a y =±b
=0
∂H z ∂n
x=± a y =±b
=0
Ez
r =a
=0
∂H z ∂r
Байду номын сангаас=0
r =a
边界条件
Et = 0 Hn = 0
cos (k x (± a )) = 0 k a = µ m = mπ cos' , x k y b = µ n = nπ cos ( k y (± b )) = 0 cos'
m n
零解从 i = 1 (第一个 0)开始 (n 是阶数, 也反映周向重复次数) 降幅驻波(Q2:以 r 衰减?)
相互可以表示成对方的级数和
·2·
