应用动量守恒定律研究人船模型问题
高中物理教研论文巧解人船模型问题(最全)word资料

高中物理教研论文巧解人船模型问题(最全)word资料巧解人船模型问题——平均动量守恒定律的应用1.平均动量守恒定律当系统在全过程中动量守恒时,则这一系统在全过程中的平均动量也守恒。
在符合动量守恒的条件下,如果物体做变速运动,为了求解位移,可用平均动量及其守恒规律来处理。
2. 人船模型如果系统是由两(或多)个物体组成的,合外力为零,且相互作用前合动量为零,我们称为人船模型。
(1)一人一船模型:如图1所示人由左端走到右端的过程中, 由动量守恒定律,得 02211=-v m v m由于在全过程动量都守恒,所以有 0211=---v m v m同乘以时间t ,得 0211=---t v m t v m即 2211s m s m =此为一人一船模型的平均动量守恒方程,且知位移与质量成反比。
又由图知 L s s =+21,解得两物体位移分别为L m m m s 2121+= Lm m m s 2112+=(2)二人一船模型:如图2所示,a 、b 两人交换位置过程中,设船c 向左运动,同理可得平均动量守恒定律的方程c c b b a a s m s m s m +=3.一题三法求解人船模型例题 如图2所示,a 、b 两人质量分别为a m 和b m ,船c 的质量为c m ,船长为L ,现在a 、b 交换位置,求船c 在该过程的位移?法1 由二人一船模型得 c c b b a a s m s m s m +=位移关系 L s s c a =+ L s s c b =-联立解得Lm m m m m s cb a ba c ++-=此解法作图较简单,但位移关系和解方程都较复杂。
法2 如图3所示,先令b 不动,a 走到右端,由一人一船模型,得 Lm m m m s cb a ac ++=1再令a 不动,让b 走到左端,在该过程中同理可得L m m m m s cb a bc ++=2由图知L m m m m m s s s cb a ba c c c ++-=-=21此解法把问题化为两个一人一船模型,根据位移和质量的反比关系可直得到结果。
人船模型解析版

人船模型一、模型建构1、人船问题:人船系统在相互作用下各自运动,运动过程中该系统所受到的合外力为零,即人和船组成的系统在运动过程中动量守恒。
2、两类问题第一类:直线运动的人船模型如图,质量为M 的船停在静止的水面上,船长为L ,一质量为m 的人,由船头走到船尾,若不计水的阻力,则整个过程人和船相对于水面移动的距离?设人在运动过程中,人和船相对于水面的速度分别为v 和u 由动量守恒定律得:mv Mu =由于人在走动过程中任意时刻人和船的速度v 和u 均满足上述关系mv M u =x t ν=,y u t=可得:mx My =x y L +=解得:M x L m M =+ my L m M=+第二类:曲线运动的人船模型如图所示,小球质量为m ,轨道质量为M ,半径为R ,将m 静止释放,不计阻力,分析结论.一、解题思路:1、确定系统动量守恒2、列平均速度动量守恒式3、列两物体位移关系式4、求解未知量 二、解题方法: 动量守恒定律 三、解题关键点: 1、确定哪个方向动量守恒 2、确定两物体位移关系 四、解题易错点位移关系运动到最低点,水平方向上动量守恒动量守恒:mv m=Mv M移动距离:mv m t=Mv M t即mx m =Mx M 位移之和:x m+x M =R联立解得:x m=Mm+M R,x M =mm+M R运动到另外一端最高点,水平方向上动量守恒动量守恒:mv m=Mv M移动距离:mv m t=Mv M t即mx m =Mx M位移之和:x m+x M =2R联立解得:x m=Mm+M·2R,x M =mm+M·2R.二、例题精析例1、气球质量200kg截有质量为50kg的人,静止在空中距地面20m 高的地方,气球下悬一质量不计的绳子,此人想从气球上沿绳慢慢下滑至地面,为安全到达地面,则这根绳至少多长?解题思路:1、确定系统动量守恒2、列平均速度动量守恒式3、列两物体位移关系式4、求解未知量解题思路:1、确定系统动量守恒2、列平均速度动量守恒式3、列两物体位移关系式4、求解未知量【解答】解:人与气球组成的系统竖直方向动量守恒由动量守恒得:m1v1﹣m2v2=0即:m1﹣m2=0绳子长度:L=s气球+s人解得:L=25m例2、如图所示,质量分别为m1和m2(m1>m2)的两个人分别站在静止于光滑水平面上的质量为M的小车的两端,小车长为L,当两人交换位置时,车将向哪个方向移动?移动多大距离?【解答】设当两人交换位置时,车将向右移动的距离为x。
动量守恒(人船模型专题)教学提纲

S2
S1
b
块由斜面顶部无初速滑到底部 时,劈移动的距离是S2多少?
分析和解答:劈和小物块组成的系统水平方向不受外力,
故水平方向动量守恒,且初始时两物均静止,设物块的水平
位移为s1,故由动量守恒定律
可得 ms1=Ms2
由几何关系可得:s1=b-s2
联立上式得 s2=mb/(M+m) 即为M发生的位移。
小结
动量守恒定律的应用Ⅰ
人船模型及应用
制作:朱正泽
复习
动量守恒定律的要点: 1、内容: 如果一个系统不受外力或所受外力之和
为零,则这个系统的总动量保持不变. 2、矢量表达式:
m1v1+m2v2=m1v1′ห้องสมุดไป่ตู้m2v2′
3、条件:系统不受外力或所受外力之和为零。
[演示1]一只小船,停在静水中,船头有一个人从船 头走向船尾,不计水的阻力。
S1
S2
代入数据联立解得:S1=8m, S2=2m
如图所示,质量为M=200kg,长为b=10m的平板车静止在光滑的水平面 上,车上有一个质量为m=50kg的人,人由静止开始从平板车左端走到 右端,求此过程中,车相对地面的位移大小?
[变式练习1]若将此题中的人换成相同
a
质量,长为a=2m的小车 m
b
(如图所示),结果又如何? M
解:由题意仍有:
—SS—12
=
M —m—
此时,小车不能视为质点
S1
S2
由几何关系知相对位移为(b-a),所以有
S1+S2=(b-a) 代入数据联立解得:S1=6.4m, S2=1.6m
m [变式3]斜面
一个质量为M,底面边长为 b
人船模型

O O ′ A B O ″ O bR 2R 人、船问题模型(C)动量守恒定律的两个推论:推论1:当系统的动量守恒时,任意一段时间内的平均动量也守恒;推论2:当系统的动量守恒时,系统的质心保持原来的静止或匀速直线运动状态不变。
例题、如图所示,长为l 、质量为M 的小船停在静水中,一个质量为m 的人立在船头,不计水的阻力。
当人从船头走到船尾的过程中,船和人对地的移位各是多大? 解一:设人行走的平均速度为v 1,在时间t 内从船头走到船尾对地位移为S 1,人行走时航速(平均)为v 2,位移为S 2,据动量守恒有 mv 1-Mv 2=0即 mS 1/t-MS 2/t=0 ∴S 1/S 2=M/m而S 1+S 2=l 解得S 1=Ml/(M+m) S 2=ml/(M+m)解二:系统质心位置保持不动,开始时人、船质心为O ′。
且OO ′=A O M m ', OO ′+O ′A=l/2 ∴ l m M M O O +=' 当人从船头走到船尾时,由于对称2l m M m O O ⋅+='' ∴ 船的位移l m M m O O S ⋅+='=22, l mM M S l S ⋅+=-=21 1.静止在空中的气球质量为M ,下面拖一条质量不计的软梯,质量为m 的人站在软梯上端距地面高为h 。
求:⑴人安全不能确定地面软梯的最小长度⑵若软梯长为h ,则人从软梯上端到下端时,人距地面还有多高?2.一质量为M 、底面边长为b 的三角形劈块静止于光滑水平地面上,如图。
有一质量为m 的物块由斜面顶部无初速滑到底部的过程中,劈块移动的距离是多少?3.某人在一只静止于水面上的小船上练习射出。
船、人连同枪(不包括子弹)及靶的总质量为M ,靶立于船头,枪内有n 颗质量均为m 的子弹,枪口到靶的距离为l ,子弹射出枪口时相对地面的速度为v ,在发射后一颗子弹时,前一颗子弹已陷入靶中,则在发射完n 颗子弹后小船后退的距离是多少?4.质量为m 、半径为R 的小球,放在半径为2R 、质量为2m 的大空心球内,大球开始静止在光滑水平面上。
人船模型
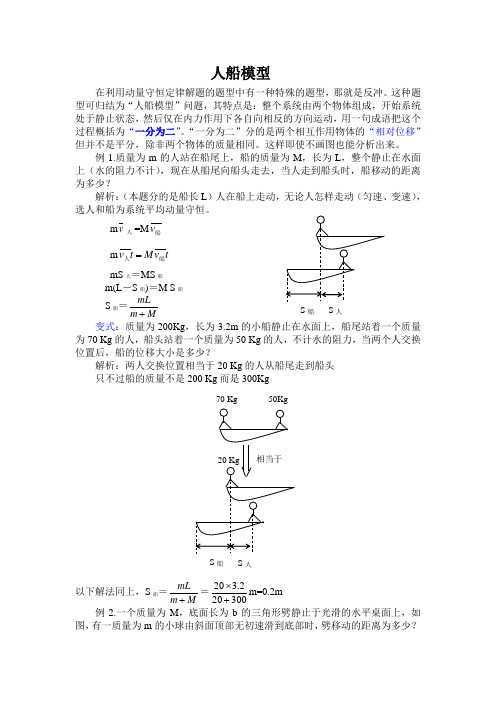
人船模型在利用动量守恒定律解题的题型中有一种特殊的题型,那就是反冲。
这种题型可归结为“人船模型”问题,其特点是:整个系统由两个物体组成,开始系统处于静止状态,然后仅在内力作用下各自向相反的方向运动,用一句成语把这个过程概括为“一分为二”。
“一分为二”分的是两个相互作用物体的“相对位移”但并不是平分,除非两个物体的质量相同。
这样即使不画图也能分析出来。
例1.质量为m 的人站在船尾上,船的质量为M ,长为L ,整个静止在水面上(水的阻力不计),现在从船尾向船头走去,当人走到船头时,船移动的距离为多少?解析:(本题分的是船长L )人在船上走动,无论人怎样走动(匀速、变速),选人和船为系统平均动量守恒。
m v 人=M 船vm t v M t v 船人=mS 人=MS 船m(L -S 船)=M S 船S 船=Mm mL + 变式:质量为200Kg ,长为3.2m 的小船静止在水面上,船尾站着一个质量为70 Kg 的人,船头站着一个质量为50 Kg 的人,不计水的阻力,当两个人交换位置后,船的位移大小是多少?解析:两人交换位置相当于20 Kg 的人从船尾走到船头只不过船的质量不是200 Kg 而是300Kg以下解法同上,S 船=M m mL +=300202.320+⨯m=0.2m 例2.一个质量为M ,底面长为b 的三角形劈静止于光滑的水平桌面上,如图,有一质量为m 的小球由斜面顶部无初速滑到底部时,劈移动的距离为多少?S 人S 船S 人S 船 50Kg 70 Kg解析:球和劈组成系统在水平方向上动量守恒(本题分的是底边长m 球v =M 劈vmS 球=MS 劈m(b-S 劈)=MS 劈S 劈=b Mm m + 例3.如图质量为m ,半径为R 的小球,放在半径为2R ,质量为2m 的大空心球内,大球开始静止在光滑水平面上,当小球从图示位置无初速地沿大球内壁滚到最低点时,大球移动的距离是多少?解析:小球和大球在水平面上动量守恒( m 小v =2m 大vmS 小=2mS 大S 小=2S 大R-S 大=2S 大S 大=31R 例4.如图所示,AB 为一光滑水平横杆,杆上套一质量为m 1 的小圆环,环上系一长为L 质量不计的细绳,绳的另一端拴一质量为m 2的小球,现将绳拉直,且与AB 平行,由此位置释放小球,当摆到与水平方向夹角为θ的位置时,求环移动距离为多少?解析:(分的是绳长L ) m 1S 环=M 2S 球m 1S 环=M 2(L-Lcos θ-S 环)S 环=212cos 1(m m L m +-)θ 劈球S 小+S 大 A B。
在四种常见模型中应用动量守恒定律(解析版)

在四种常见模型中应用动量守恒定律导练目标导练内容目标1人船模型和类人船模型目标2反冲和爆炸模型目标3弹簧模型目标4板块模型【知识导学与典例导练】一、人船模型和类人船模型1.适用条件①系统由两个物体组成且相互作用前静止,系统总动量为零;②动量守恒或某方向动量守恒.2.常用结论设人走动时船的速度大小为v 船,人的速度大小为v 人,以船运动的方向为正方向,则m 船v 船-m 人v 人=0,可得m 船v 船=m 人v 人;因人和船组成的系统在水平方向动量始终守恒,故有m 船v 船t =m 人v 人t ,即:m 船x 船=m 人x 人,由图可看出x 船+x 人=L ,可解得:x 人=m 船m 人+m 船L ;x 船=m 人m 人+m 船L3.类人船模型类型一类型二类型三类型四类型五1有一条捕鱼小船停靠在湖边码头,小船又窄又长(估计一吨左右),一位同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行码头自由停泊,轻轻从船尾上船,走到船头后停下来,而后轻轻下船,用卷尺测出船后退的距离为d ,然后用卷尺测出船长L ,已知他自身的质量为m ,则渔船的质量()A.m (L +d )dB.md (L -d )C.mL dD.m (L -d )d【答案】D【详解】因水平方向动量守恒,可知人运动的位移为(L -d )由动量守恒定律可知m (L -d )=Md解得船的质量为M =m (L -d )d故选D 。
2如图所示,滑块和小球的质量分别为M 、m 。
滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O 由一不可伸长的轻绳相连,轻绳长为L ,重力加速度为g 。
开始时,轻绳处于水平拉直状态,小球和滑块均静止。
现将小球由静止释放,下列说法正确的是( )。
A.滑块和小球组成的系统动量守恒B.滑块和小球组成的系统水平方向动量守恒C.滑块的最大速率为2m 2gLM (M +m )D.滑块向右移动的最大位移为mM +mL【答案】BC【详解】A .小球下摆过程中竖直方向有分加速度,系统的合外力不为零,因此系统动量不守恒,A 错误;B .绳子上拉力属于内力,系统在水平方向不受外力作用,因此系统水平方向动量守恒,B 正确;C .当小球落到最低点时,只有水平方向速度,此时小球和滑块的速度均达到最大,取水平向右为正方向,系统水平方向动量守恒有Mv 1-mv 2=0由系统机械能守恒有mgL =12mv 22+Mv 21解得滑块的最大速率v 1=2m 2gLM (M +m ),C 正确;D .设滑块向右移动的最大位移为x ,根据水平动量守恒得M x t -m 2L -x t =0解得x =2mM +mL ,D 错误;故选BC 。
高中物理 人船模型 易懂

重难点 人船模型1.“人船模型”问题两个原来静止的物体发生相互作用时,若所受外力的矢量和为零,则动量守恒。
在相互作用的过程中,任一时刻两物体的速度大小之比等于质量的反比。
这样的问题即为“人船模型”问题。
2.人船模型的特点(1)两物体满足动量守恒定律:m 1v 1-m 2v 2=0。
(2)运动特点:人动船动,人静船静,人快船快,人慢船慢,人左船右;人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即x 1x 2=v 1v 2=m 2m 1。
(3)应用x 1x 2=v 1v 2=m 2m 1时要注意:v 1、v 2和x 1、x 2一般都是相对地面而言的。
方法讲解例1(第一个层次)如图所示,长为L 、质量为M 的小船停在静水中,质量为m 的人从静止开始从船头走到船尾,不计水的阻力,则船和人相对地面的位移各为多少?解析:因为动量守恒,当人向左运动时,船向右运动。
设任一时刻人与船的速度大小分别为v 1、v 2,作用前都静止。
因整个过程中动量守恒,所以有mv 1=Mv 2设整个过程中的平均速度大小为v -1、v -2,则有m v -1=M v -2上式两边乘以时间t ,有m v -1t =M v -2t ,即mx 1=Mx 2且x 1+x 2=L ,解得x 1=M m +M L ,x 2=m m +M L 。
答案:m m +M L M m +ML方法讲解例2(第二个层次)如图所示,船长为2L 、质量为M 的小船停在静水中,在船中央有一个旗杆,质量为m 的人从静止开始从船头走到船尾,不计水的阻力,则船和人相对地面的位移各为多少?解析:因为动量守恒,当人向左运动时,船向右运动。
设任一时刻人与船的速度大小分别为v 1、v 2,作用前都静止。
因整个过程中动量守恒,所以有mv 1=Mv 2设整个过程中的平均速度大小为v -1、v -2,则有m v -1=M v -2前半和后半程是一样的;上式两边乘以时间t ,有m v -1t =M v -2t ,即mx 1=Mx 2且x 1+x 2=2L ,解得x 1=2M m +M L ,x 2=2m m +M L 。
动量守恒定律在“人船模型”的运用.doc

动量守恒定律在“人船模型”的运用动量守恒定律比牛顿运动定律的适用范围更广泛,是自然界的基本守恒规律之一,它既适用于宏观物体,也适用于微观粒子;既适用于低速运动物体,也适用于高速运动物体,因此,是高中物理的重点教学之一,也是高考的重要考点之一。
利用此定律只需考虑相互作用的物体作用前后动量变化的关系,从而省去了具体细节的讨论,使同学们解决一些力学问题时更简单、快捷。
“人船模型”问题是一种十分常见的题型,在研究过程当中,如果能恰当地应用动量守恒定律进行解题,会给同学们的解题带来意想不到的效果。
1.动量守恒定律及其两个推论:动量守恒定律:如果一个系统不受外力或所受外力的矢量和为零,那么这个系统的总动量保持不变。
推论1:若系统的动量守恒,则系统任意一段时间内的平均动量也守恒推论2:若系统的动量守恒,则系统的质心将保持原来匀速直线运动或静止的状态不变2.人船模型“人船模型”是由人和船两个物体构成的系统。
选取人和船为研究对象,该系统在人和船相互作用下各自运动,由于忽略水的阻力,运动过程中该系统所受到的合外力为零,即人和船组成的系统在水平方向上动量始终是守恒的。
以下分别以“一人一船”、“二人一船”模型以及人船模型的简单变形进行讨论:(1)“一人一船”模型:如图1所示,静水面上停有质量m 2,长为L 的小船,质量为m 1的人从船头走到船尾,忽略水的阻力。
人从船头走到船尾的过程中,由水平方向动量守恒可得:02211=-v m v m 由于在整个过程动量都守恒,所以根据推论1有:0211=---v m v m同乘以时间t ,得:0211=---t v m t v m , 即:2211s m s m =此为“一人一船”模型的动量守恒方程,且知人船之间的位移与质量成反比。
又由图知人船位移之和为L ,即:L s s =+21, 解得两物体位移分别为L m m m s 2121+=L m m m s 2112+= (2)“二人一船”模型如图2所示,小船c 停在静水面上,a 、b 两人从长为L 的小船上交换位置过程中,设船c 向左运动,同理可得动量守恒定律的方程: c c b b a a s m s m s m +=(3)“人船模型”的变形变形1:如图所示,质量为M 的气球下挂着长为L 的绳梯,一质量为m 的人站在绳梯的下端,人和气球静止在空中,现人从绳梯的下端往上爬到顶端时,人和气球相对于地面移动的距离?分析:由于开始人和气球组成的系统静止在空中,竖直方向系统所受外力之和为零,即竖直方向系统总动量守恒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分宜中学 卢海波
动量守衡定律是自然界最重要最普遍地归律之一,利用该定律只考虑相互作用物体作用前后动量变化地关系,省去了具体细节地讨论,为我们解决力学问题提供了一种简捷地方法和思路.资料个人收集整理,勿做商业用途人船模型问题是一种很常见地题形,在研究过程当中,如果能恰当地应用动量守恒定律进行解题,会给我们带来意想不到地效果.资料个人收集整理,勿做商业用途[例] 如图所示,静水面上停有一小船,船长 米,质量 千克,一人从船头走到船尾,人地质量 千克.那么,船移动地距离为多少?(水地阻力可以忽略不计)资料个人收集整理,勿做商业用途过程分析 当人从船头走到船尾,通过脚与船发生了作用(也可以认为走动过程就是人与船发生间歇性碰撞地过程).选取人和船为研究对象,由于不计水地阻力,所以系统在水平方向上动量守恒.资料个人收集整理,勿做商业用途解:设人从船头走到船尾,船对地地就离为,则人对地移动了 ,
根据动量守恒定律可得
( )
解得 ( ) *( ) 米
此题虽然很简单,但所展示地物理模型很重要,如果真正掌握了此题地解法,那么,下面几道题完全可以做到同法炮制,快速求解.资料个人收集整理,勿做商业用途[例] 一质量为地船,静止于湖水中,船身长,船地两端点有质量分别为和地人,且>,当两人交换位置后,船身位移地大小是多少?(不计水地阻力)资料个人收集整理,勿做商业用途过程分析 此题初看上去较上题繁杂得多,物理模型也迥然相异,但实质上是大同小异,如出一辙.试想,若把质量大地人换成两个人,其中一个人地质量为,另一个人地质量为 .由上一题可知,当两个质量都为地人互换位置之后,船将原地不动.这样一来,原来地问题就转化为上题所示地物理模型了,当质量为 地人从船地一端走到另一端,求船地位移.资料个人收集整理,勿做商业用途解:设船对地移动地位移为,则质量为 地人对地移动地位移就是 ,由动量守恒定律可得资料个人收集整理,勿做商业用途 ( 2m2) – ( ) ( )
解得
( )( )
[例] 某人在一只静止地小船上练习射击,船和人连同枪(不包括子弹)及靶地总质量为,枪内装有颗子弹,每颗子弹地质量为,枪口到靶地距离为,子弹射出枪口时相对地面地速度为,在发射一颗子弹时,前一颗粒子弹已陷入靶中,则在发射完颗子弹后,小船后退地距离为多少(不计水地阻力).资料个人收集整理,勿做商业用途过程分析 子弹发射时在枪内地运动,和击靶地过程,类似于人船模型中相互作用.连发颗子弹,相当于个人从船头走到船尾.把船、人、枪、靶和子弹作为一个系统进行研究,因该系统在水平方向上不受外力,所以在这个方向上总动量守恒.资料个人收集整理,勿做商业用途解:设一颗子弹完成射击过程地历时为,小船移动,由动量守恒定律可得
[ ( ) ] – ( )
解方程可得
(
)
因此,发射颗子弹后,小船后退地距离
( )
[例] 如图所示,在光滑水平地面上,有两个光滑地直角三形木块和,底边长分别为、,质量分别为、,若 4m ,且不计任何摩擦力,当滑到底部时,向后移了多少距离?资料个人收集整理,勿做商业用途过程分析 选定木块和整体作为研究对象,在沿斜面下滑地过程中,与人船模型类同,该系统在水平方向上所受地合外力为零,所以,在水平方向上动量守恒.资料个人收集整理,勿做商业用途解:设当沿斜面从顶端滑到底部时,向后移动了,则对地移动了 – ,由动量守恒定律得 – ( – ) 解得
( )( ) ( – )
[例] 质量为地气球下系一质量可忽略地足够长地绳子,绳子上距地面高处有一质量为地猴子.开始
时气球和猴子均静止在空中,猴子从某时刻开始沿绳子缓慢下滑,要它恰能滑到地面,开始下滑时,它下面地绳子至少应为多长?资料个人收集整理,勿做商业用途过程分析 选定气球和猴子为一个系统,在猴子沿绳子下滑着地前地整个过程中,系统在竖直方向上所受合外力为零,因此,在竖直方向上每时每刻动量守恒,与人船模型类同.资料个人收集整理,勿做商业用途解:设猴子从开始下滑到着地历时,其间气球又上升了,由动量守恒定律得
–
解得
因此,所求绳长至少应为 ( )
完稿时间:年月日星期六。
