初四数学期末试题
初四期末数学试题
初四期末数学试题一、选择题1、 -2016的相反数的倒数是（ C ）A 、2016 B 、-2016 C 、20161 D 、-201612、510000用科学记数法应记为（ C ）A 、51×104 B 、5×105 C 、5.1×105 D 、0.51×1063、若函数y=(m-2)x |m|-3是反比例函数，则m 的值是（ A ）A 、-2 B 、2 C 、±2 D 、以上都不正确4、下列运算错误的是（ B ）A 、a a ±=2B 、532a b a =⋅C 、2422)(b a b a = D 、2222a a a -=-5、已知一次函数y=ax+c 与二次函数y=ax 2+bx+c ，在同一平面直角坐标系中大致图像是（ A ）A 、B 、C 、D 、6题图7题图6、如上图在△ABC,△ADE 中,∠BAC=∠DAE=90°,AB=AC,AD-AE,点C,D,E 在一条直线上.连接BD,BE.以下四个结论:①BD=CE;②BD ⊥CE;③∠ACE+∠DBC=45°;④BE 2=2(AD 2+AB 2);其中结论正确个数是（ C ） A 、1 B 、2 C 、3 D 、47、如上图，在平面直角坐标系中，⊙A 经过原点O,并且分别与x 轴、y 轴交于B 、C 两点，已知B （8，0），C （0，6），则⊙A 的半径为（ C ）A ．3B ．4C ．5D ．88、下列哪个函数不是轴对称图形（ B ）A 、y=1-x B 、y=-1/x(x>1) C 、y=x-2x+2 D 、y=x(x ≥0) 9、在⊙O 中，圆心角∠BOC=100°,则圆周角∠BAC 度数是( D )A 、50°B 、100°C 、130°D 、50°或130° 10、已知二次函数y=x 2-2mx+m 2+3（m 为常数），下列结论正确的是（ D ）A 、当m=0时，二次函数图象顶点坐标为（0，0）B 、当m ＜0时，二次函数图象对称轴在y 轴右侧 B 、设二次函数图象与y 轴交点为A ，过A 作x 轴平行线，交图象于另一点B ，抛物线的顶点为C ，则△ABC 面积为m 3D 、该函数图象沿y 轴向下平移6个单位后，图象与x 轴两交点之间的距离为23二、填空题11、分解因式x 2-2x-4=_________________12、将抛物线y=2x 2向右平移3个单位,再向下平移1个单位,得到抛物线解析式是______________ 13、在Rt △ABC 中，∠C=90°，BC=12cm ，BC 边上的中线AD=10cm ，则sinB=______ 14、代数式111+-x 有意义的x 取值范围是__________________x ≥115、如图在扇形OAB 中，∠AOB=60°，扇形半径为r ，点C 在上，CD ⊥OA ，垂足为D ，当△OCD 的面积最大时，的长为 0.25πr16、如图，菱形纸片ABCD 中，∠A=60°，折叠菱形纸片ABCD ，使点C 落在DP （P 为AB 中点）所在的直线上，得到经过点D 的折痕DE ．则∠DEC 的大小为_______75°17、如图，在△ABC 中，∠BAC=90°，AB=5cm ，AC=2cm ，将△ABC 绕顶点C 按顺时针方向旋转45°至△A 1B 1C 的位置，则线段AB 扫过区域（图中的阴影部分）的面积为_______25π/8 cm 218、如图，Rt △ABC 的两直角边AC 边长为4，BC 边长为3，它的内切圆为⊙0，⊙0与边AB 、BC 、AC 分别相切于点D 、E 、F ，延长C0交斜边AB 于点G ．线段DG 的长___________1/715题图16题图17题图18题图三、解答题19.(1)计算：-2sin30°-(-2)3-(4-2)-1+38-+(-1)2016(2)化简求值:)252(6332--+÷--x x xx x 其中x 是一元二次方程x 2+3x-1=0的实数根.20、为响应国家的“一带一路”经济发展战略，树立品牌意识，我市质检部门对A 、B 、C 、D 四个厂家生产的同种型号的零件共2000件进行合格率检测，通过检测得出C 厂家的合格率为95%，并根据检测数据绘制了如图1、图2两幅不完整的统计图．（1）抽查D 厂家的零件为________件，扇形统计图中D 厂家对应的圆心角为_______ ； （2）抽查C 厂家的合格零件为_________件，并将图1补充完整； （3）通过计算说明合格率排在前两名的是哪两个厂家；（4）若要从A 、B 、C 、D 四个厂家中，随机抽取两个厂家参加德国工业产品博览会，请用“列表法”或“画树形图”的方法求出（3）中两个厂家同时被选中的概率．21、国家海洋局将中国钓鱼岛最高峰命名为国家海洋局将中国钓鱼岛最高峰命名为“高华峰”，并对钓鱼岛进行常态化立体巡航．如图1，在一次巡航过程中，巡航飞机飞行高度为2001米，在点A 测得高华峰顶F 点的俯角为30°，保持方向不变前进1200米到达B 点后测得F 点俯角为45°，如图2．请据此计算钓鱼岛的最 高海拔高度多少米．（结果保留整数，参考数值：3=1.732，2=1.414）22、如图所示，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=m/x （m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D．若OA=OB=OD=1．（1）求点A、B、D的坐标；（2）求一次函数和反比例函数的解析式．23、如图，点O在∠APB的平分线上，⊙O与PA相切于点C．（1）求证：直线PB与⊙O相切；（2）PO延长线与⊙O交于点E．若⊙O半径为3，PC=4．求弦CE长．24、已知二次函数y=x2+bx+c（b，c为常数）．（Ⅰ）当b=2，c=-3时，求二次函数的最小值；（Ⅱ）当c=5时，若在函数值y=l的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；（Ⅲ）当c=b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．25、在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2，；乙袋中装有3个完全相同的小球，分别标有数字-1，-2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．（1）用树状图或列表法列举点M所有可能的坐标；（2）求点M（x，y）在函数y=-x+1的图象上的概率；（3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M（x，y）能作⊙O的切线的概率．26、如图，△ABC内接于⊙O，OC和AB相交于点E，点D在OC的延长线上，且∠B=∠D=∠BAC=30°．（1）试判断直线AD与⊙O的位置关系，并说明理由；（2）AB=63，求⊙O的半径．27、某冰箱厂为响应国家“家电下乡”号召，计划生产A、B两种型号的冰箱一共100台．经预算，两种冰箱全部售出后，可获得利润不低于 4.75万元，不高于4.8万元，两种型号的冰箱生产成本和售价如下表：（1）冰箱厂有哪几种生产方案？（2）该冰箱厂按哪种方案生产，才能使投入成本最少？28、如图抛物线y=ax2+bx+c与x轴交于A,B，与y轴交于点C,OC=4，AO=2OC,且抛物线对称轴为直线x=-3．（1）求该抛物线的函数表达式；（2）己知矩形DEFG的一条边DE在线段AB上，顶点F、G分别在AC、BC上，设OD=m，矩形DEFG的面积为S，当矩形DEFG的面积S取最大值时，连接DF 并延长至点M，使FM＝2/5DF，求出此时点M的坐标；（3）若点Q是抛物线上一点，且横坐标为-4，点P是y轴上一点，是否存在这样的点P，使得△BPQ是直角三角形？如果存在，求出点P的坐标；若不存在，请说明理由．型号A型B型成本（元/台）22002600售价（元/台）28003000答案20解：（1）D厂的零件比例=1-20%-20%-35%=25%，D厂零件数=2000×25%=500件；D厂家对应的圆心角为360°×25%=90°；（2）C厂的零件数=2000×20%=400件，C厂合格零件数=400×95%=380件，如图：（3）A厂家合格率=630÷(2000×35%)=90%，B厂家合格率=370÷(2000×20%)=92.5%，C厂家合格率=95%,D厂家合格率470÷500=94%,合格率排在前两名是C,D两个厂家；（4）根据题意画树形图如下：共有12种情况，选中C、D的有2种，则P（选中C、D）=2/12=1/621解：设CF=x，在Rt△ACF和Rt△BCF中，∵∠BAF=30°，∠CBF=45°，∴BC=CF=x，CF/AC=tan30°，即AC=3x，∵AC-BC=1200米，∴3x-x=1200，解得：x=600（3+1），则DF=h-x=2001-600（3+1）≈362（米）．答：钓鱼岛的最高海拔高度约362米22解：（1）∵OA=OB=OD=1，∴点A、B、D的坐标分别为A（-1，0），B（0，1），D（1，0）；（2）∵点A、B在一次函数y=kx+b（k≠0）的图象上，∴−k+b＝0,b＝1，解得k＝1,b＝1，∴一次函数的解析式为y=x+1．∵点C在一次函数y=x+1的图象上，且CD⊥x轴，∴点C的坐标为（1，2），又∵点C在反比例函数y=m/x（m≠0）的图象上，∴m=2；∴反比例函数的解析式为y=2/x23【解答】（1）证明：连接OC，作OD⊥PB于D点．∵⊙O与PA相切于点C，∴OC⊥PA．∵点O在∠APB的平分线上，OC⊥PA，OD⊥PB，∴OD=OC．∴直线PB与⊙O相切；（2）解：设PO交⊙O于F，连接CF．∵OC=3，PC=4，∴PO=5，PE=8．∵⊙O与PA相切于点C，∴∠PCF=∠E．又∵∠CPF=∠EPC，∴△PCF∽△PEC，∴CF：CE=PC：PE=4：8=1：2．∵EF是直径，∴∠ECF=90°．设CF=x，则EC=2x．则x2+（2x）2=62，解得x=556．则EC=2x=125/524解：（Ⅰ）当b=2，c=-3时，二次函数的解析式为y=x2+2x-3=（x+1）2-4，∴当x=-1时，二次函数取得最小值-4；（Ⅱ）当c=5时，二次函数的解析式为y=x2+bx+5，由题意得，x2+bx+5=1有两个相等是实数根，∴△=b2-16=0，解得，b1=4，b2=-4，∴二次函数的解析式y=x2+4x+5，y=x2-4x+5；（Ⅲ）当c=b2时，二次函数解析式为y═x2+bx+b2，图象开口向上，对称轴为直线x=-b/2，①当-b/2＜b，即b＞0时，在自变量x的值满足b≤x≤b+3的情况下，y随x的增大而增大，∴当x=b时，y=b2+b•b+b2=3b2为最小值，∴3b2=21，解得，b1=-7（舍去），b2=7；②当b≤-b/2≤b+3时，即-2≤b≤0，∴x=-b/2，y=3/4b2为最小值，∴3/4b2=21，解得，b1=-27（舍去），b2=27（舍去）；③当-b/2＞b+3，即b＜-2，在自变量x的值满足b≤x≤b+3的情况下，y随x的增大而减小，故当x=b+3时，y=（b+3）2+b（b+3）+b2=3b2+9b+9为最小值，∴3b2+9b+9=21．解得，b1=1（舍去），b2=-4；∴b=7时，解析式为：y=x2+7x+7, b=-4时，解析式为：y=x2-4x+16．综上可得，此时二次函数的解析式为y=x2+7x+7或y=x2-4x+1625解：（1）画树状图：共有9种等可能的结果数，它们是：（0，-1），（0，-2），（0，0），（1，-1），（1，-2），（1，0），（2，-1），（2，-2），（2，0）；（2）在直线y=-x+1的图象上的点有：（1，0），（2，-1），所以点M（x，y）在函数y=-x+1的图象上的概率=2/9；（3）在⊙O上的点有（0，-2），（2，0），在⊙O外的点有（1，-2），（2，-1），（2，-2），所以过点M（x，y）能作⊙O的切线的点有5个，所以过点M（x，y）能作⊙O的切线的概率=5/926解：（1）直线AD与⊙O相切．理由如下：如图，连接OA．∵∠B=30°，∴∠AOC=2∠B=60°，∴∠OAD=180°-∠AOD-∠D=90°，即OA⊥AD，∵OA为半径，∴AD是⊙O的切线．（2）∵OA=OC，∠AOC=60°，∴△ACO是等边三角形，∴∠ACO=60°，AC=OA，∴∠AEC=180°-∠EAC-∠ACE=90°，∴OC⊥AB，又∵OC是⊙O的半径，∴AE=0.5AB=0.5×63=33，在Rt△ACE中，sin∠ACE=AE/AC=sin 60°，∴AC=6，∴⊙O的半径为627解：（1）设生产A型冰箱x台，则B型冰箱为（100-x）台，由题意得：47500≤(2800-2200)x+(3000-2600)×(100-x)≤48000解得：37.5≤x≤40∵x是正整数，∴x取38，39或40．有以下三种生产方案：A38台，B62台；A39、B61；A40、B60 （2）设投入成本为y元，由题意有：y=2200x+2600（100-x）=-400x+260000当x=40时，y有最小值．即生产A型冰箱40台，B型冰箱60台，该厂投入成本最少24400028【解答】解：（1）∵OC=4，∴点C的坐标为（0，4）．∴c=4，则抛物线解析式为y=ax2+bx+4．∵AO=2OC，则AO=8，∴点A的坐标为（-8，0）．又∵抛物线对称轴为直线x=-3，∴点B的坐标为（2，O）．∴0＝64a−8b+4,0＝4a+2b+4，解得a＝−1/4,b＝-3/2．∴该抛物线的函数表达式为y＝−1/4x2−3/2x+4．（2）∵矩形DEFG中FG∥ED，设FG与y轴交于点H，∴△CFH∽△CAO，△CHG∽△COB．∴FH/AO＝OCH/C＝HG/OB，即FH/8＝m/2．∴FH=4m，故FG=5m．设直线BC的解析式为：y=kx+b1，则4＝b1,0＝3k+b1，解得k＝−2,b1＝4．∴直线BC的解析式为y=-2x+4，则点G的坐标为（m，-2m+4）∴S=FG×GD=5m（-2m+4）=-10（m-1）2+10（5分）∵0≤m≤2，∴当m=1时，S最大．此时OD=1，OE=4，∴DE=5．过M作MM1⊥x轴于M1，则△MM1D∽△FED，∴MM1/FE＝MD/DF＝DM1/DE∵FM＝2/5DF，∴MD/DF＝7/5．则MM1/2＝DM1/5＝7/5．∴MM1＝14/5，DM1=7，则OM1=6．∴此时点M的坐标为(−6，14/5)．（3）存在．理由如下：∵点Q在抛物线上，且横坐标为-4，∴y Q=6，∴点Q坐标为（-4，6），设P的坐标为（0，n），在△BPQ中，若∠BQP为直角，则PQ2+BQ2=BP2，∴42+（n-6）2+62+（2+4）2=22+n2，解得n=10，此时点P的坐标为（0，10）．若∠QBP为直角，则PQ2=BQ2+BP2，∴42+（6-n）2=62+（2+4）2+22+n2，解得n=-2，此时点P的坐标为（0，-2）．若∠QPB为直角，则BQ2=BP2+PQ2，∴62+（2+4）2=42+（n-6）2+22+n2，解得n1＝3+17，n2＝3−17此时点P的坐标为(0，3+17)或(0，3−17)．综上所述，存在这样的点P，使得以△BPQ是直角三角形，所求的点P的坐标为：（O，10）或（0，-2）或(0，3+17)或(0，3−17)。
山东2022-2023第一学期初四数学期末考试试题
2022-2023第一学期初四数学期末考试试题一．选择题（每题3分，12道题共36分）1.在﹣1，﹣2，0，0.1这四个数中，最小的数是（）A．﹣1B．﹣2C．0D．0.12.一季度，面对国际环境更趋复杂严峻和国内疫情频发带来的多重考验，在以习近平同志为核心的党中央坚强领导下，科学统筹疫情防控和经济社会发展，初步核算，一季度国内生产总值约为27万亿元，按不变价格计算，同比增长4.8%．数据27万亿元用科学记数法表示为（）A．2.7×1013元B．2.7×1014元C．0.27×1014元D．27×1012元3．函数的自变量x 的取值范围是（）A．x ≥﹣3B．x ＞﹣3C．x ≥﹣3且x ≠0D．x ≠0且x ≠﹣34．下列说法：①三点确定一个圆，②平分弦的直径垂直于弦，③相等的圆心角所对的弦相等，④三角形的外心到三个顶点的距离相等，⑤弧长相等的弧是等弧；其中正确的有（）A．1个B．2个C．3个D．4个5.如图，一个底部呈球形的烧瓶，球的半径为5cm ，瓶内液体的最大深度CD ＝1cm ，则截面圆中弦AB 的长为（）cm ．A．4B．6C．8D．8.46.如图，点A ，B ，C 是⊙O 上的三点．若∠AOC ＝90°，∠BAC ＝35°，则∠AOB 的大小为（）A．10°B．20°C．35°D．40°7．设A （0，y 1），B （-1，y 2），C （2，y 3）是抛物线y ＝﹣（x +2）2+k 上的三点，则y 1，y 2，y 3的大小关系为（）A．y 3＞y 2＞y 1B．y 2＞y 1＞y 3C．y 1＞y 2＞y 3D．y 3＞y 1＞y 28.飞机着陆后滑行的距离s （米）关于滑行的时间t （秒）的函数解析式是s ＝60t ﹣1.5t 2，则飞机着陆后滑行到停止下来，滑行的距离为（）A．500米B．700米C．600米D．800米9.已知二次函数y ＝ax 2+bx +c 的图象如图所示，有以下结论：①abc ＞0；②a ﹣b +c ＜0；③4a +2b +c ＞0；④2a ＝b ；⑤3a +c ＜0；⑥若实数m ≠1，则a +b ＞am 2+bm 其中正确结论的个数是（）A．1个B．2个C．3个D．4个10.如图，正方形ABCD 、等边三角形AEF 内接于同一个圆，则的度数为（）A．15°B．20°C．25°D．30°11.如图，ABC 的内切圆⊙O 与,,AB BC AC 分别相切于点D ，E ，F ，连接OE ，OF ，90C ∠=︒，AC=3,BC=4,则阴影部分的面积为（）A．122π-B．142π-C．4π-D．114π-12．如图，正六边形ABCDEF 的边长为12，连接AC ，以点A 为圆心，AC 为半径画弧CE ，得扇形ACE ，将扇形ACE 围成一个圆锥，则圆锥的高为（）A．3B．6C．D．2二．填空题（每题3分，8道题共24分）13.计算：（﹣2）0﹣（）﹣1+|﹣1|+2sin30°=。
初四数学期末复习1
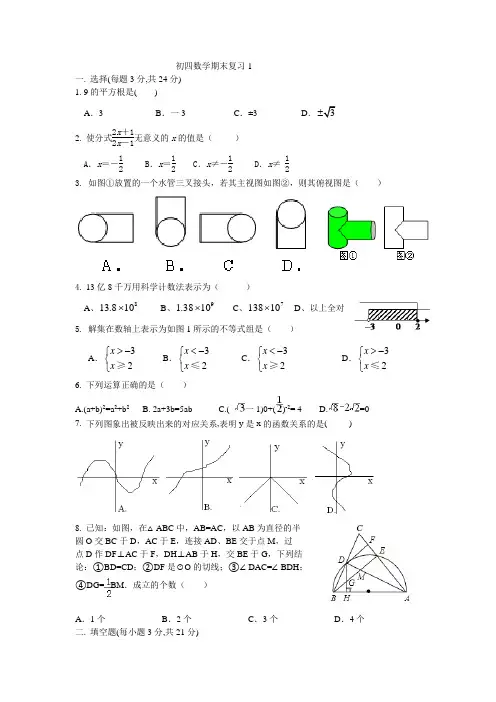
初四数学期末复习1一. 选择(每题3分,共24分)1. 9的平方根是( )A ．3B ．一3C ．±3D ．2. 使分式2x ＋12x －1无意义的x 的值是（ ） A ．x ＝－12 B ．x ＝12 C ．x ≠－12 D ．x ≠ 123. 如图①放置的一个水管三叉接头，若其主视图如图②，则其俯视图是（ ）4. 13亿8千万用科学计数法表示为（ ）A 、8108.13⨯B 、91038.1⨯C 、710138⨯D 、以上全对5. 解集在数轴上表示为如图1所示的不等式组是（ ）A ．32x x >-⎧⎨⎩≥B ．32x x <-⎧⎨⎩≤C ．32x x <-⎧⎨⎩≥D ．32x x >-⎧⎨⎩≤ 6. 下列运算正确的是（ ）A.(a+b)2=a 2+b 2B. 2a+3b=5abC.( 一1)0+()-2= 4D.=07. 下列图象出被反映出来的对应关系,表明y 是x 的函数关系的是( )8. 已知：如图，在△ABC 中，AB=AC ，以AB 为直径的半圆O 交BC 于D ，AC 于E ，连接AD 、BE 交于点M ，过点D 作DF ⊥AC 于F ，DH ⊥AB 于H ，交BE 于G ，下列结论：①BD=CD ；②DF 是⊙O 的切线；③∠DAC=∠BDH ；④DG=BM ．成立的个数（ ）9. 计算:132127-⎪⎭⎫ ⎝⎛-的结果是 .10. 图中刀柄外形是一个直角梯形(下底挖去一小半圆)，刀片上、下是平行的，转动刀片(如图)时形成∠1、∠2，则∠1＋∠2＝_______度．11. 如图，在坐标系中，点P 是第一象限内抛物线y ＝0.25x 2－1上的任意一点，P A ⊥x 轴于点A ．则OP －P A ＝ ．12. 如图，⊙O 的半径为2，点O 到直线l 的距离为3，点P 是直线l 上的一个动点，PQ 切⊙O 于点Q ，则PQ 的最小值为________．13.△ABC 中，AC=BC=4，∠ACB=900，把△ABC 旋转至△AB /C /，则阴影部分的面积是 。
张店初四期末数学试卷答案
1. 如果一个等差数列的前三项分别为3、5、7，那么这个数列的公差是多少？答案：22. 下列哪个数是负数？A. -2.5B. 3C. 0D. -1/2答案：A3. 下列哪个函数是奇函数？A. y = x^2B. y = 2xC. y = x^3D. y = 1/x答案：C4. 一个圆的半径增加了50%，那么这个圆的面积增加了多少？答案：150%5. 下列哪个方程的解集为全体实数？A. x^2 + 1 = 0B. x^2 - 1 = 0C. x^2 - 4x + 4 = 0D. x^2 + 4x + 4 = 0答案：C6. 若等差数列{an}的第一项为2，公差为3，那么第10项an是多少？答案：297. 已知一元二次方程x^2 - 5x + 6 = 0，求该方程的解。
答案：x1 = 2，x2 = 38. 在直角坐标系中，点A(2,3)关于y轴的对称点B的坐标是？答案：(-2,3)9. 一个长方体的长、宽、高分别为4cm、3cm、2cm，那么它的体积是多少？答案：24cm³10. 在△ABC中，∠A = 30°，∠B = 45°，求∠C的大小。
答案：∠C = 105°三、解答题（每题10分，共30分）11. （10分）已知函数f(x) = 2x - 3，求f(2x - 1)的表达式。
解答：f(2x - 1) = 2(2x - 1) - 3= 4x - 2 - 3= 4x - 512. （10分）已知一元二次方程x^2 - 4x + 3 = 0，求该方程的根的判别式。
解答：判别式Δ = b^2 - 4ac= (-4)^2 - 4×1×3= 16 - 12= 413. （10分）已知△ABC中，∠A = 60°，AB = 8cm，BC = 6cm，求AC的长度。
解答：根据余弦定理，AC² = AB² + BC² - 2×AB×BC×cosA= 8² + 6² - 2×8×6×cos60°= 64 + 36 - 96×1/2= 100 - 48= 52AC = √52≈ 7.21cm四、应用题（每题10分，共20分）14. （10分）某商品原价为100元，折扣率为20%，求打折后的价格。
任城区初四期末数学试卷
一、选择题（每题3分，共30分）1. 已知函数f(x) = 2x - 1，若f(x+1) = 5，则x的值为：A. 3B. 2C. 1D. 02. 在△ABC中，若∠A = 30°，∠B = 45°，则∠C的度数为：A. 75°B. 105°C. 120°D. 135°3. 下列各组数中，存在两个有理数a、b，使得a^2 + b^2 = 0的是：A. a = 1，b = 2B. a = 2，b = -2C. a = 0，b = 0D. a = -1，b = 14. 下列函数中，在定义域内为单调递增函数的是：A. y = x^2B. y = -x^2C. y = x^3D. y = -x^35. 已知等差数列{an}中，a1 = 3，公差d = 2，则第10项a10的值为：A. 15B. 18C. 21D. 246. 下列各式中，能表示x^2 + 2x + 1的是：A. (x + 1)^2B. (x - 1)^2C. (x + 2)^2D. (x - 2)^27. 在直角坐标系中，点P(2, 3)关于y轴的对称点为：A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)8. 下列各式中，能表示圆x^2 + y^2 = 4的方程的是：A. (x - 2)^2 + (y - 3)^2 = 1B. (x + 2)^2 + (y + 3)^2 = 1C. (x - 2)^2 + (y - 3)^2 = 4D. (x + 2)^2 + (y + 3)^2 = 49. 下列各组数中，能构成等比数列的是：A. 1，2，4，8，16B. 1，3，9，27，81C. 2，4，8，16，32D. 3，6，12，24，4810. 下列各式中，能表示函数y = x^2 + 1的图像向右平移1个单位后的函数是：A. y = (x - 1)^2 + 1B. y = (x + 1)^2 + 1C. y = x^2 + 2x + 1D. y = x^2 - 2x + 1二、填空题（每题5分，共25分）11. 若a > b，则|a|与|b|的大小关系为______。
初四期末数学试题
的大致图象是（）A．B．C．D．A．-2≤x≤2B．-22＜x＜22C．0≤x≤22D．-22≤x≤222题图5题图6题图7、如图抛物线y=ax2+bx+c(a≠0)过点(-1，0)和点(0，-3)，且顶点在第四象限，设P=a+b+c，则P的取值范围是（）A．-3＜P＜-1B．-6＜P＜0C．-3＜P＜0D．-6＜P＜-38、已知二次函数y=ax2+bx+c的图象与x轴交于点（-2，0）、（x1，0），且1＜x1＜2，与y轴的正半轴的交点在（0，2）的下方．下列结论：①4a-2b+c=0；②a-b+c＜0；③2a+c＞0；④2a-b+1＞0．其中正确结论的个数是（）个．A．4个B．3个C．2个D．1个A．①③④B．①②③C．①②④D．①②③④7题图9题图10题图二、填空题11、在数轴上表示实数a的点如图所示，化简2)5a+|a-2|的结果为=______(-的2倍；⑤AE=BC，其中正确的序号是_______________13题图15题图17题图18题图19题图20题图测得∠BDA=45°．已知斜坡CD坡度为i=1:3，求旗杆AB高度（3≈1.7,结果精确到个位）．求AF/FC的值．26、如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交斜边AB于点M，若H是AC 的中点，连接MH．（1）求证：MH为⊙O的切线．（2）若MH=1.5，tan∠ABC=0.75，求⊙O的半径．（3）在（2）的条件下分别过点A、B作⊙O的切线，两切线交于点D，AD 与⊙O相切于N点，过N点作NQ⊥BC，垂足为E，且交⊙O于Q点，求线段NQ的长度．27、如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D，连接BE，过点O作OC∥BE交切线DE于点C，连接AC．（1）求证：AC是⊙O的切线；（2）若BD=OB=4，求弦AE的长．28、如图，已知抛物线y=ax2+bx+c与x轴交于点A、B，与直线AC：y=-x-6交y轴于点C，点D是抛物线的顶点，且横坐标为-2．（1）求出抛物线的解析式．（2）判断△ACD的形状，并说明理由．（3）直线AD交y轴于点F，在线段AD上是否存在一点P，使∠ADC=∠PCF？若存在，直接写出点P的坐标；若不存在，说明理由．点D（1）求证：△BFD∽△ABD；（2）求证：DE=DB．存在，请说明理由．AE=7a/4，∵EF∥CD，∴AF/FC=AE/ED=7/92425∴∠COH=∠ABC，∠MOH=∠OMB，又∵OB=OM，∴∠OMB=∠MBO，∴∠COH=∠MOH，在△COH与△MOH中，OC＝OM，∠COH＝∠MOH，OH＝OH，∴△COH≌△MOH（SAS），∴∠HCO=∠HMO=90°，∴MH是⊙O的切线；（2）∵MH、AC是⊙O的切线，∴HC=MH=1.5，∴AC=2HC=3，∵tan∠ABC=3/4，∴AC/BC=3/4，∴BC=4，∴⊙O的半径为2；知：NQ=2EN=48/13∴∠ABE=60°，∵AB为圆O的直径，∴∠AEB=90°，∴AE=BE•tan60°=43 262728即∠DBE=∠BED，∴DE=DB。
初四数学期末测试题
初四期末测试题（满分：120分 时间：120分钟）一、选择题：（3×10=30分）１．如图，电线杆AB 的影子落在土坡的坡面CD 和地面BC 上，量得CD = 8米，BC = 20米，CD 与地面成30º角，且此时测得1米高的杆影长为2米，则电线杆的高度为（ ）米。
A ．9B ．28C ．14+ D．28+ 2．已知：两圆相交，其圆心距为6，一圆半径为8，则另一圆半径为r 的取值范围是（ ）A ．r >2B ．2<r <14C ．1<r <8D ．2<r<83．若二次函数y =ax 2+c ，当 x 取x 1，x 2 ，（x 1 ≠x 2）时，函数值相等，则当 x 取x 1+x 2 时,函数值为（）A ．a+cB ．a-cC ．-cD ．c4．由于被墨水污染，一道题仅能看见如下文字：，已知二次函数y = x 2+bx +c 的图象 过点（-1，0）……求证：这个二次函数的图象关于直线x = 1对称，据此信息，请你判断对此函数图象的阐述不确的是（ ）A ．过点（3，0）B ．顶点坐标为（1，-2）C ．在 x 轴上截得的线段长为4D ．与y 轴的交点是（0，-3）5．如图，圆锥的母线长是3，底面半径是1， A 是底面圆周上一点，从点A 出发绕侧面一周，再回到点A 的最短路线长是（ ）ABC． D ．3 6．将二次函数y =-2( x -1)2-2的图象向左平移1个单位，在向上平移1个单位，则所得新图象顶点为（ ）A ．（0，0）B ．（1，-2）C ．（0，-1）D ．（-2，1）7．二次函数y =ax 2+bx +c 图象如图所示，则下列式子abc ，b 2-4ac ，a +b +c ，2a +b 值为正数的有（ ）个A ．4B ．3C ．2D ．18．下列命题：①三点确定一个圆②三角形的外心到三个顶点的距离相等③直径所对的角是直角④平分弦的直径垂直于这条弦⑤圆周角等于圆心角的一半，其中正确的有（ ）个A ．1B ．2C ．3D ．4 A B DCx9．已知：AB 是⊙O 的直径，AC 、AD 是两条弦，且AB =2，AC，AD =1，则圆周角∠CAD 的度数为（ ） A ．45º或60º B ．60º C ．105º D ．15º或105º１0．如图，△ABC 中，BC =4，以 A 为圆心，2为半径的⊙A 与BC 相切于点D ，交 AB 于E ，交AC 于F ，点P 是⊙A 上的一点，且∠EPF =40º，则图中阴影部分的面积是（）A ．849π-B ．889π- C ．849π+ D ． 342π+ 二、填空：（3×10=30分）１1．△ABC 是正三角形且内接于半径为2cm 的圆，则AB 所对的弧长是 １2．二次函数y =mx 2-3x+2m-m 2的图象经过原点，则m 为１3．已知：⊙O 的圆心为坐标原点，半径为3，⊙O ’ 的圆心坐标为1），半径为1，则两圆的位置关系是１4．已知抛物线的对称轴为y 轴，其图象与x 轴关于A （-2，0），B （2，0），抛物线顶点为C ，S △ABC =4，此抛物线表达式为１5．已知关于x 的一元二次方程a x 2+b +c =3的一个根为x 1 =2，且二次函数y =a x 2+b +c 的对称轴是x =2，则抛物线的顶点坐标为１6．对称轴平行于y 轴的抛物线顶点坐标为（2，-9），且过点（-1，0），求此抛物线与x 轴两个交点间的距离为１7．△ABC 中，∠△ACB =90º，ACBC =1，将△ABC 绕C 点旋转90º后为 Rt△A ′B ′C ，再将Rt △A ′B ′C 绕B ′点旋转为Rt △A ′′B ′C ′ ，使得A 、C 、B ’、A ” 在同一直线上，则A 点运动到A ” 所走的长度为１8．Rt △ABC 中，AB =6，BC =8，则这个三角形内切圆的半径为１9．一个三角尺两直角边长分别为3cm 和4 cm ，以它的斜边为轴旋转一周，得到一个旋转体，求旋转体的全面积20．如图，AB 是圆的直径，∠DPB =60º，则CD ∶AB =A A ’A ” C ’ CB B ’ A B三、简答题：（21题每题4分，22题7分，23题8分，24题8分，25题8分，26题9分，27题12分）21．①．2sin45º+6cos30º+4tan45º②．已知：P A 、PB 为⊙O 的两条切线，切点为A ,B ，DC 切⊙O 于点E ，P A =8 cm ，∠APB =50º，则∠DOC 的度数是多少？△PDC 的周长为多少？22．右图为住宅区的两幢楼，它们的高度都是30米，两楼间的水平距离AC =24米，现需了解甲楼对乙楼采光情况的影响，当太阳光线与水平光线的夹角为30º时，求甲楼的影子落在乙楼上的高度。
初四期末考试数学试卷
一、选择题（每题5分，共25分）1. 下列各数中，绝对值最小的是（）A. -3B. 2C. -1.5D. 0.52. 已知a > b，下列不等式中正确的是（）A. a - b > 0B. a + b > 0C. a - b < 0D. a + b < 03. 在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数是（）A. 75°B. 105°C. 120°D. 135°4. 下列函数中，是反比例函数的是（）A. y = 2x + 3B. y = 3/xC. y = x^2D. y = √x5. 下列图形中，是轴对称图形的是（）A. 等腰三角形B. 平行四边形C. 梯形D. 长方形二、填空题（每题5分，共25分）6. 已知a = -3，b = 2，则a + b = ________。
7. 下列方程中，x = 2是它的解的是（）A. 2x - 1 = 3B. 2x + 1 = 3C. 2x - 1 = 1D. 2x + 1 = 18. 若sinθ = 1/2，则cosθ的值是 ________。
9. 下列数中，有理数是 ________。
10. 若x^2 - 5x + 6 = 0，则x的值为 ________。
三、解答题（共50分）11. （15分）解下列方程组：\[\begin{cases}2x + 3y = 8 \\x - y = 1\end{cases}\]12. （15分）已知函数y = -2x + 5，求以下问题：（1）当x = 3时，y的值为多少？（2）当y = -1时，x的值为多少？13. （20分）已知直角三角形ABC中，∠A = 90°，∠B = 30°，∠C= 60°，AB = 6cm，求：（1）BC的长度；（2）AC的长度；（3）三角形ABC的面积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
肇源县2013—2014学年度上学期期末质量检测初四数学试题 于红玉2.全卷共四道大题，28个小题，总分120分。
一、选择题（本大题共10小题，每小题3分，共30分。
下列各题的四个选项中，有且只有一个是正确的，请将正确选项的序号填在相应的位置上。
） 1、（改编)下列计算正确的是（ ） A 、2a 3+a 2=2a 5 B 、（﹣2ab ）3=﹣2ab 3 C 、2a 3÷a 2=2a D 错误！未找到引用源。
2、（资评)下列图形中，既是轴对称图形又是中心对称图形的有（ ）个．A 、1B 、2C 、3D 、43、（转载)由一些大小相同的小正方体搭成的几何体的主视图与左视图如图所示，则搭成这个几何体的小正方体的个数最少为（ ）4.（转载)如图是一种古代计时器——“漏壶”的示意图，在壶内盛有一定量的水，水从壶下的小孔漏出，壶壁上画有刻度， 人们可以根据壶中的水面的位置计算时间.现用x 表示时间，y 表示壶到水面的高度，下列图象适y 与xA B C D5.（转载)次函数y=ax 2+bx+c （a≠0）的图象如图所示，则下列结论中正确的是（ ）A ．a ＞0B ．当﹣1＜x ＜3时，y ＞0C ．c ＜0D ．当x ≥1时，y 随x 的增大而增大6.（转载)把不等式组的解集在数轴上表示正确的是（ ）B．（ ）8、（改编）抛物线y=ax 2+bx ﹣3过点（2，4），则代数式8a+4b+1的值为（ ）A 、﹣2B 、2C 、15D 、﹣159、（转载)已知⊙0的直径AB=40，弦CD ⊥AB 于点E ，且CD=32，则AE 的长为（ ）A 、12B 、8C 、12或28D 、8或3210、（转载)如图，在正方形ABCD 中，点O 为对角线AC 的中点，过点0作射线OM 、ON 分别交AB 、BC 于点E 、F ，且∠EOF=90°，BO 、EF 交于点P ．则． D ．A 、3B 、4C 、5D 、6密封线内不 许 答题下列结论中：（1）图形中全等的三角形只有两对；（2）正方形ABCD 的面积等于四边形OEBF 面积的4倍；（3）BE+BF=错误！未找到引用源。
0A ；（4）AE 2+CF 2=20P•OB ，正确的结论有（ ）个．A 、1B 、2C 、3D 、4二、填空题（每题3分，共18分）11，(改编)广州某慈善机构全年共募集善款5250000元，将5250000用科学记数法表示为___________ .12，(资评)若代数式有意义，则实数x 的取值范围是____________.13(改编）服装店销售某款服装，一件服装的标价为300元，若按标价的八折销售，仍可获利60元，则这款服装每件的标价比进价多____________.14（转载).把抛物线y=（x ﹣2）2﹣3向下平移2个单位，得到的抛物线与y 轴交点坐标为 ．15（转载)甲、乙、丙三人站成一排合影留念，则甲、乙二人相邻的概率是 ．16、(资评)在△ABC 中，AB=6，AC=9，点D 在边AB 所在的直线上，且AD=2，过点D 作DE ∥BC 交边AC 所在直线于点E ，则CE 的长为______． 17 (中考题)如图，OP=1，过P 作PP 1⊥OP ，得OP 1=；再过P 1作P 1P 2⊥OP 1且P 1P 2=1，得OP 2=；又过P 2作P 2P 3⊥OP 2且P 2P 3=1，得OP 3=2；…依此法继续作下去，得OP 2012= ．18.(资评)在平面直角坐标系中，已知点A （4，0）、B （﹣6，0），点C 是y 轴上的一个动点，当∠BCA=45°时，点C 的坐标为 ． 三、解答题（满分60分） 19.计算：（改编)（2﹣）2012（2+）2013﹣2﹣（）0．20（资评)先化简，再求代数式的值．，其中a=（﹣1）2012+tan60°．21（转载)如图，△ABC 中，AB=BC ，BE ⊥AC 于点E ，AD ⊥BC 于点D ，，AD 与BE 交于点F ，连接CF. (1)求证：BF=2AE; (2)若CD=2,求AD 的长.22.（转载)以“光盘”为主题的公益活动越来越受到社会的关注．某校为培养学生勤俭节约的习惯，随机抽查了部分学生（态度分为：赞成、无所谓、反对），并将抽查结B果绘制成图1和图2（统计图不完整）．请根据图中提供的信息，解答下列问题：（1）此次抽样调查中，共抽查了多少名学生？ （2）将图1补充完整；（3）根据抽样调查结果，请你估计该校3000名学生中有多少名学生持反对态度？23.（转载)如图，在平面直角坐标系中，直角梯形OABC 的边OC 、OA 分别与x 轴、y 轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，C 的坐标为（－18，0）。
（1）求点B 的坐标；（2）若直线DE 交梯形对角线BO 于点D ，交y 轴于点E ，且OE=4，OD=2BD ，求直线DE 的解析式；24.（改编)国家海洋局将中国钓鱼岛最高峰命名为“高华峰”，并对钓鱼岛进行常态化立体巡航．如图1，在一次巡航过程中，巡航飞机飞行高度为2001米，在点A 测得高华峰顶F 点的俯角为30°，保持方向不变前进1200米到达B 点后测得F 点俯角为45°，如图2．请据此计算钓鱼岛的最高海拔高度多少米．（结果保留整数，参考数值：=1.732，=1.414）25（转载)如图，AB 是⊙O 的直径，∠B=∠CAD ． （1）求证：AC 是⊙O 的切线； （2）若点E是的中点，连接AE 交BC 于点F ，当BD=5，CD=4时，求AF 的值．26（转载).在一个不透明的盒子中放有三张卡片，每张卡片上写有一个实数，分别为3，2，2+6.（卡片除了实数不同外，其余均相同）（1）从盒子中随机抽取一张卡片，请直接写出卡片上实数是3的概率； （2）先从盒子中随机抽取一张卡片，将卡片上的实数作为被减数； 卡片不放回，再随机抽取一张卡片，将卡片上的实数作为减数.请你用列表法或树状图（树形图）法，求出两次抽取的卡片上的实数之差为有理数的概率.密封 线内不 许答题取的卡片上的实数之差为有理数的概率是31=62.27.（转载)定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质：如果两个三角形是“友好三角形”,那么这两个三角形的面积相等. 理解：如图①，在△ABC 中，CD 是AB 边上的中线，那么△ACD 和△BCD 是“友好三角形”，并且S △ACD =S △BCD .应用：如图②，在矩形ABCD 中，AB=4,BC=6,点E 在AD 上，点F 在BC 上，AE=BF ，AF 与BE 交于点O.（1） 求证：△AOB 和△AOE 是“友好三角形”；（2） 连接OD ，若△AOE 和△DOE 是“友好三角形”，求四边形CDOF 的面积. 探究：在△ABC 中，∠A=30°，AB=4, 点D 在线段AB 上，连接CD ，△ACD 和△BCD 是“友好三角形”，将△ACD 沿CD 所在直线翻折，得到△A′CD ，若△A′CD 与△ABC 重合部分的面积等于△ABC 面积的41，请直接写出△ABC 的面积.28（转载)在平面直角坐标系中，已知点(2,0)A -，点(0,4)B ，点E 在OB 上，且∠OAE ＝∠OBA . （Ⅰ）如图①，求点E 的坐标；（Ⅱ）如图②，将AEO 沿x 轴向右平移得到A E O '''，连接A B BE ''、.①设AA m '=，其中02m <<，试用含m 的式子表示22A B BE ''+，并求出使22A B BE ''+取得最小值时点E '的坐标；②当A B BE ''+取得最小值时，求点E '的坐标（直接写出结果即可）．—2014学年度上学期期末质量检测 初四数试题参考答案 宋丽玲二、填空题答案：（每小题3分，共18分）11. 5.25×106 12. 01x x ≥≠且13. 120元 14. （0，-1） 15. ． 16.6或1217. ． 18. （0,12)或(0,-12)19. 解：原式= [（2﹣）（2+）]2012（2+）﹣﹣1=2+﹣﹣1图①图②=1．20. 解：原式=•=•=，当a=（﹣1）2012+tan60°=1+时，原式==．21. (1)证明：∵AD ⊥BC, ∠BAD=45°， ∴∠ABD=∠BAD=45°. ∴AD=BD ，∵AD ⊥BC, BE ⊥AC, ∴∠CAD+∠ACD=90°， ∠CBE +∠ACD=90°， ∴∠CAD=∠CBE.又∵∠CDA=∠BDF=90°， ∴△ADC ≌△BDF. ∴AC=BF.∵AB=BC,BE ⊥AC, ∴AE=EC 即AC=2AE, ∴BF=2AE;(2)解：∵△ADC ≌△BDF ∴DF=CD=2,∴在Rt △CDF 中，CF=2=+22CD DF ， ∵BE ⊥AC, AE=EC,∴AF=FC=2， ∴AD=AF+DF=2+2.22.解：（1）130÷65%=200名； （2）200﹣130﹣50=20名；（3）3000×=300名．23.解：（1）过点B 作BF⊥x 轴于F ， 在Rt△BCF 中∵∠BCO=45°， ∵C 的坐标为（－18，0），∴AB=OF=6。
∴点B 的坐标为（－6，12）。
（2）过点D 作DG⊥y 轴于点G ， ∵OD=2BD，∴OD=23OB 。
∵AB∥DG，∴△ODG∽△OBA 。
∵DG OD OG 2AB OB OA 3===，AB=6，OA=12，∴DG=4，OG=8。
∴D（－4，8），E （0，4）。
设直线DE 解析式为y=kx+b （k≠0） ∴ 4k b 8b 4-+=⎧⎨=⎩，解得k 1 b 4=-⎧⎨=⎩。
∴直线DE 解析式为y=－x+4。
密封 线内不 许 答 题x +1+1==2，=2．26.（1）31（2）画树状图得：由树状图可知，共有6种可能出现的结果，每种结果出现的可能性相同，其中两次抽取的卡片上的实数之差为有理数的结果有两种，因此，两次抽取的卡片上的实数之差为有理数的概率是31=62.27. (1)证明：∵ 四边形ABCD 为矩形， ∴AD ∥BC,∴∠EAO=∠BFO,又∵∠AOE=∠FOB,AE=BF ， ∴△AOE ≌△FOB ， ∴EO=BO.∴△AOB 和△AOE 是“友好三角形”.（2）∵△AOE 和△DOE 是“友好三角形”，∴S △AOE =S △DOE ，AE=ED=21AD=3.∵△AOB 和△AOE 是“友好三角形” ∴S △AOB =S △AOE∵△AOE ≌△FOB ， ∴S △AOE =S △FOB ， ∴S △AOD =S △ABF ，开 始322+622+6 +6 32∴S 四边形CDOF =S 矩形ABCD -２S △ABF =4×6-2×21×4×3=12.探究：2或32.28. 解：(Ⅰ)如图①，∵点A(﹣2，0)，点B(0，4)， ∴OA=2，OB=4．∵∠OAE=∠0BA ，∠EOA=∠AOB=90°， ∴△OAE ∽△OBA ，∴=，即=，解得，OE=1，∴点E 的坐标为(0，1)； (Ⅱ)①如图②，连接EE ′．由题设知AA ′=m(0＜m ＜2)，则A ′O=2﹣m ．在Rt △A ′BO 中，由A ′B 2=A ′O 2+BO 2，得A ′B 2=(2﹣m)2+42=m 2﹣4m+20．∵△A ′E ′O ′是△AEO 沿x 轴向右平移得到的，∴EE ′∥AA ′，且EE ′=AA ′． ∴∠BEE ′=90°，EE ′=m ． 又BE=OB ﹣OE=3，∴在Rt △BE ′E 中，BE ′2=E ′E 2+BE 2=m 2+9，∴A ′B 2+BE ′2=2m 2﹣4m+29=2(m ﹣1)2+27．当m=1时，A ′B 2+BE ′2可以取得最小值，此时，点E ′的坐标是(1,1)． ②如图②，过点A 作AB ′⊥x ，并使AB ′=BE=3． 易证△AB ′A ′≌△EBE ′， ∴B ′A=BE ′，∴A ′B+BE ′=A ′B+B ′A ′．当点B 、A ′、B ′在同一条直线上时，A ′B+B ′A′最小，即此时A ′B+BE ′取得最小值．易证△AB ′A ′∽△OBA ′，∴==，∴AA ′=×2=，∴EE ′=AA ′=，∴点E ′的坐标是(，1)．。