秦九韶算法实验报告
秦九韶算法介绍和实例分析

秦九韶算法介绍和实例分析具体而言,秦九韶算法通过构建一个累加器,用来存储每一次迭代计算的结果。
首先,将多项式的最高次项系数存入累加器中。
然后,通过迭代计算,将每一个次高次项的系数与上一次迭代的结果相乘,并加上该项的常数部分。
依次迭代计算,直到将所有的项都计算完毕。
最终,累加器中的值即为多项式的求值结果。
下面以一个实例来说明秦九韶算法的应用。
假设我们要求解如下多项式的值:P(x)=2x^4+3x^3-5x^2+6x-4首先,我们可以将多项式表示为累加的形式:P(x)=(((2x+3)x-5)x+6)x-4然后,我们可以使用秦九韶算法进行计算。
首先,将最高次项系数2存入累加器中。
累加器=2接下来,进行迭代计算。
首先,将累加器乘以x,并加上次高次项的常数部分3,得到结果5x+3累加器=(5x+3)然后,将累加器再次乘以x,并加上次高次项的常数部分-5,得到结果-5x^2+(5x+3)。
累加器=(-5x^2+5x+3)依次类推,进行下一次迭代计算。
最终,得到累加器的值为-4累加器=(-4)因此,多项式P(x)在x=1处的值为-4通过以上实例分析,我们可以看到,秦九韶算法通过使用累加的方式进行计算,大大减少了乘法和加法运算的次数,提高了算法的效率。
在实际应用中,秦九韶算法常用于求解多项式的值,例如在计算机图形学中,可用于求解曲线上的点的坐标。
同时,该算法还可以用于多项式的除法和求导等运算中。
总结起来,秦九韶算法是一种用于求解多项式的高效算法,通过使用累加的方式进行计算,减少了乘法和加法运算的次数。
该算法在实际应用中具有广泛的应用价值,可以提高计算效率,同时也为其他相关运算提供了基础。
秦九韶算法公式及结论

秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法。
在西方被称作霍纳算法。
秦九韶(约公元1202年-1261年),字道古,南宋末年人,出生于鲁郡(今山东曲阜一带人)。
计算方法
一般地,一元n次多项式的求值需要经过(n+1)*n/2次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法。
在人工计算时,一次大大简化了运算过程。
把一个n次多项式
改写成如下形式:
求多项式的值时,首先计算最内层括号内一次多项式的值,即
V1=an*x+a n-1
然后由内向外逐层计算一次多项式的值,即
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值。
结论:对于一个n次多项式,至多做n次乘法和n次加法。
秦九韶算法

2007-2008(2)专业课程实践论文秦九昭算法数学04 王琳,19号秦九韶算法的特典在于,它通过一次式的反复计算,逐步得出高次多项式的值。
具体地说,它将一个n 次多项式的求解问题,归结为重复计算n 个一次式a v v k n k k x --+=1,k=1,2,…,n (1) 来实现。
这种化繁为简的处理方法在数值分析中是屡见不鲜的。
现在考虑秦九韶算法的计算程序。
按式(1)计算,每求出一个“新值”v k 以后,“老值”v k 1-便失去继续保存的价值,因此可以将新值v k 存放在老值v k 1-所占用的单元内。
这样,我们只要设置一个单元v 进行累算,而将式(1)表为下列动态形式v v x a k n ⇒+∙-, k=1,2,…,n 执行这组算式之前,应先送初值a n 到单元v 中,v a n ⇒ 图描述了秦九韶算法(框1)准备部分。
单元v 送初值a n ,单元k 中送数值1.(框2)计算部分。
每循环一次,单元v 中的老值v k 1-为新值v k 所替换。
(框3)控制部分。
检查单元k 中计数值以判断循环应否结束。
当计数值为n 时输出v 中结果,否则转框4.(框4)修改部分。
修改单元k 中计数值,然后转框2再作下一步的计算。
图1#include<stdio.h>#include <math.h>float qin(float a[],int n,float x){ float r=0;int i;for(i=n;i>=0;i--)r=r*x+a[i];return r;}main(){ float a[50],x,r=0;int n,i;do{ printf("Input frequency:");scanf("%d",&n);}while(n<1);printf("Input value:");for(i=0;i<=n;i++)scanf("%f",&a[i]);printf("Input x:");scanf("%f",&x);r=qin(a,n,x);printf("Answer:%f",r);getch();}利用秦九韶算法求多项式1)(43245+-+-=x x x x x p 在3=x 时的值。
数值计算实验报告

qd.get_arr();
cout<<"x=?\n:";//x=?
cin>>x;
qd.get_x(x);
cout<<"Sum="<<qd.get_sum()<<endl;
return0;
}五.实验结果及分析
运行该程序计算多项式 得
1)在 F(x) = 9.40531
2)在 F(x) = 11.27232
3) 在F(x) = 12.29693
六.实验反思
1.秦九韶算法的作用:解决了运算次数的问题,大大减少了乘法运算的次数,提高了运算效率。
2.了解了数学计算转换为计算机计算的途径,从而探究到计算机算法与数学算法的区别,,体会到计算机对数学学习的辅助作用。
{
Calc();
returnsum;
}
private:
floatn,x;
float*p;
floatsum;
voidArr_Init()//动态数组初始化
{
p=newfloat[n+1];
if(p==NULL)//检查是否分配成功
{
cout<<"Error!"<<endl;
exit(0);
}
for(inti=0;i<=n;i++)//默认赋0值
{
public:
voidget_n(float_inpt_num)
{
n=_inpt_num;
用秦九韶算法计算多项式的值c语言

用秦九韶算法计算多项式的值c语言多项式是数学中的一个重要概念,它在各个领域都有广泛的应用。
在计算机科学中,多项式的计算也是一个常见的问题。
本文将介绍一种高效的算法——秦九韶算法,用它来计算多项式的值。
一、秦九韶算法的原理秦九韶算法是一种快速计算多项式值的算法。
它的基本思想是将多项式的系数和变量分离,然后通过递推的方式计算多项式的值。
具体来说,假设多项式为:f(x) = a0 + a1x + a2x^2 + ... + anx^n我们可以将其表示为:f(x) = a0 + x(a1 + x(a2 + ... + x(an-1 + anx)...))这样,我们就可以通过递推的方式计算多项式的值。
具体来说,我们可以从最高次项开始,依次计算每一项的值,然后将其累加起来。
这样,我们就可以在O(n)的时间复杂度内计算多项式的值。
二、用c语言实现秦九韶算法下面,我们将用c语言来实现秦九韶算法。
具体来说,我们可以定义一个数组来存储多项式的系数,然后通过循环来计算多项式的值。
代码如下:```c#include <stdio.h>double qinjiushao(double a[], int n, double x) {double result = a[n];for (int i = n - 1; i >= 0; i--) {result = result * x + a[i];}return result;}int main() {double a[] = {1, 2, 3, 4, 5};int n = 4;double x = 2;double result = qinjiushao(a, n, x);printf("f(%lf) = %lf\n", x, result);return 0;}```在这个例子中,我们定义了一个数组a来存储多项式的系数,n表示多项式的最高次数,x表示要计算的多项式的值。
秦九韶算法实验报告

《数值计算》实验报告 学院:软件学院 专业:软件工程 班级:2班 实验名称 秦九昭算法姓名 爱上辰 学号 1402120217 成绩实验报告内容要求:一.实验目的编写秦九韶算法程序,并用该程序计算多项式623)(35+-+=x x x x f在1.1=x ,2.1,3.1的值。
二.实验原理秦九韶算法实际上就是多项式的化简。
根据秦九昭算法,变换成计算机语言,求多项式的值时,首先计算最内层括号内一次多项式的值,然后由内向外逐层计算一次多项式的值,这样,求n 次多项式f(x)的值就转化为求n 个一次多项式的值。
三.实验环境Visual Studio 2013,C++语言四.实验过程(编写的程序)#include"iostream"using namespace std;void main(){int n;float a[100], x, v[100];//存放系数cout << "请输入项数:" << endl;cin >> n;cout << "请输入X 的值:" << endl;cin >> x;for (int i = 0; i < n; i++)//对每项系数进行赋值{cout << "请输入第" << i + 1 << "项的系数:" << endl;cin >> a[i];}v[0] = a[0];//秦九昭算法第一次赋值for (int j = 1; j< n;j++)//开始秦九昭算法的循环v[j] = v[j-1] * x + a[j];cout << "当x=" << x <<"时,f(x)="<< v[n-1] <<endl;system("pause");}五.实验结果及分析当X=1.1时,f(x)= 9.4035当X=1.2时,f(x)= 11.2723当X=1.3时,f(x)= 13.7039六.实验反思1.应该采用链表存贮系数,数组有限制性只能存放100项。
数值分析实验3

贵州师范大学数学与计算机科学学院学生实验报告课程名称: 数值分析 班级: 信本班 实验日期: 2013 年 9 月 3日学 号: 110703010038 姓名: 孙泽香 指导教师: 实验成绩:一、实验名称实验一:递推法的稳定性,秦九韶算法二、实验目的及要求1. 熟悉数值稳定的概念, 通过上机计算,了解舍入误差所引起的数值不稳定性.2. 培养Matlab 编程与上机调试能力.三、实验环境每人一台计算机,要求安装Windows XP 操作系统,Microsoft office2003、MATLAB6.5(或7.0)。
四、实验内容1.教材例1.13中,取16位数字计算,并分析、比较计算结果.2.设100999832()101100994321f x x x x x x x =+++++++,用秦九韶算法编程计算()f x 在1,2,3,4x =上的值.五、算法描述及实验步骤1. 设(1)从0I 尽可能精确的近似值出发,利用递推公式:115(1,2,,14)n n I I n n -=-+=, 计算从1I 到14I 的近似值;(2)从15I 较粗糙的估计值出发,用递推公式:111(15,14,,3,2)55n n I I n n -=-+=计算从1I 到14I 的近似 .2. 秦九韶算法给定n次多项式Pn(x)=a(n)x^n+a(n-1)x^(n-1)+…+a(1)x+a(0).要计算Pn(x)在x处的值。
今考虑n次多项式Pn(x),用V(k)表示第k层的值(从里面数起),依次计算 V(1)=a(n)x+a(n-1) V(2)=V(1)x+a(n-2) … V(n)=V(n-1)x+a(0).显然V(n)=Pn(x).记a(n)=V(0),上述计算过程可写成:V(0)=a(n)V(k)=V(k-1)*x+a(n-k),(k=1,2,…,n).六、调试过程及实验结果1.12 算法一:>> format long e>> syms x;>> fun=inline('1./(x+5)');>> I(1)=quad(fun,0,1);>> for n=1:14I(n+1)=1/n-5*I(n);end>> II =Columns 1 through 31.823215568047383e-001 8.839221597630853e-0025.803892011845735e-002Columns 4 through 64.313873274104657e-002 3.430633629476715e-0022.846831852616427e-002Columns 7 through 92.432507403584530e-002 2.123177267791634e-0021.884113661041828e-002Columns 10 through 121.690542805901971e-002 1.547285970490148e-0021.354479238458353e-002Columns 13 through 151.560937141041567e-002 -1.123780129001425e-0037.704747207357855e-002算法二:>> format long e>> syms x;>> fun=inline('x.^14./(x+5)');>> I(15)=quad(fun,0,1);>> for n=14:-1:1I(n)=1/(5*n)-I(n+1)/5;end>> II =Columns 1 through 31.823215567939547e-001 8.839221603022675e-0025.803891984886631e-002Columns 4 through 64.313873408900180e-002 3.430632955499104e-0022.846835222504479e-002Columns 7 through 92.432490554144271e-002 2.123261514992931e-0021.883692425035346e-002Columns 10 through 121.692648985934385e-002 1.536755*********e-0021.407133739268709e-002Columns 13 through 151.297664636989789e-002 1.203984507358747e-0021.122934606063409e-0021.13 设f(x)=101x^100+100x^99+…+3x^2+2x+1,用秦九韶算法编程计算f(x)在x=1,2,3,4上的值。
秦九韶算法
x* 3
b0 3
b1 9
b2 25
b3 75 c2 x* 237
b4 226
b5 685
c0 x* 9
c0 3
c1 18
c1 x* 54
c2 79
c3 x* 936
c4 1162
c3 312
此处 b5
p(3) 685 c4 q(3) p ' (3) 1162
数值分析实验报告
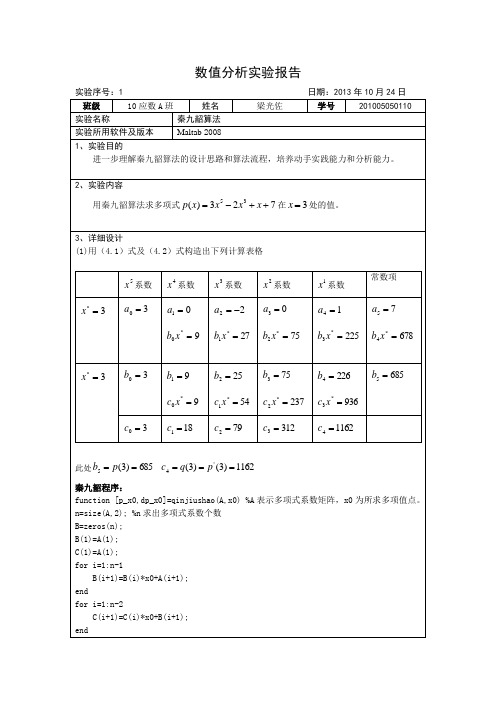
实验序号:1 班级 实验名称 实验所用软件及版本 10 应数 A 班 姓名 秦九韶算法 Maltab 2008 梁光佐 日期:2013 年 10 月 24 日 学号 201005050110
1、实验目的 进一步理解秦九韶算法的设计思路和算法流程,培养动手实践能力和分析能力。 2、实验内容 用秦九韶算法求多项式 p( x) 3x 5 2 x 3 x 7 在 x 3 处的值。
p_x=poly2sym(A,'x') %输出原多项式 p_x_1=horner(p_x) %输出嵌套的多项式 disp('-----------------------------------------------'); p_x0=B(n) %返回 p(x0)的值 dp_x0=C(n-1) %返回 p(x)的一阶导数在 x0 处的值 计算: clear A=input('给出多项式 p(x)从高次到低次的所有系数构成矩阵,缺项系数 0 补齐\nA='); disp('-----------------------------------------------'); x0=input('给出要求解的 p(x0)的点\nx0='); disp('-----------------------------------------------'); tic qinjiushao(A,x0); toc 4、实验结果与分析 给出多项式 p(x)从高次到低次的所有系数构成矩阵,缺项系数 0 补齐 A=[3 0 -2 0 1 7] ----------------------------------------------给出要求解的 p(x0)的点 x0=3 ----------------------------------------------p_x = 3*x^5 - 2*x^3 + x + 7 p_x_1 = x*(x^2*(3*x^2 - 2) + 1) + 7 ----------------------------------------------p_x0 = 685 dp_x0 = 1162 Elapsed time is 0.101758 seconds.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数值计算》实验报告 学院:软件学院 专业:软件工程 班级:2班 实验名称 秦九昭算法
姓名 爱上辰 学号 1402120217 成绩
实验报告内容要求:
一.实验目的
编写秦九韶算法程序,并用该程序计算多项式623)(35+-+=x x x x f
在1.1=x ,2.1,3.1的值。
二.实验原理
秦九韶算法实际上就是多项式的化简。
根据秦九昭算法,变换成计算机语言,求多项式的值时,首先计算最内层括号内一次多项式的值,然后由内向外逐层计算一次多项式的值,这样,求n 次多项式f(x)的值就转化为求n 个一次多项式的值。
三.实验环境
Visual Studio 2013,C++语言
四.实验过程(编写的程序)
#include"iostream"
using namespace std;
void main()
{
int n;
float a[100], x, v[100];//存放系数
cout << "请输入项数:" << endl;
cin >> n;
cout << "请输入X 的值:" << endl;
cin >> x;
for (int i = 0; i < n; i++)//对每项系数进行赋值
{
cout << "请输入第" << i + 1 << "项的系数:" << endl;
cin >> a[i];
}
v[0] = a[0];//秦九昭算法第一次赋值
for (int j = 1; j< n;j++)//开始秦九昭算法的循环
v[j] = v[j-1] * x + a[j];
cout << "当x=" << x <<"时,f(x)="<< v[n-1] <<endl;
system("pause");
}
五.实验结果及分析
当X=1.1时,f(x)= 9.4035
当X=1.2时,f(x)= 11.2723
当X=1.3时,f(x)= 13.7039
六.实验反思
1.应该采用链表存贮系数,数组有限制性只能存放100项。
2. 注意项数,有的项系数为0,导致漏输进而导致结果错误。
3.注意变量应该为float型,避免出现强制转换而出现误差。
