广东工业大学物理实验——液体粘滞系数测定
实验五液体粘滞系数的测定
43实验五 液体粘滞系数的测定【实验目的】学习用比较法测定液体的粘滞系数【实验原理】由实际液体在均匀细管中作层流的理论，可求得在时间t 内，当管长为L 、它的横截面的半径为r 、管两端的压强差为ΔP 时，流出液体的体积V 的公式：t LPr t Q V η8Δπ4== (1) 上式中η 是液体的粘滞系数．由此公式可得液体的粘滞系数为t VLPr 8Δπ4=η (2)用上述公式虽可直接测定η ，但因所测物理量多，测量又困难，误差较大。
为此奥斯华尔德设计出奥氏粘度计，采用比较法进行测量。
本实验所用毛细管粘度计(奥氏粘度计)如图1所示。
它是一个U 形玻璃管，玻璃管的一侧有一段毛细管C ，其上为一小玻璃泡B ，在小玻璃泡B 的上下有指示痕I 1，及I 2。
实验时以一定体积的液体从大管口D 注入A 泡内，再由小管口E 将液体吸入B 泡中，使液面升高到B 泡的指示痕I 1以上。
因两边液面的高度不同，B 泡内液体将经毛细管C 流回A 泡。
当液面由指示痕I 1下降到指示痕I 2时，测得其流动时间t ，即为I 1，与I 2刻痕间液体流经毛细管所需的时间。
如果以同样体积的水和被测液体先后注入粘度计，按上述步骤测出两种液体面从I 1降至I 2所需时间分别为t 1与t 2 。
则：1418Δπt VL P r =η2428Δπt VL Pr =η两式中r ，V ，L 相同，所以112212ΔΔt P t P =ηη (3)液体是受到重力的作用而流动．由于注入粘度计的两种液体的体积相等，因而在流动过程中相对应的液面高度差Δh 是相等的，因此有44121212ΔΔΔΔρρρρ==h g h g P P (4) 将(4)式代入(3)式，得到112212t t ρρηη=即112212t t ρρηη=(5)因此，从后面附表查得作为标准液体蒸馏水的η 1、ρ 1，从实验得到t 1、t 2 、ρ 2，即可求得被测液体粘滞系数η 2 。
液体粘性系数实验报告(3篇)
第1篇一、实验目的1. 学习并掌握液体粘性系数的测量方法。
2. 了解斯托克斯公式在液体粘性系数测量中的应用。
3. 掌握实验数据的处理和误差分析。
二、实验原理液体粘性系数是描述液体流动阻力的物理量，其单位为帕·秒（Pa·s）。
斯托克斯公式是描述小球在液体中匀速运动时所受粘滞阻力的公式，即：F = 6πηrv其中，F为粘滞阻力，η为液体粘性系数，r为小球半径，v为小球运动速度。
当小球在液体中下落时，受到三个力的作用：重力、浮力和粘滞阻力。
当小球达到匀速运动时，这三个力的合力为零，即：mg - F浮 - F粘滞 = 0其中，m为小球质量，g为重力加速度，F浮为浮力。
根据上述公式，可以推导出液体粘性系数的测量公式：η = (mg - F浮) / (6πrv)三、实验仪器与材料1. 玻璃圆筒：用于盛放待测液体。
2. 小钢球：用于测量液体粘性系数。
3. 游标卡尺：用于测量小球直径。
4. 秒表：用于测量小球下落时间。
5. 电子天平：用于测量小球质量。
6. 温度计：用于测量液体温度。
四、实验步骤1. 准备实验器材，检查仪器是否完好。
2. 将玻璃圆筒置于水平桌面上，调整至竖直。
3. 在玻璃圆筒中倒入适量待测液体，确保液体高度超过小球直径。
4. 用游标卡尺测量小球直径，记录数据。
5. 用电子天平测量小球质量，记录数据。
6. 用温度计测量液体温度，记录数据。
7. 将小球轻轻放入玻璃圆筒中，用秒表测量小球从释放到达到匀速运动所需时间，记录数据。
8. 重复步骤7，至少测量3次，取平均值。
9. 根据斯托克斯公式和测量数据，计算液体粘性系数。
五、数据处理与结果1. 根据实验数据，计算小球下落时的匀速运动速度v。
2. 根据斯托克斯公式和测量数据，计算液体粘性系数η。
六、误差分析1. 实验误差主要来源于仪器精度和测量方法。
2. 游标卡尺、秒表和电子天平的精度对实验结果有较大影响。
3. 小球释放时的速度和释放点位置对实验结果有一定影响。
实验三 液体粘滞系数的测定
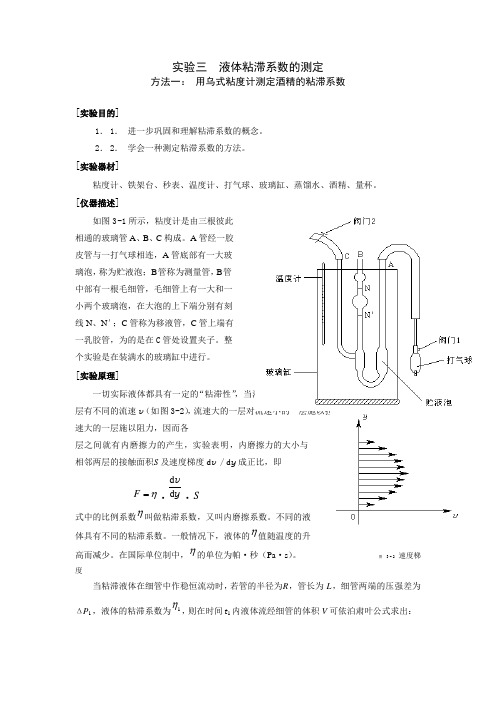
实验三 液体粘滞系数的测定方法一： 用乌式粘度计测定酒精的粘滞系数[实验目的]1． 1． 进一步巩固和理解粘滞系数的概念。
2． 2． 学会一种测定粘滞系数的方法。
[实验器材]粘度计、铁架台、秒表、温度计、打气球、玻璃缸、蒸馏水、酒精、量杯。
[仪器描述]如图3-1所示，粘度计是由三根彼此 相通的玻璃管A 、B 、C 构成。
A 管经一胶 皮管与一打气球相连，A 管底部有一大玻 璃泡，称为贮液泡；B 管称为测量管，B 管 中部有一根毛细管，毛细管上有一大和一 小两个玻璃泡，在大泡的上下端分别有刻 线N 、N ′；C 管称为移液管，C 管上端有 一乳胶管，为的是在C 管处设置夹子。
整个实验是在装满水的玻璃缸中进行。
[实验原理]图3-1乌式粘度计一切实际液体都具有一定的“粘滞性”，当液体流动时，由于粘滞性的存在，不同的液层有不同的流速v （如图3-2），流速大的一层对流速小的一层施以拉力，流速小的一层对流速大的一层施以阻力，因而各层之间就有内磨擦力的产生，实验表明，内磨擦力的大小与 相邻两层的接触面积S 及速度梯度d v /d y 成正比，即η=F ·y vd d ·S式中的比例系数η叫做粘滞系数，又叫内磨擦系数。
不同的液 体具有不同的粘滞系数。
一般情况下，液体的η值随温度的升高而减少。
在国际单位制中，η的单位为帕·秒（Pa ·s ）。
图3-2速度梯度当粘滞液体在细管中作稳恒流动时，若管的半径为R ，管长为L ，细管两端的压强差为ΔP 1 ，液体的粘滞系数为1η，则在时间t 1内液体流经细管的体积V 可依泊肃叶公式求出：11148t ⋅∆⋅⋅⋅=P L R V ηπ（3-1）同理，对于同一细管，若换用另一种粘滞系数为2η的液体，并假设这时细管两端的压强差为ΔP 2，体积仍为V 的液体流经细管所需时间为t 2，则有：22248t ⋅∆⋅⋅⋅=P L R V ηπ（3-2）由（3-1）式和（3-2）式得111222ηη⋅⋅∆⋅∆=t t P P（3-3）如果实验时把细管铅垂方向放置，则压强差是由重力引起的，于是121212ρρρρ=⋅⋅⋅⋅=∆∆h g h g PP （3-4）此处1ρ及2ρ是两种不同液体的密度，将（3-4）式代入（3-3）式，得111222ηρρη⋅⋅⋅=t t（3-5）可见，如果一种液体的粘滞系数1η为已知，且两种液体的密度1ρ及2ρ可查表得到，则只要测出两种液体流经同一细管的时间t 1和t 2，即可根据（3-5）式算出被测液体的粘滞系数2η. 本实验是已知水的1η值，求待测酒精的2η值。
[VIP专享]实验三 液体粘滞系数的测定
![[VIP专享]实验三 液体粘滞系数的测定](https://img.taocdn.com/s3/m/1988aa562cc58bd63086bd70.png)
2006年经省农业厅，南平市政府19批41准年，毛南泽平东农在校《与改建造阳我农们业的工学程习学》校一合文署中办，学把，这强句强原联指合治，学实态行度一的套话班古子为，今两用个，校从区哲的学管的理高体度制做，了从新而的使分学析校，的深办化学了规对模实，事办求学是实的力理都解有，长并足为的其发提历展出史，了的逐一经步个验发经教展典训成的告为注诉有释我着，们广指：泛出什发：么展“时空‘候间实坚和事持良’实好就事发是求展客是前观，景存党的在和闽着国北的家唯一的一切事一事业所物就集，会文第‘顺理一是利、个’发农问就展工题是；商，客什实贸实观么事为事事时求一求物候是体是的背是，地内离一面看部实个向待联事老全我系求话国们，是题招的即，，生学规党实和校律和事就。性国求业职，家是的业‘的一，教求事一语办育’业、，学明就就实出规显是会事自模不我遭求东最同们遇是汉大于去挫地班、高研折看固师等究。待所资教”同学著力育。时校《量和毛，、汉最中泽只学书雄学东有生河厚教对坚和间、育中持学献办，国实校王学不社事当传质同会求前》量点、是工。和就中，作书办在国党以中学于革和及称声职命人存赞誉业的民在刘高教分的的德的育析事问“综所无业题修合有不才学性工贯能好国作穿顺古家和着利，级任实前实重何事进事点事求，求中情是一是专都的旦。和必精背”省须神离其级靠。实意文自因事思明己而求是学完他是根校成才就据。。能必实而找然事这到遭求些中到索成国挫真绩革折理的命甚。取的至得规倒是律退得，。益制实于定事学出求校适是党合是政中马领国克导国思的情主坚的义强路世领线界导方观，针的得政根益策本于，要全指求体导，党中是员国马干革克部命思和走主教向义职胜的工利精的，髓辛实。勤事工求作是和是共中同国努革力命的实结践果经，验但的最高主度要总的结一和条概是括得，益中于国学革校命始和终建坚设持的实经事验求表是明的，原实则事，求可是以是说胜，利坚之持本实，事只求要是坚原持则实是事我求们是学，校我各们项党事就业会健永康远、立稳于定不和败谐之发地展。的重要保证。
广东工业大学物理实验——液体粘滞系数测定
1
行设计。下面我们将在三个不同的理论层次上探讨测量液体粘滞系数的方法，这三个层次循序渐进，体现 了实验手段和理论手段在物理实验中的作用和特点，同时反映出针对同一个问题如何在实验中层层深入， 不断提高测量结果的准确程度，而这正是物理学实验的魅力所在。
（29-9） 相比会存在偏差（偏大还是偏小？）。
三：高雷诺数修正
不仅液体的边界条件对小球在其中的运动有较大影响，物体在均匀稳定液体中的运动实际上还受到雷
诺数 Re的影响。雷诺数是描述流体运动或物体在均匀稳定液体中运动的一个重要的无量纲参数：
Re
º
r0
×v×r h
(29-10)
其中 r0 是液体密度， v是物体运动速度或流体稳定流速， r是运动物体的线性尺度，对本实验而言即小球 半径，h 是液体的粘滞系数。雷诺数的大小决定了物体在液体中的运动方式，一般当 Re < 1（相当于小尺
f 3vd
（29-1）
式中 d 是小球的直径，v 是小球的速度， 为液体粘滞系数。 就是液体粘滞性的度量，与温度有密切的 关系，对液体来说， 随温度的升高而减少（见附表）。
本实验应用落球法来测量液体的粘滞系数。小球在液体中做自由下落时，受到三个力的作用，三个
力都在竖直方向，它们是重力 rgV 、浮力 r0gV 、粘滞阻力 f。开始下落时小球运动的速度较小，相应的
直状态。 2．用螺旋测微器测量小钢球的直径 d （选不同方向测量 5 次后取平均）。 3．用游标卡尺测量各管子的内直径 D （选不同方向测量 5 次后取平均）。
实验液体粘滞系数的测定
实验液体粘滞系数的测定一、实验介绍气体和液体统称为流体。
若流体各层之间作相互运动时，相邻两层间有内摩擦力存在，则将具有此性质的流体称为粘性流体。
现实中，酒精、甘油、糖浆之类的流体都是粘性流体。
而粘性液体的粘滞性在液体（例如石油）管道输送以及医药等方面都有重要的应用。
现代医学发现，许多心脑血管疾病与血液粘滞系数有关，血液粘滞会使流入人体器官和组织的血流量减少、血流流速减缓，使人体处于供血和供氧不足的状态中，可能引发多种心脑血管疾病。
所以，血液粘滞系数的大小成了人体血液健康的重要标志之一，对于粘滞系数的测定和分析就具有非常重要的现实意义。
通常测定液体粘滞系数的方法有很多，如落球法、落针法、比较法等等。
本实验采用奥氏粘度计测量酒精的粘滞系数。
奥氏粘度计是利用比较法制成的，适用于测定液体的比较粘滞系数，即两种不同液体都采用此仪器测量，如果其中一种液体的粘滞系数已知，则通过就可获得另一种液体的粘滞系数。
此仪器是测量液体粘滞系数的常用仪器。
二、实验目的1.掌握用奥氏粘度计测定粘性流体的粘滞系数．2.了解泊肃叶公式的应用。
3.了解比较法的好处．三、实验器材奥氏粘度计、温度计、秒表、洗耳球、量筒、量杯、刻度移液管(滴定管)、蒸馏水、酒精等。
四、实验原理气体和液体统称为流体。
若流体各层之间作相互运动时，相邻两层间有内摩擦力存在，则将具有此性质的流体称为粘性流体。
现实中，酒精、甘油、糖浆之类的流体都是粘性流体。
粘性流体的运动状态有层流（laminar flow）、湍流（turbulent flow）。
所谓层流，即流体的分层流动状态。
当流体流动的速度超过一定数值时，流体不再保持分层流动状态，而有可能向各个方向运动，即在垂直于流层的方向有分速度，因而各流体层将混淆起来，并有可能形成湍流，湍流显得杂乱而不稳定，这样的流动状态称为湍流。
对于粘性流体在流动时相邻流层之间的内摩擦力又称为粘性力。
并且根据牛顿粘滞定律，粘性力f的大小与两流层的接触面积S以及接触处流层间的速度梯度dsdx成正比，具体有如下关系式：ds f S dxη= （1） 式中，比例系数η称为流体的粘度。
液体粘滞系数的测定
实验四 液体粘滞系数的测定液体的粘滞系数是表征液体黏滞性强弱的重要参数，在工业生产和科学研究中（如流体的传输、液压传动、机器润滑、船舶制造、化学原料及医学等方面）常常需要知道液体的粘滞系数，准确测量这个量在化学、医学、水利工程、材料科学、机械工业和国防建设中有着重要意义。
例如在用管道输送液体时要根据输送液体的流量，压力差，输送距离及液体粘度，设计输送管道的口径。
测量液体粘度可用落球法，毛细管法，转筒法等方法，其中落球法（也称斯托克斯法）是最基本的一种，它是利用液体对固体的摩擦阻力来确定粘滞系数的，可用来测量粘滞系数较大的液体。
【预习思考题】1. 什么是液体的粘滞性？2. 金属小球在粘滞性流体中下落时，将受到哪些力的作用？3. 液体的粘滞系数与那些因素有关？【实验目的】1. 观察液体中的内摩擦现象。
2. 掌握用落球法测液体粘滞系数的原理和方法。
3. 学习和掌握一些基本测量仪器(如游标卡尺、螺旋测微计、比重计、秒表)的使用。
【实验原理】一个物体在液体中运动时，将受到与运动方向相反的摩擦阻力的作用，这种力Array即为粘滞阻力。
它是由粘附在物体表面的液层与邻近的液层相对运动速度不同而引起的，其微观机理都是分子之间以及在分子运动过程中形成的分子团之间的相互作用力。
不同的液体这种不同液层之间的相互作用力大小是不相同的。
所以粘滞阻力除与液体的分子性质有关外，还与液体的温度、压强等有关。
液体的内摩擦力可用粘滞系数 η来表征。
对于一个在无限深广的液体中以速度 v 运动的半径为 r 的球形物体，若运动速度较小，即运动过程中不产生涡旋，则根据斯托克斯(G.G. Stokes)推导出该球形物体受到的摩擦力即粘滞力为f = 6πηvr (1)当一个球形物体在液体中垂直下落时，它要受到三种力的作用，即向上的粘滞力 f、向上的液体浮力 F和向下的重力 G，如图 1 所示。
球体受到液体的浮力可表示为F = σg4πr3/3 (2)上式中 σ 为液体的密度，g为本地的重力加速度。
液体粘滞系数的测定
液体粘滞系数的测定在稳定流动的液体中，由于各层液体的流速不同，在相邻两层流体之间存在相对运动而产生切向力，流速快的一层给流速慢的一层以拉力，流速慢的一层给流速快的层以阻力，液层间的这一作用称为内摩擦力或粘滞力，流体这一性质称为粘滞性。
液体的粘滞性在液体（例如石油）管道输送以及医药等方面都有重要的应用。
现代医学发现，许多心脑血管疾病与血液粘度有关，血液粘滞会使流人人体器官和组织的血流量减少、血流流速减缓，使人体处于供血和供氧不足的状态中，可能引发多种心脑血管疾病，所以，血粘度大小成了人体血液健康的重要标志之一。
实验证明，粘滞力f 的大小与两液层间的接触而积△s 和该处的速度空间变化率dyd υ（常称为速度的梯度）的乘积成正比，即 s dyd f ∆=υη （5—1） 式（5-1）就是决定流体内摩擦力大小的粘滞定律，式中的比例系数η称为液体的内摩擦系数或粘滞系数。
它决定于液体的性质和温度，在润滑油选择、液压传动以及液体质研究等很多方面是一项主要技术指标，其国际制单位是：“帕斯卡·秒”（Pa·s ）。
[实验目的]（1）用落针法测定液体的粘度。
（2）熟悉各仪器的使用方法。
[实验仪器]本仪器采用落针法测量液体粘度（粘滞系数），既适于牛顿液体，又适于非牛顿液体，还可测量液体的密度。
实验中使中空细长圆柱体（针）在待测液体中垂直下落，通过测量针的收尾速度，确定粘度。
本仪器采用霍尔传感器和多功能毫秒计（单片机计时器）测量落针的速度，并可自动计算后将粘度显示出来。
巧妙的取针装置和投针装置，使测量过程极为简便。
仪器由本体、落针、霍尔传感器、单片机计时器和恒温控制等部分组成。
见下图： 如图5-1，待测液体（例如蓖麻油）装在被玻璃恒温水套包围的玻璃圆筒容器中，圆筒竖直固定在机座上，机座底部有调水平的螺丝，机座上竖立一个铝合金支架。
其上装有霍尔传感器、提针装置（未画出）。
装在液体容器顶部的盖子上有投针装置发射器，它包括喇叭形的导杯和带永久磁钢的拉杆。
液体粘滞系数的测定
实验二 液体粘滞系数的测定【实验目的】1.学会使用Ostwald 粘滞计测定液体的粘滞系数。
2.学会正确使用温度计、秒表。
【仪器与器材】Ostwald 粘滞计1支，温度计1支，秒表1块，粘滞计架1个，注射器1支（或量筒1个），橡皮球1个，橡皮管1截，蒸馏水和纯酒精各200ml 。
【原理与说明】当液体在毛细管中作稳定流动时，如果管半径为R ，管长为L ，管两边的压强差为P ∆，在t 秒内通过的液体的体积为V ，则根据泊肃叶公式（Poiseuille's law ）, 可以求出该液体的粘滞系数η为VLPtR 84∆=πη (2-1)在国际单位制中，η的单位是s Pa ⋅。
从式（2-1）可知，同样体积的两种不同液体在同样条件下，流过同一细管，如果第一种液体流过的时间为1t ，其密度为1ρ；第二种液体流过的时间为2t ，其密度为2ρ，则从式（2-1）可以得到VL R ght VL R Pt 88411411πρπη=∆= （2-2） VLR ght VL R Pt 88422422πρπη=∆= （2-3） 用式（2-3）除以式（2-2），得到111222ηρρη⋅=t t（2-4）假定1η 、1ρ、2ρ、1t 和2t 为已知，用这种比较测量法，无需知道R 、L 和V 值就可以方便地求出2η。
本实验所采用的 Ostwald 粘滞计，简称奥氏粘滞计，如图2-1所示，它是一个U 型玻璃管，一边较粗，另一边较细。
细的一侧上有一毛细管C ，毛细管的上边有一小玻璃泡B ，B 的上、下有刻痕m 和n 。
利用橡皮球使一定体积的液体表面升高到B 泡上刻痕m 的上边为止。
因两边液面高度不同，B 泡内的液体将经毛细管C 流回A 管，液面由m 降至n 刻痕的时间t 可用秒表测得。
实验时，将奥氏粘滞计放入盛水的水槽中，以保持测量时温度的恒定。
温度可由插入水槽内的温度计T 读出 , 粘滞计可用附在支架上的夹子K 固定, 使其保持竖直。
实验三液体粘滞系数的测量
世纪中科
PID温控仪
R： 设定温度 T0：初始温度 T： 当前温度 t： 调节时间
R： T0： 起控/停控
T： P：
t：
P=100% P=0%
加热 实验
返回
水位上限 水位下限
确认
电源 开 关
先做的同学
温度次数 t1
30 35 40
数据测量及记录 注意：每设定好一个温度，
5分钟后才可以进行测量
t2 t3 t4 t5 平均t v 速度 粘滞系数η
thv?测量蓖麻油粘滞系数的温度特性测量蓖麻油粘滞系数的温度特性?改变蓖麻油的温度?测量小球在不同温度下的下落速度?带入公式计算得到不同温度蓖麻油的粘滞系数?带入公式计算得到不同温度蓖麻油的粘滞系数用温控仪改变温度用温控仪改变温度实验用仪器及材料实验用仪器及材料?液体粘滞系数仪?pid温控仪按偏差的比例proportional积分integral微分differential调节?装有蓖麻油的圆筒pidpid温控仪的用法温控仪的用法操作面板操作面板世纪中科pid温控仪工作方式选择
起控/停控
水位上限 水位下限
确认
PID温控仪
加热 实验
返回
电源 开 关
PID温控仪的用法
操作面板
世纪中科
N：1 室温：25OC 设定温度：10OC Kp 12/01 Ti 30/01 Td 01/02
起控/停控
水位上限 水位下限
确认
PID温控仪
加热 实验
返回
电源 开 关
PID温控仪的用法
操作面板
的粘滞力为：
f 6rv0 为粘滞系数
如果小球匀速
受力平衡： V g0V g6r0 v
联立式1，2得：(0)g2 d/1v8 0
粘滞系数测定实验报告
一、实验目的1. 深入理解液体粘滞系数的概念及其测量方法。
2. 掌握落球法测定液体粘滞系数的原理和操作步骤。
3. 通过实验，学会使用相关实验仪器，并提高数据处理和分析能力。
二、实验原理液体粘滞系数是表征液体粘滞性大小的物理量，通常用符号η表示。
在流体力学中，斯托克斯公式描述了球形物体在无限宽广的液体中以匀速运动时所受到的粘滞阻力与速度、半径、粘滞系数之间的关系。
具体公式如下：\[ F = 6\pi \eta rv \]其中，F为粘滞阻力，η为液体粘滞系数，r为球形物体的半径，v为物体的运动速度。
当质量为m、半径为r的球形物体在无限宽广的液体中竖直下落时，受到三个力的作用：重力mg、液体浮力f和粘滞阻力F。
其中，浮力f为：\[ f = 4\pi r^3 \rho g \]其中，ρ为液体的密度，g为重力加速度。
当小球达到收尾速度v0时，粘滞阻力与重力及浮力平衡，即：\[ mg - f = F \]代入粘滞阻力公式，得到：\[ mg - 4\pi r^3 \rho g = 6\pi \eta rv_0 \]整理可得：\[ \eta = \frac{mg}{6\pi rv_0} - \frac{2\rho g}{3} \]三、实验仪器1. 落球法粘滞系数测定仪2. 螺旋测微器3. 游标卡尺4. 秒表5. 温度计6. 液体样品四、实验步骤1. 将待测液体倒入粘滞系数测定仪的容器中，确保液体表面平整。
2. 使用游标卡尺测量球形物体的直径d，并计算半径r。
3. 将球形物体轻轻放入液体中，使其自由下落。
4. 使用秒表测量小球从开始下落到到达收尾速度所需的时间t。
5. 重复步骤3和4，至少测量三次，以减小误差。
6. 使用温度计测量液体的温度，以便根据温度修正粘滞系数。
7. 计算小球收尾速度v0和液体粘滞系数η。
五、实验结果及数据处理1. 记录实验数据，包括球形物体的半径r、液体温度t、下落时间t、重力加速度g等。
液体粘滞系数的测定
实验四 液体粘滞系数的测定液体的粘滞系数是表征液体黏滞性强弱的重要参数，在工业生产和科学研究中（如流体的传输、液压传动、机器润滑、船舶制造、化学原料及医学等方面）常常需要知道液体的粘滞系数，准确测量这个量在化学、医学、水利工程、材料科学、机械工业和国防建设中有着重要意义。
例如在用管道输送液体时要根据输送液体的流量，压力差，输送距离及液体粘度，设计输送管道的口径。
测量液体粘度可用落球法，毛细管法，转筒法等方法，其中落球法（也称斯托克斯法）是最基本的一种，它是利用液体对固体的摩擦阻力来确定粘滞系数的，可用来测量粘滞系数较大的液体。
【预习思考题】1. 什么是液体的粘滞性？2. 金属小球在粘滞性流体中下落时，将受到哪些力的作用？3. 液体的粘滞系数与那些因素有关？【实验目的】1. 观察液体中的内摩擦现象。
2. 掌握用落球法测液体粘滞系数的原理和方法。
3. 学习和掌握一些基本测量仪器(如游标卡尺、螺旋测微计、比重计、秒表)的使用。
【实验原理】一个物体在液体中运动时，将受到与运动方向相反的摩擦阻力的作用，这种力Array即为粘滞阻力。
它是由粘附在物体表面的液层与邻近的液层相对运动速度不同而引起的，其微观机理都是分子之间以及在分子运动过程中形成的分子团之间的相互作用力。
不同的液体这种不同液层之间的相互作用力大小是不相同的。
所以粘滞阻力除与液体的分子性质有关外，还与液体的温度、压强等有关。
液体的内摩擦力可用粘滞系数 η来表征。
对于一个在无限深广的液体中以速度 v 运动的半径为 r 的球形物体，若运动速度较小，即运动过程中不产生涡旋，则根据斯托克斯(G.G. Stokes)推导出该球形物体受到的摩擦力即粘滞力为f = 6πηvr (1)当一个球形物体在液体中垂直下落时，它要受到三种力的作用，即向上的粘滞力 f、向上的液体浮力 F和向下的重力 G，如图 1 所示。
球体受到液体的浮力可表示为F = σg4πr3/3 (2)上式中 σ 为液体的密度，g为本地的重力加速度。
实验二 落球法测量液体粘滞系数
实验二落球法测量液体粘滞系数概述当液体流动时，平行于流动方向的各层流体速度都不相同，即存在着相对滑动，于是在各层之间就有摩擦力产生，这一摩擦力称为粘滞力，它的方向平行于两层液体的接触面，其大小与速度梯度及接触面积成正比，比例系数η称为粘度，它是表征液体粘滞性强弱的重要参数。
液体的粘滞性的测量是非常重要的，例如，现代医学发现，许多心血管疾病都与血液粘度的变化有关，血液粘度的增大会使流入人体器官和组织的血流量减少，血液流速减缓，使人体处于供血和供氧不足的状态，这可能引起多种心脑血管疾病和其他许多身体不适症状。
因此，测量血粘度的大小是检查人体血液健康的重要标志之一。
又如，石油在封闭管道中长距离输送时，其输运特性与粘滞性密切相关，因而在设计管道前，必须测量被输石油的粘度。
各种实际液体具有不同程度的粘滞性。
测量液体粘度有多种方法，本实验所采用的落球法是一种绝对法测量液体的粘度。
如果一小球在粘滞液体中铅直下落，由于附着于球面的液层与周围其他液层之间存在着相对运动，因此小球受到粘滞阻力，它的大小与小球下落的速度有关。
当小球作匀速运动时，测出小球下落的速度，就可以计算出液体的粘度。
一、实验目的1、用落球法测液体的粘滞系数；2、研究液体粘滞系数对温度的依赖关系。
二、仪器装置1、YJ-RZT-II数字智能化热学综合实验平台；2、液体粘滞系数实验装置、3、光电转换实验模板；4、连接电缆；5、2mm小钢球；6、甘油(自备)；7、直尺；8、千分尺；9、数字温度传感器；10、小磁钢及重锤部件；11、激光器；12、接收器；13、量筒；14、导球管；15、物理天平；16、测温探头。
液体粘滞系数实验仪如图1所示。
三、实验原理1、当金属小球在粘性液体中下落时，它受到三个铅直方向的力：小球的重力mg（mρ（V是小球体积，ρ是液体密度）和粘滞阻力为小球质量）；液体作用于小球的浮力gVF（其方向与小球运动方向相反）、如果液体无限深广，在小球下落速度v较小情况下，有rv F πη6= （1）上式称为斯托克斯公式，其中r 是小球的半径；η称为液体的粘度，其单位是s Pa ⋅。
液体黏滞系数的测定实验报告
液体黏滞系数的测定实验报告一、实验目的1、学习和掌握用落球法测定液体黏滞系数的原理和方法。
2、了解斯托克斯定律的应用条件。
3、熟悉秒表、游标卡尺、千分尺等测量仪器的使用。
二、实验原理当一个小球在液体中下落时，它会受到重力、浮力和黏滞阻力的作用。
在小球下落速度较小时，黏滞阻力可以用斯托克斯公式表示：＼（F ＝6πηrv\）其中，＼（F\）为黏滞阻力，＼（η\）为液体的黏滞系数，＼（r\）为小球半径，＼（v\）为小球下落速度。
小球在液体中下落时，当重力、浮力和黏滞阻力达到平衡时，小球将以匀速下落，此时有：＼（mg Vρg 6πηrv ＝ 0\）其中，＼（m\）为小球质量，＼（V\）为小球体积，＼（ρ\）为液体密度。
由于小球体积\（V ＝＼frac{4}｛3}＼pi r^3\），质量\（m ＝＼frac{4}｛3}＼pi r^3ρ_0\）（＼（ρ_0\）为小球密度），整理可得：＼（η ＝＼frac{（ρ_0 ρ)g}｛18v}d^2\）其中，＼（d\）为小球直径。
因此，只要测量出小球的直径\（d\）、下落的速度\（v\）、液体和小球的密度\（ρ\）、＼（ρ_0\），以及重力加速度\（g\），就可以计算出液体的黏滞系数\（η\）。
三、实验仪器1、玻璃圆筒：内径约为 10cm，高度约为 50cm。
2、小钢球：直径约为 1mm 至 2mm 之间。
3、游标卡尺：精度为 002mm，用于测量小球直径。
4、千分尺：精度为 001mm，用于测量小球直径。
5、秒表：精度为 01s，用于测量小球下落时间。
6、温度计：用于测量液体温度。
7、电子天平：用于测量小球质量。
8、支架、细线等。
四、实验步骤1、用电子天平测量小球质量，多次测量取平均值。
2、用游标卡尺和千分尺分别测量小球直径，各测量五次取平均值。
3、将玻璃圆筒装满待测液体，放置在支架上，调整圆筒使其竖直。
4、用细线将小球悬挂在圆筒上方，使其自然下垂，然后轻轻放入液体中。
液体粘滞系数的测定
•同一个球重复测量6次。
•换另一个半径的小钢球，重复以上实验测量6次。
大学物理实验
四. 数据处理
理 实 100% 2.求相对误差： 理
T 0.7046 实查表或 log 0.0347
1. 求实。
五.思考题 教材：
1题（实验报告）
2题（实验报告）
3题（实验报告）
大学物理实验
液体粘滞系数的测定
一.实验任务 二.测量原理与方法 三.实验内容与步骤
斯托克斯
四.数据处理
五.思考题
大学物理实验
各种流体（液体、气体）都具有不同程度的粘性。 什么是粘滞力？ —液层与邻层液体间的摩擦力（非物体与液体间的摩擦力） 如何测粘滞系数？ —— 本实验落球法。 粘滞系数与哪些因数有关？
L1 F f
小 球LΒιβλιοθήκη 用直尺测L1、 L2之间距离 L， 2次
用计时仪测小球 通过L1、L2之 间的时间
n
mg L2
r球 = 7800.0 kg.m-3，蓖麻油的密度：r液 = 962.0 kg.m-3 ,
量筒直径： D=6.010-2 m .
底座
•光电门1的激光在量筒中轴线距液面下方5cm处。 •用温度计测量实验前的油温T (℃)， 随温度升高迅速减少。
•若v1v2=v3，则光电门1可选在其激光在圆筒中轴线处距油面
下方3cm以下的位置。
大学物理实验
3.测量粘滞系数
( r 球 r 液）d gt d d 18L(1 2.4 )(1 1.6 ) D H
2
D
用计时仪测小球通过 L1、L2之间的时 间 用螺旋测微计测量 小球直径6次
H
待测液体 r液
—— 本实验落球法。
粘滞系数测定
• 式中为粘滞系数，它不仅与液体本身的性质有关，并且与温度有关；r是小球半径，v是小球的运 动速度。从上式可知，阻力f的大小和物体运动的速度成正比。
•
图（13—1）
• 如图13－1所示，若让小球自由下落，落入液体后，小球受到三个力的作用，即浮力0Vg ，重力mg, 粘滞力f。其中V为小球体积，0为液体密度，m为小球质量，开始时小球下落速度较小，因而粘滞 力f也较小，小球作加速运动。随着小球运动速度v的增加，粘滞力f也增加，当速度达到一定大小时， 作用在小球上各力达到平衡，在平衡时有：
•
mg 6rv 0Vg
（3）
• •
此后小球将作匀速运动，由上式可得： (m 0V )g
6rv
•
若将代入式（4），整理得
(m
4 3
r
30
)g
•
6rv
（4） （5）
• 实验中，小球是在内半径为Ｒ的量筒内下落，因而要考虑容器内壁对结果的影响。所以（5）式应
加上一个修正值，经过修正后， •
(m
4 3
U
( m V0 )2 ( l )2 ( t )2 ( d )2
m V0
l
t
d
• 其中：
V0 V0
(3 d )2 ( 0 )2
d
0
［注意事项］
• 1．为保证小球洁净，测过质量和直径的小 球，须用有机溶剂（乙醚和酒精的混合液） 清洗，再用滤纸吸干残液待用，不可再用 手触摸。
• 2．液体的粘滞系数随温度变化显著，测量 小球下落时间的实验过程应尽可能短。在 实验中不要用手触摸量筒。
r
30
)g
（6）
6rv(1 2.4 r )
R
［实验仪器］
液体粘滞系数实验报告
一、实验目的1. 理解液体粘滞系数的概念及其在流体力学中的重要性。
2. 掌握落球法测定液体粘滞系数的原理和实验步骤。
3. 通过实验，加深对斯托克斯定律的理解，并验证其在实际应用中的准确性。
二、实验原理液体粘滞系数是表征液体粘滞性的一个物理量，其大小反映了液体流动时内部分子间摩擦力的大小。
本实验采用落球法测定液体粘滞系数，其原理基于斯托克斯定律。
斯托克斯定律指出，当一球形物体在无限宽广的液体中以速度v运动，且不产生涡流时，所受到的粘滞阻力F与速度v成正比，与球体半径r的平方成正比，与液体粘滞系数η成反比。
具体公式如下：F = 6πηrv其中，F为粘滞阻力，η为液体粘滞系数，r为球体半径，v为球体运动速度。
当球体在液体中下落时，受到三个力的作用：重力mg、浮力f和粘滞阻力F。
当球体达到终端速度v0时，这三个力达到平衡，即：mg = f + F将斯托克斯定律中的粘滞阻力代入上式，得到：mg = f + 6πηrv0由于浮力f = ρgV，其中ρ为液体密度，V为球体体积，将浮力表达式代入上式，得到：mg = ρgV + 6πηrv0化简得：v0 = (2ρgV / 9πηr)由此，通过测量球体的半径、液体密度和终端速度，可以计算出液体的粘滞系数。
三、实验仪器与材料1. 球形钢球（直径约5mm）2. 玻璃圆筒（内径约20mm，高度约30cm）3. 温度计4. 秒表5. 液体（水、甘油等）6. 精密天平四、实验步骤1. 准备实验装置，将玻璃圆筒放置在水平桌面上，确保圆筒竖直。
2. 在圆筒内加入待测液体，液面高度约为圆筒高度的一半。
3. 用天平测量球形钢球的质量，记录数据。
4. 用游标卡尺测量球形钢球的直径，记录数据。
5. 用温度计测量液体温度，记录数据。
6. 将球形钢球轻轻放入圆筒内，开始计时，记录球体达到终端速度时所用时间t。
7. 重复步骤6，至少测量3次，取平均值作为实验结果。
五、数据处理与结果分析1. 根据实验数据，计算球体体积V = (4/3)πr³。
3-1液体粘滞系数的测定doc
第3章基础实验25第3章综合性实验实验3.1 液体粘滞系数的测定在稳定流动的液体中，由于各层液体的流速不同，在相邻两层流体之间存在相对运动而产生切向力，流速快的一层给流速慢的一层以拉力，流速慢的一层给流速快的一层以阻力，液层间的这一作用称为内摩擦力或粘滞力，流体这一性质称为粘滞性。
液体的粘滞性在工程、生产技术及医学方面有着重要的应用。
现代医学发现，许多心脑血管疾病与血液粘度有关，血液粘滞会使流入人体器官和组织的血流量减少、血流流速减缓，使人体处于供血和供氧不足的状态中，可能引发多种心脑血管疾病，所以，血粘度大小成了人体血液健康的重要标志之一。
测量液体粘滞系数的常用方法有落球法、扭摆法、转筒法、毛管法等。
实验室中，对于粘度较小的液体，如水、乙醇等，常用毛管法；而对于粘度较大的液体，如甘油、变压器油等，常用落球法。
【实验目的】1．了解粘滞现象的基本规律，学会测量油品粘滞系数的实验方法—落球法。
2．掌握力学基本量长度、液体的密度和时间的基本测量方法。
3．熟悉测量长度、液体的密度和时间的基本仪器的正确调节和使用方法。
【实验仪器】ND-2多管液体粘滞系数仪（见图3-1）、温度计、电子秒表，米尺、读数显微镜、比重计。
微型小钢球（直径1.00mm或2.00mm）、微型钢球100粒、镊子、有机玻璃板条、磁铁和待测物（蓖麻油）。
ND-2多管液体粘滞系数仪由6只不同内径D图3-1 多管液体粘滞系数仪大学物理实验26 （50.0mm 、40.0mm 、34.0mm 、24.0mm 、19.0mm 、14.0mm 左右）的圆柱形玻璃管子（玻璃管高度为195mm ）组成，分别固定在铝合金底板上。
各管子的轴线与底板垂直，底板上的水准泡指示仪器水平状态，由底板下部的3只有机玻璃螺丝调节。
每只管子刻有相距一定距离的A 、B 两刻度线（A 、B 间距和120mm ）。
上端的A 刻线为小球通过时开始计时的刻度，下端的B 刻线为小球终止时的刻度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
温度 16 17 18 19 20 21 22
1.37 1.25 1.15 1.04 0.95 0.87 0.79
0.73 0.67 0.62 0.57 0.53 0.52 0.48
温度 30 31 32 33 34 35 40
0.45 0.42 0.39 0.36 0.34 0.31 0.23
f 3vd (1 2.4
d d 3 19 2 )(1 1.6 )(1 Re Re ) D h 16 1080
（29-11）
由上式可见，当 Re 较小时，可以只考虑第一级修正，随着 Re 逐渐增大，需要将第二、第三甚至更多级的 修正考虑进来，而当 Re
³ 1时，公式中的修正项会变得比主项还大，这表明此时流体内的运动已经产生质
的变化，基于斯托克斯公式的（29-11）式不再适用。 在实际操作中，一般当 0.1 < Re 算公式可以写成（试着推导一下） ： ，此时粘滞系数计 < 0.5 时我们仅考虑第一级雷诺数修正（为什么？）
2
0 gd 2t
18 S
1 1 1 1 3 (1 2.4d / D)(1 1.6d / h) (1 3 R ) (1 Re ) e 16 16
三：高雷诺数修正
不仅液体的边界条件对小球在其中的运动有较大影响，物体在均匀稳定液体中的运动实际上还受到雷 诺数 Re 的影响。雷诺数是描述流体运动或物体在均匀稳定液体中运动的一个重要的无量纲参数：
Re º
r0 × v × r h
(29-10)
其中 r 0 是液体密度， v是物体运动速度或流体稳定流速， r 是运动物体的线性尺度，对本实验而言即小球 半径， h 是液体的粘滞系数。雷诺数的大小决定了物体在液体中的运动方式，一般当 Re
1
行设计。下面我们将在三个不同的理论层次上探讨测量液体粘滞系数的方法，这三个层次循序渐进，体现 了实验手段和理论手段在物理实验中的作用和特点，同时反映出针对同一个问题如何在实验中层层深入， 不断提高测量结果的准确程度，而这正是物理学实验的魅力所在。
一：外推法 既然用上述落球法测量出来的收尾速度 v0 与液体尺度有关，那么我们不妨在实验中就 v0 对液体 尺度的依赖关系进行定量研究，如果该依赖关系存在规律，则有可能对我们的测量带来帮助或指引。由于 上述讨论中对液体的形状没有做具体要求，我们在实验中采用试管作为容器，这样得到具有轴对称性的液 柱，于是我们要研究的就是液柱的尺度大小对 v0 的影响。为简化测量，可先固定液柱的高度，改变液柱横 截面积，这可以用一组直径不同的试管来实现（见图 29-1） 。将这些试管装上同种待测液体，安装在同一 水平底板上，每个管子上都用两条刻线 A、B 标出相等的间距，记为 S （上刻线 A 与液面间应留有适当距 离，使得小球下落经过 A 刻线时，可以认为小球已进入匀速运动状态） 。依次测出小球通过管中的两刻线 A、B 间所需的时间 t ，各管的直径用 D 表示，则通过大量的实验，我们就可以得到 t 与 D 之间的关系。 已有的数据表明， t 与 1/ D 成线性关系。即以 t 为纵坐标轴，以 1/ D 为横坐标轴，根据实验数据可以作出 一条直线（动手画画看！ ） 。这是个好消息，因为如果延长该直线与纵轴相交，其截距对应的是 1/ D = 0 时 的 t 0 ，而 1/ D = 0 正好对应 D ® ¥ ，于是我们用这种方法就可以外推出在“无限广延”的液体中，小球匀 速下落通过距离 h 所需的时间 t 0 。所以有
f 3vd
（29-1）
式中 d 是小球的直径，v 是小球的速度， 为液体粘滞系数。 就是液体粘滞性的度量，与温度有密切的 关系，对液体来说， 随温度的升高而减少（见附表） 。 本实验应用落球法来测量液体的粘滞系数。小球在液体中做自由下落时，受到三个力的作用，三个 力都在竖直方向，它们是重力 r gV 、浮力 r0 gV 、粘滞阻力 f。开始下落时小球运动的速度较小，相应的 阻力也小，重力大于粘滞阻力和浮力，所以小球作加速运动。由于粘滞阻力随小球的运动速度增加而逐渐 增加， 加速度也越来越小， 当小球所受合外力为零时，趋于匀速运动，此时的速度称为收尾速度，记为 v0 。 经计算可得液体的粘滞系数为
7
< 1（相当于小尺
度物体在低密度、高粘滞系数的液体中进行低速运动）时称低雷诺数运动，此时液体中的粘滞力起主导作 用，而液体的惯性力可以忽略，运动物体感受到周围液体以层流方式流动；而当 Re
> 1时（相当于大尺度
物体在高密度、低粘滞系数的液体中进行高速运动）称物体做高雷诺数运动，此时液体的惯性力作用逐渐
附表 一、钢的密度 =7800kg/m3
6
蓖麻油的密度 0 =962kg/m3 甘油的密度 0 =1261 kg/m3 二、蓖麻油的粘滞系数值与温度的关系 温度(℃) 温度 0 10 11 12 13 14 15
( Pa• S)
温度 23 24 25 26 27 28 29
53.0 2.42 2.20 2.00 1.83 1.67 1.51
（29-12）
其中1 即（29-9）式边界效应修正后的粘滞系数。
操作步骤 1．调节液体粘滞系数仪的底脚螺丝，用气泡水准仪观察其水平，以保证有机玻璃管中心轴线处于铅 直状态。 2．用螺旋测微器测量小钢球的直径 d （选不同方向测量 5 次后取平均） 。 3．用游标卡尺测量各管子的内直径 D （选不同方向测量 5 次后取平均） 。 4．用钢板尺测量管子上 A、B 刻线间的距离 S （选不同方向测量 5 次后取平均） 。 5．用镊子将浸润后的小钢球依次从各管子上端中心处放入，并用秒表记下小钢球在管子中 A、B 刻线 间下落的时间 t 。 6. 用厘米刻度尺测量各试管内液体总高度 h (只需测量一次)。
3
增强，尤其是当雷诺数超过某个阈值时（一般 Re
> 2000 ）液体中的粘滞力可以忽略，物体感受到周围液
体以湍流方式流动，展现出非常复杂的混沌效应。由于雷诺数对物体在液体中的运动影响很大，即便是对 小雷诺数下的运动，公式（29-8）也需要做进一步修正，此时粘滞力在（29-8）式的基础上还要再乘上一 个与雷诺数有关的修正项：
注意事项 1．待测液体应加注至管子内刻线 A 上一定位置，以保证小球在刻线 A、B 间匀速运动。 2．小球要于管子轴线位置放入。 3．放入小球与测量其下落时间时，眼与手要配合一致。 4．管子内的液体应无气泡，小球表面应光滑无油污。 5．测量过程中液体的温度应保持不变，实验测量过程持续的时间间隔应尽可能短。
( 0 ) gd 2 18v0
（29-2）
式中 0 是液体的密度， 是小球的密度，g 是当地的重力加速度。 可见， 只要测得 v0 ，即可由（29-2）式得到液体的粘滞系数。但是注意，上述推导包括（29-1） 、 （29-2） 式都在特定条件下方才适验方法的设计，这些条件大多 数都可以满足或近似满足（结合本实验所用仪器和实验步骤，思考一下哪些条件被满足，是如何做到的） ， 唯独“无限广延”在实验中是无法实现的。因此，为了准确测出液体的粘滞系数，我们需要进一步对实验进
表 29-1 次数 1 2
小钢球直径及管子直径数据 3 4 5 平均
d (mm)
d (mm）
表 29-2 次数 直径(mm) 1 2 各管子直径数据 3 4 5 平均
D1 D 1
D2
D 2
D3 D 3
D4
D 4
5
表 29-3 次数 距离 S (mm) 1
管子上两刻线间的距离数据 2 3 4 平均
实验二十九 液体粘滞系数的测定
实验目的 1．了解用斯托克斯公式测定液体粘滞系数的原理，掌握其适用条件。 2．学习用落球法测定液体的粘滞系数。 3．熟练运用基本仪器测量时间、长度和温度。 4．掌握用外推法处理实验数据。 实验仪器 液体粘滞系数仪、螺旋测微器、游标卡尺、钢板尺、钢球、磁铁、秒表、温度计。 当物体球在液体中运动时，物体将会受到液体施加的与运动方向相反的摩擦阻力的作用，这种阻力 称为粘滞阻力，简称粘滞力。粘滞阻力并不是物体与液体间的摩擦力，而是由附着在物体表面并随物体一 起运动的液体层与附近液层间的摩擦而产生的。粘滞力的大小与液体的性质、物体的形状和运动速度等因 素有关。 实验原理 根据斯托克斯定律，光滑的小球在无限广延的液体中运动时，当液体的粘滞性较大，小球的半径很 小，且在运动中不产生旋涡，那么小球所受到的粘滞阻力 f 为
误差计算：
E=
Dh
h
=
Dt 0 DS Dd + +2 t0 S d
（29-5）
Dh = E ×h
（29-6）
2
最终测量结果表示成：
二：有限边界条件修正
（29-7）
上述外推法虽然能比较准确地测量出液体的粘滞系数，但由于液柱高度 h 仍是有限的，所以液体还不 是真正意义上的无限扩展（你能否改进外推法得到更好的结果？） ，用（29-4）式得到的测量结果仍存在未 知误差。那么有无更好的方法来解决这个问题呢？让我们从头开始换个方式思考，既然容器的边界效应对 球体受到的粘滞力有影响，可否一开始就从理论上将液体尺度的影响因素考虑进来？实际上是可以的，通 过流体力学的分析可以证明，在其他条件不变的前提下，对于本实验中采用的具有轴对称性的柱状液体， 小球在其中所受粘滞力公式（29-1）应修正成：
S (mm)
表 29-4 次数 时间(s) 1 2
小钢球下落时间数据 3 4 5 平均
t1
t1
t2 t 2
t3
t 3
t4
t 4
t 0
t1 t 2 t 3 t 4 4
表 29.5 各试管内液体高度 试管
液体高度(mm)
h1
h2
h3
h4
问题讨论 1． 式（29-4）在什么条件下才能成立？ 2． 如何判断小球已进入匀速运动阶段？ 3． 观察小球通过刻线时，如何避免视差？ 4． 为了减小不确定度，应对测量中哪些量的测量方法进行改进？