朝阳区2018-2020年初三一模数学试卷及答案
2018年北京朝阳区初三一模数学试卷

,则 3//l1
l
2//l
3,
∴ , . ∠1 = ∠3 ∠2 = ∠4
∴ . ∘ ∠1 + ∠2 = ∠3 + ∠4 = 90
5. 下列图形中,是中心对称图形但不是轴对称图形的是( ).
A.
B.
C.
D.
答案 B 解 析 中心对称有B和C,同时C还是轴对称.
6. 实数a,b,c,d在数轴上的的对应点的位置如图所示,
作法:如图,
(1)在直线a上取一点A,连接P A.
(2)分别以点A和点P 为圆心,大于 1 AP 的长为半径作弧,两弧相交于B,C两点,连接BC 交P A于点D.
2
(3)以点D为圆心,DP 为半径作圆,交直线a于点E,作直线P E.所以直线P E就是所求作的垂线.
请说明每一步的作图依据:
.
答案 解析
∴△OAB是等边三角形.
∵ , OD⊥AB
∴ , ∘ ∠AOD = ∠BOD = 30
∴ . 1
∘
∠BAD = ∠BOD = 15
2
14. 如图,在平面直角坐标系xOy中,△O′A′B′可以看作是△OAB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出
一种由△OAB得到△O′A′B′的过程:
.
x−1
+试题篮 纠错
A. x = 0
B. x = 1
C. x ≠ 0
D. x ≠ 1
答案 D
解 析 分式的分母不为零. ∵ , x − 1 ≠ 0 ∴x ≠ 1.
3. 若右图是某几何体的三视图,则这个几何体是( ).
A. 球
B. 圆柱
C. 圆锥
答案 C 解 析 主视图和左视图都是三角形,俯视图是圆点,因此是圆锥.
2018年北京市朝阳区中考一模数学试卷含答案解析 精品

2018年北京市朝阳区初三一模数学试卷一、单选题(共10小题)1.清明节是中国传统节日,它不仅是人们远足踏青的日子,更是祭奠祖先、缅怀先人的节日.市民政局提供的数据显示,今年清明节当天全市213处祭扫点共接待群众264000人,将264000用科学计数法表示应为()A.B.C.D.2.实数a,b,c,d在数轴上对应的位置如图所示,绝对值相等的两个实数是()A.与B.与C.与D.与3.有一种推理游戏叫做“天黑请闭眼”,9位同学参与游戏,通过抽牌决定所扮演的角色,事先做好9张卡牌(除所写文字不同,其余均相同),其中有法官牌1张,杀手牌2张,好人牌6张.小易参与游戏,如果只随机抽取一张,那么小易抽到杀手牌的概率是()A.B.C.D.4.下列图形选自历届世博会会徽,其中是轴对称图形的是()A.B.C.D.5.如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A = 50º,则∠BCE的度数为()A.40ºB.50ºC.60ºD.130º6.某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为()A.3300m B.2200m C.1100m D.550m 7.2022年将在北京—张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了冰壶选修课,他们被分成甲、乙两组进行训练,身高(单位:cm)如下表所示,设两队队员身高的平均数依次为,,方差依次为,,下列关系中完全正确的是()A.=,<B.=,>C.<,<D.>,>8.如图,△内接于⊙,若⊙的半径为6,,则的长为()A.2πB.4πC.6πD.12π9.我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园—玲珑塔—国家体育场—水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(–1,0),森林公园的坐标为(–2,2),则终点水立方的坐标为()A.(–2,–4)B.(–1,–4)C.(–2,4)D.(–4,–1)10.如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H 是AC边上一点,且°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的()A.线段CGB.线段AGC.线段AHD.线段CH二、填空题(共6小题)11.若二次根式有意义,则x的取值范围是____________.12.分解因式:____________.13.关于x的方程有两个不相等实数根,写出一个满足条件的k的值:k=____________.14.《孙子算经》是中国传统数学的重要著作之一,其中记载的“荡杯问题”很有趣.《孙子算经》记载“今有妇人河上荡杯.津吏问曰:‘杯何以多?’妇人曰:‘家有客.’津吏曰:‘客几何?’妇人曰:‘二人共饭,三人共羹,四人共肉,凡用杯六十五.’不知客几何?”译文:“2人同吃一碗饭,3人同吃一碗羹,4人同吃一碗肉,共用65个碗,问有多少客人?”设共有客人x人,可列方程为____________.15.在数学活动课上,小派运用统计方法估计瓶子中的豆子的数量.他先取出100粒豆子,给这些豆子做上记号,然后放回瓶子中,充分摇匀之后再取出100粒豆子,发现其中8粒有刚才做的记号,利用得到的数据可以估计瓶子中豆子的数量约为____________粒.16.阅读下面材料:数学课上,老师提出如下问题:小艾的作法如下:老师表扬了小艾的作法是对的.请回答:小艾这样作图的依据是____________.三、计算题(共1小题)17.计算:四、解答题(共12小题)18.已知,求的值.19.解不等式组并写出它的所有整数解.20.如图,E为AC上一点,EF∥AB交AF于点F,且AE = EF.求证:= 2∠1.21.台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域的交流越来越深入,2018年10月10日是北京故宫博物院成立90周年院庆日,两岸故宫同根同源,合作举办了多项纪念活动.据统计北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中北京故宫博物院藏品数量比台北故宫博物院藏品数量的2倍还多50万件,求北京故宫博物院和台北故宫博物院各约有多少万件藏品.22.如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF =∠BAE.(1)求证:四边形AEFD是平行四边形;(2)若DF=3,DE=4,AD=5,求CD的长度.23.在平面直角坐标xOy中,直线与双曲线的一个交点为A(2,4),与y 轴交于点B.(1)求m的值和点B的坐标;(2)点P在双曲线上,△OBP的面积为8,直接写出点P的坐标.24.如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.(1)求证:DB平分∠PDC;(2)若DC=6,,求BC的长.25.人口老龄化已经成为当今世界主要问题之一.北京市在上世纪90年代初就进入了老龄化社会,全市60岁及以上户籍老年人口2018年底达到279.3万人,占户籍总人口的21.2%; 2018年底比2018年底增加17.4万人,占户籍总人口的22.3%;2018年底比2018年底增加23.3万人,占户籍总人口的23%.“百善孝为先”,北京市政府越来越关注养老问题,提出养老服务新模式,计划90%的老年人在社会化服务协助下通过家庭照顾养老(即居家养老),6%的老年人在社区养老,4%的老年人入住养老服务机构.本市养老服务机构的床位总数2018年达到8.0516万张,2018年达到10.938万张,2018年达到12万张.根据以上材料回答下列问题:(1)到2018年底,本市60岁及以上户籍老年人口为__________万人;(2)选择统计表或统计图,将2018年––2018年本市60岁及以上户籍老年人口数量和占户籍总人口的比例表示出来;(3)预测2018年本市养老服务机构的床位数约为_________万张,请你结合数据估计,能否满足4%的老年人入住养老服务机构,并说明理由.26.观察下列各等式:,,,……根据上面这些等式反映的规律,解答下列问题:(1)上面等式反映的规律用文字语言可描述如下:存在两个实数,使得这两个实数的等于它们的;(2)请你写一个实数,使它具有上述等式的特征:-3=3;(3)请你再写两个实数,使它们具有上述等式的特征:-=;(4)符合上述特征的所有等式中,是否存在两个实数都是整数的情况?若存在,求出所有满足条件的等式;若不存在,说明理由.27.在平面直角坐标系xOy中,抛物线经过点(0,–3),(2,–3).(1)求抛物线的表达式;(2)求抛物线的顶点坐标及与x轴交点的坐标;(3)将(y≤0)的函数图象记为图象A,图象A关于x轴对称的图象记为图象B.已知一次函数y=mx+n,设点H是x轴上一动点,其横坐标为a,过点H作x轴的垂线,交图象A于点P,交图象B于点Q,交一次函数图象于点N.若只有当1<a<3时,点Q 在点N上方,点N在点P上方,直接写出n的值.28.在等腰三角形ABC中,AC=BC,点P为BC边上一点(不与B、C重合),连接PA,以P为旋转中心,将线段PA顺时针旋转,旋转角与∠C相等,得到线段PD,连接DB.(1)当∠C=90º时,请你在图1中补全图形,并直接写出∠DBA的度数;(2)如图2,若∠C=α,求∠DBA的度数(用含α的代数式表示);(3)连接AD,若∠C =30º,AC=2,∠APC=135º,请写出求AD长的思路.(可以不写出计算结果)29.在平面直角坐标系xOy中,A(t,0),B(,0),对于线段AB和x轴上方的点P 给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.(1)若,在点,,中,线段AB的“等角点”是;(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(6,0),∠OMN=30°.①线段AB的“等角点”P在直线MN上,且∠ABP=90°,求点P的坐标;②在①的条件下,过点B作BQ⊥PA,交MN于点Q,求∠AQB的度数;③若线段AB的所有“等角点”都在△MON内部,则t的取值范围是.答案部分1.考点:科学记数法和近似数、有效数字试题解析:科学记数法是把一个数表示成 a×的形式,其中1≤|a|<10,n为整数.所以264000=2.64 .故本题选C.答案:C2.考点:实数的相关概念试题解析:所以绝对值相等的两实数是a与d。
朝阳区初三一模数学试题及参考答案

北京市朝阳区九年级综合练习(一)数学试卷2018.5学校班级姓名考号一、选择题(本题共16分,每小题2分)下面1-8题均有四个选项,其中符合题意的选项只有..一个. 1.如图,直线a ∥b ,则直线a ,b 之间距离是 (A )线段AB 的长度 (B )线段CD 的长度 (C )线段EF 的长度 (D )线段GH 的长度2.若代数式12 x x有意义,则实数x 的取值范围是(A )x =0(B )x =1(C )x ≠0(D )x ≠13.若右图是某几何体的三视图,则这个几何体是 (A )球 (B )圆柱 (C )圆锥 (D )三棱柱4.已知l 1∥l 2,一个含有30°角的三角尺按照如图所示位置摆放,则∠1+∠2的度数为 (A )90° (B )120° (C )150° (D )180°5.下列图形中,是中心对称图形但不是..轴对称图形的是 (A )(B )(C )(D )6.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示, 下列结论①a <b ;②|b |=|d |;③a+c =a ;④ad >0中,正确的有 (A )4个(B )3个(C )2个 (D )1个7.“享受光影文化,感受城市魅力”,2018年4月15-22日第八届北京国际电影节顺利举办.下面的统计图反映了北京国际电影节﹒电影市场的有关情况.第六届和第八届北京国际电影节﹒电影市场“项目创投”申报类型统计表 根据统计图提供的信息,下列推断合理..的是 (A )两届相比较,所占比例最稳定的是动作冒险(含战争)类 (B )两届相比较,所占比例增长最多的是剧情类 (C )第八届悬疑惊悚犯罪类申报数量比第六届2倍还多(D )在第六届中,所占比例居前三位的类型是悬疑惊悚犯罪类、剧情类和爱情类 8.如图,△ABC 是等腰直角三角形,∠A =90°,AB =6,点P 是AB 边 上一动点(点P 与点A 不重合),以AP 为边作正方形APDE ,设 AP =x ,正方形APDE 与△ABC 重合部分(阴影部分)的面积为y , 则下列能大致反映y 与x 的函数关系的图象是 二、填空题(本题共16分,每小题2分) 9.赋予式子“ab ”一个实际意义:.10.如果023≠=,那么代数式)2(422n m n m +⋅-的值是. 11.足球、篮球、排球已经成为北京体育的三张名片,越来越受到广大市民的关注.下表是北京两支篮球队在2017-2018赛季CBA 常规赛的比赛成绩:设胜一场积x 分,负一场积y 分,依题意,可列二元一次方程组为.12.如图,AB ∥CD ,AB=21CD ,S △ABO :S △CDO =.13.如图,点A ,B ,C 在⊙O 上,四边形OABC 是平行四边形,OD ⊥AB 于点E ,交⊙O 于点D ,则∠BAD =度.第13题图第14题图14.如图,在平面直角坐标系xOy 中,△O'A'B'可以看作是△OAB 经过若干次图形的变化 (平移、轴对称、旋转)得到的,写出一种由△OAB 得到△O'A'B'的过程:.15.下列随机事件的概率:①投掷一枚均匀的骰子,朝上一面为偶数的概率;②同时抛掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率;③抛一枚图钉,“钉尖向下”的概率;④某作物的种子在一定条件下的发芽率.既可以用列举法求得又可以用频率估计获得的是(只填写序号).:该尺规作图的依据是?.三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题7分,第28题8分)17.计算:2sin30°+.8)4()31(01+-+-π18.解不等式组:⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x19.如图,在△ACB 中,AC =BC ,AD 为△ACB 的高线,CE 为△ACB 的中线.求证:∠DAB =∠ACE.20.已知关于x 的一元二次方程0)1(2=+++k x k x . (1)求证:方程总有两个实数根;(2)若该方程有一个根是正数,求k 的取值范围.21.如图,在△ABC 中,D 是AB 边上任意一点,E 是BC 边中点,过点C作AB 的平行线,交DE 的延长线于点F ,连接BF ,CD . (1)求证:四边形CDBF 是平行四边形;(2)若∠FDB =30°,∠ABC =45°,BC = ,求DF 的长.22.如图,在平面直角坐标系xOy 中,直线AB 与x 轴、y 轴分别交于点A 、B ,与反比例函数xky 的图象在第四象限交于点C ,CD ⊥x 轴于点D ,tan ∠OAB =2,OA =2,OD =1.(1)求该反比例函数的表达式;(2)点M 是这个反比例函数图象上的点,过点M作MN ⊥y 轴,垂足为点N ,连接OM 、AN ,如果 S △ABN =2S △OMN ,直接写出点M 的坐标.23.如图,在⊙O 中,C ,D 分别为半径OB ,弦AB 的中点,连接CD 并延长,交过点A 的切线于点E .(1)求证:AE ⊥CE .(2)若AE = ,sin ∠ADE =31,求⊙O 半径的长.24.水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚.对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:甲整理、描述数据按如下分组整理、描述这两组样本数据(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀) 分析数据两组样本数据的平均数、众数和方差如下表所示:得出结论a .估计乙大棚产量优秀的秧苗数为?株;b .可以推断出?大棚的小西红柿秧苗品种更适应市场需求,理由为.(至少从两个不同的角度说明推断的合理性)25.如图,AB 是⊙O 的直径,AB =4cm ,C 为AB 上一动点,过点C 的直线交⊙O 于D 、E 两点,且∠ACD =60°,DF ⊥AB 于点F ,EG ⊥AB 于点G ,当点C 在AB 上运动时,设AF =x cm ,DE =y cm (当x 的值为0或3时,y 的值为2),探究函数y 随自变量x 的变化而变化的 规律.(1)通过取点、画图、测量,得到了x 与y 的几组对应值,如下表:(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:点F 与点O 重合时,DE 长度约为cm (结果保留一位小数).26.在平面直角坐标系xOy 中,抛物线()2440y ax ax a =--≠与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)若方程()244=00ax ax a --≠有两个不相等的实数根,且两根都在1,3之间(包括1,3),结合函数的图象,求a 的取值范围.27.如图,在菱形ABCD 中,∠DAB =60°,点E 为AB 边上一动点(与点A ,B 不重合),连接CE ,将∠ACE 的两边所在射线CE ,CA 以点C 为中心,顺时针旋转120°,分别交射线AD 于点F ,G. (1)依题意补全图形;(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示); (3)用等式表示线段AE 、AF 与CG 之间的数量关系,并证明.28.对于平面直角坐标系xOy 中的点P 和线段AB ,其中A (t ,0)、B (t +2,0)两点,给出如下定义:若在线段AB 上存在一点Q ,使得P ,Q 两点间的距离小于或等于1,则称P 为线段AB 的伴随点. (1)当t =-3时,①在点P 1(1,1),P 2(0,0),P 3(-2,-1)中,线段AB 的伴随点是; ②在直线y =2x +b 上存在线段AB 的伴随点M 、N ,且MN =求b 的取值范围; (2)线段AB 的中点关于点(2,0)的对称点是C ,将射线CO 以点C 为中心,顺时针旋转30°得到射线l ,若射线l 上存在线段AB 的伴随点,直接写出t 的取值范围.北京市朝阳区九年级综合练习(一)数学试卷答案及评分参考2018.5一、选择题(本题共16分,每小题2分)9.答案不惟一,如:边长分别为a ,b 的矩形面积 10.4711.⎩⎨⎧=+=+.562018,631325y x y x 12.1:413.15 14.答案不唯一,如:以x 轴为对称轴,作△OAB 的轴对称图形,再将得到三角形沿向右平移4个单位长度 15.①②16.与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;直径所对的圆周角是直角三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题7分,第28题8分)17.解:原式2213212+++⨯= (4)分225+=.…………………………………………………………………5分18.解:原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式①,得5<x .………………………………………………………………………2分解不等式②,得21>x .………………………………………………………………………4分∴原不等式组的解集为521<<x .…………………………………………………………5分 19.证明:∵AC =BC ,CE 为△ACB 的中线,∴∠CAB =∠B ,CE ⊥AB .………………………………………………………………2分 ∴∠CAB +∠ACE =90°.…………………………………………………………………3分 ∵AD 为△ACB 的高线, ∴∠D =90°.∴∠DAB +∠B =90°.……………………………………………………………………4分 ∴∠DAB =∠ACE .………………………………………………………………………5分20.(1)证明:依题意,得k k 4)1(2-+=∆…………………………………………1分.)1(2-=k ……………………………………………………………2分∵0)1(2≥-k ,∴方程总有两个实数根.……………………………………………………………3分(2)解:由求根公式,得11-=x ,k x -=2.…………………………………………………4分∵方程有一个根是正数, ∴0>-k . ∴0<k .………………………………………………………………………………5分 21.(1)证明:∵CF ∥AB ,∴∠ECF =∠EBD . ∵E 是BC 中点, ∴CE =BE .∵∠CEF =∠BED , ∴△CEF ≌△BED . ∴CF =BD .∴四边形CDBF 是平行四边形.………………………………………………2分(2)解:如图,作EM ⊥DB 于点M ,∵四边形CDBF 是平行四边形,BC =24,∴2221==BC BE ,DE DF 2=. 在Rt △EMB 中,2sin =∠⋅=ABC BE EM .……………………………………3分 在Rt △EMD 中,42==EM DE .………………………………………………4分∴DF =8.……………………………………………………………………………………5分 22.解:(1)∵AO =2,OD =1,∴AD =AO+OD =3.……………………………………………………………………1分∵CD ⊥x 轴于点D , ∴∠ADC =90°.在Rt △ADC 中,6tan =∠⋅=OAB AD CD ..∴C (1,-6).……………………………………………………………………………2分∴该反比例函数的表达式是xy 6-=.…………………………………………………3分(2)点M 的坐标为(-3,2)或(53,-10).……………………………………………5分23.(1)证明:连接OA ,∵OA 是⊙O 的切线,∴∠OAE =90o (1)∵C ,D 分别为半径OB ,弦AB 的中点,∴CD 为△AOB 的中位线.∴CD ∥OA . ∴∠E =90o. ∴AE ⊥CE .…………………………………2分(2)解:连接OD ,∴∠ODB =90o.………………………………………………………………………3分∵AE = ,sin ∠ADE =31,在Rt △AED 中,23sin =∠=ADEAEAD .∵CD ∥OA , ∴∠1=∠ADE .在Rt △OAD 中,311sin ==∠OA OD .………………………………………………4分设OD =x ,则OA =3x ,∵222OA AD OD =+, ∴()()222323x x =+.解得231=x ,232-=x (舍). ∴293==x OA .……………………………………………………………………5分即⊙O 的半径长为29. 24.解:整理、描述数据按如下分组整理、描述这两组样本数据…………………………………………………………………………………………………2分得出结论a .估计乙大棚产量优秀的秧苗数为84?株;…………………………3分b .答案不唯一,理由须支撑推断的合理性.…………………………5分25.解:本题答案不唯一,如:分 (2)……………………………………………………………………………………………4分 (3)3.5.……………………………………………………………………………………6分 26.解:(1)44)2(4422---=--=a x a ax ax y .∴A (0,-4),B (2,0).…………………………………………………………2分(2)当抛物线经过点(1,0)时,34-=a .……………………………………………4分当抛物线经过点(2,0)时,1-=a . (6)分结合函数图象可知,a 的取值范围为134<≤-a .…………………………………7分27.(1)补全的图形如图所示.……………………………………………………………………………………………1分 (2)解:由题意可知,∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形,∠DAB=60°, ∴∠DAC=∠BAC=30°.........................................................................2分 ∴∠AGC=30°. ∴∠AFC =α+30°. (3)分(3)用等式表示线段AE 、AF 与CG 之间的数量关系为CG AFAE 3=+.证明:作CH ⊥AG 于点H.由(2)可知∠BAC=∠DAC=∠AGC=30°. ∴CA=CG.………………………………………………………………………………………5分∴HG=21AG. ∵∠ACE=∠GCF ,∠CAE=∠CGF , ∴△ACE ≌△GCF.……………………………………………………………………………6分∴AE=FG .在Rt △HCG 中,.23cos CG CGH CG HG =∠⋅= ∴AG =3CG .…………………………………………………………………………………7分即AF+AE =3CG .28.解:(1)①线段AB 的伴随点是:23,P P .…………………………………………2分 ②如图1,当直线y =2x +b 经过点(-3,-1)时,b =5,此时b 取得最大值.…………………………………………………………………………4分 如图2,当直线y =2x +b 经过点(-1,1)时,b =3,此时b 取得最小值. …………………………………………………………………………5分 ∴b 的取值范围是3≤b ≤5.…………………………………………………6分(2)t 的取值范围是-12.2t ≤≤…………………………………………………………8分图1 图2。
2020年北京市朝阳区中考一模数学试卷含答案解析

2020年北京市朝阳区初三一模数学试卷一、单选题(共10小题)1.清明节是中国传统节日,它不仅是人们远足踏青的日子,更是祭奠祖先、缅怀先人的节日.市民政局提供的数据显示,今年清明节当天全市213处祭扫点共接待群众264000人,将264000用科学计数法表示应为()A.B.C.D.2.实数a,b,c,d在数轴上对应的位置如图所示,绝对值相等的两个实数是()A.与B.与C.与D.与3.有一种推理游戏叫做“天黑请闭眼”,9位同学参与游戏,通过抽牌决定所扮演的角色,事先做好9张卡牌(除所写文字不同,其余均相同),其中有法官牌1张,杀手牌2张,好人牌6张.小易参与游戏,如果只随机抽取一张,那么小易抽到杀手牌的概率是()A.B.C.D.4.下列图形选自历届世博会会徽,其中是轴对称图形的是()A.B.C.D.5.如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A = 50º,则∠BCE的度数为()A.40ºB.50ºC.60ºD.130º6.某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为()A.3300m B.2200m C.1100m D.550m 7.2022年将在北京—张家口举办冬季奥运会,很多学校开设了相关的课程.某校8名同学参加了冰壶选修课,他们被分成甲、乙两组进行训练,身高(单位:cm)如下表所示,设两队队员身高的平均数依次为,,方差依次为,,下列关系中完全正确的是()A.=,<B.=,>C.<,<D.>,>8.如图,△内接于⊙,若⊙的半径为6,,则的长为()A.2πB.4πC.6πD.12π9.我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园—玲珑塔—国家体育场—水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(–1,0),森林公园的坐标为(–2,2),则终点水立方的坐标为()A.(–2,–4)B.(–1,–4)C.(–2,4)D.(–4,–1)10.如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H 是AC边上一点,且°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的()A.线段CGB.线段AGC.线段AHD.线段CH二、填空题(共6小题)11.若二次根式有意义,则x的取值范围是____________.12.分解因式:____________.13.关于x的方程有两个不相等实数根,写出一个满足条件的k的值:k=____________.14.《孙子算经》是中国传统数学的重要著作之一,其中记载的“荡杯问题”很有趣.《孙子算经》记载“今有妇人河上荡杯.津吏问曰:‘杯何以多?’妇人曰:‘家有客.’津吏曰:‘客几何?’妇人曰:‘二人共饭,三人共羹,四人共肉,凡用杯六十五.’不知客几何?”译文:“2人同吃一碗饭,3人同吃一碗羹,4人同吃一碗肉,共用65个碗,问有多少客人?”设共有客人x人,可列方程为____________.15.在数学活动课上,小派运用统计方法估计瓶子中的豆子的数量.他先取出100粒豆子,给这些豆子做上记号,然后放回瓶子中,充分摇匀之后再取出100粒豆子,发现其中8粒有刚才做的记号,利用得到的数据可以估计瓶子中豆子的数量约为____________粒.16.阅读下面材料:数学课上,老师提出如下问题:小艾的作法如下:老师表扬了小艾的作法是对的.请回答:小艾这样作图的依据是____________.三、计算题(共1小题)17.计算:四、解答题(共12小题)18.已知,求的值.19.解不等式组并写出它的所有整数解.20.如图,E为AC上一点,EF∥AB交AF于点F,且AE = EF.求证:= 2∠1.21.台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域的交流越来越深入,2020年10月10日是北京故宫博物院成立90周年院庆日,两岸故宫同根同源,合作举办了多项纪念活动.据统计北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中北京故宫博物院藏品数量比台北故宫博物院藏品数量的2倍还多50万件,求北京故宫博物院和台北故宫博物院各约有多少万件藏品.22.如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF =∠BAE.(1)求证:四边形AEFD是平行四边形;(2)若DF=3,DE=4,AD=5,求CD的长度.23.在平面直角坐标xOy中,直线与双曲线的一个交点为A(2,4),与y 轴交于点B.(1)求m的值和点B的坐标;(2)点P在双曲线上,△OBP的面积为8,直接写出点P的坐标.24.如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.(1)求证:DB平分∠PDC;(2)若DC=6,,求BC的长.25.人口老龄化已经成为当今世界主要问题之一.北京市在上世纪90年代初就进入了老龄化社会,全市60岁及以上户籍老年人口2020年底达到279.3万人,占户籍总人口的21.2%; 2020年底比2020年底增加17.4万人,占户籍总人口的22.3%;2020年底比2020年底增加23.3万人,占户籍总人口的23%.“百善孝为先”,北京市政府越来越关注养老问题,提出养老服务新模式,计划90%的老年人在社会化服务协助下通过家庭照顾养老(即居家养老),6%的老年人在社区养老,4%的老年人入住养老服务机构.本市养老服务机构的床位总数2020年达到8.0516万张,2020年达到10.938万张,2020年达到12万张.根据以上材料回答下列问题:(1)到2020年底,本市60岁及以上户籍老年人口为__________万人;(2)选择统计表或统计图,将2020年––2020年本市60岁及以上户籍老年人口数量和占户籍总人口的比例表示出来;(3)预测2020年本市养老服务机构的床位数约为_________万张,请你结合数据估计,能否满足4%的老年人入住养老服务机构,并说明理由.26.观察下列各等式:,,,……根据上面这些等式反映的规律,解答下列问题:(1)上面等式反映的规律用文字语言可描述如下:存在两个实数,使得这两个实数的等于它们的;(2)请你写一个实数,使它具有上述等式的特征:-3=3;(3)请你再写两个实数,使它们具有上述等式的特征:-=;(4)符合上述特征的所有等式中,是否存在两个实数都是整数的情况?若存在,求出所有满足条件的等式;若不存在,说明理由.27.在平面直角坐标系xOy中,抛物线经过点(0,–3),(2,–3).(1)求抛物线的表达式;(2)求抛物线的顶点坐标及与x轴交点的坐标;(3)将(y≤0)的函数图象记为图象A,图象A关于x轴对称的图象记为图象B.已知一次函数y=mx+n,设点H是x轴上一动点,其横坐标为a,过点H作x轴的垂线,交图象A于点P,交图象B于点Q,交一次函数图象于点N.若只有当1<a<3时,点Q 在点N上方,点N在点P上方,直接写出n的值.28.在等腰三角形ABC中,AC=BC,点P为BC边上一点(不与B、C重合),连接PA,以P为旋转中心,将线段PA顺时针旋转,旋转角与∠C相等,得到线段PD,连接DB.(1)当∠C=90º时,请你在图1中补全图形,并直接写出∠DBA的度数;(2)如图2,若∠C=α,求∠DBA的度数(用含α的代数式表示);(3)连接AD,若∠C =30º,AC=2,∠APC=135º,请写出求AD长的思路.(可以不写出计算结果)29.在平面直角坐标系xOy中,A(t,0),B(,0),对于线段AB和x轴上方的点P 给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.(1)若,在点,,中,线段AB的“等角点”是;(2)直线MN分别交x轴、y轴于点M、N,点M的坐标是(6,0),∠OMN=30°.①线段AB的“等角点”P在直线MN上,且∠ABP=90°,求点P的坐标;②在①的条件下,过点B作BQ⊥PA,交MN于点Q,求∠AQB的度数;③若线段AB的所有“等角点”都在△MON内部,则t的取值范围是.答案部分1.考点:科学记数法和近似数、有效数字试题解析:科学记数法是把一个数表示成 a×的形式,其中1≤|a|<10,n为整数.所以264000=2.64 .故本题选C.答案:C2.考点:实数的相关概念试题解析:所以绝对值相等的两实数是a与d。
最新-北京市朝阳区2018年初中毕业考试(一模)数学试卷

北京市朝阳区2018年初中毕业考试数学试卷 2018.4第Ⅰ卷(共30分)一、选择题(共10道小题,每小题3分,共30分)下列各题均有四个选项,其中只有一个是符合题意的.请用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑.1.在下列各数中,绝对值最大的数是A .1B .-2C .21D .13-2.2018年10月16日,新一期全球超级计算机500强榜单在美国公布,中国“天河二号”超级计算机以每秒338600000亿次浮点运算速度连续第六度称雄.将338600000用科学记数法表示为A .3.386×107B .0.3386×109C .3.386×108D .0.3386×1083. 右图是某个几何体的三视图,则这个几何体是A .圆柱B .圆锥C .三棱柱D .三棱锥4.阿仁是一名非常爱读书的学生.他制作了五张材质和外观完全一样的书签,每张书签上写有一本书的名称和作者,分别是:《海底两万里》(作者:凡尔纳,法国)、《三国演义》(作者:罗贯中)、《西游记》(作者:吴承恩)、《骆驼祥子》(作者:老舍)、《钢铁是怎样炼成的》(作者:尼·奥斯特洛夫斯基,前苏联),从这五张书签中随机抽取一张,则抽到的书签上的作者是中国人的概率是A .15B .25C .35D .455. 下列运算正确的是A .236x x x =B .632x x x ÷=C .32422x x x -=D .()236xx =6.一次函数y kx b =+的图象如右图所示, 则k,b 应满足的条件是A .0,0k b >>B .0,0k b ><C .0,0k b <>D .0,0k b <<7.如图,将一块含有45°的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,则∠2的度数是A .15°B .20°C .25°D .30°8.如图,⊙O 的半径为10,AB 是弦,OC ⊥AB 于点C , 若AB =12,则OC 的长为A .2B .C .6D .89.某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例, 右图表示的是该电路中电流I 与电阻R 之间函数关系的图象,则 电流I 关于电阻R 的函数关系式为 A .6I R =B .6I R =-C .3I R =D .2I R=10.如图,把正方形ABCD 绕它的中心O 顺时针旋转,得到正方形A ’B ’C ’D ’,旋转角大于0°小于90°.△A ’EF 的面积为S ,线段AE 的长度为x ,那么S 关于x 的函数的图象可能是机读答题卡A B C D第13题图 第14题图 第Ⅱ卷 (共70分)二、填空题 (共6道小题,每小题3分,共18分) 11. 分解因式:22ax ay -=___________.12.某校在进行―阳光体育活动‖中,统计了7位原来偏胖的学生的情况,他们的体重分别降低了5,9,3,10,6,8,5(单位:kg ),则这组数据的中位数是__________.13. 如图,若在象棋棋盘上建立直角坐标系,使―帥‖位于点(-3,-2),“炮”位于点(-2.0),则―兵‖位于的点的坐标为 . 14.如图,“吃豆小人”是一个经典的游戏形象,它的形状是一个扇形,开口∠1=60°,半径为错误!未找到引用源。
2018年朝阳区初三数学一模试题

x 1 2(x 3),
18.
解不等式组:
6x 1 2
2
x.
19. 如图,在△ACB 中,AC=BC,AD 为△ACB 的高线,CE 为△ACB 的中线. 求证:∠DAB=∠ACE.
20.已知关于 x 的一元二次方程 x2 (k 1)x k 0 .
(1)求证:方程总有两个实数根; (2)若该方程有一个根是正数,求 k 的取值范围.
点 E,作直线 PE. 所以直线 PE 就是所求作的垂线.
请回答:该尺规作图的依据是
.
三、解答题(本题共 68 分,第 17-24 题,每小题 5 分,第 25 题 6 分,第 26-27 题,每小题 7 分,第 28 题 8 分)
17.计算:2sin30°+ (1)1 (4 )0 8. 3
2.若代数式 2x 有意义,则实数 x 的取值范围是 x 1
(A)x=0
(B)x=1
(C)x≠0
(D)x≠1
3.若 右 图 是 某 几 何 体 的 三 视 图 , 则 这 个 几 何 体 是 (A)球 (B)圆 柱 (C)圆 锥 (D)三 棱 柱
4.已知 l1∥l2,一个含有 30°角的三角尺按照如图所示位置摆放,则∠1+∠2 的度数为 (A)90° (B)120° (C)150° (D)180°
25≤x<35 35≤x<45 45≤x<55 55≤x<65 65≤x<75 75≤x<85
大棚
甲
5
5
5
5
4
1
乙
2
4
6
2
(说明:45 个以下为产量不合格,45 个及以上为产量合格,其中 45~65 个为产量良好, 65~85 个为产量优秀)
2020年北京市朝阳区初三数学一模答案
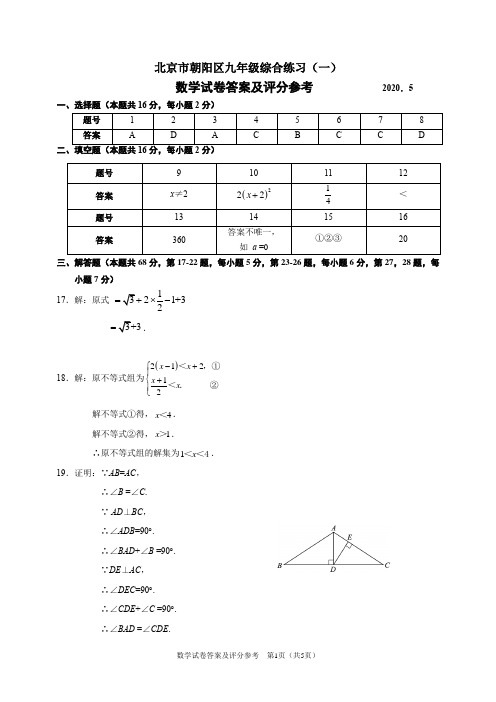
北京市朝阳区九年级综合练习(一)数学试卷答案及评分参考 2020.5一、选择题(本题共16分,每小题2分)题号 1 2 3 4 5 6 7 8 答案ADACBCCD二、填空题(本题共16分,每小题2分)三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27,28题,每小题7分) 17.解:原式 1321+32=+⨯- 3+3=.18.解:原不等式组为()21212x x x x -+⎧⎪⎨+⎪⎩<,①<. ②解不等式①得,4x <. 解不等式②得,1x >. ∴原不等式组的解集为1x <<4.19.证明:∵AB =AC ,∴∠B =∠C . ∵ AD ⊥BC , ∴∠ADB =90︒. ∴∠BAD +∠B =90︒. ∵DE ⊥AC , ∴∠DEC =90︒. ∴∠CDE +∠C =90︒. ∴∠BAD =∠CDE .题号 9 101112 答案 x ≠2 ()222x +14< 题号 13 14 15 16 答案360答案不唯一, 如 a =0①②③2020.解:(1)由题意得, 221(1)404m m ∆=+-⨯>.解得21->m . (2)答案不唯一,如:m =0.此时,方程为20x x +=. 解得1201x x ==-,.21.(1)证明:∵四边形ABCD 是平行四边形, ∴∠B =∠ADC .∵AE ⊥BC ,AF ⊥CD ,∴∠AEB =∠AFD=90°. ∵BE = DF ,∴△ABE ≌△ADF .∴AB =AD .∴四边形ABCD 是菱形.(2)解:由(1)知AD //BC .∴∠EAG =90°,∠G =∠CEG =30°. ∴EG =2AE =4.22.解:(1)3;(2)(3)31.23.(1)a =1;(2)①由题意可知图形G 是以O 为圆心,a 为半径的圆, AB ,AC ,BC 与⊙O 相切.∴∠ABM =∠NBM .∵AB =3,AC =4,BC =5, ∴∠A =90°. ∵MN ⊥BC ,∴∠A =∠BNM =90°. ∴∠BMA =∠BMN .②如图,设⊙O 与AC 的切点为D ,连接OD ,作OE ⊥MN 于点E . ∴OD ⊥AC . ∴OD = OE . ∴OE 为⊙O 的半径. ∴MN 为⊙O 的切线.∴直线MN 与图形G 的公共点个数为1.24.解:(2)m =2;(3)(4)①直线2x =.②6.25.解:(1)B (-1,1);(2)把1y =代入y x m =-+,得1x m =-.把1y =代入my x=,得x m =. ∴P (1m -,1), Q (m ,1). (3)10m -≤<或12m <≤.26.解:(1)∵抛物线231y ax ax a =-++与y 轴交于点A ,令0x =,得1y a =+. ∴A (0, a +1).(2)由抛物线231y ax ax a =-++可知3322a x a -=-=. ∴抛物线的对称轴是直线32x =.(3)对于任意的实数a ,都有+1a a >. 可知点A 总在点N 的上方.令抛物线上的点C (-2,C y ). ∴111C y a =+.①如图1,当a >0时,2C y a -->. ∴点C 在点M 的上方.结合函数图象,可知抛物线与线段MN 没有公共点. ②当a <0时,(ⅰ)如图2抛物线经过点M 时,=2C y a --.∴1=4a -.结合函数图象,可知抛物线与线段MN 恰有一个有 公共点M .(ⅰ)当14a -<<0时,可知抛物线与线段MN 没有公共点.(ⅰ)如图3,当14a <-时,2C y a --<.∴点C 在点M 的下方结合函数图象,可知抛物线与线段MN 恰有 一个有公共点.综上所述,a 的取值范围是14a -≤.27.解:(1)①补全图形,如图所示.②∠FBE = 45︒;图1图2图3(2)2DE AF=.证明:如图,作AH⊥AF,交BF的延长线于点H,设DF与AB交于点G,根据题意可知,CD= CE,∠ECD =2α,∠ABC =∠BCD =∠CDA=∠DAB=90︒.∴∠EDC=90︒-α, CB= CE,∠BCE =90︒-2α.∴∠CBE =45︒+α,∠ADF=α.∴∠ABE =45︒-α.∵BF⊥DE,∴∠BFD=90︒.∵∠AGD =∠FGB,∴∠FBG =α.∴∠FBE =∠FEB =45︒.∴FB = FE .∵AH⊥AF,∠BAD=90︒,∴∠HAB =∠F AD.∴△HAB≌△F AD.∴HB= FD, AH=AF.∴HF= DE,∠H =45︒.∴2HF AF=.∴2DE AF=.28.解:(1)(0,2);(2)如图,设以O为圆心,AB为半径的圆与直线y=1在第二象限的交点为D,作DE垂直x 轴于点E,∴OD=2,DE=1.在Rt△ODE中,根据勾股定理得OE=3.∴n的取值范围是n<3-.(3)-4<t≤-2或4323<t≤2或t =0或t=433.。
北京市朝阳区2018中考一模数学试卷(含答案)
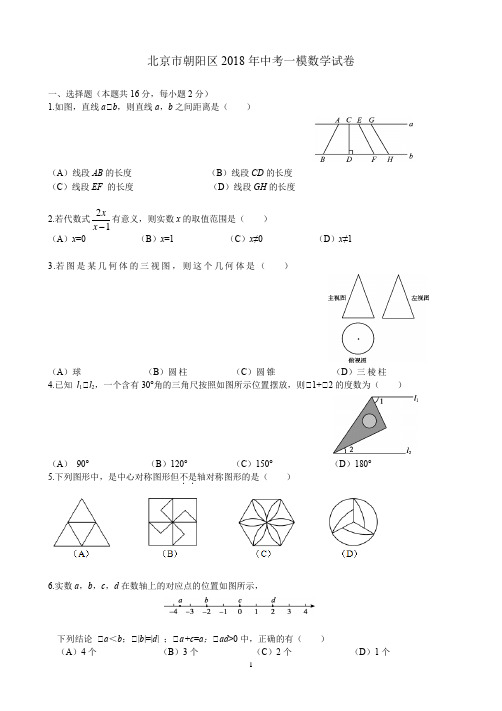
北京市朝阳区2018年中考一模数学试卷一、选择题(本题共16分,每小题2分)1.如图,直线a ∥b ,则直线a ,b 之间距离是( )(A )线段AB 的长度 (B )线段CD 的长度 (C )线段EF 的长度 (D )线段GH 的长度2.若代数式12 x x有意义,则实数x 的取值范围是( ) (A )x =0 (B )x =1 (C )x ≠0 (D )x ≠13.若图是某几何体的三视图,则这个几何体是( )(A )球 (B )圆柱 (C )圆锥 (D )三棱柱4.已知 l 1∥l 2,一个含有30°角的三角尺按照如图所示位置摆放,则∥1+∥2的度数为( )(A ) 90° (B )120° (C )150° (D )180° 5.下列图形中,是中心对称图形但不是..轴对称图形的是( )6.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,下列结论 ∥a <b ;∥|b |=|d | ;∥a+c =a ;∥ad >0中,正确的有( )7. “享受光影文化,感受城市魅力”,2018年4月15-22日第八届北京国际电影节顺利举办.下面的统计图反映了北京国际电影节﹒电影市场的有关情况.根据统计图提供的信息,下列推断合理..的是( ) (A )两届相比较,所占比例最稳定的是动作冒险(含战争)类 (B )两届相比较,所占比例增长最多的是剧情类(C )第八届悬疑惊悚犯罪类申报数量比第六届2倍还多(D )在第六届中,所占比例居前三位的类型是悬疑惊悚犯罪类、剧情类和爱情类8. 如图,∥ABC 是等腰直角三角形,∥A =90°,AB =6,点P 是AB 边上一动点(点P 与点A 不重合),以AP 为边作正方形APDE ,设AP =x ,正方形APDE 与∥ABC 重合部分(阴影部分)的面积为y ,则下列能大致反映y 与x 的函数关系的图象是( )二、填空题(本题共16分,每小题2分) 9. 赋予式子“ab ”一个实际意义: . 10.如果023≠=n m ,那么代数式)2(4322n m nm n m +⋅--的值是 . 11.足球、篮球、排球已经成为北京体育的三张名片,越来越受到广大市民的关注. 下表是北京两支篮球队在2017-2018赛季CBA 常规赛的比赛成绩:设胜一场积x 分,负一场积y 分,依题意,可列二元一次方程组为 . 12. 如图,AB∥CD ,AB=21CD ,S ∥ABO :S ∥CDO = .13. 如图,点A,B,C在∥O上,四边形OABC是平行四边形,OD∥AB于点E,交∥O于点D,则∥BAD= 度.14. 如图,在平面直角坐标系xOy中,∥O'A'B'可以看作是∥OAB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由∥OAB得到∥O'A'B'的过程:.15.下列随机事件的概率:∥投掷一枚均匀的骰子,朝上一面为偶数的概率;∥同时抛掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率;∥抛一枚图钉,“钉尖向下”的概率;∥某作物的种子在一定条件下的发芽率.既可以用列举法求得又可以用频率估计获得的是(只填写序号).16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题7分,第28题8分)17. 计算:2sin30°+ .8)4()31(01+-+-π18. 解不等式组 :⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x19. 如图,在∥ACB 中,AC =BC ,AD 为∥ACB 的高线,CE 为∥ACB 的中线.求证:∥DAB =∥ACE.20. 已知关于x 的一元二次方程0)1(2=+++k x k x . (1)求证:方程总有两个实数根;(2)若该方程有一个根是正数,求k 的取值范围.21. 如图,在∥ABC 中,D 是AB 边上任意一点,E 是BC 边中点,过点C 作AB 的平行线,交DE 的延长线于点F ,连接BF ,CD .(1)求证:四边形CDBF 是平行四边形;(2)若∥FDB =30°,∥ABC =45°,BC =4√2,求DF 的长.22. 如图,在平面直角坐标系xOy 中,直线AB 与x 轴、y 轴分别交于点A 、B ,与反比例函数xky 的图象在第四象限交于点C ,CD ∥x 轴于点D ,tan∥OAB =2,OA =2,OD =1. (1)求该反比例函数的表达式;(2)点M 是这个反比例函数图象上的点,过点M 作MN ∥y 轴,垂足为点N ,连接OM 、AN , 如果S ∥ABN =2S ∥OMN ,直接写出点M 的坐标.23. 如图,在∥O 中,C ,D 分别为半径OB ,弦AB 的中点,连接CD 并延长,交过点A 的切线于点E . (1)求证:AE ∥CE . (2)若AE =√2,sin∥ADE =31,求∥O 半径的长.24. 水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,过程如下,请补充完整.收集数据 从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数:整理、描述数据 按如下分组整理、描述这两组样本数据(说明:45个以下为产量不合格,45个及以上为产量合格,其中45~65个为产量良好,65~85个为产量优秀)分析数据 两组样本数据的平均数、众数和方差如下表所示:得出结论b.可以推断出大棚的小西红柿秧苗品种更适应市场需求,理由为.(至少从两个不同的角度说明推断的合理性)25.如图,AB是∥O的直径,AB=4cm,C为AB上一动点,过点C的直线交∥O于D、E两点,且∥ACD=60°,DF∥AB于点F,EG∥AB于点G,当点C在AB上运动时,设AF=x cm,DE=y cm(当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为cm(结果保留一位小数).26. 在平面直角坐标系xOy 中,抛物线()2440y ax ax a =--≠与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)若方程有两个不相等的实数根,且两根都在1,3之间(包括1,3),结合函数的图象,求a 的取值范围.27. 如图,在菱形ABCD 中,∠DAB =60°,点E 为AB 边上一动点(与点A ,B 不重合),连接CE ,将∠ACE 的两边所在射线CE ,CA 以点C 为中心,顺时针旋转120°,分别交射线AD 于点F ,G. (1)依题意补全图形;(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示); (3)用等式表示线段AE 、AF 与CG 之间的数量关系,并证明.()244=00ax ax a --≠28. 对于平面直角坐标系xOy中的点P和线段AB,其中A(t,0)、B(t+2,0)两点,给出如下定义:若在线段AB上存在一点Q,使得P,Q两点间的距离小于或等于1,则称P为线段AB的伴随点.(1)当t=-3时,∥在点P1(1,1),P2(0,0),P3(-2,-1)中,线段AB的伴随点是;∥在直线y=2x+b上存在线段AB的伴随点M、N,且MN=b的取值范围;(2)线段AB的中点关于点(2,0)的对称点是C,将射线CO以点C为中心,顺时针旋转30°得到射线l,若射线l上存在线段AB的伴随点,直接写出t的取值范围.北京市朝阳区2018年中考一模数学试卷参考答案及评分标准一、选择题(本题共16分,每小题2分)二、填空题 (本题共16分,每小题2分)9. 答案不惟一,如:边长分别为a ,b 的矩形面积 10.4711. ⎩⎨⎧=+=+.562018,631325y x y x 12. 1:4 13. 1514. 答案不唯一,如:以x 轴为对称轴,作∥OAB 的轴对称图形,再将得到三角形沿向右平移4个单位长度 15. ∥∥16. 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;直径所对的圆周角是直角三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26-27题,每小题7分,第28题8分) 17. 解:原式 2213212+++⨯= …………………………………………………………………4分 225+=. ……………………………………………………………………………5分18. 解:原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x解不等式∥,得 5<x . ………………………………………………………………………2分解不等式∥,得 21>x .………………………………………………………………………4分 ∥ 原不等式组的解集为521<<x . …………………………………………………………5分19. 证明:∥AC =BC ,CE 为∥ACB 的中线,∥∥CAB =∥B ,CE ∥AB . ………………………………………………………………2分 ∥∥CAB +∥ACE =90°. …………………………………………………………………3分 ∥AD 为∥ACB 的高线, ∥∥D =90°.∥∥DAB +∥B =90°. ……………………………………………………………………4分 ∥∥DAB =∥ACE . ………………………………………………………………………5分20. (1)证明:依题意,得k k 4)1(2-+=∆ ……………………………………………………1分 .)1(2-=k ……………………………………………………………2分∥0)1(2≥-k ,∥方程总有两个实数根. ……………………………………………………………3分(2)解:由求根公式,得11-=x ,k x -=2. …………………………………………………4分∥方程有一个根是正数, ∥0>-k .∥0<k .…………………………………………………………………………………5分21.(1)证明:∥CF ∥AB ,∥∥ECF =∥EBD . ∥E 是BC 中点, ∥CE =BE .∥∥CEF =∥BED , ∥∥CEF ∥∥BED . ∥CF =BD .∥四边形CDBF 是平行四边形. ……………………………………………………2分(2)解:如图,作EM ∥DB 于点M ,∥四边形CDBF 是平行四边形,BC =24, ∥2221==BC BE ,DE DF 2=.在Rt∥EMB 中,2sin =∠⋅=ABC BE EM . …………………………………………3分在Rt∥EMD 中,42==EM DE . ……………………………………………………4分∥DF =8. ……………………………………………………………………………………5分22. 解:(1)∥AO =2,OD =1,∥AD =AO+ OD =3. ……………………………………………………………………1分 ∥CD ∥x 轴于点D , ∥∥ADC =90°.在Rt∥ADC 中,6tan =∠⋅=OAB AD CD ..∥C (1,-6). ……………………………………………………………………………2分∥该反比例函数的表达式是xy 6-=. …………………………………………………3分A(2)点M 的坐标为(-3,2)或(53,-10). ……………………………………………5分23. (1)证明:连接OA ,∥OA 是∥O 的切线,∥∥OAE =90º. ………………………………1分 ∥ C ,D 分别为半径OB ,弦AB 的中点,∥CD 为∥AOB 的中位线.∥CD ∥OA . ∥∥E =90º. ∥AE ∥CE . …………………………………2分(2)解:连接OD ,∥∥ODB =90º. ………………………………………………………………………3分∥AE =,sin∥ADE =31, 在Rt∥AED 中,23sin =∠=ADEAEAD .∥CD ∥OA , ∥∥1=∥ADE .在Rt∥OAD 中,311sin ==∠OA OD .………………………………………………4分 设OD =x ,则OA =3x , ∥222OA AD OD =+, ∥()()222323x x =+.解得 231=x ,232-=x (舍). ∥293==x OA . ……………………………………………………………………5分即∥O 的半径长为29.24. 解:整理、描述数据 按如下分组整理、描述这两组样本数据…………………………………………………………………………………………………2分得出结论 a .估计乙大棚产量优秀的秧苗数为 84 株; …………………………3分b .答案不唯一,理由须支撑推断的合理性. ………………………………5分25. 解:本题答案不唯一,如:x /cm 0 0.40 0.55 1.00 1.80 2.29 2.61 3 y /cm23.683.844.003.653.132.702…………………………………………………………………………………………………1分(2)…………………………………………………………………………………………………4分(3)3.5.…………………………………………………………………………………………6分26.解:(1)44)2(4422---=--=a x a ax ax y .∥A (0,-4),B (2,0).…………………………………………………………2分 (2)当抛物线经过点(1,0)时,34-=a .……………………………………………4分 当抛物线经过点(2,0)时,1-=a . ……………………………………………6分 结合函数图象可知,a 的取值范围为134<≤-a .…………………………………7分27.(1)补全的图形如图所示.…………………………………………………………………………………………………1分(2)解:由题意可知,∠ECF=∠ACG=120°.∥∠FCG=∠ACE=α.∥四边形ABCD 是菱形,∠DAB=60°,∥∠DAC=∠BAC= 30°. ………………………………………………………………2分 ∥∠AGC=30°.∥∠AFC =α+30°. ………………………………………………………………………3分(3)用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明:作CH ∥AG 于点H.由(2)可知∠BAC=∠DAC=∠AGC=30°.∥CA=CG. ………………………………………………………………………………………5分 ∥HG =21AG. ∥∠ACE =∠GCF ,∠CAE =∠CGF ,∥∥ACE ≌△GCF. ……………………………………………………………………………6分 ∥AE =FG .在Rt △HCG 中, .23cos CG CGH CG HG =∠⋅= ∥AG =3CG . …………………………………………………………………………………7分 即AF+AE =3CG .28. 解:(1)∥线段AB 的伴随点是: 23,P P . ………………………………………………2分∥如图1,当直线y =2x +b 经过点(-3,-1)时,b =5,此时b 取得最大值.………………………………………………………………………………4分 如图2,当直线y =2x +b 经过点(-1,1)时,b =3,此时b 取得最小值. ………………………………………………………………………………5分 ∥ b 的取值范围是3≤b ≤5. ……………………………………………………6分(2)t 的取值范围是-12.2t ≤≤………………………………………………………………8分图1 图2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、填空题(本题共 16 分,每小题 2 分)
9. 赋予式子“ab”一个实际意义: .
10.如果
m 3
n 2
0
,那么代数式
3m 4m2
n n2
(2m
n)
的值是
.
11.足球、篮球、排球已经成为北京体育的三张名片,越来越受到广大市民的关注. 下表是
北京两支篮球队在 2017-2018 赛季 CBA 常规赛的比赛成绩:
2x 2.若代数式 x 1 有意义,则实数 x 的取值范围是
(A)x=0
(B)x=1
(C)x≠0
(D)x≠1
3.若 右 图 是 某 几 何 体 的 三 视 图 , 则 这 个 几 何 体 是 (A)球 (B)圆 柱 (C)圆 锥 (D)三 棱 柱
4.已知 l1∥l2,一个含有 30°角的三角尺按照如图所示位置摆放,则∠1+∠2 的度数为 (A) 90° (B)120° (C)150° (D)180°
(1)求证:方程总有两个实数根; (2)若该方程有一个根是正数,求 k 的取值范围.
21. 如图,在△ABC 中,D 是 AB 边上任意一点,E 是 BC 边中点,过点 C 作 AB 的平行线,交 DE 的延长线于点 F,连接 BF,CD.
(1)求证:四边形 CDBF 是平行四边形; (2)若∠FDB=30°,∠ABC=45°,BC=4 ,求 DF 的长.
17. 计算:2sin30°+ (1)1 (4 )0 8. 3
x 1 2(x 3),
18.
解不等式组
:
6
x 2
1
2x.
19. 如图,在△ACB 中,AC=BC,AD 为△ACB 的高线,CE 为△ACB 的中线. 求证:∠DAB=∠ACE.
20. 已知关于 x 的一元二次方程 x2 (k 1)x k 0 .
7. “享受光影文化,感受城市魅力”,2018 年 4 月 15-22 日第八届北京国际电影节顺利举办.
下面的统计图反映了北京国际电影节﹒电影市场的有关情况.
第六届和第八届北京国际电影节﹒电影市场“项目创投”申报类型统计表
申报类型 悬疑惊 剧情
爱情
喜剧
科幻
动作冒险 古装 动画 其他
届
悚犯罪
奇幻 (含战争) 武侠
两弧相交于 B,C 两点,连接 BC 交 PA 于点 D; (3)以点 D 为圆心,DP 为半径作圆,交直线 a 于
点 E,作直线 PE. 所以直线 PE 就是所求作的垂线.
请回答:该尺规作图的依据是
.
九年级数学试卷 第 4页(共 8 页)
三、解答题(本题共 68 分,第 17-24 题,每小题 5 分,第 25 题 6 分,第 26-27 题,每小题 7 分,第 28 题 8 分)
北京市朝阳区九年级综合练习(一)
数学试卷
2018.5
学校
班级
姓名
考号
考 1.本试卷共 8 页,共三道大题,28 道小题,满分 100 分。考试时间 120 分钟。
生 2.在试卷和答题卡上认真填写学校名称、姓名和准考证号。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
须 4.在答题卡上,选择题、作图题用 2B 铅笔作答,其他试题用黑色字迹签字笔作答。
队名 比赛场次 胜场
负场
积分
北京首钢
38
25
13
63
北京北控
38
18
20
56
设胜一场积 x 分,负一场积 y 分,依题意,可列二元一次方程组为 .
1
12. 如图,AB∥CD,AB= CD,S△ABO :S△CDO=
.
2
九年级数学试卷 第 3页(共 8 页)
13. 如图,点 A,B,C 在⊙O 上,四边形 OABC 是平行四边形,OD⊥AB 于点 E,交⊙O 于点
第六届
8.70% 25.30% 17.80% 12.20% 13.00% 7.80%
0 3.80% 11.40%
第八届
21.33% 19.94% 18.70% 15.37% 10.66% 7.48% 4.02% 1.39% 1.11%
根据统计图提供的信息,下列推断合.理.的是 (A)两届相比较,所占比例最稳定的是动作冒险(含战争)类 (B)两届相比较,所占比例增长最多的是剧情类 (C)第八届悬疑惊悚犯罪类申报数量比第六届 2 倍还多 (D)在第六届中,所占比例居前三位的类型是悬疑惊悚犯罪类、剧情类和爱情类
九年级数学试卷 第 2页(共 8 页)
8. 如图,△ABC 是等腰直角三角形,∠A=90°,AB=6,点 P 是 AB 边 上一动点(点 P 与点 A 不重合),以 AP 为边作正方形 APDE,设 AP=x,正方形 APDE 与△ABC 重合部分(阴影部分)的面积为 y, 则下列能大致反映 y 与 x 的函数关系的图象是
D,ቤተ መጻሕፍቲ ባይዱ∠BAD=
度.
第 13 题图
第 14 题图
14. 如图,在平面直角坐标系 xOy 中,△O'A'B'可以看作是△OAB 经过若干次图形的变化
(平移、轴对称、旋转)得到的,写出一种由△OAB 得到△O'A'B'的过程:
.
15.下列随机事件的概率:①投掷一枚均匀的骰子,朝上一面为偶数的概率;②同时抛掷两
知 5.考试结束,请将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共 16 分,每小题 2 分) 下面 1-8 题均有四个选项,其中符合题意的选项只.有.一个.
1.如图,直线 a∥b,则直线 a,b 之间距离是 (A)线段 AB 的长度 (B)线段 CD 的长度 (C)线段 EF 的长度 (D)线段 GH 的长度
枚质地均匀的硬币,两枚硬币全部正面朝上的概率;③抛一枚图钉,“钉尖向下”的概
率;④某作物的种子在一定条件下的发芽率.
既可以用列举法求得又可以用频率估计获得的是
(只填写序号).
16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线 a 和直线外一点 P. 求作:直线 a 的垂线,使它经过 P. 作法:如图, (1)在直线 a 上取一点 A, 连接 PA; (2)分别以点 A 和点 P 为圆心,大于 AP 的长为半径作弧,
九年级数学试卷 第 1页(共 8 页)
5.下列图形中,是中心对称图形但不.是.轴对称图形的是
(A)
(B)
(C)
6.实数 a,b,c,d 在数轴上的对应点的位置如图所示,
(D)
下列结论 ①a<b;②|b|=|d| ;③a+c=a;④ad>0 中,正确的有
(A)4 个
(B)3 个
(C)2 个
(D)1 个
