实验报告:贪心算法--最优装载
贪心算法之最优装载问题
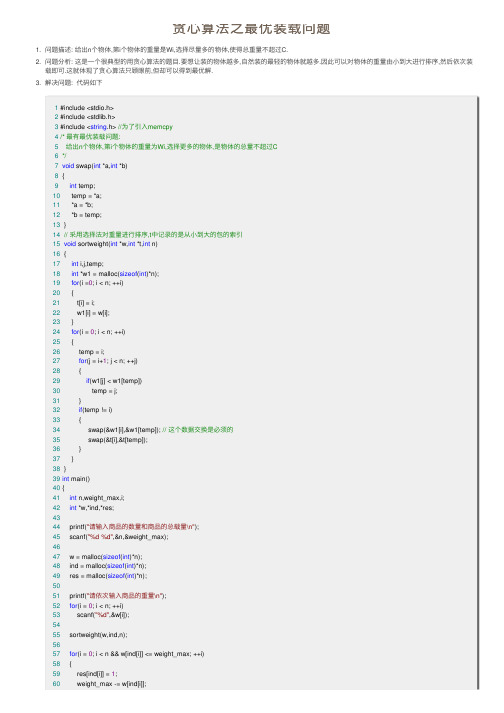
贪⼼算法之最优装载问题1. 问题描述: 给出n个物体,第i个物体的重量是Wi,选择尽量多的物体,使得总重量不超过C.2. 问题分析: 这是⼀个很典型的⽤贪⼼算法的题⽬.要想让装的物体越多,⾃然装的最轻的物体就越多.因此可以对物体的重量由⼩到⼤进⾏排序,然后依次装载即可.这就体现了贪⼼算法只顾眼前,但却可以得到最优解.3. 解决问题: 代码如下4. 1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h> //为了引⼊memcpy4/* 最有最优装载问题:5给出n个物体,第i个物体的重量为Wi,选择更多的物体,是物体的总量不超过C6*/7void swap(int *a,int *b)8 {9int temp;10 temp = *a;11 *a = *b;12 *b = temp;13 }14// 采⽤选择法对重量进⾏排序,t中记录的是从⼩到⼤的包的索引15void sortweight(int *w,int *t,int n)16 {17int i,j,temp;18int *w1 = malloc(sizeof(int)*n);19for(i =0; i < n; ++i)20 {21 t[i] = i;22 w1[i] = w[i];23 }24for(i = 0; i < n; ++i)25 {26 temp = i;27for(j = i+1; j < n; ++j)28 {29if(w1[j] < w1[temp])30 temp = j;31 }32if(temp != i)33 {34 swap(&w1[i],&w1[temp]); // 这个数据交换是必须的35 swap(&t[i],&t[temp]);36 }37 }38 }39int main()40 {41int n,weight_max,i;42int *w,*ind,*res;4344 printf("请输⼊商品的数量和商品的总载量\n");45 scanf("%d %d",&n,&weight_max);4647 w = malloc(sizeof(int)*n);48 ind = malloc(sizeof(int)*n);49 res = malloc(sizeof(int)*n);5051 printf("请依次输⼊商品的重量\n");52for(i = 0; i < n; ++i)53 scanf("%d",&w[i]);5455 sortweight(w,ind,n);5657for(i = 0; i < n && w[ind[i]] <= weight_max; ++i)58 {59 res[ind[i]] = 1;60 weight_max -= w[ind[i]];61 }62 printf("贪⼼算法求解后的结果是:\n");63for(i = 0; i < n; ++i)64 {65 printf("%d ",res[i]);66 }67 printf("\n");68return0;69 }4. 程序分析: 由于不要改变原始物体重量的值,所以在排序的时候要另外再开辟⼀个数组存储重量.并且另外开辟ind[]存放索引记录装载的顺序.ind[]存放的是重量数组中每个元素在这组数组中⼤⼩的顺序(索引).怎样在排序时记录索引需要在练习排序的时候注意下.。
贪心算法解决最优装载问题

}
}
void Loading(int x[],int w[],int c,int n,int *t) //传址
{
sort(w,t,n);
for(int i=0;i<n;i++)x[i]=0;
#include<stdlib.h>
void Swap(int &x,int &y)//交换
{
int t;
t=x;
x=y;
y=t;
}
void sort(int w[],int t[],int n)//排序,由小到大
{
for(int m=0;m<n;m++) //为每个物品编序号
{
t[m]=m;
}
int i,j;
for(int j=0; j<n && w[t[j]]<=c ; j++)
{
x[t[j]]=1;//装入
c-=w[t[j]];
}
}
int main()
{
int n,c;
cout<<"请输入物品个数:"<<endl;
cin>>n;
cout<<"请输入最大容量:"<<endl;
cin>>c;
int *t=new int[n]; //存储物品编号
二. 实验内容
贪心算法基本思想:
整体划分成部分,分而治之。每个部分中寻找最优解,然后综合所有部分最优解。这是,可能得到整体的最优解,但往往得到的是近似的最优解。
最佳装载问题的证明

x y
i 1 i i 1
最佳装载问题的证明
贪心算法一定能求得问题的最优解的例子。 设某邮政车的载重量为 c ,有 n 件邮包,每件入车内, 装载的总重量不能超过邮政车的载重 量,最佳装载要求所装入邮包的数量最大(设邮政车的容积足够大) 。
证明:令 x [ x1 ,, xn ] 为贪心算法获得的解,其中 x i =1 表示装载, 为 x i =0 表示不装载,类似的令 y 需要证明
i 1 i i 1
n
n
i
。若存在这样的 j ,则 j k ,否则 y 就不是一个可
行解。因为 x j
y j , x j 1 ,所以 y j 0 。这样的话,令 y j 1 ,若得到的
y 不是可行解,则在 j 1, n 范围内必有一个 l 使得 yl 1 。令 yl 0 ,由于
[ y1 ,, yn ] 为任意一个可行解,只
x y
i 1 i i 1
n
n
i
。不失一般性,可以假设邮包都排好序了,即
wi wi 1 1 i n ,然后分几步将 y 转化为 x ,转化过程中每一步都
产生一个可行的新 y ,且 明
y 大于等于未转化前的值,最后便可以证
n
n
i
,证明完毕。
i 1 i
n
x y
i 1 i i 1
n
n
i
实验报告:贪心算法--最优装载

XXXX 大学计算机学院实验报告计算机学院2017级软件工程专业 5 班指导教师
学号姓名2019年10 月28 日成绩
实验内容、上机调试程序、程序运行结果
System.out.print(weight[i]+" ");
}
System.out.println();
//从控制台获取集装箱的最大重量
System.out.println("请输入集装箱的最大重量:");
Scanner s = new Scanner(System.in);
maxWeight=s.nextInt();
System.out.print("可装入的集装箱有:");
//将一批集装箱装上一艘重量为80的轮船。
在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
(重量从小到大装)
for(int k=0;k<weight.length;k++){
sumWeight += weight[k];
if(sumWeight<=maxWeight){
System.out.print(weight[k]+"kg ");
}
}
}
}
②完成效果。
贪心算法之最优装载问题

贪⼼算法之最优装载问题贪⼼算法之最优装载问题1. 问题描述有⼀批集装箱要装上⼀艘重量为c的轮船,其中集装箱i的重量为W i。
最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
2. 问题分析2.1确定贪⼼策略采⽤重量最轻者先装的贪⼼选择策略,可产⽣该问题的最优解。
2.2代码求解/*** x[] 保存最优解路径数组* w[] 集装箱重量数组* c 船的载重量* n 集装箱的数量**/void Loading(int x[], int w[], int c, int n) {// 按照集装箱重量从⼩到⼤排序sort(w, n);for (int i = 1; i <= n; i++)x[i] = 0;for (int i = 1; i <= n && w[i] <= c; i++) {x[i] = 1;c -= w[i];}}2.3贪⼼选择性质设集装箱依其重量从⼩到⼤排序,(x1,x2,…,x n)是其最优解,x i={0,1},设x k是第⼀个等于1的。
(1) 如k=1,则满⾜贪⼼选择性质(2) 如k≠1,⽤x1替换x k,构造的新解同原解最优值相同,故也是最优解,满⾜贪⼼选择性质该证明⽅法只证明了任何⼀个最优解都可以转换为第⼀个集装箱上船的最优解(满⾜贪⼼策略)。
此⽅法对⼦问题同样有效,因此可以将⼀个普通最优解转化为满⾜贪⼼策略的最优解。
如(0101)⇒(1100)2.4.最优⼦结构性质最优装载问题具有最优⼦结构性质,设1⾄n个集装箱装上船的最⼤数量为T(1,n,w),则T(1,n,w)=1+T(2,n,w−w1);因T(1,n,w)是最优值,则T(2,n,w−w i)⼀定是最优值,反证法证明之反证法:如果T(2,n,w−w1)不是该问题的最优解,则存在最优值T′(2,n,w−w1)>T(2,n,w−w1),则1+T′(2,n,w−w1)=T′(1,n,w)>T(1,n,w),这与⼤前提T(1,n,w)是最优值相⽭盾,故T(2,n,w−w1)⼀定是最优值。
贪心法之最优装载问题

贪⼼法之最优装载问题概念:当⼀个问题具有最优⼦结构性质时,可⽤动态规划算法,有时会有更简单有效的算法,那就是贪⼼算法,贪⼼算法是通过⼀系列的选择来得到问题的解,贪⼼算法并不从整体最优上加以考虑,所做的选择只是在某种意义上的局部最优解。
但对范围相当⼴的许多问题能产⽣整体最优解。
在⼀些情况下,即使贪⼼算法不能得到整体最优解,但其最终结果却是最优解的很好的近似解。
贪⼼算法的基本要素:贪⼼选择性质:所求解的问题的整体最优解可以通过⼀系列局部最优的选择来,即贪⼼选择达到。
贪⼼选择所依赖的是以前所做过的选择,⽽对以后所做的选择没有关系。
最优⼦结构性质:⼀个问题的最优解包含其⼦问题的最优解。
贪⼼算法与动态规划的区别:动态规划是通过⾃底向上的⽅式解决⼦问题,贪⼼算法是通过⾃顶向下的迭代⽅式做出贪⼼选择,求解问题的最优解。
两共同点是都具有最优⼦结构性质。
最优装载问题:某艘船的载重量为C,每件物品的重量为wi,要将尽量多的物品装⼊到船上。
分析:贪⼼策略:每次都选择最轻的,然后再从剩下的n-1件物品中选择最轻的。
算法策略:把n件物品从⼩到⼤排序,然后根据贪⼼策略尽可能多的选出前i个物品,直到不能装为⽌。
这个问题⽐部分背包问题还简单,先拿轻的再拿重的可以保证最后物品装的最多。
代码如下:#include<iostream>#include<algorithm>#define MAXN 10000using namespace std;int main(){int c,n; //c:船的最⾼载重量 n:古董数量int sum=0,weight=0; //sum:装⼊的古董数量 weight:装⼊的古董重量int w[MAXN]; //单个古董对应的重量cout<<"请输⼊最⾼载重量和需载的古董数⽬:"<<endl;cin>>c>>n;cout<<"请分别输⼊这些古董的重量:"<<endl;for(int i=1;i<=n;++i)cin>>w[i];sort(w+1,w+1+n);for(int i = 1 ; i<=n ; i++){weight += w[i]; //先将重量加进去if(weight >= c){if(weight == c) //恰好装满时sum = i;elsesum = i-1; //超重了,需要减去⼀个break;}}cout<<"最多可以装"<<sum<<"个"<<endl;for(int i=1;i<=sum;++i)cout<<w[i]<<"";return0;}View Code程序运⾏结果:参考:王晓东《算法设计与分析》。
最优装载问题(贪心)

最优装载问题(贪⼼)⼀、实验内容运⽤贪⼼算法解决活动安排问题(或最优装载问题)使⽤贪⼼算法解决最优装载问题。
⼆、所⽤算法基本思想及复杂度分析1.算法基本思想贪⼼算法是指在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,它所做出的仅是在某种意义上的局部最优解。
⽤局部解构造全局解,即从问题的某⼀个初始解逐步逼近给定的⽬标,以尽可能快的求得更好的解。
当某个算法中的某⼀步不能再继续前进时,算法停⽌。
2.问题分析及算法设计问题分析:(1)给定n个古董,要把它们装到装载量为c的装载船上。
(2)⾸先需要对这n个古董进⾏质量从⼩到⼤的排序。
(3)然后每次都选择最轻的,接着再从剩下的n-1件物品中选择最轻的。
(4)重复第(3)步骤,直到当前载重量⼤于装载船的最⼤装载量,停⽌装载。
(5)此时得到最优的贪⼼⽅案,记录下装载的最⼤古董数。
算法设计:(1)算法策略:把n件物品从⼩到⼤排序,然后根据贪⼼策略尽可能多的选出前i个物品,直到不能装为⽌。
(2)特例:算法复杂度分析由最优装载问题的贪⼼选择性质和最优⼦结构性质,可知将这些古董按照其重量从⼩到⼤排序,所以算法所需的计算时间为O(nlogn)。
三、源程序核⼼代码及注释(截图)四、运⾏结果五、调试和运⾏程序过程中产⽣的问题及解决⽅法,实验总结(5⾏以上)这⾥的调试,没有什么⼤问题,单纯的依次⽐较,判断,从⽽得到结果。
这次实验让我对贪⼼算法有了更深刻的认识,其主要是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更⼩的相似的⼦问题,并使⼦问题最优,再由⼦问题来推导出全局最优解。
贪⼼算法虽然求的是局部最优解,但往往许多问题的整体最优解都是通过⼀系列的局部最优解的选择来达到的,所以贪⼼算法不⼀定可以得到能推导出问题的最优解,但其解法是最优解的近似解。
懂得算法的原理,还需要多去练习才能更好的掌握其⽤法。
源码:#include<iostream>#include<algorithm>#define MAXN 1000005using namespace std;int w[MAXN];//每件古董的重量int main(){int c,n;//c:载重量,n古董数int sum = 0;//装⼊古董的数量int tmp = 0;//装⼊古董的重量cin >> c >> n;for(int i= 1; i <= n; ++i)cin >> w[i];sort(w+1,w+1+n);for(int i = 1; i <= n; ++i){tmp += w[i];if(tmp <= c)++sum;elsebreak;}cout << sum << endl;return 0;}。
算法装载问题实验报告

一、实验背景算法装载问题(Bin Packing Problem)是组合优化领域中的一个经典问题,主要研究如何将一组物品装入有限数量的容器中,使得容器中的物品总重量不超过容器的容量,同时尽可能减少容器的数量。
该问题在实际应用中具有广泛的意义,如物流运输、资源分配、生产计划等领域。
二、实验目的1. 了解算法装载问题的基本概念和特点;2. 掌握几种常用的算法装载问题的解决方法;3. 通过实验验证不同算法在解决算法装载问题时的性能;4. 分析算法的优缺点,为实际应用提供参考。
三、实验内容1. 实验环境操作系统:Windows 10编程语言:Python 3.8实验工具:Pandas、Numpy、Scipy2. 实验方法(1)遗传算法遗传算法是一种模拟自然选择和遗传学原理的搜索启发式算法。
在算法装载问题中,可以将物品和容器看作基因,通过交叉、变异等操作,不断优化解的质量。
(2)贪心算法贪心算法是一种在每一步选择中都采取当前最优策略的算法。
在算法装载问题中,可以根据物品的重量或容器的容量,对物品进行排序,然后依次将物品装入容器。
(3)动态规划动态规划是一种将复杂问题分解为子问题,并存储子问题的解的方法。
在算法装载问题中,可以根据物品的重量和容器的容量,计算最优解。
3. 实验数据实验数据来源于一组具有不同重量和数量的物品,以及不同容量和数量的容器。
四、实验结果与分析1. 遗传算法实验结果表明,遗传算法在解决算法装载问题时具有较高的求解能力。
随着迭代次数的增加,解的质量逐渐提高,但求解时间较长。
2. 贪心算法贪心算法在解决算法装载问题时具有较快的求解速度,但解的质量相对较差。
在部分情况下,贪心算法得到的解甚至无法满足所有容器的容量要求。
3. 动态规划动态规划在解决算法装载问题时具有较高的求解质量,但求解时间较长。
对于大型问题,动态规划可能无法在合理时间内得到最优解。
五、结论通过对遗传算法、贪心算法和动态规划在算法装载问题中的应用实验,得出以下结论:1. 遗传算法具有较高的求解能力,但求解时间较长;2. 贪心算法求解速度快,但解的质量较差;3. 动态规划求解质量高,但求解时间较长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
XXXX 大学计算机学院实验报告计算机学院2017级软件工程专业 5 班指导教师
学号姓名2019年10 月28 日成绩
实验内容、上机调试程序、程序运行结果
System.out.print(weight[i]+" ");
}
System.out.println();
//从控制台获取集装箱的最大重量
System.out.println("请输入集装箱的最大重量:");
Scanner s = new Scanner(System.in);
maxWeight=s.nextInt();
System.out.print("可装入的集装箱有:");
//将一批集装箱装上一艘重量为80的轮船。
在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船。
(重量从小到大装)
for(int k=0;k<weight.length;k++){
sumWeight += weight[k];
if(sumWeight<=maxWeight){
System.out.print(weight[k]+"kg ");
}
}
}
}
②完成效果。
