算法设计与分析实验报告贪心算法

合集下载

实验三-贪心算法

StringBuffer buf=newStringBuffer();
for(inti=0;i<s.length();i++){
buf.append(getEachCode(s.substring(i,i+1)));
}
returnbuf.toString();
}
publicString getEachCode(String name){
for(inti=0;i<buffer.length();i++){
if(name.equals(codes[i].name)){
returnhuffstring[i];
}
}
return"";
}
publicvoidgetCode(intn,String[] thecodes,String thebuffer){
importjava.util.Scanner;
classHuffmanCode{
Stringname;
doubleweight;
intlc,rc,pa;
publicHuffmanCode(){
name="";
weight=0;
lc=-1;rc=-1;pa=-1;
}
}
publicclassHuffman1 {
dist[j]=newdist;prev[j]=u;}}}}
(3)运行结果
3、题目三
(1)问题分析
设G=（V，E）是连通带权图，V={1，2，…,n}。构造G的最小生成树的Prim算法的基本思想是：首先置S{1}，然后，只要S是V的真子集，就进行如下的贪心选择：选取满足条件i∈S，j∈V-S，且c[i][j]最小的边，将顶点j添加到S中。这个过程一直进行到S=V时为止。过程中所取到的边恰好构成G的一棵最小生成树。

算法设计与分析中的贪心算法与回溯法

算法设计与分析中的贪心算法与回溯法算法设计与分析领域中，贪心算法和回溯法是两种常用的解题方法。

本文将介绍这两种算法，并比较它们在不同场景下的优势和劣势。

一、贪心算法贪心算法是一种在每一步都选择当前最优解的策略，希望通过局部最优解的选择最终达到全局最优解。

贪心算法的实现较为简单，时间复杂度较低，适用于解决一些最优化问题。

贪心算法的基本思想是每次都选择当前状态下的最优解，并将其加入到解集中。

例如，在求解最小生成树的问题中，贪心算法会选择当前具有最小权值的边，并将其添加到最终结果中，直到生成树完成。

然而，贪心算法的局限性在于它只考虑了当前的最优解，无法保证找到全局最优解。

在某些问题中，贪心算法可能会陷入局部最优解而无法跳出。

因此，需要在具体问题中综合考虑问题的性质和约束条件来确定是否适合采用贪心算法。

二、回溯法回溯法是一种通过不断尝试可能的步骤来寻找问题解的方法。

它通常基于递归的思想，在每一步都尝试所有的可能选择，并逐步构建解空间，直到找到解或确定无解。

回溯法的核心思想是深度优先搜索，通过遍历解空间树来寻找解。

在每一步，回溯法都会考虑当前状态下的所有可能选择，并递归地进入下一步。

如果某一步的选择无法达到目标，回溯法会回退到上一步进行其他可能的选择。

回溯法常用于解决一些全排列、子集和组合等问题。

例如，在解决八皇后问题时，回溯法通过逐个放置皇后并进行合法性判断，直到找到所有解或遍历完所有可能的情况为止。

然而，回溯法的缺点在于其时间复杂度较高，其搜索过程包含了大量的重复计算。

因此，在使用回溯法解决问题时，需注意适当剪枝以减少搜索空间，提高算法效率。

三、贪心算法与回溯法的比较贪心算法和回溯法都是常用的算法设计与分析方法，但其适用场景和效果有所差异。

贪心算法在解决问题时能够快速找到局部最优解，并且具有较低的时间复杂度。

它适用于一些满足最优子结构性质的问题，例如最小生成树、单源最短路径等。

然而，贪心算法无法保证一定能找到全局最优解，因此需根据具体问题的特点来判断是否使用。

算法分析与设计实验报告实验5：贪心算法的应用

scanf("%d %d",&d[i].l,&d[i].r); if(d[i].l>d[i].r) swap(d[i].l,d[i].r); }
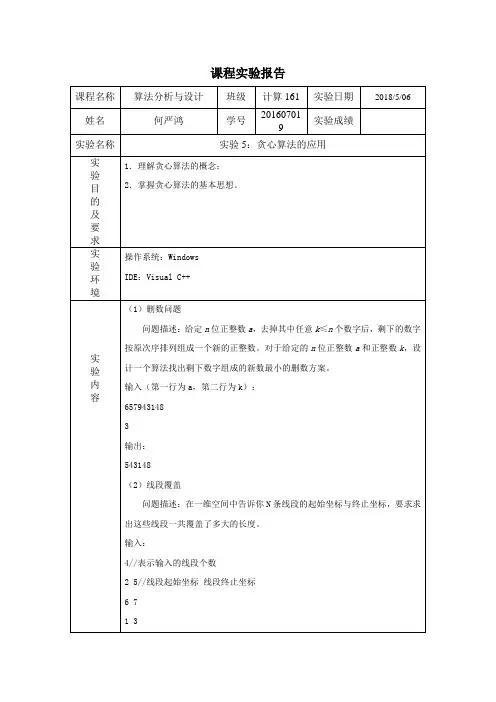
sort(d,d+n,cmp);//按纵坐标升序排列 last=d[0].r;//记录当前线段被覆盖的最大坐标值
for(int i=1;i<n;i++) { if(d[i].l<=last && d[i].r>=last)//线段 d[i]的右坐标在 last 之后，左坐标在 Last 之前的情况，即产生了覆盖。此时还要更新 last 坐标
} cout<<n.substr(0,l-s+x)<<endl;//只打印剩下的左边 l-(s-x)个数字 } return 0; } 2. #include<iostream> #include<cstdio> #include <algorithm> using namespace std; struct point {
课程实验报告
课程名称算法分析与设计班级计算 161 实验日期
姓名
何严鸿
学号 20160701 实验成绩 9
实验名称
实验 5：贪心算法的应用
实
1．理解贪心算法的概念；
验
目
2．掌握贪心算法的基本思想。
的
及
要
求
实
操作系统：Windows
验
环
IDE：Visual C++
境
（1）删数问题
2018/5/06
{
length=d[i].r-d[i-1].l; last=d[i].r; } else if (d[i].r<=last) //线段 d[i]的右坐标在 last 之内，不产生覆盖 continue; else if (d[i].l>=last) //线段 d[i]的左坐标在 Last 之后，此时 last 之后的部分不会对之前的部分产生影响，更新 last 坐标。length 的值加上之前的部分 { last=d[i-1].r; length=length+d[i].r-d[i].l; } } cout<<last<<endl; return 0; }

实验3贪心算法（定稿）

实验3贪心算法（定稿）第一篇：实验3 贪心算法（定稿）《算法设计与分析》实验报告实验3贪心算法姓名学号班级实验日期实验地点一、实验目的1、掌握贪心算法的设计思想。

2、理解最小生成树的相关概念。

二、实验环境1、硬件环境 CPU：酷睿i5 内存：4GB 硬盘：1T2、软件环境操作系统：Windows10 编程环境：jdk 编程语言：Java三、实验内容：在Prim算法与Kruskal算法中任选一种求解最小生成树问题。

1、你选择的是：Prim算法2、数据结构（1）图的数据结构——图结构是研究数据元素之间的多对多的关系。

在这种结构中，任意两个元素之间可能存在关系，即结点之间的关系可以是任意的，图中任意元素之间都可能相关。

图形结构——多个对多个，如（2）树的数据结构——树结构是研究数据元素之间的一对多的关系。

在这种结构中，每个元素对下(层)可以有0个或多个元素相联系，对上(层)只有唯一的一个元素相关，数据元素之间有明显的层次关系。

树形结构——一个对多个，如3、算法伪代码 Prim(G,E,W)输入：连通图G 输出：G的最小生成树T 1.S←{1};T=∅ 2.While V-S ≠∅ do3.从V-S中选择j使得j到S中顶点的边e的权最小；T←T∪{e}4.S←S∪{j}3、算法分析时间复杂度：O(n)空间复杂度：O(n^2)4、关键代码（含注释）package Prim;import java.util.*;publicclass Main { staticintMAXCOST=Integer.MAX_VALUE;staticint Prim(intgraph[][], intn){ /* lowcost[i]记录以i为终点的边的最小权值，当lowcost[i]=0时表示终点i加入生成树 */ intlowcost[]=newint[n+1];/* mst[i]记录对应lowcost[i]的起点，当mst[i]=0时表示起点i加入生成树 */ intmst[]=newint[n+1];intmin, minid, sum = 0;/* 默认选择1号节点加入生成树，从2号节点开始初始化*/ for(inti = 2;i<= n;i++){/* 标记1号节点加入生成树 */ mst[1] = 0;/* n个节点至少需要n-1条边构成最小生成树 */ for(inti = 2;i<= n;i++){/* 找满足条件的最小权值边的节点minid */ for(intj = 2;j<= n;j++){/* 输出生成树边的信息:起点，终点，权值 */System.out.printf(“%c1, minid + 'A''A' + 1;intj = chy-'A' + 1;graph[i][j] = cost;graph[j][i] = cost;for(intj = 1;j<= n;j++){ } graph[i][j] = MAXCOST;} } System.out.println(”Total:"+cost);} }5、实验结果（1）输入（2）输出最小生成树的权值为：生成过程：(a)(b)(d)(e)(c)四、实验总结（心得体会、需要注意的问题等）这次实验，使我受益匪浅。

贪心算法实验报告

贪心算法实验报告贪心算法实验报告引言：贪心算法是一种常用的算法设计策略，它通常用于求解最优化问题。

贪心算法的核心思想是在每一步选择中都选择当前最优的解，从而希望最终能够得到全局最优解。

本实验旨在通过实际案例的研究，探索贪心算法的应用和效果。

一、贪心算法的基本原理贪心算法的基本原理是每一步都选择当前最优解，而不考虑整体的最优解。

这种贪婪的选择策略通常是基于局部最优性的假设，即当前的选择对于后续步骤的选择没有影响。

贪心算法的优点是简单高效，但也存在一定的局限性。

二、实验案例：零钱兑换问题在本实验中，我们以零钱兑换问题为例，来说明贪心算法的应用。

问题描述：假设有不同面值的硬币，如1元、5元、10元、50元和100元，现在需要支付给客户x元，如何用最少的硬币数完成支付？解决思路：贪心算法可以通过每次选择当前面值最大的硬币来求解。

具体步骤如下：1. 初始化一个空的硬币集合，用于存放选出的硬币。

2. 从面值最大的硬币开始，如果当前硬币的面值小于等于待支付金额，则将该硬币放入集合中，并将待支付金额减去该硬币的面值。

3. 重复步骤2，直到待支付金额为0。

实验过程：以支付金额为36元为例，我们可以通过贪心算法求解最少硬币数。

首先，面值最大的硬币为100元，但36元不足以支付100元硬币，因此我们选择50元硬币。

此时，剩余待支付金额为36-50=-14元。

接下来，面值最大的硬币为50元，但待支付金额为负数，因此我们选择下一个面值最大的硬币，即10元硬币。

此时，剩余待支付金额为-14-10=-24元。

继续选择10元硬币，剩余待支付金额为-24-10=-34元。

再次选择10元硬币，剩余待支付金额为-34-10=-44元。

最后，选择5元硬币，剩余待支付金额为-44-5=-49元。

由于待支付金额已经为负数，我们无法继续选择硬币。

此时，集合中的硬币数为1个50元和3个10元，总共4个硬币。

实验结果：通过贪心算法，我们得到了36元支付所需的最少硬币数为4个。

算法分析与设计实验二贪心算法

算法分析与设计实验二贪心算法贪心算法是一种基于贪心策略的求解问题的方法，该方法在每一步都采取最优的选择，从而最终得到全局最优解。

本实验将介绍贪心算法的概念、特点以及实际应用。

1.贪心算法的概念和特点贪心算法是一种求解问题的策略，它在每一步都做出局部最优选择，以期望最终得到全局最优解。

它不考虑每一步选择的长远影响，而只关注眼前能得到的最大利益。

贪心算法有以下特点：1.1.子问题的最优解能够推导父问题的最优解：贪心算法解决的问题具有最优子结构，即问题的最优解包含其子问题的最优解。

1.2.贪心选择性质：通过选择当前最优解，可以得到局部最优解。

1.3.无后效性：当前选择的最优解不会对以后的选择产生影响。

2.实际应用2.1.背包问题背包问题是一个经典的优化问题，贪心算法可以用于解决背包问题的一种情况，分数背包问题。

在分数背包问题中，物品可以被分割成任意大小，而不仅仅是0和1两种状态，因此可以通过贪心算法求解。

2.2.最小生成树问题最小生成树问题是求解连通带权图的一种最优生成树的问题。

其中，普里姆算法和克鲁斯卡尔算法就是贪心算法的典型应用。

2.3.哈夫曼编码哈夫曼编码是一种用于对信息进行无损压缩的方法，它可以将出现频率较高的字符用较短的二进制编码表示。

贪心算法可以在构建哈夫曼树的过程中选择出现频率最低的两个字符进行合并。

3.贪心算法的设计步骤3.1.理解问题并找到最优解的子结构。

3.2.根据问题特点设计贪心策略。

3.3.利用贪心策略进行求解，并逐步推导得到全局最优解。

3.4.对求得的解进行检验，确保其满足问题的要求。

4.贪心算法的优缺点4.1.优点：贪心算法简单直观，易于实现和理解；对于一些问题，贪心算法可以得到全局最优解。

4.2.缺点：贪心算法无法保证得到问题的全局最优解；贪心策略的选择可能不唯一综上所述，贪心算法是一种基于贪心策略的求解问题的方法，通过每一步的局部最优选择，期望得到全局最优解。

贪心算法具有明显的优点和缺点，在实际应用中可以有效地解决一些问题。

计算机算法设计与分析-贪心算法

2023/10/8
计算机算法设计与分析
4
树的基本性质
连通无回路的图G称为树。树是点比边多一的连通图，G连通且q=p–1 。树是点比边多一的无回路图：G无回路且q=p–1 树若添条边就有回路：G无回路，但对任意的u,
v∈V(G)，若uvE(G)，则G+uv中恰有一条回路树若减条边就不连通：G连通，但对e∈E(G),
图条出且边权该。重回这较路n小中–的1包n条含–边1e必条1。定边该包（回括在路了实中G现必的中有n体个条现顶不为点是n。e个的这边样顶e就点i。得的令到选T’了择={G）T的+。e一1}棵–ei最。小T’生也成是树G的。生成树。又
cc矛K次不要是这((TTr盾选行保连u’’样))s。≤k择=！证通c做a故(cl权因这的T算(是T)必重为或n，法)否定–+较不者T的1c’有可是小能是条(做e图1以G的保无边法) 的G–n证回构呢：的c最–(这路成在？e最1小1条的n树)保，小生–边。，证c生1成(。必条无e成1树)须边回树≤且使构路c包含(这成e的含i有)n树，前了边–？从提e1e1条而下1。。边依
初始化：Path中仅含有源v。
2023/10/8
计算机算法设计与分析
21
最临近算法中的数据结构
图用连接矩阵W[i][j]给出，即W[i][j]为结点i到结点j的权重。
Path[]记录依次连接的城市，p记录当前到达的最后一个顶点，cost为当前路径长度。
如果节点k已经到达，则arrived[k]=true。
3
最小生成树
设G = (V, E)是一个无向连通带权图，即一个网络。E的每条边(v, w)的权为c[v][w]。

算法分析与设计实验二贪心算法

算法分析与设计实验二贪心算法实验二：贪心算法【实验目的】应用贪心算法求解活动安排问题。

【实验性质】验证性实验。

【实验要求】活动安排问题是可以用贪心算法有效求解的很好的例子。

问题：有n个活动的集合A={1,2,…,n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。

求解：安排尽量多项活动在该场地进行，即求A的最大相容子集。

设待安排的11个活动的开始时间和结束时间按结束时间的升序排列如下： i 1 2 35 3 06 4 57 5 38 6 59 7 6 10 8 8 11 9 8 12 10 2 13 11 12 14 s[i] 1 f[i] 4将此表数据作为实现该算法的测试数据。

【算法思想及采用的数据结构】【程序代码】【运行结果】【算法分析和心得体会】附加题：【实验要求】需要在某个城市的n个居民区之间铺设煤气管道，则在这n个居民区之间只要铺设n-1条管道即可。

假设任意两个居民区之间都可以架设管道，但由于地理环境的不同，所需经费不同。

选择最优的施工方案能使总投资尽可能少，这个问题即为求网的“最小生成树”问题。

参照以下居民区示意图，使得求解算法为：在可能架设的m条管道中选取n-1条，既能连通n-1个居民区，有使总投资达到“最小”。

网可采用邻接矩阵为存储结构，以定点对（i,j）的形式输出最小生成树的边。

D 23.1 675.9 C 41.1 56B A 38.2 441218.2 I 8.7 H 52.5 G 10.5E 98.7 居民区示意图 85F 79应用贪心算法策略，采用普里姆算法或Kruskal算法来求解居民区示意图的最小生成树，采用合适的数据结构。

用C语言或C++语言编写程序代码，选上述居民区示意图中的数据作为测试数据。

并调试输出正确结果。

【算法思想及采用的数据结构】【程序代码】【运行结果】【算法分析和心得体会】感谢您的阅读，祝您生活愉快。

《算法设计与分析》课程实验报告 (贪心算法(一))

《算法设计与分析》课程实验报告实验序号：07实验项目名称：实验8 贪心算法（一）一、实验题目1.删数问题问题描述：键盘输入一个高精度的正整数N（不超过250 位），去掉其中任意k个数字后剩下的数字按原左右次序将组成一个新的非负整数。

编程对给定的N 和k，寻找一种方案使得剩下的数字组成的新数最小。

若输出前有0则舍去2.区间覆盖问题问题描述：设x1,x2,...xn是实轴上的n个点。

用固定长度为k的闭区间覆盖n个点，至少需要多少个这样的固定长度的闭区间？请你设计一个有效的算法解决此问题。

3.会场安排问题问题描述：假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。

设计一个有效的贪心算法进行安排。

（这个问题实际上是著名的图着色问题。

若将每一个活动作为图的一个顶点，不相容活动间用边相连。

使相邻顶点着有不同颜色的最小着色数，相应于要找的最小会场数。

）4.导弹拦截问题问题描述：某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

某天，雷达捕捉到敌国的导弹来袭。

由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

给定导弹依次飞来的高度（雷达给出的高度数据是≤50000的正整数），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

二、实验目的（1）通过实现算法，进一步体会具体问题中的贪心选择性质，从而加强对贪心算法找最优解步骤的理解。

（2）掌握通过迭代求最优的程序实现技巧。

（3）体会将具体问题的原始数据预处理后（特别是以某种次序排序后），常能用贪心求最优解的解决问题方法。

三、实验要求（1）写出题1的最优子结构性质、贪心选择性质及相应的子问题。

（2）给出题1的贪心选择性质的证明。

（3）（选做题）：写出你的算法的贪心选择性质及相应的子问题，并描述算法思想。

算法实验报告贪心

一、实验背景贪心算法是一种在每一步选择中都采取当前状态下最好或最优的选择，从而希望导致结果是全局最好或最优的算法策略。

贪心算法并不保证能获得最优解，但往往能获得较好的近似解。

在许多实际应用中，贪心算法因其简单、高效的特点而被广泛应用。

本实验旨在通过编写贪心算法程序，解决经典的最小生成树问题，并分析贪心算法的优缺点。

二、实验目的1. 理解贪心算法的基本原理和应用场景；2. 掌握贪心算法的编程实现方法；3. 分析贪心算法的优缺点，并尝试改进；4. 比较贪心算法与其他算法在解决最小生成树问题上的性能。

三、实验内容1. 最小生成树问题最小生成树问题是指：给定一个加权无向图，找到一棵树，使得这棵树包含所有顶点，且树的总权值最小。

2. 贪心算法求解最小生成树贪心算法求解最小生成树的方法是：从任意一个顶点开始，每次选择与当前已选顶点距离最近的顶点，将其加入生成树中，直到所有顶点都被包含在生成树中。

3. 算法实现（1）数据结构- 图的表示：邻接矩阵- 顶点集合：V- 边集合：E- 已选顶点集合：selected- 最小生成树集合：mst（2）贪心算法实现```def greedy_mst(graph):V = set(graph.keys()) # 顶点集合selected = set() # 已选顶点集合mst = set() # 最小生成树集合for i in V:selected.add(i)mst.add((i, graph[i]))while len(selected) < len(V):min_edge = Nonefor edge in mst:u, v = edgeif v not in selected and (min_edge is None or graph[u][v] < graph[min_edge[0]][min_edge[1]]):min_edge = edgeselected.add(min_edge[1])mst.add(min_edge)return mst```4. 性能分析为了比较贪心算法与其他算法在解决最小生成树问题上的性能，我们可以采用以下两种算法：（1）Prim算法：从任意一个顶点开始，逐步添加边，直到所有顶点都被包含在生成树中。

算法分析与设计实验三贪心算法

实验三贪心算法实验目的1. 掌握贪心法的基本思想方法；2. 了解适用于用贪心法求解的问题类型，并能设计相应贪心法算法；3. 掌握贪心算法复杂性分析方法分析问题复杂性。

预习与实验要求1. 预习实验指导书及教材的有关内容，掌握贪心法的基本思想；2. 严格按照实验内容进行实验，培养良好的算法设计和编程的习惯；3. 认真听讲，服从安排，独立思考并完成实验。

实验设备与器材硬件：PC机软件：C++或Java等编程环境实验原理有一类问题是要从所有的允许解中求出最优解，其策略之一是“贪心法”，即逐次实施“贪心选择”：在每个选择步骤上做出的选择都是当前状态下最优的。

贪心选择依赖于在此之前所做出的选择，但不依赖于后续步骤所需要的选择，即不依赖于后续待求解子问题。

显然，这种选择方法是局部最优的，但不是从问题求解的整体考虑进行选择，因此不能保证最后所得一定是最优解。

贪心法是求解问题的一种有效方法，所得到的结果如果不是最优的，通常也是近似最优的。

实验内容以下几个问题选做一项：1. 用贪心法实现带有期限作业排序的快速算法应用贪心设计策略来解决操作系统中单机、无资源约束且每个作业可在等量时间内完成的作业调度问题。

假定只能在一台机器上处理N个作业，每个作业均可在单位时间内完成；又假定每个作业i都有一个截止期限di>0（它是整数），当且仅当作业i在它的期限截止以前被完成时，则获得pi的效益。

这个问题的一个可行解是这N个作业的一个子集合J，J中的每个作业都能在各自的截止期限之前完成。

可行解的效益值是J中这些作业的效益之和，即Σp。

具有最大效益值的可行解就是最优解。

2. 实现K元归并树贪心算法两个分别包含n个和m个记录的已分类文件可以在O（n+m）时间内归并在一起而得到一个分类文件。

当要把两个以上的已分类文件归并在一起时，可以通过成对地重复归并已分类的文件来完成。

例如：假定X1,X2,X3,X4是要归并的文件，则可以首先把X1和X2归并成文件Y1，然后将Y1和X3归并成Y2，最后将Y2和X4归并，从而得到想要的分类文件；也可以先把X1和X2归并成Y1，然后将X3和X4归并成Y2，最后归并Y1和Y2而得到想要的分类文件。

贪心算法设计实验报告

A
B
C
D
E
F
G
0
0
0
0
1
0
0
0
对表进行维护（维护后仍同上表，因为还没有两个集合合并）
0
A
B
C
D
E
F
G
0
0
0
0
1
0
0
0
C，选择第二条边 C----E （修改上表）
0
A
B
C
D
E
F
G
0
0
0
0
1
3
0
0
对上表进行维护（任同上表，因为还没有两个集合合并）
0
A
B
C
D
E
F
G
0
0
0
0
1
3
0
0
D，选择第三条边（ D-----F ） (根据条件 DF 两点不再同一集合，改边可选 ) 然后就合并 DF 两点所在的集合 D 的前去是 1，即 A 标记为 0， E 的标记也为 0，合并因为 6>1 所以表修改如下
Edge* selectionsort(Edge *array,int n)// 选择排序（对边按权重由高到低排序） {
int i,j,min,temp; for(i=0;i<n;i++) {
min=i; for(j=i+1;j<n;j++)
if(array[min].weight>array[j].weight) min=j;
在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中
只有一棵树，也即子图中含有

算法设计与分析第4章贪心算法

•
for (i=0;i<n;i++) {
•
if (d[i].w>c) break;
•
x[d[i].i]=1;
•
opt+=d[i].v;
算时间上界为 O（nlogn）。当然，为了证明算法的正确
•
c-=d[i].w;
性，还必须证明背包
•
}
•
if (i<n){
•
x[d[i].i]=c/d[i].w;
问题具有贪心选择性质。
动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。
对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。
14
4.2 贪心算法的基本要素
•
opt+=d[i].w;
•
c -= d[i].w;
•
}
•
return opt;
其中Element类说明为参见本书P115
•}
23
4.3 最优装载
2.贪心选择性质
可以证明最优装载问题具有贪心选择性质。
3.最优子结构性质
最优装载问题具有最优子结构性质。
由最优装载问题的贪心选择性质和最优子结构性质，容易证明算法loading的正确性。
7
4.1 活动安排问题
在下面所给出的解活动安排问题的贪心算法greedySelector :
• public static int greedySelector(int [] s, int [] f, boolean a[])

算法设计与分析---贪心算法实验

《算法设计与分析》实验报告
实验三
报告书
姓名指Βιβλιοθήκη 教师学号日期班级
实验内容
时间限制: 1 s
空间限制: 256000 KB
题目等级 : 钻石 Diamond
题目描述 Description
一条街的一边有几座房子。因为环保原因居民想要在路边种些树。路边的地区被分割成块，并被编号为1…n。每个块的大小为一个单位尺寸并最多可种一裸树。每个居民想在门前种些树并指定了三个号码b，e，t。这三个数表示该居民想在b和e之间最少种t棵树。当然，b≤e，居民必须保证在指定地区不能种多于地区被分割成块数的树，即要求T≤ e-b+1。允许居民想种树的各自区域可以交叉。出于资金短缺的原因，环保部门请你求出能够满足所有居民的要求，需要种树的最少数量。
9
4
1 4 2
4 6 2
8 9 2
3 5 2
样例输出 Sample Output
5
数据范围及提示 Data Size & Hint
【数据规模】
30％的数据满足0＜n ≤1000，0＜h ≤ 500；100%的数据满足n ≤30000，h ≤5000。
时间限制: 1 s
空间限制: 128000 KB
题目等级 : 黄金 Gold
错了以后想了一下，发现本题解法要改一下。首先肯定是按照损失第一降序排序，然后才是时间第二增序排序。但是贪心过程也不能直接数数。样例有一个例子就是损失多的排序后在前面，损失少的排序在后面。看起来不能兼得，但是实际上，前面那个损失大的游戏的时间不是那么急迫，是允许晚一点去执行的。这样却可以兼得。如何解决这个问题？
种树题，要求的是最少的种树的数量。也就是说，如果一个人种了一棵树，为了使得种的树最少，那就要使得这颗树尽量种在大家都想种的区域之中。每一次针对一个要种树的居民来说，如何种树才能使得以后种树的人能够尽力的享受到“我”种的树带来的好处呢？

实验3 贪心算法

淮海工学院计算机工程学院实验报告书课程名：《算法分析与设计》题目：实验3 贪心算法班级：学号：姓名：实验3 贪心算法实验目的和要求（1）了解前缀编码的概念，理解数据压缩的基本方法；（2）掌握最优子结构性质的证明方法；（3）掌握贪心法的设计思想并能熟练运用（4）证明哈夫曼树满足最优子结构性质；（5）设计贪心算法求解哈夫曼编码方案；（6）设计测试数据，写出程序文档。

实验内容设需要编码的字符集为{d 1, d 2, …, dn }，它们出现的频率为{w 1, w 2, …, wn }，应用哈夫曼树构造最短的不等长编码方案。

实验环境Turbo C 或VC++实验学时2学时，必做实验数据结构与算法//构造哈夫曼结构体struct huffman{double weight; //用来存放各个结点的权值int lchild,rchild,parent; //指向双亲、孩子结点的指针 };核心源代码#include<iostream>#include <string>using namespace std;#include <stdio.h>//构造哈夫曼结构体struct huffman{double weight;∑=j i k k aint lchild,rchild,parent;};static int i1=0,i2=0;//选择权值较小的节点int Select(huffman huff[],int i){int min=11000;int min1;for(int k=0;k<i;k++){if(huff[k].weight<min && huff[k].parent==-1){min=huff[k].weight;min1=k;}}huff[min1].parent=1;return min1;}//定义哈夫曼树，并对各个节点进行赋权值void HuffmanTree(huffman huff[],int weight[],int n) {for(int i=0;i<2*n-1;i++){huff[i].lchild=-1;huff[i].parent=-1;huff[i].rchild=-1;}for(int l=0;l<n;l++){huff[l].weight=weight[l];}for(int k=n;k<2*n-1;k++){int i1=Select(huff,k);int i2=Select(huff,k);huff[i1].parent=k;huff[i2].parent=k;huff[k].weight= huff[i1].weight+huff[i2].weight;huff[k].lchild=i1;huff[k].rchild=i2;}}//哈夫曼编码，左0右1void huffmancode(huffman huff[],int n){string s;int j;for(int i=0;i<n;i++){s="";j=i;while(huff[j].parent!=-1){if(huff[huff[j].parent].lchild==j)s=s+"0";else s=s+"1";j=huff[j].parent;}cout<<"第"<<i+1<<"个节点的哈夫曼编码为：";for(int j=s.length();j>=0;j--){cout<<s[j];}cout<<endl;}}void main(){huffman huff[20];int n,w[20];printf("请输入节点的个数:");scanf("%d",&n);for(int i=0;i<n;i++){printf("请输入第%d个节点的权值:",i+1);scanf("%d",&w[i]);}printf("\n");HuffmanTree(huff,w,n);huffmancode(huff,n);}实验结果实验体会本次实验是用贪心法求解哈夫曼编码,其实贪心法和哈夫曼树的原理是一样的,每次将集合中两个权值最小的二叉树合并成一棵新二叉树，每次选择两个权值最小的二叉树时，规定了较小的为左子树。

(算法分析与设计)2.贪心算法

n
wixi
vixi
28.2
31
31.5
...
i1
[算法思路]1).将各物体按单位价值由高到低排序.
2).取价值最高者放入背包.
3).计算背包剩余空间.
4).在剩余物体中取价值最高者放入背包.
若背包剩余容量=0或物体全部装入背包为止
算法设计与分析 > 贪心算法
背包问题的贪心算法
print tour, cost }
*该算法不能求得最优解. 算法的最坏时间复杂性为O(n2)
该问题为NP难问题.
算法设计与分析 > 贪心算法
4.7 多机调度问题
问题:设有n个独立的作业{1, 2, …, n}, 由m台相同的机器进行加工处理. 作业i所需时间为t i. 约定:任何作业可以在任何一台机器上加工处理, 但未完工前不允许中断处理,任何作业不能拆分成更小的子作业。要求给出一种作业调度方案，使所给的n 个作业在尽可能短的时间内由m台机器加工处理完成。该问题为NP完全问题.
A complete tree is filled from the left: • all the leaves are on • the same level or • two adjacent ones and • all nodes at the lowest level are as far to the left as possible.
最大相容活动子集(1, 4, 8, 11), 也可表示为等长n元数组:(1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1)
算法设计与分析 > 贪心算法
活动安排问题贪心算法
template< class Type > void GreedySelector(int n, Type s[ ], Type f[ ], bool A[] ) { A[ 1 ] = true;

贪心算法实验报告

一、实验目的通过本次实验，使学生对贪心算法的概念、基本要素、设计步骤和策略有更深入的理解，掌握贪心算法的原理和应用，并能够运用贪心算法解决实际问题。

二、实验内容本次实验主要涉及以下两个问题：1. 使用贪心算法解决单起点最短路径问题；2. 使用贪心算法解决小船过河问题。

三、实验原理1. 贪心算法贪心算法（又称贪婪算法）是一种在每一步选择中都采取当前最优的选择，从而希望导致结果是全局最优的算法。

贪心算法在每一步只考虑当前的最优解，不保证最终结果是最优的，但很多情况下可以得到最优解。

2. 单起点最短路径问题单起点最短路径问题是指在一个有向无环图中，从某个顶点出发，找到到达其他所有顶点的最短路径。

3. 小船过河问题小船过河问题是指一群人需要划船过河，船只能容纳两个人，过河后需要一人将船开回，问最少需要多久让所有人过河。

四、实验步骤及说明1. 创建图结构，包括顶点数组和边信息。

2. 使用Dijkstra算法求解单起点最短路径问题，得到最短路径和前驱顶点。

3. 使用贪心算法找到两点之间的最短距离，并更新距离和前驱顶点信息。

4. 遍历所有顶点，找到未纳入已找到点集合的距离最小的顶点，并更新其距离和前驱顶点。

5. 最终输出从源顶点到达其余所有点的最短路径。

6. 使用贪心算法解决小船过河问题，按照以下步骤进行：（1）计算所有人过河所需的总时间；（2）计算每次划船往返所需时间；（3）计算剩余人数；（4）重复（2）和（3）步骤，直到所有人过河。

五、实验结果与分析1. 单起点最短路径问题实验中，我们选取了有向无环图G，其中包含6个顶点和8条边。

使用贪心算法和Dijkstra算法求解单起点最短路径问题，得到的实验结果如下：- 贪心算法求解单起点最短路径问题的时间复杂度为O(V^2)，其中V为顶点数；- Dijkstra算法求解单起点最短路径问题的时间复杂度为O(V^2)，其中V为顶点数。

2. 小船过河问题实验中，我们选取了一群人数为10的人过河，船每次只能容纳2人。

贪心算法实现背包问题算法设计与分析实验报告

算法设计与分析实验报告实验名称贪心算法实现背包问题评分实验日期年月日指导教师姓名专业班级学号一.实验要求1. 优化问题有n个输入，而它的解就由这n个输入满足某些事先给定的约束条件的某个子集组成，而把满足约束条件的子集称为该问题的可行解。

可行解一般来说是不唯一的。

那些使目标函数取极值(极大或极小)的可行解，称为最优解。

2.贪心法求优化问题算法思想：在贪心算法中采用逐步构造最优解的方法。

在每个阶段，都作出一个看上去最优的决策（在一定的标准下）。

决策一旦作出，就不可再更改。

作出贪心决策的依据称为贪心准则（greedy criterion）。

3.一般方法1）根据题意，选取一种量度标准。

2）按这种量度标准对这n个输入排序3）依次选择输入量加入部分解中。

如果当前这个输入量的加入，不满足约束条件，则不把此输入加到这部分解中。

procedure GREEDY(A，n) /*贪心法一般控制流程*///A(1：n)包含n个输入//solutions←φ //将解向量solution初始化为空／for i←1 to n dox←SELECT(A)if FEASIBLE(solution，x)then solutions←UNION(solution，x)endifrepeatreturn(solution)end GREEDY4. 实现典型的贪心算法的编程与上机实验，验证算法的时间复杂性函数。

二.实验内容1. 编程实现背包问题贪心算法。

通过具体算法理解如何通过局部最优实现全局最优，并验证算法的时间复杂性。

2.输入5个的图的邻接矩阵，程序加入统计prim算法访问图的节点数和边数的语句。

3.将统计数与复杂性函数所计算比较次数比较，用表格列出比较结果，给出文字分析。

三.程序算法1.背包问题的贪心算法procedure KNAPSACK(P，W，M，X，n)//P(1：n)和W(1；n)分别含有按P(i)/W(i)≥P(i+1)/W(i+1)排序的n件物品的效益值和重量。

算法分析与设计实验二贪心算法

算法分析与设计实验二贪心算法贪心算法（Greedy Algorithm）是一种常用的算法设计方法，其核心思想是在每一步都做出当前情况下最优选择，以期望最终得到全局最优解。

本实验主要介绍贪心算法的原理、应用和分析。

一、贪心算法的原理贪心算法的基本思路是在每一步都做出当前情况下最优选择，并且不考虑当前选择对后续选择的影响。

贪心算法通常采用贪心选择策略和最优子结构两个基本要素。

1.贪心选择策略贪心选择策略是指在每一步都选择当前情况下最优解的策略。

这种策略要求我们能够证明，通过选择当前最优解，可以使得问题的规模减小到原问题的一个子问题，并且该子问题的最优解一定包含在全局最优解中。

2.最优子结构最优子结构是指问题的最优解包含其子问题的最优解。

贪心算法求解问题的过程通常包括两个步骤，选择最优子结构和利用最优子结构得到最优解。

二、贪心算法的应用1.集合覆盖问题集合覆盖问题是指在给定的一组集合中，找出最小的子集合，使得这些子集合的并集包含所有的元素。

贪心算法可以通过每一步选择包含最多未覆盖元素的集合，直到覆盖所有元素为止。

2.挑选活动问题挑选活动问题是指在给定一组活动的起始时间和结束时间，找出最大的相容活动子集合。

贪心算法可以通过每一步选择结束时间最早的活动，之后将该活动与其他相容的活动进行比较，从而得到最大的相容活动子集合。

3.分数背包问题分数背包问题是指在给定一组物品和一个背包容量的情况下，选择部分物品放入背包，使得放入背包的物品总价值最大。

贪心算法可以通过每一步选择单位重量价值最高的物品，直到背包容量不足为止。

三、贪心算法的分析贪心算法通常具有高效性和近似最优性的特点。

由于贪心算法每一步都选择当前最优解，不进行回溯和剪枝的操作，因此贪心算法的时间复杂度较低。

然而，贪心算法并不总能得到问题的最优解，它通常只能得到近似最优解。

贪心算法的近似性证明可以分为两步。

首先，我们需要证明贪心选择策略的正确性，即每一步选择的最优解一定包含在全局最优解中。

算法分析与设计实验报告--贪心法 (2)

例1已知如下图所示的单行线交通网，每弧旁的数字表示通过这条单行线所需要的费用，现在某人要从v1出发，通过这个交通网到v8去，求使总费用最小的旅行路线。
Dijkstra方法的基本思想是从vs出发，逐步地向外探寻最短路。执行过程中，与每个点对应，记录下一个数(称为这个点的标号)，它或者表示从vs到该点的最短路的权(称为P标号)、或者是从vs到该点的最短路的权的上界(称为T标号)，方法的每一步是去修改T标号，并且把某一个具T标号的改变为具P标号的点，从而使G中具P标号的顶点数多一个，这样至多经过n-1(n为图G的顶点数)步，就可以求出从vs到各点的最短路。
if(D[j]>D[min]+graph[min][j]||D[j]==-1)
{D[j]=D[min]+graph[min][j]; //每次迭代求最小值，最后一次即为到源点的最短路径
P[j]=min;
}
}
}
void main()
{instital(R, B, D, P);
theshortestway(R, B, D, P);
using namespace std;
int const ZUSHU = 5;
int Ling[] = {50,20,10,5,1};
int GeShu[ZUSHU];
void ZhaoLing(int n)
{for(int i=0;i<ZUSHU;i++)
{GeShu[i] = n / Ling[i];n = n % Ling[i];}
（1）初始时，S中仅含有源节点。
（2）设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，用数组D[i]记录顶点i当前所对应的最短特殊路径长度。

算法设计与分析实验报告贪心算法

实验三-贪心算法

算法设计与分析中的贪心算法与回溯法

算法分析与设计实验报告 实验5：贪心算法的应用

实验3贪心算法（定稿）

贪心算法 实验报告

算法分析与设计实验二贪心算法

计算机算法设计与分析-贪心算法

算法分析与设计实验二贪心算法

《算法设计与分析》课程实验报告 (贪心算法(一))

算法实验报告贪心

算法分析与设计实验三贪心算法

贪心算法设计实验报告

算法设计与分析第4章贪心算法

算法设计与分析---贪心算法实验

实验3 贪心算法

(算法分析与设计)2.贪心算法

贪心算法实验报告

贪心算法实现背包问题算法设计与分析实验报告

算法分析与设计实验二贪心算法

算法分析与设计实验报告--贪心法 (2)

算法分析与设计实验报告实验5：贪心算法的应用

贪心算法实验报告