物理化学笔记
物理化学课堂笔记
第一章:化学热力学一．绪论。
1.物理化学从化学现象与物理现象之间的联系着手，用物理学的理论和实验方法来研究化学变化，相变化及其P，V，T，物理变化本质。
了解物质的性质与其结构之间的关系规律的科学。
（简而言之就是用物理方法研究化学问题）其它定义：研究物质系统发生 pVT 变化、相变化和化学变化过程的基本原理，主要是平衡规律和速率规律以及与这些变化规律有密切联系的物质结构及性质（宏观性质、微观性质、界面性质和分散性质等）。
2.物理化学的基本组成①化学热力学：任一过程的方向和限度。
（研究化学反应的方向与限度。
例如：合成氨、人造金刚石、人造饼干等等。
）②化学动力学：任一过程的速度和机理（一个过程具体的每个步骤）。
（研究化学速率与反应机理，例H2与O2混合。
鞭炮。
4.电化学、表面化学、胶体化学。
）③结构化学：（研究物质结构与性质之间内在联系。
）3.研究方法①热动力学方法：以大量指点所构成的宏观系统为研究对象，直接从宏观实验和观察为基础，处理问题只关注起始和终止，不考虑宏观物体个别分子的行为不研究宏观系统个别粒子的结构及其变化的具体细节。
②统计力学方法：从宏观到微观的方法研究对象：大量粒子组成的宏观系统出发点：系统中微观粒子的性质（如质量、振动频率、转动惯量等）③量子力学方法：以量子力学为基础，以原子和分子为研究对象，揭示物质性质及其内在关系。
1-1基本性质（Basic Concept）1.系统和环境（System and Surrounding）①System: The materials of interest is defined as system.（研究的物质被定义为系统）Surrounding: The everything else is defined as surrounding.(其余的东西被定义为环境)②系统的分类（Classification of system）根据系统和环境，物质和能量交换方式，系统可分为敞开系统（Open），封闭系统（Closed），隔离系统（isolated）。
物理化学知识点(全)
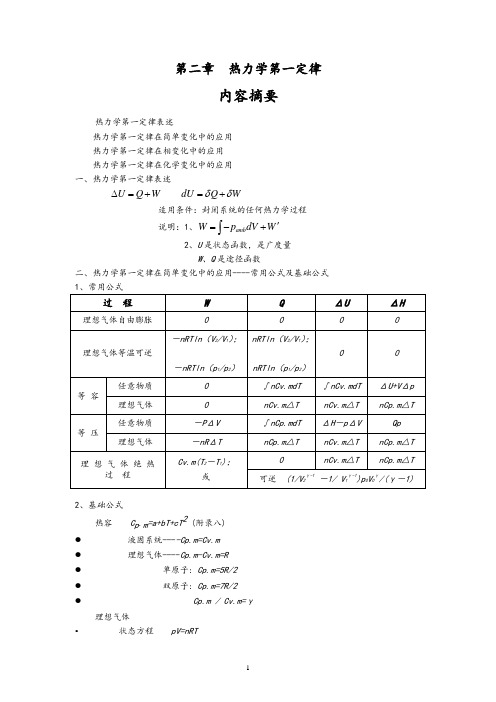
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件：封闭系统的任何热力学过程 说明：1、amb W p dV W '=-+⎰2、U 是状态函数，是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 过 程WQΔUΔH理想气体自由膨胀理想气体等温可逆－nRTln （V 2/V 1）； －nRTln （p 1/p 2） nRTln （V 2/V 1）；nRTln （p 1/p 2）0 0等 容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等 压任意物质－P ΔV ∫nCp.mdT ΔH －p ΔV Qp 理想气体－nR ΔT nCp.m △TnCv.m △T nCp.m △T 理 想 气 体 绝 热过 程 Cv.m(T 2－T 1)；或nCv.m △TnCp.m △T可逆 (1/V 2γ-1－1/ V 1γ-1)p 0V 0γ/(γ－1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、 可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m － p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = －Δ蒸发H m (T)Δ凝固H m (T) = －Δ熔化H m (T) Δ凝华H m (T) = －Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点： 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
物理化学笔记
中科院—中科大《物理化学》考研笔记第一章热力学第一定律二、热力学平衡n 如果体系中各状态函数均不随时间而变化，我们称体系处于热力学平衡状态。
严格意义上的热力学平衡状态应当同时具备三个平衡：2. 机械平衡：n 体系的各部分之间没有不平衡力的存在，即体系各处压力相同。
§2、热力学第一定律n 对于宏观体系而言，能量守恒原理即热力学第一定律。
n 热力学第一定律的表述方法很多，但都是说明一个问题¾能量守恒。
例如：一种表述为:n “第一类永动机不可能存在的”n 不供给能量而可连续不断产生能量的机器叫第一类永动机。
一、热和功热和功产生的条件：n 与体系所进行的状态变化过程相联系，没有状态的变化过程就没有热和功的产生。
符号表示：n 功W：体系对环境作功为正值，反之为负值。
n 热Q：体系吸热Q为正值，反之Q为负值。
二、热力学第一定律的数学表达式DU = Q－W （封闭体系）•如果体系状态只发生一无限小量的变化，则上式可写为：dU = dQ－dW （封闭体系）例1：设有一电热丝浸于水中，通以电流，如果按下列几种情况作为体系，试问DU、Q、W的正、负号或零。
（a）以电热丝为体系；（b）以电热丝和水为体系；（c）以电热丝、水、电源和绝热层为体系；（d）以电热丝、电源为体系。
解答：DU Q W（a）+ －－（b）+ －－（c）0 0 0（d）－－0三、膨胀功（体积功）：Wen 功的概念通常以环境作为参照系来理解，微量体积功dW e可用P外×dV表示：dWe = P外×dV式中P外为环境加在体系上的外压，即环境压力P环。
n 不同过程膨胀功：u （1）向真空膨胀We = P外×DV = 0u （2）体系在恒定外压的情况下膨胀We = P外×DVu （3）在整个膨胀过程中，始终保持外压P外比体系压力P小一个无限小的量dP此时，P外= P－dP，体系的体积功：We =∫V1V2 P外·dV =∫V1V2 （P－dP）dV= ∫V1V2 P dV此处略去二级无限小量dP·dV，数学上是合理的；即可用体系压力P代替P外。
物化笔记总结
第一章 热力学第一定律一、基本概念系统与环境， 状态与状态函数， 广度性质与强度性质， 过程与途径， 热与功， 内能与焓。
二、基本定律热力学第一定律： ΔU=Q+W 。
焦耳实验： ΔU=f(T ) ; ΔH=f(T) 三、基本关系式1、体积功的计算 6W= －p e dV恒外压过程： W= －p e ΔVln V 1 = nRT ln p2可逆过程： W=nRT V p2 12、热效应、焓等容热： Q V =ΔU (封闭系统不作其他功) 等压热： Q p =ΔH (封闭系统不作其他功) 焓的定义： H=U+pV ; dH=dU+d(pV)ϕT2C dT焓与温度的关系： ΔH= T p13、等压热容与等容热容热容定义： C V= (?U?T )V ； C p = ( ??T H )p定压热容与定容热容的关系：C C = nRV热容与温度的关系： 四、第一定律的应用1、理想气体状态变化 C p =a+bT+c’2T等温过程： ΔU =0 ; ΔH=0 ; W=－Q= ϕ p e dV 等容过程： W=0 ; Q =ΔU= ϕ C V dT ; ΔH= ϕ C p dT等压过程： W=－p e ΔV ; Q =ΔH=ϕC pdT ; ΔU= ϕ C VdT可逆绝热过程：Q=0 ; 利用p 1 V 1γ=p 2 V 2γ 求出 T 2,W =ΔU=ϕC VdT ;ΔH= ϕ C p dT不可逆绝热过程： Q=0 ;p1利用 C V (T 2-T 1)=－p e (V 2-V 1)求出 T 2,ϕC dT ϕ C dTW =ΔU= V ;ΔH= p2、相变化可逆相变化： ΔH=Q=n Δ_H ；W ＝－p(V2-V 1)=－pV g =－nRT ; ΔU=Q+W3、热化学物质的标准态；热化学方程式；盖斯定律；标准摩尔生成焓。
摩尔反应热的求算：H 9 (298) = ϖ H 9(B,298)反应热与温度的关系—基尔霍夫定律：[?( H )rm ] =ϖ C (B) B p ,m 。
(仅供参考)物理化学笔记
*注意!由於放射性同位素的化學性質與該元素非放射性同位素基本相同,
因此放射性同位素可在各種化學反應中作為示蹤原子.(物理性質略有不同)
O
O
e.g.酯化作用 CH3-CO18H + CH3CH2OH→CH3COCH2CH3 + H2O18
" 鈷-60 放出的γ輻射可以用作殺死癌細胞 (1998 ASL 1)
相對同位素質量,相對原子質量和相對分子質量 " 相對分子質量 : 無單位 , 摩爾質量 : 有單位 (1999 AL 1)
1.4 摩爾概念 , 摩爾濃度(略)
c摩爾是物質的量的基本單位,這個數量等於 12.000 克同位素 12C 所含的碳原 子個數,相等於 6.022×1023,它是一個常#43; 2I-(aq) + 2H+(aq) → I2(aq) + H2O(l) +Cl-(aq) I2(aq) + 2S2O32-(aq) → 2I-(aq) + S4O62-(aq)
*注意事項! 由於 I2(l)具有揮發性,又有毒,易因揮發造成誤差及造成危險.因此 在實驗時,我們使用 I2(aq),即將 I2 溶於 KI(aq)之中產生的液體-- I3-(aq).
1.5 法拉第和摩爾
法拉第是指一摩爾電子的電量
法拉第電解定律
第一定律 : 電解時,電極析出的生成物質量與通入電量成正比.
第二定律 : 電解時,析出 1 摩爾物質所需的電量與它的離子所帶電荷成正比.
Q 1F
= 96485C,∴一粒電子的電量(電荷) =
96485 6.022 ×1023
= 1.6022 ×10−19 C
1.3 質譜儀 氣化室:氣化固體,電離室:產生陽離子,加速電場,再由偏轉磁場 令正離子偏轉,正離子愈輕,偏轉程度愈大.在特定電場/磁場下,只有特定質量 電荷比的離子才可擊中儀器末端的離子探測器. (2001 AL)
物理化学的知识点总结
物理化学的知识点总结一、热力学1. 热力学基本概念热力学是研究能量转化和传递规律的科学。
热力学的基本概念包括系统、环境、热、功、内能、焓、熵等。
2. 热力学第一定律热力学第一定律描述了能量守恒的原理，即能量可以从一个系统转移到另一个系统，但总能量量不变。
3. 热力学第二定律热力学第二定律描述了能量转化的方向性，熵的增加是自然界中不可逆过程的一个重要特征。
4. 热力学第三定律热力学第三定律表明在绝对零度下熵接近零。
此定律是热力学的一个基本原理，也说明了热力学的某些现象在低温下会呈现出独特的特性。
5. 热力学函数热力学函数是描述系统状态和性质的函数，包括内能、焓、自由能、吉布斯自由能等。
二、化学热力学1. 热力学平衡和热力学过程热力学平衡是指系统各个部分之间没有宏观可观察的能量传输，热力学过程是系统状态发生变化的过程。
2. 能量转化和热力学函数能量转化是热力学过程中的一个重要概念，热力学函数则是描述系统各种状态和性质的函数。
3. 热力学理想气体理想气体是热力学研究中的一个重要模型，它通过状态方程和理想气体定律来描述气体的性质和行为。
4. 热力学方程热力学方程是描述系统热力学性质和行为的方程，包括焓-熵图、温度-熵图、压力-体积图等。
5. 反应焓和反应熵反应焓和反应熵是化学热力学研究中的重要参数，可以用来描述化学反应的热力学过程。
三、物质平衡和相平衡1. 物质平衡物质平衡是研究物质在化学反应和物理过程中的转化和分配规律的一个重要概念。
2. 相平衡相平衡是研究不同相之间的平衡状态和转化规律的一个重要概念，包括固相、液相、气相以及其之间的平衡状态。
3. 物质平衡和相平衡的研究方法物质平衡和相平衡的研究方法包括热力学分析、相平衡曲线的绘制和分析、相平衡图的绘制等。
四、电化学1. 电解质和电解电解质是能在水溶液中发生电离的化合物，电解是将电能转化为化学能或反之的过程。
2. 电化学反应和电势电化学反应是在电化学过程中发生的化学反应，电势是描述电化学系统状态的一个重要参数。
物理化学笔记(附例题)
用分析天平称取 1.2346g K2Cr2O7 基准物质，溶解后转移至 100.0mL 容量
瓶中定容，试计算 c(K2Cr2O7)和 c( 1 6 K 2 Cr2 O 7 ) 解：已知
m(K 2 Cr2 O 7 )＝1.2346g
M ( K 2 Cr2 O 7 )＝ 294.18g mol－1
1 －1 M (1 ＝ 49.03g mol－1 6 K 2 Cr2 O 7 )＝ 294.18g mol 6
表 1－2 类 型 粒子直径/nm ＜1 分散系名称 真溶液 分子、离子 分散系 分散系分类（二） 主要特征 最稳定，扩散快，能透过滤纸及半透 膜，对光散射极弱。 很稳定，扩散慢，能透过滤纸及半透 膜，对光散射极弱，粘度大。 稳定，扩散慢，能透过滤纸，不能透 过半透膜，光散射强。 不稳定，扩散慢，不能透过滤纸及半 透膜，无光散射 多 相 系 统 单 相 系 统
1 1 n( KMnO 4 ) ＝5n（5KMnO4） 5 5
可见，基本单元的选择是任意的，它既可以是实际存在的，也可以根据需要而人为设定。
1mol 物质的质量称为该物质的 “摩尔质量” ，符号为 M，单位为 kg·mol 1，常用单 － － 位为 g·mol 1。例如 1mol 12C 的质量是 0.012kg，则 12C 的摩尔质量 M(C)＝12 g·mol 1。 － 任何分子、原子或离子的摩尔质量，当单位为 g·mol 1 时，数值上等于其相对原子 质量、相对分子质量或离子式量。若用 m 表示 B 物质的质量，则该物质的物质的量为：
（3）NaCl 饱和溶液中
n( NaCl) ＝ 3.173g / 58.44g mol－1 ＝ 0.0542mol n(H 2 O) ＝ (12.003－3.173)g / 18g mol－1 ＝ 0.491mol
物理化学下册笔记
物理化学下册笔记摘要：一、引言二、物理化学基本概念1.物理化学的研究对象2.物理化学的研究方法三、物理化学的核心理论1.热力学1.1 热力学第一定律1.2 热力学第二定律1.3 热力学第三定律2.动力学2.1 反应速率理论2.2 化学反应动力学2.3 物质传递过程动力学四、物理化学的应用领域1.化学工程2.能源与环境3.材料科学4.生命科学五、物理化学的发展趋势与前景一、引言物理化学作为化学的一个重要分支，研究内容涉及物质在各种条件下的性质、组成、结构、变化规律等。
物理化学在理论研究和实际应用中具有广泛的应用价值，为我国科学技术的发展作出了巨大贡献。
本文将简要介绍物理化学的基本概念、核心理论及其应用领域，并展望物理化学的发展趋势与前景。
二、物理化学基本概念物理化学的研究对象是物质，研究内容包括物质的组成、结构、性质、变化规律等。
物理化学的研究方法主要有实验方法和理论方法，其中实验方法包括测量、观察和模拟等；理论方法包括数学建模、逻辑推理和归纳等。
三、物理化学的核心理论物理化学的核心理论包括热力学和动力学。
热力学主要研究物质的宏观热力学性质，如热、功、熵等，以及它们之间的相互关系。
动力学主要研究物质微观粒子在各种条件下的运动、碰撞、反应等过程。
1.热力学热力学是物理化学的一个分支，主要研究物质的宏观热力学性质及其相互关系。
热力学主要包括三个定律：第一定律、第二定律和第三定律。
1.1 热力学第一定律热力学第一定律，又称能量守恒定律，表明能量在不同形式之间可以相互转化，但总能量守恒。
1.2 热力学第二定律热力学第二定律，又称熵增加原理，表明自然过程总是朝着熵增加的方向1.3 热力学第三定律热力学第三定律，又称绝对零度定律，表明在绝对零度时，物质的熵等于零。
2.动力学动力学是物理化学的另一个分支，主要研究物质微观粒子在各种条件下的运动、碰撞、反应等过程。
动力学主要包括反应速率理论、化学反应动力学和物质传递过程动力学。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2004年中科院—中科大《物理化学》考研笔记第一章热力学第一定律二、热力学平衡n 如果体系中各状态函数均不随时间而变化，我们称体系处于热力学平衡状态。
严格意义上的热力学平衡状态应当同时具备三个平衡：2. 机械平衡：n 体系的各部分之间没有不平衡力的存在，即体系各处压力相同。
§2、热力学第一定律n 对于宏观体系而言，能量守恒原理即热力学第一定律。
n 热力学第一定律的表述方法很多，但都是说明一个问题¾能量守恒。
例如：一种表述为:n “第一类永动机不可能存在的”n 不供给能量而可连续不断产生能量的机器叫第一类永动机。
一、热和功热和功产生的条件：n 与体系所进行的状态变化过程相联系，没有状态的变化过程就没有热和功的产生。
符号表示：n 功W：体系对环境作功为正值，反之为负值。
n 热Q：体系吸热Q为正值，反之Q为负值。
二、热力学第一定律的数学表达式DU = Q－W （封闭体系）•如果体系状态只发生一无限小量的变化，则上式可写为：dU = dQ－dW （封闭体系）例1：设有一电热丝浸于水中，通以电流，如果按下列几种情况作为体系，试问DU、Q、W的正、负号或零。
（a）以电热丝为体系；（b）以电热丝和水为体系；（c）以电热丝、水、电源和绝热层为体系；（d）以电热丝、电源为体系。
解答： DU Q W（a） + －－（b） + －－（c） 0 0 0（d）－－ 0三、膨胀功（体积功）：Wen 功的概念通常以环境作为参照系来理解，微量体积功dWe可用P外×dV表示： dWe = P外×dV式中P外为环境加在体系上的外压，即环境压力P环。
n 不同过程膨胀功：u （1）向真空膨胀We = P外×DV = 0u （2）体系在恒定外压的情况下膨胀We = P外× DVu （3）在整个膨胀过程中，始终保持外压P外比体系压力P小一个无限小的量 dP此时，P外= P－dP，体系的体积功：We =∫V1V2 P外·dV =∫V1V2 （P－dP）dV= ∫V1V2 P dV此处略去二级无限小量dP·dV，数学上是合理的；即可用体系压力P代替P外。
n 封闭、理气、恒温可逆膨胀功：We = ∫V1V2 P外·dV = ∫V1V2 P·dV= ∫V1V2 nRT/V dV = nRT∫V1V2 dV/V= nRT ln (V2 /V1) = n RT ln (P1/P2)n *上述三种膨胀过程，体积功不同。
四、可逆相变及其膨胀功对于可逆蒸发过程：We = ò P外dV = ò PdV = P DV若蒸气为理想气体，则：We = P× nRT/P = nRT （n：蒸发液体mol数）*此式也适用于固体的可逆升华。
五、恒容和恒压下的热量（交换）n Qv = ∆U （封闭体系、 Wf =0 、恒容过程）n Q P = ∆H （封闭体系、 Wf =0 、恒压过程）六、理想气体的内能（U）和焓（H）(U/V)T > 0 （实际气体）(U/P)T < 0 （实际气体）( U/V )T = 0 （理想气体）( U/P )T = 0 （理想气体）U = U ( T ) （理想气体）H = H ( T ) （理想气体）七、恒容热容、恒压热容n 恒容热容： CV = dQV / dTn 恒压热容： CP = dQP / dTn 封闭、恒容、无非体积功下： ( dU )v = Cv dTn 封闭、恒压、无非体积功下： (dH)P = Cp dTn C P – C v = nR （理气、无非体积功）n 通常情况下采用的经验公式有以下两种形式:CP, m = a + bT + cT2 + …（CP, m为摩尔恒压热容）CP, m = a + bT +c ¢/ T2 + …P V g = 常数…①TV g-1 = 常数…②T g / P g－1 = 常数…③n 式①②③表示理想气体、绝热可逆过程、dWf = 0时的T，V，P之间的关系； n 这组关系方程式叫做“过程方程”；n 只适合理气绝热可逆过程，这和理气“状态方程”：PV = nRT （适合任何过程的热力学平衡体系）是有区别的。
n 对于不可逆的绝热过程，上述“过程方程”不能适用。
但下式仍然成立：dU = －dW， DU =－W （绝热）dU = －dWe ，DU =－We （绝热, Wf = 0）DU = CV（T2-T1）（理气、绝热、Wf =0）DH = CP（T2-T1）（理气、绝热、Wf =0）九、焦-汤系数n 气体经节流膨胀后温度随压力的变化率即焦-汤系数mJ-T = ( T/P )HmJ-T = 0 ( 理想气体 )n 只有在 mJ-T > 0 时，节流过程才能降温。
§3、热化学一、恒容反应热和恒压反应热Qv = D r U （dV=0，Wf =0）Dr U = ( SU ) 产－( SU ) 反QP = Dr H （dP = 0，Wf =0）Dr H = ( SH ) 产－( SH ) 反n Q p = Q v + Dn RT二、赫斯定律（盖斯定律）1、赫斯定律表述：n 一化学反应不论是一步完成还是分几步完成，其热效应总是相同的，即反应热只与反应的始态和终态有关，而与反应所经历的途径无关。
2、赫斯定律适用条件：n 所涉及的化学步骤都必须在无非体积功（Wf =0）、恒压或恒容条件下（通常恒压）。
3、赫斯定律的意义：n 奠定了整个热化学的基础，使热化学方程能象普通代数一样进行运算，从而可根据已经准确测定的反应热来计算难以测量或不能测量的反应的热效应。
例2、已知下列反应的Dr Hmo（298.15K）（1） CH3COOH（l）+ 2O2（g）® 2CO2（g）+ 2H2O(l)D1H =－208 kcal/mol（2） C（s）+ O2（g）® CO2（g）D2H =－94.0 kcal/mol（3） H2（g）+ 1/2 O2（g）® 2H2O (l)D3H =－68.3 kcal/mol请计算反应:（4） 2C（s）+ 2H2（g）+ O2（g）® CH3COOH（l）D4H = ? (乙酸的生成热)解：反应（4） =（2）×2 +（3）×2 －（1）\ D4H =（－94.0）×2+（－68.3）×2 －（－208）= －116.6 kcal/mol三、生成热（生成焓）n 任意反应的反应热 DrH 等于产物的生成焓（热）减去反应物的生成焓，即： DrH =（SDf H）P－（SDf H）R五、自键焓计算反应热n 键焓：拆散气态化合物中某一类键而生成气态原子所需要的能量平均值。
Dr Hm（298K）= （S e）R－（S e）P六、离子生成焓n 公认：H+（¥，aq）的离子生成焓等于零，可确定其它离子的相对生成焓。
七、溶解热和稀释热（略）§4、反应热与反应温度的关系—基尔霍夫方程n （DrH /T）p = DrC Pn DrH2－DrH1= òDrH1DrH2d(DrH ) = òT1T2 DrCPdTn DrH2-DrH1= Da (T2-T1)+ (Db/2) (T22-T12) + (Dc/3) (T23-T13)n Dr H = DrH0+ò Dr CP dT (DrH0为积分常数)其中：CP, m = a + bT + cT2 + …（CP, m为摩尔恒压热容）CP, m = a + bT +c ¢/ T2 + …Dr C P= ( SCP )P－( SCP )R§5、热力学第一定律的微观说明n 了解： dU = dQ－dＷ中热和功的微观本质：- dＷ = S ni d ein 功来源于能级的改变（升高或降低），但各能级上粒子数不变所引起的能量的变化。
dQ = S ei d nin 热是由于粒子在能级上重新分布而引起的内能的改。
n 能量均分原理Þ 简单小分子的定容摩尔热容：单原子分子：Cv = (3/2)R，双原子分子：Cv = (5/2)R 或 (7/2)R（高温）。
n 例1氧弹中盛有1 mol CO(g)和0.5 mol O2 (g)，起始状态为py，300 K时，反应：n DrHmy = -281.58 kJn CO2的CV,m=(20.96+0.0293T/K) J·K-1·mol-1。
假定气体服从理想气体方程。
计算终态时氧弹的温度及压力。
n [答] 反应恒容绝热进行，n ΔrH(T)=ΔrU(T)+ΔnRTn 故ΔU ==[-280 332.9+0.01465(T/K)2+20.96(T/K)-7606.5]J = 0n 解得T =3775 K,n p = 850 kPan 例2n py,298 K时，乙醇(l)的DcHmy = -1366.9 kJ·mol-1, CO2(g)和H2O(l)的DfHmy 分别为-393.5和-285.9 kJ·mol-1。
n （1）写出乙醇燃烧反应以及CO2(g)，H2O(l)的生成反应的热化学方程式。
n （2）计算C2H5OH(l)的标准摩尔生成热。
n （3）若2.0 mol C2H5OH(l)在氧弹中燃烧，其热效应QV为多少？第二章热力学第二定律§1、热力学第二定律的经典表述A. 克劳修斯（Clausius）表述：不可能把热从低温物体传到高温物体，而不引起其他变化。
B. 开尔文（Kelvin）表述：不可能从单一热源取出热使之完全变为功，而不发生其他变化。
n 或者说：“不可能设计成这样一种机器，这种机器能循环不断地工作，它仅仅从单一热源吸取热量变为功，而没有任何其他变化。
”n “第二类永动机是不可能造成的。
”§2、卡诺循环n 一、卡诺循环各过程热功转化计算二、热机效率（h）n 可逆卡诺机：h = 1－(T1/ T2) （理想或实际气体）n 若可逆卡诺机倒开，制冷机冷冻系数：b = Q¢1/(-W) = T1 / ( T2－T1)n 热机效率：h £ 1－(T1/ T2)n 对可逆卡诺循环，有(Q1/ T1) + (Q2 / T2) = 0§3、熵的概念引入∮(dQr / T ) = 0•任意可逆循环过程ABA的热温商的闭合曲线积分为零。
n 积分值∫AB dQr / T 表示从A® B体系某个状态函数的变化值。
定义这个状态函数为“熵 S ”。
n 当体系的状态由A变到B时，熵函数的变化为：DSA®B = SB-SA = ∫AB dQr / Tn 如果变化无限小，可写成(状态函数的) 微分形式：d S = dQr / T包含两层含义：（1）熵变量DSA®B是状态函数S的变量，只取决于始、终态，熵变量DSA®B 值刚好与A®B 可逆过程的热温商相等，事实上DSA®B大小与实际过程是否可逆无关, 即使A®B是不可逆过程，其熵变量也是此值。