营改增误区系列-6%销项税率的一般纳税人不能抵扣税率为17%的进项税[税务筹划优质文档]
六年级上册计算题可打印
1、直接写得数。
1＋5％＝14％＋35％＝14％÷35％＝2÷25％＝34＋12＝85×0.375＝0.8×25＝0.25÷34＝2、能简算的要简算。
1－14517×16＋5÷1745×58＋45×43－4520×720×99＋7202022×2020202134×58＋14×0.625＋58 57－59×57713÷8＋613×18＋187378÷1773、解方程。
60％x＋25＝40x－10％x＝18x＋30％x＝521、直接写得数。
38＋120％＝1％＋99％＝100×1－10％＝36％＋1.8＝45÷815＝1621×712＝914÷187＝1322×1126＝2、能简算的要简算。
225×67＋33×225＋÷1561413×14－141335×2.8＋2.7×35713÷40×539×1218×112＋13×180.375×1.83＋2.17×383、解方程。
23�÷45＝5423�＋13＝1223�＝8×341、直接写得数。
47×8＝314÷121＝ 1.1×799＝24×56×0＝335×76＝1724×1217＝ 1.8×54＝13％×2552＝2、能简算的要简算。
42×23÷＋54×38＋34÷831645÷114＋58÷17＋58÷2－13×78÷×5812÷247÷12756÷3、解方程。
食品科学中几个常用的法定计量单位
按照《中华人民共和国计量法》、国务院《关于在我国统一实行法定计量单位的命令》所 规定的《中华人民共和国法定计量单位》及《全面推行我国法定计量单位的通知》规定，我 国从 1991 年 1 月起，除个别特殊领域外，不允许再使用非法定计量单位。但目前，在报刊、 杂志上，在科研院所、企事业单位的分析化验中，仍存在大理使用不符合国家规定的量和单 位[93] i 。
食品分析中常用法定计量单位浅议
按照《中华人民共和国计量法》、国务院《关于在我国统一实行法定计量单位的命令》、《中 华人民共和国法定计量单位》及《全面推行我国法定计量单位的通知》规定，我国从 1991 年 1 月起，除个别特殊领域外，禁止使用非法定计量单位。但目前在报刊、杂志上，企事业单位 的分析化验中，仍在大量使用不符合国家规定的量和单位。
＝纳（10-9）。故前面诺贝尔奖例，不应该用毫微微秒，应该用 10-15 s（飞秒，fs）。
2．3 （离心机的）转速：应该用 r/min(转每分)，而不可再用“rpm”；
2．4 粘度单位：用 Pa⋅s（帕斯卡秒），不应再用“泊、厘泊”。
2．5 组合单位的分子、分母一般不同时采用词头。加词头时，一般应加在分子中的第一个
1．我国法定计量单位及其构成
我国《计量法》第三条规定：国家采用国际单位制单位。国际单位制单位和国家选定的
其他计量单位，为国家法定计量单位。国家法定计量单位的名称、符号由国务院公布。非国
家法定计量单位应当废除。废除的办法由国务院制定。
我国法定计量单位的构成， 从《计量法》规定可见，我国法定计量单位由两大部分构成，
� M 作词头符号表示“兆”，m 作词头符号表示“毫”，m 作长度单位符号表示“米”，m(斜 体)可作量的符号用。
聚四氟乙烯材料力学性能参数表(参考模板)
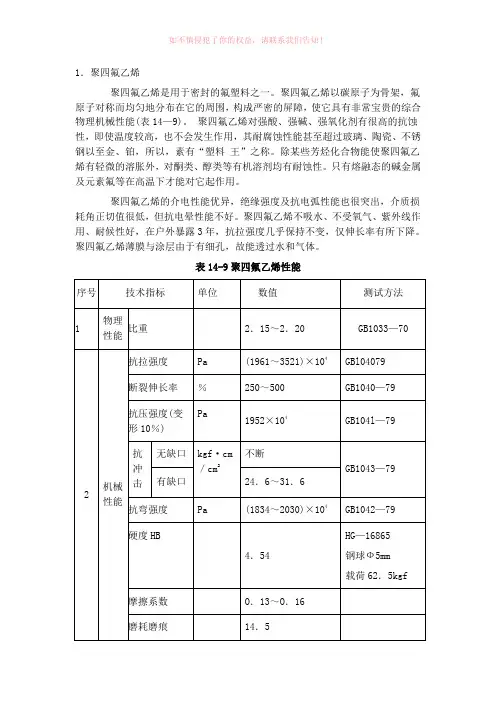
1．聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。
聚四氟乙烯以碳原子为骨架，氟原子对称而均匀地分布在它的周围，构成严密的屏障，使它具有非常宝贵的综合物理机械性能(表14—9)。
聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性，即使温度较高，也不会发生作用，其耐腐蚀性能甚至超过玻璃、陶瓷、不锈钢以至金、铂，所以，素有“塑料王”之称。
除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外，对酮类、醇类等有机溶剂均有耐蚀性。
只有熔融态的碱金属及元素氟等在高温下才能对它起作用。
聚四氟乙烯的介电性能优异，绝缘强度及抗电弧性能也很突出，介质损耗角正切值很低，但抗电晕性能不好。
聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好，在户外暴露3年，抗拉强度几乎保持不变，仅伸长率有所下降。
聚四氟乙烯薄膜与涂层由于有细孔，故能透过水和气体。
表14-9聚四氟乙烯性能聚四氟乙烯在200℃以上，开始极微量的裂解，即使升温到结晶体熔点327℃，仍裂解很少，每小时失重为万分之二。
但加热至400℃以上热裂解速度逐渐加快，产生有毒气体，因此，聚四氟乙烯烧结温度一般控制在375～380℃。
聚四氟乙烯分子间的范德华引力小，容易产生键间滑动，故聚四氟乙烯具有很低的摩擦系数及不粘性，摩擦系数在已知固体材料中是最低的。
聚四氟乙烯的导热系数小，该性能对其成型工艺及应用影响较大。
其不但导热性差，且线膨胀系数较大，加入填充剂可适当降低线膨胀系数。
在负荷下会发生蠕变现象，亦称作“冷流”，加入填充剂可减轻蠕变程度。
聚四氟乙烯可以添加不同的填充剂，选择的填充剂应基本满足下述要求：能耐380℃高温即四氟制品的烧结温度；与接触的介质不发生反应；与四氟树脂有良好的混入性；能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。
常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。
如填充玻璃纤维或石墨，可提高四氟制品的耐磨、耐冷流性，填充MoS2可提高其润滑性，填充青铜、钼、镍、铝、银、钨、铁等，可改善导热性，填充聚酰亚胺或聚苯酯，可提高耐磨性，填充聚苯硫醚后能提高抗蠕变能力，保证尺寸稳定等。
安全气囊系统标定规范
有／无
11
9#
侧面变形壁
50
4X2
有／无
12
10#
侧面柱撞
29
4X4
有／无
13
8#
14
11#
误用＋路试
10 ° 正面 40%偏置固定壁
15
4X4 4X2
有／无 有／有
禁止开启
15
12#
o
o
正面固定壁
24
4X2
有／有
必须开启
16
13#
17
14#
10 英寸对中柱撞 左 30 ° 正面固定壁
32
4X4
有／有
5
5#
碰撞形式 左 30 ° 正面固定壁
碰撞车速 驱动型式 安全带／气襄 气襄开启特性
32
4X4
有／无
6
6#
40%偏置变形壁 CECE R94)
56
4X4
有／无
7
7#
8
2#
9
8#
10
4#
数据 提取 试验
卡车护栏 侧面变形壁 侧面变形壁 侧面变形壁
35
4X2
有／无
15
4X2
有／无
24
4X4
有／无
35
4X4
序号 1 2 3 4 5 6 7 8 9 10 11 12
项目 头部加速度 － 时间图表
胸骨位移 － 时间图表 胸部粘性指数－时间图表
胸部加速度 － 时间图表 大腿骨力 －时间图表 颈部X方向力 －时间图表 颈部Y方向弯矩－ 时间图表 颈部Z方向力 －时间图表 小腿左上胫骨指数－时间图表 小腿左下胫骨指数－时间图表 小腿右上胫骨指数－ 时间图表 小腿右下胫骨指数－时间图表
七年级数学上册期中考试试卷
七年级数学上册期中考试试卷说到数学有很多人都会头痛觉得很难，其实大家只要认真的做题就不会很难的，下面小编就给大家整理一下七年级数学，欢迎大家来学习哦有关七年级数学上册期中联考试卷一、选择题(每题3分，共计36分)1.﹣2的相反数的倒数是( )A.﹣B.﹣2C.D.22.在有理数(﹣1)2、、﹣|﹣2|、(﹣2)3中负数有( )个.A.4B.3C.2D.13.下列说法中正确的是( )A.0既不是整数也不是分数B.整数和分数统称有理数C.一个数的绝对值一定是正数D.绝对值等于本身的数是0和14. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作.根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为 ( )A. B. C. D.5.如图，四个有理数在数轴上的对应点M，P，N，Q，若点M，N表示的有理数互为相反数，则图中表示绝对值最小的数的点是( )A.点MB.点NC.点PD.点Q6.下列各组的两项是同类项的是( )A.3m2n2与3m3n2B.2xy与 yxC.53与a3D.3x2y2与4x2z27.下列计算正确的是( )A.2a+b=2abB.﹣5a2+3a2=﹣2C.3x2 y﹣3xy2=0D.8.下列各组数相等的一组是 ( )A.∣-3∣和-(-3)B. -1-(-4)和-3C. D.9. 下列利用等式的性质错误的是( )A. 由a=b,得到5-2a=5-2bB. 由 ,得到a=bC. 由a=b,得到ac=bcD. 由a=b,得到10.下列说法正确的是( )A.单项式22x3y4的次数9B.x+ 不是多项式C.x3﹣2x2y2+3y2是三次三项式D.单项式的系数是11. 如图,两个天平都平衡,则与2个球体质量相等的正方体的个数为( )A.2B.3C. 4D.512. 如图是一个运算程序的示意图，若开始输入x的值为81，则第2014次输出的结果为( )A.3B.27C.9D.1Ⅱ卷二、填空题(本大题共8小题，每小题3分，共24分)13.近似数2.40×104精确到位.14.若a﹣2b=3，则2a﹣4b﹣5= .15.某商品进价a元，商店将价格提高30%作零售价销售，在销售旺季过后，商店以8折的价格开展促销活动，这时一件商品的售价为16.在多项式中，次数最高的项的系数是 .17.若与是同类项，且它们的和为0，则 .18.已知，，若多项式不含一次项，则m= .19.飞机的无风航速为a千米/时，风速为20千米/时，飞机顺风飞行4小时的行程与飞机逆风飞行3小时的行程相差多少千米? .20.【阅读】计算1+3+32+33+…+3100的值，令M=1+3+32+33+ (3100)则3M=3+32+33+…+3101，因此3M﹣M=3101﹣1，所以，即仿照以上推理计算：1+5+52+53+…+52017的值是 .三、解答题(本题共60分)21、(1)(3分) 计算：(2)(5分)先化简，再求值：，其中a=-2，b=2 .22.(本题满分6分)已知a、b互为相反数，c、d互为倒数，|m|=3，求的值。
PID参数设定方法
PID 参数的设定：是靠经验及工艺的熟悉，参考测量值跟踪与设定值曲线，从而
PID 控制器参数的工程整定,各种调节系统中 P.I.D 参数经验数据以下可参照：
& w * m * W # l 4 x
: E " [ 9 p : S 4 a * [ $ h
1 g # n 4 r ' [ & ] ' N 0 E ' M 7 { 6 e
. y " C 4 Z . t ) b
PID 控制器的参数整定是控制系统设计的核心内容。 它是根据被控过程的特性确 定 PID 控制器的比例系数、 积分时间和微分时间的大小。PID 控制器参数整定的 方法很多，概括起来有两大类：一是理论计算整定法。它主要是依据系统的数学 模型， 经过理论计算确定控制器参数。这种方法所得到的计算数据未必可以直接 用，还必须通过工程实际进行调整和修改。二是工程整定方法，它主要依赖工程 经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被 广泛采用。PID 控制器参数的工程整定方法，主要有临界比例法、反应曲线法和 衰减法。三种方法各有其特点，其共同点都是通过试验，然后按照工程经验公式 对控制器参数进行整定。 但无论采用哪一种方法所得到的控制器参数，都需要在 实际运行中进行最后调整与完善。 现在一般采用的是临界比例法。利用该方法进 行 PID 控制器参数的整定步骤如下：(1)首先预选择一个足够短的采样周期让系
� 使用 Kp 自适应功能有增加系统的快速响应及减少系统振荡
� 微分时间约为积分时间的 1/10----1/5 ，如果系统扰动比较大， 则微分时间应设得小一些
PID 参数是根据控制对象的惯量来确定的。大惯量如：大烘房的温度控制，一般 P 可在 10 以上,I=3-10,D=1 左右。小惯量如：一个小电机带一水泵进行压力闭环控制，一般只用 PI 控 制。P=1-10,I=0.1-1,D=0,这些要在现场调试时进行修正的。 1、让调节器参数积分系数 S0=0，实际微分系数 k=0，控制系统投入闭环运行，由小到大 改变比例系数 S1，让扰动信号作阶跃变化，观察控制过程，直到获得满意的控制过程为止。
粤语(白话)对照大全
比D常用广州话你睇下（给些常用广州话你看一下）乜（mie，0/6)廿（nian，0/9）= <数> 二十卅（sa，0/6）= <数> 三十冇（mao，2/9）= 没有；例如：有冇钱？=有没有钱？甴曱（gad zad ,0/1）= 蟑螂叻（le,0/7）= 很棒；例如：佢啲成绩好叻啵=他的成绩很厉害呵冚（hem，0/1）= 全部？；例如：冚家铲=全家死光光氹（dang，2/9）= 哄；例如：氹你开心=哄你开心攰（gui，5/8）= 累佢（qu，3/8）= 他或她；例如：距系边个？=他是谁？呃（e，2/0）= 骗；例如：呃神骗鬼抦（bing，2/8）= 殴打；例如：我哋去抦果条友=我们去揍那个家伙拎（lin，0/9）= 提、拿拗（ao，0/1）= 矛盾咁（gan，3/4）= 如此、这样；例如：咁啊？=这样啊？咗（zuo，2/2）= 了；例如：食咗饭未？=吃了饭没有？呢（ne，0/1）、哩（li，0/7）= 这；例如：呢啲事=这些事乸（na，0/3）= 雌性；例如：鸡乸=母鸡咦（yi，7/4）、噫(yi，7/6)= 感叹词，啊（表奇怪）；例：咦？咯（lo，0/1）= 语气助词咩（mie，0/3）= 什么；例如：有咩事？=有什么事？咪（mi，1/7）= 不要；例如：咪走~=不要走~系（xi，7/9）= 是；例如：系乜嚟架？=是什么东西来的？*（diao，0/3）= 操唓（che，1/5）= 语气助词，表示鄙夷=切哽（geng，1/1）=当然；例如：哽系=当然是唔（wu，3/9）= 不；例如：唔系=不是俾（bi，3/5）= 给；例如：你俾我啦~=你给我吧~屙（e，3/3）= 排泄；例如：屙尿=拉尿掂（dian，0/6）= 完结或状态佳之意；例如：搞掂=办妥掟（ding，2/5）= 扔啫（ze，2/2）= 语气助词；例如：唔系啫=不是的啰（luo，3/4）= 语气助词/啰嗦念（nian，1/7）= 想；例如：我念咁做唔好嘎？=我想这样做不好吧？啖（dan，2/7）= 口；例如：咬一啖=咬一口啵（bo，3/2）= 语气助词靓（liang，1/4）= 漂亮或表示幼稚；例如：靓仔=帅哥/小子揾（wen，2/0）= 找、挣；例如：揾食=谋生睇（di，3/2）= 看；例如：睇电视=看电视嗟（jue，1/7）= 语气助词，感叹声；例如：嗟~好吧毙咩？=切~很了不起么？嘅（ge，4/6）= 的；例如：你嘅道服呢？=你的道服呢？喔（wo，1/5）= 语气助词嗮（sai，0/8）= 语气助词浪费嗰（go，0/1）= 那；例如：嗰啲=那些嘞（le，0/9）= 语气助词嘢（ge，4/7）= 东西；例如：有嘢睇=有东西看嘈（cao，0/6）= 吵；例如：嘈乜鬼=吵什么东西嘎（ga，0/4）= 语气助词；例如：唔系咁嘎~= 不是这样的~嘥（sai，0/9）= 浪费、错过；例：咁好嘅机会嘥咗=这么好的机会错过了嗻（zhe，2/7）= 语气助词；例如：我先至23嗻=我才23呀~潎（pie，0/9）= 闪，走人撩（liao，0/3）= 挑逗；例如：撩是斗非=若是生非瞓（fen，5/6）= 睡；例如：眼瞓=困顿嬲（niao，0/6）= 生气/一向；例如：我好嬲/必嬲喺咁嘅=我很生气/向来都是这样的嫐（nao,1/8）解释同上嚟（li，9/7）= 来；例如：入嚟=进来囖（lo,0/2）语气助词吤（ge,4/4）例：将啲橙搣开一吤吤（一片片）你（ni,2/0）女嘅“你”惗（nie,4/3）想例：成日惗埋晒啲衰嘢撇（pie,2/2）闪，走人蠹(du,1/7)例：一蠹尿淠( pei,3/8)例：一淠屎氽(tun,0/6)例：一氽水嗌(wo,2/1)嚄(wo,2/3)谂(shen,2/3)晏(yan,5/7) 晏昼（下午）；食晏（吃午饭）嗤(chi ,3/8) 打乞嗤(打喷嚏)啋(cai,1/4) 啋理佢都傻(傻瓜才理他)嚿(huo,3/1)一嚿石头（一块石头）啩(gua,1/9) 你会应承啩？（你会答应吧？）掴(guo,1/4)掴几巴（打几个耳光）揩(kai,0/2) 揩油（占小便宜）嚡(hai ,1/8)粗糙：条脷好嚡（舌头很粗糙）悭(qian,3/2)悭钱（省钱）呷(xia ,1/7)呷醋（吃醋）喐(yu ,11/5) 喐手（动手）唔系"郁"邋(la,1/1)遢(ta ,1/7)踎(meo,0/1) 近读某；即蹲；佢哋习惯踎住食嘅（他们习惯蹲着吃）啱(ngam,0/1) 唔啱着（不合穿）；啱先（刚才）奀(en,0/5) 近读银；奀瘦（瘦弱）闩(shuan, 0/3)读山，闩门（关门）呔(dai,1/4)车呔（车胎）唞(teo,0/1) 早唞（晚安）；唞凉（乘凉）劏(tang,3/1)劏猪（杀猪）嘞lei le（lei) kafl 我识做嘞（我懂得怎样做了）啰luo luo klqy 行啰（走吧）罅xia xia rmhh 读喇；窿罅（洞隙）唥lang lang kuwc 唥钟（响铃）嚟li li ktqi 行嚟行去（走来走去）孻nai nai bvhl 近读拉，子尽为孻；如孻仔拉心肝攋la la rgkm 读赖；攋低条锁匙（漏了带钥匙）躝lan lan khui 近读兰；爬有虫躝嚟躝去；滚躝尸擸la la rvln 读纳；擸擸埋埋一大堆（收刮了不少东西）捩lie lie rynd 近读厉；捩横曲折，捩手掟咗佢（转头就扔掉它）簕le le tafl 刺；玫瑰花好多簕冧min min pssu 撞冧（撞倒）；花冧（花蕾）；好冧（好甜蜜）笠li li tuf 笠衫；执笠（破产）邋遢la ta la ta vlqp jnpd 邋遢（肮脏）褛lv lv puov 乌蝇褛马尾——一拍两散脷lei li（lei) etjh 猪脷（猪舌头）叻le le kln 你真系叻（你真能干）僆lian lian wlph 僆仔（细路仔），看不起时用，非写为靓仔摙lian lian rlph 近读连；摙死你（卡死你）靓liang liang gemq 靓女（美女）；心情好靓（心情很好）拎lin lin rwyc 拎畀我（拿给我）鹩哥liao liao dujg 即八哥攞luo luo rlxy 攞钱（取钱）碌lu lu dviy 一碌木睩lu lu hviy 睩大眼（争大眼）渌lu lu iviy 渌下筷子（烫一下筷子）辘lu lu lynx 车辘（车轮）挛luan luan yorj 挛毛（曲头发）捋luo luo refy 读劣；捋高衫袖M开头唔wu wu kgkg 唔紧要（不要紧）孖ma ma bbg 孖仔（孪生儿子）溦mei mei imgt 雨溦溦（小雨），非写为微嫲ma ma vyss 祖母，习惯上较多称阿嫲擘bo bo nkur 读ma:k；擘大个口（张大个口）蜢meng meng jblg 蝗虫掹meng meng rblg 拉，拽：掹衫尾（拽着衣服下摆）咪mi mi koy 你咪理（你别管）唛ma ma（mai) kgty 商标（唛头）；一唛米（一筒米）癦me me ulff 即痣炆wen wen oyy 炆就是普通话的焖抆wen wen ryy 近读吻；抆屎（擦屁股）乜mie mie（nie) nnv 乜名？（什么名？）踎? meo khgk 近读某；即蹲；佢哋习惯踎住食嘅（他们习惯蹲着吃）咩mie mie kudh 你唔知道咩？（你不知道吗？）孭me mie（me) bmy 读咩；孭仔（背孩子）屘man man ntfb 屘近读尾；屘二（倒数第二眯mi mi hoy 眯埋眼（合上眼）搣mie mie rdgt 近读灭；搣到好痛（捏得好痛）篾mie mie tldt 竹篾（竹子剖成的长条薄片）嚤mo mo kysr 缓慢；佢（他）行得好嚤。
2023年甘肃省兰州市中考数学真题(解析版)
2023年兰州市初中学业水平考试数 学注意事项：1．全卷共120分，考试时间120分钟．2．考生必须将姓名、准考证号、考场号、座位号等个人信息填（涂）写在答题卡上．3．考生务必将答案直接填（涂）写在答题卡的相应位置上．一、选择题（本大题共12小题，每小题3分，共36分）1. －5的相反数是( ) A. 15− B. 15 C. 5 D. -5【答案】C【解析】【分析】根据相反数的定义解答即可�【详解】-5的相反数是5�故选C �【点睛】本题考查了相反数，熟记相反数的定义：只有符号不同的两个数互为相反数是关键�2. 如图，直线AB 与CD 相交于点O ，则BOD ∠=（ ）A. 40°B. 50°C. 55°D. 60°【答案】B【解析】【分析】利用对顶角相等得到BOD AOC ∠=∠，即可求解．【详解】解：读取量角器可知：50AOC ∠=°，∴50BOD AOC ∠=∠=°，故选：B ．【点睛】本题考查了对顶角相等，量角器读数，是基础题．3. 计算：255a a a −=−（ ） A. 5a −B. 5a +C. 5D. a【答案】D【解析】【分析】分子分解因式，再约分得到结果． 【详解】解：255a a a −− ()55a a a −=−a =，故选：D ．【点睛】本题考查了约分，掌握提公因式法分解因式是解题的关键．4. 如图1是我国古建筑墙上采用的八角形空窗，其轮廓是一个正八边形，窗外之境如同镶嵌于一个画框之中．如图2是八角形空窗的示意图，它的一个外角1∠=（ ）A. 45°B. 60°C. 110°D. 135°【答案】A【解析】 【分析】由正八边形的外角和为360°，结合正八边形的每一个外角都相等，再列式计算即可．【详解】解：∵正八边形的外角和为360°，∴3601=458°∠=°， 故选A 【点睛】本题考查的是正多边形的外角问题，熟记多边形的外角和为360°是解本题的关键． 5. 方程213x =+的解是（ ）A. 1x =B. =1x −C. 5x =D. 5x =−【答案】A【解析】 【分析】分式方程去分母转化为整式方程，求出整式方程解得到x 的值，经检验即可得解．【详解】解：去分母得：23x =+，解得=1x −，经检验=1x −是分式方程的解．故选：A ．【点睛】本题考查了解分式方程，熟练掌握解分式方程的方法是解题的关键．6. 如图1是一段弯管，弯管的部分外轮廓线如图2所示是一条圆弧 AB ，圆弧的半径20cm OA =，圆心角90AOB ∠=°，则»=AB （ ）A. 20cm πB. 10cm πC. 5cm πD. 2cm π【答案】B【解析】 【分析】根据弧长公式求解即可．【详解】解：弧的半径20cm OA =，圆心角90AOB ∠=°，∴»902010180AB ππ×==， 故选：B ．【点睛】题目主要考查弧长公式，熟练掌握运用弧长公式是解题关键．7. 已知二次函数()2323y x =−−−，下列说法正确的是（ ） A. 对称轴为2x =−B. 顶点坐标为()2,3C. 函数的最大值是－3D. 函数的最小值是－3【答案】C【解析】 【分析】根据二次函数的图象及性质进行判断即可．的【详解】二次函数()2323y x =−−−的对称轴为2x =，顶点坐标为()2,3− ∵30−<∴二次函数图象开口向下，函数有最大值，为=3y − ∴A 、B 、D 选项错误，C 选项正确故选：C【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数图象和性质是解题的关键．8. 关于x 的一元二次方程20x bx c ++=有两个相等的实数根，则()2212b c −+=（ ） A. －2B. 2C. －4D. 4【答案】A【解析】 【分析】由一元二次方程根的情况可得240b c −=，再代入式子即可求解．【详解】∵关于x 的一元二次方程20x bx c ++=有两个相等的实数根∴240b c ∆=−=∴()2221242022b c b c −+=−−=−=−， 故选：A .【点睛】本题考查一元二次方程根的判别式，熟练掌握一元二次方程根的判别式是解题的关键．9. 2022年我国新能源汽车销量持续增长，全年销量约为572.6万辆，同比增长91.7%，连续8年位居全球第一．下面的统计图反映了2021年、2022年新能源汽车月度销量及同比增长速度的情况．（2022年同比增长速度20222021100%2021−×年当月销量年当月销量年当月销量）根据统计图提供的信息，下列推断不合理的是（ ）A. 2021年新能源汽车月度销量最高是12月份，超过40万辆B. 2022年新能源汽车月度销量超过50万辆的月份有6个C. 相对于2021年，2022年新能源汽车同比增长速度最快的是2月份，达到了181.1%D. 相对于2021年，2022年从5月份开始新能源汽车同比增长速度持续降低【答案】D【解析】【分析】根据折线图逐项分析即可得出答案．【详解】解：A、2021年新能源汽车月度销量最高是12月份，超过40万辆，推断合理，本选项不符合题意；B、2022年新能源汽车月度销量超过50万辆的月份有6个，推断合理，本选项不符合题意；C、相对于2021年，2022年新能源汽车同比增长速度最快的是2月份，达到了181.1%，推断合理，本选项不符合题意；D、相对于2021年，2022年从6月份开始新能源汽车同比增长速度持续降低，原说法推断不合理，本选项符合题意；故选：D．【点睛】此题考查了折线统计图，从折线统计图中获取数据做出分析，正确识别图中的数据是解题的关键．10. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法．如《淮南子天文训》中记载：“正朝夕：先树一表东方；操一表却去前表十步，以参望日始出北廉．日直入，又树一表于东方，因西方之表，以参望日方入北康．则定东方两表之中与西方之表，则东西也．”如图，用几何语言叙述作图方法：已知直线a和直线外一定点O，过点O作直线与a平行．（1）以O为圆心，单位长为半径作圆，交直线a于点M，N ；（2）分别在MO 的延长线及ON 上取点A ，B ，使OA OB =；（3）连接AB ，取其中点C ，过O ，C 两点确定直线b ，则直线a b ∥．按以上作图顺序，若35MNO ∠=°，则AOC ∠=（ ）A 35°B. 30°C. 25°D. 20°【答案】A【解析】 【分析】证明35NMO MNO ∠=∠=°，可得23570AOB ∠=×°=°，结合OA OB =，C 为AB 的中点，可得35AOC BOC ∠=∠=°．【详解】解：∵35MNO ∠=°，MO NO =，∴35NMO MNO ∠=∠=°，∴23570AOB ∠=×°=°，∵OA OB =，C 为AB 的中点，∴35AOC BOC ∠=∠=°，故选A ．【点睛】本题考查的是圆的基本性质，等腰三角形的性质，平行线的判定，三角形的外角的性质，熟记等腰三角形的性质是解本题的关键．11. 一次函数1y kx =−的函数值y 随x 的增大而减小，当2x =时，y 的值可以是（ ） A. 2B. 1C. －1D. －2【答案】D【解析】 【分析】根据一次函数的增减性可得k 的取值范围，再把2x =代入函数1y kx =−，从而判断函数值y 的取值．【详解】∵一次函数1y kx =−函数值y 随x 的增大而减小 ∴0k <∴当2x =时，211yk =−<−.的故选：D【点睛】本题考查一次函数的性质，不等式的性质，熟悉一次函数的性质是解题的关键．12. 如图，在矩形ABCD 中，点E 为BA 延长线上一点，F 为CE 的中点，以B 为圆心，BF 长为半径的圆弧过AD 与CE 的交点G ，连接BG ．若4AB =，10CE =，则AG =（ ）A. 2B. 2.5C. 3D. 3.5【答案】C【解析】 【分析】利用直角三角形斜边中线的性质求得5BG BF ==，在Rt ABG △中，利用勾股定理即可求解.【详解】解：∵矩形ABCD 中，∴90ABC BAC ∠=∠=°，∵F 为CE 的中点，10CE =， ∴152BG BF CE ===，在Rt ABG △中，3AG，故选：C. 【点睛】本题考查了矩形的性质，直角三角形斜边中线的性质，勾股定理，掌握“直角三角形斜边中线的长等于斜边的一半”是解题的关键.二、填空题（本大题共4小题，每小题3分，共12分）13. 因式分解：2225x y −=______． 【答案】()()55x y x y +−【解析】【分析】直接利用平方差分解即可．【详解】解：()()222555x y x y x y −=+−． 故答案为：()()55x y x y +−．【点睛】本题考查因式分解，解题的关键是熟练掌握平方差公式．14. 如图，在ABCD Y 中，BD CD =，AE BD ⊥于点E ，若70C ∠=°，则BAE ∠=______°．【答案】50【解析】【分析】证明70DBC C ∠=∠=°，18027040BDC∠=°−×°=°，由AB CD ∥，可得40ABE BDC ∠=∠=°，结合AE BD ⊥，可得904050BAE ∠=°−°=°．【详解】解：∵BD CD =，70C ∠=°，∴70DBC C ∠=∠=°，18027040BDC∠=°−×°=°， ∵ABCD Y ，∴AB CD ∥，∴40ABE BDC ∠=∠=°，∵AE BD ⊥，∴904050BAE ∠=°−°=°；故答案为：50【点睛】本题考查的是等腰三角形的性质，平行四边形的性质，三角形的内角和定理的应用，熟记基本几何图形的性质是解本题的关键．15. 如图，将面积为7的正方形OABC 和面积为9的正方形ODEF 分别绕原点O 顺时针旋转，使OA ，OD 落在数轴上，点A ，D 在数轴上对应的数字分别为a ，b ，则b a −=______．【答案】3−【解析】【分析】分别求出两个正方形的边长，从而得到a ，b 的值，代入计算即可．【详解】∵正方形OABC 的面积为7，正方形ODEF 的面积为9OD=∴OA=，3b=即a=3b a−=∴3故答案为：3【点睛】本题考查算术平方根的意义，在数轴上表示实数，正确求出算术平方根是解题的关键．16. 某学习小组做抛掷一枚瓶盖的实验，整理的实验数据如下表：累计抛50 100 200 300 500 1000 2000 3000 5000 掷次数盖面朝28 54 106 158 264 527 1056 1587 2850 上次数盖面朝0.56000.54000.53000.52670.52800.52700.52800.52900.5300上频率下面有三个推断：①通过上述实验的结果，可以推断这枚瓶盖有很大的可能性不是质地均匀的；②第2000次实验的结果一定是“盖面朝上”；③随着实验次数的增大，“盖面朝上”的概率接近0.53．其中正确的是______．（填序号）【答案】①③【解析】【分析】根据表中数据及频率估计概率依次判断即可．【详解】解：①通过上述实验的结果，发现盖面朝上的次数多与累计次数的一半，可以推断这枚瓶盖有很大的可能性不是质地均匀的，故正确；②实验是随机的，第2000次实验的结果不一定是“盖面朝上”，故错误；③随着实验次数的增大，“盖面朝上”的概率接近0.53����．故答案为：①③．【点睛】题目主要考查频率估计概率，结合表中数据求解是解题关键．三、解答题（本大题共12小题，共72分）17.【解析】【分析】根据二次根式乘法，加减法运算法则计算即可．【详解】解：原式＝−【点睛】本题考查了二次根式的混合运算，熟练掌握二次根式的化简方法是解题的关键．18. 计算：()()()2234x y x y y y +−−−．【答案】23x y −【解析】【分析】先计算平方差公式及单项式乘以多项式，然后计算加减法即可．【详解】解：()()()2234x y x y y y +−−−222=434x y y y −−+23x y =−．【点睛】题目主要考查整式的乘法运算及加减运算，熟练掌握运算法则是解题关键．19. 解不等式组：312(1)223x x x x −>+ + >− ． 【答案】34x <<【解析】【分析】分别解不等式组中的两个不等式，再取两个不等式的解集的公共部分即可． 【详解】解：312(1)223x x x x −>+ +>−①②， 由①得：32>21x x −+，解得：>3x ，由②得：2>36x x +−，解得：4x <，∴不等式组的解集为：34x <<．【点睛】本题考查的是一元一次不等式组是解法，掌握解一元一次不等式组的方法与步骤是解本题的关键．20. 如图，反比例函数()0ky x x=<与一次函数2y x m =−+的图象交于点()1,4A −，BC y ⊥轴于点D ，分别交反比例函数与一次函数的图象于点B ，C ．（1）求反比例函数ky x=与一次函数2y x m =−+的表达式； （2）当1OD =时，求线段BC 的长． 【答案】（1）反比例函数的表达式为4y x=−；一次函数的表达式为22y x =−+； （2）142BC =． 【解析】【分析】（1）利用待定系数法即可求解；（2）先求得直线BC 的表达式为1y =，再分别求得B C 、的坐标，据此即可求解． 【小问1详解】解：∵反比例函数()0ky x x=<的图象经过点()1,4A −， ∴144k =−×=−，∴反比例函数的表达式为4y x=−； ∵一次函数2y x m =−+的图象经过点()1,4A −， ∴()421m =−×−+， ∴2m =，∴一次函数的表达式为22y x =−+； 【小问2详解】 解：∵1OD =，∴()01D ，，∴直线BC 的表达式为1y =， ∵1y =时，14x=−， 解得4x =−，则()41B −，， ∵1y =时，122x =−+， 解得12x =，则112C，， ∴()114422BC =−−=． 【点睛】本题考查一次函数、反比例函数图象上点的坐标特征，待定系数法是求函数解析式的基本方法． 21. 综合与实践问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9：“平分一个已知角．”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA 和OB 上分别取点C 和D ，使得OC OD =，连接CD ，以CD 为边作等边三角形CDE ，则OE 就是AOB ∠的平分线．请写出OE 平分AOB ∠的依据：____________； 类比迁移：（2）小明根据以上信息研究发现：CDE 不一定必须是等边三角形，只需CE DE =即可．他查阅资料：我国古代已经用角尺平分任意角．做法如下：如图3，在AOB ∠的边OA ，OB 上分别取OM ON =，移动角尺，使角尺两边相同刻度分别与点M ，N 重合，则过角尺顶点C 的射线OC 是AOB ∠的平分线，请说明此做法的理由； 拓展实践：（3）小明将研究应用于实践．如图4，校园的两条小路AB 和AC ，汇聚形成了一个岔路口A ，现在学校要在两条小路之间安装一盏路灯E ，使得路灯照亮两条小路（两条小路一样亮），并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等．试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规．．．．．．．．．．在对应的示意图5中作出路灯E 的位置．（保留作图痕迹，不写作法）【答案】（1）SSS ；（2）证明见解析；（3）作图见解析； 【解析】【分析】（1）先证明()SSS OCE ODE ≌，可得AOE BOE ∠=∠，从而可得答案；（2）先证明()SSS OCM OCN ≌，可得AOC BOC ∠=∠，可得OC 是AOB ∠的角平分线； （3）先作BAC ∠的角平分线，再在角平分线上截取AE AD =即可． 【详解】解：（1）∵OC OD =，CE DE =，DE DE =， ∴()SSS OCE ODE ≌， ∴AOE BOE ∠=∠， ∴OE 是AOB ∠的角平分线； 故答案为：SSS（2）∵OM ON =，CM CN =，OC OC =， ∴()SSS OCM OCN ≌， ∴AOC BOC ∠=∠， ∴OC 是AOB ∠的角平分线； （3）如图，点E 即为所求作的点；．【点睛】本题考查的是全等三角形的判定与性质，角平分线的定义与角平分线的性质，作已知角的角平分线，理解题意，熟练的作角的平分线是解本题的关键．22. 如图1是我国第一个以“龙”为主题的主题公园——“兰州龙源”．“兰州龙源”的“龙”字主题雕塑以紫铜铸造，如巨龙腾空，气势如虹，屹立在黄河北岸．某数学兴趣小组开展了测量“龙”字雕塑CD 高度的实践活动．具体过程如下：如图2，“龙”字雕塑CD 位于垂直地面的基座BC 上，在平行于水平地面的A 处测得38BAC ∠=°、53BAD ∠=°，18m AB =．求“龙”字雕塑CD 的高度．（B ，C ，D 三点共线，BD AB ⊥．结果精确到0.1m ）（参考数据：sin 380.62°≈，cos380.79°≈，tan 380.78°≈，sin 530.80°≈，cos530.60°≈，tan 53 1.33°≈）【答案】“龙”字雕塑CD 的高度为9.9m ． 【解析】【分析】在Rt ABC △和Rt △ABD 中，分别求得BC 和BD 的长，据此求解即可. 【详解】解：在Rt ABC △中，18m AB =，38BAC ∠=°，∴()tan 380.781814.04m BC AB =°≈×=， 在Rt △ABD 中，18m AB =，53BAD ∠=°，∴()tan 53 1.331823.94m BD AB =°≈×=， ∴()23.9414.049.9m CD BD BC =−=−=, 答：“龙”字雕塑CD 的高度为9.9m ．【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．23. 一名运动员在10m 高的跳台进行跳水，身体（看成一点）在空中的运动轨迹是一条抛物线，运动员离水面OB 的高度()m y 与离起跳点A 的水平距离()m x 之间的函数关系如图所示，运动员离起跳点A 的水平距离为1m 时达到最高点，当运动员离起跳点A 的水平距离为3m 时离水面的距离为7m ．（1）求y 关于x 的函数表达式；（2）求运动员从起跳点到入水点的水平距离OB 的长． 【答案】（1）y 关于x 的函数表达式为2210y x x =−++； （2）运动员从起跳点到入水点的水平距离OB的长为(1m +． 【解析】【分析】（1）由题意得抛物线的对称轴为1x =，经过点()010，，()37，，利用待定系数法即可求解； （2）令0y =，解方程即可求解． 【小问1详解】解：由题意得抛物线的对称轴为1x =，经过点()010，，()37，， 设抛物线的表达式为2y ax bx c ++，∴1210937ba c abc −= = ++=，解得1210a b c =− = = ， ∴y 关于x 的函数表达式为2210y x x =−++； 【小问2详解】解：令0y =，则22100x x −++=，解得1x =±， ∴运动员从起跳点到入水点的水平距离OB的长为(1m ．【点睛】本题考查了二次函数在实际问题中的应用，数形结合并熟练掌握运用待定系数法求抛物线的解析式是解题的关键．24. 如图，矩形ABCD 的对角线AC 与BD 相交于点O ，CD OE ∥，直线CE 是线段OD 的垂直平分线，CE 分别交OD AD ，于点F ，G ，连接DE ．（1）判断四边形OCDE 的形状，并说明理由； （2）当4CD =时，求EG 的长．【答案】（1）四边形OCDE 是菱形，理由见解析 （2）EG =． 【解析】【分析】（1）证明COD △和EOD △是等边三角形，即可推出四边形OCDE 是菱形；（2）利用含30度角的直角三角形的性质以及勾股定理求得DF 和CF的长，利用菱形的性质得到EF CF ==，在Rt CGF △中，解直角三角形求得GF 的长，据此求解即可．【小问1详解】证明：四边形OCDE 是菱形，理由如下， ∵矩形ABCD 的对角线AC 与BD 相交于点O ，∴1122OCOD AC BD ===， ∵直线CE 是线段OD 的垂直平分线， ∴CO CD =，EO ED =，∴CO CD OD ==，即COD △是等边三角形，∴60OCD DCO DOC ∠=∠=∠=°，1302OCF DCF OCD ∠=∠=∠=°， ∵CD OE ∥，∴60EOD EDO CDO ∠=∠=∠=°， ∴EOD △等边三角形， ∴CO CD EO ED ===， ∴四边形OCDE 是菱形；是【小问2详解】解：∵直线CE 是线段OD 的垂直平分线，且30DCF ∠=°， ∴122DF CD ==，CF =，由（1）得四边形OCDE 是菱形，∴EF CF ==，在Rt DGF 中，9030GDF ODC ∠=°−∠=°，∴tan 302GF DF =°=，∴EG EF GF =−． 【点睛】本题考查了菱形判定和性质，等边三角形的判定与性质，解直角三角形，线段垂直平分线的性质，解答本题的关键是明确题意，找出所求问题需要的条件．25. 某校八年级共有男生300人，为了解该年级男生排球垫球成绩和掷实心球成绩的情况，从中随机抽取40名男生进行测试，对数据进行整理、描述和分析，下面是给出的部分信息．信息一：排球垫球成绩如下图所示（成绩用x 表示，分成六组：A ． 10x <；B ． 1015x ≤<；C ． 1520x ≤<；D ． 2025x ≤<；E ． 2530x ≤<；F ． 30x ≤）．信息二：排球垫球成绩在D ． 2025x ≤<这一组的是： 20，20，21，21，21，22，22，23，24，24信息三：掷实心球成绩（成绩用y 表示，单位：米）的人数（频数）分布表如下： 分组 6.0y < 6.0 6.8y ≤< 6.87.6y ≤< 7.68.4y ≤< 8.49.2y ≤< 9.2y ≤人数2m10962信息四：这次抽样测试中6名男生的两项成绩的部分数据如下：学生学生1 学生2 学生3 学生4 学生5 学生6的排球垫球 26 25 23 22 22 15 掷实心球▲7．87．8▲8．89．2根据以上信息，回答下列问题： （1）填空：m =______；（2）下列结论正确的是_____；（填序号）①排球垫球成绩超过10个的人数占抽取人数的百分比低于60%； ②掷实心球成绩的中位数记为n ，则6.87.6n ≤<；③若排球垫球成绩达到22个及以上时，成绩记为优秀．如果信息四中6名男生的两项成绩恰好为优秀的有4名，那么学生3掷实心球的成绩是优秀．（3）若排球垫球成绩达到22个及以上时，成绩记为优秀，请估计全年级男生排球垫球成绩达到优秀的人数．【答案】（1）11 （2）②③ （3）75人 【解析】【分析】（1）由总人数减去各小组已知人数即可得到答案；（2）由排球垫球成绩超过10个的人数除以总人数可判断①，由中位数的含义可判断②，分三种情况进行分析讨论可判断③，从而可得到答案；（3）由样本的百分率乘以总人数即可得到答案． 【小问1详解】解：由题意可得：4021096211m −−−−−； 【小问2详解】①排球垫球成绩超过10个的人数占抽取人数的百分比为3690%40=，故①不符合题意； ②∵掷实心球成绩排在第20个，第21个数据落在6.87.6y ≤<这一组， ∴掷实心球成绩的中位数记为n ，则6.87.6n ≤<；故②符合题意； ③由排球垫球成绩达到22个及以上时，成绩记为优秀．∴从这点出发可得：学生1，学生2，学生3，学生4，学生5为优秀， ∵信息四中6名男生的两项成绩恰好为优秀的有4名， ∴若学生1为优秀，则学生4不为优秀，可得学生3优秀； 若学生4为优秀，学生1不为优秀，可得学生3优秀；学生1，学生4不可能同时为优秀，∴学生3掷实心球的成绩必为优秀，故③符合题意； 故答案为：②③ 【小问3详解】排球垫球成绩达到22个及以上时，成绩记为优秀，估计全年级男生排球垫球成绩达到优秀的人数为103007540×=（人）． 【点睛】本题考查的是从频数分布表，统计表中获取信息，利用样本估计总体，熟练的从频数分布表与统计表中获取互相关联的信息是解本题的关键．26. 如图，ABC 内接于O ，AB 是O 的直径， BCBD =，DE AC ⊥于点E ，DE 交BF 于点F ，交AB 于点G ，2BOD F ∠=∠，连接BD ．（1）求证：BF 是O 的切线； （2）判断DGB 的形状，并说明理由； （3）当2BD =时，求FG 的长．【答案】（1）见解析 （2）DGB 是等腰三角形，理由见解析 （3）4FG = 【解析】【分析】（1）连接CO ，根据圆周角定理得出2BOD BOC BAC ∠=∠=∠，根据已知得出F BAC ∠=∠，根据DEAC ⊥得出90AEG ∠=°，进而根据对等角相等，以及三角形内角和定理可得90FBG AEG ∠=∠=°，即可得证；（2）根据题意得出 AD AC =，则ABD ABC ∠=∠，证明EF BC ∥，得出AGE ABC ∠=∠，等量代换得出FGB ABD ∠=∠，即可得出结论；（3）根据FGB ABD ∠=∠，AB BF ⊥，设FGB ABD α∠=∠=，则90DBF F α∠=∠=°−，等边对等角得出DB DF =，则224FG DG DB ===． 【小问1详解】证明：如图所示，连接CO ，� BCBD =， ∴2BOD BOC BAC ∠=∠=∠， ∵2BOD F ∠=∠， ∴F BAC ∠=∠， ∵DEAC ⊥，∴90AEG ∠=°， ∵AGE FGB ∠=∠ ∴90FBG AEG ∠=∠=°，即AB BF ⊥，又AB 是O 的直径， ∴BF 是O 的切线； 【小问2详解】� BCBD =，AB 是O 的直径， ∴ AD AC =，BC AC ⊥， ∴ABD ABC ∠=∠， ∵DEAC ⊥，BC AC ⊥，∵EF BC ∥， ∴AGE ABC ∠=∠， 又AGE FGB ∠=∠，∴FGB ABD ∠=∠，∴DGB 是等腰三角形，【小问3详解】�FGB ABD ∠=∠，AB BF ⊥，设FGB ABD α∠=∠=，则90DBF F α∠=∠=°−，∴DB DF =，∴224FG DG DB ===．【点睛】本题考查了切线的判定，等腰三角形的性质与判定，圆周角定理，熟练掌握以上知识是解题的关键．27. 在平面直角坐标系中，给出如下定义：P 为图形M 上任意一点，如果点P 到直线EF 的距离等于图形M 上任意两点距离的最大值时，那么点P 称为直线EF 的“伴随点”．例如：如图1，已知点()1,2A ，()3,2B，()2,2P 在线段AB 上，则点P 是直线EF ：x 轴的“伴随点”．（1）如图2，已知点()1,0A ，()3,0B ，P 是线段AB 上一点，直线EF 过()1,0G −，T两点，当点P 是直线EF 的“伴随点”时，求点P 的坐标；（2）如图3，x 轴上方有一等边三角形ABC ，BC y ⊥轴，顶点A 在y 轴上且在BC 上方，=OC ，点P 是ABC 上一点，且点P 是直线EF ：x 轴的“伴随点”．当点P 到x 轴的距离最小时，求等边三角形ABC 的边长；（3）如图4，以()1,0A ，()2,0B ，()2,1C 为顶点的正方形ABCD 上始终存在点P ，使得点P 是直线EF ：y x b =−+的“伴随点”．请直接写出b 的取值范围． 【答案】（1）()3,0P（2）2（3）11b −≤≤【解析】【分析】（1）过点P 作PQ EF ⊥于点Q ，根据新定义得出2PQ =，根据已知得出30TGO ∠=°，则24GP PQ ==，即可求解；（2）当P 到x 轴的距离最小时，点P 在线段BC 上，设ABC 的边长为a ，以C 为圆心a 为半径作圆，当C 与x 轴相切时，如图所示，切点为H ，此时点P 是直线EF ：x 轴的“伴随点”．且点P 到x 轴的距离最小，则C 的纵坐标为a ，即CH a =，ABC 是等边三角形，且BC y ⊥轴，设BC 交于点D ，则AD BC ⊥，得出1,2C a a ，根据=OC （3）当四边形ABCD 是正方形时，()1,1D ，连接CA 并延长交y 轴于点M ，直线AC 的解析式为1y x =−，得出()0,1M −，可得P ，则当点P 与点A 重合时，当点P 与C 点重合时，求得两个临界点时的b 的值，即可求解．【小问1详解】解：如图所示，过点P 作PQ EF ⊥于点Q ，�()1,0A ，()3,0B ，则2AB =，点P 是直线EF 的“伴随点”时，�2PQ =，∵()1,0G −，T，∴1OG TO ==，，�tan TGO ∠∴30TGO ∠=°，∴24GP PQ ==， ∴()3,0P ；【小问2详解】解：当P 到x 轴的距离最小时，∴点P 在线段BC 上，设ABC 的边长为a ，以C 为圆心a 为半径作圆，当C 与x 轴相切时，如图所示，切点为H ，此时点P 是直线EF ：x 轴的“伴随点”．且点P 到x 轴的距离最小，则C 的纵坐标为a ，即CH a =，�ABC 是等边三角形，且BC y ⊥轴，设BC 交于点D ，则AD BC ⊥，�BD DC =12a =， �1,2C a a，∵=OC ∴22152a a +=，解得：2a =或2−（舍去）∴等边三角形ABC 的边长为2【小问3详解】解：如图所示，当四边形ABCD 是正方形时，()1,1D ，连接CA 并延长交y 轴于点M ，∵()1,0A ，()2,0B ，()2,1C∴1AB =，AC =�()1,0A ，()2,1C设直线AC 的解析式为y mx n =+，则 021m n m n += +=解得11m n = =−∴直线AC 的解析式为1y x =−，∴直线,AC EF 垂直，当0x =时，1y =−∴()0,1M −，�AM AC =，即得P 到直线EF ，则当点P 与点A 重合时，P 是直线EF ：y x b =−+的“伴随点”． 此时()0,1M −在y x b =−+上，则01b +=−，解得：1b =-，当点P 与C 点重合时，则EF 过点A ，此时01b =−+，解得：1b =，∴11b −≤≤．【点睛】本题考查了几何新定义，解直角三角形，切线的性质，直线与坐标轴交点问题，正方形的性质，理解新定义是解题的关键．28.综合与实践【思考尝试】（1）数学活动课上，老师出示了一个问题：如图1，在矩形ABCD 中，E 是边AB 上一点，DF CE ⊥于点F ，GD DF ⊥，AG DG ⊥，AG CF =．试猜想四边形ABCD 的形状，并说明理由；【实践探究】（2）小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形ABCD 中，E 是边AB 上一点，DF CE ⊥于点F ，AH CE ⊥于点H ，GD DF ⊥交AH 于点G ，可以用等式表示线段FH ，AH ，CF 的数量关系，请你思考并解答这个问题；【拓展迁移】（3）小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD 中，E 是边AB 上一点，AH CE ⊥于点H ，点M 在CH 上，且AH HM =，连接AM ，BH ，可以用等式表示线段CM ，BH 的数量关系，请你思考并解答这个问题．【答案】（1）四边形ABCD 是正方形，证明见解析；（2）FH AH CF =+；（3）MC =，证明见解析；【解析】【分析】（1）证明ADG CDF ≌，可得AD CD =，从而可得结论； （2）证明四边形DGHF 是矩形，可得90G DFC ∠=°=∠，同理可得：ADG CDF ∠=∠，证明ADG CDF ≌，DG DF =，AG CF =，证明四边形DGHF 是正方形，可得HG HF =，从而可得结论；（3）如图，连接AC ，证明90AHE ABC ∠=∠=°，AC AB=，45BAC ∠=°，AHE CBE ∽，可得AE HE CE BE=，再证明HEB AEC ∽，可得HBE MCA ∠=∠，证明AHB AMC ∽，可得HB AB MC AC == 【详解】解：（1）∵GD DF ⊥，DF CE ⊥，AG DG ⊥，∴90G DFC ∠=∠=°，90ADG ADF ∠+∠=°，∵矩形ABCD ，∴90ADC ADF CDF ∠=°=∠+∠，∴ADG CDF ∠=∠，∵AG CF =，∴ADG CDF ≌，∴AD CD =，∴矩形ABCD 是正方形．（2）∵DF CE ⊥，AH CE ⊥，GD DF ⊥，∴90DFH H GDF ∠=∠=∠=°，∴四边形DGHF 是矩形，∴90G DFC ∠=°=∠，同理可得：ADG CDF ∠=∠，∵正方形ABCD ，∴AD CD =，∴ADG CDF ≌，∴DG DF =，AG CF =，∴四边形DGHF 是正方形，∴HG HF =，∴FH HG AH AG AH CF ==+=+．（3）如图，连接AC ，∵AH CE ⊥，正方形ABCD ，∴90AHE ABC ∠=∠=°，AC AB =，45BAC ∠=°，∵AEH CEB ∠=∠，∴AHE CBE ∽， ∴AE HECE BE =，∵BEH AEC ∠=∠，∴HEB AEC ∽，∴HBE MCA ∠=∠，∵,AH CE AH HM ⊥=， ∴45HAM BAC ∠=°=∠，∴HAE MAC ∠=∠，∴AHB AMC ∽，∴HBAB MC AC ==∴MC =．【点睛】本题考查的是矩形的判定与性质，正方形的判定与性质，全等三角形的判定与性质，相似三角形的判定与性质，作出合适的辅助线，构建相似三角形是解本题的关键．。
不同回流比对精馏分离效果的影响
17
参考文献
1.1 理论塔板
若气、液两相在塔板上接触时间足够长，使得离开该塔板的气、液两相互呈 平衡，即������������ 与������������ 平衡， ，则称该塔板为理论板。实际上由于塔板上气液接触时间 有限，������������ 与������������ 难以达到平衡，即理论板是不存在的。理论板作为衡量塔板分离效 率的依据和标准[2]。
1、流量计 2、进料阀 3、进料泵 4、热交换器 5、塔板 6、原料罐 7、残液罐 8、产品罐 9、反应釜 3
2.1 全回流
配制浓度为 18.1%的乙醇水溶液原料液加入贮缺罐中， ，打开进料阀，由进 料泵将原料打入塔釜中，观察塔釜的液位高度，进料至容积的 2/3 处停止进料。 打开塔顶冷凝器的冷却水，调节为 140L/h，关闭进料阀，启动电加热管电源， 调节加热功率为 90%，并关闭塔顶出料管路，使整塔处于全回流状态。经过 2 小时后，塔顶回流量、温度、塔釜温度稳定后，开始进入部分回流状态。
引言
精馏是化工分离工程中最基本、最重要的单元操作之一。在精馏的操作中, 回流比（R）是关系着精馏产品质量的重要参数。每当塔顶馏出液浓度下降或需 要进一步提高塔顶馏出液浓度时, 通常都以增加回流比的操作方式使产品得以 提高。 间歇操作回流比得出产品浓度一般都是变化的。本文通过实验讨论连续操 作过程中不同回流比对精馏分离效果的影响。
14
反应条件：回流温度 27.1℃，进料温度 40.3℃，������������ =0.897，������������ =0.178。 塔板层数 1 2 3 4 5 6 7 8 9 R=1 74.8 75.3 75.3 75.8 76.1 76.5 76.5 79.3 84.3 全回流温度 部分回流温度 78.8 80.4 81.1 84.3 85.0 85.2 85.2 87.7 88.3
2024最新(青岛版)六年级上册数学期末练习题,期末检测试卷及答案 山东六三制专用
六年级上册数学期末试题（青岛版）一．选择题（四个选项中只有一个符合题意。
本大题共12小题，每小题2分，共24分）1.百分数又叫做百分率或百分比。
为了便于统计和比较，我们通常会把一些分数改写成百分数的形式来表示。
下面百分数中，（）可以超过100%。
A.出勤率B.成活率C.今年工厂产值增长率D.产品合格率2.小明在做科学实验时发现一瓶盐水的含盐率看不清楚了。
于是，他从容器中倒出了100克盐水，经过加热稀释得到了25克盐。
小明经过计算用标签标注了该盐水的含盐率（）。
A.20%B.75%C.25%D.33%3.“车轮形状为什么选择圆形？”下面解释最合理的是（）。
A.圆是曲线图形B.圆有无数条半径，而且都相等B.圆很美观 D.圆的周长是直径的π倍4.爸爸骑共享单车回家，13小时走了全程的23。
这里的13是把（）看作单位“1”，平均分成3份，表示这样的1份。
A.13小时B.23C.全程D.1小时5.下面涂色部分不能表示3×1的是（）。
A B C D6.8:9的前项增加24，要使比值不变，后项应增加（）。
A.24B.27C.32D.367.甲、乙两数的差为9，甲数与乙数的比是5:2，则乙数是（）。
A.15B.9C.6D.38.一个正方形骰子的六个面上分别有1、2、3、4、5、6个点，如果抛出这个正方形骰子，朝上的面是（）的可能性最小。
A.偶数B.奇数C.合数D.质数9.水结成冰后，体积增加了111，冰融化成水后，体积减少了（）。
A.110B.111C.112D.11310.0.33，33.3%，13，310这四个数中，从大到小排在第二的是（）。
A.0.33B.33.3%C.13D.31011.有两堆棋子，从第一堆拿15到第二堆后，两堆棋子数量正好相等，那么原来第二堆棋子与第一堆棋子数量的比是（）。
A.5：3B.3：5C.5：4D.5：612.如右图，A、B两只小蚂蚁从甲到乙分别走两条路，比较这两条路线（）A.蚂蚁A走的长B.蚂蚁B走的长B.一样长 D.无法确定13.下图中圆的面积是28.26cm2，平行四边形的面积是（）。
二年级上册数学试题-周周练习题(第十三周)(含答案)沪教版
中只有一个人说了真话， 你知道是谁打扫了教室吗？ 小伟说： “不是我做的。” 小安说： ”也不是我做的。” 小云说： “是小安做的。”
4
沪教版二年级数学上册周周练（第十五周） 参考答案
一． 直接写出得数。 36--;-4= 9 1 00 — 2 7 —34=39 52+33— 28= 57 6X6 =36 32--;-4= 8
3
4. 学校买了几袋笔记本， 每袋有10本， 平均分给6个班级， 每个班分8 本， 还剩下2本， 学校买了几袋笔记本？
5. 赵奶奶家有两盆小鱼， 大盆有32条小鱼， 小盆有14条小鱼， 每次从 大盆抓3条小鱼放进小盆里， 抓几次两个盆的小鱼数量相等？
七． 拓展与提高。 1. 把下面的图形加 一条直线， 使它变成 一 个有6个直角的图形。
就是分18 72=9条，两个盆就一 样多
＼了。每次抓3条，需要抓： 973=3次。
答： 抓 3次两个盆的小鱼数量相等。
七． 拓展与提高。 1. 把下面的图形加 一条直线， 使它变成 一个有 6个直角的图形。
2. 数一 数， 下图中共有多少个角？
1+2+3+4+5+6+7 =28(个）
8
沪教版二年级数学上册周周练（第十五周） 整理与提高（一）
D.44---;-6
四． 列式计算。
2
1. 56里面有几个7? 54里面有几个6? 24 . 个6加上3个6是多少？ 3. 被除数是63, 商是9, 除数是多少？
48 . 个8比4个8多多少？ 五． 应用题。
1. 一本童话书有60页， 笑笑已经看了12页， 如果剩下的每天看6页， 需要几天能把这本书看完？
2023届三湘名校高三3月第二次大联考数学试卷及答案
三湖名校教育联盟·2023届高三第二次大联考科目：数学（试题卷）注意事项：1.本试题卷共6页，共22个小题。
总分150分，考试时间120分钟。
2.接到试卷后，请检查是否有缺页、缺题或字迹不清等问题。
如有，请及时报告监考老师。
3.答题前，务必将自己的姓名、考号写在答题卡和l 该试题卷的封面上，并认真核对条形码的姓名、考号和平斗目。
4.作答时，请将答案写在答题卡上。
在草稿纸、试题卷上答题无效。
5.考试结束后，将本试题卷和答题卡一并交囚。
姓名准考证号率元首飞考试JI顶利！绝密食启用前三湘名校教育联盟•2023届高三第二次大联考数学一、单项选择题：本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合题目要求的－1.已知集合A ={x l x 1-5.:i_·-6�0,xE R } ,ff!IJ C.A =A.（一1,6)B.(-6, 1)C.(2,3) D .[-6,1]+t 2.已知α，b E R,i 为虚数单位，若一一.，.－＝l-2i ,Y !IJ l a 十b i l =2+,A. 3B. 5C.9D.253.从I ,2，…J这丸个数字中任取两个，这两个数的和为质数的概率为I －3A4 8一. 9 ，、7·－-· 18 。
!1. 364.已知定义在E R上的函数J(x ）满足J(-x)=-J(x),f(x+2)=-f(2-x ），且当:r E<-2,2)时，只x）＝川－3x ，则函数f(.2－）在［－6,6］上的零点个数为A.9 B.] 1c.13D.155.函数f（川＝Asin (w 2+g,) (w>O, O ＜ψ＜旧的部分图象如l到所示，则下列说法正确的是A. f(x)=2sin(fx咔）yB.E画数f （川的单i古iJ:i差t('j区间为［6阳－2,6阳＋l]CkEZ)C .函数f(x）在区｜可［一缸，2π］上有且仅有5个零点D丽数g(:r)=f(x)+f(.1+1)的最大街为2../35 26.设α＝τ一·－；；：：.，b=2一In 2,c ＝在一τ，贝I J‘’、fe“Jlx)=As i 叫，，，x ＋ψ）...A.α＞b>cB. c ＞α＞bC. c >b ＞α。
期末复习重要考点02 《整式的加减》十二大考点题型(热点题型+限时测评)(原卷版)
（人教版）七年级上册数学期末复习重要考点02《整式的加减》十二大重要考点题型【题型1用含字母的式子表示数量关系】1．（2023秋•和平区校级月考）某班有x个男生，其中女生人数占45%，那么这个班级共有（）人．A．45%B．（1﹣45%）x C．45%D．1−45%2．（2023秋•梁子湖区期中）某商店举行促销活动，其促销的方式为“消费超过100元时，所购买的商品按原价打九折后，再减少30元”．若某商品的原价为x元（x＞100），则购买该商品实际付款的金额（单位：元）是（）A．90%（x﹣30）B．90%x﹣30C．10%x﹣30D．10%（x﹣30）3．（2023秋•梁子湖区期中）如图，池塘边有一块长为a米，宽为b米的长方形土地，现将其余三面都留出宽是1.5米的小路，中间余下的长方形部分做菜地，则菜地的周长为（）A．（a+2b﹣4）米B．（a+2b﹣12）米C．（2a+2b﹣9）米D．（2a+2b）米4．（2022秋•高新区期末）某地居民生活用水收费标准：每月用水量不超过20立方米，每立方米a元；超过部分每立方米（a+2）元．该地区某家庭上月用水量为25立方米，则应缴水费（）A．25a元B．（25a+10）元C．（25a+50）元D．（20a+10）元5．（2022秋•靖远县期末）一个两位数，十位上的数字为a，个位上的数字比十位上的数字少2，则这个两位数为（）A．11a﹣20B．11a+20C．11a﹣2D．11a+26．（2023•南岗区校级三模）随着通讯市场竞争的日益激烈，某品牌的手机价格春节期间降低了a元，五一前后又下调了25%，该手机现在的价格是b元，则原来的价格是元．7．（2023秋•临平区月考）一件商品每件成本a元，原来按成本价增加20%定出价格，现在由于库存积压减价，按原价打九折出售，现在每件可以盈利元．8．（2023秋•盐湖区期中）某公园准备修建一块长方形草坪，长为35m，宽为25m．并在草坪上修建如图所示的十字路，已知十字路宽x m，则修建的十字路的面积是m2．（用含x的代数式表示）【题型2单项式、多项式、整式相关概念】1．（2023秋•娄底期中）在﹣a，2，2，2+3，m3n2，xy﹣1，0，52中，是单项式的有（）A．6个B．5个C．4个D．3个2．（2023秋•梁子湖区期中）下列关于单项式−B23的说法中，正确的是（）A．系数是﹣3，次数是2B．系数是﹣3，次数是3C．系数是−13，次数是2D．系数是−13，次数是3 3．（2023秋•通道县期中）多项式2xy2−3237−1的次数是，常数项是．4．（2023秋•镇赉县校级期末）在代数式x2+5，﹣1，﹣3x+2，π，5，x2+1r1，5x中，整式有（）A．3个B．4个C．5个D．6个5．（2022秋•市中区期末）下列叙述，错误的是（）A．单项式2x2y3的次数是5B．32是三次单项式，系数是3C．252−22+1是四次三项式D．有理数与数轴上的点一一对应6．（2023秋•南关区期末）将多项式3xy3﹣x2y3﹣9y+x3按x的升幂排列的结果是（）A．x3﹣9y﹣x2y3+3xy3B．x3﹣x2y3+3xy3﹣9yC．﹣9y+x3+3xy3﹣x2y3D．﹣9y+3xy3﹣x2y3+x37．（2022秋•富平县期末）多项式6x2+5xy2﹣4xy﹣3y2中所有二次项系数的和是（）A．4B．3C．2D．﹣18．下列说法：①2的系数是2；②多项式2x2+xy2+3是二次三项式；③x2﹣x﹣2的常数项为2；④在1，2x+y，132，54，0中，整式有3个．其中正确的有（）A．1个B．2个C．3个D．4个【题型3综合利用单项式、多项式的相关概念求值】1．若单项式−35B3的系数是m，次数是n，则m+n＝（）A．75B．115C．175D．1952．已知﹣4x2yz m是关于x，y，z的5次单项式，m是常数，则m的值是（）A．1B．2C．3D．4 3．（2022秋•甘谷县校级期末）若52|U−14(+1)2−3是关于x、y的三次三项式，则m＝．4．（2023秋•双峰县期中）若x n+1+（m﹣1）x+8是关于x的三次二项式，则m＝，n＝．5．（2023秋•邹城市期中）已知m，n为常数，代数式2x2y+mx3﹣n y+xy化简之后为单项式，则m+n＝．6．（2022秋•秦都区期末）若关于x，y的多项式3x2﹣2x m+1y﹣1的次数是5，单项式﹣x的系数是n，求m+n的值．7．（2022秋•南江县校级月考）已知多项式﹣3x m+1y3+x3y﹣3x4﹣1是五次四项式，单项式3x3n y2的次数与这个多项式的次数相同．（1）求m，n的值；（2）把这个多项式按x降幂排列．8．已知：−12a2n b2﹣m是关于a，b的六次单项式，23a2b n+1+ab﹣2a2+b﹣5是关于a，b的四次多项式，求|m2﹣2m+n2|的值．【题型4合并同类项与去括号】1．（2022秋•南浔区期末）下列各式中是同类项的为（）A．5x2y与﹣3xy2B．xyz与﹣4xyC．﹣32与x2D．﹣3x2y与3x2y2．（2022秋•灵宝市期末）下列各组中的两项，不是同类项的是（）A．﹣x2y和2x2y B．23和32C．﹣m3n2与12m2n3D．2πR与π2R3．（2022秋•市中区期末）若﹣5a4b m﹣1与﹣a n b是同类项，则m﹣n的值为（）A．0B．1C．﹣1D．﹣24．（2023秋•贵州期末）下列合并同类项的结果中，正确的是（）A．﹣3ab﹣3ab＝0B．y﹣3y＝﹣2yC．2m3+3m3＝5m6D．3a2﹣a2＝35．（2022秋•新会区期末）下列计算中，去括号正确的是（）A．﹣2（3x+1）＝6x﹣2B．﹣2（3x+1）＝6x+2C．﹣2（3x+1）＝﹣6x﹣2D．﹣2（3x+1）＝﹣6x+26．（2022秋•嵩县期末）下列各式中，去括号或添括号正确的是（）A．a2﹣（﹣b+c）＝a2﹣b+cB．﹣2x﹣t﹣a+1＝﹣（2x﹣t）+（a﹣1）C．3x﹣[5x﹣（2x﹣1）]＝3x﹣5x﹣2x+1D．a﹣3x+2y﹣1＝a+（﹣3x+2y﹣1）7．先去括号，再合并同类项：（1）3a﹣b+（5a﹣3b+3）；（2）（2b﹣3a）﹣（2a﹣3b+1）；（3）4x2+2（x2﹣y2）﹣3（x2+y2）．8．（2023秋•沙坪坝区校级月考）化简：（1）（m+n）﹣[3m+2（﹣m+n）]；（2）（4a2b2﹣5ab2）﹣（3a2b2+4ab2）；（3）3x2﹣{6xy+[4x2﹣8y2﹣（4xy﹣6y2）]﹣3x2}．【题型5整式的化简求值---直接代入求值】1．（2022秋•保亭县期末）先化简，再求值：3x2y2﹣（4xy2﹣3）+（﹣5xy2﹣3x2y2），其中x＝3，y＝﹣1．2．（2023秋•东丰县期末）先化简，后求值：3（a2﹣ab+7）﹣2（3ab﹣a2+1）+3，其中a＝2，b=13．3．（2023秋•昌邑区期中）先化简，再求值：3x2y﹣[3x2y﹣（2xy2﹣x2y）﹣4x2y]﹣xy2，其中x＝1，y＝﹣1．4．（2023秋•利辛县期中）先化简，再求值：32−[22−2(B−322)+B]+32，其中a为最小的正整数，b为最大的负整数．5．（2022秋•澄城县期末）先化简，再求值：5ab2﹣[2a2b﹣（4ab2﹣2a2b）]，其中a、b满足|a﹣2|+（b+1）2＝0．6．（2023秋•建昌县期中）求−13−2(+132)−(23+132)的值，其中（x﹣2）2+|y+1|＝0．7．（2022秋•安新县期末）已知A＝x2﹣3xy﹣y，B＝﹣x2﹣xy+3y．（1）①化简A+B；②当﹣ab y与122是同类项时，求A+B的值；（2）若x是﹣2的倒数，y是最大的负整数，求A﹣3B的值．【题型6整式的化简求值---整体代入求值】1．（2023秋•东丰县期末）已知3m2﹣2m＝1，则代数式9m2﹣6m﹣5的值是．2．（2023秋•天长市期中）若a2﹣2b2﹣2＝0，则﹣3a2+6b2+2023的值为．3．（2023秋•宝鸡期中）已知当x＝﹣3时，ax3﹣bx+5＝9，则x＝3时，ax3﹣bx+9的值为．4．（2023秋•北碚区校级期中）已知实数a，b，x，y满足a+b＝2，x+y＝3，ax+by＝4，则（a2+b2）xy+ab （x2+y2）＝．5．（2023秋•永福县期中）已知A＝3x2﹣x+2y﹣4xy，B＝2x2﹣3x﹣y+xy．（1）化简：2A﹣3B；（2）若+=−67，xy＝1，求2A﹣3B的值．6．已知a﹣b＝5，﹣ab＝3，求(7+4+B)−6(56+−B)的值．7．（2022秋•平定县期末）综合与探究【阅读理解】“整体思想”是一种重要的数学思想方法，在多项式的化简求值中应用极为广泛．比如，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a﹣b）看成一个整体，则4（a﹣b）﹣2（a﹣b）+（a﹣b）＝（4﹣2+1）（a﹣b）＝3（a﹣b）．【尝试应用】根据阅读内容，运用“整体思想”，解答下列问题：（1）化简8（a+b）+6（a+b）﹣2（a+b）的结果是．（2）化简求值，9（x+y）2+3（x+y）+7（x+y）2﹣7（x+y），其中+=12．【拓展探索】（3）若x2﹣2y＝4，请求出﹣3x2+6y+2的值．【题型7整式加减中的错看问题】1．（2022秋•离石区期末）小文在做多项式减法运算时，将减去2a2+3a﹣5误认为是加上2a2+3a﹣5，求得的答案是a2+a﹣4（其他运算无误），那么正确的结果是（）A．﹣a2﹣2a+1B．﹣3a2+a﹣4C．a2+a﹣4D．﹣3a2﹣5a+62．（2022秋•渠县校级期末）有一道题目是一个多项式A减去多项式2x2+5x﹣3，小胡同学将2x2+5x﹣3抄成了2x2+5x+3，计算结果是﹣x2+3x﹣7，这道题目的正确结果是（）A．x2+8x﹣4B．﹣x2+3x﹣1C．﹣3x2﹣x﹣7D．x2+3x﹣73．（2022秋•内江期末）黑板上有一道题，是一个多项式减去3x2﹣5x+1，某同学由于大意，将减号抄成加号，得出结果是5x2+3x﹣7，这道题的正确结果是（）A．8x2﹣2x﹣6B．14x2﹣12x﹣5C．2x2+8x﹣8D．﹣x2+13x﹣94．（2023秋•长春期末）有这样一道题目：“先化简，再求值：（2x3﹣3x2y﹣2xy2）﹣2（x3﹣xy2+y3）+3（x2y﹣y3），其中=13，y＝﹣2．”粗心的龙龙在计算时把“x=13”错抄成“x=17”，但他计算的结果却是正确的．请通过计算说明理由，并求出这个代数式的值．5．（2023春•楚雄州期末）已知A＝3x﹣4xy+2y，小明在计算2A﹣B时，误将其按2A+B计算，结果得到7x+4xy﹣y．（1）求多项式B．（2）求2A﹣B的正确结果是多少？6．（2022秋•台山市期末）小红做一道数学题“两个整式A，B，已知B为4x2﹣5x﹣6，试求A+2B的值“．小红误将A+2B看成A﹣2B，结果答案（计算正确）为﹣7x2+10x+12．（1）求整式A；（2）求出当x＝﹣3时，A+2B的值．【题型8整式加减中与某个字母（某项）无关问题】1．（2023秋•十堰期中）若代数式x2+ax﹣（bx2﹣x﹣3）的值与字母x无关，则a﹣b的值为（）A．0B．﹣2C．2D．12．（2023秋•禹州市期中）若多项式（2k+3）x2y+3x﹣7x2y﹣5y+1中不含x2y的项，则k的值为．3．（2022秋•蚌埠期末）已知A＝3a2﹣ab+b+2，B＝3a2﹣2ab+4b﹣1，若A﹣B的值与b无关，则a的值为．4．（2023秋•清苑区期中）已知代数式A＝4x2﹣mx+2m，B＝2x2﹣mx+x，若A﹣2B的值与x的取值无关，则m的值为（）A．3B．2C．1D．05．（2022秋•烟台期末）若代数式3x2+ax+4﹣（bx2+2x）的值与x的取值无关，化简求值：2（a2b+ab2）﹣3（a2b﹣3）﹣2ab2﹣1．6．（2023秋•天长市期中）已知：A＝2a2﹣5ab+3b，B＝4a2+6ab+8a．（1）化简：2A﹣B；（2）若a＝﹣2，b＝1，求2A﹣B的值；（3）若代数式2A﹣B的值与a无关，求此时b的值．【题型9整式加减与数轴、绝对值的结合】1．（2023秋•宁江区期末）已知有理数a、b、c在数轴上的对应点如图所示，|a﹣b|+|b﹣c|﹣|c﹣a|的结果（）A．a﹣b B．b+c C．0D．a﹣c2．（2022秋•洪山区校级期末）数轴上，有理数a、b、﹣a、c的位置如图，则化简|a+c|+|a+b|+|c﹣b|的结果为（）A．2a+2c B．2a+2b C．2c﹣2b D．03．（2023秋•东丰县期末）已知a，b，c在数轴上的位置如图所示，求|a﹣b|﹣|b+c|+|a﹣b|﹣|c﹣b|的值．4．（2023秋•禹州市期中）已知数轴上A，B，C三点对应的数分别是a，b，c，若a＜0，b＜0，|a|＜|b|，c 为最小的正整数．（1）请在数轴上标出A，B，C三点的大致位置；（2）化简：|a﹣b|﹣2|b﹣a﹣c|+|b﹣2c|．5．（2022秋•黔西南州期末）有理数a，b，c在数轴上的位置如图：（1）用“＞”或“＜”填空a0，b0，c﹣b0，ab0．（2）化简：|a|﹣|b+c|﹣|a﹣c|．6．（2023秋•江都区期中）已知有理数a、b、c在数轴上的位置如图所示，且|a|＝|b|．（1）求a+b和的值；（2）填空：a0；a+b0；c﹣a0；c﹣b0；﹣2b0；（3）化简：|a|﹣|a+b|﹣|c﹣a|+|c﹣b|﹣|﹣2b|．【题型10利用整式加减解决实际问题】1．（2022秋•侯马市期末）长方形一边的长为3m+2n，与其相邻的另一边的长比它长m﹣n，则这个长方形的周长是（）A．7m+3n B．7m+5n C．14m+10n D．14m+6n2．（2023秋•临沭县期中）已知B，C，D三个车站的位置如图所示，B，C两站之间的距离是2a﹣b，B，D两站之间的距离是72a﹣2b﹣1，则C，D两站之间的距离是（）A．112a﹣3b﹣1B．32a+b+1C．32a﹣b﹣1D．32a﹣3b﹣13．（2022秋•涧西区校级期末）如图，两个矩形的一部分重叠在一起，重叠部分是面积是4的正方形，则阴影部分的面积为（）A．ab+cd﹣4B．ab+cd+4C．ab+cd﹣8D．ab+cd+84．（2023•青羊区校级自主招生）如图1，将一个边长为m的正方形纸片剪去两个小长方形得到一个如图2所示的图形，再将剪下的两个小长方形拼成如图3所示的一个新的长方形，则图3中的长方形的周长为（）A．2m﹣3n B．4m﹣8n C．2m﹣4n D．4m﹣10n5．（2022秋•安乡县期末）如图，从一个长方形铁皮中剪去一个小正方形，长方形的长为2a米，宽为b米，小正方形的边长为a米．（1）求剩余铁皮的面积；（2）当a=23，b＝1时，求剩余铁皮的面积．6．（2022秋•碑林区校级期中）某超市销售茶壶、茶杯，每只茶壶定价20元，每只茶杯定价4元．今年“双十一”期间开展促销活动，向顾客提供两种优惠方案：方案一：每买一只茶壶就赠一只茶杯；方案二：茶壶和茶杯都按定价的90%付款．某顾客计划到这家超市购买6只茶壶和x只茶杯（茶杯数多于6只）．（1）用含x的代数式分别表示方案一与方案二各需付款多少元？（2）当x＝25时，若规定每位顾客只能在以上两种方案中任选一种，请通过计算说明该顾客选择上面两种购买方案中哪一种更省钱？7．（2022秋•安定区期末）某家具厂生产一种课桌和椅子课桌每张定价200元，椅子每把定价80元，厂方在开展促销活动期间，向客户提供两种优惠方案：方案一：每买一张课桌就赠送一把椅子；方案二：课桌和椅子都按定价的80%付款．某校计划添置100张课桌和x把椅子（x＞100）．（1）用含x的代数式分别表示方案一与方案二各需付款多少元？（2）当x＝300时，通过计算说明该校选择上面的两种购买方案哪种更省钱？（3）当x为何值时，按两种优惠方案购买付款金额相同？【题型11利用整式加减进行新定义运算】1．现规定一种新的运算：=ad﹣cb，则B−32−2−2B−2−5的值是．2．（2023•任城区校级三模）定义：若a+b＝ab，则称a、b是“西溪数”，例如：3+1.5＝3×1.5，因此3和1.5是一组“西溪数”，若m、n是一组“西溪数”，则2mn﹣（3mn﹣m﹣n﹣6）的值为．3．（2023秋•长清区期中）定义新运算“⊗”与“⊕”：a⊗b＝2a+b，a⊕b＝a﹣2b．（1）请分别计算1⊗3和2⊕（﹣1）的值；（2）化简：[m⊗（﹣n）]﹣[（﹣n）⊕m]．4．（2023•陈仓区三模）一个三位数整数，a代表这个整数最左边的数，b代表这个整数最右边的数．若r2正好为剩下的中间数，则这个三位数就叫平衡数，例如：357满足3+72=5，357就是平衡数．（1）判断：468平衡数；（填“是”或“不是”）（2）证明：任意一个三位数的平衡数一定能被3整除．5．（2022秋•工业园区校级月考）定义一种新运算：观察下列各式：1⊙3＝1×4+3＝7；3⊙（﹣1）＝3×4﹣1＝11；5⊙4＝5×4+4＝24；4⊙（﹣3）＝4×4﹣3＝13．（1）请你想一想：a⊙b＝；（2）若a≠b，那么a⊙b b⊙a（填“＝”或“≠”）；（3）先化简，再求值：（a﹣b）⊙（2a+b），其中a＝1，b＝2．6．（2023秋•乐至县校级期中）对于任何数，我们规定：=ad﹣bc．例如：1234=1×4﹣2×3＝4﹣6＝﹣2．（1）按照这个规定，请你化简：−5284；（2）按照这个规定，当a2﹣4a+2＝0时，求+23−1−3的值．【题型12整式中的规律探究问题】1．（2023秋•天长市期中）观察下列关于x的单项式，探究其规律：﹣2x，4x2，﹣6x3，8x4，﹣10x5，12x6，…按照上述规律，第2023个单项式是（）A．﹣4046x2022B．4046x2022C．﹣4046x2023D．4046x20232．（2022秋•舒城县期末）观察一组数据：1，1，2，4，7，11，16，22，29，…，若记第一个数为a1，记第二个数为a2，…，记第n个数为a n.通过计算a2﹣a1，a3﹣a2，a4﹣a3，…发现它们有一定的规律，由此规律推算a100的值应为（）A．5152B．5051C．4951D．48523．（2023秋•贵州期末）如图图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中共有6个小圆圈，第②个图形中共有9个小圆圈，第③个图形中共有12个小圆圈，…，按此规律，则第⑲个图形中小圆圈的个数为（）A．60B．63C．66D．694．有一组多项式：a+b2，a2﹣b4，a3+b6，a4﹣b8，…，请观察它们的构成规律，用你发现的规律写出第10个多项式为．5．（2023•白银模拟）下列图形都是由完全相同的小梯形按一定规律组成的，如果第1个图形的周长为5，那么第个图形的周长为32．6．（2023秋•盐湖区期中）由白色小正方形和灰色小正方形组成的图形如图所示，则第n个图形中白色小正方形和灰色小正方形的个数总和为个．（用含n的代数式表示）7．（2023秋•连山区期中）下列图形按一定规律排列，观察并回答：（1）依照此规律，第4个图形共有个★，第7个图形共有个★；（2）第n个图形中有★个；（3）根据（2）中的结论，第几个图形中有2023个★？1．（2022秋•岱岳区期末）一种商品进价为每件m元，按进价增加40%出售，后因库存积压降价，按售价的八折出售，此时售价为（）A．1.25m元B．1.12m元C．1.32m元D．0.98m元2．（2023秋•桐城市期中）下列说法正确的是（）A．2x3+1是单项式B．﹣a3的系数是1C．3m2﹣1是三次多项式D．2是单项式3．（2022秋•烟台期末）若﹣5x a+1y b﹣2与7x3y2是同类项，则a、b的值分别是（）A．a＝2，b＝4B．a＝4，b＝0C．a＝2，b＝﹣4D．以上都不对4．（2023秋•水城区期中）下列去括号正确的是（）A．﹣（a+b﹣c）＝﹣a+b﹣c B．﹣（a+b﹣c）＝﹣a﹣b+cC．﹣（﹣a﹣b﹣c）＝﹣a+b+c D．﹣（a﹣b﹣c）＝﹣a+b﹣c5．（2023秋•灞桥区校级期中）已知A＝2a2+3ab﹣2a﹣1，B＝﹣a2+ab﹣1，若A+2B的值与a的取值无关，则b的值为（）A．23B．13C．25D．356．（2022秋•河池期末）若A＝2x2+x+1，B＝x2+x，则A、B的大小关系（）A．A＞B B．A＜B C．A＝B D．不能确定7．（2023秋•德惠市期末）某同学上学时步行，回家时乘车，路上共用a小时．如果往返都乘车，则共需b小时，那么往返都步行需要小时．8．（2022秋•海阳市期末）若多项式﹣2x|m|﹣（m﹣2）x﹣1是关于x的二次三项式，则m的值为．9．（2022秋•潍坊校级期末）已知x2﹣x﹣4＝0，则2﹣3x2+3x的值．10．（2023秋•温江区校级期中）化简下列式子：（1）3x﹣2y﹣x﹣6y+2；（2）（2a2+1）﹣（2﹣3a2）；（3）3（x2﹣2xy）﹣2（﹣3xy+y2）；（4）3m2n﹣[2m2n﹣（2mn﹣m2n）﹣4m2]．11．（2023秋•咸宁期中）已知关于x，y的多项式15r12+B−43+1（m是自然数）．（1）当m＝1时，该多项式是次项式；（2）该多项式的次数最小是次；（3）若该多项式是八次多项式，且单项式182K3与该多项式的次数相同，求（﹣m）3+2n的值．12．（2023秋•恩施市校级月考）已知a、b、c在数轴上的位置如图，化简|2b+c|+|a﹣2c|﹣|b+c﹣a|﹣|b﹣a|．13．（2022秋•仁怀市期末）先化简，再求值：3B2−2(2+32B2−2)，其中a，b满足：|+1|+(−12)2=0．14．（2023秋•靖江市校级期中）已知代数式A＝2m2+3my+2y﹣1，B＝m2﹣my．（1）化简3A﹣2（A+B）；（2）若（m﹣1）2+|y+2|＝0，求3A﹣2（A+B）的值；（3）若3A﹣2（A+B）的值与y的取值无关，求m的值．15．（2023秋•信丰县期中）【教材呈现】如图是人教版七年级上册数学教材76页的部分内容．把（a+b）和（x+y）各看作一个整体，对下列各式进行化简：4（a+b）+2（a+b）﹣（a+b）＝（2+3﹣1）（a+b）＝4（a+b）．“整体思想”是中学数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．（1）【问题解决】把（x﹣y）2看成一个整体，求将2（x﹣y）2﹣5（x﹣y）2+（x﹣y）2合并的结果；（2）【简单应用】①已知a2+a＝1，则2a2+2a+2020＝；②已知a+b＝﹣3，求5（a+b）+7a+7b+11的值；（3）【拓展提高】已知a2﹣2ab＝﹣5，ab+2b2＝﹣3，求代数式32−92B+32的值．16．（2022秋•宁强县期末）某商场销售一种乒乓球拍和乒乓球，乒乓球拍每副定价80元，乒乓每盒定价20元，“国庆节”假期期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．方案一：买一副乒乓球拍送一盒乒乓球；方案二：乒乓球拍和乒乓球都按定价的90%付款．某客户要到该商场购买乒乓球拍20副，乒乓球x盒（x＞20且为整数）．（1）用含x的代数式表示按两种方案购买各需付款多少元？（2）若x＝30，通过计算说明此时按哪种方案购买较合算；（3）当x＝30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．。
2024-2025学年上学期六年级期末考试数学试卷及答案
2024-2025学年六年级上学期期末考试数学试卷一、反复比较，慎重选择。
（将正确答案的序号填在括号内）1. 下列数中，（）与其它几个数不同．A. 8%B. 0.08C. 百分之八D.主102.一批优质花生的出油率大约是（）A. 5%B. 50%c. 100%D. 105%1 13. 1路公交车，开到靖宇小学站时，车上人数的先下车－后，又上来这时车上人数的－，上8 8 车和下车人数比较（） A. 上车的多B. 下车的多C. 同样多D. 无法确定4. 书法兴趣小组中女生人数是男生的85%。
下面的说法中，错误的是（）A. 男生人数比女生多。
B. 男生比女生少了15%。
C. 男生人数和女生人数的比是20:17。
D. 如果女生85人，那么男生有100人。
5. 估算下面4个算式的计算结果，最大的是（）1A. 120x (1 + -) 1B. 120x (1 -寻1 C. 120+ (1 +-)5 D. 120+ (1 --) 526. 一辆小车－小时行驶30千米，求行1千米所需的时间，列式正确的是（） 52 A. -+ 30 5 2 B. -X 30 5 2C. 30 +亏 2D. 30 X (1-岁3 3 7. 把一根绳子剪成两段，第一段长－米，第二段占全长的－，两段相比()7 7A. 第一段长C . 两段一样长B. 第二段长D. 无法比较8. 把20克盐溶解在100克水中，盐和盐水的最简整数比是（）A. 20: 100B. 1: 5C. 1: 61-4． D 9. "车轮的形状为什么选择圆形？＂，下面的解释中最合理的是() A. 圆形很美观 B. 圆的周长是直径的TI 倍C. 圆是曲线图形D. 圆有无数条半径，而且都相等10. 下图各图正方形的大小相等，阴影部分面积与其他三幅图不同的是()A.w B曰c.M 二、认真读题，谨慎填空。
（） 11. 45d m 2 =—m 2 （）（） 24分＝—时（）312. 200kg的－是kg,45m比m 少10%。
9笔画的所有字
9笔画咤垞姹差查査秅紁臿茬茶荖差茈虿浐觇尝昶欩牊钞俥砗疢眈胂茞乗侱城娍宬峸柽洆浈爯荿郢勅哆垑奓姼彖恀恜拸持炽竾胝胣茬荎郗盅种茧茺衶重侴俦牰欪祝竐除穿舡荈剏疮春陙荃兹呲垐差庛柌泚祠茈茦茨茲徔怱促殂洒疩拵籿侳剉哒垯炟畓羍耷胆荅荙带待怠柋殆毒玳贷単唌柦眈砃胆衴垱挡荡洮陦陟俤哋埅帝柢牴約胝虳垫扂敁涎点玷屌盄咥哋垤峌恎挕昳柣绖胅轶娗庰訂酊垌姛峒峝恫挏昸栋氡洞胨迵剅郖钭陡度毒独笃段耑垖怼追盹盾砘逇钝哆哚垛垜尮度挅挆柁柂柮炧炨茤俄咢咹哑垩姶峉砈峎乻咡峏洏洱耏荋贰饵垡峜珐疺発罚茷阀畈舤埅眆钫昲朏祓胇胐茷贲费飛盼砏秎竕衯贲封甮疯盽砜逄風俌俘俛垘复峊怤枹柎柫氟洑炥玸畉畐砆祓祔罘胕茯荂衭訃負赴郙郛韨鳬尜釓垓姟峐荄钙阂乹柑竿虷缸舡钢勂叝诰郜咯挌牁牱紇茖虼阁革饹给哏茛畊秔郠宫拱紅羾虹垢姤枸玽耇耉茩逅钩怘故柧牯胍轱骨剐括挂胍适恠枴柺冠泴矜覌俇咣垙姯洸茪垝姽恑攱洼癸皈茥贵軌闺鬼浑咶圀活哈虾咳孩骇凾炶虷顸垳巷狠绗侴侾勂昦秏竓茠郝垎峆曷柇洽狢盇籺紇贺阂饸哏很恨拫狠姮恆恒绗訇哄垬娂沗洚洪竑紅缸羾荭虹訇侯厚垕後洉矦茩逅峘怘恗浒烀瓳祜胍胡轷咶哗姡狯砉骅咶徊奐宦峘洹狟荁恍洸炾皇茫荒衁咴哕廽徊恛恢拻挥洃洄浍绘芔茴荟虺袆诲迴韋俒昬浑荤咟活砉钬卽叝咭哜垍姞姫峜急挤既洁洎济狤皍笈紀級结给茍茤荠計迹革叚拮挟架枷柙毠浃玾珈胛荚郟饸俭剑姦姧柬洊牮茛茧荐贱钘奖姜将洚紅绛茳虹咬姣娇峤峧挍挢浇狡绞茭茮荞觉訆饺骄拮拾栉洁狤界畍疥皆砎祖紇结衸诫迼勁巹津浕矜砛荕荩衿觔亰俓剄勁婙浄烃秔穽胫荆荊陘侰垧扃炯逈柩柾觓赳韭举侷枸柤狊矩秬莒钜姢巻帣挗柽珏疦砄绝虳觉俊姰袀訇軍郡钧陖咯垰胩咳垲奒恺闿看砍衎砊荒钪拷洘剋勀勊咳垎客峇恪柯炣牁牱珂科胢轲垦狠胫挎敂眍俈挎枯绔胐轱咵垮姱恗挎荂哙浍狯俇匩哐恇昿洭诳贶奎尯茥姡括挄适剌柆俫栏烂览俍郞咾姥恅栎狫窂络荖浌饹垒洡类俐俚俪厘峛峢栃栎疬砅类茘荔赲轹郦俩娈栏炼亮俍俩咧姴挒挘洌茢迾临恡昤朎柃炩玲瓴斿柳栁桞泵浏珋昽栊珑胧剅娄垏峍栌胪轳娈孪峦峈洛烁络荦骆蚂閁骂派脉荬厖恾笀茫冒昴柕眊贸凂昧某栂眉祙美袂迷虻咪峚弭洣祕祢迷俛勉眄面玅眇秒竗钞咩旀勄敃昬珉盿砇闽姳洺眀茗冒尛帞昩枺洦脉冒哞恈敄某洠姥峔恈牳畆畒胟南哪娜拏衲钠柰耏耐迺侽南柟垴恼挠哪哪氞耐哛昵柅祢籾胒衵逆哖姩峊枿陧拰柠衂钮哝挊浓怒娜挪砈浌眍禺紆鸥巼派皅趴钯俖哌派叛柈洀牉盼眅砏砙胖厖胖逄炮炰爮胞俖姵斾昢朏柸胐胚盆恲挷竼迸毗毘砒便扁骈品姘拼泵砏俜屏帡枰洴玶胓荓哛敀昢洦珀癹匍哛巬陠俟咠契柒甭疧砌竐荠衹峠帢恰洽胢乹俔前拪柑牵粁茜荨钤将羗鸧俏峤茭荍荞诮陗匧契砌窃亲侵矜衿钦亲氢甠轻桏俅恘秋秌觓訄訅酋釓斪朐枸浀祛胊胠姾峑弮恮泉洤畎荃荈卻染珃衻袇娆绕荛饶姙紉荏衽乺乼乽挘衵栄狨绒茙茸荣柔帤洳茹盶耎挪栍洒飒思俕桒乺洓洒穼剎柵栅砂埏挻柵栅炶狦珊舢陝垧姠恦殇柖牊玿厙奓拾虵侺信哂姺昚柛氠珅甚矧神穼籸胂乗殅牲珄省竔胜陞兘冟咶姼室宩屍屎峕峙恀恃拭拾施是昰枾柿浉炻狮甚眂祏蚀贳适郝食垨狩荍首侸俆俞兪凁咰姝怷树洙竖荗除耍咰帥拴閂说盾顺帥洬烁说俟俬娰思枱柶洠牭祠食娀柗诵送凁叜叟俗洬选砕虽狲荪洓挞狧羍荅闼枱炱炲胎钛怹炭眈胆荨挡咷挑洮逃贷俤剃厗洟荑恬殄沗畋畑盷胋宨庣恌挑祒赵贴亭厛娗庭挺涏烃莛哃垌姛峒峝恫恸洞炵狪统茼迵重钭凃突彖砖侻俀追退窀侻柁柝砖说哇娃徍挖洼砙歪弯笂紈徍皇威峗峞洈洧為畏胃韋昷珉闻挝侮俉卼垭屋敄洿诬误郚钨係俙咥屎巼徆怷怸恄恓既枲洒洗盻茜诶郗郤饻俠叚峡挟昰柙洽炠狭疨虾陜俔咸唌姭姺宪挦显枮洒洗涎盷省県籼胘陥险亯响姠巷庠恦洋相舡蚃项饷香侾削咲哓姣恔枵洨狡茭骁骄卸垥奊契峫恊拹挟洩炧炨籺衸頁亲信盺哘型星洐省研胜荇荥钘陘哅恟洶修咻庥茠俆叙咻恤昫欨洫浒砉胥须咺宣昡洵炫玹盷绚选削泶勋峋巺徇恂挦洒洵浔狥紃荀荤荨迿逊陖哑垭娅挜柙疨砑鸦俨兗匽咽唌埏姲姶姸娫弇彥彦恹洇涎狠狿研砚莚衍险养垟徉昜柍殃洋炴羏胦咬垚姚峣柼洮玅穾約荛药要轺钥亱咽峫拽捓枼洇頁俋咦咿奕姨峓帟帠庡弈恞拸施昱昳枱枻柂洂洟洢洫浂玴珆瓵疫羿胣舣荑虵蚁衵袂贻轶迻釔食饻垔垠姻泿洇洕狠胤茵荫音骃映栍盈矨荥荧郢哟俑勇勈栐哊囿姷宥峟幽怣斿柚牰疣祐羑诱迶俁俞俣兪哊挧昱狱禹禺秗竽紆舁茟茰虶语剈垣怨爰盶貟院陨哕恱栎約药说钥恽昷畇盾眃秐貟郧陨乽咱拶沯哉洅咱拶昝沯匨栆草蚤則柞荝怎咤奒奓挓柞柤查柵査栅炸眨虴夈粂战栈毡觇飐粀垗昭柖炤狣盄蚤赵侲姫帧弫挋昣浈珍珎胗貞轸陣鸩埩峥帧拯挣政炡狰俧咥咫姪峙庢庤恉挃指昵枳柣栀栉洔洷疧砋祑祗秓秖胑胝衹衼轵郦陟柊盅种茽衳衶重钟冑咮昼洀洲炿祝紂胄荮诪轴壴柚柱柷殶洙炢炷祝笁胑茱茿轴除挝拽孨専砖耑壵荘追盹窀胗斫浊炪兹呰呲咨姕姿秭籽耔茈茡茲荢虸总昮疭奏乼俎柤爼珇祖洅侳昨柞祚胙侶垏垒律挔捛闾籹衂虐侶挔捛律闾籹虐柘砓籷15笔画錒僾皚磑躷蝻鞌鞍墺嶴懊澆澳磝鴁墢罷罷瘢螁魬鳻磅镑暴緥蕔褒褴髱鴇輩鋇撪獖幤潷獘罷罼豍貏駜髲魮稹箯糄編緶艑蝙諚標熛膘諘鋲麃憋瘪镔墢嶏嶓撥播暴潑潘蕃踣鋍镈餑駊郶餔踩儏噆慙憯撡槽鄵憡噌層嶒缯擑艖儃嘽嬋幝廛撣潹潺緾蕆諂鋓閳骣廠瑺膓誯嘮嘲樔潮窲趠麨徹撤澈夦瞋諃賝霃噌憕撐撑撜樘澂澄緽趟噄墀徲慗殦漦瘛瞝翨褫誺踟遲骴齒徸憃憧樁潼緟蝩衝儊嘼廚樗篨諔諸鋤嘬膗暷篅噇幢撞牕瘡篅箺膞蝽醇諁趠踔輟醊龊糍縒螆賜辤飺餈骴暰樅樬潨熜牕瑽璁緫聦聪誴賨賩趣噈憱數槭趣踧醋麄撺鋑槯璀膵趡踤墫壿澊撮歵縒噠墶撘薘褟觰鞑叇曃緿蝳駘儋勯嘾彈憚撢撣潬潭賧儅瞊蕩趤噵導稻艔衜德噔墱嬁嶝澄慸敵樀潪甋締蝭踧题瘨蕇踮殦調踔艓蝶踢濎薡墥嬞懂箽蕫諌鋀餖獤蝳覩賭醏閬緞憞銳鋭頧墩墪壿撴潡凙墯橢縅噁蕚遻鋨頞頟颚额餓魤墢撥罸蕟髮噃墦嬎嬏幡憣樊潘範蕃魬魴鴋墢廢蕜蕟誹髴墳幩憤濆獖瞓蕡魵鳻僼篈鄷鋒鴌鴀嘸幞撫敷澓緮膚蕧蝜蝠蝮賦頫駙髴鳺鴔麩嘠噶槪骸橄槹皜稾稿鋯镐噶嶱擖獦镉鞈韐頜骼緪縆羮賡鲠匔澒碽銾鋛鞏撀穀緱褠骺嫴穀篐縎踻銽頢颳樌瘝輨横黆儈劊劌嬀嶡嶲撅撌暩槶槻槼潙螝磙緷輥鲧膕虢輠蝦襅鞐頦骸憨暵澏熯銲鋎鋡頜魧嘷暭澔獋皜皞諕镐蝎頜鹤嘿潶鞎撔横澋撔澒篊谾銾鋐篌糇翭骺幠戯撫槲槴歑熩箶糊蝴衚魱鳸嫿槬樗澅蕐螖諣踝輠鋘錵褢諙踝槵歓緩鲩鴅曂横熿璜皝篁艎蝗噅噕噧圚墯嬇寭慧憓戯撝暳槥潓翬蕙蝰螝輝輠麾緡劐劇嘰嶯撃撠暩槣樍樭潗濈畿瘠稷稽箿緝蕀蕺觭諅諆賫踑踖踦躸鞊鲫鹡齑價稼蝦鋏镓鞈頡頬駕儉劍劎墹樫澗熞箭箴糋緘翦蕑蕳諌諓賤趝踐踺險鲣鳽鹣僵嵹摾槳漿獎蔃螀儌劋噍嫶嬌嶕嶠嶣徺憍撟撹樔潐澆皛膠蕉蕎價擑潔羯蝔褯誱踕镼鞊頡魪僸凚嶜槿歏殣瑾璡觐鋟鹶黅幜憬擏澋璄靚幜熲皛駉慦樛蝤劇勮屦聥蝺諊諏趜踘踙踞躹鋤鋦駒鮔蕊踡鋑鋗镌韏餋噊噘嶡嶥憰撅撧潏熦爴獗瘚蕝蕞蕨觮镼鴂鴃寯懏餕鲪錺磕輡槺廤靠髛嶱樖瞌磕緙艐蝌課躻錒頦銵錓毆瞉褲骻儈墤蕢鄶鋛嘳嬇憒撌槶潰篑聧聩聭蕢蝰踩熴瑻醌閫噋頢蝲賚賫厱澜褴醂羮鋃閬嘮嶗憦撈潦澇獠躼樂樏畾磊蕌頛頪踜輘氂漦犛糎蔾蝷褵鋫鋰錺镉鲡鲤黎劆匳噒嫾憐碾磏稴練聨聫褳鲢樑諒輛輬靚嘹嫽寮嶚嶛憭撩敹潦熮獠缭遼巤颲凛凜嶙撛潾獜遴輘霊駖劉澑熮瑬瘤磂罶膢鋶镏駠鹠樓熡甊篓耧膢蝼噜戮撸樐樚澛熝膔觮趢踛辘醁魯魲論踚輪樂躶摩犘碼罵魸嘪蕒蝐賣邁槾樠澫熳璊瞒瞢氂犛瞐艒蝐蝥貓髳嬍篃蝐蝞鋂霉暪樠璊瞒儚橗瞑瞢蕄蝱鄸冪樒澠瞑糆緜緡緬臱蝒麪麫廟篎緲慜憫潣澠緡瞑嘿墨嫼摩瘼瞐瞙镆魩魹黙蝥艒霂誽镎魶魸摨褦蝻撓澆鬧縇餒殢縌觬誽貎輗鹝鹢撚撵碾輦嬈樢噛摰槷槸諗踗踙镊镍澝儂辳褥駑撋諾蹃噢縇歐毆熰甌縅耦膒蕅鴎潖輫樊潘盤磐鋬磅褜髱麃嶏賠輫醅霈噴濆嘭憉澎踫輣輧駍僻劈嶏磇罷蕃諀隦駓髬髲魮鴄篇緶翩蝙諚輧頨骿膘飘麃撆暼瘪慿箳輧頩潑駊噗墣撲暴潽獛舖舗諩鋪噐慼憇槣槭璂磎禥稽緝蕲襅觭諆賫踑踦擖儙厱槧潛潜篏羬蕁諐谴遷鋟嵹樯漒蔃僺嘺墝墧嫶嶠嶣憔撬碻箾蕉蕎鞒頝骹篋蕺踥噙嶔嶜撳擒斳槿鋟頜鳹慶擏樈漀磘請匔瞏窮璆篍緧蝤蝵銶敺毆璖蝺觑誳趣镼閴駈麹権踡韏墧慤確碻趞蝽嘫髯嬈蕘遶熱槦穃縙蝾褣镕糅蝚蕠蝡褥撋緛蝡蕊蕋蕤銳鋭潤撒潵僿毿潵犙糂馓磉褬艘槭澁縇槮儍噎擑樧閯霅魦鲨墠墡撣潬潸澘缮覢曏樉殤熵賞潲蕱審槮糂諗鋠震頣魫憴澠箵縄蕂奭箷翨蝨銴餙餝駛鲥鳾熟艏數樗樜樞潻澍熟蔬豎樉瞓誰蕣數箾嘶噝廝撕澌磃禩緦蕬賜鋖駟慫憽樬濍艘螋憟樎樕潥碿躻鋉餗撰選嬘澻熣穂誶賥遺潠箰蕵樎璅撻澾褟誻踏鞈曃駘儃嘽嘾墰墵彈憛憳撢歎潬潭瘫蕁蕈談賧醈劏樘磄糃羰膛蕩蝪趟躺镋醄鞉躻鋱滕蕛邆徲歒殢漽緹蕛蝭踢銻题髰磌窴覥賟頲斢窱調踔鋚鞗頫髫鲦蝶鋨濎聤蝏頲憅潼獞蕫斢緰鋀鋵墥槫墤尵噋魨橢駝駞鞋潫澫翫豌踠鋄鋔魭鲩誷輞寪慰潙潿熨熭犚磑緭緯蔿蝛蝟衛覣諉踓遺醀韑頠緼蕰魰鳼鴍瞈鹟踒噁墲嫵廡憮潕箼蕪蝥躻遻鋈鋘鋙嘶嘻噏嬆嬉嶲憘戯撕擕槢潝潟澌澙瘜磎縅膝蕮覤遲瞎磍縀蕸蝦諕霅嫺嫻憪撊撏暹澖稴箲線羬誸賢銽鋧險韯曏樣橡箱緗膷嘵憢撨獟獢皛箾誵銷霄骹勰噧寫屧撷擑擕暬潰緤緳縀缬蝎蝢鞋頡廞鋅箵篂鋞嘼糔銹噓嬃歔獝稸糈緖緰縃蔬蕦蝑豫魣儇撰暶潠璇盤禤箮翧蝖誸選鋗馔樰膤勲噀噚撏潠潭潯蕁蕈蕥襅鴉嬊嶖戭樮蝘谳醃險颜餍魇鴈樣餋駚儌嬈嶢嶤樂獟磘窯窰蕘鴁鹞噎擖擛曄潱皣瞱鄴靥餘儀億嬄撎槷槸毅熠熤熪熼瘞篒誼踦輢遺镒鹝鹢黓噖慭戭殥潭潯璌癊磤緸誾趛鞇影樱潁瑩璄璎禜膡蝿槦牅禜銿颙鲬憂槱牖牗蕕蝣蝤魷噊噢墺慾歶潏澳熨獝稶窳緰羭聥蓹蕍薁蝓諛豫賣遹鋊鋙雓頨餘魣鳿龉緣縁蜵蝝蝯褤駌魭樂箹銳閱閲奫澐熨磒緷緼蕓蕰蕴蝹鋆錺魳儎噆撍暫糌賛銺駔槽璅樍歵稷諎赜鞐增憎缯鋥樝觰霅駘嫸嶘谵輚醆骣幥暲樟璋賬嘲踔駋潧磌稹箴鋴镇震駗鴆徵撜趟鋥嬂幟徵慹憄摨摯漐潪熫稺膣觯質踬踯遲鋕鳷徸潨潼緟銿僽皺調諏賙輖駎嘱樦橥澍濐諔諸豬鋳駐檛膼撰瑼甎磗篆膞颛馔幢撞樁縋諈醊諄劅蕞諁諑踔鋜瘠糍輜鋅餈魸鼒樅熜熧糉緫緵縂翪艐蝬踨踪諏趣槭踤駔蕝蕞醉噂墫壿嶟撙遵嘬撮醋履慮樓氀箻膟膢魯㲶鋝鋢㨼鋝鋢㨼履氀慮箻膟㲶磔赭踷輙銸。
广东省惠州市2024-2025学年高三上学期第二次调研考试 数学 含解析
惠州市2025届高三第二次调研考试试题数学全卷满分150分，时间120分钟．2024.10注意事项：1答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上．2．作答单项及多项选择题时，选出每个小题答案后，用2B铅笔把答题卡上对应题目的答案信息点涂黑如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效．3非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效一、单项选择题：本题共8小题，每小题满分5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分l已知集合A={�2�x<5}，集合B={xl x2-4x<O}，则A^B=( ）A.(o,s)B.[2,4) c.(4,5) o.(-00,O)u[2,+oo)2已知复数z满足z2+l = 0,则lz+ll=( )A.3B.2C.l D．五3已知等差数列{a,,}前9项的和为27，如＝8，则a.oo= ()A.100B.99C.98 0.974在正方体ABCD-'4iB1Cp1中，棱BC,A戊的中点分别为E,F，则直线E F与平面ABBA所成角的正弦值为（）石 B. 森2石 D. 痀5已知向凳a,b满足：a=(✓3,1)，叫＝石，（兹－b ）·6=3，则向豐6在向榄五上的投影向榄为（）A胃气）B[竿i)C［告）叶亨订6已知函数f(x)=log2厅－2ax),aeR,则“a:s;O"是“函数f(x)在(1，七吩上单调递增＂的（）A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件7已知“水滴＂的表面是一个由圆锥的侧面和部分球面（常称为“球冠”)所围成的几何体如图所示，将“水滴＂的轴截面看成由线段AB,AC 和优弧BC所围成的平面图形，其中点B,C 所在直线与水平面平行，AB和AC与圆弧相切已知“水滴＂的“竖直高度”与“水平宽度”(“水平宽度”指的是平行千水4平面的直线截轴截面所得线段的长度的最大值）的比值为－，则sin乙BAC=<A3416 24A.-B .- C.—D .—55252538在统计某学校所有选择理科和文科的学生数据中，发现理科生多千文科生，女生多千男生，则关千本次学生样本的数据中，结论一定成立的是（）A理科男生多千文科女生B文科女生多千文科男生C理科女生多干文科男生D理科女生多于理科男生二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求全部选对的得6分，部分选对的得部分分，有选错的得0分9某公司为保证产品生产质量，连续10天监测某种新产品生产线的次品件数，得到关千每天出现的次品的件数的一组样本数据：3,4, 3, 1,5, 3, 2,5, 1, 3则关千这组数据的结论正确的是（）A极经是4B众数小千平均数c ．方差是2D数据的第80百分位数为4.510函数f (x) =A sin (cvx+ <p)(A> O,a> > 0树<§）的部分图象如图所示，现将f(x )的图象向左平移巴6个单位长度，得到函数g(x)的图象，则下列结论正确的是(2亡7兀X12兀A.<p =－一6B.(i)=2c ．函数）1= xf (x ＋王）是奇函数12 D.g (x )=2c os （2x -¾)II 如图，心形曲线L:x 2+(y -|入扩＝1与Y 轴交于A ,B 两点，点P 是L 上的一个动点，则（）ypXBA点［孚叩11(-1,1.）均在L 上B.IO月的最大值和最小值之和为3C 点P 的纵坐标的最大值为J5D.I PAl+IPB 怍2石三、填空题：本题共3小题，每小题5分，共15分．12．在（x+1)5的二项展开式中，各项的系数和为13椭圆于fi =l (a >b>O )的左、右顶点分别是A 、B ，左、右焦点分别是R 、F2，若I A F.I ,I F.Fzl,IF.纠成等比数列，则此椭圆的离心率e=.14若关千X的方程ln(ax4)＝[二了有实根，则a江护的最小值为四、解答题：本题共5小题，共77分解答应写出必要的文字说明、证明过程或演算步骤15（本题满分13分）已知函数f(x)=�X 2一x-2ln x(l)求曲线y=f(x)在点(l,f(1)）处的切线方程：(2)求函数f(x)在区间[1,e]上的晟小值16（木题满分15分）如图，四棱锥P-ABCD中，PA J_底面ABCD,AB II CD,AD=CD=l.乙BAD=120'，乙ACB=90°.D C(l)求证：BC上平面PAC:(2)若PA＝石，求平面PCD与平面PCA夹角的余弦值l7 （本题满分15分）已知双曲线C:x2-y2=l及直线l:y＝虹－1(])若l与C有两个不同的交点，求实数K的取值范围：(2)若l与C交千A,B两点，O是坐标原点，且t:.OAB的面积为J5，求实数K的值18（本题满分17分）记t:,.ABC的内角A,B,C的对边分别为a,b,c,已知a<b<c且tanA,tanB, t anC均为整数(I)求tanA,tanB, t anC的值，(2)设AC的中点为D,求乙CDB的余弦值19（本题满分17分）若数列{a,,}(1 s n s k, n E N*, k EN*）满足a,，叶0,1}，则称数列{a,,｝为K项0-1数列，由所有k项0-1数列组成集合M ks4)时，a,,=0,求数列{(-l)飞，｝的所有(])若伈｝是12项0-1数列，当且仅当n=3p(p E N*,p项的和；(2)从梊合M人．中仔意取出两个数列｛动，｛丸｝，记X=区|a,－b/|i=I＠求随机变量X的分布列，并证明：E(X)＞一：k2＠若用某软件产生k(k2'.:2)项0-1数列，记事件A =“第一次产生数字1"'B=“第二次产生数字l"'且0<P(A ) <1,0<P (B) <l若P(BIA)<P(B区），比较P(Al B)与P(AI B )的大小惠州市2025届高三第二次调研考试试题高三数学参考答案与评分细则一、单项选择题：本题共8小题，每小题满分5分，共40分．题号2345 678答案BDc BAADcl 【解析】因为B ={xl O < x <4}，所以A nB={xl 2�x<4}故选：B 2【解析】因为z 2+l=O,即z 2= -1,所以z ＝土，所以卜＋11=11士11=f言75了＝J5故选：D.的公妇为d，由已知得：｛9a, +36d =273【解析】设等劳数列{a ,,}，解得a,= -1, cl = 1,a, +9d =8所以a 100=a , + 99d = -1 + 99 = 98故选：C.4【解析】连接FB ，在正方体ABCD -f\B ,C 1D 1中，BC..l 平面A BB A ，棱BC 的中点为E,则BE..l 平面A BB I A ，而BFc 平面A BB A ，故BE..l BF,则乙EFB 即为迎线EF 与平面A BB I A 所成角，设正方体棱长为2,则BE=l,BF=.JB I F 2+B阻＝j了I ＝心，BE1✓6则EF =✓BF 2+BE 2＝拆，故sin乙E FB =－－＝－－＝一－故选：BEF拆6A lni ,DI L ,“K ,＇,'…,'} ，夕,j A5【解析】由例＝石，（2ii-b)·b =3,得2li·b -lbi 2=2li·b -2=3,即a 6=－525由已知得la:1=2,所以向摄6在向量a上的投影向量为彗向＝＼卢＝｀石，l)＝厂产，i)故选：A .as l6【解析】若函数f(x)在（l，切）上单调递增，则｛，解得a5-，Il-2a之02所以“a�O"是＂函数f(x)在(1.冲~)上单调递增”的充分不必要条件．故选：A7【解析】设优弧BC 所在圆的圆心为O,半径为R,连接OA ,OB ,OC 易知“水滴＂的＂竖直商度”为OA +R, OA +R 45 “水平宽度”为2R,由题意知＝一，解得OA=－R 因为AB 与圆弧相切千点B ,2R 3 3OB R 3 所以B 在Rt 心ABO 中，sin乙BAO =—=—=－冗OA 5 :::...R5，又乙BAO e l 0，一，（』4所以COS乙BAO=.Jl-sm 汔BAO ＝一，由对称性知，5乙BAO ＝乙CA O,则乙BAC=2乙BAO,3 4 24所以sin 乙BAC=2sin 乙BAOcos 乙BA0=2x-=-x-=—故选：D.5 5 258【解析】根据已知条件设理科女生有x 1人，理科男生有X 2人：文科女生有）'1人，文科男生有）5人；根据题意可知：X 1 + X 2 > Y i + Y 2'X i +Y i > X 2 + Y 2'根据同向不等式可加的性质有：X 1 + X 2 + X 1 + Y 1 > Y 1 + Y 2 + X 2 + Y 2'即X 1> Y 2，所以理科女生多千文科男生，C正确其他选项没有足够证据论证故选：C .二、多项选择题：本题共3小题，每小题满分6分，共18分．在每小题给出的四个选项中，有多项符合题目要求全部选对得6分，部分选对得部分分，有选错的得0分．题号I 9 I 10 I 11全部正确选项I A D I ABO I ACD9【解析】数据从小到大排列为：1,1, 2, 3, 3, 3, 3, 4, 5, 5对千A,该组数据的极差为5-1=4,故A正确：对于B,众数为3,平均数为lx2+2+3x4+4+5x210=3,两者相等，故B错误；对干C,方差为而伈－3)2x2+(2-3)2xl+(3-3)2x4+(4-3)2xl+(S-3)2x2] = 1.8,故C错误，对千D,10x80%=8,这组数据的第80百分位数为第8个数和第9个数的平均数4.5,故D正确故选：AD.10【解析】由图像可知：f(x)ma x = 2, A= 2:又f(0)=2s叩＝－l,故sinrp＝一L，又lrp|＜巴，所以rp＝－巴，所以A项正确，2 2 6已知f（气＝2sin（五0－勹＝0,由五点作图法可知：卫坛－巴＝亢，解得：OJ=2'所以B项正l2 12 6 l2 6确；故f(x) =2sin（三）则xj.（咕）＝2xsin2x设h(x)=xf.（咕）＝2xsin2x则h(-x)= 2(-x)sin(-2x) =2.xsin2x= h(x)，所以函数y=.-1;小号）是偶函数，故C项错误g(x)=f(x十艺）＝2s i n[2(x+：)－去］＝2s i n(2x＋艺）＝2c o s[�-(2x＋艺）］=2cos甘－2x)=2cos（三），所以D项正确故选：ABD.五II【解析】A选项，经验算，点(—,0和(-1,1)的坐标满足曲线L的方程x2 +(y-lxl)2 =L所以` o)和(-l,l）均在L上故2A项：确B 选项，I OP l ＝心三了，因为曲线L:x江(y-I 入扩＝l 关千Y 轴对称，当x 以0时，x 2 +(y-x)2 =l,设x=cos0, y-x= s in0,0e[－豆］，2 2.l+co s20 所以IOPl 2=.,\,:2+y 2=cos 20+(cos0+sin0)2 =l+�+sin20 23 1 3森l =-＋sin20+－cos20=－＋—sin (20 + rp ),其中tanrp ＝一，2 22 22 所以OP l min =[工石－�,10P 1m ax =[工石＋12 2 2 2 2 2，所以10月的最大值和最小值之和为石，故B项错误；C 选项，因为曲线L:x 2+(y -l x 忙＝1关千Y 轴对称，当x习0时，x 2+(y-x)2 =I ,则(y-x)2 =1-.,\,，2，所以y =x 土』7了因求，占P 的纵坐标的最大值，故取y =x+.[i':了，2又y 2=(x ＋石二了）＝1+2x../I 二了＝1+2[x.了7平1+.,\,;2+(l －入＂2)=2（当且仅当x 2＝上时等号2成立），所以y�.,fi ，故C项正确；x -D 选项，IPA I +I P B� 2✓3等价千点P 在椭圆上－＋—＝1内（包含椭圆），由B 项可知，即满足：322(cos0+sin0)2 +3cos 20 � 6,即2(l+sin20)+3(1+cos20)�6，整理得：23 4sin20 + 3cos20 � 5,即5sin(20+/3）�5'其中其中tan/3＝－，即sin(20+/3）�l 恒成立，则故D4项正确故选：A BD .三、填空题：本题共3小题，每小题5分，共15分．12.32五5314.e i12.【解析】当x =l 时，二项式展升式各项的系数和为25=32故答案为：3213【解析】由题意知I Mi l =a-c,I F;Fz l =2c,IF;科＝c+a,且三者成等比数列，则IFiFi l 2= IAF;I .I F;BIl石石即4c 2= (c-a )(c +a )= c 2 -a 2,所以e 2=－，所以e =—故答案为：—－55514【解析】设方程ln （釭＋勹＝k的实根为X。
低电荷态类硅离子能级的解析计算
低电荷态类硅离子能级的解析计算陈展斌【期刊名称】《《湖南工业大学学报》》【年(卷),期】2019(033)005【总页数】8页(P84-91)【关键词】硅原子; 相对论; 能量; 解析式; 变分法【作者】陈展斌【作者单位】湖南工业大学理学院湖南株洲 412007【正文语种】中文【中图分类】O562.31 研究背景多电子体系一直是原子物理工作者感兴趣的研究对象[1-4]。
硅原子及类硅离子最外层具有4 个电子，处于亚稳态。
由于其良好的物理性质，因而具有广泛的应用前景。
近年来，关于硅的应用研究成果层出不穷，如太阳能材料，团簇以及纳米复合材料方面都取得了很大的成功。
随着有机硅数量和品种的持续增长，应用领域不断拓宽，并形成了化工新材料的重要产品体系。
伴随着科学技术的发展，硅的应用领域还将进一步扩大。
这些应用也促进了人们对硅原子的结构和性质的研究。
利用多组态狄拉克福克方法和活动空间近似，Wu M.等[5]研究了中性硅原子的能级能量、跃迁几率和超精细结构。
利用多通道量子亏损理论，Liang L.等[6-7]计算了中性硅原子3pns 3P0（n=7～35）和3pnd 3P0（n=6～17）的能级和寿命。
利用相对论哈特利福克方法，B.C.Fawcett 等[8]计算了3s23p2-3s3p3 和3s23p2-3s23p3d 跃迁的波长和振子强度，并与实验结果进行了比较。
尽管目前已经有一些关于硅原子结构与性质的报道，然而由于复杂的物理体系，硅原子结构的计算大部分采取数值近似的方法，解析计算的研究非常匮乏。
本文基于多电子精细结构哈密顿和不可约张量理论[4]，在考虑电子间交换相互作用以及内外壳层电子的不同屏蔽效应的基础上，推导了中性硅原子和低电荷态类硅离子Z=14～17 能级的非相对论和相对论修正项的解析表达式。
分析了各相对论修正项的贡献，并与已有的实验结果进行比较。
2 理论2.1 非相对论能量公式的推导由量子力学知识可知，硅原子的非相对论哈密顿可以表示为[4]式中Z 为核电荷数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【精品优质】价值文档首发！营改增误区系列:6%销项税率的一般纳税人不能抵扣税率为17%的
进项税[税务筹划优质文档]
导读：提供税率为6%的现代服务业服务的一般纳税人，收到的增值税专用发票，按发票注明的增值税额抵扣（包括17%或13%等高于6%的增值税税率）
政策依据：
财税［2016］36号文件第二十五条规定：下列进项税额准予从销项税额中抵扣：
（一）从销售方取得的增值税专用发票（含税控机动车销售统一发票，下同）上注明的增值税额。
（二）从海关取得的海关进口增值税专用缴款书上注明的增值税额。
（三）购进农产品，除取得增值税专用发票或者海关进口增值税专用缴款书外，按照农产品收购发票或者销售发票上注明的农产品买价和13%的扣除率计算的进项税额。
计算公式为：
进项税额=买价×扣除率
买价，是指纳税人购进农产品在农产品收购发票或者销售发票上注明的价款和按照规定缴纳的烟叶税。
购进农产品，按照《农产品增值税进项税额核定扣除试点实施办法》抵扣进项税额的除外。
（四）从境外单位或者个人购进服务、无形资产或者不动产，自税务机关或者扣缴义务人取得的解缴税款的完税凭证上注明的增值税额。
误区解读：。