二维图形裁剪
计算机图形学二维图形的裁剪

垂直并指向屏幕里面,即右手坐标系中Z轴的负方向。 反过来,如果P在该边界线的左边(即外侧),这时AB×AP的方向与X-
Y平面垂直并指向屏幕外面,即右手坐标系中Z轴的正方向。 设:点P(x,y)、点A(xA,yA)、点B(xB,yB), 向量AB={(xB-xA),(yB-yA)}, 向量AP={(x-xA),(y-yA)}, 那么AB×AP的方向可由下式的符号来确定:
依次下去,相对于第三条、第四条边界线进行裁剪,最后输出的多边 形顶点序列即为所求的裁剪好了的多边形。如下图所示。
7.3.1 Sutherland-Hodgeman多边形裁剪
新的多边形顶点序列产生规则: 在用窗口一条边界及其延长线裁剪一个多边形时,该边界线把平面分
成两个部分:一部分称为边界内侧;另一部分称为边界外侧。 如下图所示,依序考虑多边形的各条边。假设当前处理的多边形的边为
V=(xB-xA)·(y-yA)-(x-xA)·(yB-yA)
(3-14)
因此,当V≤0时,P在边界线内侧; 而V>0时,P在边界线外侧。
练习
Sutherland-Hodgeman多边形裁剪中,常用向量叉积法来测试当前点P是 否在边界内侧。已知窗口边界A(30,100)、B(40,180),某点P(50, 300),请 问点P在边界内侧吗?
7.3 多边形的裁剪
多边形裁剪的常用算法 1.Sutherland-Hodgeman多边形裁剪 2.Weiler-Atherton任意多边形裁剪
7.3.1 Sutherland-Hodgeman多边形裁剪
Sutherland-Hodgman算法也叫逐边裁剪法,该算法是萨瑟兰德 (I.E.Sutherland)和霍德曼(Hodgman)在1974年提出的。这种算法采用了 分割处理、逐边裁剪的方法。 一、Sutherland-Hodgeman多边形裁剪算法思想:
二维图形的裁剪1

7.2.1 Cohen-Sutherland算法
2、判别 根据C1和C2的具体值,可以有三种情况: (1)C1=C2=0,表明两端点全在窗口
内,因而整个线段也在窗内,应予保留。
(2)C1&C2≠0(两端点代码按位作逻辑 乘不为0),即C1和C2至少有某一位同时为1,
表明两端点必定处于某一边界的同一外侧,因
Cohen-Sutherland 算法 (编码算法)
算法思想:
第一步 判别线段两端点是否都落在窗口内,如果是, 则线段完全可见;否则进入第二步; 第二步 判别线段是否为显然不可见,如果是,则裁 剪结束;否则进行第三步 ; 第三步 求线段与窗口边延长线的交点,这个交点将 线段分为两段,其中一段显然不可见,丢弃。 对余下的另一段重新进行第一步,第二步判断, 直至结束
裁剪过程是递归的。
7.2.1 Cohen-Sutherland算法
二、Cohen-Sutherland算法步骤:
1、分区编码 延长裁剪边框将二维平面分成九个区域,每个区域各用一个四位二进 制代码标识。各区代码值如图中所示。 四位二进制代码的编码规则是:
(1)第一位置1:区域在左边界外侧 (2)第二位置1:区域在右边界外侧 (3)第三位置1:区域在下边界外侧 (4)第四位置1:区域在上边界外侧 裁剪窗口内(包括边界上)的区域,四位二进制代码均为0。 设线段的两个端点为P1(x1,y1)和P2(x2,y2),根据上述规则, 可以求出P1和P2所在区域的分区代码C1和C2。
7.2.1 Cohen-Sutherland算法
一、Cohen-Sutherland算法思想: 该算法也称为编码算法,首先对线段的两个端点按所在的 区域进行分区编码,根据编码可以迅速地判明全部在窗口内的 线段和全部在某边界外侧的线段。只有不属于这两种情况的线 段,才需要求出线段与窗口边界的交点,求出交点后,舍去窗 外部分。 对剩余部分,把它作为新的线段看待,又从头开始考虑。 两遍循环之后,就能确定该线段是部分截留下来,还是全部舍 弃。
CG11-二维图形裁剪
二维裁剪:线段裁剪 线段裁剪处理的基础有两个方面:
● 对象裁剪方法 ● 其它裁剪方法
– 尤其是对不能确定的线段,要计算 它与裁剪边界的交点,再通过对线 段的端点进行“内 - 外检测”来处 理线段。
裁剪
裁剪后
线段裁剪举例
☆二维裁剪定义 线段P1P2 ☆点的裁剪 由下端点 P1 开始,依次按左、右、 P2 ☆线段裁剪 上、下边界对 P1 检查,发现端点位 ● 线段裁剪举例 P2’ ◘ 算法举例 于裁剪窗口下。
裁剪窗口
二维裁剪时机选择
☆二维裁剪定义
◘ 二维裁剪时机
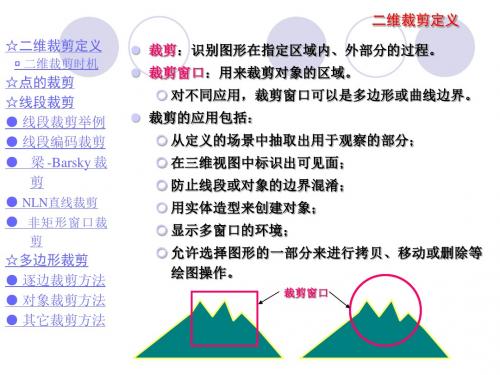
裁剪算法可用于世界坐标系中, 世界坐标系下的裁剪只有窗口内的部分映射到设备 空间中,而将落在窗口外的图形部分删除。
☆点的裁剪 ☆线段裁剪 ● 线段裁剪举例 ● 线段编码裁剪 ● 梁 -Barsky 裁 剪 ● NLN直线裁剪 ● 非矩形窗口裁
基本认识:裁剪窗口是二维对象;线段是一维对 象,两个对象维数不同不便比较。 解决思路:将待裁剪线段及裁剪矩形窗口均看作 点集,那么,裁剪结果即为两点集的交集。
解决办法:
设:P1P2所在直线为L; 记:该直线(或其延长线)与裁剪窗口的两交点 为Q1Q2,称为Q1Q2诱导窗口,它是一维的。 P1P2 关于矩形窗口的裁剪结果与 P1P2 关于诱 导窗口的裁剪结果是一致的
◘ 区域码生成 ◘ 内外点判断 ◘ 算法举例 ◘ 算法举例(续)
– 根据线段端点的区域码,可快速判断线段是否完全在裁 剪窗口内或外:
完全在窗口边界内的线段两个端点的区域码均为0000;
两个端点区域码同样位置都为 1的线段完全在裁剪矩形外。
– 测试线段更好的方法是对两个端点的区域码进行逻辑与 操作:
图形学二维裁剪实验报告

专业班级:学号:姓名:一、试验名称:二维裁剪二、试验目的:在二维观察中,需要在观察坐标系下对窗口进行裁剪,即只保留窗口内的那部分图形,去掉窗口外的图形。
二维裁剪是用计算机生成图形最基本的技能,通过本实验使学生掌握如何用计算机进行二维裁剪并熟悉开发环境。
三、实验原理:算法源代码:void CMyView::OnDraw(CDC* pDC){CMyDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data herePoint FrameLT,FrameRB;Point P[5];FrameLT.x=150;FrameLT.y=150;FrameRB.x=320;FrameRB.y=320;pDC->Rectangle((int)FrameLT.x,(int)FrameLT.y,(int)FrameRB.x,(int)FrameRB. y);for(int i = 0; i < 5; i++){P[i].x = (float)(260 + 150*cos(72*i*PI/180) +0.5);P[i].y = (float)(260 + 150*sin(72*i*PI/180) +0.5);}专业班级:学号:姓名:pDC->MoveTo((int)P[0].x,(int)P[0].y);pDC->LineTo((int)P[2].x,(int)P[2].y);pDC->LineTo((int)P[4].x,(int)P[4].y);pDC->LineTo((int)P[1].x,(int)P[1].y);pDC->LineTo((int)P[3].x,(int)P[3].y);pDC->LineTo((int)P[0].x,(int)P[0].y);}void CMyView::Code(Point FrameLT,Point FrameRB,Point P,unsigned char *Flag){unsigned char flag=0;if(P.x<FrameLT.x) flag+=1;if(P.x>FrameRB.x) flag+=2;if(P.y>FrameRB.y) flag+=4;if(P.y<FrameLT.y) flag+=8;(*Flag)=flag;}void CMyView::Clipping(Point FrameLT,Point FrameRB,Point LineSP,Point LineEP){CClientDC dc(this);unsigned char flagSP,flagEP,flagAND,flagOR;double k=(LineEP.y-LineSP.y)/(LineEP.x-LineSP.x);Code(FrameLT,FrameRB,LineSP,&flagSP);Code(FrameLT,FrameRB,LineEP,&flagEP);专业班级:学号:姓名:flagAND=flagSP & flagEP;if(flagAND!=0)return;while(flagSP!=0||flagEP!=0){flagOR=flagSP|flagEP;if((flagOR&0x01)==1){if((flagSP&0x01)==1){LineSP.y=(float)(LineSP.y+k*(FrameLT.x-LineSP.x)); LineSP.x=FrameLT.x;Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.y=(float)(LineEP.y+k*(FrameLT.x-LineEP.x)); LineEP.x=FrameLT.x;Code(FrameLT,FrameRB,LineEP,&flagEP);}}if((flagOR&0x02)==2){if((flagSP&0x02)==2){LineSP.y=(float)(LineSP.y+k*(FrameRB.x-LineSP.x)); LineSP.x=FrameRB.x;专业班级:学号:姓名:Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.y=(float)(LineEP.y+k*(FrameRB.x-LineEP.x)); LineEP.x=FrameRB.x;Code(FrameLT,FrameRB,LineEP,&flagEP);}}if((flagOR&0x04)==4){if((flagSP&0x04)==4){LineSP.x=(float)(LineSP.x+(FrameRB.y-LineSP.y)/k); LineSP.y=FrameRB.y;Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.x=(float)(LineEP.x+(FrameRB.y-LineEP.y)/k); LineEP.y=FrameRB.y;Code(FrameLT,FrameRB,LineEP,&flagEP);}}if((flagOR&0x08)==8){专业班级:学号:姓名:if((flagSP&0x08)==8){LineSP.x=(float)(LineSP.x+(FrameLT.y-LineSP.y)/k); LineSP.y=FrameLT.y;Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.x=(float)(LineEP.x+(FrameLT.y-LineEP.y)/k); LineEP.y=FrameLT.y;Code(FrameLT,FrameRB,LineEP,&flagEP);}flagAND=flagSP&flagEP;if(flagAND!=0)return;}dc.MoveTo((int)LineSP.x,(int)LineSP.y);dc.LineTo((int)LineEP.x,(int)LineEP.y);}}void CMyView::OnCut() //裁剪{// TODO: Add your command handler code hereCClientDC dc(this);CPen pen(PS_SOLID,1,RGB(255,255,255));CPen *pOldpen = dc.SelectObject(&pen);专业班级:学号:姓名:CBrush*pBrush=CBrush::FromHandle((HBRUSH)GetStockObject(NULL_BRUSH));dc.SelectObject(pBrush);Point FrameLT,FrameRB;Point P[5];FrameLT.x=150;FrameLT.y=150;FrameRB.x=320;FrameRB.y=320;dc.Rectangle((int)FrameLT.x,(int)FrameLT.y,(int)FrameRB.x,(int)FrameR B.y);for(int i = 0; i < 5; i++){P[i].x = (float)(260 + 150*cos(72*i*PI/180) +0.5);P[i].y = (float)(260 + 150*sin(72*i*PI/180) +0.5);}dc.MoveTo((int)P[0].x,(int)P[0].y);dc.LineTo((int)P[2].x,(int)P[2].y);dc.LineTo((int)P[4].x,(int)P[4].y);dc.LineTo((int)P[1].x,(int)P[1].y);dc.LineTo((int)P[3].x,(int)P[3].y);dc.LineTo((int)P[0].x,(int)P[0].y);dc.SelectObject(pOldpen);专业班级:学号:姓名:dc.Rectangle((int)FrameLT.x,(int)FrameLT.y,(int)FrameRB.x,(int)FrameR B.y);Clipping(FrameLT,FrameRB,P[0],P[2]);Clipping(FrameLT,FrameRB,P[2],P[4]);Clipping(FrameLT,FrameRB,P[4],P[1]);Clipping(FrameLT,FrameRB,P[1],P[3]);Clipping(FrameLT,FrameRB,P[3],P[0]);}四、实验总结:裁剪处理的主要步骤是:①图元关于窗口内外关系的判别;②图元与窗口的求交。
中间区段法裁剪

中间区段法裁剪
中间区段法裁剪(Middle Segment Clipping)是计算机图形学
中一种常用的二维裁剪算法,主要用于裁剪直线和多边形等图形。
中间区段法裁剪的基本思想是:首先确定裁剪窗口的边界,并将其等分为上、下、左、右四个方向的区段。
接着,根据裁剪窗口与图形在平面上的相对位置关系,决定各个区段是否需要进行裁剪。
最终,根据裁剪结果进行图形的显示或丢弃。
具体裁剪过程如下:
1. 确定裁剪窗口的边界:左边界(Xmin)、右边界(Xmax)、上边界(Ymin)和下边界(Ymax)。
2. 以直线为例,对于每一条线段,根据起点(P1)和终点
(P2)的位置关系,判断其是否需要进行裁剪。
3. 首先根据P1和P2的水平位置关系判断是否在裁剪窗口的
左右区段内。
若在同一区段内,则根据垂直位置关系进一步判断是否在裁剪窗口的上下区段内。
若在裁剪窗口内,则直接保留该线段。
若跨越区段边界,则根据裁剪窗口与线段的交点计算新的起点和终点,并进行裁剪。
4. 根据裁剪结果进行线段的显示或丢弃。
中间区段法裁剪的优点是相对简单、高效,适用于直线和多边形等较简单的图形。
缺点是无法处理曲线和复杂图形的裁剪。
在实际应用中,可以与其他裁剪算法结合使用,以实现更复杂的图形裁剪效果。
计算机图形学第6章二维图形的裁剪

• 重点:掌握二维图形点、线段、多边形和字符的裁剪算法 。
• 难点:理解二维图形的裁剪算法思想并且用C语言进行算法 的实现。
一、裁剪的意义 为了描述图形对象,我们必须存储它的全部信息,但有时为了达到分 区描述或重点描述某一部分的目的,往往将要描述的部分置于一个窗口内, 而将窗口外的部分“剪掉”,这个处理过程叫做裁剪,裁剪在计算机图形 处理中具有十分重要的意义。 裁剪实质上是从数据集合中抽取信息的过程,这个过程是通过一定的 计算方法来实现。
7.2.2 中点分割算法
二、中点分割算法实现: 1、将直线的两端点P1、P2编码得:C1、C2; 2、判别 根据C1和C2的具体值,可以有三种情况: (1)C1=C2=0,表明两端点全在窗口内,因而整个线段也在窗内, 应予保留。 (2)C1&C2≠0(两端点代码按位作逻辑乘不为0),即C1和C2至少 有某一位同时为1,表明两端点必定处于某一边界的同一外侧,因而整个线 段全在窗外,应予舍弃。 (3)不属于上面两种情况,均需要求交点。
如果上面四个不等式中任何一个不满足,则点(x,y)位于窗口之 外。 对于任意多边形窗口,需要根据多边形内点的判别准则进行判断。
7.2 线段的裁剪
直线段的裁剪比点复杂,其裁剪方法又是多边形裁剪和三维图形裁剪的 基础。 一、直线裁剪的基本思想 判断直线与窗口的位置关系: 1.确定直线是完全可见; 2.部分可见; 3.还是完全不可见。 对部分可见线段,求出它与窗口边界的交点,并将窗口内的线段输出。
一、中点分割算法思想: 1、中点公式
7.2.2 中点分割算法
2、中点分割法求交点的规则 如图中所示,当线段P1P2求出中点P后,舍弃线段的哪部分,由下面 两条规则决定:
中点分割法求交点规则
计算机图形学第7章二维图形的裁剪(2_3)

7.3.1 Sutherland-Hodgeman多边形裁剪 3、对多边形的n条边进行处理,对当前点号的考虑为:0~n-1。
for(i=0;i<n;i++) { if(当前第i个顶点是在边界内侧) /*对左边界:p[i][0]>=xmin */ { if(flag!=0) /*前一个点在外侧吗?*/ { flag=0;/*从外到内的情况,将标志置0,作为下一次循环的前一点标志*/ j++; q[j][0]=求出交点的x方向分量; /*将交点q放入新多边形*/ q[j][1]=求出交点的y方向分量; } j++; q[j][0]= p[i][0]; /*将当前点p放入新多边形*/ q[j][1]= p[i][1]; } else { if(flag==0) /*前一个点在内侧吗?*/ { flag=1;/*从内到外的情况,将标志置1,作为下一次循环的前一点标志*/ j++; q[j][0]=求出交点的x方向分量; /*将交点q放入新多边形*/ q[j][1]=求出交点的y方向分量; } } s[0]=p[i][0]; /*将当前点作为下次循环的前一点*/ s[1]=p[i][1]; }
7.2.3 梁友栋-Barsky裁剪算法
XWmin X 1 Xu ' XWmax X 1 Xu ' YWmin Y1 Yu ' YWmax Y1 Yu '
XWmin X 1 Xu '
这四个不等式可以表示为:
XWmax X 1 Xu ' YWmin Y1 Yu ' YWmax Y1 Yu '
7.2.3 梁友栋-Barsky裁剪算法
[计算机软件及应用]二维图形裁剪
![[计算机软件及应用]二维图形裁剪](https://img.taocdn.com/s3/m/1f91f2d47c1cfad6195fa79e.png)
①若P1P2完全在窗口内,则显示该线段P1P2,简称“取”之;
②若P1P2完全在窗口外,则丢弃该线段,简称“舍”之;
③若线段既不满足“取”的条件,也不满足“舍”的条件,则 求线段与窗口边界的交点,在交点处把线段分为两段,其 中一段完全在窗口外,可舍弃之,然后对另一段重复上述 处理。
核心思想:分区编码和线段分割。
当Qi =0时 若Di <0 时,线段不可见
(如图中AB,有QR=0,DR<0)
若Di >0 时, 分析另一D, (如图中的EF就是这种情况,它使QL=0, DL>0和QR=0,DR>0。这时由于EF和x=xL 及x=xR平行,故不必去求出EF和x=xL及 x=xR的交点,而让EF和y=yT及y=yB的交点 决定直线段上的可见部分。)
#define LEFT 1 #define RIGHT 2 #define BOTTOM 4 分区编码方法:图形区域划分成九个区域。 #define TOP 8
编码原则
四位编码 1111 表示端点所处的位置:
1 1 1 1
(--->) 上 下 右 左
第一位为“1”时,表示点在y=yT的上方; 第二位为“1”时,表示点在y=yB的下方;
例:分别给下列直线段编码,并判断是否需要剪裁。
P2
C2=1010
C
C1=0001
P2
C2=0000
D A P1 P2
C1=0000
P2
C2=0000
P1 B P1
C1=0100 C2=0101
P1
C1=0101
例:Cohen-SutherLand算法过程:
过程: 1)输入线段AB的两端点坐标A(x0,y0)、B(x1,y1),以及裁剪窗口的四 条边界:yt,yb,xl,xr。 2)对AB编码,A的编码codeA=0001,B的编码为codeB=0110。 3)线段AB裁剪的基本过程(按左右下上的顺序): ①由于codeA | codeB≠0,对AB不能全部保留;又因为codeA & codeB=0,对 AB不能全部舍弃,因此要对AB进行求交处理。 ②由codeA=0001知A在窗口左边外侧,按左右下上的顺序求AB与窗口左边 交点为P1,AP1必在窗口外,故裁剪掉,并用A替换P1。如图(b)所示。 (交点替换是为了方便编程循环)。 ③对P1B重复上述处理。A(原P1)编码为0000,B编码为0110;由于A(原 P1)已在窗口内,交换A和B的坐标值与编码,则B编码为0000,A编码变为 0110,按左右下上顺序求得右交点为P3;A(原B)P3必在窗口外,故裁剪掉, 并用A替换P3。如图(c)所示。 ④A的编码还没有达到0000,再求得下边交点为P2,AP2必定在窗口外,故 裁剪掉,并用A替换P2。如图(d)所示。 ⑤对剩下的直线段AB再进行判断,现在A编码为0000,B编码为0000,由于 codeA | codeB=0,全在窗口中,故全部保留。 最后得到裁剪后的线段为AB,算法结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“取景器”=窗 口
视区1 视区2 (viewport)
裁剪的目的
判断图形元素是否落在裁剪窗口之内并找出其位
于内部的部分
裁剪处理的基础
图元关于窗口内外关系的判别 图元与窗口的求交 假定条件 矩形裁剪窗口:[xmin,xmax]×[ymin,ymax]
待裁剪点或线段:
• 点裁剪
– 点(x, y)在窗口内的充分必要条件是:
Sutherland-Hodgman算法
思路:将多边形边界作为一个整体,分而治之。将多 边形的各边先相对于窗口的某一条边界进行裁剪,然 后将裁剪结果再与另一条边界进行裁剪,如此重复多 次,便可得到最终结果。 流水线过程(左上右下):左边的结果是上边的开始。 亦称逐边裁 剪算法
– 内侧空间与外侧空间 – 多边形的边与半空间的关系
E
A
A
B B F
三、多边形裁剪
• 错觉:直线段裁剪的组合? 关键:要保持窗口内多边形的边界部分,而且要将窗
框的有关部分按一定次序插入多边形的保留边界之间, 从而使剪裁后的多边形的边仍然保持封闭状态。
• 新的问题:
1)边界不再封闭,需要用窗口边界的恰当部分来封闭 它,如何确定其边界?
2)一个凹多边形可能被裁剪成几个小的多边形,如何 确定这些小多边形的边界?
对余下的另一段重新进行第一步,第二步判断,
直至结束
编码判断
当线段的两个端点的编码的逻辑“与”非零时 ,线段
为显然不可见的。也可以进行“按位与”运算,可知
这两个端点是否同在视区的上、下、左、右; 如code1=0101,code2=0110,则code1&code2=0100,表示 在窗口下方。 问题:显然可见的编码如何判断??
t0
P0 P1 1
t2 t1
t3
3.始边和终边的确定及交点计算:
令 QL= △x QR= △x QB= △y QT= △y DL= x0-xL DR= xR-x0 DB= y0-yB DT= yT-y0
参数交点为: ti= Di / Qi i=L,R,B,T
Qi <0 ti为与始边交点参数
Qi >0
线段的参数表示
x=x0+t△x
y=y0+t△y △x=x1-x0
0<=t<=1 △y=y1-y0
窗口边界的四条边分为两类:始边和终边。
若x 0 x xL为始边,x xR为终边。 若x 0 x xL为终边,x xR为始边。 若y 0 y y B为始边,y yT 为终边。 若y 0 y y B为终边,y yT 为始边。
y
其中k为斜率。上述直线方程与窗口各边界的交点为:
x2 x1
( x x1 ) y1 k ( x x1 ) y1
左:
右: 下: 上:
x xL k y k ( x L x1 ) y1
x xR k y k ( x R x1 ) y1
x min x x max
y min y y max
问题:对于任何多边形窗口,如何判别?
P1 Wyt P3 P2
Wyb
Wxl Wxr
二、线段裁剪
C A
y=yT E y=yB
B
D
线段相对于该窗口的情况有:
x=xL
x=xR
①线段全部位于窗口的内部(A); ②线段全部位于窗口外部(B、C); ③线段的中间部分在窗口内,而二端点在窗口外部 (D); ④线段的一端在窗口内,而另一端在窗口外(E)。
光标看作小的裁剪窗口。)
梁友栋-Barsky算法
设要裁剪的线段是P0P1。 P0P1和窗口边界交于 A,B,C,D四点,见图。 算法的基本思想是从A,B 和P0三点中找出最靠近的 P1点,图中要找的点是P0。 从C,D和P1中找出最靠近 P0的点。图中要找的点是 C点。那么P0C就是P0P1线 段上的可见部分。
例:分别给下列直线段编码,并判断是否需要剪裁。
P2
C2=1010
C
C1=0001
P2
C2=0000
D A P1 P2
C2=0000
P1 B P1
C1=0100 C2=0101
P2
C1=0000
P1
C1=0101
例:Cohen-SutherLand算法过程:
过程: 1)输入线段AB的两端点坐标A(x0,y0)、B(x1,y1),以及裁剪窗口的四 条边界:yt,yb,xl,xr。 2)对AB编码,A的编码codeA=0001,B的编码为codeB=0110。 3)线段AB裁剪的基本过程(按左右下上的顺序): ①由于codeA | codeB≠0,对AB不能全部保留;又因为codeA & codeB=0,对 AB不能全部舍弃,因此要对AB进行求交处理。 ②由codeA=0001知A在窗口左边外侧,按左右下上的顺序求AB与窗口左边 交点为P1,AP1必在窗口外,故裁剪掉,并用A替换P1。如图(b)所示。 (交点替换是为了方便编程循环)。 ③对P1B重复上述处理。A(原P1)编码为0000,B编码为0110;由于A(原 P1)已在窗口内,交换A和B的坐标值与编码,则B编码为0000,A编码变为 0110,按左右下上顺序求得右交点为P3;A(原B)P3必在窗口外,故裁剪掉, 并用A替换P3。如图(c)所示。 ④A的编码还没有达到0000,再求得下边交点为P2,AP2必定在窗口外,故 裁剪掉,并用A替换P2。如图(d)所示。 ⑤对剩下的直线段AB再进行判断,现在A编码为0000,B编码为0000,由于 codeA | codeB=0,全在窗口中,故全部保留。 最后得到裁剪后的线段为AB,算法结束。
1)求出直线P0P1与窗口的交点I,如图(a)所示。
2)取P0 I线段显示,擦除I P1线段,并将P1替换I,即 得P0P1线段,裁剪结束。如图(b)所示。
P0 I
P0 P1
P1
(a) (b)
求线段与窗口交点
P1 设线段两端点坐标为:( x1,y1 ) 和 P2 ( x2,y2 ) 则过这两点 y2 y1 的直线方程为:
二维图形裁剪
裁剪概述
直接求交算法; Cohen-Sutherland算法;(重点,算法实现) 梁友栋-Barsky算法
线段裁剪
多边形裁剪
Sutlerland_Hodgman算法(难点,算法实现)
Weiler-Athenton算法
字符裁剪
一、裁剪概述
裁剪:是裁去窗口之外物体或物体部分的一种操作。
ti为与终边交点参数
当Qi =0时 若Di <0 时,线段不可见
(如图中AB,有QR=0,DR<0)
若Di >0 时, 分析另一D, (如图中的EF就是这种情况,它使QL=0, DL>0和QR=0,DR>0。这时由于EF和x=xL 及x=xR平行,故不必去求出EF和x=xL及 x=xR的交点,而让EF和y=yT及y=yB的交点 决定直线段上的可见部分。)
待裁剪线段和窗口的关系 线段完全可见 显然不可见 线段至少有一端点在窗口之外,但非显然不可见
裁剪
保留
丢弃 为提高效率,算法设计时应考虑: (一)快速判断线段完全在窗口内或外的情形; (二) 设法减少裁剪情形中求交次数和每次求交时所需的计算量。
直接求交算法
基本思想是:判断直线与窗口的位置关系,确定该直 线是完全可见、部分可见或完全不可见,然后输出处 于窗口内线段的端点,并显示此线段。
#define LEFT 1 #define RIGHT 2 #define BOTTOM 4 分区编码方法:图形区域划分成九个区域。 #define TOP 8
编码原则
四位编码 1111 表示端点所处的位置:
1 1 1 1
(--->) 上 下 右 左
第一位为“1”时,表示点在y=yT的上方; 第二位为“1”时,表示点在y=yB的下方;
编码判断
当线段的两个端点的编码的逻辑“与”非零时 ,线段
为显然不可见的。也可以进行“按位于”运算,可知
这两个端点是否同在视区的上、下、左、右; 如code1=0101,code2=0110,则code1&code2=0100,表示 在窗口下方。 问题:显然可见的编码如何判断??
对一条线段的可见性测试方法: (1)若线段两个端点的四位二进制编码全为0000,即两端 点编码逻辑或运算为0,那么该线段完全位于窗口内,可直 接保留; (2)对两端点的四位二进制编码进行逻辑与运算,若结果 不为零,那么整条线段必位于窗口外,可直接舍弃; (3)否则,这条线段既不能直接保留,也不能直接舍弃, 它可能与窗口相交。 此时,需要对线段进行再分割,即找到与窗口边线的一个交 点,根据交点位置,赋予四位二进制编码,并对分割后的线 段按照一定的顺序(如左右下上)进行检查,决定保留、舍 弃或再次进行分割。重复这一过程,直到全部线段均被舍弃 或保留为止。
①若P1P2完全在窗口内,则显示该线段P1P2,简称“取”之;
②若P1P2完全在窗口外,则丢弃该线段,简称“舍”之;
③若线段既不满足“取”的条件,也不满足“舍”的条件,则 求线段与窗口边界的交点,在交点处把线段分为两段,其 中一段完全在窗口外,可舍弃之,然后对另一段重复上述 处理。
核心思想:分区编码和线段分割。
C
y=yT A E y=yB
练习:请给出右图的线 段端点编码(端点编码:
定义为它所在区域的编码)
B
D
x=xL
x=xR
Cohen-Sutherland 算法步骤
第一步 判别线段两端点是否都落在窗口内,如果是,
则线段完全可见;否则进入第二步;
第二步 判别线段是否为显然不可见,如果是,则裁 剪结束;否则进行第三步 ; 第三步 求线段与窗口边延长线的交点,这个交点将 线段分为两段,其中一段显然不可见,丢弃。
