希望杯教程 四年级数学第二讲(计数问题)
第九届小学“希望杯”全国数学邀请赛四年级第二试真题.

第九届小学“希望杯”全国数学邀请赛四年级第二试真题一填空(每小题5分,共60分)1.计算:234+432-4×8+330÷5=2.四(1)班全体同学站成一排,当从左往右报数时,小华报:18;当从右往左报数时,小华报:13。
那么,该班有学生名。
3.如果25×口÷3×15+5=2005,那么口_________.4.。
图1是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有个。
5.在括号内填上两个相邻的整数,使等式11112()()=-成立。
6.由数字0,3,6组成的所有三位数的和。
7.某种品牌的电脑降价20%后,每台售价为4592元,则该品牌电脑降价前每台售价______元。
8.已知两个自然数的积是35,差是2,则这两个自然数的和是_______。
9.把1991,1992,1993,1994,1995分别填入图2中的5个方格中,使得横排的三个方格中的数的和等于竖列的三个方格中的数的和。
则中间方格中能填的数是。
10.图2是3×3的正方形网格,1与2相比,较大的是__________。
11.小明从家出发,先向东偏北30°的方向跑了350米到达点A ,接着向北偏西30°的方向跑了200米到达点B ,然后又向西偏南30°的方向跑了350米到达点C ,这时小明距家 米。
12.在图5的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N= 。
二、解答题(每小题15分,共60分)每题都要写出推算过程。
13.将一副三角板摆放在一起(可以叠放),使同时出现15°,30°,45°,60°,75°,90°,105°这七个角,请画图说明并表示出这些角。
14.连续写出从1开始的自然数,写到2008时停止,得到一个多位数:123456789…2008请说明:这个多位数除以3,得到的余数是几?为什么?15.甲、乙、丙三辆车同时从A 地出发驶向B 地,依次在出发后5小时、5512 小时、612小时与迎面驶来的一辆卡车相遇。
2024希望杯复赛四年级试题答案解析.pptx

【解析】击-砺=100“+1昉+C-100r_10/,-。=100(«-c)-(«-c)=200-2
=198
5、正方形A的边长是10,若正方形B,C的边长都是自然数,且B1C的面积和等于A的面
积,则B和C的边长的和是
.
【答案】14
【解析】B1C的面积和等于A的面积,即B1C的面积和是10x10=100,则tP+c⅛100,
2024希望杯复赛四年级试题答案解析
2024年第14届四年级希望杯复赛解析 一、填空题(每小题5分,共60分) 1、计算:2024×2024-2024×2024+2024×2024-2024×2024= . 【答案】1 【解析】 2016×2014-20l3×20l5+2012×2015-2013×2016 =2。I6χ(2。I4-2。I3)-2。I5×(2。I3-2。I2) =20l6×l-20l5×l =1 2、60的不同约数(1除外)的个数是 【答案】11 【解析】60=l×60=2×30=3×2。=4×15=5×12=6×10. 60的约数(1除外)有:2、3、4、5、6.10、12、15,20、30、60,共11个。 3、今年丹丹4岁,丹丹的苦爸28岁,a年后,苦苦的年龄是丹丹年龄的3倍,则a的值
所以正方形e的面积是:6×6=36(平方厘米) 14、有两块地,平均亩产板食675千克,耳中第一块地是5亩,亩产辐食705千克,假如 其次块地亩产粮食650千克,那么,其次块地有多少亩? 【解析】第一块地总共比平均少:(705-675)×5=150(千克) 所以其次块地比平均多150千克 只次块地的亩数:150÷(675-650)=6(亩) 4个连续的自然数,从小到大依次是11的倍数、7的倍数、5的倍数、3的倍数,求这4个自然数的和的最小值. 【解析】方法一:设这4个连续的自然数为a、a+1、a+2.a+3∙ 依据题京,a+3是3的倍数,所以,a也是3的倍数,而a是11的倍数,则a是33的倍数. 又因为第三个数a+2是5的倍数,个位为0或者5. 则第一个数a的个位应当为3或者8. 又a是33的倍数, a最小为33x1=33,后面的数为34、35、36,而34不是7的俄,解除. a可以为33×6=168,后面的数为169、170、171,而169不是7的倍数,解除.
4四年级希望杯答案及过程

四年级希望杯1、计算:19×75+23×25=【答案】2000【考点】四则运算【解析】原式=1425+575=20002、定义新运算:a△b=(a+b)×b,a□b=a×b+b,如:1△4=(1+4)×4,1□4=1×4+4按从左到右的顺序计算:1△2□3=【答案】21【考点】定义新运算【解析】1△2=(1+2)×3=6,6□3=6×3+3=213、abc是三位数,若a是奇数,且abc是3的倍数,则abc最小是【答案】111【考点】数论【解析】a为奇数,且要求最小,则a=1,b=0又要求为3的倍数,则a+b+c为3的倍数,所以c=24、三个连续的自然数的乘积是120,它们的和是【答案】15【考点】分解质因数【解析】120=2×2×2×3×5=4×5×6,则他们三个数的和为155、已知x,y是大于0的自然数,且x+y=150。
若x是3的倍数,y是5的倍数,则(x,y)的不同取值有对【答案】9【考点】数论【方法】由题意得,x,y为3和5的公倍数才符合要求,公倍数有15、30、45、60、75、90、105、120、135则共有9对不同取值6、如果8×(2+1÷x)=18,则x=【答案】4【考点】解方程【解析】等式两边分别除以8,得2+1÷x=2.25,再等式两边分别减去2得1÷x=0.25,则x=47、观察以下的一列数:11,17,23,29,35,……若从第n个数开始,每个数都大于2017,则n=【答案】336【考点】等差数列【解析】等差数列中,项数=(末项-首项)÷公差+1,则n最小为(2017-11)÷6+1,则n=3368、图1由20个方格组成,其中含有A的正方形有个【答案】13【考点】图形计算【解析】含有A的正方形边长为1的有1个,边长为2的有4个,边长为3的有6个,边长为4的有2个,共有1+4+6+2=13个9、图2由12个面积为1的方格组成,则图中和阴影梯形面积相同的长方形有个【答案】10【考点】图形计算【过程】由题意可知阴影部分面积为3,则面积为3的长方形竖着排列有4个,横着排列有6个,则面积为3的长方形共有4+6=10个10、某学习小组数学成绩的统计图如图3,该小组的平均成绩是分【答案】90【考点】平均数问题【解析】平均成绩为(6×85+3×89+5×95+1×98)÷(6+3+5+1)=9011、今年,小军5岁,爸爸31岁,再过年,爸爸的年龄是小军的3倍【答案】8【考点】年龄问题【解析】年龄差为31-5=26(岁),且年龄差不变,当爸爸年龄是小军年龄的3倍时,则差了2倍,则小军的年龄为26÷2=13岁,则13-5=8岁12、10个连续的自然数从大到小排列,若最后6个数的和比钱4个数的和的2倍大15,则这10个数中最小的数是【答案】6【考点】数论【解析】由题意,我们只知道这10个数是连续的,那我们可以用符号来表示最小的数字(如△),那么其它的9个数字就是△+1,△+2,△+3,……,△+913、如图4,把一个边长是5cm的正方形纸片沿虚线分为5个长方形,然后按照箭头标记的方向和长度移动其中的4个长方形,则所得图形的周长是 cm【答案】40【考点】巧算周长【解析】按照要求平移后周长增加了,增加的部分为每两层中间相隔的部分,从上往下第一层与第二层之间分别增加2+2=4,第二层与第三层之间分别增加2+1=3,第三层与第四层之间分别增加1+1=2,第四层与第五层之间分别增加1+0=1,则平移后不规则图形周长为4×5+4×2+3×2+2×2+1×2=4014、在一个长方形内画3个圆,这个长方形最多可被分为部分【答案】15【考点】图形计数【解析】想要分成的部分最多,则要求三个圆分别相交且和长方形的四条边分别相切,则共分成15部分15、2017年3月19日是星期日,据此推算,2017年9月1日是星期【答案】五【考点】周期问题【解析】3月19号到9月1号共12+30+31+30+31+31+1=166天,166÷6=23……5,则9曰1号为星期五16、观察7=5×1+2,12=5×2+2,17=5×3+2,这里,7,12,17被叫做“3个相邻的被5除余2的数”,若有3个相邻的被5除余2的数的和等于336,则其中最小的数是【答案】107【考点】数论【方法】由题意知,336÷5=67……1,因为3个连续被5除余2的数,则这三个数中共有67-1=66个5,又知3个数为连续数,则分别有21、22、23个5,所以最小的数为21×+2=10717、甲,乙,两人分别从A,B两地同时出发,相向而行,甲到达A,B中点C时,乙距C 点还有240米,乙到达C点时,甲已经超过C点360米,则两人在D点相遇时,CD的距离是米【答案】144【方法】行程问题【解析】由题意知相同时间内,乙走240米,甲走360米,即乙跑2米,甲跑3米。
四年级希望杯考辅第二讲教师版

第二讲应用题和几何专题一、和、差、倍问题和差问题是已知大小两个数的和与两个数的差,求大小两个数各是多少的应用题。
为了解答这种应用题,首先要弄清两个数相差多少的不同叙述方式.有些题目明确给了两个数的差,而有些应用题把两个数的差“暗藏”起来,我们管暗藏的差叫“暗差”。
例:“把姐姐的铅笔拿出3支后,姐姐、弟弟的铅笔支数就同样多.”这说明姐姐的铅笔比弟弟多3支,也说明姐姐和弟弟铅笔相差3支。
和倍问题是已知大小两个数的和与它们的倍数关系,求大小两个数的应用题.为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示两种量间的这种关系,以便于找到解题的途径。
“差倍问题”就是已知两个数的差和它们的倍数关系,求这两个数。
差倍问题的解题思路与和倍问题一样,先要在题目中找到1倍量,再画图确定解题方法.被除数的数量和除数的倍数关系要相对应,相除后得到的结果是一倍量,然后求出另一个数,最后再写出验算和答题。
【例1】549是甲、乙、丙、丁4个数的和.如果甲数加上2,乙数减少2,丙数乘以2,丁数除以2以后,则4个数相等.求4个数各是多少?分析上图可以看出,丙数最小.由于丙数乘以2和丁数除以2相等,也就是丙数的2倍和丁数的一半相等,即丁数相当于丙数的4倍.乙减2之后是丙的2倍,甲加上2之后也是丙的2倍.根据这些倍数关系,可以先求出丙数,再分别求出其他各数。
解:①丙数是:(549+2-2)÷(2+2+1+4)=549÷9=61②甲数是:61×2-2=120③乙数是:61×2+2=124④丁数是:61×4=244验算:120+124+61+244=549120+2=122124-2=12261×2=122244÷2=122【例2】两块同样长的花布,第一块卖出31米,第二块卖出19米后,第二块是第一块的4倍,求每块花布原有多少米?分析已知两块花布同样长,由于第一块卖出的多,第二块卖出的少,因此第一块剩下的少,第二块剩下的多.所剩的布第二块比第一块多31-19=12(米).又知第二块所剩下的布是第一块的4倍,那么第二块比第一块多出的12米正好相当于所剩布的(4-1)倍,这样,第一块所剩布的长度即可求出(见上图)。
第2讲.四年级希望杯复赛.教师版

个.
[分析]图中的正方形一共有 4 4 3 3 2 2 1 1 30 (个), 其中,含“ A ”的正方形有 1 4 4 1 10 (个), 所以不含“ A ”的正方形有 30 10 20 (个).
|四年级 第二讲
希望杯 2 试辅导班 ·教师版|
计数问题
【例 1】(第一届 2 试试题)数一数:图中共有
个正方形.
【分析】设图中最小的正方形的边长是 1,则边长为 1 的正方形共有 4 个;边长为 2 的正方形共有 17 个; 边长为 4 的正方形共有 9 个;边长为 3 的正方形共有 4 个;边长为 4 的正方形有 1 个.所以图中 共有正方形 4 17 9 4 1 35 (个). [拓展](第五届 2 试试题)图中,不含“ A ”的正方形有
1
【例 2】(第一届 2 试试题)将边长为正整数 n 的正方形平均分成 n 2 个小正方形, 每个小正方形的顶点称为 格点.例如,左图中的黑点是边长为 2 的正方形的格点. 如右图,在边长为 12 的正方形中有四个完全相同的直角三角形.如果三角形的一条直角边是 3, 那么这四个三角形各边共经过多少个格点(每个格点只计一次)?
|四年级 第二讲
希望杯 2 试辅导班 ·教师版|
3
【例 7】(第六届 2 试试题)已知一列数: 5 , 4 , 7 ,1 , 2 , 5 , 4 , 3 , 7 ,1 , 2 , 5 , 4 , 3 , 7 ,1 , 2 , 5 , 4 , 3 ,……,由此可推出第 2008 个数是________。 【分析】观 察 数 列 发 现 , 除 前 两 个 数 字 之 外 , 7 , 1 , 2 , 5 , 4 , 3 六 个 数 字 周 期 出 现 , 因 为 (2008 2) 6 334 2 ,所以第 2008 个数是 1 。 【例 8】(第一届 2 试试题)在计算机中,对于如图左,图中的数据(或运算)的读法规则是:先读第一分支 圆圈中的,再读与它相连的第二分支左边的圆圈中的,最后读与它相连的第二分支右边的圆圈中 的,也就是说,对于每一个圆圈中的数据(或运算)都是按“中→左→右”的顺序. 如:下图左表示: 2 3 ,下图中表示: 2 3 2 1 ,则下图右表示的式子的运算结果是 .
四年级数学希望杯第二讲(教师版).doc

四年级希望杯2试真题选讲〔2〕一、计数问题1、甲乙丙3个小朋友站成一排照相,共有______种不同的排列方法?解答:甲乙丙甲丙乙乙丙甲乙甲丙丙甲乙丙乙甲一共6种2、用1元,2元和5元的纸币,有______种不同的方法凑出6元钱解答:5+12+2+22+2+1+12+1+1+1+11+1+1+1+1+1共有5种方法3、数一数,图中有_________个三角形。
解答:先数最小的,有12个再数由4个小三角形组成的,有6个最后数由9个三角形组成的,有2个因此一共有20个4、如下图,在2×2方格中,画一条直线最多穿过3个方格;在3×3方格中,画一条直线最多穿过 5个方格;那么在5×5方格中,画一条直线,最多穿过_________个方格。
解答:如图,最多穿过9个方格5、六一儿童节,四位小朋友各做了一个小礼物准备相互赠送,但要求自己不得留下自己做的礼物,他们收到礼物的不同方式有_____种。
解答:设这四个小朋友分别是a,b,c,d收到a送的礼物有三种可能,不妨先设为b用心爱心专心1那么b送的礼物如果给a,那么必然是c和d交换礼物,这是一种送的礼物如果给了c,,那么c不能给a只能给d,所以d要给a,这也是一种同理b的礼物给了d又是一种那么总共就是3种,a送给b有3种,给c和d也是3种因此加起来就是9种.二、几何图形问题1、将一张长方形纸对折再对折〔如图2〕,然后沿着图中的虚线剪下,得到①、②两局部,将①展开后得到的平面图形一定是__________。
〔填“三角形〞、“长方形〞、“梯形〞或“菱形〞〕解答:菱形〔可以实际操作一下〕2、以下图是3×3的正方形方格,1与2相比,较大的是__________.解答:显然1较大3、以下各图中,阴影局部的面积与整个图形面积的比值最大的是图_________。
解答:A的比值是1/3.的比值是3/8的比值是1/4的比值是1/4所以最大的是B4、将图中所示的三角形ABC分成面积相等的四个局部,请给出三种不同的分法。
2004年四年级希望杯第2届解析讲解

第二届(2004)希望杯数学(01)一、填空题1.计算:234+432-4×8+330÷5=700。
左式=234+432-32+66=(234+66)+(432-32)=300+400=7002.如果&=+÷10,那么2&5= 2.5。
3.某校四年级有两个班,其中甲班有人,乙班比甲班多3人,则该校四年级共有学生人2a+3。
4.将数16表示成两个自然数的和的形式,则所表示成的两个数的最大乘积是64。
5.在括号内填上两个相邻的整数,使等式=成立。
3、46.在月球表面,白天阳光垂直照射的地方的温度高达127℃,夜晚的温度下降到零下183℃,则月球表面昼夜温差(最高与最低温度的差)是310 ℃。
127-(-183)=127+183=3107.北京到西安的飞机票价是每张960元。
张老师想从网上订购一张从北京到西安的飞机票。
海蓝票务中心的机票以九五折出售,但每张票要加收30元送票费;云天票务中心的机票不打折,但免费送票。
张老师从票务中心购买飞机票更省钱。
(填“海蓝”或“云天”)海蓝的票优惠5%,960x5%=48元,大于送票费,所以合算的8.一个数除以3的余数是2,除以5的余数是1,则这个数除以15的余数是11解:设这个数y,则y=3a+2 ; y=5b+1 (a,b为自然数)5y=15a+10 ; 3y=15b+36y=30b+6后式-前式,得y=30b-15a-4 =30b-15(a-1)+15-4 =15(2b-a+1)+119.如果,=2×2,……,=25×25,且+……+=5525,那么++……+=。
=32+(2x3)2+……+(25x3)2=32x(12+22+……252)=9x5525=4972510.如图,有一条长方形跑道,甲从A点出发,乙从C点同时出发,都按顺时针方向奔跑,甲每秒跑5米,乙每秒跑4.5米。
当甲第一次追上乙时,甲跑了圈。
相对论思考模式:甲追上乙,需要多跑16米,(10+6)甲的速度比乙每秒快0.5m,(5-4.5)那么甲追上乙,花的时间是,16÷0.5=32秒可知甲跑的距离是:32×5 =160 米圈数:160÷(16×2)=5圈11.三个不同的一位数的和等于10,用这三个一位数组成三位数,其中最大的是910 。
四年级希望杯2试试题及答案
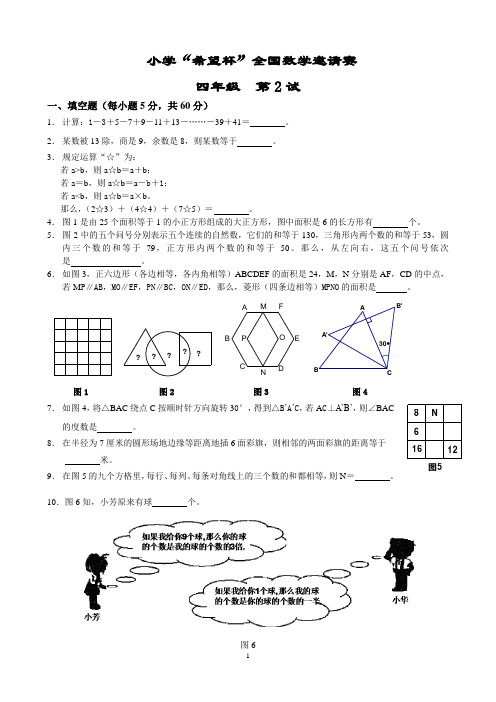
小学“希望杯”全国数学邀请赛四年级 第2试一、填空题(每小题5分,共60分)1. 计算:1-3+5-7+9-11+13-……-39+41= 。
2. 某数被13除,商是9,余数是8,则某数等于 。
3. 规定运算“☆”为: 若a>b ,则a ☆b =a +b ;若a =b ,则a ☆b =a -b +1; 若a<b ,则a ☆b =a ×b 。
那么,(2☆3)+(4☆4)+(7☆5)= 。
4. 图1是由25个面积等于1的小正方形组成的大正方形,图中面积是6的长方形有 个。
5. 图2中的五个问号分别表示五个连续的自然数,它们的和等于130,三角形内两个数的和等于53,圆内三个数的和等于79,正方形内两个数的和等于50。
那么,从左向右,这五个问号依次是 。
6. 如图3,正六边形(各边相等,各内角相等)ABCDEF 的面积是24,M ,N 分别是AF ,CD 的中点,若M P ∥AB ,MO ∥EF ,PN ∥BC ,ON ∥ED ,那么,菱形(四条边相等)MPNO 的面积是 。
?????O P NMFEDCBAB'A'CBA30图1 图2 图3 图4 7. 如图4,将△BAC 绕点C 按顺时针方向旋转30°,得到△B ’A ’C ,若A C ⊥A’B’,则∠BAC的度数是 。
8. 在半径为7厘米的圆形场地边缘等距离地插6面彩旗,则相邻的两面彩旗的距离等于米。
9. 在图5的九个方格里,每行、每列、每条对角线上的三个数的和都相等,则N = 。
10.图6知,小芳原来有球 个。
图6图512N166811.小明从家出发,先向东偏北30°的方向跑了350米到达点A,接着向北偏西30°的方向跑了200米到达点B,然后又向西偏南30°的方向跑了350米到达点C,这时小明距家米。
12.山上,几个牧童在放羊。
如果每人放5只羊,则有3只羊没人管;如果一半的牧童每人放4只羊,其余的牧童每人放7只羊,则每只羊都有人管。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
希望杯教程四年级数学第二讲(计数问题)四年级数学第二讲(计数问题)
一、知识回顾
1. 枚举法:不重不漏。
适合情况是
2. 加法原理:完成一件事情,有n类方法,第1类中有m1种方法,第2类中有m2
种方法,??,第n类有mn种方法,则完成这件事情的方法一共有:
能用加法原理解决的问题的特点是:
3. 乘法原理:完成一件事情,若需要n个步骤,第1步有m1种方法,第二步有m2
种方法,??,第n步有mn种方法,则完成这件事情的方法一共有:
注意点是:
4. 抽屉原理:桌子上有10个苹果,要把这10个苹果放到9个抽屉里,我们发现无
论怎么放,至少会有一个抽屉里面放()个苹果。
如果要把桌上的21个苹果放到10个抽屉里,至少有一个抽屉里放()个苹果。
如果要把桌上的56个苹果放到10个抽屉里,至少有一个抽屉里要放()个苹果。
5. 容斥原理:也就是说在不考虑重叠的情况下,把包含于某内容中的所有对象的数
目先计算出来,然后再把重复计数的数目去掉,使得计算的结果既无重复又无遗漏。
(1)如果计数的事物有A、B两类,
那么A类和B类元素个数总和(A∪B)= (2)如果被计数的事物有A、B、C三类,那么A类、B类和C类元素个数总和:
(A∪B∪C)=
6. 此外,常用的计数方法还有排列组合、标数法、捆绑法、排除法、归纳法、整体法、递推法等。
二、典型例题
例1:下图中,以点A、B、C、D、E、F、G为端点的线段有多少条?
例2:小林有2件上衣,4条裤子,3双皮鞋,她能有()种不同的穿戴形式。
例3:从5幅楷体,3幅隶书,2幅草体书法作品中选取不同类型的2幅临摹,共有多少种不同的选法?
例4:把24个苹果最多分给几个小朋友,才能保证至少有一个小朋友分得7个苹果。
例5:四年级一班第2小组共12人,其中5人会打乒乓球,8人会下象棋,3人既会
打乒乓球又会下象棋。
那么这个小组中既不会打乒乓球又不会下象棋的有多少人?
例6:布袋中有38个同样大小的小球,其中白、黄、红三种颜色的球各有15个,另
外还有3个蓝色球,3个绿色球和2个紫色球。
问:至少取出多少个球,才能使取出的球
中至少有4个球同色?
例7:学校教学楼有5级台阶,如果规定一步只能走1级或2级台阶,那么走完这5
级台阶共有多少种不同的走法?
例8:左下图中共有多少条对称轴?例9:右下图中不含“A”的正方形有多
少个?
例10:图中共有多少个正方形,多少个三角形?
三、练习巩固
1. 在线段AB上插入7个点,则共增加了多少条线段?
2. 书架的第一层有依次排列的10本不同的故事书,现将2本不同的小说书也插入第
1层,问:有多少种不同的放法?
3. 四年级共有48人,其中的23人参加科技小组,26人参加文艺小组,12人两个小
组都参加了,则有多少人两个小组都没有参加?
4. 某届欧洲足球锦标赛共有16支球队参加比赛,先平均分成4个小组进行小组赛,
每组中每2支球队之间都要赛一场,那么这四个小组一共要进行多少场小组赛?
5. 甲、乙两个人各买了同样的一盒信纸和信封,若甲给每个信封里装1张信纸,剩
50张信纸;若乙将3张信纸装进一个信封的话,剩50个信封。
则原来一盒里装有多少个
信封?装有多少张信纸?
6. 把100个小球放在几个盒子里,要求每个盒子中的小球的个数都含有数字8\(比如:放在3个盒子中的小球个数可以是8,8,84)。
现在要将这100个球放到5个盒子里,则各个盒子中的小球的个数分别是多少?
7. 四年级一、二、三、四、五班进行拔河比赛,每两班都要比赛一次。
到现在为止,一班已经比赛了4次,二班赛了3次,三班赛了2次,四班赛了1次。
则五班赛了多少次?
8. 东风小学四年级3个班的全体学生报名参加第七届“希望杯”全国数学邀请赛,
一班和二班共有67人参加,二班和三班共有64人参加,一班和三班共有63人参加。
那
么参加比赛的一班有几人?二班有几人?三班有几人?
9. 学校举办庆“六一”书画展,学校橱窗里展出了各个年级学生的书画作品,其中有24幅不是四年级的,有22幅不是五年级的,四五年级的学生作品共有10幅,则除四五年级之外的其他年级的作品共有多少幅?
10. 下图中各有多少条对称轴?
11. 左下图中共有多少个三角形? 12. 右下图中正方形网格上共有多少条线段?
13. 下图中一共有多少个正方形?
14. 有10个2分硬币和10个5分硬币,用这些硬币可以构成的币值有多少种?
15. “福娃”作为2021年奥运会吉祥物深受人们喜爱,下图中不包括“福娃迎迎”(用●表示)的正方形有多少个?
16. 如图中,顺次连接正方体的三个顶点A,B,C,得到等边三角形ABC。
像这样的等边三角形还可以画出多少个?
17. 左下图是由25个面积等于1的小正方形组成的大正方形,则图中面积是6的长方形有多少个?
18. 右上图中,每个小正方形的面积都是1平方厘米,则在此图中最多可以画出多少个面积是2平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。
19. 如图,白色和黑色的三角形按顺序排列,当两种三角形相差12个时,白色三角形有多少个?
??
20. 小明先用围棋子围成一个正方形,然后将这些棋子围成一个等边三角形,等边三角形每边比正方形每边多用6枚棋子。
这些棋子一共有多少枚?
感谢您的阅读,祝您生活愉快。
