结构弹性稳定计算
《结构力学》习题集及答案（下册）第十章结构弹性稳定计算
第十章 结构弹性稳定计算一、判断题：1、稳定方程即是根据稳定平衡状态建立的平衡方程。
2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。
3、在稳定分析中，有n 个稳定自由度的结构具有n 个临界荷载。
4、两类稳定问题的主要区别是：荷载—位移曲线上是否出现分支点。
5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。
6、能量法确定临界荷载的依据是势能驻值原理。
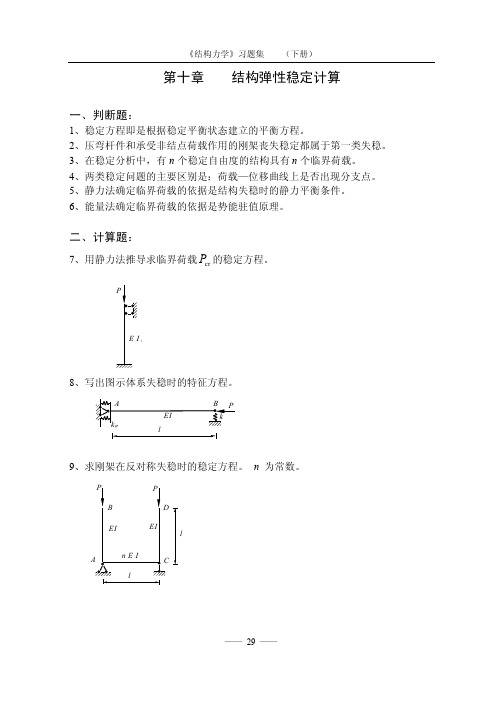
二、计算题：7、用静力法推导求临界荷载cr P 的稳定方程。
PE I ,l8、写出图示体系失稳时的特征方程。
k lEIk AB P9、求刚架在反对称失稳时的稳定方程。
n 为常数。
l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。
转动刚度kl k r 2=，k 为弹簧刚度。
P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。
已知弹簧刚度l EI k 33= 。
PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。
PEI l13、用静力法求图示结构的临界荷载cr P ，欲使B 铰不发生水平移动，求弹性支承的最小刚度k 值。
PlEI A Bk14、用静力法确定图示具有下端固定铰，上端滑动支承压杆的临界荷载crP。
P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。
设失稳时两柱的变形曲线均为余弦曲线：yxh=-δπ(cos).12提示：cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。
PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆，AB段失稳时变形曲线设为：()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。
l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ，设变形曲线为正弦曲线。
混凝土结构的稳定性计算原理
混凝土结构的稳定性计算原理一、前言混凝土结构的稳定性计算是建筑学中的重要组成部分。
混凝土结构的稳定性是指在荷载作用下，结构不发生破坏或者失稳的能力。
计算混凝土结构的稳定性是为了保证结构的安全性，避免人员和财产的损失。
本文将对混凝土结构的稳定性计算原理进行详细的阐述。
二、混凝土结构的稳定性计算的基本原理混凝土结构的稳定性计算基本上是按照以下步骤进行的：1. 确定结构的荷载2. 确定结构的内力3. 确定结构的稳定性4. 确定结构的尺寸和构造三、确定结构的荷载在建筑设计中，荷载是指对于结构体系所施加的所有重力和外力的合力。
荷载的种类包括自重、活载、风载、地震载、温度载等。
在计算荷载时，需要根据国家有关规定和标准，对各种荷载进行分类和确定。
四、确定结构的内力在确定结构的内力时，需要根据荷载作用下结构的受力特点，进行弹性力学分析计算。
弹性力学分析计算包括静力学、动力学、弹性理论、塑性理论等。
其中，静力学是最常用的分析方法。
在静力学分析中，通常采用平衡方程和受力平衡方程进行计算。
五、确定结构的稳定性在确定结构的稳定性时，需要分析结构的承载能力和稳定性能力。
承载能力是指结构在荷载作用下的破坏承载能力，稳定性能力是指结构在荷载作用下的稳定能力。
结构的稳定性分析包括弯曲稳定性、剪切稳定性、压缩稳定性、扭转稳定性、屈曲稳定性等。
在计算稳定性时，要考虑结构的材料和断面性质、受力形式和结构的几何形状等因素。
六、确定结构的尺寸和构造在确定结构的尺寸和构造时，需要根据结构的荷载和内力计算结果，确定结构的尺寸和构造。
结构的尺寸和构造要满足强度、刚度、稳定性和经济性的要求。
在设计时，还需要考虑施工的可行性和建筑的使用要求等因素。
七、混凝土结构的稳定性计算的具体方法混凝土结构的稳定性计算的具体方法包括以下几个方面：1. 计算结构的荷载：根据建筑设计规范和标准，确定结构所受的各种荷载。
2. 计算结构的内力：根据荷载作用下结构的受力特点，运用弹性力学分析方法，计算结构的内力。
ANSYS 入门教程 - 结构的弹性稳定性分析
ANSYS 入门教程- 结构的弹性稳定性分析2011-01-09 15:06:42| 分类：默认分类| 标签：|字号大中小订阅第7 章结构弹性稳定分析7.1 特征值屈曲分析的步骤7.2 构件的特征值屈曲分析7.3 结构的特征值屈曲分析一、结构失稳或结构屈曲：当结构所受载荷达到某一值时，若增加一微小的增量，则结构的平衡位形将发生很大的改变，这种现象叫做结构失稳或结构屈曲。
结构稳定问题一般分为两类:★第一类失稳：又称平衡分岔失稳、分枝点失稳、特征值屈曲分析。
结构失稳时相应的载荷可称为屈曲载荷、临界载荷、压屈载荷或平衡分枝载荷。
★第二类失稳：结构失稳时，平衡状态不发生质变，也称极值点失稳。
结构失稳时相应的载荷称为极限载荷或压溃载荷。
●跳跃失稳：当载荷达到某值时，结构平衡状态发生一明显的跳跃，突然过渡到非邻近的另一具有较大位移的平衡状态。
可归入第二类失稳。
★结构弹性稳定分析= 第一类稳定问题ANSYS 特征值屈曲分析（Buckling Analysis）。
★第二类稳定问题ANSYS 结构静力非线性分析，无论前屈曲平衡状态或后屈曲平衡状态均可一次求得，即“全过程分析”。
这里介绍ANSYS 特征值屈曲分析的相关技术。
在本章中如无特殊说明，单独使用的“屈曲分析”均指“特征值屈曲分析”。
7.1 特征值屈曲分析的步骤①创建模型②获得静力解③获得特征值屈曲解④查看结果一、创建模型注意三点：⑴仅考虑线性行为。
若定义了非线性单元将按线性单元处理。
刚度计算基于初始状态（静力分析后的刚度），并在后续计算中保持不变。
⑵必须定义材料的弹性模量或某种形式的刚度。
非线性性质即便定义了也将被忽略。
⑶单元网格密度对屈曲载荷系数影响很大。
例如采用结构自然节点划分时（一个构件仅划分一个单元）可能产生100% 的误差甚至出现错误结果，尤其对高阶屈曲模态的误差可能更大，其原因与形成单元应力刚度矩阵有关。
经验表明，仅关注第1 阶屈曲模态及其屈曲载荷系数时，每个自然杆应不少于 3 个单元。
起重机弹性约束杆挠度影响系数及稳定性计算
起重机弹性约束杆挠度影响系数及稳定性计算设-~'I-制造孙.辩豪秆芎礞?锻虞琵起重机弹性约束杆挠度影响系数及稳定性计算//√刘明思陆念力孙善利起重机结构压弯构件的稳定性计算与轴压构件稳定性计算的重要区别在于压弯构件不仅要考虑一类分支失稳,还要考虑由于压弯效应引起的边缘屈服.由于轴压力的作用,使压弯构件中产生附加弯矩和附加挠度.因此承受轴力的梁比无轴力梁的挠度与弯矩要大,通常我们用轴力影响系数,来描述压弯梁跨中挠度与弯矩的放大倍数.铁摩辛柯曾就承受端弯矩,跨中集中力O,均布力q三种不同荷载情况时的两端简支压弯梁的跨中挠度放大系数r提出了一个统一的近似表达式LlJ:f『二(1)式中:尸——轴压力;——轴压临界力,:起重机设计规范(GB3811—83)中的压弯构件稳定验算公式即采用了此放大系数.由于规范公式的推导原型是针对两端铰接梁的,能否适用于其它约束条件的压弯梁尚需证明.本文将就弹性约束下压弯梁的临界力和挠度加以分析,给出精确的轴压临界力方程和挠度表达式,并证明在弹性约束情况下轴力引起的跨中挠度放大仍可用式(1)表达,但式中轴压临界力尸是对应弹性约束梁的.1弹性约束压弯梁的端转角与跨中挠度已知,两端受等弯矩的铰支压弯梁端转角9和跨中挠度分别表示为:M/taIlMr^,猫—zJ=(3)1厂五式中:——轴力系数,=刍38丁下Hf.i_嘏上.,卜_———击——一I1!.1二仁1.堕堑卫四—j圈1设压弯梁端部转动刚度为椰/f,则当受弹性约束的梁发生端部转角时,相当于在梁端施加一反向力矩Mo:一卿日/f,则当受弹性约束的梁发生端部转角时,相当于在梁端施加一反向力矩Mo=一卿日/f,此端弯矩引起的相应转角与挠度为:MoZo面=一(4)Z等?一?(5)转动刚度系数日与轴力系数相关,见公式(26),(27).以下分别就图1中的三种受荷形式的压弯梁的跨中挠度与梁端转角进行推导.(1)受等端弯矩肘的弹性约束压弯梁图1(a)梁端转角和跨中挠度表示为::?(6)面'oJt筑感攮猢HIa=?+将式(4),(5)代人(6),(7)整理得设计制造(7)2弹性约束压弯梁的轴力影响系数=一M/?—_=_tal—luE12urJtanu(8)一,/一Ml24_二堕l一一8Elu(2ucosu+rlsinu):黥(9)8一,(2)跨中受集中力Q的弹性约束压弯粱图1(b)梁端转角和跨中挠度为:=?+(1o)d=E/?+oO…)一48l,.,"将式(4),(5)代人(1O),(11)得:=籀×(12,a=【一.(!=堂1c阻2u(2u+~Ttanu)j:苏fl3)(3)受均布荷载q的弹性约束压弯粱图1(c)粱端转角和跨中挠度表为::.+(14)'—一【l4J=384E/?鼍(15)一5～o将式(4),(5)代人(14),(15)得:=×c一『(塑==12.一384日【51.丝立跚_15u(2ucosu+rlsinu)j=384/E,4口(17)式(9),(13),(17)中的厶,,.,分别表示对应图1(a),(b),(c)三种情况的挠度放大系数,它们是轴力系数和转动刚度系数的函数.挠度放大系数前的系数项则为轴力P和转角刚度均为0时的粱跨中挠度.在轴力P=0(即//.=O)的情况F,弹性约束粱的挠度放大系数变为:l_田=,唧(18):(19)8一+4"厶:(20)一10+5,,舯,,分别称为对应弯距,横向集中力Q,均布力q引起的转动刚度影响系数,而将,呷,,(,称为轴力P引起的轴力影响系数:i=|=(2ucosu(21)一u+sInu)如=fo/foo=×(一3r/(1(-eo+~u胁)22k…zz),IM3一u3cu(u+开胁u), =|q对:(28ecu一2一2一一5(10+).…一…r/~art)(23)ZUc08U+U,轴力影响系数表示是在弹性约束条件下,有轴力作用时,压弯粱的跨中挠度相对无轴力作用时粱的跨中挠度的放大系数.从这个意义上说,规范中所用的式(1),实质上是无弹性约束梁的轴力影响系数.式(1)是图1三种情况的特例口=0时,三个部分精确轴力影响系数表达式的统一近似表达式,它可达到很高的精度.文献[1]指出,当轴力P<0.6P时,该式误差不超过2%.在弹性约束情况下,图1中三种受荷形式的压弯梁挠度的轴力影响系数是否仍可用如式(1)的公式表达?换言之,式(21),(丝),(23)能否统一用式(1)近似代替?回答是肯定的.表1给出了不同转动刚度系数口条件下精确轴力影响系数与近似表达式结果的比较.但必须指出近似表达式(1)中,轴压临界力P也须与端部转动刚度相对应.9设计制造袅1P,P-q=0.O0011.1140.21.257031.441041.6861.1101.2471.4231.6581.1111.2511.4301.6691.1111.2501.4291.667…l=1.O0…I|f0lfi.i151.I101.1J21.1Jl 0.21.2581.2471.2511.250 0.31.4421.4231.4311.429 0.41.6891.6581.6701.667 0.52.0341.9862.0062.000 0.62.5512.4792.5082.500 5.0P,P,呷蛔靠f011.1131l1011121.111 021.253124712521.250 031.4351.42414311.429041.6761.鲫1.6711.667052.0151.9902.0072.000062.5242.4842.5102500=10.0P,P,呷矗f0.11.1呻1.1101.1111.1l10.21.2451.2481.2501.2500.31.4191.4251.4291.4290.41.6531.66016681.6670.51.9791.99120o22.0000.62.4692.4862.姗2.5003弹性约束压弯梁的临界轴力压弯梁因轴荷达到临界力而屈曲时,粱的跨中挠度将为不定式或无穷大.当轴力影响系数的表达式分母为零时挠度将成为0/o不定式或无穷大.因此我们从式(21),(22),(23)分母的公共项中得到屈曲条件式:2ueosu~sinu:0(24)由此式求出对应屈曲的轴压系数n,则得到轴压临界力:P;T4u2El(25)将屈曲条件式改写为:[Knu=一2u/r](26)因为形如诅n=一Ax的方程的近似解为::丌(A>0)iA>uJ故得式(26)的近似解:u=舞(27)相应临界力近似值为:()(28)式(28)为临界力的近似解,在精确度要求更高的场合,可借助计算机,直接解超越方程(24)或(26).表2给出了不同转角刚度系数条件下,由精确的式(24)和近似的式(28)得出的计算长度系数,临界力可表达为::(29)一()衰2(式24)(式28)0.01嗍1.嗍0.50.9156O.90oo100.830.8333200.77430.75003.00.0.70004.00.6863066675.00.6,980.642910.00.59190.583320.00.54870.545550.00.51990.5192100.00.51∞0.5098500.00.锄O.502o1000.00.50100.5010∞0.姗0.姗参考文棘1铁摩辛柯着,张福洪译.弹性稳定理论.科学出版社, 1958刘明思,陆念力,咭尔滨建筑大学机电系,1.50006哈尔滨西大直街66号孙善利,牡丹江塔机厂收稿日期2000.o2.06编辑:孔庆璐。
钢结构公式大全
钢结构公式大全1. 钢结构自重计算公式：自重= A × B × C × D × G其中，A为钢结构体积，B为钢的密度，C为钢板厚度，D为钢板长度，G为钢板宽度。
2. 钢结构荷载计算公式：荷载= Qk × γk + Qd × γd + Qe × γe + Qs × γs其中，Qk为永久荷载，γk为永久荷载的安全系数；Qd为可变荷载，γd 为可变荷载的安全系数；Qe为地震荷载，γe为地震荷载的安全系数；Qs为风荷载，γs为风荷载的安全系数。
3. 钢结构强度计算公式：强度= σb × A /γm其中，σb为钢材的抗拉强度，A为受力面积，γm为安全系数。
4. 钢结构刚度计算公式：刚度= EI / L其中，E为弹性模量，I为截面惯性矩，L为长度。
5. 钢结构稳定性计算公式：稳定性= Ncr / N其中，Ncr为临界承载力，N为实际承载力。
6. 钢结构焊接强度计算公式：焊接强度= 0.7 × Fexx × A / γw其中，Fexx为焊接材料的抗拉强度，A为焊缝截面积，γw为焊接安全系数。
7. 钢结构的变形计算公式：变形= F × L / (A × E)其中，F为受力，L为长度，A为截面积，E为弹性模量。
8. 钢结构的屈曲计算公式：Pcr = π² × E × I / L²其中，Pcr为临界压力，E为弹性模量，I为截面惯性矩，L为长度。
9. 钢结构的板材抗弯计算公式：M = σ × W / y其中，M为弯矩，σ为应力，W为截面模量，y为离心距。
10. 钢结构的悬挂索计算公式：T = F / cosθ其中，T为索力，F为受力，θ为倾角。
以上是钢结构常用的计算公式，但实际应用中还需根据具体情况进行调整和修正。
结构力学 结构的极限荷载与弹性稳定图文
A
B
D
C
l/3
l/3
l/3
解: AB段极限弯矩为 M u ，BC段极限弯矩为Mu。
塑性铰的可能位置：A、B、D。
A l/3
B
Mu B
l/3
FPu
DC Mu
D
l/3
§11-4 超静定结构的极限荷载计算
1）B、D截面出现塑性
FPu
铰，由弯矩图可知，只 有当 Mu 3Mu 时，此破
A l/3
B
Mu B
分析：(1) 图(a)表示截面处于弹性阶段。
该阶段的最大应力发生在截面最外纤维处，
称为屈服极限y，此时的弯矩Ms称为弹性 s a)
极限弯矩，或称为屈服弯矩。即：
s
MS
bh2 6
s
y0
（2）图(b）—截面处于弹塑性阶段，
y0
截面外边缘处成为塑性区，应力为常数， s b)
§11-2 基本概念
=s；在截面内部(|y|y0)则仍为弹性区，称为弹性
2
C l
2 4
B Mu
由We=Wi，可得 所以有1 4q源自l 24M uqu
16M l2
u
三次超静定 三个塑性铰
§11-4 超静定结构的极限荷载计算
例11-4-3 已知梁截面极限弯矩为Mu ，求极限荷载 。 解:塑性铰位置：A截面及梁上最大弯矩截面C。
q
qu
A
l
BA
Mu A
Mu C C B
l-x
x
例11-1-1 设有矩形截面简支梁在跨中承受集中荷载 作用(图a)，试求极限荷载FPu 。
解：由M图知跨中截面 弯矩最大，在极限荷载作用 下，塑性铰将在跨中截面形 成，弯矩达极限值Mu(图b)。
钢结构 计算公式
钢结构计算公式钢结构是一种常用的建筑结构形式，在工程计算中有一些常见的计算公式。
本文将介绍一些常见的钢结构计算公式，并对其进行详细解析。
一、钢结构的设计载荷计算公式1.自重计算公式钢结构的自重是指结构本身的重量，可通过以下公式计算：自重 = 单位长度重量 x 结构长度2.活载计算公式活载是指建筑物使用过程中产生的临时荷载，可通过以下公式计算：活载 = 活载系数 x 单位面积活载3.风荷载计算公式风荷载是指风力对建筑物产生的荷载，可通过以下公式计算：风荷载 = 风压 x 结构面积二、钢结构的强度计算公式1.抗弯强度计算公式抗弯强度是指钢结构在受到弯曲力作用时的抵抗能力，可通过以下公式计算：抗弯强度 = 弯矩 x 距离 / 截面惯性矩2.抗剪强度计算公式抗剪强度是指钢结构在受到剪切力作用时的抵抗能力，可通过以下公式计算：抗剪强度 = 剪力 x 距离 / 截面面积3.抗压强度计算公式抗压强度是指钢结构在受到压力作用时的抵抗能力，可通过以下公式计算：抗压强度 = 压力 / 截面面积4.抗拉强度计算公式抗拉强度是指钢结构在受到拉力作用时的抵抗能力，可通过以下公式计算：抗拉强度 = 拉力 / 截面面积三、钢结构的稳定性计算公式1.屈曲强度计算公式屈曲强度是指钢结构在受到压力作用时发生屈曲破坏的能力，可通过以下公式计算：屈曲强度 = 屈曲载荷 / 截面面积2.稳定系数计算公式稳定系数是指钢结构在受到外力作用时的稳定性能，可通过以下公式计算：稳定系数 = 屈曲载荷 / 临界载荷四、钢结构的挠度计算公式1.弹性挠度计算公式弹性挠度是指钢结构在受到荷载作用时的弹性变形程度，可通过以下公式计算：弹性挠度 = (荷载 x 距离^4) / (8 x 弹性模量 x 截面惯性矩)2.塑性挠度计算公式塑性挠度是指钢结构在受到荷载作用时的塑性变形程度，可通过以下公式计算：塑性挠度 = (荷载 x 距离^3) / (48 x 弹性模量 x 截面惯性矩)3.总挠度计算公式总挠度是指钢结构在受到荷载作用时的弹性变形和塑性变形之和，可通过以下公式计算：总挠度 = 弹性挠度 + 塑性挠度通过以上公式的计算，可以得到钢结构在不同荷载条件下的各项参数，从而进行合理的设计和施工。
常见的钢结构计算公式
常见的钢结构计算公式钢结构是一种使用钢材构筑的建筑结构，具有高强度、刚度和耐久性。
在进行钢结构设计时，一般需要运用一系列的计算公式和方法，以确保结构的安全性和稳定性。
下面将介绍一些常见的钢结构计算公式。
1.弹性极限计算公式：在静力设计中，钢材的弹性极限可以通过以下公式计算：Fy = Ag × fy其中，Fy为弹性极限力；Ag为截面的毛面积；fy为材料的屈服点。
2.构件稳定性计算公式：钢结构构件在承受压力时会发生稳定性问题，所以需要计算其稳定性能。
常用的公式有：Pu = Fcr × Ag其中，Pu为构件的压力力；Fcr为构件的临界强度；Ag为构件的截面积。
3.弯曲计算公式：钢结构常常承受弯曲力，采用以下公式计算弯曲强度：Mcr = π² × E × I / L²其中，Mcr为构件的临界弯矩；E为弹性模量；I为截面的抵抗矩；L为构件的长度。
4.疲劳强度计算公式：钢结构在长期使用过程中可能出现疲劳破坏，需要计算其疲劳强度。
一般采用以下公式：S=K×Fs×Fc×Fi×S′其中，S为构件的疲劳强度；K为系数；Fs为构件的应力范围；Fc为理论疲劳强度调整系数；Fi为不同种类的载荷影响系数；S′为基本疲劳强度。
5.刚度计算公式：刚度是钢结构抵抗外力和变形的能力，可以通过以下公式计算：k=(4×E×I)/L其中，k为构件的刚度；E为弹性模量；I为截面的抵抗矩；L为构件的长度。
6.连接的计算公式：钢结构的连接通常通过螺栓、焊接等方式实现。
连接的承载能力可以通过以下公式计算：Rn=φ×An×Fv其中，Rn为连接的承载能力；φ为安全系数；An为焊接或螺栓连接的有效截面积；Fv为连接的剪切力。
这些是钢结构设计中一些常见的计算公式，但实际计算中还应考虑不同情景和特点，以及遵从相关的设计规范和标准。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3 结构弹性的稳定计算
3.2稳定问题的分析方法——静力法
根据临界状态的静力特征而提出的确定临界荷载的方法，称为静 力法。
静力法的要点： 是在原始平衡路径Ⅰ之外寻找新的平衡路径Ⅱ，确定二者交叉的 分支点，由此求出临界荷载。
3 结构弹性的稳定计算
3 结构弹性的稳定计算
3.1两类稳定问题概述
3.2稳定问题的分析方法——静力法
目
3.3稳定问题的分析方法——能量法
录
3.4 剪力对临界荷载的影响
3.5 组合压杆的稳定
3.6 窄条梁的稳定
3 结构弹性的稳定计算
3.1两类稳定问题概述
从稳定性角度来考察，平衡状态有三种不同的情况： ⑴稳定平衡状态 ⑵不稳定平衡状态 ⑶中性平衡状态 结构稳定计算理论：小挠度理论（通常采用），优点：方法简
性杆，在铰结点B和C处为弹性支承，其刚度系数都为k。试求其临界荷载Pcr。
图3－5 两个自由度的体系 （a）原始平衡形式；（b）平衡的新形式
3 结构弹性的稳定计算
例3-1(续1)
解：设体系由原始平衡状态(图3-5(a)的水平位置)转到任意变形的新状态
(图3-5(b))，设B点和C点的竖向位移分别为y1和y2，相应的支座反力分别为
其重点是在内力的计算上。对大多数结构，通常其应力都处于弹性范围内而且变 形很小。因此，认为荷载与变形之间呈线性关系，并按结构未变形前的几何形状 和位置来进行计算，叠加原理适用，通常称此种计算为线性分析或一阶分析。对 于应力虽处于弹性范围但变形较大的结构（如悬索），因变形对计算的影响不能 忽略，应按结构变形后的几何形状和位置来进行计算，此时，荷载与变形之间已 为非线性关系，叠加原理不再适用，这种计算称为几何非线性分析或二阶分析。
这是关于y1和y2的齐次方程。
3 结构弹性的稳定计算
例3-1(续2)
如果系数行列式不等于零，即 kl 2P P 0 P kl 2P
则零解(即y1和y2全为零)是齐次方程(a)的唯一解。也就是说，原始平衡形式 是体系唯一的平衡形式。
如果系数行列式等于零，即
kl 2P P 0
(b)
P kl 2P
3 结构弹性的稳定计算
其他结构可能出现的分支点失稳现象
图3－2 分支点失稳
（a）受结点荷载的刚架；（b）受水压力的圆拱；（c）窄条梁
3 结构弹性的稳定计算
3.1.2极值点失稳 压杆的非完善体系(图3-3(a)、(b))：具有初曲率和承受偏心荷载的压杆。
图3－3 极值点失稳
（a）有初弯曲的压杆；（b）偏心荷载压杆；（c）P－Δ曲线
R1 ky1 同时，A点和D点的支座反力为
R2 ky2
X A P
YA
Py1 l
YD
Py2 l
变形状态的平衡条件为
MC/ 0
(C/左)
k y1l
Py1 l
2l
Py 2
0
MB/ 0
( B/右)
k y2 l
Py 2 l
2l
Py1
0
Py1 kl 2Py2 0
形式。为了得到非零解，齐次方程(3-2)的系数应为零，即
Pl k 0 (3-3)
式(3-3)称为特征方程。由特征方程得知，第二平衡路径Ⅱ为水平直线。由两
条路径的交点得到分支点，分支点相应的荷载即为临界荷载，因此
Pcr
k l
(3-4)
3 结构弹性的稳定计算
例3-1 图3-5(a)所示是一个具有两个变形自由度的体系，其中AB、BC、CD各杆为刚
则除零解外，齐次方程(a)还有非零解。也就是说，除原始平衡形式外，体系
还有新的平衡形式。这样，平衡形式即具有二重性，这就是体系处于临界状态的
简支压杆的完善体系或理想体系(图3-1(a))：杆件轴线是理想的直线（没有初 曲率），荷载P是理想的中心受压荷载（没有偏心）。
图3－1 分支点失稳
（a）理想的中心受压杆； （b）P－Δ曲线
在分支点B处，原始平衡路径Ⅰ与新平衡路径Ⅱ同时并存，出现平衡形式的二 重性，原始平衡路径Ⅰ由稳定平衡转变为不稳定平衡，出现稳定性的转变。具有 这种特征的失稳形式称为分支点失稳形式。分支点对应的荷载称为临界荷载，对 应的平衡状态称为临界状态。分支点失稳又称为第一类失稳。
单，结论基本正确。 大挠度理论，特点：结论精确，方法复杂。 随着荷载的逐渐增大，结构的原始平衡状态可能由稳定平衡状态 转变为不稳定平衡状态。这时原始平衡状态丧失其稳定性，简称为 失稳。 结构失稳的两种基本形式：分支点失稳和极值点失稳。下面以压 杆为例加以说明。
3 结构弹性的稳定计算
3.1.1分支点失稳
3 结构弹性的稳定计算
3.2.1静力法确定有限自由度体系的临界荷载 图3-4（a）中，AB为刚性压杆，底端A为弹性支承，其转动刚度系数为k。
图3－4 单自由度失稳
（a）原始平衡形式；（b）平衡的新形式
杆AB处于竖直位置时的平衡形式（图3-4（a））是其原始平衡形式。
3 结构弹性的稳定计算
3.2.1静力法确定有限自由度体系的临界荷载（续）
稳定问题的着眼点不是放在计算最大应力，而是研究荷载与结构内部抵抗力 之间的平衡上，看这种平衡是否处于稳定状态，即要找出变形开始急剧增长的临 界点，并找出与临界状态相应的最小荷载（临界荷载）。由于它的计算要在结构 变形后的几何形状和位置上进行，其方法也属于几何非线性范畴，叠加原理不再 适用，故其计算也属二阶分析。
现在寻找杆件处于倾斜位置时新的平衡形式(图3-4(b))。
根据小挠度理论，其平衡方程为 (3-P1l) M A 0
由于弹性支座的反力矩MA＝kθ，所以
Pl k (03-2)
式(3-2)是以位移θ为未知量的齐次方程。齐次方程有两类解：即零解和非零
解。零解(θ＝0)对应于原始平衡形式，即平衡路径Ⅰ；非零解(θ≠0)是新的平衡
在极值点处，平衡路径由稳定平衡转变为不稳定平衡。这种失稳形式称为极 值点失稳。其特征是平衡形式不出现分支现象，而P-Δ曲线具有极值点。极值点 相应的荷载极大值称为临界荷载。极值点失稳又称为第二类失稳。
3 结构弹性的稳定计算
稳定问题与强度问题的区别说明 强度问题是指结构在稳定平衡状态下它的最大应力不超过材料的允许应力，