Excel求置信区间的方法
excel计算回归模型的置信区间

excel计算回归模型的置信区间回归模型的置信区间是在统计学中常用的一种方法,用于评估回归模型的预测结果的准确性和可靠性。
在实际应用中,我们经常需要使用回归模型来预测某个变量的取值,并对预测结果进行评估。
通过计算回归模型的置信区间,我们可以得到一个范围,该范围内包含了预测结果的真实值的概率。
让我们先了解一下回归模型的基本概念。
回归模型是一种用于研究变量之间关系的统计模型,它可以帮助我们理解和预测一个变量(因变量)与其他变量(自变量)之间的关系。
回归模型的基本形式可以表示为:Y = β0 + β1X1+ β2X2 + ... + βnXn + ε,其中Y是因变量,X1、X2、...、Xn是自变量,β0、β1、β2、...、βn是回归系数,ε是误差项。
在实际应用中,我们通常使用最小二乘法来估计回归系数,即通过最小化观测值与回归模型预测值之间的差距来确定回归系数的值。
然而,由于样本数据的限制,我们无法得到准确的回归系数值,因此需要进行统计推断来评估回归模型的预测结果的准确性。
回归模型的置信区间是一种常用的统计推断方法,用于估计回归模型预测结果的不确定性。
置信区间表示了对于给定置信水平的情况下,预测结果的真实值落在一个区间内的概率。
通常,我们使用95%的置信水平,即置信区间的宽度为95%。
计算回归模型的置信区间需要考虑多个因素,包括样本的大小、回归系数的估计值、自变量的取值以及残差的方差等。
在进行计算之前,我们需要对回归模型做一些假设,包括误差项服从正态分布、观测值之间独立等。
一种常用的计算回归模型置信区间的方法是基于t分布。
根据中心极限定理,当样本容量足够大时,回归系数的估计值近似服从正态分布。
因此,我们可以使用t分布来计算回归系数的置信区间。
具体而言,回归模型的置信区间可以表示为:估计值±t值×标准误差,其中估计值是回归系数的估计值,t值是与给定置信水平和自由度相关的临界值,标准误差反映了回归系数估计值的不确定性。
excel 斜率置信区间 -回复

excel 斜率置信区间-回复Excel 斜率置信区间是用来衡量回归分析的斜率参数的可靠性和确定性的。
在统计学中,回归分析是研究变量之间关系的一种方法,而斜率是描述这种关系强度和方向的重要指标。
通过计算斜率的置信区间,我们可以判断斜率参数的可靠性,以及此参数估计的波动范围。
斜率置信区间是指在给定置信水平下,斜率的真实值有多大概率落在某个区间内。
通常情况下,我们可以使用Excel来计算斜率置信区间,以下是一步一步的说明。
1. 收集数据:首先,我们需要收集相关变量的数据,这些变量应该存在某种联系。
例如,如果我们想研究身高和体重之间的关系,我们可以收集一组样本数据,包括身高和体重的观测值。
2. 插入数据:一旦数据收集完毕,我们可以将这些数据插入Excel中的数据表。
我们需要确保每个变量都有相应的列,并将数据以适当的格式输入。
3. 绘制散点图:为了可视化变量之间的关系,我们可以使用Excel中的散点图功能绘制出数据的散点图。
选择身高作为自变量(X轴),体重作为因变量(Y轴),然后选择散点图类型。
4. 添加趋势线:为了更好地描述变量之间的关系,我们可以为散点图添加趋势线。
选择散点图上的任意散点,然后右键单击选择“添加趋势线”。
在弹出的对话框中,选择合适的线性趋势线。
5. 计算斜率:一旦趋势线添加完成,我们可以通过点击趋势线上的右键,选择“趋势线的格式设置”来查看趋势线参数。
其中一个参数就是斜率。
6. 计算标准误差:标准误差是衡量斜率参数估计的准确性的指标之一。
在Excel中,标准误差可以通过参考计算斜率的公式和相关数据来计算。
标准误差可以使用“STERR”函数完成。
7. 确定置信水平:在计算斜率置信区间之前,我们需要确定置信水平。
通常,常见的置信水平包括95和99。
我们可以根据实际需求选择适当的置信水平。
8. 计算置信区间:一旦有了标准误差和置信水平,我们可以使用Excel 中的T分布或Z分布来计算斜率的置信区间。
使用EXCEL进行区间估计及确定样本容量

使用EXCEL进行区间估计及确定样本容量区间估计和确定样本容量是统计学中非常重要的概念。
在进行统计分析时,我们通常有一个总体参数需要估计,但是通常我们无法获得整个总体的数据,而只能获得样本数据。
因此,我们需要使用区间估计来估计参数的范围,并且需要确定样本容量来保证估计的准确性和可靠性。
区间估计是通过样本数据来对总体参数进行估计,并给出一个范围区间来表达不确定性。
常用的区间估计方法有置信区间和预测区间。
在Excel中,我们可以使用函数来进行区间估计。
首先,我们需要计算样本的均值和标准差。
假设有一个包含样本数据的列A,我们可以使用AVERAGE函数来计算样本均值,使用STDEV函数来计算样本标准差。
例如,我们有一个含有100个观测值的样本,可以使用以下公式计算样本均值和样本标准差:样本均值:=AVERAGE(A1:A100)样本标准差:=STDEV(A1:A100)接下来,我们可以使用Excel的统计函数来计算置信区间的上限和下限。
假设我们要计算一个95%的置信区间,我们可以使用以下公式:置信区间下限:=CONFIDENCE.NORM(0.05,STDEV(A1:A100),COUNT(A1:A100))置信区间上限:=CONFIDENCE.NORM(0.05,STDEV(A1:A100),COUNT(A1:A100))其中,0.05为置信水平,STDEV(A1:A100)为样本标准差,COUNT(A1:A100)为样本容量。
另外,我们也可以使用Excel的数据分析工具来进行区间估计。
首先,我们需要安装数据分析工具包(如果未安装),然后找到"数据"选项卡,点击"数据分析",选择"t检验:配对两样本"或者"z检验:两样本或一个样本平均值"。
在打开的对话框中,填入相应的参数,例如选择样本数据的范围,设置置信水平等。
点击"确定"后,Excel会自动计算出区间估计的结果。
excel 拟合 置信区间 -回复

excel 拟合置信区间-回复Excel是一款功能强大的电子表格软件,广泛应用于商务分析、数据处理和科学计算等领域。
其中,拟合和置信区间是Excel中非常重要的概念和功能。
本文将以"Excel拟合置信区间"为主题,一步一步回答相关问题,帮助读者了解如何在Excel中进行拟合和计算置信区间。
第一步:了解拟合和置信区间的概念拟合是指根据已知数据点找到一个最佳的数学函数来描述数据间的关系。
在Excel中,可以通过使用拟合函数来计算并绘制与数据集最匹配的曲线。
常用的拟合函数有线性拟合、多项式拟合、指数拟合等。
置信区间是对拟合结果的不确定性进行估计的一种统计方法。
在拟合过程中,我们往往希望得到一个置信区间,以评估曲线对真实数据集的拟合程度。
置信区间可以告诉我们在一定置信水平下,估计值的不确定性范围。
第二步:准备数据集在Excel中进行拟合和计算置信区间之前,我们需要准备一个数据集。
假设我们有一个销售额与广告费用的关系的数据集,其中广告费用作为自变量,销售额作为因变量。
数据集至少需要包含2列,一列为自变量数据,一列为因变量数据。
第三步:进行数据拟合在Excel中,数据拟合可以通过选择合适的函数来实现。
对于线性拟合,我们可以使用“LINEST”函数。
对于多项式拟合,可以使用“TREND”函数。
其他类型的拟合函数可以在Excel的函数库中找到。
1. 打开Excel并加载数据集。
2.确定需要进行的拟合类型,并选择相应的拟合函数。
3.在单元格中输入拟合函数,并在拟合函数的参数中选择数据集的自变量和因变量范围。
4.按下"Enter"键,即可得到拟合结果。
第四步:计算置信区间在Excel中,可以使用"CONFIDENCE"函数来计算置信区间。
该函数需要拟合的标准误差和所需的置信水平作为输入参数。
1. 确定置信水平(通常为95或99)。
2.使用Excel中的"STDEV"函数来计算标准误差。
excel 拟合 置信区间

excel 拟合置信区间摘要:一、背景介绍1.Excel 在数据分析中的应用2.拟合函数在Excel 中的重要性3.置信区间的概念二、Excel 中拟合函数的应用1.线性拟合2.多项式拟合3.指数拟合4.对数拟合5.其他拟合函数三、Excel 中计算置信区间的步骤1.选择数据2.确定置信水平3.使用内置函数计算置信区间4.结果解读四、拟合函数与置信区间的实际应用案例1.数据分析2.预测趋势3.市场调研4.科学研究正文:在当今这个大数据时代,Excel 作为一款功能强大的数据处理软件,被广泛应用于各个领域。
在数据分析过程中,拟合函数和置信区间的应用尤为重要,它们可以帮助我们更好地理解数据,从而做出更准确的决策。
本文将详细介绍Excel 拟合函数在置信区间计算中的应用。
首先,我们需要了解Excel 中拟合函数的应用。
Excel 提供了丰富的拟合函数,包括线性拟合(SLOPE 和INTERCEPT)、多项式拟合(POLY)、指数拟合(EXPONENTIAL)和对数拟合(LOGARITHMIC)等。
这些拟合函数可以帮助我们更好地理解数据之间的关系,从而为后续的数据分析提供便利。
其次,我们需要了解如何在Excel 中计算置信区间。
计算置信区间的步骤如下:首先选择需要计算置信区间的数据,然后确定置信水平(通常为95%),接着使用Excel 内置的函数(如STDEV.S、VAR.S 等)计算标准误差,最后使用公式计算置信区间。
需要注意的是,计算置信区间的过程中要确保数据的可靠性。
在实际应用中,拟合函数和置信区间可以帮助我们更好地分析数据、预测趋势和进行市场调研。
例如,在市场调研中,我们可以使用Excel 的拟合函数预测产品的销售趋势,并根据置信区间评估预测结果的可靠性。
在科学研究中,拟合函数可以帮助我们建立实验模型,而置信区间则可以用于评估实验结果的准确性。
总之,Excel 中的拟合函数和置信区间在数据分析中具有重要意义。
在Excel中求回归分析的预测区间置信区间
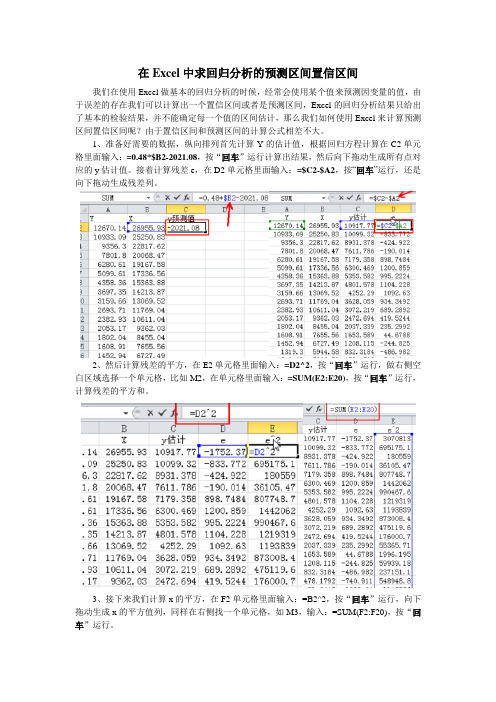
在Excel中求回归分析的预测区间置信区间我们在使用Excel做基本的回归分析的时候,经常会使用某个值来预测因变量的值,由于误差的存在我们可以计算出一个置信区间或者是预测区间,Excel的回归分析结果只给出了基本的检验结果,并不能确定每一个值的区间估计,那么我们如何使用Excel来计算预测区间置信区间呢?由于置信区间和预测区间的计算公式相差不大。
1、准备好需要的数据,纵向排列首先计算Y的估计值,根据回归方程计算在C2单元格里面输入:=0.48*$B2-2021.08,按“回车”运行计算出结果,然后向下拖动生成所有点对应的y估计值。
接着计算残差e,在D2单元格里面输入:=$C2-$A2,按“回车”运行,还是向下拖动生成残差列。
2、然后计算残差的平方,在E2单元格里面输入:=D2^2,按“回车”运行,做右侧空白区域选择一个单元格,比如M2,在单元格里面输入:=SUM(E2:E20),按“回车”运行,计算残差的平方和。
3、接下来我们计算x的平方,在F2单元格里面输入:=B2^2,按“回车”运行,向下拖动生成x的平方值列,同样在右侧找一个单元格,如M3,输入:=SUM(F2:F20),按“回车”运行。
4、接下来我们计算估计误差,先在K2单元格计算出x的均值,输入:=AVERAGE(B2:B20),按“回车”运行。
在K3输入需要计算得X值,比如这里的3000,在K5单元格里面输入:=SQRT($M$2/17*(1/18+($K$3-$K$2)^2/$M$3)),按“回车”运行输出误差值。
如果计算得是置信区间的话,可以另外选择单元格输入:=SQRT($M$2/17*(1+1/18+($K$3-$K$2)^2/$M$3)),按“回车”运行。
5、计算预测区间的上限和下限在J9单元格里面输入:=$M$5-TINV(0.05,17)*$K$5,按“回车”运行,作为下限值。
在K9单元格里面输入:=$M$5+TINV(0.05,17)*$K$5,按“回车”运行,作为上限值。
正态分布置信区间Excel计算公式

05
注意事项
样本量大小的影响
样本量大小
样本量越大,置信区间的宽度越窄,即 置信水平越高。在Excel中,可以使用 NORM.INV函数计算正态分布的置信区 间,其中需要输入样本量大小作为参数 之一。
VS
样本代表性
样本必须具有代表性,否则计算出的置信 区间可能不准确。在选择样本时,应尽量 确保其能够反映总体特征。
置信水平的选择
常用的置信水平
常用的置信水平有90%、95%和99%。不 同的置信水平对应着不同的置信区间宽度。 在Excel中,NORM.INV函数也接受置信水 平作为参数之一。
决策依据
选择合适的置信水平对于决策至关重要。例 如,在假设检验中,如果选择的置信水平过 低,可能会导致错误的结论。
置信区间的解释与解读
应用
用于检验假设的置信区间,判断样本数据是 否符合预期的总体分布。
样本均值的置信区间
计算公式
$[bar{x} - frac{s}{sqrt{n}} times
z_{alpha/2},
bar{x}
+
frac{s}{sqrt{n}}
times
z_{alpha/2}]$
解释
其中,$bar{x}$表示样本均值, $s$表示样本标准差,$n$表示样 本数量,$z_{alpha/2}$表示标准 正态分布的下(或上)临界值。
函数返回值:在给定置信 水平和标准差下,样本大 小为size的连续型变量的 置信区间宽度。04实例ຫໍສະໝຸດ 析假设检验中的正态分布置信区间
计算公式
$P(mu - sigma < X < mu + sigma) = 1 alpha$
解释
其中,$P$表示概率,$mu$表示总体均值, $sigma$表示总体标准差,$X$表示样本数据, $alpha$表示显著性水平。
[整理版]EXCEL区间估计
![[整理版]EXCEL区间估计](https://img.taocdn.com/s3/m/91f92735bdd126fff705cc1755270722192e59dc.png)
区间估计计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单。
1、单一总体均值的区间估计在2σ未知时,均值μ的置信区间:),(22n sz x n s z x αα+-例1:一家保险公司收集到由36位投保人组成的随机样本,得到每位投保人的年龄数据如下图7-1所示。
试建立投保人年龄95%的置信区间。
图7-1 36个投保人年龄的数据具体操作步骤如下:①在单元格C3输入样本数(n)=36。
②计算平均数和标准差。
在单元格C4输入平均数公式:= A VERAGE (E1:J6),在单元格C5输入样本标准差公式:= STDEV (E1:J6)。
③在单元格C6输入置信度(1-α)=95%,在单元格C7中输入显著水平(α)=5%。
④计算Z 值,在单元格C8中输入 =NORMSINV (1-C7/2)⑤计算置信区间上限和下限。
在单元格C9输入求置信区间下限公式:=C4-C8*C5/SQRT(C3),在单元格C10输入求置信区间上限公式:= C4+C8*C5/SQRT(C3)。
⑥在单元格C11输入求置信区间公式:=CONCA TENA TE("(",C9,",",C10,")")。
由上可得置信区间为(36.96, 42.04),如图7-2所示。
图7-2 单一总体均值的区间估计2、单一总体比例的区间估计: 置信区间为:)/)1(,/)1((2/2/n q q z q n q q z q -+--αα 例2:美国某调查机构想了解美国民众对政府某项税收议案的态度,调查了1000位美国人,结果发现5成人表示支持,4成人表示反对,1成人既不支持,也不反对。
试估计支持比例的95%置信区间。
操作步骤如下:①在单元格C3输入样本数(n)=1000。
②在单元格C4输入样本中支持百分比(q)=0.5。
③在单元格C5输入置信度(1-α)=95%,在单元格C6输入显著水平(α)=5%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用Excel求置信区间
一、总体均值的区间估计
(一)总体方差未知
例:为研究某种汽车轮胎的磨损情况,随机选取16只轮胎,每只轮胎行驶到磨坏为止。
记录所行驶的里程(以公里计)如下:
假设汽车轮胎的行驶里程服从正态分布,均值、方差未知。
试求总体均值μ的置信度为的置信区间。
步骤:
1.在单元格A1中输入“样本数据”,在单元格B4中输入“指标名称”,在单元格C4中输入“指标数值”,并在单元格A2:A17中输入样本数据。
2.在单元格B5中输入“样本容量”,在单元格C5中输入“16”。
3.计算样本平均行驶里程。
在单元格B6中输入“样本均值”,在单元格C6中输入公式:“=AVERAGE(A2,A17)”,回车后得到的结果为。
4.计算样本标准差。
在单元格B7中输入“样本标准差”,在单元格C7中输入公式:“=STDEV(A2,A17)”,回车后得到的结果为。
5.计算抽样平均误差。
在单元格B8中输入“抽样平均误差”,在单元格C8中输入公式:“=C7/SQRT(C5)” ,回车后得到的结果为。
6.在单元格B9中输入“置信度”,在单元格C9中输入“”。
7.在单元格B10中输入“自由度”,在单元格C10中输入“15”。
8.在单元格B11中输入“t分布的双侧分位数”,在单元格C11中输入公式:“ =TINV(1-C9,C10)”,回车后得到α=的t分布的双侧分位数t=。
9.计算允许误差。
在单元格B12中输入“允许误差”,在单元格C12中输入公式:“=C11*C8”,回车后得到的结果为。
10.计算置信区间下限。
在单元格B13中输入“置信下限”,在单元格C13中输入置信区间下限公式:“=C6-C12”,回车后得到的结果为。
11.计算置信区间上限。
在单元格B14中输入“置信上限”,在单元格C14中输入置信区间上限公式:“=C6+C12”,回车后得到的结果为。
(二)总体方差已知
仍以上例为例,假设汽车轮胎的行驶里程服从正态总体,方差为10002,试求总体均值μ的置信度为的置信区间。
1.在单元格A1中输入“样本数据”,在单元格B4中输入“指标名称”,在单元格C4中输入“指标数值”,并在单元格A2:A17中输入样本数据。
2.在单元格B5中输入“样本容量”,在单元格C5中输入“16”。
3.计算样本平均行驶里程。
在单元格B6中输入“样本均值”,在单元格C6中输入公式:“=AVERAGE(A2,A17)”,回车后得到的结果为。
4.在单元格B7中输入“标准差”,在
单元格C7中输入“1000”。
5.计算抽样平均误差。
在单元格B8中输入“抽样平均误差”,在单元格C8中输入公式:“=C7/SQRT(C5)” ,回车后得到的结果为250。
6.在单元格B9中输入“置信度”,在单元格C9中输入“”。
7. 在单元格B10中输入“自由度”,在单元格C10中输入“15”。
8. 在单元格B11中输入“标准正态分布的双侧分位数”,在单元格C11中输入公式:“=NORMSINV”,回车后得到α=的标准正态分布的双侧分位数2=。
9.计算允许误差。
在单元格B12中输入“允许误差”,在单元格C12中输入公式:“=C11*C8”,回车后得到的结果为490。
10.计算置信区间下限。
在单元格B13中输入“置信下限”,在单元格C13中输入置信区间下限公式:“=C6-C12”,
回车后得到的结果为。
11.计算置信区间上限。
在单元格B14中输入“置信上限”,在单元格C14中输入置信区间上限公式:“=C6+C12,回车后得到的结果为。
二、总体方差的区间估计(μ未知)
例:假设从加工的同一批产品中任意抽取20件,测得它们的平均长度为12厘米,方差为平方厘米,求总体方差的置信度为95%的置信区间。
为构造区间估计的工作表,我们应在工作表的A列输入计算指标,B列输入计算公式,C列输入计算结果。
提示:
① 本表C列为B列的计算结果,当在B列输入完公式后,即显示出C列结果,这里只是为了让读者看清楚公式,才给出了B列的公式形式。
② 统计函数“=CHINV(α,df)”,给出概率水平为α、自由度为v的χ2分布上侧分位数。
具体使用方法,可以在Excel的函数指南中查看。
综上所述,我们有95%的把握认为该批零件平均长度的方差在至之间。
三、总体比例的区间估计
市大专以上学历的从业人员专业不对口的比率。
于是随机抽取了一个由1500人组成的样本进行调查,其中有450人说他们从事的工作与所学专业不对口。
试在95%的置信度下构造出该市专业不对口人员所占比率的置信区间。
n(1由于样本容量很大,n=1500,)
-p
样本比例和
都大于5,故可用正态分布逼近。
构造区间估计的工作表,我们应在工作表的C列输入计算指标,D列输入计算公式,E列输入计算结果。
① 本表E列为D列的计算结果,当输入完公式后,即显示出E列结果,这里只是为了让读者看清楚公式,才给出了D列的计算公式。
② 统计函数“=CONFIDENCE(α,β,δ)”,给出置信水平为1-α、样本比例标准差为β和样本容量为δ的总体比例的误差范围。
具体使用方法,可以在Excel的函数指南中查看。
