3.4 角动量定理 角动量守恒定律
合集下载
Ch3.4(角动量定理和角动量守恒定律)

分量式
M
M
x
yF z zF y
zF x xF z
y
M z xF y yF x
3) 作用于质点上所有力矩的矢量和,等于合力的力矩。
i
M
i
r F1 r F 2 r F n
r ( F1 F 2 F n ) r F M
1 p1
m
v1
m
2
B p2
r sin
r1
r2
L 2 r2 p 2 sin 2 mr 2 v 2 sin 2 mv 2 OD
O
讨论:
① 作直线运动的质点, r 和 p 可能逐点变化,但 d r sin 保持不变。
② 对不同参考点的角动量一般不同。 ③ 若 p m v 不变,则:L1 L 2 ,即匀速直线运动 的质点对同一参考点的角动量守恒 L C 。
一、角动量 (一)质点的角动量 1. 定义:某一质点,动量 对 O 点的径矢为 r ,则它 对 O 点的角动量(动量矩)为 注意:
x
P
z
L
p sin
O
r sin
r
y
p
m
p cos
(1)大小: L rp sin mrv sin 方向: 用右手螺旋定则确定。 (2)相对性 ① 对不同的参考系,矢径不同,动 量不同,角动量也不同。 ② 参考点不同, 矢径不同,角动量也不同。
L L1 L 2 L n r1 p 1 r2 p 2 rn p n
角动量 角动量守恒定律大学物理

对定轴转动的刚体 Miin 0 ,合外力矩
M
Miex
d dt
(
mi
ri
2
)
d(J
dt
)
d( J )
dL
M
dt dt
第3章 守恒定律
12
大学物
理学
第二版
t2 t1
Mdt
L2
L1
t2 t1
Mdt
L2
L1
当转轴给定时,作用在物体上的冲量 矩等于角动量的增量.——定轴转动的角 动量定理
第3章 守恒定律
然长度处以
垂直于弹簧运动,当
弹簧与初始位置垂直时,弹簧长度
v
求此时滑块的速度.
v0
第3章 守恒定律
图 3.4
大学物 理学
第二版
【解】 由角动量和机械能守恒
结论:对于有心力问题,系统对力心处的 角动量守恒.
第3章 守恒定律
大学物
理学
第二版
三、角动量守恒定律的应用
(1)常平架回转仪(陀螺仪) (2)直升飞机尾翼
质点角动量定理的推导
L r p r mv
dL
d
(r
p)
r
dp
dr
p
dt dt dr v,v p 0
dt dL
dt
r
dp
r
F
dt
dt
dt
第3章 守恒定律
4
大学物
理学
第二版
dL
M
dt
作用于质点的合外力对参考点 O 的力 矩,等于质点对该点 O 的角动量随时间的 变化率.
13
大学物
理学
第二版
对定轴转动的刚体,受合外力矩M,
刚体定轴转动的角动量定理和角动量守恒定律

刚体定轴转动的角动量定理和角动量守恒定律
1、刚体定轴转动的角动量
刚体绕定轴转动的角动量等于刚体对该轴的转动惯量与角速度的乘积;方向与角速度的方向相同。
2、刚体定轴转动的角动量定理
(1)微分形式:刚体绕某定轴转动时,作用于刚体的合外力矩,等于刚体绕该定轴的角动量随时间的变化率。
(2)积分形式:当物体绕某定轴转动时,作用在物体上的冲量矩等于角动量的增量。
3、刚体定轴转动的角动量守恒定律
如果物体所受的合外力矩等于零,或者不受外力矩作用,物体的角动量保持不变。
练习:1角动量守恒的条件是 。
0=M 11222
1ωωJ J Mdt t t -=⎰刚体 ) 21J J ==ωJ 恒量
ωJ L =()ωJ dt d dt dL M ==。
角动量、角动量守恒
T
(3) )
m, l
联立(1)、(2)、(3)式求解 式求解 联立
mg
1 T = mg 4
例5:在光滑水平桌面上放置一个静止的质量 : 可绕中心转动的细杆, 为 M、长为 2l 、可绕中心转动的细杆,有一质 、 量为 m 的小球以速度 v0 与杆的一端发生完全弹 性碰撞, 性碰撞,求小球的反弹速度 v 及杆的转动角速 度ω。 解:在水平面上,碰撞 在水平面上, 过程中系统角动量守恒, 过程中系统角动量守恒,
∆A/ ∆t = 恒 量
两个共轴飞轮转动惯量分别为J 例1:两个共轴飞轮转动惯量分别为 1、J2, 角速度分别为 ω1 、ω2,求两飞轮啮合后共同 啮合过程机械能损失。 的角速度 ω 。啮合过程机械能损失。 J1 J2 解:两飞轮通过摩 擦达到共同速度,合 擦达到共同速度 合 外力矩为0, 外力矩为 ,系统角 动量守恒。 动量守恒。
定义:力对某点 的力矩等于力的作用点 定义:力对某点O的力矩等于力的作用点 的矢量积。 的矢径 r 与力F的矢量积。 v v
v Mo
ϕ
注意: 注意: 1)大小: o = rF sin ϕ )大小: M v v 的方向 2)方向: × F )方向: r 3)单位:牛顿米 )单位: v r 4)当 F ≠ 0 时, ) 有两种情况 Mo = 0 v A) r = 0 ) B)力的方向沿矢径的方向( sin ϕ = 0) )力的方向沿矢径的方向(
ω1 L0 = L = C J1ω1 + J2ω2 = (J1 + J2 )ω
ω2
J1ω1 + J2ω2 共同角速度 ω = J1 + J2
啮合过程机械能损失
∆E = E − E0
1 1 1 2 2 2 ∆E = (J1 + J2 )ω − ( J1ω1 + J2ω2 ) 2 2 2 J1ω1 + J2ω2 其中 ω = J1 + J2
3.4 角动量定理 角动量守恒定律

大小:
L r P sin
r, P
S
P
r
O
特例:质点作圆周运动
方向:垂直
组成的平面
L M L2 T
L rp mr v
1
SI
k g m /s
2
量纲:
讨论
惯性参照系
(1) 质点的动量矩(角动量)与质点的动量及位矢(取决 于固定点的选择)有关; (2) 当质点作平面运动时,质点对运动平面内某参考点 O 的动量矩也称为质点对过O 垂直于运动平面的轴的 动量矩 ; L
dr dt
二、力对定点的力矩
dL dt
d r p dt
dr dt
o
p r
dp dt
p v p 0
dL dt r dp dt rF M
M
F
O .
定义
为力对定点O的力矩 M rF 力对O 点的力矩 大小: M r F sin
M
A
r Lo T
A
R T 0
R
r
mg
O
m gR sin m gr
LA R mv
r
对于O点:
M
g
M
A
r T
rT cos
LO r m v
r mg
m gr
质点作任何运动都可以用角动量来描述其运动状态。 例 质点对圆心的动量矩。 行星在椭圆轨道上的动量矩。
F 0 P 0
M 0 L 0
形式上完全相同,所以记忆上就可简化。从动量定理变换到 角动量定理,只需将相应的量变换一下,名称上改变一下。
L r P sin
r, P
S
P
r
O
特例:质点作圆周运动
方向:垂直
组成的平面
L M L2 T
L rp mr v
1
SI
k g m /s
2
量纲:
讨论
惯性参照系
(1) 质点的动量矩(角动量)与质点的动量及位矢(取决 于固定点的选择)有关; (2) 当质点作平面运动时,质点对运动平面内某参考点 O 的动量矩也称为质点对过O 垂直于运动平面的轴的 动量矩 ; L
dr dt
二、力对定点的力矩
dL dt
d r p dt
dr dt
o
p r
dp dt
p v p 0
dL dt r dp dt rF M
M
F
O .
定义
为力对定点O的力矩 M rF 力对O 点的力矩 大小: M r F sin
M
A
r Lo T
A
R T 0
R
r
mg
O
m gR sin m gr
LA R mv
r
对于O点:
M
g
M
A
r T
rT cos
LO r m v
r mg
m gr
质点作任何运动都可以用角动量来描述其运动状态。 例 质点对圆心的动量矩。 行星在椭圆轨道上的动量矩。
F 0 P 0
M 0 L 0
形式上完全相同,所以记忆上就可简化。从动量定理变换到 角动量定理,只需将相应的量变换一下,名称上改变一下。
物理-定轴转动刚体的角动量定理和角动量守恒定律

或 Lz = I = 恒量
当刚体相对惯性系中某给定转轴的合外力矩为 零时,该刚体对同一转轴的角动量保持不变。
——对转轴的角动量守恒定律
二、定轴转动中的角动量守恒
说明 1、 关于该守恒定律的条件:
Mz Miz 0
特别地,若每一个力的力矩均为零,即 则
二、定轴转动中的角动量守恒
M iz ri Fi sini 0 的几种情况
10
f
20
O1 R1 A
R2 O2 fB
随堂练习
当两圆柱接触处无相对滑动时,两者转速相反
10
20
O1 R1 A
R2 O2 B
且两者接触点的线速率相等!
二、定轴转动中的角动量守恒
由定轴转动的角动量定理
Mz
dLz dt
若刚体所受对转轴的合外力矩 M z 0,则有
dLz d ( I ) 0
dt
dt
二、定轴转动中的角动量守恒
(3) 对共轴非刚体系(其中各质元到转轴的距离可 变则)系:统的转动惯量可变,此时系统对转轴的角动量守恒,
即:I =恒量
• 特别地,若各质元的 保持一致,
Lz =I =恒量
当 I 增大时, 就减小; 当 I 减小时, 就增大 。
二、定轴转动中的角动量守恒
例如:花样滑冰运动员在冰面上旋转时 运动了角动量守恒定律
(1)
(2)
(3)
二、定轴转动中的角动量守恒
2、对转轴的角动量守恒定律的适用范围: • 不仅适用于刚体, • 也适用于绕同一转轴转动的任意质点系。
二、定轴转动中的角动量守恒
3、对转轴的角动量守恒的几种典型表现 (1) 对定轴刚体:I 不变, 大小和方向均不变;
3_4角动量 角动量守恒定律.

t1
Mdt
J2
J1
4 – 4 角动量 角动量守恒定律
第四章 刚体的转动
刚体定轴转动的角动量定理
t2 t1
Mdt
J2
J1
刚体转动的角动量定理:刚体所受的冲量矩等于 刚体转动角动量的增量.
3 刚体定轴转动的角动量守恒定律
若 M 0 ,则 L J 常量
刚体所受的合力矩为零时,刚体转动角动量为一 恒矢量.
1 (1 ml 2 ma2 ) 2
23
W 1 J 2
2
mga(1 cos30) mg l (1 cos30)
2
v g(2 3)(ml 2ma)(ml2 3ma2 ) 6 ma
4 – 4 角动量 角动量守恒定律
第四章 刚体的转动
例3 质量很小长度为l 的均匀细杆,可绕过其中心 O
o
m'
30
L mr2 J
a
mva ( 1 ml 2 m a2 )
3
v m
3mva m'l 2 3ma2
4 – 4 角动量 角动量守恒定律
m'l
3mva 2 3ma2
射入竿后,以子弹、细杆和 地球为系统 ,机械能守恒 .
第四章 刚体的转动
o 30
a v m'
4 – 4 角动量 角动量守恒定律
第四章 刚体的转动
力的时间累积效应 冲量、动量、动量定理.
力矩的时间累积效应
冲量矩、角动量、
角动量定理.
一 质点的角动量定理和角动量守恒定律
质点运动状态的描述
p mv Ek mv2 2
Mdt
J2
J1
4 – 4 角动量 角动量守恒定律
第四章 刚体的转动
刚体定轴转动的角动量定理
t2 t1
Mdt
J2
J1
刚体转动的角动量定理:刚体所受的冲量矩等于 刚体转动角动量的增量.
3 刚体定轴转动的角动量守恒定律
若 M 0 ,则 L J 常量
刚体所受的合力矩为零时,刚体转动角动量为一 恒矢量.
1 (1 ml 2 ma2 ) 2
23
W 1 J 2
2
mga(1 cos30) mg l (1 cos30)
2
v g(2 3)(ml 2ma)(ml2 3ma2 ) 6 ma
4 – 4 角动量 角动量守恒定律
第四章 刚体的转动
例3 质量很小长度为l 的均匀细杆,可绕过其中心 O
o
m'
30
L mr2 J
a
mva ( 1 ml 2 m a2 )
3
v m
3mva m'l 2 3ma2
4 – 4 角动量 角动量守恒定律
m'l
3mva 2 3ma2
射入竿后,以子弹、细杆和 地球为系统 ,机械能守恒 .
第四章 刚体的转动
o 30
a v m'
4 – 4 角动量 角动量守恒定律
第四章 刚体的转动
力的时间累积效应 冲量、动量、动量定理.
力矩的时间累积效应
冲量矩、角动量、
角动量定理.
一 质点的角动量定理和角动量守恒定律
质点运动状态的描述
p mv Ek mv2 2
角动量 角动量守恒定律
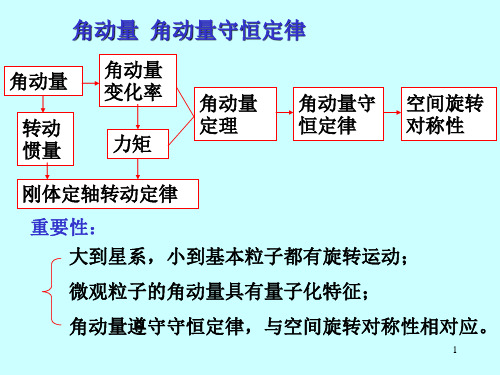
r为力的作用点到 参考点的位置矢量
20
2) 力对定轴的力矩
z
Mz
o
d
F F //
r
F
M r F r ( F// F ) r F// r F
第一项
力F对O点的力矩 (F不在转动平面内):
M1 r F//
dL 可得 M r F dt
对 N 个质点 m1, m2 ,, mN 组成的质点系,由
dL1 r1 F1外 F1内 M 1外 M 1内 dt 两边求和得 dL2 r2 F2外 F2内 M 2外 M 2内 dL总 d dt Li dt i dt M i 外 M i内 dLN i i 24 rN FN外 FN内 M N外 M N内 dt
z
vi
转轴与其转动平面交点
o
转动 平面
mi 对 o 的角动量: Lio ri mi vi
大小:Lio ri mi vi mi ri 2 Lio 方向:沿 2 即 Lio mi ri
o圆周运动半径为 ri
o ri
mi
6
定义:质点 mi 对其转动平面上圆心 o 点的角动 量的大小,称为质点对转轴的角动量。
11
m 1 L3 L3 1 2 m L 12 L 3 8 8
(2) 轴过一端端点
dm
o
x
J r dm x dm
2 2 L
L
x
2
若使用平行轴定理:
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 动量矩守恒定律是物理学的基本定律之一,它不仅 动量矩守恒定律是物理学的基本定律之一, 适用于宏观体系,也适用于微观体系, 适用于宏观体系,也适用于微观体系,且在高速低 速范围均适用; 速范围均适用; (2) 动量守恒与角动量守恒 是相互独立的定律; 是相互独立的定律; 通常对有心力: (3) 通常对有心力: 过 点 F O点, M=0, 动量矩守恒
§3.4 角动量定理 角动量守恒定律
一,质点对定点的角动量 二,力对定点的力矩 三,质点的角动量定理 角动量守恒定律 四,质点系的角动量问题
1
第点O的动量矩 角动量) 一. 质点对定点 的动量矩 角动量
定义
L = r ×P
S
L
L = r × P = r ×m v
m
r0
v
R
OM
v0
θ
质点的动量矩守恒 1 GMm 1 2 GMm 2 mv0 = mv 2 r0 2 R
mv0r0sinθ = mvR
v0r0sinθ v= = 4v0sinθ R
3GM v =v0 1+ 2 v 2R 0
1/ 2
1 3GM sinθ = 1+ 2 4 2R 0 v
尾部添矩) (趣称 头上长角 尾部添矩)
16 第3章动量与角动量
�
动量定理
动量矩定理
dP F= dt
t2
dL M = dt
t2
∫ F dt = Δ P
t1
∫ M dt = Δ L
t1
F = 0 P = 0
M = 0 L = 0
形式上完全相同,所以记忆上就可简化. 形式上完全相同,所以记忆上就可简化.从动量定理变换到 上完全相同 简化 角动量定理,只需将相应的量变换一下,名称上改变一下. 角动量定理,只需将相应的量变换一下,名称上改变一下.
11
掠面 速度
行星对太阳的位矢在相等 的时间内扫过相等的面积
第3章动量与角动量
例2 发射一宇宙飞船去考察一 质量为 M ,半径为 R 的行 星, 以速度v 当飞船静止于空间距行星中心 4 R 时,以速度 0发射一 的仪器.要使该仪器恰好掠过行星表面. 质量为 m 的仪器.要使该仪器恰好掠过行星表面. 角及着陆滑行的初速度. 求 θ角及着陆滑行的初速度. 角及着陆滑行的初速度 引力场(有心力) 解 引力场(有心力) 系统的机械能守恒
L = rpsinα = mrvsinα
大小: 大小:
α
r
P
O
L = r P sin α
特例: 特例:质点作圆周运动
方向: 方向:垂直 r, P 组成的平面
L = rp = mrv
1
SI
2
kgm 2 /s
量纲: 量纲: L = M L 2 T
第3章动量与角动量
讨论
惯性参照系
(1) 质点的动量矩(角动量)与质点的动量及位矢(取决 质点的动量矩(角动量)与质点的动量及位矢( 位矢 于固定点的选择)有关; 于固定点的选择)有关; (2) 当质点作平面运动时,质点对运动平面内某参考点 当质点作平面运动时, O 的动量矩也称为质点对过 垂直于运动平面的轴的 的动量矩也称为质点对过O 动量矩 动量矩 L ;
M外 = 0
L = 0
L = const.vector
如果作用在质点系合外力矩沿某轴的投影为零, 如果作用在质点系合外力矩沿某轴的投影为零,则沿此轴动 沿某轴的投影为零 量矩守恒, 量矩守恒,如 L =常 常 量 M =0
z
Z
14 第3章动量与角动量
盘状星系
15
角动量守恒的结果
第3章动量与角动量
比较
MA = R ×T
Mg = R×mg
= mgR sin θ = mgr
LA = R×mv M A = r ×T
r mg υ
R r
O
对于O点 对于 点:
= rT cos θ
LO = r × mv
第3章动量与角动量
Mg = r×mg
7
= mgr
质点作任何运动都可以用角动量来描述其运动状态. 质点作任何运动都可以用角动量来描述其运动状态. 例 质点对圆心的动量矩. 行星在椭圆轨道上的动量矩. 质点对圆心的动量矩. 行星在椭圆轨道上的动量矩.
第3章动量与角动量
二,力对定点的力矩
定义 为力对定点O的力矩 M = r × F 为力对定点 的力矩
M
大小: 大小:
M = r F sin
方向: 方向:垂直 r , F 组成的平面
o
r
d
SI
M = ML2T 2 Nm 量纲: 量纲:
m
F
讨论 力对O (1) 力对 点的力矩
Mo
F
O .
MO = r × F
得 微分形式 冲量矩 积分形式 说明
d(m ) dr v dL d + ×m v = ( r ×m ) = r × v dt dt dt dt
r ×F = M
v ×m = 0 v
dL M = dt
t2
或写成
M dt = dL
∫ M dt = ΔL
t1
质点所受合力矩的 冲量矩 冲量矩等于质点的 动量矩 动量矩的增量
i i i
∑r×
i i
fi = 0
内力对定点的力矩之和为零
(自证 自证) 自证
质点系内的重要结论之三 dL L = ∑ Li M外 = i dt
13 第3章动量与角动量
冲量矩
∫t M外dt = ∫L dL = L2 L1 = L
1 1
t2
L2
(1)质点系所受合外力矩的冲量矩等于质点系动量矩的增量; (1)质点系所受合外力矩的冲量矩等于质点系动量矩的增量; 质点系所受合外力矩的冲量矩等于质点系动量矩的增量 (2) 内力对定点的力矩之和为零,只有外力矩才能改变系 内力对定点的力矩之和为零, 统的总角动量. 统的总角动量. 3. 质点系动量矩守恒定律 对质点系
12
1/ 2
第3章动量与角动量
四,质点系的动量矩
1. 对定点的动量矩
P2
P1
L = ∑ Li = ∑ ri × Pi
i i
o
r2
r1
质点系对参考点O 质点系对参考点 的动量矩就是质点系所有质点对同一参 考点的动量矩的矢量和 2. 质点系的动量矩定理
d Li ∑ M i =∑ d t i i M = ∑ M i = ∑ ri × Fi + ∑ ri × f i
θ A
F τ
F⊥
Fn
x
y
z
M= x
M = r × F = Mx x + My y + Mz z
6 第3章动量与角动量
y z FxFyFz
(3)力对任意点的力矩,在通过该点的任一轴上的投影, (3)力对任意点的力矩,在通过该点的任一轴上的投影, 力对任意点的力矩 等于该力对该轴的力矩. 等于该力对该轴的力矩. 例2:圆锥摆球在水平面内匀速转 : A r 分别讨论对固定点A和 点 动,分别讨论对固定点 和O点, r Lo T θ 小球受的张力矩,重力矩和角动量. 小球受的张力矩,重力矩和角动量. LA 对于A点 解: 对于 点
力矩的方向由右螺旋法则确定
5 第3章动量与角动量
r
(2) 力对定轴力矩的矢量形式
z
F//
F
MZ = r × F⊥
Mz (F) = F⊥h = Fr τ
力矩的方向由右螺旋法则确定 对轴的力矩 在具体的坐标系中, 在具体的坐标系中,力矩在各坐标轴 的分量,就叫对轴的力矩. 的分量,就叫对轴的力矩.
h
r
O
(3) 质点对某点的动量 矩,在通过该点的 任意轴上的投影就 等于质点对该轴的 动量矩; 动量矩;
LO′
LO
O′
S
P
α
r
O
3
第3章动量与角动量
(4) 对轴的动量矩 在具体的坐标系中,动量矩在各坐标轴的分量, 在具体的坐标系中,动量矩在各坐标轴的分量, 就叫对轴的动量矩. 就叫对轴的动量矩.
L = r × P = Lx x + Ly y + Lz z
第3章动量与角动量
10
行星在速度和有心力所组成的平面内运动 例如 由动量矩守恒定律可导出行星运动的开普勒 第二定律. 第二定律. 行星受到的合外力矩
r r r M = r ×F = 0
L
r r r L = r × mυ = C
υ
r r F
α
m
r
r rsinα L = mvrsinα = m t 1 r r rsinα S 2 = 2m = 2m t t
(1) 冲量矩是质点动量矩变化的原因; 冲量矩是质点动量矩变化的原因; (2) 质点动量矩的变化是力矩对时间的积累结果. 质点动量矩的变化是力矩对时间的积累结果.
9 第3章动量与角动量
dL =0 若 M =0 dt
讨论
2. 质点动量矩守恒定律 r
r r r r L = r × P = C 常矢量
——质点动量矩守恒定律 质点动量矩守恒定律
L
m1 υ
o
r
m υ
m2 υ
r2
o
r 1
抛出物体对O点的动量矩. 直线运动的物体对 点的动量矩. 点的动量矩. 抛出物体对 点的动量矩. 直线运动的物体对O点的动量矩 点的动量矩
y
m1 υ
m2 υ
r
o
8
m υ
r 1
x
r2
x
o
第3章动量与角动量
三,质点的角动量定理 角动量守恒定律
1. 动量矩定理
dP F = dt
