实验三MATLAB符号计算
如何在Matlab中进行符号计算

如何在Matlab中进行符号计算Matlab是一种非常强大的数学计算软件,除了常见的数值计算,也可以进行符号计算。
符号计算是一种基于数学符号的计算方法,可以进行代数运算、求解方程、求导、积分等一系列符号运算。
在Matlab中进行符号计算,可以帮助我们更好地理解数学概念、解决复杂的数学问题。
本文将介绍如何在Matlab中进行符号计算,包括符号变量的定义、基本运算、方程求解、求导和积分等方面。
一、符号变量的定义在Matlab中进行符号计算,需要首先定义符号变量。
符号变量是用来表示未知数和函数的数学符号,可以使用syms关键字来定义。
例如,我们可以定义一个符号变量x,并进行一些基本操作。
```syms x;f = x^2 + sin(x);```在上述代码中,我们定义了一个符号变量x,并定义了一个函数f,代表x的平方加上sin(x)。
在后续的运算中,可以使用这些符号变量进行计算。
二、基本运算在Matlab中进行符号计算时,可以进行基本的数学运算,包括加减乘除、幂运算、开方等。
这些运算符在符号计算中与数值计算中的用法一致。
例如,我们可以进行如下的运算:```syms x;f = x^3 + 2*x^2 - x + 1;g = diff(f, x);```在上述代码中,我们定义了一个函数f,然后使用diff函数对f进行求导,将结果赋值给变量g。
通过这样的方式,可以方便地进行复杂的数学运算。
三、方程求解在Matlab中进行符号计算时,经常需要解方程。
Matlab提供了solve函数,可以对方程进行求解。
例如,我们可以解一个简单的一次方程:```syms x;eqn = 2*x + 3 == 7;sol = solve(eqn, x);```上述代码中,我们定义了一个方程eqn,然后使用solve函数求解方程,将结果赋值给变量sol。
在Matlab中可以同时解多个方程,并得到符号解或数值解。
四、求导和积分除了基本运算和方程求解,Matlab还提供了求导和积分的函数,方便进行符号计算。
Matlab中的符号计算方法

Matlab中的符号计算方法在数学和科学领域,符号计算是一个重要的工具。
它可以帮助我们进行精确的数学计算和推理,而不仅仅是依赖计算机的数值近似。
Matlab作为一个强大的数值计算软件,也提供了丰富的符号计算功能,用于代数运算、微积分和代数方程求解等方面。
本文将介绍Matlab中的一些常用的符号计算方法和技巧。
一、符号变量在Matlab中,我们可以通过声明符号变量来表示符号对象。
符号变量通常用小写字母表示,例如x、y、z等。
使用符号变量,我们可以进行各种代数运算,例如加法、减法、乘法和除法等。
下面是一些示例:syms x y zf = x^2 + y^2 - z^2;g = (x + y + z)^3;h = sin(x) * cos(y);通过声明符号变量,并使用这些变量进行计算,我们可以得到精确的结果,而不是使用数值近似。
二、符号表达式在Matlab中,符号表达式是由符号变量和运算符组成的一种数据类型。
使用符号表达式,我们可以构建复杂的代数表达式和方程。
例如,我们可以定义一个符号表达式f表示一个多项式函数,并对其进行运算:f = x^3 - 2*x^2 + x - 1;我们可以对符号表达式进行加减乘除等运算,并得到一个新的符号表达式。
三、代数方程求解在解决数学问题时,我们经常需要求解代数方程。
Matlab提供了强大的符号求解工具,可以帮助我们求解各种类型的代数方程。
例如,我们可以使用solve函数求解一元方程:syms xeqn = x^2 - 3*x + 2 == 0;sol = solve(eqn, x);通过solve函数,我们可以找到满足方程eqn的所有解,并将其存储到sol变量中。
除了一元方程,Matlab还支持多元方程的求解。
例如,我们可以使用solve函数求解一个二元方程组:syms x yeqn1 = x + 2*y == 5;eqn2 = x - y == 1;sol = solve([eqn1, eqn2], [x, y]);通过solve函数,我们可以找到满足方程组eqn1和eqn2的所有解,并将其存储到sol变量中。
实验MATLAB符号计算

5.1
5.1.1
【例5.1.1-1】符号常数形成中的差异
a1=[1/3,pi/7,sqrt(5),pi+sqrt(5)]%<1>
a2=sym([1/3,pi/7,sqrt(5),pi+sqrt(5)])%<2>
a3=sym([1/3,pi/7,sqrt(5),pi+sqrt(5)],'e')%<3>
char
CMs =
sym
(4)
isa(Mn,'double'),isa(Mc,'char'),isa(Ms,'sym')
ans =
1
ans =
1
ans =
1
(5)
whos Mn Mc Ms
Name Size Bytes Class
Mc 1x9 18 char array
Mn 2x2 32 double array
Ms 2x2 312 sym object
Grand total is 21 elements using 362 bytes
5.1.4
【例5.1.4-1】对独立自由符号变量的自动辨认。
(1)
syms a b x X Y;k=sym('3');z=sym('c*sqrt(delta)+y*sin(theta)');
MATLAB数值计算和符号运算
贵州大学实验报告
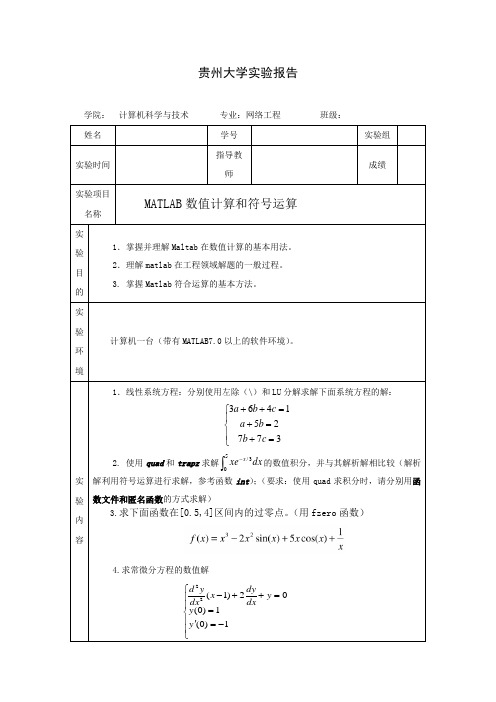
学院:计算机科学与技术专业:网络工程班级:
姓名
学号
实验组
实验时间
指导教师
成绩
实验项目名称
MATLAB数值计算和符号运算
实验目的
1.掌握并理解Maltab在数值计算的基本用法。
2.理解matlab在工程领域解题的一般过程。
3. 掌握Matlab符合运算的基本方法。
实验环境
计算机一台(带有MATLAB7.0以上的软件环境)。
实验内容
1.线性系统方程:分别使用左除(\)和LU分解求解下面系统方程的解:
2. 使用quad和trapz求解 的数值积分,并与其解析解相比较(解析解利用符号运算进行求解,参考函数int);(要求:使用quad求积分时,请分别用函数文件和匿名函数的方式求解)
实验代码
第一题
a=[3 6 4;1 5 0;0 7 7]
b=[1;2;3]
x=a\b
[L,U]=lu(a)
x=U\(L\b)
第二题
functiony=fun(x)
y=x.*exp(-(x./3));
Q1=quad('fun',0,5)
Q2=quad(@(x)(x.*exp(-(x./3))),0,5)
b=[400;440;484;532.4];
x0=[0.5;0.5;0.5;0.5];
[x,fval]=fmincon('fun',x0,A,b)
实验结果
第一题
第二题
第三题
第四题
第五题
第六题ห้องสมุดไป่ตู้
MATLAB实验报告三
掌握符号计算的基本方法;
三、使用仪器、材料
掌握程序设计控制流、M 函数文件、编写程序。
一台装有MATLAB7.0或以上的计算机
二、实验内容
1. 2.
计算二重积分 1
2
x2
四、实验过程原始记录(程序、数据、图表、计算等)
1
( x y )dydx。
2 2
63
1.
计算二重积分 1
2
Байду номын сангаас
x2
1
( x 2 y 2 )dydx
2.请分别写出用 for 和 while 循环语句计算 K 2i 1 2 2 2... 2 63 的程
i 0
63
序。此外,还请写出一种避免循环的计算程序。
4. 等比数列公式法
2 求一阶微分方程 x at bt, x(0) 2 的解
五、实验结果及分析
5.
2 2 求方程 x y 1, xy 2 的解。(提示:正确使用 solve)
广州大学学生实验报告
开课学院及实验室:
学院 机电学院
计算机 301B
电气 122 姓名 黄柱
2014 年
学号 成绩 指导 老师
5 月 20 日
年级、专 业、班
1207300074
实验课程名称 实验项目名称
MATLAB 语言及应用
实验三
符号计算及程序设计
姚菁
一、实验目的 二、实验内容 三、使用仪器、材料 四、实验过程原始记录(程序、数据、图表、计算等) 五、实验结果及分析 一、实验目的
请分别写出用 for 和 while 循环语句计算 K 2i 1 2 2 2... 2 63 的
MATLAB实验三参考答案

how =collect(x)
4、求下列函数的极限(写出命令) (1) lim
cos x e x 0 x4
x2 2
syms x; limit('(cos(x)-exp(-1/2*x^2))/(x^4)',x,0) -1/12 (2) lim
2 x ln 2 x 1 x 0 1 cos x
syms n; S=symsum(1/((3*n-2)*(3*n+1)),n,1,inf) 8、试求出函数 f ( x )
sin x 的麦克劳林幂级数展开式的前 9 项,并求出关于 x=2 x 3x 2
2
的 Taylor 幂级数展开式的前 5 项。(命令 taylor 或者 taylortool)
河南财经政法大学数学与信息科学学院 1
实验报告
结果: EXPR =(x^2+x*exp(-t)+1)*(x+exp(-t)) expr1 =x^3+2*exp(-t)*x^2+(1+exp(-t)^2)*x+exp(-t) expr2 =x*exp(-t)^2+(2*x^2+1)*exp(-t)+(x^2+1)*x 3、factor(因式分解),simple(简化运算,对表达式尝试多种不同的算法进行简化,并以最 简化形式给出,How 中记录的为简化过程中使用的方法, )指令的使用 syms a x; f1=x^4-5*x^3+x^2+5*x-6; factor(f1) x^4-5*x^3+x^2+5*x-6 f2=x^2-a^2; factor(f2) (x-a)*(x+a) f3=2*sin(x)^2-cos(x)^2 [y , how]=simple(f3) y 为 f 的最优化简形式,How 中记录的为简化过程中使用的方法 y =-3*cos(x)^2+2 how =simplify [y , how]=simple(f1) y =x^4-5*x^3+x^2+5*x-6
matlab符号计算实验报告

1. 已知x=6,y=5,利用符号表达式求z =>> syms x >> z=(x+1)/(sqrt(x+3)-sqrt(y)); >> subs(z,x,5) ans =6/(8^(1/2)-y^(1/2)) >> subs(ans,6) ans = 15.83382. 分解因式。
(1)x y -44; >> syms x y >> factor(x^4-y^4) ans =(x-y)*(x+y)*(x^2+y^2)(2)x x x +++64212575151 >> syms x >> factor(125*x^6+75*x^4+15*x^2+1) ans =(5*x^2+1)^33. 化简表达式(1)sin cos cos sin ββββ-1212;>> syms x y >> f=sin(x).*cos(y)-cos(x).*sin(y); >> sfy1=simple(f) 结果:sfy1 =sin(x-y)(2)x x x +++248321>> syms x >> f=(4*x^2+8*x+3)/(2*x+1);sfy1=simplify(f) sfy1 =2*x+34、求下列极限,将完成实验的程序写到文件sy1.m 中:(1) (2) (3) (4)(5) (1)>> syms x >> F1=atan(x)/(x); >> w=limit(F1) w =1(2)>> syms x F2=((1+x)/(1-x))^(1/x); >> w=limit(F2) w =exp(2)(3)>> syms x F3=(x.*log(1+x))/(sin(x^2)); >> w=limit(F3) w =1(4)>> syms x F4=atan(x)/(x); >> w=limit(F4,x,inf) w =0(5)>> syms x F5=(1/(1-x)-1/(1-x^3)); >> w=limit(F5,x,1) w =NaN5、求下列函数的导数,将完成实验的程序写到文件sy2.m 中:1、 >> x = sym('x'); >> y1=(cos(x))^3-cos(3*x); >> diff(y1)ans =-3*cos(x)^2*sin(x)+3*sin(3*x)2、 >> x = sym('x'); >> y2=x.*sin(x).*(log(x)); >> diff(y2)ans =sin(x)*log(x)+x*cos(x)*log(x)+sin(x)3、>> x = sym('x'); >> y3=(x.*exp(x)-1)/sin(x); >> diff(y3)ans =(exp(x)+x*exp(x))/sin(x)-(x*exp(x)-1)/sin(x)^2*cos(x)4、 x x x x F 1011lim 2⎪⎭⎫ ⎝⎛-+=→31115lim()11x F x x →=---20sin )1ln(lim 3x x x F x +=→x x F x arctan lim 10→=arctan 4lim x x F x →∞=xx y 3cos cos 13-=xx x y ln sin 2=x xe y xsin 13-=cos x y e x =>> x = sym('x');y=cos(x).*exp(x); >> diff(y) ans =-sin(x)*exp(x)+cos(x)*exp(x)5、 >> x = sym('x');y=x^2.*sin(x); >> diff(y) ans = 2*x*sin(x)+x^2*cos(x)6、求下列函数的积分1、syms x a b c;int(sin(a*x).*sin(b*x).*sin(c*x)) ans =-1/4/(c+a-b)*cos((c+a-b)*x)+1/4/(-c+a-b)*cos((-c+a-b)*x)+1/4/(c+a+b)*cos((c+a+b)*x)-1/4/(-c +a+b)*cos((-c+a+b)*x) 2、>> syms x ;int(x^5+x^3-sqrt(x)/4) ans =1/6*x^6+1/4*x^4-1/6*x^(3/2)3、>> syms x ;int(x.*exp(x)/(x+1)^2,x,0,1) ans =1/2*exp(1)-1 4、 >> syms x y;F=int(int('x/(1+x*y)',x,0,1),y,0,1) F =2*log(2)-15、 由曲面22y x z +=,1=z ,2=z 所围成 >> syms x y z;F=int(int(int('x^2+y^2',x,-inf,inf),y,-inf,inf),z,1,2) F =Inf7、求下列级数的和(1) (2)(1)>> syms n;symsum(2*n-1/2^n,1,Inf) ans =Inf(2)syms n;symsum(1/n*(2*n-1),1,Inf) ans =Inf8、将函数 展开成2-x 的幂级数>> syms x;mtaylor(1/(x^2+5*x-3),x-2) 2sin 2y x x=⎰cxdx bx ax sin sin sin dx x x x )4(35⎰-+⎰+102)1(dx x xe x ⎰⎰+D dxdy xy x 1]1,0[]1,0[⨯=D ⎰⎰⎰Vzdxdydz 11212n n n I ∞=-=∑211(21)n I n n ∞==+∑21()53f x x x =+-。
matlab符号计算实验总结

matlab符号计算实验总结
在这个实验中,我们使用了MATLAB中的符号计算工具,通过创建符号变量和符号表达式来进行数学计算和推导。
这些符号计算工具能够处理代数运算、微积分、方程求解等复杂的数学问题。
在实验过程中,我们首先学习了如何创建符号变量。
通过使用
'sym'函数,我们可以将常规变量转换为符号变量,从而进行符号计算。
例如,我们可以定义一个符号变量x:x = sym('x')。
接下来,我们学习了如何使用符号变量进行代数运算。
通过将符号变量组合成符号表达式,我们可以进行加减乘除等代数运算。
例如,我们可以定义一个符号表达式y = x^2 + 2*x + 1,并对其进行简化或展开操作。
除了代数运算,我们还学习了如何进行微积分计算。
通过使用符号变量和符号表达式,我们可以对函数进行求导和积分操作。
例如,我们可以对一个符号表达式y = x^3求导,并得到其导数表达式。
在实验中,我们还学习了如何使用符号计算工具解方程。
通过使用'solve'函数,我们可以求解方程的根。
例如,我们可以解一个一元二次方程,找到其根的解析解。
通过这个实验,我深刻理解了符号计算在数学问题中的重要性。
它能够帮助我们更好地理解数学概念和定理,并能够进行复杂的数学推导和计算。
MATLAB中的符号计算工具提供了强大的功能和简便的操作,使得数学问题的解决变得更加高效和准确。
总的来说,这个实验让我对MATLAB中的符号计算有了更深入的
了解和掌握。
我相信在今后的学习和研究中,这些符号计算工具将对我有很大的帮助。
