掌门人一对一全套资料高一数学1-5指数与指数函数
2024年新高一数学讲义(人教A版2019必修第一册)指数及其运算(解析版)
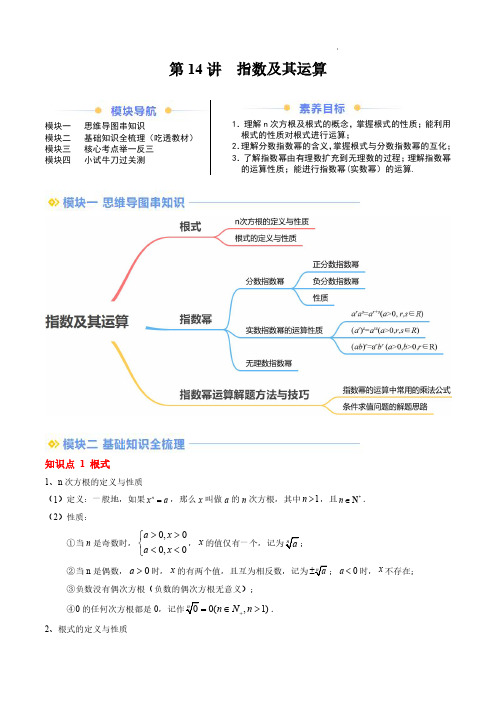
第14讲指数及其运算模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解n 次方根及根式的概念,掌握根式的性质;能利用根式的性质对根式进行运算;2.理解分数指数幂的含义,掌握根式与分数指数幂的互化;3.了解指数幂由有理数扩充到无理数的过程;理解指数幂的运算性质;能进行指数幂(实数幂)的运算.知识点1根式1、n 次方根的定义与性质(1)定义:一般地,如果n x a =,那么x 叫做a 的n 次方根,其中1n >,且*n ∈N .(2)性质:①当n 是奇数时,0,00,0>>⎧⎨<<⎩a x a x ,x;②当n 是偶数,0>a 时,x的有两个值,且互为相反数,记为;0<a 时,x 不存在;③负数没有偶次方根(负数的偶次方根无意义);④0的任何次方根都是00(,1)n N n +=∈>.2、根式的定义与性质(1n 叫做根指数,a 叫做被开方数.(2)性质:(1n >,且n *∈N)n =a;,,,.⎧⎪=⎨⎪⎩为奇数为偶数n a n a n 知识点2指数幂1、分数指数幂(1)正分数指数幂:规定:mn a=()0,,,1a m n n *>∈>N (2)负分数指数幂:规定:1mn m naa-==()0,,,1a m n n *>∈>N (3)性质:0的正分数指数幂等于0,0的负分数指数幂没有意义.【要点辨析】分数指数幂的注意事项:①分数指数幂是指数概念的又一推广,分数指数幂mna 不可理解为mn个a 相乘,它是根式的一种新的写法.在这样的规定下,根式与分数指数幂是表示相同意义的量,只是形式不同而已.化成分数指数幂的形式时,不要轻易对mn进行约分.③在保证相应的根式有意义的前提下,负数也存在分数指数幂,如()235-=()345-=就没有意义.2、实数指数幂的运算性质①(0,,)+=>∈r s r s a a a a r s R .②()=sra rs a (0,,)a r s >∈R .③()=r ab r r a b (0,0,)a b r >>∈R .3、无理数指数幂一般地,无理数指数幂a α(0a >,α为无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.【注意】(1)对于无理数指数幂,我们只需要了解两点:①它是一个确定的实数;②它是有理数指数幂无限逼近的结果.(2)定义了无理数指数幂之后,幂的指数就由原来的有理数范围扩充到了实数范围.知识点3指数幂运算解题方法与技巧1、指数幂的运算中常用的乘法公式(1)完全平方公式:222()2a b a ab b -=-+;222()2a b a ab b +=++;(2)平方差公式:22()()a b a b a b -=-+;(3)立方差公式:3322()()a b a b a ab b -=-++;(4)立方和公式:3322()()a b a b a ab b +=+-+;(5)完全立方公式:33223()33a b a a b ab b -=-+-;33223()33a b a a b ab b +=+++.2、条件求值问题的解题思路(1)将条件中的式子用待求式表示出来,进而代入化简得出结论;(2)当直接代入不易时,可以从总体上把握已知式和所求式的特点,从而巧妙求解,一般先利用平方差、立方和(差)以及完全平方公式对其进行化简,再用整体代入法来求值;(3)适当应用换元法,能使公式的使用更加清晰,过程更简洁.考点一:根式的概念及辨析例1.(23-24高一上·全国·专题练习)若a 是实数,则下列式子中可能没有意义的是()AB C D 【答案】D【解析】A.R a ∈有意义;B.R a ∈有意义;C.R a ∈有意义;D.a<0无意义;故选:D【变式1-1】(23-24高一上·全国·课后作业)R a ∈,下列各式一定有意义的是()A .2a -B .14a C .23a D .0a【答案】C【解析】对于A ,当0a =时,2a -无意义,A 不是;对于B ,当a<0时,14a 无意义,B 不是;对于C ,23a =C 是;对于D ,当0a =时,0a 无意义,D 不是.故选:C【变式1-2】(2023高一·江苏·a 的取值范围是()A .0a ≥B .1a ≥C .2a ≥D .Ra ∈【答案】B有意义,得102R a a -≥⎧⎨-∈⎩,解得1a ≥,所以a 的取值范围是1a ≥.故选:B【变式1-3】(223-24高一下·贵州遵义·月考)若34(12)x --有意义,则实数x 的取值范围为【答案】1(,)2-∞【解析】由34(12)x --120x ->,解得12x <,故答案为:1(,2-∞.考点二:利用根式的性质化简求值例2.(23-24高一上·北京·期中)下列各式正确的是()A 3=-Bx=C 2=D .01a =【答案】C【解析】A 3=,故A 错误;B x =,故B 错误;C2=,故C 正确;D :01a =,当0a ≠时成立,故D 错误;故选:C.【变式2-1】(23-24高一上·贵州贵阳·月考)若0ab <,则化简)A .-1B .0C .1D .2【答案】B【解析】=a b a b ⎛=+ ⎝因为0ab <,所以,a b 异号,0a b a b +=,所以0a b a b a b a b a b++==,所以,0=.故选:B.【变式2-2】(23-24高一上·全国·+【答案】6-6(446-+=-.【变式2-3】(23-24高一上·甘肃兰州·期中)(多选)若412x<-3的结果可能为()A .210x -B .46x -C .24x -+D .410x --【答案】AC 【解析】由题意知412x <-,即4102x-<-,即202x x +>-,故(2)(2)0,2x x x +->∴<-或2x >,3|2|3x =+-3523210,23523352324,2x x x x x x x x x x ----=->⎧=--+-=⎨-+++-=-+<-⎩,故选:AC考点三:根式与分数指数幂互化例3.(23-24高一上·湖南株洲·月考)下列关于nm a -(),m n *∈N 的形式的运算正确的是()A.538-=B.538-=C.538-=D .()328--【答案】A【解析】由于5353818-==A 正确,B ,C 错误;()328--=D 错误,故选:A【变式3-1】(23-24高一上·浙江杭州·期中)(多选)下列各式正确的是()A .46a=B 5=-C.(36=D .23a -=【答案】AC【解析】对于A :4263a a ==A正确;对于B 5=,故B 错误;对于C:(2636===,故C 正确;对于D:23231aa-==D 错误.故选:AC【变式3-2】(23-24高一上·江西新余·期中)(多选)下列根式与分数指数幂的互化中正确的有()A .)130xx -=≠B()120a a =≥C.21320,0)x y x y -=>>D .3142(0)x x ⎤=->【答案】BC【解析】对选项A :)130xx -=≠,错误;对选项B()1313220a a a ⎛⎫==≥ ⎪⎝⎭,正确;对选项C22133212(0,0)y x y x y x-==>>,正确;对选项D:33214432(0)x x x⎛⎫==>⎪⎝⎭,错误;故选:BC【变式3-3】(23-24高一上·广东广州·期中)用分数指数幂表示并计算下列各式(式中字母均正数),写出化简步骤.154m⋅【答案】(1)14b;(2)1【解析】(1=111224b b⎛⎫===⎪⎝⎭.(2)154m⋅11111532423651641m m m m mm m+-⋅⋅====⋅.考点四:利用指数幂运算性质化简例4.(23-24高一上·全国专题练习)下列等式一定成立的是()A.1332a a a⋅=B.11220⋅=a a C.329()a a=D.111362a a a÷=【答案】D【解析】对于A:11311333262a a a a+⋅==,故A错误;对于B:11212221⋅==a a a a,故B错误;对于C:326()a a=,故C错误;对于D:1111132362a a a a÷==,故D正确;故选:D【变式4-1】(23-24高一上·广东江门·期中)102x=,103y=,则10x y+=.【答案】6【解析】102x=Q,103y=,101010236x y x y+∴=⋅=⨯=,故答案为:6.【变式4-2】(23-24高一上·河南·期中)若a b =,则()2312222a b ab ---⎡⎤=⎢⎥⎣⎦.【答案】1【解析】由题意,0,0a b >>,所以()()231222232246a b ab a b a b -----⎡==⎤⎢⎥⎣⎦,又11322,2a b --===,所以原式6411223222221----⎛⎫⎛⎫=⋅=⋅= ⎪ ⎪⎝⎭⎝⎭.故答案为:1.【变式4-3】(23-24高一上·江西九江·期中)化简或计算下列各式.(1)121121332a b a b ---⎛⎫ ⎪;(2)()10.52332770.02721259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭.【答案】(1)1a;(2)0.09【解析】(1)原式2111111111532322132623615661ab a baba aa b⎛⎫⨯--⎪⎝⎭---+--⋅====.(2)原式22333273550.0910001033⨯⎛⎫⎛⎫==+-= ⎪⎪⎝⎭⎝⎭.考点五:解简单的指数方程例5.(23-24高一·全国·专题练习)方程11416x -=的解为()A .2B .﹣2C .﹣1D .1【答案】C 【解析】∵1214416x --==,∴x ﹣1=﹣2,∴x =﹣1.故选:C .【变式5-1】(22-23高一上·河北沧州·期中)关于x 的方程112250x x +--+=的解的个数为()A .0B .1C .2D .4【答案】B【解析】解:原方程即222502xx ⨯-+=,化简可得()2225220x x ⨯+⨯-=,令2(0)x t t =>,可得22520t t +-=,该方程有且只有一个正根,由于2x t =单调递增,所以t 与x 一一对应,即原方程只有一个解.故选:B .【变式5-2】(23-24高一上·北京顺义·期中)关于x 的方程422x x -=的解为.【答案】1x =【解析】由422x x -=可得()22220x x --=,即()()21220x x+-=,因为20x >,可得22x =,故1x =.所以,方程关于x 的方程422x x -=的解为1x =.故答案为:1x =.【变式5-3】(22-23高三·全国·对口高考)方程(2522xx x -+=的解为.【答案】5x =或12x =【解析】由题意可得(2599222222xxx x x -+⎛⎫=== ⎪⎝⎭,所以25922x x x -+=,即221150x x -+=,解得5x =或12x =,故答案为:5x =或12x =考点六:整体换元法解决条件求值例6.(23-24高一下·辽宁抚顺·开学考试)已知12a a+=,则1122a a -+等于()A .2B .4C .2±D .4±【答案】A【解析】112221()2224a a a a-+=++=+=,所以11222a a -+=.故选:A.【变式6-1】(23-24高一上·全国·专题练习)已知11223a a -+=,则33221122a a a a--++的值为.【答案】6【解析】因为11223a a-+=,所以2112223a a -⎛⎫+= ⎪⎝⎭,即129a a -++=,所以17a a -+=,所以3333112222a aa a --⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭22111111222222a a a a a a ---⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=+-⋅+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()()11122371181a a a a --⎛⎫=++=⨯- ⎝-=⎪⎭,所以332211221863a a a a--+==+.【变式6-2】(23-24高一上·全国·专题练习)已知11223x x -+=,计算:22111227x x x x x x---+-+++.【答案】4【解析】因为11223x x-+=,所以211229x x -⎛⎫+= ⎪⎝⎭,所以129x x -++=,所以17x x -+=,所以()2127x x -+=,即22249x x -++=,所以2247x x -+=,所以22111227477473x x x x x x---+--==++++.【变式6-3】(23-24高一上·湖南娄底·期末)已知11223a a -+=,求下列各式的值:(1)1a a -+;(2)33222232a a a a --+-+-.【答案】(1)7;(2)13【解析】(1)由题意11223a a-+=,所以21112222327a a a a --⎛⎫+=+-=-= ⎪⎝⎭.(2)由题意11223a a -+=,所以()()1111212233222222213371331512744534a a a a a a a a a a a a ------⎛⎫⎛⎫- ⎪⎪⨯--+-⎝⎭⋅⎝⎭==-==+--+++-.一、单选题1.(23-24高一上·青海海南·期中)已知R a ∈,则下列各式一定有意义的是()A .2a -B .13a C .12a D .0a 【答案】B【解析】对于A ,由221aa -=可知,0a =时表达式无意义;对于B ,根据幂函数性质可知,R a ∈时,表达式13a 恒有意义;对于C,易知12a =a<0时,表达式无意义;对于D ,当0a =时,0a 无意义;故选:B2.(23-24高一上·陕西咸阳·期末)化简32的结果为()A .5BC .5-D.【答案】A【解析】332232232332555⨯⎛⎫=== ⎪⎝⎭=,故选:A3.(23-24高一上·北京大兴·月考)已知0a >=()A .12a B .32a C .2a D .3a 【答案】A12a ==,故选:A4.(23-24高一上·安徽淮南·月考改编)下列根式与分数指数幂的互化错误的是()A()120a a =>B.)340xx -=>C.)21320,0x y x y -=>>D .()32140x x =>【答案】B【解析】对于A()1313220a a a ⎛⎫==> ⎪⎝⎭,故A 正确;对于B选项,)334410xx x -⎛⎫=> ⎪⎝⎭,故B 错误;对于C,)21321210,0x y x y x-=>>,故C 正确;对于D ,)()33321444320x x x ⎛⎫===> ⎪⎝⎭,故D 正确.故选:B .5.(23-24高一上·江苏泰州·期中)已知14x x -+=,则22x x -+等于()A .6B .12C .14D .16【答案】C【解析】由14x x -+=可得:()2122216x x x x --+=++=,则2214x x -+=.故选:C.6.(23-24高一上·四川德阳·月考)010.256371.586-⎛⎫⨯-++= ⎪⎝⎭()A .110B .109C .108D .100【答案】A【解析】原式()11133333112344131442222223221083331210810231-⎛⎫=+=+= ⎪⎝⎭⎛⎫⎛⎫⎛⎫⨯+⨯+⨯-=⨯+-⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:A.二、多选题7.(23-24高一上·四川成都·期中)以下运算结果等于2的是()AB .C .D【答案】BCD 【解析】对于Aπ44π=-=-,不合题意;对于B ,2=,符合题意;对于C ,()22=--=,符合题意;对于D 22=-=,符合题意.故选:BCD8.(23-24高一上·浙江·月考)已知0a >,0b >,则下列各式正确的是()A π3=-B 1=C .m na-=D .121133332463b ab a b ---⎛⎫÷-=- ⎪⎝⎭【答案】ABD【解析】A 选项:由π30->π3=-,A 选项正确;B ()11111123612312600222221a b b a ab a b ⎛⎫⎛⎫-⨯-+⨯ ⎪ ⎪--⎝⎭⎝⎭⎡⎤====⎢⎥⎣⎦,B 选项正确;C 选项:m na-=C 选项错误;D 选项:112121101333333331246663b ab a a b a b b ⎛⎫⎛⎫------- ⎪ ⎪⎝⎭⎝⎭⎛⎫÷-=-=-=- ⎪⎝⎭,D 选项正确;故选:ABD.三、填空题9.(22-23高一上·上海奉贤·期末)化简()222a b ⋅=(其中0a >,0b >).【答案】4ab【解析】()((42222222a b ab ab ⨯⋅=⋅=.故答案为:4ab .10.(23-24高一上·全国·单元测试)方程2129240x x +-⋅+=的解集是.【答案】{1,2}-【解析】令2x t =,则0t >,方程可化为22940t t -+=,解得12t =或4t =,所以,122x=或24x =,解得=1x -或2x =.所以,方程的解集为{1,2}-.故答案为:{1,2}-.11.(23-24高一上·重庆沙坪坝·期中)已知12102α-=,131032β=,则314210βα+=(填数值)【答案】2【解析】()()31131113113142513422342242101010=322222βαβα⎛⎫⎛⎫⨯⨯+-⨯+- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=⨯⨯=== ⎪ ⎪⎝⎭⎝⎭.故答案为:2四、解答题12.(23-24高一上·安徽马鞍山·期中)化简求值:(1)()12120.344⎛⎫+ ⎪⎝⎭(2)20.5231103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭;【答案】(1)52;(2)0【解析】(1)()120120.344⎛⎫+ ⎪⎝⎭1293511422⎛⎫=+=+= ⎪⎝⎭.(2)20.5231103522216274--⎛⎫⎛⎫⎛⎫-⨯-⨯÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222364493322220273444-⎛⎫⎛⎫⎛⎫⎛⎫⨯-÷=-⨯-⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭13.(23-24高一上·辽宁丹东·期中)已知正实数a 满足11221a a --=.(1)求1a a -+的值;(2)求33221122a a a a---+的值.【答案】(1)3;(2)5【解析】(1)将11221a a --=两边平方得121a a -+-=,所以13a a -+=.(2)因为a 是正实数,令1122(0)a a x x -+=>,则2125x a a -=++=,所以x =可得()33111222214a aa a a a ---⎛⎫-=-++= ⎪⎝⎭,所以33221122a a a a---==+。
重点高中数学知识点完整结构图-掌门1对1

高中数学知识点完整结构图-掌门1对 1高中数学知识点1 集合函数附:一、函数的定义域的常用求法:1、分式的分母不等于零;2、偶次方根的被开方数大于等于零;3、对数的真数大于零;4、指数函数和对数函数的底数大于零且不等于1;5、三角函数正切函数tan y x =中()2x k k Z ππ≠+∈;余切函数cot y x =中;6、如果函数是由实际意义确定的解析式,应依据自变量的实际意义确定其取值范围。
二、函数的解析式的常用求法:1、定义法;2、换元法;3、待定系数法;4、函数方程法;5、参数法;6、配方法三、函数的值域的常用求法:1、换元法;2、配方法;3、判别式法;4、几何法;5、不等式法;6、单调性法;7、直接法四、函数的最值的常用求法:1、配方法;2、换元法;3、不等式法;4、几何法;5、单调性法五、函数单调性的常用结论: 1、若(),()f xg x 均为某区间上的增(减)函数,则()()f x g x +在这个区间上也为增(减)函数 2、若()f x 为增(减)函数,则()f x -为减(增)函数3、若()f x 与()g x 的单调性相同,则[()]y f g x =是增函数;若()f x 与()g x 的单调性不同,则[()]y f g x =是减函数。
4、奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反。
5、常用函数的单调性解答:比较大小、求值域、求最值、解不等式、证不等式、作函数图象。
六、函数奇偶性的常用结论:1、如果一个奇函数在0x =处有定义,则(0)0f =,如果一个函数()y f x =既是奇函数又是偶函数,则()0f x =(反之不成立)2、两个奇(偶)函数之和(差)为奇(偶)函数;之积(商)为偶函数。
3、一个奇函数与一个偶函数的积(商)为奇函数。
4、两个函数()y f u =和()u g x =复合而成的函数,只要其中有一个是偶函数,那么该复合函数就是偶函数;当两个函数都是奇函数时,该复合函数是奇函数。
高一数学指数函数ppt课件

图像法
运算性质法
利用指数函数的运算性质,如乘法公 式和指数法则,推导出奇偶性的判断 方法。例如,若f(x)和g(x)都是奇函数, 则f(x)*g(x)也是奇函数。
通过观察指数函数的图像,判断其是 否关于原点对称或关于y轴对称,从而 确定函数的奇偶性。
06 典型例题解析与 课堂互动环节
典型例题选讲及思路点拨
指数函数的图像关于y轴对称。
当a>1时,函数在定义域内单调递增,图 像上升;当0<a<1时,函数在定义域内单 调递减,图像下降。
指数函数图像特点 函数图像过定点(0,1)。
指数函数性质探讨
指数函数的单调性
01
当a>1时,函数在R上单调递增;当0<a<1时,函数在R上单调
递减。
指数函数的周期性
02
指数函数不是周期函数。
应用举例
$3^4 = (frac{3}{2})^4 times 2^4$
对数转换
当底数不同且难以直接 计算时,可通过对数转 换为相同底数进行计算。
应用举例
比较 $7^{10}$ 和 $10^7$ 的大小,可转 换为比较 $10 times
log7$ 和 $7 times log10$。
复杂表达式化简技巧
利用指数函数构建可持续增长模型,可以预测未来经济发展的趋势和可能遇到的问 题,帮助学生了解经济增长的复杂性和不确定性。
05 指数函数图像变 换与性质变化规 律
平移、伸缩变换对图像影响
平移变换
指数函数图像沿x轴或y轴平移,不改 变函数的形状和周期性,只改变函数 的位置。
伸缩变换
通过改变函数的参数,实现对指数函 数图像的横向或纵向伸缩,从而改变 函数的周期和振幅。
掌门人一对一全套资料高一数学1-5指数与指数函数

已知函数 f(x)=2x,等差数列{an}的公差为 2,若 f(a2 +a4+a6+a8+a10)=4,则 log2[f(a1)·f(a2)·f(a3)·…·f(a10)] =________.
2019/12/24
解析:∵f(a2+a4+a6+a8+a10)=4,f(x)=2x, ∴a2+a4+a6+a8+a10=2, ∵{an}为公差 d=2 的等差数列, ∴a1+a2+…+a10=2(a2+a4+a6+a8+a10)-5d=- 6. ∴log2[f(a1)·f(a2)·…·f(a10)] =log2[2a1·2 a2·…·2 a10]=log22a1+a2+…+a10=-6.
2019/12/24
解析:令 t=ax,则 y=t2+2t-1,对称轴方程为 t= -1,
若 a>1,∵x∈[-1,1],t=ax∈1a,a, y 最大值=a2+2a-1=14,∵a>0,∴a=3.
若 0<a<1,∵x∈[-1,1],∴t=ax∈a,1a, y 最大值=1a2+21a-1=14, ∵0<a<1,∴a=13,∴a=3 或13.
∴bb··aa= 3=624 ②
①
②÷①得 a2=4,
又 a>0,且 a≠1,∴a=2,b=3,
∴f(x)=3·2x.
2019/12/24
(2)由(1)知 a=2,b=3,∴(1a)x+(1b)x-m≥0 在(-∞, 1]上恒成立,即 m≤(12)x+(13)x 在(-∞,1]上恒成立.
2019/12/24
答案:D
2019/12/24
指数函数的单调性
[例 3] 已知 log1 b<log1 a<log1 c,则( )
清华掌门人一对一全套资料高一数学1-2 函数及其表示

2019/4/17
③反函数法 ——利用函数和它的反函数的定义域与 值域的关系,通过求反函数的定义域,得到原函数的值 cx+ d 域. 形如 y= (a≠ 0)的函数的值域, 均可使用反函数 ax+ b 法. 此外, 这种类型的函数值域也可使用“分离常数法” 求解.
2019/4/17
④判别式法 —— 把函数转化成关于 x 的二次方程 F(x, y)=0,通过方程有实根,判别式 Δ≥0,从而求得 a1x2+ b1x+ c1 原函数的值域. 形如 y= 2 ( a1 , a2 不同时为零 ) a2x + b2x+ c2 的函数的值域常用此法求解. 前提条件:函数的定义域应为 R;分子、分母没有 公因式.
2019/4/17
(3)求函数值域的方法 求函数的值域是高中数学的难点,它没有固定的方 法和模式.常用的方法有: ①直接法 ——从自变量 x 的范围出发,通过观察和 代数运算推出 y= f(x)的取值范围; ②配方法 ——配方法是求“二次型函数”值域的基 本方法, 形如 F(x)= af 2(x)+ bf(x)+ c 的函数的值域问题, 均可使用配方法.
2019/4/17
(2)基本初等函数的值域 ① y= kx+ b(k≠ 0)的值域为 R. ② y= ax2+ bx+ c(a≠ 0)的值域是:当 a>0 时,值域
4ac- b2 为 ,+∞ ;当 4a
a<0
2 4 ac - b 时,值域为 . -∞, 4a
2019/A 到 B 的映射, 且 a∈A, b∈ B,如果元素 a 和元素 b 对应,那么我们把元素 b 叫 做元素 a 的象,元素 a 叫做元素 b 的原象.
2019/4/17
2.函数 (1)定义 设 A、B 是非空的数集,如果按照某种确定的对应关 系 f,使对于集合 A 中的任意一个数 x,在集合 B 中都有 唯一确定的数 f(x)和它对应, 那么就称 f:A→ B 为集合 A 到集合 B 的一个函数,记作 y= f(x),x∈ A.其中,x 叫做 自变量, x 的取值范围 A 叫做函数的定义域,与 x 的值
高一数学1到5章知识点

高一数学1到5章知识点高中数学是学生们面临的一门必修课程。
从高一开始,学生将逐步接触到数学的不同领域和知识点。
本文将讨论高一数学的1到5章知识点,包括函数、三角函数、数列与数学归纳法、排列与组合以及概率等内容。
1. 函数在高中数学的1章中,学生首先学习了函数的概念和表示方法。
函数是一种对应关系,将自变量的取值映射到因变量的取值。
函数的表示方法有多种形式,如函数表、函数图像和函数式。
在学习函数的过程中,学生将接触到函数的定义域、值域和奇偶性等概念。
2. 三角函数在高一数学的2章中,学生开始学习三角函数的知识。
三角函数是与角度相关的一类函数,包括正弦函数、余弦函数和正切函数等。
学生需要掌握三角函数的定义、性质和图像等内容。
此外,学生还需要学习三角函数的基本关系式和解三角方程的方法。
3. 数列与数学归纳法在高一数学的3章中,学生将学习数列与数学归纳法的知识。
数列是一系列有序的数按照一定规律排列而成的。
学生需要掌握常见数列的定义、性质和求和公式等内容。
同时,数学归纳法是一种证明方法,通过证明某个命题在满足初始条件的情况下对所有自然数成立,从而得出结论。
4. 排列与组合在高一数学的4章中,学生开始学习排列与组合的知识。
排列与组合是数学中的一类问题,涉及到从一组元素中选择若干个进行排列或组合的方式。
学生需要了解排列与组合的定义、计算公式和应用等内容。
此外,学生还需要掌握排列与组合之间的互相转化关系。
5. 概率在高一数学的5章中,学生将学习概率的知识。
概率是研究随机事件发生的可能性的数学方法。
学生需要了解概率的定义、性质和计算方法等内容。
在学习概率的过程中,学生还将接触到事件的互斥与独立性、条件概率和贝叶斯定理等概念。
通过学习这些知识点,学生将逐渐建立起数学的基础,为后续的学习打下坚实的基础。
高中数学不仅仅是考试的内容,更是培养学生思维能力和解决问题的能力的重要工具。
因此,学生需要通过不断的练习和思考来巩固和应用所学知识,才能真正理解数学的魅力和应用的价值。
高一数学指数及指数函数基础知识

高一数学指数及指数函数1•根式的性质(3)负数没有偶次方根 (4)零的任何正次方根都是零2•幕的有关概念 (1)正整数指数幕:naa a a ..… n...... a (n N )(2)零指数幕a 01(a 0)1⑶负整数指数幕 a p-(a 0.p N )a pm(4)正分数指数幕a nnma (a0, m, n N ,且 n 1) (5)负分数指数幕a m1 nm(a0, m, n N ,且 n 1)a 石(6)0的正分数指数幕等于0,0的负分数指数幕无意义3•有理指数幕的运算性质rr s⑶(ab) a a ,(a0,b 0, r Q)4、指数函数的定义:函数y a% 0且a °叫做指数函数,其中x 是自变量,函数定义域是R 。
① 若a 0,则当x 0时,『0;当x 0时,a x 无意义.1 1② 若a 0,则对于X 的某些数值,可使a 无意义•如(2),这时对于 4,2,等等,在实数范围内函数值不存在•③ 若a 1,则对于任何x R ,a x 1,是一个常量,没有研究的必要性• 对于任何x R ,「都有意义,且『0.因此指数函数的定义域是R ,值域是(°)有些函数貌似指数函数,实际上却不是,如y 『k (a 0且 a 1,k Z );x有些函数看起来不像指数函数,实际上却是,如y a (a 0且a 1),因为它可 x1 1 1 0 1 a ,其中a ,且a(1)当n 为奇数时,有n a na(2)当n 为偶数时,有;a" a a, (a 0) a, (a 0)r sr s .八 亠、(1) a a a ,(a 0, r, s Q)/ r、srs , -亠、⑵(a )a ,(a 0,r,s Q)以化为y5、函数的图象(1)①特征点:指数函数y = a x (a > 0且a ^ 1) 的图象经过两点(0 , 1)和(1,a).②指数函数y = a x (a > 0且a 工1)的图象中,y = 1 反映了它的分布特征;而直线x = 1 与指数函数图象的交点(1,a)的纵坐 标则直观反映了指数函数的底数特 征,称直线x = 1和y = 1为指数函 数的两条特征线•(2)、函数的图象单调性当a > 1时,函数在定义域范围内 呈单调递增; 当0v a v 1时,函数在定义域范围 内呈单调递减; 推论:(1)底互为倒数的两个函数图像关于y 轴对称(2)当a > 1时,底数越大,函数图象越靠近丫轴;当0v a v 1时,底数越小, 函数图象越靠近丫轴。
高一数学《指数函数与对数函数》PPT课件

(1)
1 x 2
1
x2
2
x2
x 1
5
1
1
x2 x 2 5
1
(2)(x 2
)3
1
(x 2
)3
1
(x 2
1
x 2 )[(x
x 1 ) 1]
x x 1 3 x 0
5(3 1)
6. 4
3
36 3
81 9 2
7. 2 3 3 1.5 6 12 6
8.设 mn>0,x= m n ,化简:A= 2 x2 4 .
⑵ y 3 5x1 ⑶ y 2 x 1
函数的定义域就是使函数表达式有意义的自变量 x的取值范围。
(1)定义域为{x|x≠1};
1
0 x 1
值域为{y|y>0且y≠1}
1
⑴ y 0.4 x1
⑵ y 3 5x1 ⑶ y 2 x 1
(2)
定义域为{x|
x
1 5
}
值域为{y|y≥1}
5x 1 ≥0
BC A
A’ B’ C’
f(a)=SAA’C’C-SAA’B-SB’C’C
(f2()af)(a)1 g(a) 1a(a2
2
2
ag(a2) 2 aa11)
1 [( a 2 a 1) ( a 1 a )] 2
1(
1
1
)0
2 a 2 a 1 a 1 a
7. (★★★★)当a≠0时,y=ax+b 和 y=bax
y 1 x 2
y 1 x
1
2
把 y 轴右边的图形翻折到 y 轴的左边
3. 作出函数 y= │ 2x -1│的图像
y= │ 2x -1│
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;
a2=
|a|
;
n
an=
a |a|
,n为奇数, ,n为偶数.
2019/8/28
(3)分数指数幂
m
an
=n
am
;
-
a
m n
=
1
m
=
1
.(a>0,m,n∈N,且
a n n am
n>1) (4)指数幂的运算性质
ar·as=ar+s,(ar)s=ar·s,
(a·b)r=ar·br.(a>0,b>0,r,s∈R)
∴bb··aa= 3=624 ②
①
②÷①得 a2=4,
又 a>0,且 a≠1,∴a=2,b=3,
∴f(x)=3·2x.
2019/8/28
(2)由(1)知 a=2,b=3,∴(1a)x+(1b)x-m≥0 在(-∞, 1]上恒成立,即 m≤(12)x+(13)x 在(-∞,1]上恒成立.
令 g(x)=(12)x+(13)x, 则 g(x)在(-∞,1]上单调递减, ∴m≤g(x)min=g(1)=12+13=56, 故所求实数 m 的取值范围是(-∞,56].
2019/8/28
化简:(1) 51+2-( 3-1)0- 9-4 5=________;
2
1
1
1
1
5
(2)(2a 3 b 2 )( - 6a 2 b 3 )÷( - 3a 6 b 6 ) =
__________.(a>0,b>0)
2019/8/28
解析:(1)原式= 5-2-1- 5-22 =( 5-2)-1-( 5-2)=-1.
解析:0<a<1 时,f(x)=ax 在[1,2]上单调递减, ∴a-a2=a3,∴a=23; a>1 时,f(x)=ax 单调递增,∴a2-a=a3, ∴a=43. 答案:43或23
2019/8/28
三、解题技巧 1.比较一组幂式、对数式形式的数的大小时,一般 先区分正、负(与 0 比);正数再与 1 比较,找出大于 1 的 和小于 1 的;底数相同的幂式,用指数函数的单调性; 底数相同的对数式用对数函数的单调性;指数相同的幂 式用幂函数的单调性或指数函数的图象;真数相同的对
2019/8/28
解析:令 t=ax,则 y=t2+2t-1,对称轴方程为 t= -1,
若 a>1,∵x∈[-1,1],t=ax∈1a,a, y 最大值=a2+2a-1=14,∵a>0,∴a=3.
若 0<a<1,∵x∈[-1,1],∴t=ax∈a,1a, y 最大值=1a2+21a-1=14, ∵0<a<1,∴a=13,∴a=3 或13.
2019/8/28
第五节
指数与指数函数
2019/8/28
2019/8/28
重点难点 重点:①指数幂的运算法则. ②指数函数的概念、图象与性质. 难点:①根式与分数指数幂的运算. ②a>1 与 0<a<1 时,指数函数图象、性质的区别. ③指数函数图象与性质的应用和简单指数方程、不 等式的求解.
答案:D
2019/8/28
(文)(2011·杭州月考)函数 y=a|x|(a>1)的图象是( )
2019/8/28
解析:y=a|x|=aax-x
x≥0 ,当 x≥0 时,与指数 x<0
函数 y=ax(a>1)的图象相同;当 x<0 时,y=a-x 与 y=ax
的图象关于 y 轴对称,由此判断 B 正确.
∵49<34,
∴49
3 2
3 3 <4 2
,∴23
3<34
3 2
.
2019/8/28
二、分类讨论的思想 [例 2] 函数 f(x)=ax(a>0 且 a≠1)在[1,2]上的最大值 比最小值大a3,则 a 的值为________.
2019/8/28
2019/8/28
解析:∵y=log1 x 为减函数,log1 b<log1 a<log1 c
2
2
2
2
∴b>a>c
又 y=2x 为增函数 ∴2b>2a>2c 故选 A.
答案:A
2019/8/28
已知集合 M={-1,1},N={x|12<2x<4,x∈Z},则
M∩N 等于( )
A.{-1,1}
B.{-1}
x<0
a>1
y>1
0<y<1
0<a<1
0<y<1
y>1
2019/8/28
误区警示 1.忽视底数 a>1 与 0<a<1 时性质的区别及函数的值 域致误.解题的每一步要等价转化. 2.比较幂值大小时,要注意区分底数相同还是指数 相等.是用指数函数的单调性,还是用幂函数的单调性 或指数函数的图象解决.要注意图象的应用,还应注意 中间量 0、1 等的运用.指数函数的图象在第一象限内底 大图高(逆时针方向底数依次变大).
2019/8/28
(文)若关于 x 的方程 25-|x+1|-4·5-|x+1|-m=0 有实 根,则实数 m 的取值范围是________.
2019/8/28
解析:令 t=5-|x+1|知 t2-4t=m, 则有 m=t2-4t=(t-2)2-4. ∵t∈(0,1],∴m∈[-3,0).
答案:[-3,0)
2019/8/28
知识归纳 1.整数指数幂的运算性质 (1)am·an= am+n ,(am)n= am·n , (a·b)n= an·bn .(m、n∈Z)
2019/8/28
(2)xn=a,(n∈N,n>1)⇔x=n a,n为奇数, x=±n aa>0,n为偶数.
n (
a)n=
a
因此应有||22ab--11||==ab ,解得ab= =01 , 所以有 a+b=1,选 A.
答案:A
2019/8/28
点评:本题解题的关键在于首先由函数的值域推出 b>a≥0,从而避免了对 a、b 的各种可能存在情况的讨论, 然后根据函数的单调性,建立关于 a、b 的方程组求解.
2019/8/28
3.用换元法解题时,要注意“新元”的取值范围.
2019/8/28
2019/8/28
一、数形结合的思想
[例 1]
比较233 与34
3 2
的大小.
2019/8/28
解析:在同一直角坐标系中作出函数 y=49x 与 y=34
x 的图象,考察 x=32时 y 值大小,
2019/8/28
数式用对数函数的图象;底数不同、指数也不同的幂式 或底数不同、真数也不同的对数式可引入中间量转化或 化成同底,另外要注意指对互化的灵活运用.
2019/8/28
2.在指数里含有未知数的方程的解法. (1)形如 af(x)=ag(x)(a>0,a≠1)的方程,化为 f(x)=g(x) 求解; (2)形如 af(x)=bg(x)(a>0,b>0,a≠1,b≠1)的方程, 两边取对数; (3)形如 a2x+b·ax+c=0 的方程,用换元法令 ax=t 化为二次方程求解.
2019/8/28
2.指数函数的图象和性质
指数函数
定义
y=ax(a>0,a≠1)
图象
2019/8/28
指数函数
(1)定义域:R
(2)值域:(0,+∞)
(3)过(0,1)点,即 x=0 时,y=1. 性 (4)当 a>1 时,在 R 上是增函数; 质 当 0<a<1 时,在 R 上是减函数.
x>0
2019/8/28
2.(文)若 log2a<0,12b<1,则(
2019/8/28
2019/8/28
指数幂的运算
[例 1] 化简:
4 (1)(1-a)
a-1 13=________;
3 (2) xy2· xy-1· xy=________;
(3)0.25-0.5+217-
1 3
-6250.25=________.
2019/8/28
解析:(1)原式=(1-a)(a-1)
2019/8/28
答案:D
2019/8/28
指数函数的单调性
[例 3] 已知 log1 b<log1 a<>2a>2c
B.2a>2b>2c
C.2c>2b>2a
D.2c>2a>2b
分析:可先由对数函数 y=log1 x 的单调性得出 a、b、
2
c 的大小,再由 y=2x 的单调性得出结论.
2019/8/28
2019/8/28
一、选择题
1.已知 f(x)=2x+2-x,若 f(a)=3,则 f(2a)=( )
A.5
B.7
C.9
D.11
[答案] B
2019/8/28
[解析] ∵f(x)=2x+2-x,f(a)=3,∴2a+2-a=3,f(2a) =22a+2-2a=(2a)2+(2-a)2=(2a+2-a)2-2=9-2=7.
-
3 4
=-(a-1)(a-1)
-
3 4
=-(a-1)
4
=-4
a-1.
(2)原式=[xy2(xy-1)
11
]2 3
1
(xy) 2
=(xy x y ) x y 2
1 2
11 -2 3
1 2
1 2
3 31
11
11
