七年级数学下册第六章数据与统计图表.频数与频率练习浙教版
七下第6章数据与统计图表6-4频数与频率1新版浙教版

3.6, 3.8, 3.4, 3.4,3.5, 2.8,3.3,
极差为:2 组别(kg)
4.0, 4.5, 3.6, 3.5,3.7, 3.7
人数
2、组距哪里来?
2.8~3.2
3.2~3.6 3.6~4.0 4.0~4.4 4.4~4.8
?
组距自己定
(经验之谈:数据个数在100以内 时通常按数据的多少分成5~12组)
划记
人数
为了不使数据不落在各组的边界 上,边界值比实际数据多取一位.
最大值 - 最小值 组距
=
2 0.
4
=
5
把数据分成6组
注意:数据个数在50个以内 常分成5-8组;数据个数在50100个常分成8-12组.
提炼概念 列频数统计表的一般步骤如下:
2.确定各组的边界值. 3.列表,填写组别和统计各组频数.
4.7, 2.9, 3.2, 3.5, 3.6, 4.8,4.3,
3.6, 3.8, 3.4, 3.4,3.5, 2.8,3.3, 4.0,
4.5, 3.6, 3.5,3.7, 3.7
组别(kg) 划记
人数 3、边界值怎么取? 为了使数据不落在各组的边界
2.75~3.15
上,在组距不变的情况下,我
6.4 频数与频率(1)
新知导入
情境引入
人们在获得一组数据后,经常需要了解数据的分布情况. 下面我们用一个具体的例子来说明反映数据分布情况的统计方法.
从某地区妇产医院获得2010年10月份在该院出生的20名新生婴儿
体重如下(单位:kg): 4.7, 2.9, 3.2, 3.5 3.6, 4.8, 4.3, 3.6 3.8, 3.4, 3.4, 3.5 2.8, 3.3, 4.0, 4.5 3.6, 3.5, 3.7, 3.7
201X年春七年级数学下册第6章数据与统计图表6.4第2课时频率练习(新版)浙教版

6.4 频数与频率第2课时频率知识点1频率为了了解数据分组后各组频数的大小在总数中所占的份量,常常需要求出各组频数与数据总数的比.每一组数据频数与数据总数的比叫做这一组数据(或事件)的频率,频率×100%即为百分比.1.某校抽取了40名同学进行体能测试,其中获得优秀的频数是5,则获得优秀的频率是( )A.5 B.0.5 C.0.25 D.0.125知识点2频数与频率(1)频率=频数样本的容量;(2)各小组的频率之和为1,各小组的频数之和等于样本的容量.2.某校七年级(1)班某次数学测试成绩如下(单位:分):63 84 91 53 69 81 61 69 91 7875 81 80 67 76 81 79 94 61 6989 70 70 87 81 86 90 88 85 6771 82 87 75 87 95 53 65 74 77(1)请你把频数表补充完整;成绩x(分)划记频数频率50≤x<6020.05060≤x<70正90.22570≤x<80正正0.25080≤x<90正正140.35090≤x<100正5(2)(3)如果60分以上(包括60分)为及格,80分以上(包括80分)为优秀,求这次考试的及格率和优秀率.探究频率在实际生活中的应用下表是某校两个班级期中数学成绩统计结果:项目班级优秀人数及格人数不及格人数总人数甲2045550乙1838240(1)甲、乙两班中,哪个班级的优秀人数、及格人数多?哪个班级的优秀率高?高多少?哪个班级的及格率高?高多少?(2)你觉得哪个班级的成绩较好?根据是什么?比较两个班级的学习成绩,用频数和频率哪个好?为什么?[归纳总结] (1)判断成绩的好坏,主要看优秀率、及格率的高低;(2)要明确频数与频率的意义.1.下列说法正确的是( )A.频数表示所有对象出现的次数B.频率表示每个对象出现的次数C.所有频率之和等于1D.频数和频率都不能够反映每个对象出现的频繁程度2.某校对学生参加体育锻炼的时间进行调查,将所得数据分成5组.已知第一组的频率是0.18,第二、三、四小组的频率之和为0.62,故第五组的频率是( )A.0.20 B.0.09C.0.31 D.不能确定3.王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )A.16 B.14C.4 D.6二、填空题4.2015·漳州我市今年中考数学学科开考时间是6月22日15时,数串“201506221500”中“0”出现的频数是________.5.某商店在8月份售出同一品牌四种规格的空调台数分别是:1匹的14台;1.2匹的24台,1.5匹的8台,2匹的4台.那么该商店售出的空调中,规格为________匹的频数最大,是________,频率是________.6.已知样本75,71,73,75,77,79,75,78,80,79,76,74,75,77,76,72,74,75,76,78,这20个数据中,最大值是________,最小值是________,它们的差是________;如果取组距为2,那么这组数据应该分为________组;如果用x表示其中任意一个数据,第一组的数据范围为________,75≤x<77这组数据的频数是________,频率是________.三、解答题7.从某班抽取30名学生的一次数学测试成绩如下表(单位:分):(2)①及格(60分及以上为及格)率是多少?若80分以上(含80分)为优秀,则优秀率是多少?②哪个分数段的人数最多?有多少人?占总人数的百分比是多少?记录方式如下:如果一个顾客购买某一品牌的饮料,就将这一饮料的名称记录一次.下表是她记录的原始资料:(2)如果让你给冷饮店提出进货建议,你会有什么建议呢?详解详析【预习效果检测】 1.D2.解:(1)空格内分别填入10,0.125.(2)80≤x <90分数段的学生最多,50≤x <60分数段的学生最少. (3)及格率为3840×100%=95%,优秀率为1940×100%=47.5%.【重难互动探究】例 解:(1)甲班的优秀人数与及格人数都比乙班多. 由题意可知甲班的优秀率=2050×100%=40%,乙班的优秀率=1840×100%=45%,所以乙班的优秀率高,高5%.由题意可知甲班的及格率=4550×100%=90%,乙班的及格率=3840×100%=95%,所以乙班的及格率高,高5%.(2)乙班的成绩较好,因为乙班的优秀率与及格率都比甲班高.比较两个班级的学习成绩用频率好,频数大小与总人数多少有直接关系,频率是频数在总人数中所占的百分比,不受总人数的影响.【作业高效训练】 [课堂达标]1.[解析] C 本题考查了频数与频率的概念.注意频数是指每个对象出现的次数,频率是指每个对象出现的次数与总次数的比值.它们能够反映每个对象出现的频繁程度.故选C.2.[解析] A 第五组的频率为1-0.18-0.62=0.20. 3.A4.[答案] 45.[答案] 1.2 24 0.48[解析] 售出最多的是1.2匹的,为24台;各种规格的空调总共售出了14+24+8+4=50(台),故1.2匹的占2450=0.48,即其频率为0.48.6.[答案] 80 71 9 5 71≤x <73 8 0.47.解:(1)频数依次是6,12,6,3,3;频率依次是0.2,0.4,0.2,0.1,0.1. (2)①及格率是90%,优秀率是60%.②80~89分的人数最多,有12人,占总人数的40%. [数学活动][解析] 按品牌分组统计,绘制统计表,根据频数分布提出建议. 解:(1)根据原始资料进行频数统计,绘制的频数、频率统计表如下:此进货时可口可乐、百事可乐按0.3∶0.225,即4∶3的比例进货,且这两种饮料的和占五种饮料的52.5%左右,其余三种占47.5%左右,且“露露”略高于三种的平均数.。
浙教版七年级下册数学第六章 数据与统计图表含答案

浙教版七年级下册数学第六章数据与统计图表含答案一、单选题(共15题,共计45分)1、一次数学测试后,某班60名学生的成绩被分为5组,第一至第四组的频数分别为8、10、16、 14,则第五组的频率是()A.0.1B.0.2C.0.3D.0.42、为了解九年级1200名学生的身高情况,小李同学采用合理的方式随机抽查了200名学生的身高为样本进行统计,其中身高在170cm~175cm有80人,那么估计该校九年级同学身高在170cm~175cm的人数是()人.A.40B.400C.480D.5003、下列调查中,最适合采用普查方式的是()A.坐飞机前对乘客的安检B.了解兰州的猪肉市价格C.对黄河水质情况的调查D.兰州市对垃圾分类处理知晓率的调查4、某校七(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是()A.从图中可以直接看出喜欢各种球类的具体人数B.从图中可以直接看出全班的总人数C.从图中可以直接看出全班同学一学期来喜欢各种球类的变化情况D.从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系5、下列调查中,适宜采用全面调查方式的是()A.调查一架“歼20”战机各零部件的产品质量B.调查某品牌圆珠笔芯的使用寿命C.调查市场上酸奶的质量情况D.调查我市市民对上届巴西奥运会吉祥物的知晓度6、下列事件中,最适合采用全面调查的是()A.对全国中学生节水意识的调查B.对某批次灯泡的使用寿命的调查 C.对某个班级全体学生出生日期的调查 D.对春节联欢晚会收视率的调查7、小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有()人.A.1080B.900C.600D.1088、母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况。
浙教版七年级下册数学第六章 数据与统计图表含答案

浙教版七年级下册数学第六章数据与统计图表含答案一、单选题(共15题,共计45分)1、小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:则通话时间不超过15 min的频率为( )A.0.1B.0.4C.0.5D.0.92、在最近很火的节目《中国诗词大会》中,除才女武亦姝实力超群外,其他选手的实力也不容小觑.以下是随机抽取的10名挑战者答对的题目数量的统计:这10名挑战者答对题目数量中的中位数和众数分别是()A.4和5B.5和4C.5和5D.6和53、在对n个数据进行整理的频率分布表中,各组的频数与频率之和分别等于()A.n,1B.n,nC.1,nD.1,14、为了了解南京市八年级学生的身高情况,请你运用所学的统计知识,将解决上述问题要经历的几个重要步骤进行排序.①用样本估计总体;②整理数据;③设计调查问卷④分析数据;⑤收集数据.则正确的排序为()A.⑤③②④①B.③⑤②①④C.③⑤②④①D.③⑤④②①5、某中学各年级人数如图所示,根据图中的信息,下列结论错误的是()A.七、八年级的人数相同B.九年级的人数最少C.女生人数多于男生人数D.女生人数少于男生人数6、下列说法中,正确的是()A.为检测我市正在销售的酸奶质量,应该采用抽样调查的方式B.两名同学连续五次数学测试的平均分相同,方差较大的同学数学成绩更稳定C.抛掷一个正方体骰子,点数为奇数的概率是D.“打开电视,正在播放广告”是必然事件7、下列调查中,适宜采用全面调查方式的是()A.了解我县中小学生课后的手机使用情况B.了解一批手机电池的使用寿命C.了解我县初中生的视力情况D.了解全班学生参加社会实践活动的情况8、下列说法中,正确的是()A.为检测我市正在销售的酸奶质量,应该采用抽样调查的方式B.在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 C.某同学连续10次抛掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30% D.“2012年将在我市举办全运会,这期间的每一天都是晴天”是必然事件.9、某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设①踢毽子;②篮球;③跳绳;④乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下不完整的两个统计图,依据图中信息,得出下列结论中正确的是( )A.本次共调查300名学生B.扇形统计图中,喜欢篮球项目的学生部分所对应的扇形圆心角大小为45°C.喜欢跳绳项日的学生人数为60人 D.喜欢篮球项目的学生人数为30人10、如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断()A.甲公司销售量多B.乙公司销售量多C.两家销售量一样多D.不能判断11、某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手的得分情况进行统计,绘成如图所示的得分成绩统计图,下列四个论断:①众数为6分;②有8名选手的成绩高于8分;③中位数是8分;④得6分和9分的人数一样多,其中正确的是()A.①②③B.②③④C.①②④D.①②③④12、在某次数学测试中,满分为100分,各测试内容及所占分值的分布情况如下扇形统计图,则以下结论正确的是()①一元一次不等式(组)部分与二元一次方程组部分所占分值一样②因式分解部分在试卷上占10分③整式的运算部分在整张试卷中所占比例为25%④观察、猜想与证明部分的圆心角度数为72°A.①②③B.②③④C.①④D.①②③④13、从某校九年级中随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,5分.将测量的结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是()A.1B.2C.3D.414、下列叙述正确的是()A.“如果a,b是实数,那么a+b=b+a”是不确定事件B.“某班50位同学中恰有2位同学生日是同一天”是随机事件C.为了了解一批炮弹的杀伤力,采用普查的调查方式比较合适D.某种彩票的中奖概率为,是指买7张彩票一定有一张中奖15、安居物业管理公司对某小区一天的垃圾进行了分类统计,下图是分类情况的扇形统表,若一天产生的垃圾约为,估计该小区一个月(按30天计)产生的可回收垃圾重量约是( )A. B. C. D.二、填空题(共10题,共计30分)16、已知一组数据有40个,把它分成五组,第一组、第二组、第四组、第五组的频数分别是10,8,7,6,第三组频数是________.17、①了解全国中小学生每天的零花钱;②了解一批灯泡的平均使用寿命;③调查20~25岁年轻人最崇拜的偶像;④对患甲型H7N9的流感患者同一车厢的乘客进行医学检查.上述调查适合做普查的是:________.18、下图是根据某中学为地震灾区玉树捐款的情况而制作的统计图,已知该校在校学生3000人,请根据统计图计算该校共捐款________元。
初一七年级数学下册第六章数据与统计图表频数与频率二练习浙教版
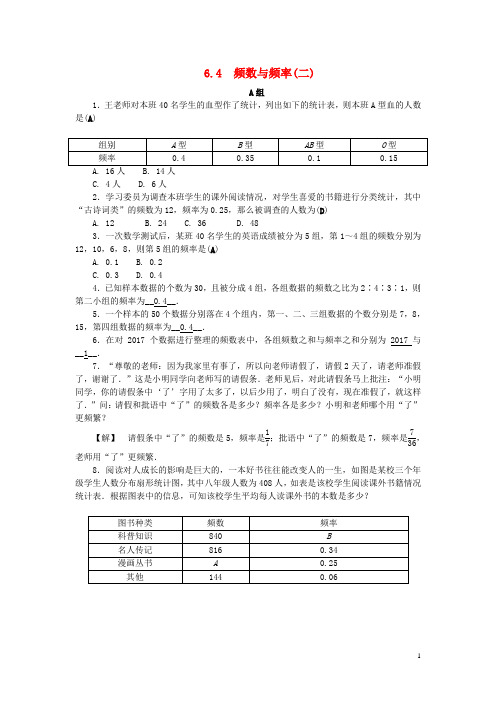
6.4 频数与频率(二)A 组1.王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A 型血的人数是(A )A. 16人B. 14人C. 4人D. 6人2.学习委员为调查本班学生的课外阅读情况,对学生喜爱的书籍进行分类统计,其中“古诗词类”的频数为12,频率为0.25,那么被调查的人数为(D )A. 12B. 24C. 36D. 483.一次数学测试后,某班40名学生的英语成绩被分为5组,第1~4组的频数分别为12,10,6,8,则第5组的频率是(A )A. 0.1B. 0.2C. 0.3D. 0.44.已知样本数据的个数为30,且被分成4组,各组数据的频数之比为2∶4∶3∶1,则第二小组的频率为__0.4__.5.一个样本的50个数据分别落在4个组内,第一、二、三组数据的个数分别是7,8,15,第四组数据的频率为__0.4__.6.在对2017个数据进行整理的频数表中,各组频数之和与频率之和分别为2017与__1__.7.“尊敬的老师:因为我家里有事了,所以向老师请假了,请假2天了,请老师准假了,谢谢了.”这是小明同学向老师写的请假条.老师见后,对此请假条马上批注:“小明同学,你的请假条中‘了’字用了太多了,以后少用了,明白了没有,现在准假了,就这样了.”问:请假和批语中“了”的频数各是多少?频率各是多少?小明和老师哪个用“了”更频繁?【解】 请假条中“了”的频数是5,频率是17;批语中“了”的频数是7,频率是736,老师用“了”更频繁.8.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,如表是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是多少?,(第8题))【解】 ∵八年级的人数是408人,占1-38%-28%=34%, ∴全校人数有408÷34%=1200(人). 又∵图书总数是816÷0.34=2400(本),∴该校学生平均每人读课外书2400÷1200=2(本).B 组9.某自来水公司为了解居民某月用水情况,随机抽取了20户居民的月用水量x (m 3),绘制出表格,则月用水量x <3的频率是(C )A. 0.15B. 0.3C. 0.8D. 0.9【解】 由图可得,月用水量x <3的总户数为1+2+3+4+3+3=16, ∴频率=1620=0.8.10.把容量是50的样本分成6组,其中有1组的频数是14,有2组的频数均是10,有2组的频率均是0.14,则剩下一组的频数是__2__,频率是__0.04__.【解】 剩下一组的频数是50-14-2×10-2×(50×0.14)=2,频率是2÷50=0.04. 11.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了如下尚不完整的频数表:=84,=0.33.(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最多? 最喜爱阅读哪类读物的学生最少?(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?【解】 (1)m 0.42=220.11,∴m =84.220.11=66n,∴n =0.33. (2)最喜爱阅读文学类的学生最多,最喜爱阅读艺术类的学生最少. (3)1200×0.33=396(人).答:估计该校1200名学生中最喜爱阅读科普读物的学生有396人.12.某班学生的数学期末成绩(成绩为整数,单位:分)的频数表如下,根据表中提供的信息回答下列问题:(2)在表中,频率m =__0.05__,频数n =__18__. (3)在表中,频数最小的一组的范围是49.5~59.5.(4)若成绩大于或等于80分为优秀,大于或等于60分为及格,求该班的优秀率和及格率.【解】 (1)a =9÷0.15=60.(2)m =3÷60=0.05,n =60×0.30=18. (4)优秀率为(0.30+0.10)×100%=40%, 及格率为(1-0.05)×100%=95%.数学乐园13.某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,划分等级后的数据整理如下表:(1)本次问卷调查抽取的样本容量为200,表中的值为0.6.(2)计算“非常了解”所对应的扇形圆心角的度数,并补全扇形统计图.,(第13题))(3)若该校有1500名学生,请根据调查结果,估算这些学生中“比较了解”垃圾分类知识的人数约为多少.【解】 (1)样本容量为36÷0.18=200,m =120200=0.6. (2)“非常了解”所对应的扇形圆心角的度数为0.2×360°=72°. 补图如解图所示.,(第13题解))(3)1500×0.6=900(人).答:这些学生中“比较了解”垃圾分类知识的人数约为900.。
2020春浙教版七年级数学下册 第6章 6.4 频数与频率

17.为了了解男生的身高情况,抽测了某校 17 岁的 50 名男生的 身高,将数据分成 7 组,列出了相应的频数表(部分未列出) 如下:
请回答下列问题:
(1)请将上述频数表填写完整; 解:4;0.08;17;0.12 (2)估计这所学校 17 岁男生中,身高不低于 1.655 m 且不高于 1.715 m 的学生所占的百分比; 解:11+5017×100%=56%.
3.【2019 春·温州期末】陈老师对 56 名同学的跳绳成绩进行了统 计,跳绳个数 140 个以上的有 28 名同学,则跳绳个数 140 个以上的频率为( C ) A.0.4 B.0.2 C.0.5 D.2
4.小明为一组数据制作频数表,他了解到这组数据的最大值是 40,最小值是 16,准备分组时取组距为 4.为了使数据不落在 边界上,他应将这组数据分成( ) A.6 组 B.7 组 C.8 组 D.9 组
【点拨】∵这组数据的最大值是 40,最小值是 16, ∴这组数据的最大值与最小值的差为 40-16=24. ∵24÷4=6,且数据不落在边界上, ∴这组数据的组数为 6+1=7(组). 故选 B.
【答案】B
5.将 50 个数据分成三组,其中第一组和第三组的频率之和为 0.7,则第二组的频数是( C ) A.0.3 B.0.7 C.15 D.35
(2)参加这次测试的男生有多少人? 解:参加这次测试的男生有0.714=50(人).
15.为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临 之际,某校团委组织了以“珍爱生命,学会生存,感恩父母” 为主题的教育活动,在学校随机调查了 50 名同学平均每周 在家做家务的时间,统计并制作了如下所示的频数表和如图 所示的统计图:
9.某学校为了了解七年级学生参加课外兴趣小组活动情况,随 机调查了 40 名学生,将结果绘制成了如图所示的条形统计 图,则参加绘画兴趣小组的频率是( D ) A.0.1 B.0.15 C.0.25 D.0.3
浙教版数学 七年级下册第六章频数统计表同步测试卷含参考答案
浙教版数学七年级下册第六章数据与统计图表6.4频数统计表同步测试卷一.选择题(共10小题,3*10=30)1.一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分()A.10组B.9组C.8组D.11组2.某校为了了解学生在校午餐所需的时间,统计了20名同学在校午餐所需的时间,获得如下的数据(单位:分):12,12,15,10,16,18,19,18,20,27,22,25,20,18,18,20,15,16,21,16.若将这些数据以4分为组距进行分组,则组数是()A.4组B.5组C.6组D.7组3.数据3,1,5,1,3,4中,数据“3”出现的频数是()A.1 B.2 C.3 D.44.已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5,12,8,则第三组的频数为()A.0.375 B.0.6 C.15 D.255.下面是一组同学的跳远成绩(单位:cm):455425438402398435395438426382390460388412420430442418454428396435438428415441根据这些成绩设计频数统计表,下列分组合适的是()A.381~401401~421421~441441~461B.381.5~401.5401.5~421.5421.5~441.5441.5~461.5C.382.5~402.5402.5~422.5422.5~442.5442.5~462.5D.382~402402~422422~442442~4626.已知数据:10,8,6,10,8,13,11,10,12,7,9,8,12,9,11,12,9,10,11,10,那么频数为4的一组是()A.5.5~7.5 B.7.5~9.5C.9.5~11.5 D.11.5~13.57.已知样本:7,8,10,14,9,7,12,11,10,8,13,10,8,11,10,9,12,9,13,11,那么这组样本数据落在范围8.5~11.5的频数应该是()A.8 B.12 C.10 D.138.体育委员统计了七(1)班全体同学60秒跳绳的次数,并列出下面的频数分布表:给出以下结论:①全班有52个学生;②组距是20;③组数是7;④跳绳次数在100≤x<140范围的学生约占全班学生总数的67%.其中正确结论的个数是( )A.1个B.2个C.3个D.4个9.一组数据的最大值与最小值的差是80,若确定组距为9,则可分为()A.7组B.8组C.9组D.12组A.1月至2月B.2月至3月C.3月至4月D.4月至5月10. 旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )A.小王随机抽取了100名员工B.在频数分布表中,组距是2000,组数是5组C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%D.在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有37人二.填空题(共6小题,3*6=18)11.某次测验后,60~70分这组人数占全班总人数的20%,若全班有45人,则该组的频数为_______.12.国际奥委会于2001年7月13日通过投票确定2008年奥运会举办城市,北京获得总计105张选票中的56张,得票率超过50%,获得奥运会举办权,北京得票的频数是_________.13、某校为了了解学生在校午餐所需的时间,统计了20名同学在校午餐所需的时间,获得如下的数据(单位:分):12,12,15,10,16,18,19,18,20,27,22,25,20,18,18,20,15,16,21,16.若将这些数据以4分为组距进行分组,则组数是________组.14、七(2)班数学测验成绩如下:77,74,65,53,95,87,84,63,91,53,69,81,61,69,91,78,75,81,80,67,76,81,61,69,79,94,86,70,70,87,81,86,90,88,85,67,71,82,87,75,落在79.5~89.5内数据的频数为__________.15.某次测验后,60~70分这组人数占全班总人数的20%,若全班有45人,则该组的频数为________.16.在一列数1,2,3,4,…,1000中,数字“0”出现的频数是___________.三.解答题(共7小题,52分)17.(6分) 某校抽检64个学生的体重如下(单位:kg):38323940354537384029394137423934363933423644332940353937463931393642384136443834383841393934364830313742424534334843413539444344将以上数据分为4组,列频数统计表.18. (6分) 某中学为了让学生了解环保知识,增强环保意识,举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计,请你解答下列问题:(1)全体参赛学生中,估计竞赛成绩落在哪组范围内的人数最多?(2)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的学生人数约为多少人?19.(6分) 课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.根据图中提供的信息,解答下面的问题:(1)本次调查的样本容量为______;(2)求表格中的a的值,并在图中补全条形统计图;(3)该校现有1200名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?20.(8分) 某厂抽查40名女工的年龄如下(单位:岁):25,27,28,23,26,25,28,21,30,24,25,28,22,27,26,29,25,24,25,26,27,23,24,22,26,28,23,29,27,26,25,23,27,24,22,26,30,25,23,28.取组距为2岁列频数统计表.21.(8分) 某次钓鱼比赛后,裁判员制作了一张如下所示的频数分布表.(1)请你完成频数分布表:(2)估计这组数据的最大值与最小值的差至多为多少,分组时的组距为多少?(3)共有多少人参加这次比赛?(4)哪一个成绩段的参赛者最多?哪一个成绩段的参赛者最少?(5)钓到11条以上(含11条)的参赛者有多少人,占参赛者总人数的百分之几?22. (8分) 去年以来,我国中东部地区持续出现雾霾天气,我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:请根据图表中提供的信息解答下列问题:(1)填空:m=____,n=____,扇形统计图中E组所占百分比为____;(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数.23.(10分) 某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成频数表和扇形统计图(如图),请根据所提供的信息解答下列问题:(1)求频数表中的m和n的值;(2)求扇形统计图中,E组所对应的扇形圆心角的度数;(3)请你估计该校九年级的学生中,体育综合测试成绩不少于80分的大约有多少人?参考答案1-5 ABBCB6-10 DCDCC11. 912. 56 13. 5 14. 14 15. 9 16. 19217. 解:最大值是48,最小值是29,最大值与最小值的差是48-29=19,取组距是5 kg ,则可以分为4组:18. 解:(1)估计竞赛成绩在80.5~90.5分的人数最多; (2)该校成绩优秀的学生人数约为1250×900=216(人).19. 解:(1)50(2)a =50-10-20-15=5,补图略(3)1200×15+550=480(名).答:估计该校共有480名学生课外阅读时间不少于1小时20解:最大值是30岁,最小值是21岁,(30-21)÷2=4.5,所以分5组 正 正正21. 解:(1)(2)这组数据的最大值与最小值的差至多为29,分组时的组距为5; (3)参加这次比赛的总人数为1+7+5+11+15+6=45(人);(4)由频数表可知,成绩在20.5~25.5条范围内的参赛者最多,在0.5~5.5条范围内的参赛者最少;(5)钓到11条以上(含11条)的参赛者有5+11+15+6=37(人),约占参赛者总人数的3745×100%≈82%。
精品解析浙教版初中数学七年级下册第六章数据与统计图表专题训练试题(含答案及详细解析)
初中数学七年级下册第六章数据与统计图表专题训练(2021-2022浙教考试时间:90分钟,总分100分)班级:__________ 姓名:__________ 总分:__________一、单选题(10小题,每小题3分,共计30分)1、在大课间活动中,同学们积极参加体育锻炼.小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,下列说法不正确...的是()A.第四小组有10人B.本次抽样调查的样本容量为50C.该校“一分钟跳绳”成绩优秀的人数约为480人D.第五小组对应圆心角的度数为452、九年级一班同学根据兴趣分成 A、B、C、D、E 五个小组,把各小组人数分布绘制成如图所示的不完整统计图.则 D 小组的人数是()A.10 人B.l1 人C.12 人D.15 人3、下列采用的调查方式中,不合适的是()A.了解澧水河的水质,采用抽样调查.B.了解一批灯泡的使用寿命,采用全面调查.C.了解张家界市中学生睡眠时间,采用抽样调查.D.了解某班同学的数学成绩,采用全面调查.4、为了解学生体育锻炼的用时情况,陈老师对本班50名学生一天的锻炼时间进行调查,并将结果绘制成如图统计图,那么一天锻炼时间为1小时的人数占全班人数的()A.14% B.16% C.20% D.50%5、空气是由多种气体混合而成的,为了简明扼要的介绍空气的组成情况,较好的描述数据,最适合使用的统计图是()A.扇形图B.条形图C.折线图D.直方图6、某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )A.得分在70~80分的人数最多B.该班的总人数为40C.人数最少的得分段的频数为2 D.得分及格(≥60分)的有12人7、每年4月23日是“世界读书日”,为了了解某校八年级500名学生对“世界读书日”的知晓情况,从中随机抽取了50名学生进行调查.在这次调查中,个体是()A.500名学生B.所抽取的50名学生对“世界读书日”的知晓情况C.50名学生D.每一名学生对“世界读书日”的知晓情况8、2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误..的是()A.1月份销售为2.2万辆B.从2月到3月的月销售增长最快C.4月份销售比3月份增加了1万辆D.1~4月新能源乘用车销售逐月增加A B C D E F共6门选修课,选取了若干学生进行了我最喜欢的一门9、某学校准备为七年级学生开设,,,,,选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).下列说法不正确的是()A.这次被调查的学生人数为400人B.E对应扇形的圆心角为80C.喜欢选修课F的人数为72人D.喜欢选修课A的人数最少10、对某市某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),绘制成如图所示统计图.已知选择鲳鱼的有40人,那么选择黄鱼的有()A.20人B.40人C.60人D.80人二、填空题(5小题,每小题4分,共计20分)1、为完成下列任务,你认为用什么调查方式更合适?(选填“全面调查”或“抽样调查”)(1)了解一批圆珠笔芯的使用寿命________.(2)了解全班同学周末时间是如何安排的________.(3)了解我国八年级学生的视力情况________.(4)了解中央电视台春节联欢晚会的收视率________.(5)了解集贸市场出售的蔬菜中农药的残留情况________.(6)了解里约奥运会100米决赛参赛运动员兴奋剂的使用情况________.2、为了了解2021年昆明市七年级学生下学期期末考试的数学成绩,从中随机抽取了1000名学生的数学成绩,在本次抽样调查中,个体是_______.3、如图为某市未来几天的每日最高气温与最低气温的变化趋势图,根据图中信息可知,最大的温差是______.4、已知某组数据的频数为63,样本容量为90,则频率为____.5、超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间1-2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为________.三、解答题(5小题,每小题10分,共计50分)1、吴老师为了解本班学生的数学学习情况,对某次数学考试成绩(成绩取整数,满分为100分)作了统计,绘制成如下频数分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:(1)补全频数分布表和频数分布直方图;(2)如果用扇形统计图表示这次数学考试成绩,那么成绩在69.5~79.5范围内的扇形圆心角的度数为________度.2、中秋节是中国四大传统节日之一,中秋文化在世界上影响广泛,吃月饼是中秋节的一项重要习俗.下面图表是华联超市中秋节当天所销售月饼的一些信息,请根据图表中信息解答下面的问题.(1)C品牌月饼一共卖了个,总价是元.(2)A品牌月饼单价是B品牌月饼单价的1,A、B品牌的月饼单价各多少元?2m)如下:请你根据上述信息,绘制相应的频数直方图.4、小颖一天的时间安排统计图如图所示.(1)根据图中的数据制作扇形统计图,表示小颖一天的时间安排;(2)比较两幅统计图的不同;(3)制作扇形统计图表示你一天的作息情况.5、如果你们学校需要建造新的自行车停车棚,至少需要多大面积?解决这个问题你需要哪些数据?你准备如何收集这些数据?---------参考答案-----------一、单选题1、D【分析】结合条形图和扇形图,求出样本人数,进行解答即可.【详解】根据直方图可知第二小组人数为10人,根据扇形图知第二小组占样本容量数的20%,则抽取样本人数为1020%50÷=人,故B选项正确;所以,第四小组人数为50410166410-----=人,故A选项正确;第五小组对应的圆心角度数为636043.250︒⨯=︒,故D选项错误;用样本估计总体,该校“一分钟跳绳”成绩优秀的人数约为1064120048050++⨯=人,故C选项正确;故选:D.【点睛】本题综合考查总体、个体、样本、样本容量,以及扇形统计图和频数(率)分布直方图.准确理解总体、个体、样本、样本容量、扇形统计图和频数(率)分布直方图等的相关概念是关键.2、C【分析】从条形统计图可看出 A 的具体人数,从扇形图找到所占的百分比,可求出总人数,然后结合 D所占的百分比求得 D小组的人数.【详解】总人数=510%=50(人),D 小组的人数=50×86.4360=12(人)),故选C.【点睛】本题考查了条形统计图、扇形统计图、用样本估计总体,读懂统计图,从不同的统计图中找到必要的信息进行解题是关键.3、B【分析】根据调查对象的特点,结合普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果接近准确数值,从而可得答案.【详解】解:了解澧水河的水质,采用普查不太可能做到,所以采用抽样调查,故A合适,了解一批灯泡的使用寿命,不宜采用全面调查,因为调查带有破坏性,故B不合适,了解张家界市中学生睡眠时间,工作量大,宜采用抽样调查,故C合适,了解某班同学的数学成绩,采用全面调查.合适,故D合适,故选B.【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.4、D【分析】根据条形统计图中的数据,可以计算出一天锻炼时间为1小时的人数占全班人数的百分比,从而可以解答本题.【详解】解:由题意可得,25÷(8+25+10+7)×100%=0.5×100%=50%,即一天锻炼时间为1小时的人数占全班人数的50%,故选:D.【点睛】本题考查样本估计总体,从条形统计图中读取信息是解题的关键.5、A【详解】根据题意,得要求直观反映空气的组成情况,即各部分在总体中所占的百分比,结合统计图各自的特点,应选择扇形统计图.故选A.6、D【详解】试题分析:A、得分在70~80分之间的人数最多,有14人,此选项正确;B、该班的总人数为4+12+14+8+2=40人,此选项正确;C、得分在90~100分之间的人数最少,有2人,频数为2,此选项正确;D、及格(≥60分)人数是12+14+8+2=36人,此选项错误.故选D.点睛:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.7、D【分析】个体是总体中的每一个调查的对象,据此判定即可.【详解】在这次调查中,个体是每一名学生对“世界读书日”的知晓情况故选:D.【点睛】本题考查了调查中个体的定义,掌握理解个体的概念是解题关键.8、D【详解】【分析】观察折线统计图,一一判断即可.【解答】观察图象可知:A. 1月份销售为2.2万辆,正确.B. 从2月到3月的月销售增长最快,正确.C.4.3 3.31-=, 4月份销售比3月份增加了1万辆,正确.D. 1~4月新能源乘用车销售先减少后增大.故错误.故选D.【点评】考查折线统计图,解题的关键是看懂图象.9、B【分析】根据表格和扇形图,通过计算,对每个选项分别进行判断,即可得到答案. 【详解】解:这次被调查的学生人数为:60÷15%=400(人),故A正确;∵D所占的百分比为:100100%=25%400⨯,A所占的百分比为:40100%=10%400⨯,∴E对应的圆心角为:360(118%10%15%12%25%)36020%72︒⨯-----=︒⨯=︒;故B错误;∵喜欢选修课F的人数为:40018%=72⨯(人),故C正确;∵喜欢选修课C有:40012%=48⨯(人),喜欢选修课E有:40020%=80⨯(人),∴喜欢选修课A的人数为40人,是人数最少的选修课;故D正确;故选:B.【点睛】本题考查了条形统计图、扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.10、D【分析】扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.【详解】解:鱼类总数:40÷20%=200(人),选择黄鱼的:200×40%=80(人),故选D.【点睛】本题考查的是扇形统计图.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键;扇形统计图直接反映部分占总体的百分比大小.二、填空题1、抽样调查全面调查抽样调查抽样调查抽样调查全面调查【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.【详解】(1)了解一批圆珠笔芯的使用寿命,具有破坏性,故适合用抽样调查.(2)了解全班同学周末时间是如何安排的,数量较小,故适合用全面调查.(3)了解我国八年级学生的视力情况,数量较大,故适合用抽样调查.(4)了解中央电视台春节联欢晚会的收视率,数量较大,故适合用抽样调查.(5)了解集贸市场出售的蔬菜中农药的残留情况,具有破坏性,故适合用抽样调查.(6)了解里约奥运会100米决赛参赛运动员兴奋剂的使用情况,数量较小,准确度要求高,故适合用全面调查.故答案为:抽样调查,全面调查,抽样调查,抽样调查,抽样调查,全面调查【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.2、每名考生的数学成绩.【分析】根据个体是总体中的每一个考查的对象,进而得出答案.【详解】解:从中随机抽取了1000名学生的数学成绩进行统计分析,则在该统计调查中,个体是每名考生的数学成绩.故答案为:每名考生的数学成绩.【点睛】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.3、10【分析】求出每天的最高气温与最低气温的差,再比较大小即可.【详解】解:∵由折线统计图可知,15日温差=4−(−3)=7;16日温差=4−(−6)=10;17日温差=2−(−6)=8;18日温差=2−(−2)=4;19日温差=1−(−5)=6;20日温差=1−(−1)=2;∴最大的温差是10.故答案为:10.【点睛】本题考查了折线统计图的应用以及有理数的减法,掌握有理数减法法则是解答本题的关键.有理数减法法则:减去一个数,等于加上这个数的相反数.4、0.7【分析】根据频率=频数÷总数,求解即可.【详解】这组数据的频率63÷90=0.7,故答案为:0.7.【点睛】本题考查了频率的计算公式,解答本题的关键是掌握公式:频率=频数÷总数.5、16【分析】根据题意和频数分布直方图可以得到这个时间段内顾客等待时间不少于5分钟的人数,找出等待5—6分钟,6—7分钟与7—8分钟的人数相加即可.【详解】解:由频数分布直方图可得,这个时间段内顾客等待时间不少于5分钟的人数为:9+5+2=16,故答案为:16.【点睛】本题考查频数分布直方图,解题的关键是明确题意,利用数形结合的思想解答问题.三、解答题1、(1)见解析;(2)72【分析】(1)根据69.5-79.5这一组的频数为10,频率为0.2,求出总人数,由此进行求解即可;(2)依据扇形的圆心角度数=360°×占比进行求解即可.【详解】解:(1)∵69.5-79.5这一组的频数为10,频率为0.2,∴总人数=10÷0.2=50人,∴59.5-69.5这一组的人数=50×0.1=5人,∴89.5-100.5这一组的频率=6÷50=0.12,列表如下:补全统计图如下:(2)由题意可得成绩在69.5~79.5范围内的扇形圆心角的度数=360°×0.20=72°,故答案为:72.【点睛】本题主要考查了频率与频数分布表,频数分布直方图,求扇形圆心角度数,解题的关键在于能够熟练掌握相关知识进行求解.2、(1)1000,2500;(2)A品牌月饼的单价是1.5元,B品牌月饼的单价是3元.【分析】(1)把超市三种月饼总销售量看作单位“1”,其中A品牌的占20%,求出三种月饼的总数是多少个,C品牌占50%,用总数乘50%就是C品牌的个数,最后根据总价=单价×数量求出C品牌的总价;(2)由A品牌月饼的单价是B品牌粽子的12,设B品牌月饼的单价为x元,则A品牌月饼的单价为12x元,然后根据总价=单价×数量,列方程解答后,即可求出各自的单价.【详解】解:(1)400÷20%=2000(个),2000×50%=1000(个),1000×2.5=2500(元),所以,C品牌月饼一共卖了1000个,总价是2500元.故答案为:1000,2500.x元,由题意得:(2)设B品牌月饼的单价为x元,则A品牌月饼的单价为12x=4900-2500600x+400×12解得x=3,=1.5(元).3×12所以,A品牌月饼的单价是1.5元,B品牌月饼的单价是3元.【点睛】此题考查了理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息解决有关的实际问题。
七年级数学下册 第6章 数据与统计图表 6.4 频数与频率(第2课时)校本作业(A本)(新版)浙教版
6.4 频数与频率(第2课时)课堂笔记1. 为了了解数据分组后各组频数的大小在总数中所占的份量,常常需要求出各组频数与数据总数的比. 每一组数据频数与数据总数的比叫做这一组数据(或事件)的频率,频率×100%即为百分比.2. 频率=频数/样本容量,样本容量=频数/频率,频数=样本容量×频率.注意:(1)频数与频率反映的是一组数据中各个数据出现的频繁程度,出现得越频繁,频数越大,频率也越大;出现的次数越少,频数越小,频率也越小.(2)各小组频率之和为1,各小组频数之和等于样本容量.3. 能根据样本频率来估计总体的数据分布情况.分层训练A组基础训练1.王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是()A. 16人B. 14人C. 4人D. 6人2. 将一个有40个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为()A. 6B. 0.9C. 6.67D. 1 3.(苏州中考)一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是()A. 0.1B. 0.2C. 0.3D. 0.44. 小敏统计了全班50名同学最喜欢的学科(每个同学只选一门学科). 统计结果显示:最喜欢数学和科学的频数分别是13和10,最喜欢语文和英语的人数的频率是0.3和0.2,其余的同学最喜欢社会. 则下列错误的是()A. 最喜欢语文的人数最多B. 最喜欢社会的人数最少C. 最喜欢数学的人数和最喜欢语文的人数之和超过总人数的一半D. 最喜欢科学的人数比最喜欢英语的人数要少5. 为了了解某地七年级男生的身高情况,从当地某学校选取了一个容量为60的样本,60名男生的身高(cm)分组情况如下表所示,则表中a,b的值分别是()A. 18,0.6B. 0.1,18C. 18,0.1D. 0.3,0.16. 从500个数据中用适当的方法抽取50个作为样本进行统计,频数统计表中,126.5~130.5这一组的频率是0.12,那么估计总体数据落在126.5~130.5之间的个数为()A. 120B. 60C. 12D. 67. 已知样本数据个数为30,且被分成4组,各组数据个数之比为2∶4∶3∶1,则第二小组的频率为 .8.为了了解某校九年级男生的身高情况,该校从九年级随机找来50名男生进行了身高测量,根据测量结果(测量结果均为整数,单位:cm)列出了如下频数表:根据表中提供的信息回答下列问题:(1)在表中,数据在164.5~168.5cm范围内的频数是,176.5~180.5cm范围内的频率是;(2)在表中,频率最大的一组数据的范围是 cm;(3)估计该校九年级男生身高在172cm以上(不包含172cm)的约占 %.9.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了如下尚不完整的频数表:(1)表中m=,n=;(2)在这次抽样调查中,最喜爱阅读哪类读物的学生最多?最喜爱阅读哪类读物的学生最少?(3)根据以上调查,试估计该校1200名学生中最喜爱阅读科普读物的学生有多少人?B组自主提高10.某班学生的数学期末成绩(成绩为整数,单位:分)的频数表如下,根据表中提供的信息回答下列问题:(1)求该班学生的总人数a;(2)在表中,频率m=,频数n=;(3)在表中,频数最小的一组的范围是;(4)若成绩大于或等于80分为优秀,大于或等于60分为及格,求该班的优秀率和及格率.C组综合运用11.某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:(1)本次问卷调查抽取的样本容量为,表中m的值为;(2)计算“非常了解”所对应的扇形圆心角的度数,并补全扇形统计图;(3)若该校有1500名学生,请根据调查结果,估算这些学生中“比较了解”垃圾分类知识的人数约为多少.参考答案6.4 频数与频率(第2课时)【分层训练】1—6. AAADCB7. 0.48. (1)12 0.08 (2)168.5~172.5 (3)369. (1)84 0.33(2)最喜爱阅读文学类的学生最多(84人),最喜爱阅读艺术类的学生最少(22人). (3)1200×0.33=396(人).10. (1)a =9÷0.15=60. (2)0.05 18 (3)49.5~59.5(4)优秀人数为18+6=24人,故优秀率为6024×100%=40%. 及格人数为60-3=57人,故及格率为6057×100%=95%. 11. (1)200 0.6(2)“非常了解”所对应的扇形圆心角的度数为0.2×360°=72°. 补图如图所示.(3)1500×0.6=900(人).答:这些学生中“比较了解”垃圾分类知识的人数约为900人.本文档仅供文库使用。
七年级数学下册第六章数据与统计图表6.4频数与频率一练习新版浙教版
6.4 频数与频率(一)A 组1.某校学生会成员的年龄如下表所示,则出现频数最多的年龄是(B )C. 13或15D. 22.有若干个数据,最大值是124,最小值是104,用频数表描述这组数据时,若取组距为3,则应分为(B )A. 6组B. 7组C. 8组D. 9组3.小明随机写了一串数字“123321223311”,则出现数字“3”的频数是(B ) A. 3 B. 4 C. 5 D. 64.在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频数是总数的15,则第六组的频数是(B )A. 10B. 5C. 15D. 205.如表所示是某校七年级(8)班共50位同学身高情况的频数表,则表中的组距是__7__,身高最大值与最小值的差至少是__14__cm.3.14159265358979423846264338327950288.试用画“正”字的方法记录圆周率的上述近似值中各数字出现的频数(完成下表).67.体育委员统计了全班同学60 s 跳绳的次数,并列出频数表如下:(2)组距是多少?组数是多少?(3)跳绳次数在120≤x <160范围内的学生有多少?【解】 (1)全班共有2+4+21+13+8+4=52(名)学生. (2)组距是80-60=20,组数是6.(3)跳绳次数在120≤x <160范围内的学生有13+8=21(人).B 组8.若数据3,0,m ,-1的极差是5,则m 的值为(C ) A. -2 B. 4C. -2或4D. 不确定【解】 当m 为最大值时,m -(-1)=5,得m =4;当m 为最小值时,3-m =5,得m =-2;当m 既不是最大值,又不是最小值时,3-(-1)=4≠5,不可能.故m 的值为-2或4.9.为了解某校七年级学生每天干家务的平均时间,小颖同学在该校七年级每班随机抽查5名学生,统计这些学生2017年3月每天干家务的平均时间(单位:min),绘制成如下统计表(其中A 表示0~10 min ,B 表示11~20 min ,C 表示21~30 min ,时间取整数):__25____12.5%____40__(2)该校七年级共有240名学生,其中大约有__150__名学生每天干家务的平均时间是11~20 min. 【解】 (1)由题意,得c =1025%=40,a =40×62.5%=25, b =540×100%=12.5%. (2)240×62.5%=150(名).10.某校为了了解学生的身高情况,抽测了60名17岁男生的身高,将数据分成7组,列出了相应的频数表如下:正正 正正 正正正(1)表中的组距是多少?最大数据与最小数据的差至多是多少? (2)这60名17岁男生中,身高在哪个范围内的频数最多?(3)这60名17岁男生中,身高不低于1.655 m 且不高于1.715 m 的学生所占的百分比是多少? 【解】 (1)组距=1.775-1.745=0.03(m).最大数据与最小数据的差至多是7×0.03=0.21(m). (2)身高在1.685~1.715 m 范围内的频数最多.(3)身高不低于1.655 m 且不高于1.715 m 的学生所占的百分比为11+1760×100%≈46.7%.数学乐园11.某校七年级(1)班50名学生参加1 min 跳绳体育考试.1 min 跳绳次数与频数经统计后绘制成下面的频数表(60~70表示为大于等于60并且小于70,其余类同)和扇形统计图.110~120 224~254 3 B 100~110 194~224 9 90~100 164~194 m C 80~90 148~164 12 70~80 132~148 n D60~70 116~132 2 0~60 0~116 0(第11题)(1)求m ,n 的值.(2)求该班1 min 跳绳成绩在80分以上(含80分)的人数占全班人数的百分比. (3)根据频数表估计该班学生1 min 跳绳考试的平均分. 【解】 (1)由题意,得 ⎩⎪⎨⎪⎧3+9+m +12+n +2=50,9+m =50×54%,解得⎩⎪⎨⎪⎧m =18,n =6. (2)(3+9+18+12)÷50×100%=84%.(3)用各分数段的组中值(两个边界值的平均数)来代替该组分数,可得平均分为(115×3+105×9+95×18+85×12+75×6+65×2)÷50=92(分).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.4 频数与频率(一)
1.某校学生会成员的年龄如下表所示,则出现频数最多的年龄是(B)
C. 13 或15
D. 2
2.有若干个数据,最大值是124,最小值是104,用频数表描述这组数据时,若取组距为3,则应分为(B)
A. 6组
B. 7 组
C. 8组
D. 9 组
3. 小明随机写了一串数字“ 123321223311',则出现数字“ 3”的频数是(B)
A. 3
B. 4
C. 5
D. 6
4. 在一次数学测试中,某班50名学生的成绩分为六组,
第一组到第四组的频数分别为
1
6, 8, 9, 12,第五组的频数是总数的?则第六组的频数是(B)
5
A. 10
B. 5
C.15
D. 20
5•如表所示是某校七年级(8)班共50位同学身高情况的频数表,则表中的组距是
身高最大值与最小值的差至少是_14_ cm.
6.把圆周率算到小数点后面35位得到
3. 14159265358979423846264338327950288.
试用画“正”字的方法记录圆周率的上述近似值中各数字出现的频数(完成下表).
【解】
7.体育委员统计了全班同学60 s跳绳的次数,并列出频数表如下:
(2) 组距是多少?组数是多少?
(3) 跳绳次数在120W x v 160范围内的学生有多少?
【解】⑴全班共有2+ 4 + 21 + 13 + 8+ 4= 52(名)学生.
⑵组距是80-60=20,组数是6.
⑶跳绳次数在120W x v160范围内的学生有13+8=21(人).
&若数据3, 0, m - 1的极差是5,则m的值为(C)
A. - 2
B. 4
C. —2或4
D.不确定
【解】当m为最大值时,n—( —1) = 5,得n= 4;当m为最小值时,3 —n= 5,得m =—2;当m既不是最大值,又不是最小值时,3 —( —1) = 4工5,不可能.故m的值为—2 或4.
9. 为了解某校七年级学生每天干家务的平均时间,小颖同学在该校七年级每班随机抽查5名学生,统计这些学生2017年3月每天干家务的平均时间(单位:min),绘制成如下统计表(其中A表示0〜10 min , B表示11〜20 min , C表示21〜30 min,时间取整数):
25 12.5%
(2) 该校七年级共有240名学生,其中大约有150名学生每天干家务的平均时间是
11 〜20 min.
【解】(1)由题意,得
10 c=
25%=
40, a=
40X
62.5 %
= 25,
5 b= X
100%=
12.5%.
40
(2)240 X 62.5 %= 150(名).
10. 某校为
了了解学生的身高情况,抽测了60名17岁男生的身高,将数据分成7组,
1.625
〜
-1.655正_6
1.655
〜
-1.685正正-11
1.685 〜1.715正正正T17
1.715
〜
-1.745正_ 6
1.745
〜
-1.775iF4
请根据频数表回答下列问题:
(1) 表中的组距是多少?最大数据与最小数据的差至多是多少?
(2) 这60名17岁男生中,身高在哪个范围内的频数最多?
(3) 这60名17岁男生中,身高不低于 1.655 m且不高于1.715 m的学生所占的百分比
是多少?
【解】⑴组距=1.775 —1.745 = 0.03(m).最大数据与最小数据的差至多是7X 0.03
=0.21(m).
(2) 身高在1.685〜1.715 m范围内的频数最多.
11 + 17
(3) 身高不低于1.655 m且不高于1.715 m的学生所占的百分比为亦x100济46.7%.
数学乐园
11.某校七年级(1)班50名学生参加1 min跳绳体育考试.1 min跳绳次数与频数经统计后绘制成下面的
频数表(60〜70表示为大于等于60并且小于70,其余类同)和扇形统计图.
等级分数段(分)
1 min跳绳
次数段
频数A
120254〜3000
110〜120224〜2543 B
100〜110194〜2249
90 〜100164〜194m
C
80 〜90148〜16412
70 〜80132〜148n
D
60 〜70116〜1322
0〜600 〜1160
(1) 求m n的值.
(2) 求该班1 min跳绳成绩在
(3)根据频数表估计该班学生
1 min跳绳考试的平均分.
【解】(1)由题意,得
3 + 9+ 12+ n+ 2 = 50,
9+ m= 50 x 54%
80分以上(含80分)的人数占全班人数的百分比.
m= 18
解得’
n= 6.
⑵(3 + 9+ 18 + 12) - 50X 100%= 84%.
(3)用各分数段的组中值(两个边界值的平均数)来代替该组分
可得平均分为(115 X3数,
+ 105X 9+ 95X 18+ 85X 12+ 75X 6+ 65X 2)- 50= 92(分).。
