四年级奥数教程及训练-05枚举法解题
奥数-枚举法
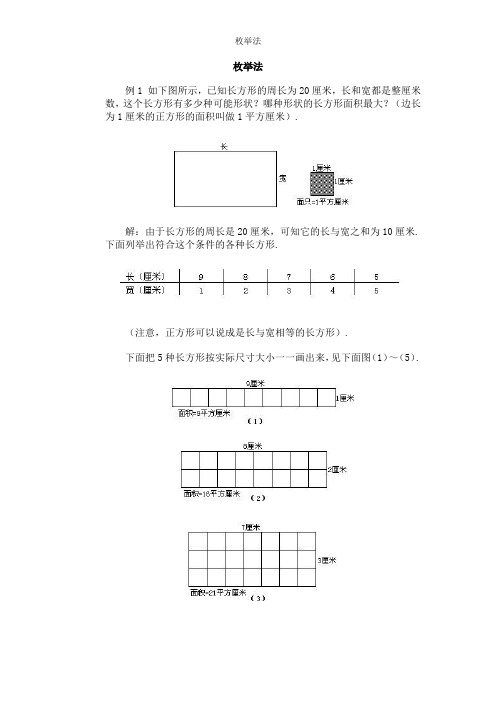
枚举法例1 如下图所示,已知长方形的周长为20厘米,长和宽都是整厘米数,这个长方形有多少种可能形状?哪种形状的长方形面积最大?(边长为1厘米的正方形的面积叫做1平方厘米).解:由于长方形的周长是20厘米,可知它的长与宽之和为10厘米.下面列举出符合这个条件的各种长方形.(注意,正方形可以说成是长与宽相等的长方形).下面把5种长方形按实际尺寸大小一一画出来,见下面图(1)~(5).例2 如右图所示,ABCD是一个正方形,边长为2厘米,沿着图中线段从A到C的最短长度为4厘米.问这样的最短路线共有多少条?请一一画出来.解:将各种路线一一列出,可知共6条,见下图.注意,如果题中不要求将路径一一画出,可采用如右图所示方法较为便捷.图中交点处的数字表示到达该点的路线条数,如O点处的数字2,表示由A到O有2条不同的路径,见上图中的(1)和(2);又H点处的数字3的意义也如此,见上图中的(1)、(2)、(3)可知有3条路径可由A到H.仔细观察,可发现各交点处的数字之间的关系,如O点的2等于F点和E点的数字相加之和,即1+1=2,又如,C点的6等于G点和H点的数字相加之和,即3+3=6.例3 在10和31之间有多少个数是3的倍数?解:由尝试法可求出答案:3×4=12 3×5=15 3×6=18 3×7=213×8=24 3×9=27 3×10=30可知满足条件的数是 12、15、18、21、24、27和30共7个.注意,倘若问10和1000之间有多少个数是3的倍数,则用上述一一列举的方法就显得太繁琐了,此时可采用下述方法:10÷3=3余1,可知10以内有3个数是3的倍数;1000÷3=333余1,可知1000以内有333个数是3的倍数;333-3=330,则知10~1000之内有330个数是3的倍数.由上述这些例题可体会枚举法的优点和缺点及其适用范围.例4 两个整数之积为144,差为10,求这两个数?解:列出两个数积为144的各种情况,再寻找满足题目条件的一对出来:1 2 3 4 6 8 9 12144 72 48 36 24 18 16 12可见其中差是10的两个数是8和18,这一对数即为所求.例5 12枚硬币的总值是1元,其中只有5分和1角的两种,问每种硬币各多少个?解:列举出两种硬币的可能搭配:可见满足题目要求的搭配是:四个5分币,八个1角币.例6 小虎给4个小朋友写信.由于粗心,在把信纸装入信封时都给装错了.4个好朋友收到的都是给别人的信.问小虎装错的情况共有多少种可能?解:把4封信编号:1,2,3,4.把小朋友编号,友1,友2,友3,友4.并假定1号信是给友1写的,2号信是给友2写的,3号信是给友3的,4号信是给友4写的:再把各种可能的错装情况列成下表:说明:如第一种错收情况是友1得2号信,友2得了1号信,友3得了4号信,友4得了3号信.。
小学奥数知识点趣味学习--枚举法

小学奥数知识点趣味学习——枚举法运用枚举法解题的关键是要正确分类,要注意以下两点:一是分类要全,不能造成遗漏;二是枚举要清,要将每一个符合条件的对象都列举出来。
【典型例题】【例1】:从小华家到学校有3条路可以走,从学校到岐江公园有4条路可以走,从小华家到岐江公园,有几种不同的走法?【试一试】1. 从甲地到乙地,有3条公路直达,从乙地到丙地有2条铁路可以直达,从甲地到丙地有多少种不同的走法?2. 新华书店有3种不同的英语书,4种不同的数学读物销售,小明想买一种英语书和一种数学读物,共有多少种不同的买法?【例2】把4个同样的苹果放在两个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?【试一试】1.把5个同样的苹果放在两个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?2.把7个同样的苹果放在三个同样的盘子里,不允许有的盘子空着不放,问共有多少种不同的分法?【例3】从1~6这六个数字中,每次取2个数字,这两个数字的和都必须大于7,能有多少种取法?【试一试】1.从1~9这九个数字中,每次取2个数字,这两个数字的和都必须大于10,能有多少种取法?2.从1~19这十九个数字中,每次取2个数字,这两个数字的和都必须大于20,能有多少种取法?【例4】一个长方形的周长是22米,如果它的长和宽都是整米数,那么这个长方形的面积有多少种可能值?【试一试】1.一个长方形的周长是30厘米,如果它的长和宽都是整厘米数,那么这个长方形的面积有多少种可能值?2.把15个玻璃球分成数量不同的4堆,共有多少种不同的分法?【例5】有4位小朋友,寒假中互相通一次电话,他们一共打了多少次电话?【试一试】1.6个小队进行排球比赛,每两队比赛一场,共要进行多少次比赛?2.有8位小朋友,要互通一次电话,他们一共打了多少次电话?。
5 枚举法(精英)

第五讲枚举法年级姓名学号【知识要点】用枚举法解题时需要掌握以下三点:1、列举时应注意依秩序,有条理地列举,不能杂乱无章地罗列。
2、根据题意,按范围和各种情况分类考虑,做到既不重复又不遗漏。
3、排除不符合条件的情况,不断缩小列举的范围。
【例题精讲】例1、明明从家到学校有2条路可走,从学校到少年宫有4条路可走,明明从家经过学校到少年宫共有几种走法?例2、用5、6、7三张数字卡片可以排出哪几个没有重复数字的三位数?例3、某副食品商店现存有5千克重的糖果10箱,2千克重的糖果4箱,1千克重的糖果6箱。
一位顾客要买10千克糖果,为了携带方便要求不开箱。
问怎例4、有1克,2克,4克,8克的砝码各一只,用它们每称一次得一个重量,求一共可以称出多少种不同的重量?例5、两个自然数的积是96,它们的和是22。
问这两个自然数分别是多少?例6、一副扑克牌,去掉大小王还剩52张。
把这52张扑克牌按照顺序和花色在桌面上摆放整齐,正面全部朝上。
然后把所有的黑桃、红桃都翻过来(正面朝下);接着把J、Q、K翻过来(使正面朝上的变朝下,正面朝下的又变成朝上)。
问正面朝上的牌共有多少张?正面朝下的牌共有多少张?【为了掌握】1、有一个三位数,十位上的数字比个位上的数字大3,百位上的数字是个位上的数字的平方,问这个三位数是多少?2、某班学生订阅A、B、C三种杂志,每人最多订阅两种,最少订阅一种,问共有多少种订阅方法?3、马拉松长跑比赛中有100名运动员,分别给他们1—100的号码布,问号码布上有数字7的运动员有多少名?4、有红、黄、蓝色的小旗各1面,从中选用1面、2面或3面升上旗杆,做出各种不同信号,问一共可以做多少种不同信号?(顺序不同表示不同信号)5、已知三个自然数的积等于12,这三个自然数分别是多少?6、把分别写上5,6,7,8的四张卡片,排成一个三位数,使它是5的倍数,请你把所有这样的三位数写出来。
7、用分别写有2,3,4的三张卡片,能排成多少个不同的三位偶数?写出这些数来。
(完整版)小学奥数枚举法题及答案【三篇】

小学奥数枚举法题及答案【三篇】导读:本文小学奥数枚举法题及答案【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【篇一】枚举法问题在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始,按顺时针方向,每隔一个球,取走一个球;每隔一个球,取走一个球;……他一直这样操作下去,当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗?答案与解析:根据题中所说的操作方法,他在第一圈的操作中,取走的是排在黄球中第2、4、6、……1994位置上的黄球,这时圆周上除了一个红球外,还剩下1994÷2=997个黄球。
在第二圈操作时,他取走了这997个黄球中,排在第1、3、5、7、……995、997位置上的黄球,这时圆周上除了一个红球外,还剩下997—(997+1)÷2=498个黄球。
他又要继续第三圈操作了,他隔过红球,又取走了这498个黄球中,排在第1、3、5、……495、497的位置上的黄球,这时圆周上除了一个红球外,还剩下498÷2=249个黄球。
因为在上一圈操作时,排在这498个黄球中最后一个位置上的黄球没有被取走,所以他再进行操作时,第一个被取走的就是那个红球,这时,他的操作停止,圆周上剩下249个黄球。
【篇二】在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始,按顺时针方向,每隔一个球,取走一个球;每隔一个球,取走一个球;……他一直这样操作下去,当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗? 答案与解析:根据题中所说的操作方法,他在第一圈的操作中,取走的是排在黄球中第2、4、6、……1994位置上的黄球,这时圆周上除了一个红球外,还剩下1994÷2=997个黄球。
在第二圈操作时,他取走了这997个黄球中,排在第1、3、5、7、……995、997位置上的黄球,这时圆周上除了一个红球外,还剩下997—(997+1)÷2=498个黄球。
四年级奥数枚举法和列表法

枚举法[知识要点]一般地,根据问题要求,一一列举问题,并加以解决,最终达到解决整个问题的目的。
这种分析问题、解决问题的方法,称之为枚举法。
运用枚举法解决应用题时,必须注意无重复、无遗漏。
为此必须力求有次序、有规律地进行枚举。
[典型例题]例1 用7、4、2三张数字卡片,能排成多少个无重复数字的三位数,它们分别是哪几个数?例2 用数字2,4,5,可以组成多少个无重复数字的三位数?分别是哪几个数?其中最大、最小各是多少?例3 小明有面值为5角邮票一枚、8角的邮票两枚,他用这些邮票能付多少种不同的邮资(寄信时,所需邮票的钱数?)2.用一台天平和重1克、3克、9克的砝码各一个(不用其他物体当砝码),当砝码只能放在同一盘内时,可称出不同的重量有多少种?3.把6支相同的铅笔分给3个小朋友,使每个小朋友都分到铅笔,那么有多少种不同的分法?4.用2张10元和1张50元一共可以组成多少种币值(组成的钱数)?5.麦当劳推出一种优惠活动,汉堡类有:A、鸡腿汉堡 B、麦辣鸡腿汉堡;饮料类有:C、雪碧 D、可口可乐;冰淇淋类有:(1)草莓冰淇淋(2)奶油冰淇淋汉堡只能选一种,饮料只能选一种,冰淇淋只能选一种,每次各类选一种,有多少种不同的选择,它们分别是哪些?1.用数字4,8,9,可以组成多少个无重复数字的三位数?分别是哪些数?2.用数字0,1,4可组成多少个无重复数字的三位数?分别哪些?3.由1角,2角,5角元的人民币各一张,一共可以组成多少种币值。
(组成的钱数)4.有7本相同的书,分别借给2名同学,每人至少借一本,有多少种不同的借法?列表法解应用题【典型例题】例1 华仔、小方、小米粥三人去商店买相同的书包,小米粥买了4个,用去256元钱,华仔买了6个,用去多少钱?小方花了320元能买多少个? 请根据要解决的问题,找出需要的条件列表整理并解答. (1)华仔用了多少元? (2)小方买了多少个?练习1 小林、小强、小冬三人去商店买同样的彩笔,小林用30元买了5盒,小强买了3盒,小冬买彩笔共用了48元。
四年级下册数学试题-奥数培优:用枚举法解应用题(含答案)全国通用

课题第十五讲:用枚举法解应用题教学内容养鸡场的工人,小心翼翼地把鸡蛋从筐里一个一个往外拿,边拿边数,筐里的鸡蛋拿光了,有多少个鸡蛋也就数清了.这种计数的方法就是枚举法.一般地,根据问题要求,一一列举问题的解答,或者为了解决问题的方便,把问题分为不重复、不遗漏的有限种情况,一一列举各种情况,并加以解决,最终达到解决整个问题的目的.这种分析问题、解决问题的方法,称之为枚举法。
运用枚举法解应用题时,必须注意无重复、无遗漏.为此必须力求有次序、有规律地进行枚举。
.用数字1,2,3可以组成多少个不同的三位数?分别是哪几个数?根据百位上数字的不同,我们可将它们分成三类:第1类:百位上的数字为1,有123,132;第2类:百位上的数字为2,有213,231;第3类:百位上的数字为3,有312,321.所以可以组成123,132,213,231,312,321,共6个三位数..小明有面值为5角、8角的邮票各两枚,他用这些邮票能付多少种不同的邮资(寄信时,所需邮票的钱数)?我们可根据小明寄信时所用邮票枚数的多少,把它们分成四类.解第1类:用l枚邮票时有5角、8角2种;第2类:用2枚邮票时有1元、1元3角、1元6角3种;第3类:用3枚邮票时有1元8角、2元l角2种;第4类:用4枚邮票时只有2元6角1种.共有2+3+2+l=8(种).答能付8种不同的邮资.(1)用3、4、7三张数字卡片,可以排成几个不同的三位数?其中最小的三位数是多少?最大的三位数是多少?(2)用3张10元和2张50元一共可以组成多少种币值(组成的钱数)?.用一台天平和重l克、3克、9克的砝码各一个(不再用其他物体当砝码),当砝码只能放在同一盘内时,可称出不同的重量有多少种?共有三个重量各不相同的砝码,可以取出其中的一个、两个或三个来称不同的重量,一一列举这三种情况.解取一个砝码可称l克、3克、9克的重量,有3种;取两个砝码可称;1+3= 4(克),1+9=10(克),3+9=12(克)的重量,有3种;取全部三个砝码可称:1+3+9 =13(克)的重量,有1种.注意到1,3,9,4,10,12,13各不相同,故可称出不同的重量有3+3+1=7(种).说明用树形图可以把解题过程显示出来..课外小组组织30人做游戏,按1~30号排队报数,第一次报数后,单号全部站出来;以后每次余下的人中第一个人开始站出来,隔一人站出来一人.到第几次这些人全部都站出来了?最后站出来的人应是第几号?根据题目的特点,先用排列法把题中的条件、问题排列出来,再用枚举法完成题目的要求.条件:(1)排队编号:1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30.(2)第一次报数后单号全部站出来.(3)以后每次:从余下的第一人站出来起,隔一人站出来一人.问题:到第几次这些人全部都站出来了?最后站出来的是第几号?解次数出队号码第一次1,3,5,7,9,11,13,15,17,19,21,23,25,27,29第二次2,6,10,14,18,22,26,30第三次4,12,20,28第四次8,24第五次16从上表的列举中,我们毫无遗漏地排列,得出到第五次这些人全都站出来了,最后一人是第16号.(1)把7支相同的铅笔分成3份,那么有多少种不同的分法?(2)有甲、乙、丙、丁、戊五个足球代表队进行比赛,每个队都要和其他队赛一场,总共要赛多少场?.A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共有种.解如图15 -1,A第一次传给B,到第五次传回A有5种不同方式,同理,A第一次传给C,也有5种不同方式,所以,不同的传球方式共有10种,.用长48厘米的铁丝围成各种长方形(长和宽都是整厘米数,且长和宽不相等),围成的最大一个长方形面积是多少平方厘米?各种长方形的长与宽之和都是48÷2=24(厘米).解由于各种长方形的长、宽都是整厘米数,且不相等,并且和为24厘米,可以列表如下:长23 22 21 20 19 18 17 16 15 14 13宽 1 2 3 4 5 6 7 8 9 10 11因为23×1< 22×2<…<14×10< 13×11,所以符合条件的最大长方形的面积是13×11=143(平方厘米)答围成的最大一个长方形的面积是143平方厘米.此题用列举法思维,达到了快速、简捷的解题目的.从以上各例可以看到,利用树形图或列表分析的方法解答应用题,往往是非常有效的,它能把抽象、复杂的事情清楚、直观地展现在我们面前,为解题提供思路,另外,我们还应体会到,用枚举法解应用题的关键是准确分类,为此,必须注意两点:l.分类要全,分类不全.就会造成遗漏.分类确定之后,要把每一类中每一个符合条件的对象都列举出来.2.分类要清,因为如果分不清,使第1类中有第2类、第2类中有第3类,互相包含,那么就会有重复.这样结果也就很难正确了.(1)从A城到B城可乘火车、汽车、轮船;从B城到C城可乘火车、汽车、轮船、飞机,某人从A城开始游览,经B城到C城共有多少种走法?(2)A、B、C三个自然数的乘积是6,求A、B、C三个自然数分别可能是几?(A、B、C可以是不同的数,也可以是相同的数)最有魅力的23个问题1900年8月8日,在巴黎第二届国际数学家大会上,有个年轻的科学家正在演讲,大家都被他讲的内容深深吸引,安静地听他演讲,每个人的眼睛里都闪烁着激动的光芒.当他结束演讲的时候,刚才还静悄悄的大厅里,顿时爆发出雷鸣般的掌声,这个轰动了全场的人是谁呢?他讲的是什么令人激动的内容呢?他就是德国的希尔伯特.他提出了今后一百年里数学家应当努力解决的23个问题.这就是著名的“希尔伯特23个问题”.这个时候,希尔伯特心里的石头才落了地.刚才,他还在担心自己演讲的内容听众会不会接受呢.和下面的听众一样,希尔伯特也非常激动,此时的他,心潮澎湃,看来,我选择这个伟大的演讲题目果然没有错!原来,在来参加这次会议之前,希尔伯特一直在犹豫演讲的题目:是讲我自己的数学研究成果呢?还是讲一讲我对今后数学发展的看法呢?他写了一封信给自己的好朋友——数学家闵可夫斯基,征求他的意见,闵可夫斯基回信写道:“最有吸引力的题材莫过于展望数学的未来……这样的题材,将会使你的演讲在今后几十年里成为人们议论的话题,”这样,希尔伯特就下定决心了,他整理了自己的看法,一共提出了23个问题.从那以后,全世界几乎所有的数学家,都被他的23个问题吸引,这23个问题成为20世纪数学学科发展的缩影.著名的“哥德巴赫猜想”就是第8个问题中的一部分,对这些问题的研究有力地推动了20世纪数学的发展,难怪有人说:“希尔伯特就像风笛手,他那甜蜜的笛声诱惑了如此众多的老鼠,跟着他跳进了数学的深河,”今天,我们似乎还能听到那甜蜜笛声的召唤呢!一、填空题1.从甲地到乙地有2条路可走,由乙地到丙地有3条路可走,那么由甲地经乙地到丙地共有____条路可走,2.有4个足球队参加“希望杯”足球比赛,每两个队都必须比赛一场,共比赛____场;如果进行淘汰赛,最后决出冠军共需比赛____场.3.甲、乙、丙、丁站成一排照相,但甲必须站在两头,共有____种不同的排法.4.从3,6,7,8这四张数字卡片中,任取3张,排成三位数,能排成____个不同的三位数,最大的三位数是____,最小的三位数是____.5.从两张5元币、五张2元币、十张1元币中,拿出10元钱买钢笔,一共有____种不同的拿法.6.用1,0,3,5这四个数可以组成____个四位数.二、选择题7.有7张卡片上写着数字2,3,4,5,6,7,8,从中抽出两张,组成的所有的两位数是奇数的个数是().(A) 21 (B) 42 (C) 24 (D) 188.两人见面要握一次手,照这样规定,6人见面共握手().(A) 24次(B) 15次(C) 30次(D) 12次9.有红、黄、蓝色的小旗各1面,从中选用l面、2面或3面升上旗杆,组合出各种不同信号,一共可以组合不同信号().(A)5种(B)6种(C) 10种(D) 15种10.已知三位数的各位数字之和等于8,那么这样的三位数共有().(A) 28个(B) 30个(C) 32个(D) 36个三、简答题11.有四张8角邮票与三张1元邮栗,用这些邮票中的一张或若干张能得出多少种不同的邮资?一.填空题(每题6分,共48分)1.如图,一条直线上有四个点,那么这条直线上有______条线段,有______条射线.2.甲、乙、丙、丁站成一排照相,但甲和乙必须站在两头,共有______种不同的站法.3.从分别写有2、3、4、5的四张卡片中任取两张,作两个一位数乘法,有______种不同的乘法算式,有______个不同的积,4.从7、4、2、O四张数字卡片中,挑选三张排成三位数,能排成______个不同的三位数,5.婷婷有3种不同颜色的上衣,5种不同颜色的裙子,那么她共有______种不同的穿法.6.由10元、50元、100元的人民币各一张,一共可以组成______种币值(组成的钱数).7.如图,数出图中所有的正方形的个数是______个,8.在上题4×4的方格图中放A、B两枚棋子(棋子放在空格中),要求两枚棋子不在同一行,也不在同一列,共有______种放法.二、选择题(每题8分,共24分)9.有4本不同的书,分别借给2名同学,每人借一本,不同的借法有( )种.(A)12 (B)6 (C) 10 (D)810.把5件相同的礼物分给3个小朋友,使每个小朋友都分到礼物,分礼物的不同方法一共有( )种.(A)2种 (B)3种 (C)5种 (D)6种11.如图,甲地到乙地有三条路可通,从乙地到丙地有两条路可通,从丙地到丁地有三条路可通,从甲地到丁地有两条路可通.从甲地到丁地共有( )种不同的走法.(A) 20 (B) 10 (C) 36 (D) 24三、解答题(每题12分,共48分)12.甲、乙、丙三人约好每人报名参加数学、英语、美术、音乐四个课外小组中的一个,那么,报名的结果会出现多少种不同的情形?13.有8张卡片,上面分别写着自然数1至8,见下图.从中取出3张,要使这3张卡片上的数字之和为9,问有多少种不同的取法?14.有正方体一个,它的六个面上分别标有数字1、2、3、4、5、6,将这个正方体投掷两次.问:两次向上的一面数字之和为偶数的情况有多少种?15.小王有10张1元的人民币.5张2元的人民币,2张5元的人民币,要拿出10元买一本书,可以有多少种拿法?你最对了吗?答案:1.6,8.2.4种,甲一丙一丁一乙,甲一丁一丙一乙,乙一丙一丁一甲,乙一丁一丙一甲.3.12,6.枚举:2×3、2×4、2×5、3×4、3×5、4×5共六个乘法算式,交换两因数位置,又得到六个乘法算式.因此,共有12个乘法算式,有6个不同的积.4.18个,百位上可排7、4、2三个数,先考虑7排在百位上,共有六种情况(如图),同理,2排在百位上,4排在百位上也各有六种情况,所以不同的三位数共有6×3 = 18(个).5.15.每种颜色的上衣可配5种不同颜色的裙子,则3种不同颜色的上衣配5种不同颜色的裙子,共有穿法为:5×3=15(种).6.7种.10元、50元、100元、(10+50)= 60元、(10+100)= 110元、(50+100)=150元、(10+ 50+100)=160元.7.30.分四种情况计数:(1)边长为1个单位的正方形有16个;(2)边长为2个单位的正方形有9个;(3)边长为3个单位的正方形有4个;(4)边长为4个单位的正方形有1个.共有:16+9+4+1= 30(个)正方形.8.144.由于两枚棋子要一枚一枚地放,所以可分两步完成这件事,第一步放棋子A,A可以放在16个方格中任意一个,有16种放法;第二步放棋子B,由于A棋子所在的行与列的方格中不能再放,故B只能放在剩下的9个方格中,有9种放法,根据乘法原理得:16×9=144(种).所以,共有144种放法.9.A. 4×3 = 12(种).10.D. 5件礼物分成三组,有两种不同的分组法:1,1,3或1,2,2.每种分组法有3种不同的排列,故有6种不同的分法.11.A.从甲到丁有以下路径:(1)甲→丁(有2种不同走法);(2)甲→乙→丙→丁(有3×2×3=18种不同走法).所以共有:2+18=20(种)不同的走法.12.64种,三人报名参加课外小组,彼此互不影响.甲报名,可报4个小组中的一个,有4种报名方法,同理,乙、。
小学奥数枚举法解题方法的介绍
小学奥数枚举法解题方法的介绍
有关小学奥数枚举法解题方法的介绍
甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘。
到现在为止,甲赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘。
问小强赛了几盘?
解:作表3-2。
甲已经赛了4盘,就是甲与乙、丙、丁、小强各赛了一盘,在甲与乙、丙、丁、小强相交的那些格里都打上√;乙赛的盘数,就是除了与甲赛的那一盘,又与丙和小强各赛一盘,在乙与丙、小强相交的那两个格中都打上√;丙赛了两盘,就是丙与甲、乙各赛一盘,打上√;丁与甲赛的那一盘也打上√。
丁未与乙、丙、小强赛过,在丁与乙、丙与小强相交的格中都画上圈。
根据条件分析,填完表格以后,可明显地看出,小强与甲、乙各赛一盘,未与丙、丁赛,共赛2盘。
答:小强赛了2盘。
四年级奥数计数的基本方法枚举树
计数的基本方法---枚举树(2.28)“树形图”是数学中应用最为广泛的图形之一,在数学计数问题中,每当我们面对一些非常规的题目一筹莫展时、无从下手时,枚举法往往可以发挥巨大的威力。
枚举法又叫穷举法,顾名思义,就是把所有符合题目条件的对象一一列举出来,然后根据要求从中挑选出合理的。
但是怎样在枚举的过程中既不重不漏地枚举出所有符合条件的对象呢?“树形图”就可以使我们的枚举过程不仅形像直观,而且有条理又不易重复或遗漏,使人一目了然一.树形图在组合计算中的应用例1.用一台天平和重1克、3克、9克的砝码各一个(不再用其它物体当砝码),当砝码只能放在同一盘内时,可称出不同的重量有多少种?例2.甲乙两人进行乒乓球比赛,规定谁先胜三场谁胜。
第一场甲胜。
问到决出最后的胜负为止,共有几种不同的情形?其中甲胜的情形有几种?例3.某人游览 A ,B,C 三个风景区,计划旅游5天。
由A区开始游览,一天换一个风景区,最后又回到A区,试问有多少种游览路线?例4.小马虎给4位同学写信,由于粗心,他在把信装入信封时给弄错了,结果四位同学都没有收到小马虎给自己写的信,而是收到了他写给别的同学的信,请问一共有多少种可能情形?(PS.本题是组合数学中著名的“错装信封问题”把n个已写好相应地址的信封任意打乱。
问,所有信纸全都装错了信封的情况有多少种?例5.下图中有6个点,9条线段,一只蚂蚁从A点出发,沿着某几条线段爬到F点,行进中,同一个点或同一条线段只能经过一次,这只蚂蚁最多有多少种不同的爬行路线?例6.对自然数作如下操作:如果是奇数就减去1,如果是偶数就除以2,如此操作直到结果变为1为止。
那么经过6次操作后使结果变成1的数有几个?二.枚举树在决策问题中的应用枚举树不仅可以帮助我们去计数,还可以帮我们在众多的决策中选择出一组最优的策略。
例7.四皇后问题是将4个棋子放在4X4的格子里,使得不会有两个棋子在同一行、同一列或对角线上。
(用象棋术语来讲,该问题是如何将4个皇后放在4X4的棋盘中,并且使得没有皇后能攻击对方)例8.设有13个银币,标号为1、2、3、……13。
奥数教程(第八版)四年级 第12讲 用枚举法解应用题
经典例题精讲 四年级
第12讲 用枚举法解应用题
主讲老师: Mathematical Olympiad Tutorial
第12讲 用枚举法解应用题
例1 有三张数字卡片,分别为 4 , 9 , 0 。 从中挑出两张排成一个两位数,一共可以排 成多少个两位数?
第12讲 用枚举法解应用题
第12讲 用枚举法解应用题
例5 计划将甲、乙、丙三种不同的树苗种植在一条 直路的同一侧,要求相邻的两棵树苗不能相同, 那么考虑前5棵,第1棵与第5棵同是甲种树苗 的种法共有 6 种。 解: 画树状图枚举如下:
因此,第1棵与第 5棵同是甲种树苗 的种法共有6种。
第12讲 用枚举法解应用题
例6 用长48厘米的铁丝围成各种长方形(长和宽都 是整厘米数,且长和宽不相等),围成的最大 一个长方形面积是多少平方厘米? 解: 列表如下:
(2)剩下1张5元,取出 1+10+50+100=161(元);
(3)剩下1张10元,取出 1+5+50+100=156(元);
第12讲 用枚举法解应用题
例3 你的口袋里有1元、5元、10元、50元、100元 的纸币各1张。如果每次取出4张计算它们的钱 数,共有 5 种不同的钱数。
解: (4)剩下1张50元,取出 1+5+10+100=116(元);
圆珠笔 橡皮 签字笔 (支 ) (块) (支)
圆珠笔 橡皮 签字笔 (支 ) (块) (支)
第12讲 用枚举法解应用题
例4 一个文具店中橡皮的售价为每块5角,圆珠笔 的售价为每支1元,签字笔的售价为每支2元5 角。小明要在该店花5元5角购买其中的两种文 具,他有多少种不同的选择? 解: 5+2+1=8(种), 所以他有8种不同的选择。
四奥第4讲 枚举法
第四讲枚举法教学课题:枚举法教学课时:两课时教学目标:1.经历枚举的过程,让学生形成分类枚举的思维习惯。
2.通过操作发展学生的枚举能力,形成比较抽象的数学思维。
教学重难点:经历枚举过程,进行恰当的分类,做到枚举不重不漏。
教具准备:本周通知:教学过程:一、故事导入师:最近老师在看一部讲述骗子的英国电视剧《飞天大盗》,这部剧讲的是一群高智商的骗子如何去骗一些贪婪的人的钱。
昨天讲到这样一个故事,他们把一个贪婪狡诈的银行家骗上钩了,但是如何把他锁在保险箱里的钱偷到手呢?问题就来了——保险箱需要输入一个三位数的密码,密码都是由1~3这3个数字其中三个组成的。
电视放到这里就给观众留下了一个悬念,问我们,最多需要试多少次才能把密码试出来呢?那同学们你们愿意试试吗?生:(七嘴八舌)123!231!……师:同学们各有各的想法,都很棒。
但是我们想想,什么叫“最多需要试多少次”呢?生:就是看着这1、2、3能组成多少个三位数!(如果学生答不出来由老师引导)师:恩,XXX答得非常对!就是看1、2、3能组成多少个三位数!那究竟怎么去写才能够保证我没有写重复或者漏掉呢,这就是我们今天要学习的——枚举法。
二、例题精讲例1、有红、黄、蓝色的小旗各1面,我们可以把不同数量、不同顺序的旗子挂在旗杆上表示不同的信号,那么一共可以表示出多少种不同信号?【考虑顺序不同信号不同的情况】【思路点拨】和放砝码、取硬币一样,将取出小旗的面数进行分类一面:3种两面:6种三面:6种 3+6+6=15种例2、从3名男生、2名女生中选出三名升旗手,其中至少有1名男生,共有多少种不同的选法?【思路点拨】分类枚举,一个男生的情况:3 两个男生的情况:6 三个男生的情况:13+6+1=10种例3、一个长方形的周长是30厘米,如果它的长和宽都是整厘米数,那么这个长方形的面积有多少种可能?师:咱们一起来回忆一下,我们长方形的面积公式是?生:长方形的面积=长×宽师:很好,看来大家并没有因为放暑假而把知识还给老师。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级奥数第五讲
枚举法解应用题
【知识要点和基本方法】
一般地,根据问题要求,一一枚举问题的解答,或者为了解决问题的方便,把问题分为不重复、不遗漏的有限种情况,一一枚举各种情况,并加以解决,最终达到解决整个问题的目的,这种分析问题、解决问题的方法,称之为枚举法,我们也可以通俗地称枚举法为举例子。
枚举法是一种常见的数学方法,当然枚举法也存在一些问题,那就是容易遗漏掉一些情况,所以应用枚举法的时候选择什么样的标准尤其重要。
【例题精选】
例1.用数字1,2,3可以组成多少个不同的数字?分别是哪几个数?
分析:根据百位上数字的不同,我们可以把它们分为三类:
第1类:百位上的数字为1,有123,132;
第2类:百位上的数字为2,有213,231;
第3类:百位上的数字为3,有312,321。
所以可以组成123,132,213,231,312,321,共6个三位数。
课堂练习题:
用0、6、7、8、9这五个数字组成各个数位上数字不相同的两位数共有多少个?
例2.小明有面值为5角、8角的邮票各两枚。
他用这些邮票能付多少种不同的邮资(寄信时,所需邮票的钱数)
分析:我们可根据小明寄信时所用邮票枚数的多少,把它们分成四类——一枚、二枚、三枚、四枚。
一枚:5角
二枚:10角,13角
三枚:18角,21角
四枚:26角
课堂练习题:
10元钱买6角邮票和8角邮票共14张,问两种邮票各多少张?
例3.用一台天平和重1克、3克、9克的砝码各一个(不再用其他物体当砝码),当砝码只能放在一个盘内时,可称出不同的重量有多少种?
分析:共有三个重量各不相同的砝码,可以取出其中的一个、两个或三个来称不同的重量,一一列举这三种情况。
1个:1克,3克,9克
2个:4克,10克,12克
3个:13克
同学们可以思考一下:如果砝码可以放天平的两边,又能称出多少不同的重量?
例4.课外小组组织30人做游戏,按1-30号排队报数。
第一次报数后,单号全部站出来;以后每次余下的人中第一个人开始站出来,隔一人站出来一人。
到第几次这些人全部站出来了?最后站出来的人应是第几号?
分析:根据题目的特点,先用排列法把题中的条件、问题排列出来,再用枚举法完成题目的要求。
例5.用长48厘米的铁丝围成各种长方形(长和宽都是整厘米数,且长和宽部不相等),围成的最大一个长方形面积是多少平方厘米?
分析:各种长方形的长和宽之和都是48÷2=24(厘米)。
两数的和一定,当两数越接近,它们的乘积越大,当两数相等的时候,乘积最大。
例6.商店出售饼干,现存10箱5千克重的,4箱2千克重的,8箱1千克重的。
一顾客要买9千克饼干,为了便于携带要求不开箱。
营业员有多少种发货方法?
分析:买9千克饼干要求不开箱,从题目告诉的条件来看,并不难做到,但问题是求“有多少种发货方法?”这意味着要求无遗漏、无重复的把各种发货的可能性都考虑到,显然用枚举法是一种好方法。
用列表的形式,为了避免重复、遗漏,可先取5千克重的箱,再取2千克重的箱,最后取1千克重的箱。
例7 将三个相同的小球放入A、B、C三个盒子中,一共有多少种方法?
分析:三个球相同,所以就考虑盒子,分别有下面这样的方法:0,0,3;0,1,2;0,2,1;0,3,0;3,0,0;1,2,0;1,1,1;2,1,0;2,0,1;1,0,2;一共有10种不同的方法。
【听课记录】
【课后练习题】
1.从甲地到乙地有2条路可走,由乙地到丙地有3条路可走,那么由甲地经乙地到丙地共有几条路可走?
2.有4个小足球队参加“希望杯”足球比赛,每两个队都必须比赛一场,共比赛多少场?如果进行淘汰赛,最后决出冠军共需多少场比赛?
3.甲、乙、丙、丁站成一排照相,但甲必须站在两头,共有多少种不同的排法?
4.从3、6、7、8四张数字卡片中,任取3张,排成三位数,能排成多少个不同的三位数?最大的三位数是多少?最小的三位数是多少?
5.从两张5元币、五张2元币、十张1元币中,拿出10元钱买钢笔,一共有多少种不同的拿法?
6.用1、0、3、5这四个数可以组成多少个四位数?
7.有7张卡片上写着数字2、3、4、5、6、7、8,从中抽出两张,组成的所有的两位数是奇数的个数是多少?
8.两人见面要握一次手,照这样规定,6人见面共握多少次手?
9.有红、黄、蓝色的小旗各1面,从中选出1面、2面或3面升上旗杆,作出各种不同的信号,一共可以作几种不同的信号?
10.已知三位数的各位数字之和等于8,那么这样的三位数共有多少个?
11.有四张8角邮票与三张1元邮票,用这些邮票中的一张或若干张能得出多少种不同的邮资?
12.已知三个自然数的积等于12,这三个自然数分别是多少?
13.现有1克、2克、3克重的天平砝码,要用10个砝码称出重20克的物体。
(1)在取出的砝码中,1克重的有3个,那么3克重的砝码应有多少个?
(2)如果任一种砝码至少取一个,那么除情况(1)外,取出的砝码还有哪几种情况?
14.某食堂的菜单如下:
汤类:A. 鸡蛋汤;B. 三鲜汤。
菜类:C. 炒肉丝;D. 红烧猪肉;E. 炒青菜。
饮料类:(1)高橙;(2)健力宝;(3)葡萄酒。
每顿饭若只能各类选一种,试问:
(1)可以有多少种不同的选购方法?(2)请写出这些选购菜单。
15.5个茶杯的价钱分别是8角、6角、5角、4角和3角,3个茶盘的价格分别是9角、7角和2角,如果一个茶杯配一个茶盘,一共可以配成多少种不同价格的茶具?。
