电子技术基础课后答案_第四版_数字部分(康华光编)
电子技术基础(数字)康华光课后解答

VNLA(max) =VIL(max) —VOL(max) =0.8V—0.4V=0.4V
2.4
0.4
2
0.8
逻辑门 B
3.5
0.2
2.5
0.6
逻辑门 C
4.2
0.2
3.2
0.8
解:根据表题 3.1.1 所示逻辑门的参数,以及式(3.1.1)和式(3.1.2),计算出逻 辑门 A 的高电平和低电平噪声容限分别为:
VNHA =VOH (min) —VIH (min) =2.4V—2V=0.4V
(2) L D(A C)
(3) L (A B)(C D)
2.2.2 已知函数 L(A,B,C,D)的卡诺图如图所示,试写出函数 L 的最简与 或表达式
解: L(A, B,C, D) BCD BCD BCD ABD 2.2.3 用卡诺图化简下列个式 (1) ABCD ABCD AB AD ABC 解: ABCD ABCD AB AD ABC ABCD ABCD AB(C C)(D D) AD(B B)(C C) ABC(D D) ABCD ABCD ABCD ABCD ABCD ABCD ABCD
解: A ABC ACD (C D)E
A( 1 B C) A C D C D E
A A C D C D E
AB +AB
1 0 0 1
A CD CDE A CD E 2.1.4 用代数法化简下列各式 (3) ABC(B C) 解: ABC(B C) (A B C)(B C)
(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H 1.4 二进制代码 1.4.1 将下列十进制数转换为 8421BCD 码: (1)43 (3)254.25 解:(43)D=(01000011)BCD 1.4.3 试用十六进制写书下列字符繁荣 ASCⅡ码的表示:P28 (1)+ (2)@ (3)you (4)43 解:首先查出每个字符所对应的二进制表示的 ASCⅡ码,然后将二进制码转换 为十六进制数表示。 (1)“+”的 ASCⅡ码为 0101011,则(00101011)B=(2B)H (2)@的 ASCⅡ码为 1000000,(01000000)B=(40)H (3)you 的 ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为
数字电路考研康华光电子技术基础数字部分考研真题与笔记

数字电路考研康华光电子技术基础数字部分考研真题与笔记一、数电考研考点复习笔记1.1 复习笔记本章是《电子技术基础数字部分》的开篇,主要讲述了模拟信号和数字信号以及数字信号的描述方法,进而讨论了数制、二进制的算术运算、二进制代码和数字逻辑的基本运算,是整本教材的学习基础。
笔记所列内容,读者应力求理解和熟练运用。
一、模拟信号与数字信号1模拟信号和数字信号(见表1-1-1)表1-1-1 模拟信号和数字信号2数字信号的描述方法(见表1-1-2)表1-1-2 数字信号的描述方法3数字波形详细特征(1)数字波形的两种类型见表1-1-3表1-1-3 数字波形的类型(2)周期性和非周期性与模拟信号波形相同,数字波形亦有周期型和非周期性之分。
周期性数字波形常用周期T和频率f来描述。
脉冲波形的脉冲宽度用表示,所以占空比(3)实际数字信号波形在实际的数字系统中,数字信号并不理想。
当从低电平跳变到高电平,或从高电平跳到低电平时,边沿没有那么陡峭,而要经历一个过渡过程。
图1-1-1为非理想脉冲波形。
图1-1-1 非理想脉冲波形(4)波形图、时序图或定时图波形图、时序图或定时图概述见表1-1-4。
表1-1-4 波形图、时序图或定时图概述时序图和定时图区别与特征见表1-1-5。
表1-1-5 时序图、定时图特征二、数制1几种常用的进制(见表1-1-6)表1-1-6 几种常用的进制2进制之间的转换(1)其他进制转十进制任意一个其他进制数转化成十进制可用如下表达式表示:其中R表示进制,Ki表示相应位的值。
例如(二进制转十进制):(1011.01)2=1×23+0×22+1×21+1×20+0×2-1+1×2-2=(11.25)10。
(2)十进制转二进制①整数部分的转换:将十进制数除以2,取所余数为k0;将其商再除以2,取其余数为k1,……以此类推,直到所得商等于0为止,余数k n…k1k0(从下往上排)即为二进制数。
电子技术基础课后答案第四版数字部分康华光编

电子技术基础课后答案第四版数字部分康华光编1.1.1 一数字信号的波形如图1.1.1所示,试问该波形所代表的二进制数是什么?解:0101 10101.2.1 试按表1.2.1所列的数字集成电路的分类依据,指出下列器件属于何种集成度器件:(1) 微处理器;(2) IC 计算器;(3) IC 加法器;(4) 逻辑门;(5) 4兆位存储器IC 。
解:(1) 微处理器属于超大规模;(2) IC 计算器属于大规模;(3) IC 加法器属于中规模;(4) 逻辑门属于小规模;(5) 4兆位存储器IC 属于甚大规模。
1.3.1 将下列十进制数转换为二进制数、八进制数、十六进制数和8421BCD 码(要求转换误差不大于2-4): (1) 43 (2) 127 (3) 254.25 (4)2.718解:(1) 43D=101011B=53O=2BH ; 43的BCD 编码为0100 0011BCD 。
(2) 127D=1111111B=177O=7FH ; 127的BCD 编码为0001 0010 0111BCD 。
(3) 254.25D=11111110.01B=376.2O=FE.4H ; 0010 0101 0100.0010 0101BCD 。
(4) 2.718D=10.1011 0111B=2.56O=2.B7H ; 0010.0111 0001 1000BCD 。
1.3.3 将下列每一二进制数转换为十六进制码: (1) 101001B (2) 11.01101B 解:(1) 101001B=29H (2) 11.01101B=3.68H 1.3.4 将下列十进制转换为十六进制数: (1) 500D (2) 59D (3) 0.34D (4) 1002.45D 解:(1) 500D=1F4H (2) 59D=3BH (3) 0.34D=0.570AH (4) 1002.45D=3EA.7333H1.3.5 将下列十六进制数转换为二进制数: (1) 23F.45H (2) A040.51H解:(1) 23F.45H=10 0011 1111.0100 0101B(2) A040.51H=1010 0000 0100 0000.0101 0001B 1.3.6 将下列十六进制数转换为十进制数: (1) 103.2H (2) A45D.0BCH 解:(1) 103.2H=259.125D (2) A45D.0BCH=41024.046D2.4.3 解:(1) LSTTL 驱动同类门mA I OL 8(max)= mA I IL 4.0(max)= 204.08==mA mAN OLmA I OH 4.0(max)= mA I IH 02.0(max)= 2002.04.0==mA mAN OHN=20(2) LSTTL 驱动基本TTL 门mA I OL 8(max)= mA I IL 6.1(max)= 56.18==mA mAN OLmA I OH 4.0(max)= mA I IH 04.0(max)= 1004.04.0==mA mAN OHN=5 2.4.5 解:E D BC AB E D BC AB L +++=⋅⋅⋅=__________________________2.6.3 解:B=0时,传输门开通,L=A ;B=1时,传输门关闭,A 相当于经过3个反相器到达输出L ,L=A A B L 0 0 0 0 1 1 1 0 1 1 1 0所以,B A B A B A L ⊕=+= 2.7.1 解:C ,__________BC C B =D ,__________DE D E =__________DE BC ⋅,______________________________________________________)(DE BC A DE BC A +=⋅__________GF AF ⋅,_______________________________________________________________________)()(G A EF GF AF E GF AF E +=+=⋅____________________________________________________________________)()()()(G A EF DE BC A G A EF DE BC A L +++=+⋅+= 2.7.2 解:B A B A B A B A AB A B B A ⊕=+=+⋅=⋅⋅)(__________________________B A L ⊕==A ⊙B 2.9.11 解:当没有车辆行驶时,道路的状态设为0,有车辆行驶时,道路的状态为1;通道允许行驶时的状态设为1,不允许行驶时的状态设为0。
《数字电子技术》康华光 习题&解答 第十章 模数与数模转换器
《数字电子技术》康华光 习题&解答第十章 模数与数模转换器10.1 D/A 转换器,其最小分辨电压V LSB =4mV ,最大满刻度输出电压V om =10V ,求该转换器输入二进制数字量的位数。
该转换器输入二进制数字量的位数为12。
10.2 在10位二进制数D/A 转换器中,已知其最大满刻度输出模拟电压V om =5V ,求最小分辨电压V LSB 和分辨率。
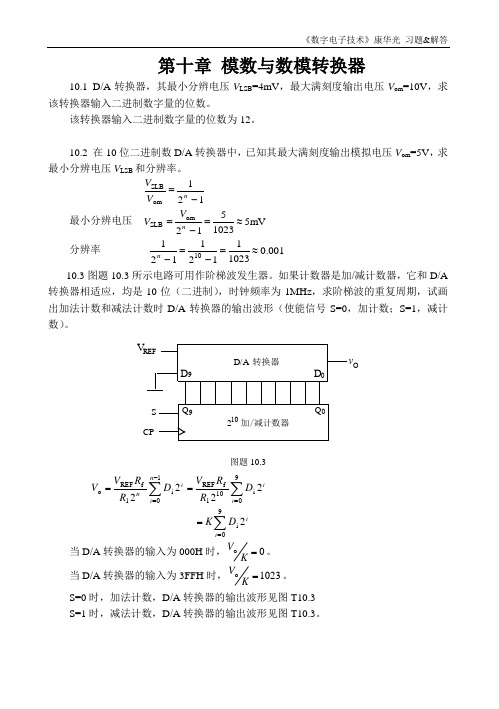
121omSLB -=nV V最小分辨电压 mV51023512om SLB ≈=-=nV V分辨率001.01023112112110≈=-=-n10.3图题10.3所示电路可用作阶梯波发生器。
如果计数器是加/减计数器,它和D/A 转换器相适应,均是10位(二进制),时钟频率为1MHz ,求阶梯波的重复周期,试画出加法计数和减法计数时D/A 转换器的输出波形(使能信号S=0,加计数;S=1,减计数)。
V R EF9D D 0D /A 转换器2加/减计数器10Q Q 9S C POv图题10.3ii in i nDR R V DR R V V 22229i101f REF 1i1f REF o ∑∑=-===i i D K 29i ∑==当D/A 转换器的输入为000H 时,o =K V 。
当D/A 转换器的输入为3FFH 时,1023o=KV 。
S=0时,加法计数,D/A 转换器的输出波形见图T10.3 S=1时,减法计数,D/A 转换器的输出波形见图T10.3。
S =1时,减法计数阶梯波的重复周期T =2n T PC =1024×10-6≈1mS10.4 在A/D 转换过程中,取样保持电路的作用是什么?量化有哪两种方法,他们各自产生的量化误差是多少?应该怎样理解编码的含义,试举例说明。
在A/D 转换过程中,取样保持电路的作用是:对输入的模拟信号在一系列选定的瞬间取样,并在随后的一段时间内保持取样值,以便A/D 转换器把这些取样值转换为输出的数字量。
电子技术基础(数字部分)_数电_(第五版)康华光主编[1]
![电子技术基础(数字部分)_数电_(第五版)康华光主编[1]](https://img.taocdn.com/s3/m/66203cec551810a6f5248631.png)
现系统功能。使硬件设计软件化。
1、设计: 在计算机上利用软件平台进行设计 原理图设计 设计方法 VerlogHDL语言设计 状态机设计
1.1.2、数字集成电路的分类及特点
1、数字集成电路的分类 根据电路的结构特点及其对输入信号的响应规则的不同, --数字电路可分为组合逻辑电路和时序逻辑电路。
nnbbbbn????????????????????????????????????????????22221n1n2211d对于二进制的小数部分可写成1n2n1n1201d22222??????????????????????????????????????????????nbbbbn将上式两边分别乘以2得1?b由此可见将十进制小数乘以2所得乘积的整数即为不难推知将十进制小数每次除去上次所得积中的整数再乘以2直到满足误差要求进行四舍五入为止就可完成由十进制小数转换成二进制小数
系数 一般表达式: 各位的权都是10的幂。
( N )D K i 10i
i
位权Βιβλιοθήκη 任意进制数的一般表达式为:
(N) r K i r i
i
1.2.2 二进制
1、二进制数的表示方法 二进制数只有0、1两个数码,进位规律是:“逢二进一” .
例如:1+1= 10 = 1×21
b. 小数的转换: 对于二进制的小数部分可写成
( N ) D b1 2 1 b 2 2 2 b (n 1) 2 (n 1) b n 2 n
将上式两边分别乘以2,得
2 ( N ) D b1 2 0 b 2 2 1 b(n 1) 2 (n 2) b n 2 (n 1)
模电“电子技术基础”康华光-ch9-1rcforel

新型半导体材料和工艺的发展 将为模拟电路带来新的突破,
提升性能和降低成本。
05
本章习题及解答
本章习题
1. 什么是RC电路?它在 电子技术中有哪些应用?
3. 描述RL电路的特点和计 算方法。
2. 如何计算RC电路的时 间常数?
4. 在RC电路中,如何通 过改变电阻或电容来影响 输出波形?
习题答案及解析
答案
RC电路是由电阻(R)和电容(C)组成的电路,通常用于滤波、积分、微分等电子技 术应用。
解析
该题考查了RC电路的基本概念和在电子技术中的应用,需要理解RC电路的组成和作用。
习题答案及解析
2. 答案及解析
1
2
答案:RC电路的时间常数(τ)可以通过公式计 算:τ = R × C。其中,R是电阻的阻值,C是电 容的容量。
3
解析:该题考查了RC电路时间常数的计算方法, 需要掌握时间常数的基本概念和计算公式。
习题答案及解析
答案
RL电路是由电阻(R)和电感(L)组成的电路,其特点是具有感抗,能够阻碍 电流的变化。计算方法包括感抗的计算公式Xl=2πfL。
解析
该题考查了RL电路的特点和计算方法,需要理解RL电路的组成和感抗的概念, 并掌握计算公式。
模电“电子技术基础”康 华光-ch9-1rcforel
• 引言 • 模电的基本概念 • 康华光-ch9-1rcforel章节概述 • 模电的应用与发展趋势 • 本章习题及解答
01
引言
课程背景
电子技术基础是电子、通信、计算机 等相关专业的必修课程,是学习其他 专业课程的基础。
随着信息技术的发展,电子技术基础 课程在各个领域的应用越来越广泛, 对于培养学生的实践能力和创新思维 具有重要意义。
电子技术基础(数字)康华光课后答案

(A)
(B)
(C)
(D)
解:对于图题 3.1.12(a)所示的 CMOS 电路,当 EN =0 时, TP2 和TN 2 均导通,
TP1 和 TN1 构成的反相器正常工作,L= A ,当 EN =1 时,TP2 和TN 2 均截止,无论
A 为高电平还是低电平,输出端均为高阻状态,其真值表如表题解 3.1.12 所示, 该电路是低电平使能三态非门,其表示符号如图题解 3.1.12(a)所示。
A
L
00Βιβλιοθήκη 1010
1
0
1
1
高阻
3.1.12(a)
A
L
0
0
0
0
1
1
1
0
高阻
1
1
高阻
3.1.12(b)
EN A
0
0
L 高阻
0
1
高阻
1
0
0
1
1
1
3.1.12(c
A
L
0
0
1
0
1
0
1
0
高阻
1
1
高阻
3.1.12(d)
3.2.2 为什么说 TTL 与非门的输入端在以下四种接法下,都属于逻辑 1:(1)输 入端悬空;(2)输入端接高于 2V 的电源;(3)输入端接同类与非门的输出高电 压 3.6V;(4)输入端接 10kΩ 的电阻到地。 解:(1)参见教材图 3.2.4 电路,当输入端悬空时,T1 管的集电结处于正偏,Vcc 作用于 T1 的集电结和 T2,T3 管的发射结,使 T2,T3 饱和,使 T2 管的集电极 电 位 Vc2=VcEs2+VBE3=0.2+0.7=0.9V , 而 T4 管 若 要 导 通 VB2=Vc2≥VBE4+VD=0.7+0.7=1.4V,故 T4
康华光《电子技术基础-数字部分》配套题库-课后习题(锁存器和触发器)

图 5-9
5 / 20
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.2.6 试用 1 片八 D 锁存器 74HC373 设计一个能锁存 2 位 BCD 码信号的锁存电路。
假定三态输出使能端 OE =0,锁存器原输出 Q7Q6Q5Q4=1001(9D),Q3Q2Q1Q0=0100
变。 (3)当 CP 由 1 跳变到 0 后,则再次重复(1)的过程。
5.3.2 触发器的逻辑电路如图 5-12 所示,确定其应属于何种电路结构的触发器。
7 / 20
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-12 解:该电路是由两个逻辑门控 SR 锁存器级联构成的主从 SR 触发器。 5.3.3 触发器的逻辑电路如图 5-13 所示,确定其应属于何种电路结构的触发器。
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 5 章 锁存器和触发器 5.2 锁存器
5.2.1 分析图 5-1 所示电路的功能,列出功能表。
图 5-1 解:由电路图可得: 因此锁存器的功能表,如表 5-1 所示。
表 5-1
5.2.2 用 CMOS 电路 74HCT02 或非门构成消除机械开关抖动影响的电路如图 5-2 所
示,试画出在开关 S 由位置 A 到 B 时 Q 和 Q 端的波形。如改用 TTL 电路 74LS02 实现,
R1、R2 取值的大致范围为多少?整个电路的功耗会发生什么变化?
1 / 20
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 5-2
解:开关接通 A 点时,Q=0, Q=1 。当开关触点拨离 A 点瞬间,由于 Q=1 的作用,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.1 一数字信号的波形如图1.1.1所示,试问该波形所代表的二进制数是什么?解:0101 10101.2.1 试按表1.2.1所列的数字集成电路的分类依据,指出下列器件属于何种集成度器件:(1) 微处理器;(2) IC 计算器;(3) IC 加法器;(4) 逻辑门;(5) 4兆位存储器IC 。
解:(1) 微处理器属于超大规模;(2) IC 计算器属于大规模;(3) IC 加法器属于中规模;(4) 逻辑门属于小规模;(5) 4兆位存储器IC 属于甚大规模。
1.3.1 将下列十进制数转换为二进制数、八进制数、十六进制数和8421BCD 码(要求转换误差不大于2-4):(1) 43 (2) 127 (3) 254.25 (4) 2.718 解:(1) 43D=101011B=53O=2BH ; 43的BCD 编码为0100 0011BCD 。
(2) 127D=1111111B=177O=7FH ; 127的BCD 编码为0001 0010 0111BCD 。
(3) 254.25D=11111110.01B=376.2O=FE.4H ; 0010 0101 0100.0010 0101BCD 。
(4) 2.718D=10.1011 0111B=2.56O=2.B7H ; 0010.0111 0001 1000BCD 。
1.3.3 将下列每一二进制数转换为十六进制码:(1) 101001B (2) 11.01101B解:(1) 101001B=29H (2) 11.01101B=3.68H1.3.4 将下列十进制转换为十六进制数:(1) 500D (2) 59D (3) 0.34D (4) 1002.45D解:(1) 500D=1F4H (2) 59D=3BH (3) 0.34D=0.570AH(4) 1002.45D=3EA.7333H1.3.5 将下列十六进制数转换为二进制数:(1) 23F.45H (2) A040.51H解:(1) 23F.45H=10 0011 1111.0100 0101B(2) A040.51H=1010 0000 0100 0000.0101 0001B1.3.6 将下列十六进制数转换为十进制数:(1) 103.2H (2) A45D.0BCH解:(1) 103.2H=259.125D (2) A45D.0BCH=41024.046D2.4.3 解:(1) LSTTL 驱动同类门mA I O L 8(max)= mA I IL 4.0(max)= 204.08==mA mA N OLmAI O H 4.0(max)= mA I IH 02.0(max)= 2002.04.0==mA mAN OHN=20 (2) LSTTL 驱动基本TTL 门mA I O L 8(max)= mA I IL 6.1(max)= 56.18==mA mAN OLmAI O H 4.0(max)= mA I IH 04.0(max)= 1004.04.0==mA mA N OHN=5 2.4.5 解:ED BC ABE D BC AB L +++=⋅⋅⋅=__________________________ 2.6.3 解:B=0时,传输门开通,L=A ;B=1时,传输门关闭,A 相当于经过3个反相器到达输出L ,L=AA B L0 0 00 1 11 0 11 1 0 所以,B A B A B A L ⊕=+=2.7.1 解:C ,__________BC C B =D ,__________DE D E =__________DE BC ⋅,______________________________________________________)(DE BC A DE BC A +=⋅__________GF AF ⋅,_______________________________________________________________________)()(G A EF GF AF E GF AF E +=+=⋅____________________________________________________________________)()()()(G A EF DE BC A G A EF DE BC A L +++=+⋅+= 2.7.2 解:B A B A B A B A AB A B B A ⊕=+=+⋅=⋅⋅)(__________________________B A L ⊕==A ⊙B 2.9.11 解:当没有车辆行驶时,道路的状态设为0,有车辆行驶时,道路的状态为1;通道允许行驶时的状态设为1,不允许行驶时的状态设为0。
设A 表示通道A 有无车辆的状态,B1、B2表示通道B1、B2有无车辆的情况,LA 表示通道A 的允许行驶2121B B A B B A A LA ⋅+=⋅⋅+= ()21______________21______B B A B B A LA LB +=⋅+==3.1.2 用逻辑代数证明下列不等式 (a) B A B A A +=+由交换律 ))((C A B A BC A ++=+,得B A B A A A B A A +=++=+))(( (b) AC AB C AB C B A ABC +=++ACAB B C A C B C A C B C B BC A C AB C B A ABC +=+=+=++=++)()()( (c) ()E CD A E D C CD A C B A A ++=++++()ECD A E CD CD A E D C CD A A E D C CD A C B A A ++=++=+++=++++_____)(3.1.3 用代数法化简下列等式 (a) )(A BC AB + AB AB ABC A BC AB =+=+)((b) ))((B A B A +B A B A B A =+))(((c) )(_______C B BC A +C AB C C B C A C B AB C B C B A C B BC A +=++++=+++=+))(()(_______(d) B C CB BC A ABC A ++++_____C A B C CB BC A ABC A +=++++_____(e) ____________________________B A B A B A AB +++0_____________________________________=+=+++A A B A B A B A AB (f) ____________________________________________________________________________)()()()(B A B A B A B A ⋅++++B A B A B A B B A B A B A B AB B A B A B A B A B A B A B A B A =+=+++=⋅⋅+⋅+=⋅++++)())(()()()()()()()()(___________________________________________________________________________________________________________(g) ))((C B A C B A ++++B AC B A C B A +=++++))(((h) C B A ABC C B A C B A ++++ C A C B C B A C B C B A A C B A ABC C B A C B A +=++=++=++++(i) _____________________________)(B A AB ++B A B A B A B A AB B A AB ⊕=++=+⋅=++))(()()(__________________________________(j) B A C A ABC B +++C A AC B C A ABC B B A C A ABC B ++=++=+++ (k) C B ABCD D BC ABD D ABC ++++DB C B AB D A C A B D C AD AC B D B C B ABD ABC D C B ABD ABC C D C B ABD ABC C B ABCD D BC ABD D ABC ++=+++=+++=+++=+++=+++=++++)()()()((l) __________________________________________________C AB C B BC A AC +++BC BC BC A C B A BC C B A BC A ABC C B A C B BC A AC C AB C B BC A AC =+=++=+++=++⋅+⋅+=+++)())(()()()(__________________________________________________ (m) __________________________________________________)(B A B A ABC B A +++)()()(____________________________________________________________________________________________________________________________________________________________________=+++=++=+++=+++A C B A A C B A BA AB BC B A B A B A ABC B A3.1.4 将下列各式转换成与 – 或形式 (a) __________________D C B A ⊕⊕⊕(1)当0________=⊕B A ,1__________=⊕D C 时,真值为1。
于是AB=01,CD=00或CD=11时,真值为1;AB=10,CD=00或CD=11时,真值为1。
则有四个最小项不为0,即D C B A 、BCD A 、D C B A 、CD B A(2)当1________=⊕B A ,0__________=⊕D C 时,真值为1。
AB=00,CD=10或CD=01时,真值为1;AB=11,CD=10或CD=01时,真值为1。
则有四个最小项不为0,即D C B A 、D C B A 、D ABC 、D C AB∑=⊕⊕⊕)14,13,11,8,7,4,2,1(__________________m D C B A(b) __________________________________________________________________D A D C D C B A +++++++D BC AC DCD BD BC AD AC D B A D C D A D C D C B A D A D C D C B A ++=+++++=+++=+++++=+++++++))(())(())((__________________________________________________________________(c) ______________________________________________________________________AB BC BD AC ⋅⋅⋅CA D C D AB CB BC A B AD C D A C B B A B A C B D B C A ABBC BD AC AB BC BD AC +++=+++++++=+++++=⋅+⋅=⋅⋅⋅))(())((__________________________________________________________________________________________3.1.7 利用与非门实现下列函数 (a) L=AB+AC_______________________AC AB L ⋅=(b) _____________)(C A D L +=_____________________________)(C A D C A D L =+=(c) ____________________))((D C B A L ++=__________________________________________))((D C B A D C B A L =++= 3.2.2 用卡诺图法化简下列各式(a) C AB C B BC A AC +++______________________C C AB C C AB C AC CAB C B BC AC C AB C B BC A AC =+=++=+++=+++____________________________________________________(b) C B A D A B A D C AB CD B A ++++C AD A B A C D D A B A D A D C A B A D A D C B B A D A D C AB B A C B A D A B A D C AB CD B A ++=++=++=++=++=++++)()((c) __________________)()()(B A D C A BD C D B B A ++++BCD AB D C B C B A DAB BCD ABD D C B C B A ABD C A BD D C B C B A B A D C A BD C D B B A +++=++++=++++=++++)()()()(__________________ (d) __________)()()(C B A D B C A D C B D CD B A +++++ ∑=++++++++=++++=+++++)14,12,11,9,6,5,4,1()()()(5414614129111__________m m m m m m m m m m CB A D BCD AB D C B CD B A C B A D B C A D C B D CD B A D B A D C A D B ++ (e) ∑=)15,14,13,12,10,9,8,7,6,5,4,3(),,,(m D C B A LCD B A D AC D C A D B C B AB +++++ (f) ∑=)14,913,8,7,6,5,2,1,0(),,,(m D C B A LD BC D C A BC A D C C B ++++ (g) ∑∑+=)15,11,7,5,3,2()13,9,6,4,1,0(),,,(d m D C B A LD A +(h) ∑∑+=)11,10,9,3,2,1()15,14,13,0(),,,(d m D C B A LAC AD B A ++ 3.3.4 试分析图题3.3.4所示逻辑电路的功能。
