多因素试验结果的统计分析
多因素试验的名词解释
多因素试验的名词解释
多因素试验是指在研究对象的多个因素中，通过对这些因素进行同时处理、组合配对，从而得到各个因素之间相互影响的结果。
该试验方法可以帮助研究者深入理解各个因素对研究对象的影响程度，从而为进一步改进或优化研究对象的相关问题提供科学依据。
多因素试验的最大特点在于能够同时考察多个因素对结果的影响，而不需要单独研究每个因素的影响。
通过将多个因素进行组合配对，研究者可以得到更为全面和准确的数据，从而更好地解释因素之间的关系。
在进行多因素试验时，研究者需要明确各个因素的选择范围和水平，即确定每个因素的不同取值。
通过多次实验，每次实验选取不同的取值组合，研究者可以获取不同条件下的实验结果，进而分析和评估各个因素对结果的影响。
这种方法可以帮助研究者更加准确地把握各个因素的作用，找出主导因素和次要因素，并确定最佳因素组合。
多因素试验的结果分析可以采用统计学方法，如方差分析等。
通过统计学的手段，可以对不同因素水平组合下的实验结果进行比较，进而判断各个因素对结果的显著性影响和相互作用关系。
这种分析方法可以在一定程度上帮助研究者排除干扰因素，减少误差，提高实验结果的可靠性。
总而言之，多因素试验是一种能够同时考察多个因素影响的实验方法。
通过对各个因素进行组合处理，研究者可以全面了解各因素对结果的影响，找出主导因素并确定最佳因素组合。
该方法可以提供科学依据，帮助研究者解决实际问题，并在实践中发挥重要作用。
多因素方差分析结果解读
多因素方差分析结果解读多因素方差分析（MultivariateAnalysisofVariance，简称MANOVA）是一种用于检验多个自变量对一个因变量的影响的统计分析方法，它主要应用于研究多个自变量的整体影响，以及多个自变量之间的交互影响。
在多因素方差分析中，研究者需要对自变量、因变量、因素、水平、抽样设计和拟合统计模型等参数进行合理安排并给出具体分析方法、统计检验方法以及分析结果解读方法，以便得出准确的分析结果。
本文主要就如何正确解读多因素方差分析结果做一个讨论。
首先要明确的是，多因素方差分析结果从两个角度进行解读：整体的影响和交互的影响。
在解读多因素方差分析结果的整体影响时，关键是检验多个自变量对因变量的影响，这通常是通过检验拟合模型的F统计量来实现的，如果F统计量达到显著性水平（一般认为是α=0.05），则可以得出多个自变量对因变量有统计学意义的整体影响的结论，但不能准确判断具体哪个自变量对因变量最有影响力，需要进一步解读它们之间的交互影响。
多因素方差分析的另一个重点是检验多个自变量之间的交互影响，它是检验多个自变量对因变量的影响的补充，可以更精确地判断出多个自变量之间的某种特定关系。
这里有几种常用的检验交互影响的方法：F检验、Wilks’检验、Hotelling-Lawley Trace检验以及Bartlett-Box F检验、Roy’s大F检验等，其中F检验用于检验各个因素与交互因素之间的关系；Wilks’检验和Hotelling-Lawley Trace检验用于检验因素之间以及因素与交互因素之间的关系；Bartlett-Box F检验和Roy’s大F检验则用于检验因素、交互因素与因变量之间的关系。
总的来说，在解读多因素方差分析结果时，要同时检验多个自变量对因变量的影响和多个自变量之间的交互影响，不仅要给出准确的分析方法和统计检验方法，而且要根据检验结果准确解读分析结果，以便正确地概括出多个自变量对因变量的整体影响及多个自变量之间的具体关系，以达到准确仿真分析实际情况的目的。
14 现况调查的统计分析策略——多因素线性回归分析(2)残差分析
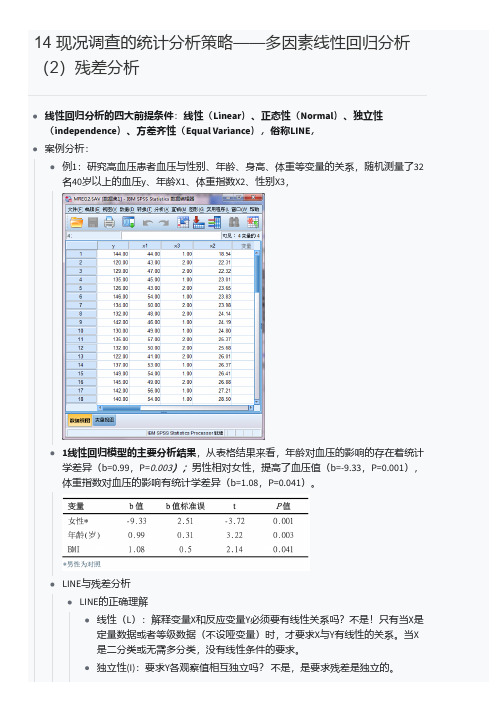
14 现况调查的统计分析策略——多因素线性回归分析（2）残差分析线性回归分析的四大前提条件：线性（Linear）、正态性（Normal）、独立性（independence）、方差齐性（Equal Variance），俗称LINE，案例分析：例1：研究高血压患者血压与性别、年龄、身高、体重等变量的关系，随机测量了32名40岁以上的血压y、年龄X1、体重指数X2、性别X3，1线性回归模型的主要分析结果，从表格结果来看，年龄对血压的影响的存在着统计学差异（b=0.99，P=0.003）；男性相对女性，提高了血压值（b=-9.33，P=0.001），体重指数对血压的影响有统计学差异（b=1.08，P=0.041）。
LINE与残差分析LINE的正确理解线性（L）：解释变量X和反应变量Y必须要有线性关系吗？不是！只有当X是定量数据或者等级数据（不设哑变量）时，才要求X与Y有线性的关系。
当X是二分类或无需多分类，没有线性条件的要求。
独立性(I)：要求Y各观察值相互独立吗？不是，是要求残差是独立的。
正态性(N)：要求Y各观察值正态分布吗？不是，是要求残差正态分布。
方差齐性（E）：要求不同的解释变量X时，反应变量Y方差相等吗？没错，但是对于多因素回归分析，更加合理的理解是在不同Y预测值情况下，残差的方差变化不大。
残差线性回归按变量数量的多少可以分为：简单线性回归和多重线性回归。
简单线性回归，也就是有一个自变量，数学上表达为一元一次函数，其模型可以表示如下：上述公式是基于样本得到的结果，b0和b1均为统计量，若该公式拓展到总体人群，则为公式中参数解释如下：其中，关键的指标即为b1和β1，他们称之为回归系数，反映的是x对y的影响力，是当x每改变一个观测单位时所引起y的改变量。
值得注意的是，这里x是真实的变量值x，而y带了一顶帽子，并非是y的真实值，而是成为y的预测值或者估计值。
通过x产生的预测值ŷ，是接近于y 但不等于y。
医学统计学 多元线性回归 多因素统计分析方法
病型 男 女
B药物治疗高血压疗效的男女比较
治疗例数
有效例数
有效率/%
50
36
72.0
50
44
88.0
X2=4.000, P=0.046
两种药物治疗高血压的疗效比较
药物 A药 B药
治疗例数 100（轻70，重30） 100（轻35，重65）
有效例数 95 80
有效率/% 95.0 86.0
⑴拆分两两比较（轻重分别比较）
b2
-.088 -.088
The independent variable is x1.
回归方程为： yˆ 18.662 1.633x
b3 .000
直线回归分析步骤小结
1、分析是否符合LINE条件： ⑴绘制散点图；⑵学生化残差图；⑶P-P图。 2、求回归方程：全模型（所有的回归方程都求） 3、回归效果判断：（哪种回归方程最好？确定 系数最大、最熟悉、最简单的模型） 4、结论：有无回归关系，列出回归方程。
1、直线性：x和y必需呈直线趋势(Linear)，且Y必 须是随机变量，X可以是计量、计数、等级资料。
2、独立性：各观测点相互独立，即任意两个观测 点的残差的协方差为0。(Independent) 3、正态性：残差服从正态分布。（Normality） 4、方差齐性：残差的大小不随变量取值水平的改 变而改变。(Equal variance, or homogeneity)
要解决上述问题，必须采用多因素分析的方法。
医学统计学的发展
空间：单因素 多因素 时间：随机过程（时间序列）
常用的多因素分析方法：多元方差分析、 多重线性回归、协方差分析、判别分析、 聚类分析、主成分分析、因子分析、典型 相关分析、logistic回归分析、Cox回归分 析等。
流行病学常用多因素回归统计分析
流行病学常用多因素回归统计分析流行病学中常常使用多因素回归模型来分析和解释疾病的发病风险及其与不同危险因素之间的关系。
多因素回归分析是一种统计方法，可以探究多个危险因素对疾病的影响，同时考虑其他潜在影响因素的调整。
多因素回归分析可以用来识别和评估与疾病相关的危险因素，同时控制其他潜在危险因素的影响。
它可以提供关于各个危险因素对疾病贡献的估计值，并确定其统计显著性。
在进行多因素回归分析之前，需要进行数据收集和整理。
一般来说，多因素回归分析需要考虑以下几个步骤：1.变量选择：根据研究的目的和疾病的特点，选择与疾病相关的变量。
这些变量可以包括患者的基本特征（如年龄、性别）、生活方式（如饮食、运动）和环境因素（如空气污染、水质）等。
2.数据收集和整理：收集相关的数据，并进行数据清洗和整理。
确保数据的准确性和完整性。
3.建立回归模型：根据研究的目的和变量的特征，选择合适的回归模型。
常用的回归模型包括线性回归模型、逻辑回归模型等。
4.模型拟合：将收集到的数据应用到回归模型中，进行参数估计和模型拟合。
拟合后可以得到危险因素的估计系数、标准误差、置信区间和P值等。
5.结果解释：根据模型拟合的结果，评估每个危险因素对疾病的影响，并进行解释。
可以根据估计系数和其置信区间来判断危险因素的显著性和贡献。
6.效应调整：对于其他可能的潜在影响因素，可以进行调整处理，检验危险因素对疾病的独立贡献。
调整常用的方法包括多元回归、对匹配等。
7.结果报告：根据分析结果，撰写分析报告，并对结果进行解释和讨论。
多因素回归分析在流行病学中的应用非常广泛。
它可以帮助科研人员确定疾病的风险因素，为预防和控制疾病提供科学依据。
通过多因素回归分析，可以了解各个危险因素之间的相互作用关系，为制定有效的公共卫生政策和预防措施提供指导。
总之，多因素回归分析是流行病学中常用的统计分析方法，可以评估和解释疾病的发病风险及其与多个危险因素之间的关系。
它在流行病学研究和公共卫生实践中具有重要的应用价值。
多因素方差分析23460
3 0.0 35 a
3 .0 0 0
3 0.0 35 a
3 .0 0 0
3 0.0 35 a
3 .0 0 0
3 0.0 35 a
3 .0 0 0
.54 1 a
3 .0 0 0
.54 1 a
3 .0 0 0
.54 1 a
3 .0 0 0
.54 1 a
3 .0 0 0
Error df 3 6.0 00 3 6.0 00 3 6.0 00 3 6.0 00 3 6.0 00 3 6.0 00 3 6.0 00 3 6.0 00
a
11
SPSS统计软件
交叉设计方差分析
例2. 以睡眠时间增加量(小时)为效应，观察 A、B两种药物对改善失眠者的睡眠效果。已 知A、B之间没有交互作用，并且收治的失眠 患者不多，共12名。应采用何种设计较合理？ (数据睡眠.sav)
a
12
SPSS统计软件design） 基本模式
SPSS统计软件
复习
1、某医生为了研究一种四类降糖新药的疗效，以统一的纳 入和排除标准选择了60名2型糖尿病患者，按完全随机设 计方案将患者分为三组进行双盲临床试验。其中，降糖新 药高剂量组21人、低剂量组19人、对照组20人。对照组服 用公认的降糖药物，治疗4周后测得其餐后两小时血糖的 下降值，问治疗4周后，餐后2小时血糖下降值的三组总体
a.
a Design: Intercept+分 组
Within Subjects Design: weight
Sig. .329 .317 .368 .547
31
SPSS统计软件
重复测量资料的方差分析
下表为受试者内因素、受试者内因素与自变量的一级交互作用的多元 方差分析统计学检验结果。
统计分析
2
140
1
7.5
1
5
图1-6Post Hoc MultipleComparisons for Observed Means对话框
8）选择保存运算值
图1-7Save对话框
9）在主对话框中单击“Options”按钮，打开“Options”输出设置对话框，见图1-8
图1-8“Options”输出设置对话框
10）设置完成后，在多因素方差分析窗口框中点击“OK”按钮，SPSS就会根据设置进行运算，并将结算结果输出到SPSS结果输出窗口中。
不同湿度（b）对粘虫历期的偏差均方是322.000，F值为18.575，显著性水平是0.000，即p<0.05存在显著性差异；
不同温度和不同湿度（a*b）共同对粘虫历期的偏差均方是19.809，F值为1.143，显著性水平是0.358，即p>0.05存在不显著性差异。
3）多重比较
由于方差不齐次性，应选择方差不具有齐次性时的“Tamhane's T2”t检验进行配对比较。表1-4多重比较表就是“温度”各水平“Tamhane's T2”方法比较的结果。
温度25℃与27℃、29℃和31℃之间都有显著性差异；温度27℃与25℃、29℃和31℃之间都有显著性差异；温度29℃与26℃和27℃之间都有显著性差异；与31℃无显著性差异；温度31℃与25℃和27℃之间都有显著性差异；与29℃无显著性差异。不同湿度水平之间无显著性差异存在。
多元回归分析
某地区病虫测报站用相关系数法选取了以下4个预报因子；x1为最多连续10天诱蛾量(头)；x2为4月上、中旬百束小谷草把累计落卵量(块)；x3为4月中旬降水量(毫米)，x4为4月中旬雨日(天)；预报一代粘虫幼虫发生量y（头/m2）。分级别数值列成表2-1。
多因素方差分析公式了解多因素方差分析的计算公式
多因素方差分析公式了解多因素方差分析的计算公式多因素方差分析公式——了解多因素方差分析的计算公式多因素方差分析是一种统计方法，用于分析多个因素对观察结果的影响。
它通过比较不同因素水平下的观察值差异来判断这些因素对实验结果的影响程度。
在多因素方差分析中，我们需要了解与计算一些重要的公式。
1. 多因素方差分析的总平方和（SS_total）公式：SS_total = SS_between + SS_within其中，SS_total是总平方和，表示所有观测值与总均值之间的偏离程度；SS_between是组间平方和，表示不同因素水平下的观测值与总均值之间的偏离程度；SS_within是组内平方和，表示同一因素水平下的观测值与该水平下的均值之间的偏离程度。
2. 多因素方差分析的组间平方和（SS_between）公式：SS_between = ∑(ni * (μi - μ)²)其中，ni是第i组的观测值个数，μi是第i组观测值的均值，μ为所有观测值的总均值。
3. 多因素方差分析的组内平方和（SS_within）公式：SS_within = ∑∑((Xij - μi)²)其中，Xij表示第i组的第j个观测值，μi为第i组观测值的均值。
4. 多因素方差分析的组间平均平方（MS_between）公式：MS_between = SS_between / (k - 1)其中，k为不同因素水平的个数。
5. 多因素方差分析的组内平均平方（MS_within）公式：MS_within = SS_within / (N - k)其中，N为总观测值的个数。
6. 多因素方差分析的F统计量公式：F = MS_between / MS_withinF统计量用于判断不同因素水平的均值之间的差异是否显著。
若F 值大于某个临界值，则认为不同因素水平的均值存在显著差异。
通过以上公式，我们可以计算出组间平方和、组内平方和、组间平均平方、组内平均平方和F统计量，从而进行多因素方差分析。
多因素分析
Sig. .000 .000 .000 .000 .000
注意：当因子A与B间的交互作用有统计学意 义时，对A（或B）的单独作用的解释须小心。 本例，用B药时，用A药病人比不同时用A药的 病人的红细胞数均数大，不用B药时，用A药 病人比不同时用A药的病人的红细胞数均数也 大，故可说明A药有效。但有时可能出现这种 情况，用B药时，用A药病人比不同时用A药的 病人的红细胞数均数大，不用B药时，用A药 病人比不同时用A药的病人的红细胞数均数小， 此时就不能简单地说A药有利于病人红细胞数 增加，需分别就用B药和不用B药两种情况说 明A药的作用。对B作用的作用的解释也是如 此。
三因子方差分析
例题 某研究者以大白鼠作试验， 观察指标是肝重与体重之比（5%）， 主要想了解正氟醚对观察指标的作用， 同时要考察用生理盐水和用戊巴比妥 作为诱导药对正氟醚毒性作用有无影 响，对不同性别大白鼠诱导的作用有 何不同，以及对不同性别大白鼠正氟 醚的作用是否相同。
A因子
不用 不用 不用 不用 用 用 用 用
总体均数
111 112 Байду номын сангаас21 122 211 212 221 222
Tes ts o f Bet ween -Subj ects Effe cts Dependent Variable: Y Type III Sum Source of Squares df Mean Square Corrected Model 4.218 a 7 .603 Intercept 769.081 1 769.081 A 2.017E-03 1 2.017E-03 B 7.707E-02 1 7.707E-02 C .799 1 .799 A * B 1.904 1 1.904 B * C 5.227E-02 1 5.227E-02 A * C 1.335 1 1.335 A * B * C 4.860E-02 1 4.860E-02 Error 2.685 16 .168 Total 775.984 24 Corrected Total 6.903 23 a. R Squared = .611 (Adjusted R Squared = .441)
多因素方差分析结果解读
多因素方差分析结果解读多因素方差分析是一种统计学方法，用于衡量研究变量之间的统计关系，以了解不同变量之间的交互作用。
多因素方差分析(ANOVA)可以使科学家、工程师和其他研究者探索并发现不同因素（变量）之间的关系，以便对有效的解释和可视化的信息进行解读。
本文将讨论多因素方差分析结果解读的基本概念，以及基于多因素方差分析数据分析结果正确解读的重要性。
首先，需要了解多因素方差分析的基本知识和步骤。
“多因素方差分析”是一种在统计学中用来确定多个变量之间关系的统计方法。
它可以在每个变量之间检测不同水平的均方差，以了解变量之间的交互作用。
这种分析通过定义变量并应用严格的统计标准来识别和分析变量之间的关系。
多因素方差分析的结果解释是有价值的，因为它们可以帮助研究者了解不同变量之间的关系，从而推断其中的交互作用。
多因素方差分析结果的正确解读可以帮助科学家和其他研究者更好地了解和探究变量之间的关系，以便建立准确有效的模型。
进行多因素方差分析时，最重要的是执行正确的统计分析，以便对数据进行准确描述。
多因素方差分析结果解释也是一种重要的工具，可以帮助研究者确定变量之间的关系，从而建立有效的模型。
正确的解释需要考虑变量之间的相关性，以及它如何影响整个分析的结果。
多因素方差分析的结果可以很好地说明变量之间的关系。
研究者可以根据结果检查各个变量之间的相关性，以及每个变量如何影响研究结果。
多因素方差分析结果解释可以帮助研究者更好地识别和分析变量之间的关系，从而建立有效的模型。
多因素方差分析结果解释的重要性在于它可以帮助研究者更加准确地了解研究问题，并对不同变量之间的相互作用做出准确的推断。
多因素方差分析的结果可以帮助研究者了解具体的研究内容，从而更好地回答研究问题。
总之，多因素方差分析结果解释在研究变量之间关系的统计学中十分重要，可以帮助研究者更加准确地了解研究变量之间的关系，并对不同变量之间的相互作用做出准确的推断。
正确理解和使用多因素方差分析结果解释，可以帮助研究者更好地利用和分析其研究结果，从而产生更有效的解决方案。
临床试验常用统计分析方法多因素
临床试验常用统计分析方法多因素临床试验是评估医疗干预效果和安全性的重要手段。
在设计和执行临床试验时，统计分析方法是必不可少的工具，用于解释和推断干预效果是否显著。
而多因素分析是其中一种常用的统计分析方法，它可以同时考虑多个潜在的干预因素，从而更全面地评估干预效果。
多因素分析的基本原理是，对于一个特定的效果变量（如疾病预后的恢复情况），它可能受到多个因素的影响（如性别、年龄、治疗方法等）。
通过多因素分析，可以控制其他可能的混杂因素，以便更准确地评估某个特定因素对于效果变量的影响。
在进行多因素分析时，常见的方法包括多元线性回归分析、Cox比例风险回归分析和Logistic回归分析等。
多元线性回归分析是一种用于评估一个或多个连续因变量与一个或多个连续或分类自变量之间关系的方法。
在临床试验中，多元线性回归分析可以用来评估干预因素对于连续效果变量（如血压水平）的影响。
通过控制其他可能的干扰因素，可以较为准确地估计干预因素对于效果变量的影响大小。
Cox比例风险回归分析是一种用于评估一个或多个预测因素对于生存分析结果的影响的方法。
在临床试验中，Cox比例风险回归分析常用于评估干预因素对于患者生存时间的影响。
通过控制其他可能的干扰因素，可以更准确地估计干预因素对于生存时间的影响。
Logistic回归分析是一种用于评估一个或多个预测因素对于二分类结果（如生存与死亡）的影响的方法。
在临床试验中，Logistic回归分析可以用于评估干预因素对于二分类效果变量（如治疗反应）的影响。
通过控制其他可能的干扰因素，可以较为准确地估计干预因素对于二分类效果变量的影响。
除了上述常见的多因素分析方法外，还有一些其他的方法可以用于多因素分析，如生存树分析、随机森林等。
这些方法在临床试验中的应用可以根据试验设计、数据类型以及研究问题的特点来选择。
多因素分析在临床试验中的应用具有重要意义。
通过控制其他可能的干扰因素，多因素分析可以准确评估干预因素对于效果变量的影响，从而为临床决策提供更可靠的依据。
临床试验中常见的统计分析方法与解读技巧
临床试验中常见的统计分析方法与解读技巧在医学领域，临床试验是评估新药、新疗法或新治疗方案的有效性和安全性的重要手段。
然而，仅仅通过试验结果的直观观察并不能得出准确的结论，这时就需要借助统计学的方法来进行数据分析和解读。
本文将介绍一些临床试验中常见的统计分析方法和解读技巧，以便读者能更加全面地理解试验结果。
一、描述性统计分析描述性统计分析是临床试验数据分析的第一步，它主要用于总结和描述数据的特征，包括测量指标的中心趋势和离散程度。
常用的描述性统计分析方法有：平均值、中位数、标准差、频率分布等。
平均值是描述数据集中趋势的指标，它表示数据的集中程度。
但是，在临床试验中，由于样本容量较小，数据容易受到极端值的影响，因此还需考虑使用中位数来描述数据的中心趋势。
标准差是描述数据离散程度的指标，它反映了数据集中的个体与平均值之间的差异。
较大的标准差说明数据的离散程度较大，反之亦然。
频率分布是将数据分成不同区间，并记录每个区间内数据的个数或百分比，用于描述数据的分布情况。
通过频率分布，我们可以了解到数据在不同区间内的分布状况，以及数据呈现的特点。
二、假设检验与置信区间假设检验是临床试验中常用的统计分析方法之一，它用于判断试验结果是否具有统计学意义。
假设检验一般包括建立原假设和备择假设、选择统计量、设定显著性水平和计算p值等步骤。
在假设检验中，我们首先建立原假设（H0）和备择假设（H1）。
原假设通常是认为两组样本的差异没有统计学意义，备择假设则相反。
然后选择适当的统计量（如t值、χ²值等），计算p值。
p值是在原假设成立的条件下，观察到样本结果或更极端结果发生的概率。
最后，根据显著性水平（一般为0.05），判断p值是否小于显著性水平，若小于则拒绝原假设，否则则接受原假设。
置信区间是另一种常用的分析方法，它用来估计样本的真实参数范围。
在临床试验中，我们往往关注新治疗方案的效果是否超过了一定的临界值。
通过构建置信区间，我们可以得到一个范围，表示真实参数值可能落在该范围内的概率。
SPSS统计分析教程多因素方差分析
多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程，检验不同水平组合之间因变量均数，由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用，也可以分析因素之间的交互作用，以及分析协方差，以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来，且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量，协变量与因变量不彼此独立。
因素变量是分类变量，可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
[例子]研究不同温度与不同湿度对粘虫发育历期的影响，得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表数据保存在“”文件中，变量格式如图5-1。
1）准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量，因素变量温度“A”，湿度为“B”变量，重复变量“重复”。
然后输入对应的数值，如图5-6所示。
或者打开已存在的数据文件“”。
图5-6 数据输入格式2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“General Linear Model”项，在右拉式菜单中点击“Univariate”项，系统打开单因变量多因素方差分析设置窗口如图5-7。
图5-7 多因素方差分析窗口3）设置分析变量设置因变量:在左边变量列表中选“历期”，用向右拉按钮选入到“Dependent Variable：”框中。
设置因素变量:在左边变量列表中选“a”和“b”变量，用向右拉按钮移到“Fixed Factor(s):”框中。
可以选择多个因素变量。
由于内存容量的限制，选择的因素水平组合数(单元数)应该尽量少。
如何进行实验结果的统计分析
如何进行实验结果的统计分析实验结果的统计分析对于科学研究具有重要意义，它可以帮助我们从大量数据中获取有关实验现象的有效信息。
本文将介绍如何进行实验结果的统计分析，以及一些常用的统计方法和工具。
一、实验结果的收集和整理在进行实验之前，我们首先需要明确实验的目的和研究的问题，然后设计实验过程和实验方案。
在实验过程中，我们要严格按照实验方案进行操作，并记录每一步实验的细节。
实验完成后，我们需要将实验得到的数据进行整理，包括数据的分类、整合和清洗等步骤。
二、数据的描述和可视化在进行实验结果的统计分析之前，我们需要对数据进行描述和可视化，以便更好地理解和分析数据。
常用的描述性统计方法包括计算平均值、标准差、中位数等，这些指标可以帮助我们了解数据的分布和集中趋势。
此外，我们还可以使用直方图、散点图、饼图等图表形式来可视化数据，直观地呈现实验结果。
三、假设检验假设检验是判断实验结果是否具有统计学意义的重要方法。
在进行假设检验时，我们需要明确一个原假设和一个备选假设，并进行统计推断。
常用的假设检验方法包括 t 检验、方差分析、卡方检验等，这些方法可以帮助我们确定实验结果中的差异是否是由随机因素引起的。
四、相关分析相关分析可以用来研究实验结果之间的关系。
由于实验结果往往包含多个变量，我们可以通过计算相关系数来判断这些变量之间是否存在相关性。
常用的相关分析方法包括皮尔逊相关系数、斯皮尔曼等级相关系数等，这些方法可以帮助我们了解实验结果之间的相关性及其强弱程度。
五、回归分析回归分析是用来研究自变量和因变量之间关系的统计方法。
在进行回归分析时，我们需要首先选择合适的回归模型，然后利用最小二乘法等方法对模型参数进行估计，最后对回归模型进行检验和解释。
回归分析可以帮助我们预测和探究实验结果受哪些因素的影响，从而提供科学依据。
六、统计软件和工具在进行实验结果的统计分析时，我们可以借助各种统计软件和工具来提高效率和准确性。
常用的统计软件包括SPSS、R、Python等，它们提供了丰富的统计分析函数和图表绘制功能，能够辅助我们进行数据处理和结果分析。
临床试验结果的统计分析
临床试验结果的统计分析随着医学研究的发展，临床试验结果的统计分析成为了评估药物和治疗方法疗效的重要手段之一。
统计分析能够帮助我们从大量的数据中提取有效信息，为临床实践和决策提供科学依据。
本文将介绍临床试验结果统计分析的一般步骤和常用的分析方法。
一、临床试验结果统计分析的步骤1. 数据清理和整理在进行统计分析之前，首先需要对收集到的数据进行清理和整理。
这包括检查数据的完整性、一致性和准确性，处理缺失和异常值，规范数据格式等。
2. 描述性统计分析描述性统计分析是对试验数据进行整体概括和描述的方法。
通过计算平均数、标准差、中位数、分位数等统计指标，可以对数据的分布、集中趋势和离散程度进行描述，帮助我们了解试验的基本情况。
3. 假设检验假设检验是用来判断实验结果是否具有统计学意义的方法。
在临床试验中，我们常常会对治疗组和对照组之间的差异进行比较。
通过设立零假设和备择假设，利用适当的统计检验方法，比如t检验、方差分析、卡方检验等，可以确定两组数据之间是否存在显著差异。
4. 效应量计算效应量是衡量治疗效果的一个指标，它可以描述治疗组和对照组之间的差异大小。
常用的效应量指标有标准化均值差异（Cohen's d）、相关系数等。
计算效应量有助于我们评估治疗的临床意义和实践应用价值。
5. 置信区间估计置信区间是对参数估计的一个范围性描述。
通过计算置信区间，我们可以得到参数估计的上下限，从而判断试验结果的稳定性和可靠性。
一般情况下，置信区间取95%或99%。
二、常用的临床试验结果统计分析方法1. 差异性分析差异性分析是比较治疗组和对照组之间差异的方法。
根据数据类型和分布情况的不同，可以选择t检验、方差分析、非参数检验等方法进行差异性分析。
2. 关联性分析关联性分析用于评估变量之间的相关关系。
常用的方法包括皮尔逊相关系数、斯皮尔曼相关系数等。
关联性分析可以帮助我们了解变量之间的关联程度，为进一步的研究和分析提供依据。
统计分析方法(t检验、单因素方差分析和多因素方差分析)
两组独立样本的比较：独立样本t检验 在变量视图中填入变量：这里的X为需分析数据，G代表分组
在数据视图中录入数据： G下方的数据1、2为分组 X下方的数据为相应的分组 对应的需要分析的数据
在工具栏里选择分析——描述统计——探索
将X选入因变量列表，G选入因子列表， 然后单击绘制
勾选带检验的正态图，其余的 可按照默认值 单击继续
在输出页面中找到上述表格，如果sig即P值，大于0.05，说明该 组数据属于正态性数据，可以继续进行独立样本的t检验；如果 有任何一组P值小于0.05，则需改用非参数检验
数据符合正态时，在工具栏中选 择分析，在下拉菜单中选择比较 均值，再选择独立样本T检验
将X选入检验变量，G选入分组变 量，然后点击定义组，组1后填 入1，组2后填入2，继续——确定
在输出页面中找到上述表格，如果sig即P值，大于0.05，说明两组数据方差齐，则 看第一行数据，如果小于0.05，说明两组数据方差不齐，则看第二行数据；sig的 值即为最终所需P值。
单因素方差分析
数据录入后，进行正态性检验，方法 见4、5、6页PPT。检验结果需要全部 正态才能进行单因素方差分析，否则 需要用非参数检验，但非参数检验没 有两两比较。
分析——比较均值——单因素ANOVA 将X选入因变量列表，G选入因子列表 中，单击两两比较，选择LSD，继续， 单击选项，选择方差同质性检验，继 续——确定
方差齐性检验结果显著性大于0.05， 说明方差齐，可以进行单因素方差分 析，如果显著性小于0.05，则说明方 差不齐，则不能进行单因素方差分析
该表为总体的显著性
该表为两两比较的结果 1 2 为1组与2组比较
田间试验与统计分析 第八章 多因素试验设计与统计分析
两因素随机区组试验 总变异=区组间+处理间（A因素+B因素+ AXB互作）+误差
两因素裂区试验 总变异=区组间+处理间（ A因素+B因素+ AXB互作）+主区 误差+副区误差
激素2
63
激素3
64
激素4
62
激素5
61
组（B）
II
III
IV
62
61
60
65
68
65
61
61
60
67
63
61
65
62
64
62
62
65
例2:两因素完全随机试验 -组合内有重复观察值
肥料 重复
土壤种类
施用A1、A2、A3三 种类
种肥料于B1、B2、
B1
B2
B3
B3 三 种 土 壤 ， 以 A1 1
区组I 8 7 6 9 7 8 7 8 10 70 7.78
区组II 8 7 5 9 9 7 7 7 9 68 7.56
区组III T
8
24
6
20
6
17
8
26
6
22
6
21
6
20
8
23
9
28
63
201
7
平均 8 6.7 5.7 8.7 7.3 7 6.7 7.7 9.3
7.4
按品种和密度作两向分组整理成下表2： 表2 品种A和密度B的两向表
三因素三水平正交试验统计分析数据
环境因子对某农药在土壤中降解的影响
在土壤温度、土壤含水量、土壤 pH 三个因素三个水平下进行正交试验（无交互作用），则某农药在土壤中的降解试验分别有 9 个处理，即：
9 个处理为：
在加入土壤后不同时间（ 0、 3、 7、14、21、30、60、120、180 d）检测某农药的含量，换算成残留百分数（ %）如下：
请问该如何分析这些数据？用 SAS和 SPSS均可，可以的话将过程附在 word中，并要有结果分析哦，谢谢！
1
睡不着，看到你的帖子了，让我帮你试一下吧！把数据拷进来，对应关系是否没错，你自己校对吧，我只说方法。
定义好了之后，选择分析方法 --- 重复测量（如果你觉得还有更好的方法，请介绍给我。
）
2
照此办理即
可
3
什么变量，因子的，该放哪里，就放哪里
吧！
4
模型选的可是没有交互效应呀，这是你说的，我不知道你为什么敢这么确定？
5
一路 OK下来，终于给出结果了。
一大堆东西，能看懂多少，看多少吧！下面表格才可能
真有用。
只有温度 P<0.05, 哈哈，其它因子没啥作用！这个结果我不信，但数据就是这
样说的。
祝你好运！
6。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(1)结果整理
将试验所得结果按处理和区组两向分 组整理成表；
资料处理与区组两向表
ⅠⅡ
Ⅲ Tt
A1
B1
17 15 13 45
B2
11 14 13 38
B3
12 8 8 28
A2
B1
19 13 11 43
B2 20 19 13 52
B3
17 16 18 51
SSr
Tr2 C ab
SSt
Tt2 C r
SSA
TA2 C rb
SSB
TB2 C ra
SSAB SSt SSA SSB
SSe SST SSr SSA SSB SSAB
SST SSr SSt
SST x2hij C
MS MSr MSt MSA MSB
MSe
二因素随机区组的期望均方
变异 来源 区组 A B A×B 误差
期望均方
固定模型
随机模型
σ2e+abκ2β σ 2e+rbκ2A σ2e+ raκ2B σ2e+ rκ2(A×B) σ2e
σ2e+abσ2β σ2e+rσ2(A×B) +rbσ2A σ2e+rσ2(A×B) +raσ2B σ2e+rσ2A×B
:
2 B
0; H0
:
2 AB
0;
其F值都是以误差项的均方为分母的。
当选用随机模型：
• 测验
H0
:
2
0; H0
:
2 AB
0;
应以误差项均方为分母；
而测验
H0
:
2 A
0;
H
0
:
2 B
0;
需以互作项的均方为分母。
二因素随机区组与单因素随机区组的差别：二因 素试验的处理项可以再分解为A因素水平间、B因素 水平间和AB互作三部分，因此二因素处理项的平方 和与自由度亦可作相应的剖分：
肥
Ⅰ
A2 B2
A2 B3
A1 A3 B1 B3
A3 A1 B1 B2
A3 B4
A1 B4
A1 A3 A2 A2 B3 B2 B4 B1
A1 A2 A3 A2 A1 A3 A1 A2 A1 A2 A3 A3
Ⅱ B4 B4 B2 B1 B2 B3 B1 B2 B3 B3 B4 B1
瘦
2、二因素随机区组试验的结果分析
假定有一个A、B二因素试验，a=3, b=4, 随机 区组设计，重复两次r=2，该试验共有12个水平 组合.
B1
B2
B3
B4
A1
A1B1
A1B2
A1B3
A1B4
A2
A2B1
A2B2
A2B3
A2B4
A3
A3B1
A3B2
A3B3
A3B4
因重复2次，故应先划分为两个区组；又因有 12个水平组合，故每区组划分为12个试验小区。
r
a
b
a
b
h Ai Bj (AB)ij (AB)ij 0
1
1
1
1
1
因此，在可加性的假设下，二因素随机区 组试验结果的总变异可分解为区组间、处理间 和试验误差三部分，而处理又可分解为A因素、 B因素和A×B互作三个部分。
二因素随机区组试验设计可参照单因素随机 区组试验进行，唯一不同点是二因素随机区组试 验把各因素不同水平组合当作单因素试验中的处 理看待，并按随机的原则排列在各区组。
第八章 多因素试验结果的统计分析
• 二因素随机区组设计的结果分析 • 三因素随机区组设计的结果分析 • 二因素裂区设计的结果分析
§8.1 多因素随机区组试验的统计分析
一、二因素随机区组试验结果的方差分析 1、二因素随机区组试验的线性模型和期望均方
设有A、B两个试验因素，A因素有a个水平,B 因素有b个水平 , 采用随机区组设计，重复r次。 该二因素试验共有ab个水平组合，每一个水平组 合有r个观察值。则该试验共有rab个观察值。
二因素随机区组试验
变异来源
DF
区组
r-1
处理
ab-1
A因素
a-1
B因素
b-1
A×B互作
(a-1)(b-1)
误差
(ab-1)(r-1)
单因素随机区组试验
变异来源 DF
区组
r-1
处理
k-1
误差 (k-1)(r-1)
变异来源 区组
处理
A
B A×B MSA×B 误差
总变异
二因素随机区组设计的平方和与均方
SS
在二因素试验中，由于有两个试验因素， 其处理效应由三部分构成，即：
tij Ai Bj ( AB)ij
故二因素随机区组试验中每一观察值的线性 模型为：
xhij x h Ai Bj ( AB)ij ehij
式中，h=1, 2，…，r； i =1, 2, …, a； j =1, 2，…，b;
σ2e
对于多因素试验而言，效应模型的不同 将导致F测验的方法不同。
对固定模型来说，各变异项的均方除误 差均方即构成相应的F测验。
但对随机模型来说，区组变异和互作变 异用误差均方进行F测验；而A 、B的变异则 应用互作项的均方进行F测验。
当选用固定模型：
H0
:
2
0; H0
:
2 A
0; H0
SSt = SSA + SSB + SSA×B
(ab-1)=(a-1)&#和；SSA×B 为互作项平方 和 ;SSA为A因素平方和； SSB为B因素平方和。
二、二因素随机区组试验结果的分析实例(固定模 型）
【例8.1】玉米品种与施肥二因素随机区组试 验，A因素有A1，A2，A3(a=3)三个品种，B因素有 B1，B2，B3(b=3)三个施肥水平，重复3次(r=3)， 小区计产面积20m2，田间排列和小区产量(kg)如 图8.1，试作分析。
A3
B1 19 18 16 53
B2 10 8 10 28
B3 9
8
7 24
Tr 134 119 109 362(T)
再按品种(A)和施肥(B)作两向分组整理成表。
资料品种(A)与施肥(B)两向表
B1
B2
B3 TA
A1 45 38 28 111
A2 43 52 51 146
玉米品种与施肥随机区组试验田间排列和小区产量 Ⅰ A2B3 A1B2 A2B1 A2B3 A3B3 A2B2 A1B3 A3B1 A1B1
10 11 19 17 9 20 12 19 17 Ⅱ A2B2 A2B1 A2B3 A1B2 A1B3 A3B2 A1B1 A3B3 A3B1
19 13 16 14 8 8 15 8 18 Ⅲ A1B3 A3B3 A1B2 A3B1 A1B1 A2B1 A3B2 A2B2 A2B3