局部应力应变法
疲劳强度设计

疲劳强度设计对承受循环应力的零件和构件,根据疲劳强度理论和疲劳试验数据,决定其合理的结构和尺寸的机械设计方法。
机械零件和构件对疲劳破坏的抗力,称为零件和构件的疲劳强度。
疲劳强度由零件的局部应力状态和该处的材料性能确定,所以疲劳强度设计是以零件最弱区为依据的。
通过改进零件的形状以降低峰值应力,或在最弱区的表面层采用强化工艺,就能显著地提高其疲劳强度。
在材料的疲劳现象未被认识之前,机械设计只考虑静强度,而不考虑应力变化对零件寿命的影响。
这样设计出来的机械产品经常在运行一段时期后,经过一定次数的应力变化循环而产生疲劳,致使突然发生脆性断裂,造成灾难性事故。
应用疲劳强度设计能保证机械在给定的寿命内安全运行。
疲劳强度设计方法有常规疲劳强度设计、损伤容限设计和疲劳强度可靠性设计。
简史19 世纪40 年代,随着铁路的发展,机车车轴的疲劳破坏成为非常严重的问题。
1867年,德国A.沃勒在巴黎博览会上展出了他用旋转弯曲试验获得车轴疲劳试验结果,把疲劳与应力联系起来,提出了疲劳极限的概念,为常规疲劳设计奠定了基础。
20 世纪40 年代以前的常规疲劳强度设计只考虑无限寿命设计。
第二次世界大战中及战后,通过对当时发生的许多疲劳破坏事故的调查分析,逐渐形成了现代的常规疲劳强度设计,它非但提高了无限寿命设计的计算精确度, 而且可以按给定的有限寿命来设计零件,有限寿命设计的理论基础是线性损伤积累理论。
早在1924年,德国A.帕姆格伦在估算滚动轴承寿命时,曾假定轴承材料受到的疲劳损伤的积累与轴承转动次数(等于载荷的循环次数)成线性关系,即两者之间的关系可以用一次方程式来表示。
1945 年,美国M.A. 迈因纳根据更多的资料和数据,明确提出了线性损伤积累理论,也称帕姆格伦-迈因纳定理。
随着断裂力学的发展,美国 A.K. 黑德于1953 年提出了疲劳裂纹扩展的理论。
1957年,美国P.C.帕里斯提出了疲劳裂纹扩展速率的半经验公式。
局部应力应变法

1引言局部应力应变法是在缺口应变分析和低周疲劳基础上发展起来的一种疲劳寿命估算方法,因此,它特别适用于低周疲劳。
而推广应用于高周疲劳时,由于它没有考虑表面加工和尺寸等因素的影响(这些因素对低周疲劳无影响,而对高周疲劳的影响则是不可忽视的),就存在一些明显的不足,因此,本文对局部应力应变法应当如何考虑表面加工等因素的影响问题进行了专门研究。
另外,单轴载荷下的局部应力应变法已经比较成熟,而多轴应力下的局部应力应变法则研究较少,很不成熟。
为了能将局部应力应变法成功地应用于多轴疲劳,本文还对多轴应变下的局部应力应变法进行了研究。
2多轴应变下的局部应力应变法2.1对称循环对于结构钢,可使用单轴载荷下的方法,分别得出第一主应力方向、第二主应力方向和第三主应力方向的局部应变-时间历程和局部应力-时间历程,并对最大主应力用雨流法或有效系数法进行循环计数,判别出一系列封闭的滞回环。
再根据每个滞回环的三个主应变范围值,按第四强度理论或第三强度理论进行等效应变范围计算及寿命估算。
2.1.1按第四强度理论等效应变εq的表达式为:(1)式中:ε1、ε2、ε3——第1、第2和第3主应变;ν——泊松比。
将上式改写为应变范围的形式,可得:(2)令:(3)则得:(4)再将单轴载荷下的应变-寿命曲线中的Δε用等效应变范围Δεq取代,并与式(3)联立可得:(5)上式右侧第一项为弹性分量,其ν值等于0.3;而第二项为塑性分量,其ν值等于0.5。
这样便可以将第一项的ν值以0.3代入,第二项的ν值以0.5代入。
于是,上式可以变为:(6)由式(4)可知,Δε′q与ν值无关,因此就可以很方便地利用式(6)进行寿命估算,式(6)便是第四强度理论的多轴疲劳应变-寿命曲线。
在进行损伤计算时,需要使用Δεqp/Δεqe值,Δεqp为等效塑性应变范围,Δεqe为等效弹性应变范围,它们用下面方法算出:对峰谷点分别用下式计算等效应力范围Δσq:(7)则:(8)对于Δεqp,可以先由式(3)得:Δε′q=(1+ν)Δεq=1.3Δεqe+1.5Δεqp从而可得:(9)进行损伤计算的方法和所采用的损伤式均与单轴应力相同,只须在计算时以Δεqe代替Δεe,Δεqp代替Δεp,并以式(6)代替单轴载荷下的应变-寿命曲线。
涡轮叶片高低周疲劳分析方法总结论文综述

本次毕业设计论文的内容是涡轮叶片高低周疲劳分析方法的总结与对比。
涡轮叶片是航空发动机工作环境最恶劣 ,结构最复杂的零件之一 ,也是发动机断裂故障多发件之一。
由于发动机工作时涡轮叶片始终在高温下承受复合载荷的作用,因此它的高周疲劳寿命和低周疲劳寿命的计算至关重要。
高周疲劳是指破坏循环数大于104~105的疲劳,高周疲劳的情况下,其应力水平低于弹性极限,没有明显的宏观塑性变形,应力与应变呈线性关系。
低周疲劳是指破坏循环数小于104~105的疲劳,低周疲劳的情况下,其应力水平高于弹性极限,有明显的宏观塑性变形,应力与应变呈非线性关系。
在《高周疲劳和低周疲劳统一的能量表征方法研究》一文中,对高周疲劳和低周疲劳预测模型进行了研究,提出了一种能够将高周疲劳和低周疲劳统一表征的能量形式参量。
用统一的能量形式表征参量对高温合金GH141的760摄氏度高周疲劳和低周疲劳数据进行处理,得到理想的能量-寿命方程。
用1Cr11Ni2W2MoV 钢500摄氏度和粉末盘材料FGH95d 600摄氏度高温低周疲劳和高周疲劳数据对统一表征方法进行验证,验证结果表明,用能量形式的表征参量能够得到理想的能量-寿命方程。
疲劳试验通常可以通过控制应变或控制应力来进行。
按照控制方式可以将疲劳分为应力疲劳和应变疲劳。
材料发生了塑性变形进入屈服阶段后,小的应力变化将引起大的变形,此时进行疲劳试验时多采用应变控制,材料的疲劳寿命一般比较短,因此通常也叫低周疲劳而当材料在没有进入屈服阶段前,采用应力和采用应变都可以进行疲劳试验,通常控制应力来进行疲劳实验,材料的疲劳寿命一般比较长,因此,通常也叫高周疲劳。
三参数幂函数能量方法寿命预测模型:采用应力控制的方式进行高周疲劳实验,用应力参量来表征高周疲劳的寿命特征;采用应变控制的方式进行低周疲劳实验,用应变参量或能量参量来表征低周疲劳的寿命特征。
如果能够用能量参量来表征高周疲劳的寿命特征,那就可以将高周疲劳和低周疲劳统一起来用一个表征参量进行表征,从而就不需将疲劳划分为高周疲劳和低周疲劳,但能量表征同时需要应力和应变参量。
疲劳基础知识介绍

2.疲劳基础知识 疲劳基础知识
疲劳源区 裂纹扩展区
宏观断口
疲劳断口一般可分为 三个区:疲劳源区、 三个区:疲劳源区、 裂纹扩展区( 裂纹扩展区(光滑区 和瞬时断裂区( )和瞬时断裂区(粗 糙)
瞬时断裂区
2.疲劳基础知识 疲劳基础知识
描述交变应力的基本量
最大应力, 最大应力,最小应力σ
常用导出量
max
2.疲劳基础知识 疲劳基础知识 疲劳曲线
交变应力σ与疲劳寿命N(循环次 数)与之间的关系曲线成为疲劳 曲线(S-N曲线) 图1为材料的疲劳曲线 AB段——静应力强度状况 BC段——低周疲劳(能够见到材 料已发生塑性变形) CD段——有限寿命疲劳阶段 CD段可以用下式描述 σm N = C rN
m σ rN N = σ rm N 0 = C m τ rN N = τ rm N 0 = C ′
图1 材料的疲劳曲线
2.疲劳基础知识 疲劳基础知识
高周疲劳(N>105) 高周疲劳
• 作用于零件、构件上的应力较低, ,工作应力低于材料的屈服极限,甚 至低于弹性极限。 • 描述高周疲劳,用S-N曲线(即σ-N N曲线)。高周疲劳范围内,由于试 样主要产生的只是弹性变形,塑性变形很小 塑性变形很小,用应变也很难测量,这 时采用S-N 曲线。 • 弹簧、传动轴等的疲劳属于此类。 。
1.概述 概述
疲劳破坏与传统静力破坏的本质区别
静力破坏 一次最大载荷作用下的破坏 疲劳破坏 多次反复载荷作用下的破坏
小于屈服极限或强度极限不 远小于静强度极限甚至小于屈服极限就可 能破坏 发生破坏 通常产生明显的塑性变形 通常没有外在宏观的显著塑性变形 通常没有外在宏观的显著塑性变形,破坏 形式像脆性破坏,不易察觉 断口粗粒状或纤维状 两个区域特征:平滑区,粗粒状或纤维状 两个区域特征 抗力主要取决于材料本身 抗力与材料的组成、构件的形状或尺寸、 抗力与材料的组成 表面加工状况、使用条件及外部工作环境 表面加工状况 有关
局部应力应变分析法

局部应力应变分析法在静态方法中,常用的局部应力应变分析方法有三种:线弹性解法、非线性有限元法和局部拉伸演变法。
线弹性解法是指基于线弹性材料模型进行的应力应变分析。
该方法适用于线弹性材料,在局部区域内根据材料的线弹性特性,通过求解弹性力学方程得到应力和应变的分布情况。
非线性有限元法是指通过有限元分析方法,考虑材料的非线性特性进行的应力应变分析。
该方法适用于材料存在非线性行为的情况,可以更准确地描述材料的应力和应变分布。
局部拉伸演变法是指通过对材料进行局部拉伸或压缩,观察材料的应力应变行为,推断材料的局部应力应变分布。
该方法适用于对材料进行局部应变实验的情况,可以直接观测到材料的应力和应变的分布情况。
在动态方法中,常用的局部应力应变分析方法有高速摄影、应变计和激光光弹法。
高速摄影是指采用高速摄影技术对材料或结构进行快速动态观测,通过观察影像的变化来分析局部应力应变分布。
该方法适用于高速冲击或振动实验,可以直观地观察到材料或结构的应力和应变分布情况。
应变计是一种用于测量材料或结构应变的传感器。
通过将应变计安装在材料或结构的局部区域,可以测量该区域的应变,并根据线弹性理论求解应力分布。
该方法适用于对局部应变进行精确测量的情况,可以得到较准确的局部应力应变分布。
激光光弹法是一种利用激光照射材料或结构,通过测量激光的反射或散射来分析材料的应力应变分布的方法。
该方法适用于光学材料或结构,可以非接触地获取材料或结构的应力和应变分布情况。
综上所述,局部应力应变分析法是研究材料或结构在局部区域的应力和应变分布的一种方法。
通过静态方法和动态方法,可以使用不同的分析技术来研究局部应力应变分布。
这些方法在工程设计和材料研究中具有广泛的应用,可以帮助工程师和科学家更好地理解材料和结构的性能,并进行相应的设计和改进。
06-07疲劳断裂分析4-2
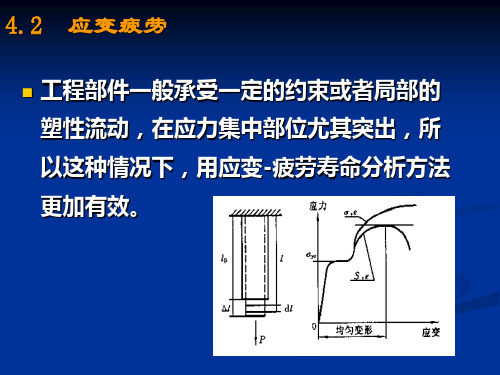
4.2
应变疲劳
3.局部应力-应变法:局部应力应变的确定
解:1)缺口的应力-应变响应
p ( np e ) K
4.2
应变疲劳
3.局部应力-应变法:局部应力应变的确定
解:2)缺口的应力-应变响应如图所示,根据稳态环可 知:
3)将其带入ε-N曲线:
则可求得:N=12470循环
p ( np e ) K
4.2
应变疲劳
3.局部应力-应变法:局部应力应变的确定 在循环载荷作用下,缺口的局部应力-应变也是随时 间变化,此时用反映材料性能的循环应力-应变曲线代 替单调应力-应变曲线,反向加载后,应力-应变响应应 当由滞后环来描述,还要考虑缺口应力集中的影响。
p ( np e ) K
4.2
1 n'
p ( np e ) K
4.2
应变疲劳
材料记得曾为反向加载所 中断的应力-应变路径 应变第二次到达某处, 该处曾经发生过反向应 变,则形成封闭环; 过了封闭环顶点以后, σ-ε路径不受封闭环的 影响,仍然记得原有路 径
④ 循环应力-应变曲线:材料的记忆特性
材料的记忆特性图
4.29
b 疲劳强度指数(-0.06 -0.14,可取-0.1);
典型应变-寿命曲线
c-疲劳延性指数(-0.5 0.7,可取-0.6)
p ( np e ) K
4.2
应变疲劳
当 ea= pa时,有:
2.应变寿命曲线(ε-N曲线)
f
'
E 可得 :
(2 N )b= f '(2 N )c
p ( np e ) K
4.2
应变疲劳
疲劳分析方法
疲劳寿命分析方法摘要:本文简单介绍了在结构件疲劳寿命分析方法方面国内外的发展状况,重点讲解了结构件寿命疲劳分析方法中的名义应力法、局部应力应变法、应力应变场强度法四大方法的估算原理。
疲劳是一个既古老又年轻的研究分支,自Wohler将疲劳纳入科学研究的范畴至今,疲劳研究仍有方兴未艾之势,材料疲劳的真正机理与对其的科学描述尚未得到很好的解决。
疲劳寿命分析方法是疲分研究的主要内容之一,从疲劳研究史可以看到疲劳寿命分析方法的研究伴随着整个历史。
金属疲劳的最初研究是一位德国矿业工程帅风W.A.J.A1bert在1829年前后完成的。
他对用铁制作的矿山升降机链条进行了反复加载试验,以校验其可靠性。
1843年,英国铁路工程师W.J.M.Rankine对疲劳断裂的不同特征有了认识,并注意到机器部件存在应力集中的危险性。
1852年-1869年期间,Wohler对疲劳破坏进行了系统的研究。
他发现由钢制作的车轴在循环载荷作用下,其强度人大低于它们的静载强度,提出利用S-N 曲线来描述疲劳行为的方法,并是提出了疲劳“耐久极限”这个概念。
1874年,德国工程师H.Gerber开始研究疲劳设计方法,提出了考虑平均应力影响的疲劳寿命计算方法。
Goodman讨论了类似的问题。
1910年,O.H.Basquin提出了描述金属S-N曲线的经验规律,指出:应力对疲劳循环数的双对数图在很大的应力范围内表现为线性关系。
Bairstow通过多级循环试验和测量滞后回线,给出了有关形变滞后的研究结果,并指出形变滞后与疲劳破坏的关系。
1929年B.P.Haigh研究缺口敏感性。
1937年H.Neuber指出缺口根部区域内的平均应力比峰值应力更能代表受载的严重程度。
1945年M.A.Miner 在J.V.Palmgren工作的基础上提出疲劳线性累积损伤理论。
L.F.Coffin和S.S.Manson各自独立提出了塑性应变幅和疲劳寿命之间的经验关系,即Coffin—Manson公式,随后形成了局部应力应变法。
疲劳分析的各种方法
疲劳寿命预测方法很多。
按疲劳裂纹形成寿命预测的基本假定和控制参数,可分为名义应力法、局部应力一应变法、能量法、场强法等。
2.4.1.1名义应力法名义应力法是以结构的名义应力为试验和寿命估算的基础,采用雨流法取出一个个相互独立、互不相关的应力循环,结合材料的S -N曲线,按线性累积损伤理论估算结构疲劳寿命的一种方法。
基本假定:对任一构件(或结构细节或元件),只要应力集中系数K T相同,载荷谱相同,它们的寿命则相同。
此法中名义应力为控制参数。
该方法考虑到了载荷顺序和残余应力的影响,简单易行。
但该种方法有两个主要的不足之处:一是因其在弹性范围内研究疲劳问题,没有考虑缺口根部的局部塑性变形的影响,在计算有应力集中存在的结构疲劳寿命时,计算误差较大;二是标准试样和结构之间的等效关系的确定十分困难,这是由于这种关系与结构的几何形状、加载方式和结构的大小、材料等因素有关。
正是因为上述缺陷,使名义应力法预测疲劳裂纹的形成能力较低,且该种方法需求得在不同的应力比R和不同的应力集中因子K T下的S-N曲线,而获得这些材料数据需要大量的经费。
因而名义应力法只适用于计算应力水平较低的高周疲劳和无缺口结构的疲劳寿命。
近年来,名义应力法也在不断的发展中,相继出现了应力严重系数法(S. ST)、有效应力法、额定系数法(DRF)等。
2.1.2.2局部应力一应变法局部应力一应变法的基本思想是根据结构的名义应力历程,借助于局部应力-应变法分析缺口处的局部应力。
再根据缺口处的局部应力,结合构件的S-N曲线、材料的循环。
一曲线、E -N曲线及线性累积损伤理论,估算结构的疲劳寿命。
基本假定:若一个构件的危险部位(点)的应力一应变历程与一个光滑小试件的应力一应变历程相同,则寿命相同。
此法中局部应力一应变是控制参数。
局部应力一应变法主要用于解决高应变的低周疲劳和带缺口结构的疲劳寿命问题。
该方法的特点是可以通过一定的分析、计算将结构上的名义应力转化为缺口处的局部应力和应变。
航空飞行器用减压阀特性研究方法探析
航空飞行器用减压阀特性研究方法探析杨星1严洪英2(1.国营第570厂四川宜宾644000;2.海军装备部四川宜宾644000)摘要:复杂的航空环境对航空器用减压阀的特性、振动、噪声及疲劳寿命特性等提出了更高的要求。
本文针对目前国内外军用航空器用减压阀在设计和使用过程中的静、动态特性分析方法,以及振动、噪声和疲劳寿命设计等进行整理和分析,并针对我国目前航空器用减压阀疲劳寿命设计方法和疲劳损伤积累理论等进行综述。
综合国内外发展历程和发展现状,数值仿真和工程计算技术的发展使得目前特性研究方法已经日渐成熟。
关键词:航空器减压阀特性振动和噪声疲劳寿命中图分类号:V228文献标识码:A文章编号:1674-098X(2021)08(b)-0004-05Brief Analysis of Research Methods on the Characteristics of Pressure Reducing Valve for Aviation AircraftYANG Xing1YAN Hongying2(1.State Owned No.570Plant,Yibin,Sichuan Province,644000China;2.Equipment Department of People'sLiberation Army Navy,Yibin,Sichuan Province,644000China)Abstract:The complex aviation environment puts forward higher requirements on the characteristics,vibration, noise and fatigue life characteristics of aircraft pressure reducing valves.In this paper,the static and dynamic characteristic analysis methods,vibration,noise and fatigue life design of pressure reducing valves for military aircraft at home and abroad are sorted and analyzed,and the fatigue life design methods and fatigue damage accumulation theory of pressure reducing valves for aircraft in China are summarized.The development of numerical simulation and engineering calculation technology makes the characteristic research methods mature day by day.Key Words:Aviation aircraft;Pressure reducing valve;Characteristic;Vibration and noise;Fatigue life静态分析和动态分析是航空用减压阀特性分析的两个重要方面。
局部应力应变法及其设计数据_赵少汴
时使用循环应力- 应变曲线。
( 4) 绘出如图 1 所示的局部应力- 应变响应图。
这时, 局部应力应变形成若干个封闭的滞回环。
# 当 $Ep / $Ee \1 时, 使用塑性线计算损伤与 试验结果符合较好, 这时:
Di =
1 Np
i
=
2(
$Epi 2Rcf
)
-
1 c
( 16)
# 当 $Ep / $Ee [ 011 时, 用弹性线计算损伤与 试验结果符合较好, 这时:
明了其寿命估算过程。还提供了 10 种常用国产机械材料的低周应 变疲劳性能试验数据。
关键词: 循环应力- 应变曲线; 应变- 寿命曲线; 损伤 计算式; 疲劳寿命估算
中图分类号: T H123 文献标识码: A
1引言
E=
Ee+
Ep =
R E
+
R1 ( Kc ) nc
式中: E) ) ) 真应变( 总应变) ;
荷块的损伤为:
( 1)
常规疲劳设计法以名义应力为基本设计参数, 按名义应力进行疲劳设计。而实际上, 决定零构件 疲劳强度和寿命的应变集中处的最大局部应力和应 变。因此, 近代在应变分析和低周疲劳的基础上, 提 出了一种新的疲劳寿命估算方法 ) ) ) 局部应力应变 法。它的设计思路是, 零构件的疲劳破坏, 都是从应 变集中部位的最大应变处起始, 并且在裂纹萌生以 前都要产生一定的塑性变形, 局部塑性变形是疲劳 裂纹萌生和扩展的先决条件。因此, 决定零构件疲 劳强度和寿命的是应变集中处的最大局部应力和应 变。只要最大局部应力应变相同, 疲劳寿命就相同。 因而有应力集中零构件的疲劳寿命, 可以使用局部 应力应变相同的光滑试样的应变- 寿命曲线进行计 算, 也可使用局部应力应变相同的光滑试样进行疲 劳试验来模拟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b s 1.2时,为循环软化; b s 1.2 ~ 1.4时,为可能硬化,也可 能软化。
4.应力-应变迟滞回线
材料在循环载荷作用下得到的应力-应变迹线称为迟 滞回线。 大多数工程材料的稳定迟滞回线与循环应力-应变曲 线之间有着简单的近似关系,即迟滞回线与放大1 倍的单轴循环应力-应变曲线形状相似。
1 1
(5 12)
n
(5 13)
弹性应变 塑性应变
循环应力应变曲线 材料在循环加载下的应力应变响应称为循环应力-应变曲线. 低周疲劳中的应力-应变关系不能用单调应力-应变关系来表示,需要用循环 应力-应变关系来表达. 应力应变迟滞回线(滞后环) 迟滞பைடு நூலகம் 线面积 代表塑 性变形 时外力 所做的 功或所 消耗的 能量。
在寿命较短的情况下,设计应力或应变水平可以高一些,以充分发 挥材料的潜力。这样可能使构件的某些高应力处进入塑性屈服。
众所周知,对于延性较好的材料,屈服后应变的变化大,应
力的变化小,因此用应变作为低周疲劳性能的控制参量比应 力更好。
载荷水平高(超过屈服应力)、寿命短(<104),称之为
应变疲劳或低周应变疲劳。
第5节 局部应力应变分析法
1
机械强度与可靠性——
第6章 局部应力应变分析法
5.1 概述
对于应力水平较低,寿命长的情况,用应力-寿命曲线(S-
N曲线)描述材料/零件的疲劳特性是恰当的。
许多工程构件,在整个使用寿命期内,所经历的载荷次数并
不多。
例如:压力容器若每天承受两次载荷循环,则在30年的使用期内, 载荷的总循环数还不到2.5*104次。
(5 7)
式中, p 为塑性应变;
n为应变硬化指数; K为单调强度指数,即 p 1时的真应变。
材料的真断裂强度σf与真断裂延性εf
f
Pf Af
(5 8)
A0 1 ln (5 9) A 1 式中,Pf 为断裂载荷; Af 为断裂时的截面积; f ln (A A0 ) ; A
将 f 和 f 代替式( 5 7)中的和 p,可得:
f K ( f )n
或者
(5 10)
K
f
f
n
(5 11)
把式( 5 11)代入( 5 7),可得: n p f f 所以总应变为:(材料 真应力 应变曲线表达式) f E f
低循环103~(104~105)
估算裂纹形成寿命 材料循环应力-应变曲线, ε-N曲线 塑性变形较大,应力应 变不成正比
变形
机械强度与可靠性——
第6章 局部应力应变分析法
5.2 低周疲劳
低周疲劳与高周疲劳
一般将失效循环数小于104-105次循环的疲劳称为低周疲劳;
将失效循环数大于104-105循环的疲劳称为高周疲劳。
一次拉伸试验得到a图中的OA段; 一次压缩试验得到a图中的OB段; BOA称为单调应力-应变曲线,一 般只考虑OA段。
先加载到A点,然后卸载到O点,再加载到B 点,再加载到C点(与A重合)循环应力应 变曲线。 加载和卸载应力应变迹线ABC形成一个闭环。 (迟滞回线、迟滞环) 在循环载荷下得到的应力应变迹线叫应力应变迟滞回线。
缺点
主要解决低周循环疲劳问题,不能用于无限寿命计算。对有限寿命的高循 环段(105~106),计算结果没有名义应力法好。 该方法目前还不够完善,还不能考虑尺寸因素和表面状况的影响,用于高 周循环的误差较大。 该方法目前仅限于对单个零件进行分析。对于复杂的连接件,由于难以进 行精确的应力应变分析,目前还难以使用该方法。
快速试验法中的多级法和增级法
循环应力-应变曲线表达式
循环应力-应变曲线可用单调应力-应变曲线相似的公式来表达:
K' ( p )n
'
(5 14 )
1
f K ( f )n K
(5 10) (5 11)
K ' E K' p f ( f )n
使用若干个试样,每一个试样在一定的应力幅值 下循环,直到得到一条稳定的闭合迟滞回线。将 迟滞回线的端点连接起来,得到的光滑曲线即为 循环应力应变曲线。
快速试验
多级法
用一个试样在低应力幅下循环达到稳定,然后逐级 增加应力幅值,得到一系列稳定的闭合回线。
增级法
试样所受的应力幅值先逐渐减小,再逐渐增大,构 成一个循环块,再继续做这种循环块的试验,直到 稳定。循环稳定时各迟滞回线端点的连线即为循环 应力-应变曲线。
应力-应变迟滞回线
5.材料的记忆特性
记忆特性:材料在循环加载下,当后级载荷 的绝对值大于前级载荷时,材料仍按照前级 迹线的变化规律继续变化。
第1次升载时,按循环应力-应变曲线由O->A, 然后按迟滞回线由A->B,之后按迟滞回线升载 ->C。
当由C点降载至D时,在B点前按以C点为原点 的迟滞回线降载,降至B点后,则按照原来的 变化规律,按以A点为原点的迟滞回线变化降 载至D。 由D点升载时,在达到A点前,按以D点为原点 的迟滞回线变化。 到达A点后,若继续升载,则按原来的变化规 律,仍按循环应力-应变曲线的变化继续变化 至E。
循环硬化与循环软化只是在开始时产生, 随着循环次数的增加,达到一定次数以 后,材料对变形的抗力趋于稳定。 大多数材料在达到疲劳寿命的一半时, 应力应变曲线达到稳定。
循环应力应变曲线 在应变比R=-1下,对不同的应变幅值,可得到 不同的稳定循环迟滞回线。 以为ε横坐标、 σ为纵坐标连接起来的这些迟滞 环顶点的曲线称为材料的循环应力应变曲线。 循环应力应变的测定方法 多试样等幅阶梯加载法(常规方法)
材料的记忆特性
二. 应变-寿命(ε-N)曲线
1. 应变-寿命关系
曼森-科芬方程 一点的总应变=弹性应变+塑性应变 试验表明,在双对数坐标上,弹性应变、塑性应变与循环疲劳寿命的关系成 一直线,可表示为:
' p e f ' c (2N )b f (2N ) 2 2 2 E
(5 13)
与单调应力应变曲线的 比较:
式中,为应力幅;K ' 为循环强度系数; n '为循环应变硬化指数, 取值范围0.10 ~ 0.20;
K为单调强度系数; n为应变硬化指数;
'f 为疲劳强度系数, 'f f b 350MPa;
1 A 为疲劳延性系数, f ln 0 ln A 1
在曼森-科芬方程(5-20)中:
弹性线 塑性线
' e f (2N )b 2 E p ' c f (2N ) 2
(5 21) (5 22)
将式(5-20)、(5-21)和(5-22)画在同一坐标图上,得到通用斜率法的应变 寿命曲线。
弹性线和塑性线的交点 所对应的寿命 N称为 转变寿命NT , NT 104 ~ 105。
(5 1)
e
(5 2)
式中,P为外载荷; A0为试样初始面积;
真实应力
l0为试样初始基长;
l为l0的增量;
真实应变
P A
(5 3)
l
l0
dl l
(5 4)
式中,P为外载荷; A为试样瞬时截面积; l为试样瞬时长度;
真实应力应变σ,ε与工程应力应变S,e的关系 发生颈缩之前, σ 和ε可以用下式计算
l A0 S S A l S(1 e ) 0 l l dl ln l ln(1 e ) l l 0
0
(5 5) (5 6)
材料的真应力与塑性应变间的关系为
K ( p )n
低周疲劳采用局部应力应变法求解,基本的材料曲线为:
循环应力-应变曲线;
应变-寿命曲线。
6
一.循环应力-应变曲线与单调应力-应变曲线
单调应力-应变曲线(材料在单调加载下的应力-应变曲线) 曲线分为“工程应力-应变曲线”和“真实应力-应变曲线”
工程应力
S
工程应变
P A0
l l0
'
'
n'
(5 15) (5 16)
f
f
n
1
' f f
1
p f f
n
(5 12)
1
n'
(5 17)
1
' f ' E
n'
(5 18)
n f E f 弹性应变 塑性应变
N NT时,塑性应变占优势, 属于低周疲劳。
(5 20)
式中, 2 N为疲劳寿命;
'f 为疲劳强度系数,简化 计算中取 'f f ; 'f 为疲劳延性系数,简化 计算中取 'f f ;
b为疲劳强度指数(弹性 线的斜率), 一般取b 0.05 ~ 0.12; c为延性指数(塑性线的 斜率), 一般,延性材料 c 0.6,高强度合金 c 0.5。
循环硬化与循环软化
金属材料在低周疲劳初期,由于循环应力的作用会出现循环硬化和 循环软化现象。
循环硬化:在应变范围Δε为常数的情况下,应力随着循环次数的增加而 增加。或者说材料变形抗力随循环次数的增加而增加,然后达到稳定状 态的过程。 另一种定义:在应力幅σa为常数的情况下,应变幅εa随着循环次数的增 加而逐渐减少,最后趋于稳定的过程。 循环软化:与循环硬化相反,在应变幅εa为常数的情况下,应力幅sa随着 循环次数的增加而逐渐减少。
