自组织竞争神经网络与SOM网络kohonen网络共66页
自组织竞争神经网络SOM65页PPT

40.5 -90
13
43 -90
14
43 -81
15
47.5 -81
16
42
-81
x2
x4
17
42 -80.5
18
43.5 -80.5
19
43.5
-75
20
48.5
-75
28
x5
训练 次数
1
W1
W2
18.43 -180
x3
2
-30.8 -180
3
7 -180
X3
00..770077
X4
00..3943297 X5
0.6 0.8
解:为作图方便,将上述模式转换成极坐标形式 :
X1136.89o X2180oX314.45X4170oX5153.13o
竞争层设两个权向量,随机初始化为单位向量:
cos XT Xi
X Xi
类1
类2
T
(b)基于余弦法的相似性测量
的夹角小于a,两类模式向量的
夹角大于a。余弦法适合模式向
量长度相同和模式特征只与向量
方向相关的相似性测量。
11
§4.2 竞争学习的概念与原理 竞争学习原理
竞争学习规则——Winner-Take-All
网络的输出神经元之间相互竞争以求被激活, 结果在每一时刻只有一个输出神经元被激活。 这个被激活的神经元称为竞争获胜神经元,而
其它神经元的状态被抑制,故称为Winner Take All。
12
1.向量归一化 首先将当前输入模式向量
X和竞争层中各神经元对应的内星向量Wj 全部进行归一化处理; (j=1,2,…,m)
自组织竞争神经网络

第23页
3.搜索阶段:
由Reset信号置获胜阶段无效开始,网络进入搜索 阶段。此时R为全0,G1=1 ,在C层输出端又得到了此 次输入模式X。所以,网络又进入识别及比较阶段,得 到新获胜节点(以前获胜节点不参加竞争)。这么重 复直至搜索到某一个获胜节点K,它与输入向量X充分 匹配到达满足要求为止。模式X编制到R层K节点所连 模式类别中,即按一定方法修改K节点自下而上和自上 而下权向量,使网络以后再碰到X或与X相近模式时, R层K节点能很快取得竞争胜利。若搜索了全部R层输 出节点而没有发觉有与X充分靠近模式,则增设一个R 层节点以表示X或与X相近模式。
⑥ 警戒线检测。设向量X中不为0个数用||X||表示,可
有 n || X || xi
n
||C'|| w' j *iXi i1
(5.3.1)
i 1
n
||C'|| w' j *iXi
(5.3.2)
i1
若||C||/||X||>成立,则接收j*为获胜节点,转⑦。
不然发Reset信号,置j*为0(不允许其再参加竞争),
信号1:输入X第i个分量Xi。 信号2:R层第j个单元自上而下返回信号Rj。 信号3:G1控制信号。 设C层第i个单元输出为Ci。 Ci依据“2/3规则”产 生,即Ci含有三个信号中多数相同值。 网络开始运行时, G1 =1,R层反馈信号为0。
自组织竞争神经网络
第18页
2.R 层结构:
R层功效结构相当于一个前向竞争网络,假设输出 层有m个节点,m类输入模式。输出层节点能动态增加, 以满足设置新模式类需要。设由C层自下而上连接到R 层第j个节点权向量用Wj={w1j,w2j,..,wnj} 表示。C层输出向量C沿Wj向前馈送,经过竞争在R层 输出端产生获胜节点,指示此次输入向量类别。
自组织神经网络

自组织网络学习算法的MATLAB MATLAB实现 2.6.3 自组织网络学习算法的MATLAB实现
例2-5 人口分类是人口统计中的一个重要指 现有1999 10个地区的人口出生比例情况 1999共 标,现有1999共10个地区的人口出生比例情况 如下: 如下: 出生男性百分比分别为:0.5512 0.5123 0.5087 0.5001 0.6012 0.5298 0.5000 0.4965 0.5103 0.5003; 出生女性百分比分别为:0.4488 0.4877 0.4913 0.4999 0.3988 0.4702 0.5000 0.5035 0.4897 0.4997
自组织特征映射学习算法原理 Kohonen自组织特征映射算法,能够自动 找出输入数据之间的类似度,将相似的输 入在网络上就近配置。因此是一种可以构 成对输入数据有选择地给予响应的网络。 类似度准则 n 2 欧氏距离 d j = (xi − wij )
∑
i=1
2.6.2自组织特征映射网络的学习算法 2.6.2自组织特征映射网络的学习算法
2.6.1 自组织特征映射神经网络结构
竞争层
输入层
SOM神经网络结构 SOM神经网络结构
2.6.1 自组织特征映射神经网络结构
输入层
竞争层
SOM神经网络平面示意图 SOM神经网络平面示意图
2.6.1 自组织特征映射神经网络结构
竞争层 输入层
SOM神经网络立体示意图 SOM神经网络立体示意图
2.6.2自组织特征映射网络的学习算法 2.6.2自组织特征映射网络的学习算法
自组织网络学习算法的MATLAB MATLAB实现 2.6.3 自组织网络学习算法的MATLAB实现 例2-5源程序
神经网络及应用第五章自组织竞争神经网络

5.2 自组织特征映射神经网络
1981年,自组织特征映射网(Self-Organizing Feature Map, SOFM)由芬兰Helsink大学的T. Kohonen教授提 出,又称Kohonen网。 Kohonen认为,一个神经网络接受外界输入模式时, 将会分为不同的对应区域,各区域对输入模式具有不 同的相应特征,而这个过程是自动完成的。 自适应特征映射正式根据这一看法提出的,其特点与 人脑的自组织特性相类似。
5.1 竞争学习的概念与原理
前20次训练中两个权向量的变化情况:
解:将上述模式转换为极坐标形式 X 1 = 1∠36.89o X 2 = 1∠ − 80o X 3 = 1∠45o X 4 = 1∠ − 70o X 5 = 1∠53.13o 竞争层设两个权向量,随机初始化单位向量 1 −1 W1 (0) = 1∠0o W2 (0) = 1∠180o 0 0 取学习率η=0.5,按1~5的顺序依次输入模式向量,调整权值, 每次修改后重新进行归一化。
5.1.2 竞争学习原理 竞争学习规则 胜者为王(Winner-Take-All)
1)向量归一化 首先将自组织网络中的当前输入模式向量X和竞争层中各神 经元对应的内星权向量 Wj (j=1,2,…,m)全部进行归一化处理, ) ) 得到 X 和 W j (j=1,2,…,m)
内星节点:总是接受来自其他神经元的输入加权信号,是信号 的汇聚点,对应的权值向量称为内星权向量。 外星节点:总是向其他神经元发出输出加权信号,是信号的发 散点,对应的权值向量称为外星权向量。
5.2 自组织特征映射神经网络
SOFM网的输出阵列
5.2 自组织特征映射神经网络
5.2.3 权值调整域
SOFM采用Kohonen算法,该算法在胜者为王算法基础上加以改 进而成的,其主要区别在于调整权向量与侧抑制的方式不同: – 胜者为王算法中,只有竞争获胜神经元才能调整权向量,其 他任何神经元都无权调整。 – SOFM网的获胜神经元对其临近神经元的影响是由近及远, 由兴奋逐渐转变为抑制,因此其学习算法中不仅获胜神经元 本身要调整权向量,它周围的神经元在其影响下也要程度不 同地调整权向量。
自组织竞争神经网络
dj =
n
∑ (x
i =1
i
− wi j ) 2
∆wi j = η h( j , j*)( xi − wi j )
j − j*2 h ( j , j *) = exp − σ2
自组织竞争神经网络算法能够进行有效的自适应分类,但它仍存在一些问题: 学习速度的选择使其不得不在学习速度和最终权值向量的稳定性之间进行折中。 有时有一个神经元的初始权值向量离输入向量太远以至于它从未在竞争中获胜, 因 此也从未得到学习,这将形成毫无用处的“死”神经元。
网络结构
%1.ÎÊÌâÌá³ö X=[0 1;0 1]; clusters=8; points=10; std_dev=0.05; P=nngenc(X,clusters,points,std_dev); plot(P(1,:),P(2,:),'+r'); title('ÊäÈëÏòÁ¿'); xlabel('P(1)'); ylabel('P(2)'); %2.ÍøÂçÉè¼Æ net=newc([0 1;0 1],8,.1) w=net.IW{1}; plot(P(1,:),P(2,:),'+r'); hold on; circle=plot(w(:,1),w(:,2),'ob') %3.ÍøÂçѵÁ· net.trainParam.epochs=7; net=train(net,P) w=net.IW{1}; delete(circle); plot(w(:,1),w(:,2),'ob'); %4.ÍøÂç²âÊÔ p=[0.5;0.2]; a=sim(net,p)
自组织特征映射神经网络(SOM)

二、学习算法
1 算法 I: (i) 初始化:
- 各权矢量
W j 的确定
wji (0) ← Small random numbers(也可根据先验知识); , k ← 0; (ii) 输入 X(k) , 对 W 做下述操作: j c 求出 与 X(k) 最接近的权矢量 W , q 2 1/ 2 min{ W j − X (k ) = Wq − X (k ) = d q , ( X − Y = ( ∑ i ( xi − yi ) ) ) j d 定义单元 q 所在的邻域为 Nq (tk ), 将 Nq (tk ) 中各单元的权进行修改, 其它权值不变:
的改进使其与当前单元对应的权值修改次数有关随修改次数增加使关于算法的收敛性简述设可将输入样本集合划分为每个中有一个中心矢量聚类中心在物理上竞争学习算法competitivelearningcl典型的无教师学习unsupervisedlearning算法
CH.6
自组织特征映射神经网络
Neural Network
⎡P ⎢ 1,1 ⎢ P2,1 ⎢ P ⎢ ⎣ 3,1
共7396个训练矢量。 码本规模:N=512 用 SOM 网络进行矢量量化,实现图像数据压缩
(3) 学习算法
(取定 L、N) (i) 初始化: Wj (0) ← [0,255] 之间的随机数; (ii) 构造图像矢量样本集 { X(k) }, (iii) 输入 X(k), 由各 U j计算出 (iv) 由输出单元 U 在所有 out (v) (vi)
d1 U1
…
dj
Uj
Wj
… U N
dN
SOM
xn
dj
中,找出最小距离
(3) 于是令:
⎧1 , if j = q yj = ⎨ ⎩0 , if j ≠ q
自组织神经网络
❖
PR
- Rx2 矩阵确定输入范围
❖
Di
- 第i层神经元个数,缺省为5× 8
❖ TFCN
- 拓扑函数,缺省为 'hextop'.
❖ DFCN
- 距离函数,缺省为 'linkdist'.
❖
OLR
- 排序阶段学习率,缺省为0.9.
❖ OSTEPS - 排序阶段最大学习步骤,缺省为1000.
❖
TLR
- 调整阶段学习率,缺省为0.02;
例:LVQ网络的设计
❖ 设定输入样本和期望输出 ❖ 构建并设置网络参数 ❖ 根据训练样本对网络进行训练 ❖ 用训练样本测试网络 ❖ 用新样本测试网络 ❖ 讨论比例的影响
小结
❖ 何谓自组织:没有答案的学习
❖ 自组织竞争神经网络的基本概念
神经元:输入与权值的负距离加上阈值 网络结构:竞争网络 学习方法:Kohonen和阈值学习规则 用途:聚类
❖
TND
- 调整阶段最大学习步骤,缺省为1
例八:SOFM网络的构建和训练
❖ 构建网络 ❖ 设置训练样本 待聚类样本 ❖ 观察训练前网络的状态 ❖ 根据样本进行训练
排序阶段 粗调 调整阶段 细调
❖ 观察训练后网络的状态
例九:一维SOFM网络设计
❖ 输入为二维向量,神经元分布为一维 ❖ 将二维空间的特征映射到一维拓扑结构 ❖ 步骤
* IW 1 ,1 ( q 1 )
若分类不正确:
修正第 i个神经元的权值更远离
该样本
i i - ( p ( q ) i ) * IW 1,1 ( q )
* IW 1 ,1 ( q 1 )
* IW 1 ,1 ( q 1 )
竞争型神经网络与自组织神经网络
竞争型神经网络是基于无监督学习的神经网络的一种重要类型,作为基本的网络形式,构成了其他一些具有组织能力的网络,如学习向量量化网络、自组织映射网络、自适应共振理论网络等。
与其它类型的神经网络和学习规则相比,竞争型神经网络具有结构简单、学习算法简便、运算速度快等特点。
竞争型神经网络模拟生物神经网络系统依靠神经元之间的兴奋、协调与抑制、竞争的方式进行信息处理。
一个竞争神经网络可以解释为:在这个神经网络中,当一个神经元兴奋后,会通过它的分支对其他神经元产生抑制,从而使神经元之间出现竞争。
当多个神经元受到抑制,兴奋最强的神经细胞“战胜”了其它神经元的抑制作用脱颖而出,成为竞争的胜利者,这时兴奋最强的神经元的净输入被设定为 1,所有其他的神经元的净输入被设定为 0,也就是所谓的“成者为王,败者为寇”。
一般说来,竞争神经网络包含两类状态变量:短期记忆变元(STM)和长期记忆变元(LTM)。
STM 描述了快速变化的神经元动力学行为,而 LTM 描述了无监督的神经细胞突触的缓慢行为。
因为人类的记忆有长期记忆(LTM)和短期记忆(STM)之分,因此包含长时和短时记忆的竞争神经网络在理论研究和工程应用中受到广泛关注。
竞争性神经网络模型图自组织特征映射神经网络(简称SOM),是由输入层和输出层组成的单层神经网络,主要用于对输入向量进行区域分类。
SOM是一种无导师聚类,能将一维输入模式在输出层映射成二维离散图形,此图形分布在网格中,网格大小由m*n 表示,并保持其拓扑结构不变,从而使有相似特征的神经元彼此靠近,不同特征的神经元彼此远离,最终实现区分识别样品的目的。
SOM 通过学习输入向量的分布情况和拓扑结构,靠多个神经元的协同作用来完成模式分类。
当神经网络接受外界输入模式时,神经网络就会将其分布在不同的对应区域,并且记忆各区域对输入模式的不同响应特征,使各神经元形成有序的空间分布。
当输入不同的样品光谱时,网络中的神经元便随机兴奋,经过SOM 训练后神经元在输出层有序排列,作用相近的神经元相互靠近,作用不同的神经元相互远离。
《自组织神经网络》PPT课件
x3
2 -30.8 -180
3
7 -180
x1
4
-32 -180
5
11 -180
6
24 -180
7
24 -130
w2
w1
8 9
10
34 34 44
-130 -100 -100
11
40.5 -100
12
40.5 -90
13
43 -90
14
43 -81
15
47.5 -81
16
42 -81
x2
x4
17
42 -80.5
Wˆ j*T Xˆ
max (
j{1, 2 ,...,m}
Wˆ j
T
Xˆ )
竞争学习规则——胜者为王(Winner-Take-All)
3.网络输出与权值调整
1 j j* o j (t 1) 0 j j*
Wj* (t 1) Wˆ j* (t) Wj* Wˆ j* (t) (t)(Xˆ Wˆ j* )
47.5 -81
16
42 -81
x2
x4
17
42 -80.5
18 43.5 -80.5
19 43.5 -75
20 48.5 -75
x5
训练 次数
W1
W2
1 18.43 -180
x3
2 -30.8 -180
3
7 -180
x1
4
-32 -180
5
11 -180
w1
6 7
24 -180 24 -130
8
x5
训练 次数
W1
W2
1 18.43 -180
第5章自组织竞争网络
距离,结果是离得最近的那个*获胜。
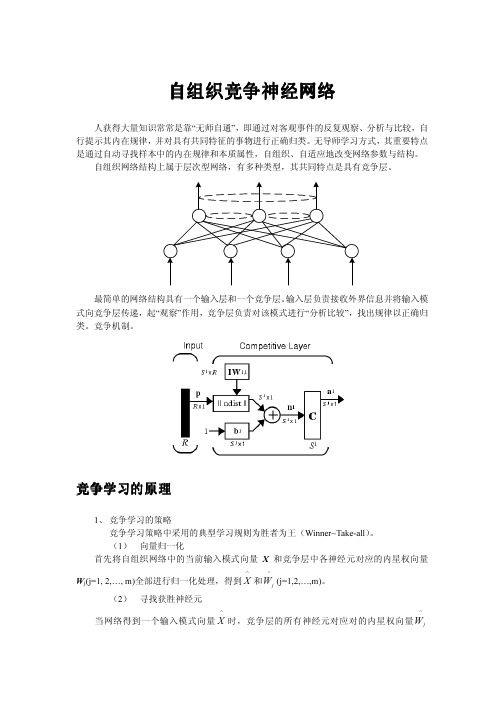
人工神经网络及应用
第五章 自组织竞争神经网络
主讲 何东健
人获得大量知识常常是靠“无师自通”,即通过 对客观事物的反复观察、分析与比较,自行揭示其 内在规律,并对具有共同特征的事物进行正确归类。
自组织神经网络的无导师学习方式类似于大脑中 生物神经网络的学习,其最重要的特点是通过自动 寻找样本中的内在规律和本质属性,自组织、自适 应地改变网络参数与结构。
将上式展开,并利用单位向量的特点,可得
可见,欲使两单位向量的欧式距离最小,须使两
向量的点积
最大。
(3)网络输出与权值调整
算法规定,获胜神经元输出为1,其余输出为0。
即只有获胜神经元才有权调整其权向量wj,调整后权向 量为
α∈(0,1]为学习率,其值随着学习的进展而减小。可 以看出,当j≠j*时,权值得不到调整,实质是“胜者” 对它们进行了强侧抑制,不允许兴奋。
获胜神经元有最大权值调整 量,邻近神经元有稍小调整 量,距离越大,权的调整量 越小,到某一距离R时,调 整量为0。距离再远,调整 量略负,更远时又回到0
由a中2个曲线合成 墨西哥帽函数 与生物系统相似 但计算复杂
大礼帽函数
厨师帽函数
4.2.3 SOFM网的运行原理与学习算法
1.运行原理: 训练和工作两个阶段。 训练阶段:随机输入样本。对某个输入模式,输出层 会有某个神经元获胜。获胜神经元周围的神经元因侧 向相互作用也产生较大响应,于是获胜神经元及其优 胜邻域内神经元所连接的权向量均向输入向量的方向 根据距离作程度不同的调整。大量样本调整网络的权 值,最后使输出层各神经元成为对特定模式类敏感的 神经细胞,对应的内星权向量成为各输入模式类的中 心向量。当两个模式类的特征接近时,代表这两类的 神经元在位置上也接近。从而在输出层形成样本模式 类分布情况的有序特征图。
