中考平行四边形经典中考习题
中考复习之——平行四边形经典练习题(3套)附带详细解答过程

练习1一、选择题(3′×10=30′)1.下列性质中,平行四边形具有而非平行四边形不具有的是().A.内角和为360° B.外角和为360° C.不确定性 D.对角相等2.Y ABCD中,∠A=55°,则∠B、∠C的度数分别是().A.135°,55° B.55°,135° C.125°,55° D.55°,125°3.下列正确结论的个数是().①平行四边形内角和为360°;②平行四边形对角线相等;③平行四边形对角线互相平分;④平行四边形邻角互补.A.1 B.2 C.3 D.44.平行四边形中一边的长为10cm,那么它的两条对角线的长度可能是().A.4cm和6cm B.20cm和30cm C.6cm和8cm D.8cm和12cm5.在Y ABCD中,AB+BC=11cm,∠B=30°,S Y ABCD=15cm2,则AB与BC的值可能是(). A.5cm和6cm B.4cm和7cm C.3cm和8cm D.2cm和9cm6.在下列定理中,没有逆定理的是().A.有斜边和一直角边对应相等的两个直角三角形全等;B.直角三角形两个锐角互余;C.全等三角形对应角相等;D.角平分线上的点到这个角两边的距离相等.7.下列说法中正确的是().A.每个命题都有逆命题 B.每个定理都有逆定理C.真命题的逆命题是真命题 D.假命题的逆命题是假命题8.一个三角形三个内角之比为1:2:1,其相对应三边之比为().A.1:2:1 B.12:1 C.1:4:1 D.12:1:29.一个三角形的三条中位线把这个三角形分成面积相等的三角形有()个.A.2 B.3 C.4 D.510.如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=•14,•AC=19,则MN的长为().A.2 B.2.5 C.3 D.3.5二、填空题(3′×10=30′)11.用14cm长的一根铁丝围成一个平行四边形,短边与长边的比为3:4,短边的比为________,长边的比为________.12.已知平行四边形的周长为20cm,一条对角线把它分成两个三角形,•周长都是18cm,则这条对角线长是_________cm.13.在Y ABCD中,AB的垂直平分线EF经过点D,在AB上的垂足为E,•若Y ABCD•的周长为38cm,△ABD的周长比Y ABCD的周长少10cm,则Y ABCD的一组邻边长分别为______.14.在Y ABCD中,E是BC边上一点,且AB=BE,又AE的延长线交DC的延长线于点F.若∠F=65°,则Y ABCD的各内角度数分别为_________.15.平行四边形两邻边的长分别为20cm,16cm,两条长边的距离是8cm,•则两条短边的距离是_____cm.16.如果一个命题的题设和结论分别是另一个命题的______和_______,•那么这两个命题是互为逆命题.17.命题“两直线平行,同旁内角互补”的逆命题是_________.18.在直角三角形中,已知两边的长分别是4和3,则第三边的长是________.19.直角三角形两直角边的长分别为8和10,则斜边上的高为________,斜边被高分成两部分的长分别是__________.20.△ABC的两边分别为5,12,另一边c为奇数,且a+b+•c•是3•的倍数,•则c•应为________,此三角形为________三角形.三、解答题(6′×10=60′)21.如右图所示,在Y ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,求Y ABCD的周长.22.如图所示,在Y ABCD中,E、F是对角线BD上的两点,且BE=DF.求证:(1)AE=CF;(2)AE∥CF.FCDAEB23.如图所示,Y ABCD的周长是103+62,AB的长是53,DE⊥AB于E,DF⊥CB交CB•的延长线于点F,DE的长是3,求(1)∠C的大小;(2)DF的长.24.如图所示,Y ABCD中,AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、•∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其它条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程(要求:•推理过程中要用到“平行四边形”和“角平分线”这两个条件).25.已知△ABC的三边分别为a,b,c,a=n2-16,b=8n,c=n2+16(n>4).求证:∠C=90°.26.如图所示,在△ABC中,AC=8,BC=6,在△ABE中,DE⊥AB于D,DE=12,S△ABE=60,•求∠C的度数.27.已知三角形三条中位线的比为3:5:6,三角形的周长是112cm,•求三条中位线的长.28.如图所示,已知AB=CD,AN=ND,BM=CM,求证:∠1=∠2.29.如图所示,△ABC的顶点A在直线MN上,△ABC绕点A旋转,BE⊥MN于E,•CD•⊥MN 于D,F为BC中点,当MN经过△ABC的内部时,求证:(1)FE=FD;(2)当△ABC继续旋转,•使MN不经过△ABC内部时,其他条件不变,上述结论是否成立呢?30.如图所示,E是Y ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF =S△EFC.答案:一、1.D 2.C 3.C 4.B 5.A 6.C 7.A 8.B 9.C 10.C二、11.3cm 4cm 12.8 13.9cm和10cm 14.50°,130°,50°,130° • •15.10 16.结论 题设 17.同旁内角互补,两直线平行 18.519.13 直角 三、21.Y ABCD 的周长为20cm 22.略23.(1)∠C=45° (2)DF=224.略 25.•略 26.∠C=90° 27.三条中位线的长为:12cm ;20cm ;24cm 28.提示:连结BD ,取BD•的中点G ,连结MG ,NG29.(1)略 (2)结论仍成立.提示:过F 作FG ⊥MN 于G 30.略练习2一、填空题(每空2分,共28分)1.已知在中,AB =14cm ,BC =16cm ,则此平行四边形的周长为 cm .2.要说明一个四边形是菱形,可以先说明这个四边形是 形,再说明(只需填写一种方法)3.如图,正方形ABCD 的对线AC 、BD 相交于点O . 那么图中共有 个等腰直角三角形.4.把“直角三角形、等腰三角形、等腰直角三角形”填入 下列相应的空格上.(1)正方形可以由两个能够完全重合的 拼合而成; (第3题) (2)菱形可以由两个能够完全重合的 拼合而成;ABCDO(3)矩形可以由两个能够完全重合的 拼合而成. 5.矩形的两条对角线的夹角为ο60,较短的边长为12cm ,则对角线长为 cm . 6.若直角梯形被一条对角线分成两个等腰直角三角形,那么这个梯形中除两个直角外,其余两个内角的度数分别为 ο和 ο.7.平行四边形的周长为24cm ,相邻两边长的比为3:1,那么这个平行四边形较短的边长为 cm .8.根据图中所给的尺寸和比例,可知这个“十”字标志的周长为 m .(第8题) (第10题)9.已知平行四边形的两条对角线互相垂直且长分别为12cm 和6cm ,那么这个平行四边形的面积为 2cm .10.如图,l 是四边形ABCD 的对称轴,如果AD ∥BC ,有下列结论: (1)AB ∥CD ;(2)AB=CD ;(3)AB ⊥BC ;(4)AO=OC .其中正确的结论是 . (把你认为正确的结论的序号都填上) 二、选择题(每题3分,共24分)11. 如果一个多边形的内角和等于一个三角形的外角和,那么这个多边形是( )A 、三角形B 、四边形C 、五边形D 、六边形12.下列说法中,错误的是 ( ) A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形 C. 平行四边形的对角相等 D.对角线互相垂直的四边形是平行四边形 13.给出四个特征(1)两条对角线相等;(2)任一组对角互补;(3)任一组邻角互补;(4)是轴对称图形ABCDOl但不是中心对称图形,其中属于矩形和等腰梯形共同具有的特征的共有 ( ) A.1个 B.2个 C.3个 D.4个 14. 四边形ABCD 中,AD//BC ,那么的值可能是( )A 、3:5:6:4B 、3:4:5:6C 、4:5:6:3D 、6:5:3:415.如图,直线a ∥b ,A 是直线a 上的一个定点,线段BC 在直线b 上移动,那么在移动过程中ABC ∆的面积 ( )A.变大B.变小C.不变D.无法确定(第15题) (第16题) (第17题)16.如图,矩形ABCD 沿着AE 折叠,使D 点落在BC 边上的F 点处,如果ο60=∠BAF ,则DAE ∠ 等于 ( )A.ο15B.ο30C.ο45D.ο6017.如图,在ABC ∆中,AB=AC =5,D 是BC 上的点,DE ∥AB 交AC 于点E ,DF ∥AC 交AB 于点F , 那么四边形AFDE 的周长是 ( ) A.5 B.10 C.15 D.2018.已知四边形ABCD 中,AC 交BD 于点O ,如果只给条件“AB ∥CD ”,那么还不能判定四形 ABCD 为平行四边形,给出以下四种说法:(1)如果再加上条件“BC=AD ”,那么四边形ABCD 一定是平行四边形; (2)如果再加上条件“BCD BAD ∠=∠”,那么四边形ABCD 一定是平行四边形; (3)如果再加上条件“AO=OC ”,那么四边形ABCD 一定是平行四边形; (4)如果再加上条件“CAB DBA ∠=∠”,那么四边形ABCD 一定是平行四边形 其中正确的说法是( )ABCDEFABCa bA.(1)(2)B.(1)(3)(4)C.(2)(3)D.(2)(3)(4) 三、解答题(第19题8分,第20~23题每题10分,共48分) 19.如图,中,DB=CD ,ο70=∠C ,AE⊥BD 于E .试求DAE ∠的度数.(第19题)20.如图中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG ,ο100=∠DGE . (1)试说明DF=BG ; (2)试求AFD ∠的度数.(第20题)21.工人师傅做铝合金窗框分下面三个步骤进行:AB CD EABCDFEG(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH ;(2)摆放成如图②的四边形,则这时窗框的形状是形,根据的数学道理是: ;(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: .(图①) (图②) (图③) (图④) (第21题)22.李大伯家有一口如图所示的四边形的池塘,在它的四个角上均有一棵大柳树,李大伯开挖池塘,使池塘面积扩大一倍,又想保持柳树不动,如果要求新池塘成平行四边形的形状.请问李大伯愿望能否实现?若能,请画出你的设计;若不能,请说明理由.(第22题)ABC D答案1.60.2.平行四边形;有一组邻边相等.3.8. 提示:它们是.,,,,,,,ACD BCD ABC ABD AOD COD BOC AOB ∆∆∆∆∆∆∆∆4.(1)等腰直角三角形; (2)等腰三角形; (3)直角三角形.5.24.6. 135; 45.7.3.8.4. 提示:如图所示,将“十”字标志的某些边进行平移后可得到一个边长为1m 的正方 形,所以它的周长为4m .(第8题) 9. 36. 提示:菱形的面积等于菱形两条对角线乘积的一半. 10. (1)(2)(4). 提示:四边形ABCD 是菱形. 11.B. 12.D. 13.C. 14.C.15.C. 提示:因为ABC ∆的底边BC 的长不变,BC 边上的高等于直线b a ,之间的距离也不变,所以ABC ∆的面积不变.16.A. 提示:由于()BAF DAE FAE DAE FAE ∠-=∠=∠∠∠ο9021,所以通过折叠后得到的是由 . 17.B.提示:先说明DF=BF,DE=CE,所以四边形AFDE 的周长=AF+DF+DE+AE=AF+BF+CE+AE=AB+AC. 18.C.19.因为BD=CD ,所以,C DBC ∠=∠又因为四边形ABCD 是平行四边形,所以AD ∥BC ,所以,DBC D ∠=∠因为οοοο20709090,,=-=∠-=∠∆⊥D DAE AED BD AE 中所以在直角.20.(1)因为四边形ABCD 是平行四边形,所以AB=DC ,又AF=CG ,所以AB -AF=DC -CG,即GD=BF,又 DG ∥BF,所以四边形DFBG 是平行四边形,所以DF=BG ;(2)因为四边形DFBG 是平行四边形,所以DF ∥GB,所以AFD GBF ∠=∠,同理可得DGE GBF ∠=∠,所以ο100=∠=∠DGE AFD .21.(1)平行四边,两组对边分别相等的四边形是平行四边形;(2)矩,有一个是直角的平行四边形是矩形.22.如图所示,连结对角线AC 、BD,过A 、B 、C 、D 分别作BD 、AC 、BD 、AC 的平行线,且这些 平行线两两相交于E 、F 、G 、H ,四边形EFGH 即为符合条件的平行四边形.练习31、把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图).试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想.AB C D EFGH D CA B GH FE2、四边形ABCD 、DEFG 都是正方形,连接AE 、CG .(1)求证:AE =CG ;(2)观察图形,猜想AE 与CG 之间的位置关系,并证明你的猜想.3、将平行四边形纸片ABCD 按如图方式折叠,使点C 与A 重合,点D 落到D ′ 处,折痕为EF .(1)求证:△ABE ≌△AD ′F ;(2)连接CF ,判断四边形AECF 是什么特殊四边形?证明你的结论.挑战自我:A B CDEFD ′1、 (2010年眉山市).如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ABC 的度数为( )A .90°B .60°C .45°D .30°2、(2010福建龙岩中考)下列图形中,单独选用一种图形不能进行平面镶嵌的图形是( )A. 正三角形B. 正方形C. 正五边形D. 正六边形3.(2010年北京顺义)若一个正多边形的一个内角是120°,则这个正多边形的边数是( )A .9B .8C .6D .44、(2010年福建福州中考)如图4,在□ABCD 中,对角线AC 、BD 相交于点O ,若AC=14,BD=8,AB=10,则△OAB 的周长为 。
中考数学真题分类汇编及解析(二十七)平行四边形

(2022•广东中考)如图,在▱ABCD 中,一定正确的是( )A .AD =CDB .AC =BD C .AB =CD D .CD =BC【解析】选C .因为四边形ABCD 是平行四边形,所以AB =CD 。
(2022•舟山中考)如图,在△ABC 中,AB =AC =8.点E ,F ,G 分别在边AB ,BC ,AC 上,EF ∥AC ,GF ∥AB ,则四边形AEFG 的周长是( )A .32B .24C .16D .8【解析】选C .因为EF ∥AC ,GF ∥AB ,所以四边形AEFG 是平行四边形,∠B =∠GFC ,∠C =∠EFB ,因为AB =AC ,所以∠B =∠C ,所以∠B =∠EFB ,∠GFC =∠C ,所以EB =EF ,FG =GC ,因为四边形AEFG 的周长是AE +EF +FG +AG ,所以四边形AEFG 的周长是AE +EB +GC +AG =AB +AC ,因为AB =AC =8,所以四边形AEFG 的周长是AG +AC =8+8=16。
(2022•泰安中考)如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,点E 为BC 的中点,连接EO 并延长交AD 于点F ,∠ABC =60°,BC =2AB .下列结论:①AB ⊥AC ;②AD =4OE ;③四边形AECF 是菱形;④S △BOE =14S △ABC ,其中正确结论的个数是( )A .4B .3C .2D .1【解析】选A .因为点E 为BC 的中点,所以BC =2BE =2CE ,又因为BC =2AB ,所以AB =BE ,因为∠ABC =60°,所以△ABE 是等边三角形,所以∠BAE =∠BEA =60°,(2022•达州中考)如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是()A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF【解析】选B.因为D,E分别是AB,BC的中点,所以DE是△ABC的中位线,所以DE∥AC,DE=12 AC,A、当∠B=∠F,不能判定AD∥CF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;B、因为DE=EF,所以DE=12DF,所以AC=DF,因为AC∥DF,所以四边形ADFC为平行四边形,故本选项符合题意;C、根据AC=CF,不能判定AC=DF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;(2022•宜宾中考)如图,在△ABC 中,AB =AC =5,D 是BC 上的点,DE ∥AB 交AC 于点E ,DF ∥AC 交AB 于点F ,那么四边形AEDF 的周长是( )A .5B .10C .15D .20【解析】选B .因为DE ∥AB ,DF ∥AC ,所以四边形AFDE 是平行四边形,∠B =∠EDC ,∠FDB =∠C因为AB =AC ,所以∠B =∠C ,所以∠B =∠FDB ,∠C =∠EDF ,所以BF =FD ,DE =EC ,所以C ▱AFDE =AB +AC =5+5=10。
人教中考数学平行四边形综合经典题附答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).(1)当点N落在边BC上时,求t的值.(2)当点N到点A、B的距离相等时,求t的值.(3)当点Q沿D→B运动时,求S与t之间的函数表达式.(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF 与四边形PQMN的面积比为2:3时t的值.【答案】(1)(2)2(3)S=S菱形PQMN=2S△PNQ=t2;(4)t=1或【解析】试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;(3)当0≤t≤时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当≤t≤时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.(4)MN、MQ与边BC的有交点时,此时<t<,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.试题解析:(1)∵△PQN与△ABC都是等边三角形,∴当点N落在边BC上时,点Q与点B重合.∴DQ=3∴2t=3.∴t=;(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,∴PD=DQ,当0<t<时,此时,PD=t,DQ=2t∴t=2t∴t=0(不合题意,舍去),当≤t<3时,此时,PD=t,DQ=6﹣2t∴t=6﹣2t,解得t=2;综上所述,当点N到点A、B的距离相等时,t=2;(3)由题意知:此时,PD=t,DQ=2t当点M在BC边上时,∴MN=BQ∵PQ=MN=3t,BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①,当0≤t≤时,S△PNQ=PQ2=t2;∴S=S菱形PQMN=2S△PNQ=t2,如图②,当≤t≤时,设MN、MQ与边BC的交点分别是E、F,∵MN=PQ=3t,NE=BQ=3﹣2t,∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,∵△EMF是等边三角形,∴S△EMF=ME2=(5t﹣3)2.;(4)MN、MQ与边BC的交点分别是E、F,此时<t<,t=1或.考点:几何变换综合题2.如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M 沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.(1)P点的坐标为多少(用含x的代数式表示);(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.【答案】(1)P点坐标为(x,3﹣x).(2)S的最大值为,此时x=2.(3)x=,或x=,或x=.【解析】试题分析:(1)求P点的坐标,也就是求OM和PM的长,已知了OM的长为x,关键是求出PM的长,方法不唯一,①可通过PM∥OC得出的对应成比例线段来求;②也可延长MP交BC于Q,先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长,然后根据PM=AB﹣PQ来求出PM的长.得出OM和PM的长,即可求出P点的坐标.(2)可按(1)②中的方法经求出PQ的长,而CN的长可根据CN=BC﹣BN来求得,因此根据三角形的面积计算公式即可得出S,x的函数关系式.(3)本题要分类讨论:①当CP=CN时,可在直角三角形CPQ中,用CQ的长即x和∠ABC的余弦值求出CP的表达式,然后联立CN的表达式即可求出x的值;②当CP=PN时,那么CQ=QN,先在直角三角形CPQ中求出CQ的长,然后根据QN=CN﹣CQ求出QN的表达式,根据题设的等量条件即可得出x的值.③当CN=PN时,先求出QP和QN的长,然后在直角三角形PNQ中,用勾股定理求出PN 的长,联立CN的表达式即可求出x的值.试题解析:(1)过点P作PQ⊥BC于点Q,有题意可得:PQ∥AB,∴△CQP∽△CBA,∴∴解得:QP=x,∴PM=3﹣x,由题意可知,C(0,3),M(x,0),N(4﹣x,3),P点坐标为(x,3﹣x).(2)设△NPC的面积为S,在△NPC中,NC=4﹣x,NC边上的高为,其中,0≤x≤4.∴S=(4﹣x)×x=(﹣x2+4x)=﹣(x﹣2)2+.∴S的最大值为,此时x=2.(3)延长MP交CB于Q,则有PQ⊥BC.①若NP=CP,∵PQ⊥BC,∴NQ=CQ=x.∴3x=4,∴x=.②若CP=CN ,则CN=4﹣x ,PQ=x ,CP=x ,4﹣x=x , ∴x=;③若CN=NP ,则CN=4﹣x .∵PQ=x ,NQ=4﹣2x ,∵在Rt △PNQ 中,PN 2=NQ 2+PQ 2,∴(4﹣x )2=(4﹣2x )2+(x )2, ∴x=.综上所述,x=,或x=,或x=.考点:二次函数综合题.3.如图①,在等腰Rt ABC 中,90BAC ∠=,点E 在AC 上(且不与点A 、C 重合),在ABC △的外部作等腰Rt CED △,使90CED ∠=,连接AD ,分别以AB ,AD 为邻边作平行四边形ABFD ,连接AF .()1请直接写出线段AF ,AE 的数量关系;()2①将CED 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断线段AF ,AE 的数量关系,并证明你的结论;②若25AB =2CE =,在图②的基础上将CED 绕点C 继续逆时针旋转一周的过程中,当平行四边形ABFD 为菱形时,直接写出线段AE 的长度.【答案】(1)证明见解析;(2)①AF 2AE =②42或22.【解析】【分析】 ()1如图①中,结论:AF 2AE =,只要证明AEF 是等腰直角三角形即可; ()2①如图②中,结论:AF 2AE =,连接EF ,DF 交BC 于K ,先证明EKF ≌EDA 再证明AEF 是等腰直角三角形即可;②分两种情形a 、如图③中,当AD AC =时,四边形ABFD 是菱形.b 、如图④中当AD AC =时,四边形ABFD 是菱形.分别求解即可.【详解】()1如图①中,结论:AF 2AE =.理由:四边形ABFD 是平行四边形,AB DF ∴=,AB AC =,AC DF ∴=,DE EC =,AE EF ∴=,DEC AEF 90∠∠==,AEF ∴是等腰直角三角形,AF 2AE ∴=.故答案为AF 2AE =.()2①如图②中,结论:AF 2AE=.理由:连接EF ,DF 交BC 于K .四边形ABFD 是平行四边形,AB//DF ∴,DKE ABC 45∠∠∴==,EKF 180DKE 135∠∠∴=-=,EK ED =,ADE 180EDC 18045135∠∠=-=-=,EKF ADE ∠∠∴=,DKC C ∠∠=,DK DC ∴=,DF AB AC ==,KF AD ∴=,在EKF 和EDA 中,EK ED EKF ADE KF AD =⎧⎪∠=∠⎨⎪=⎩,EKF ∴≌EDA ,EF EA ∴=,KEF AED ∠∠=,FEA BED 90∠∠∴==,AEF ∴是等腰直角三角形,AF 2AE ∴=.②如图③中,当AD AC =时,四边形ABFD 是菱形,设AE 交CD 于H ,易知EH DH CH 2===22AH (25)(2)32=-=,AE AH EH 42=+=,=时,四边形ABFD是菱形,易知如图④中当AD AC=-=-=,AE AH EH32222综上所述,满足条件的AE的长为4222【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质、勾股定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,寻找全等的条件是解题的难点,属于中考常考题型.4.如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;(2)当∠B=70°时,求∠AEC的度数;(3)当△ACE为直角三角形时,求边BC的长.【答案】(1)()22303y x x x =-++<<;(2)∠AEC =105°;(3)边BC 的长为2117+. 【解析】试题分析:(1)过A 作AH ⊥BC 于H ,得到四边形ADCH 为矩形.在△BAH 中,由勾股定理即可得出结论.(2)取CD 中点T ,连接TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∠AET =∠B =70°.又AD =AE =1,得到∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,即可得到结论.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 解△ABH 即可得到结论.②当∠CAE =90°时,易知△CDA ∽△BCA ,由相似三角形对应边成比例即可得到结论. 试题解析:解:(1)过A 作AH ⊥BC 于H .由∠D =∠BCD =90°,得四边形ADCH 为矩形. 在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,∴22221y x =+-, 则()22303y x x x =-++<<(2)取CD 中点T ,联结TE ,则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD ,∴∠AET =∠B =70°.又AD =AE =1,∴∠AED =∠ADE =∠DET =35°.由ET 垂直平分CD ,得∠CET =∠DET =35°,∴∠AEC =70°+35°=105°.(3)分两种情况讨论:①当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2.②当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-- 则22411724AD CA x x AC CB x x -=⇒=⇒=-(舍负) 易知∠ACE <90°,所以边BC 117+ 综上所述:边BC 的长为2117+.点睛:本题是四边形综合题.考查了梯形中位线,相似三角形的判定与性质.解题的关键是掌握梯形中常见的辅助线作法.5.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.(1)试猜想AE与GC有怎样的关系(直接写出结论即可);(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.(3)在(2)中,若E是BC的中点,且BC=2,则C,F两点间的距离为.【答案】(1) AE=CG,AE⊥GC;(2)成立,证明见解析;2.【解析】【分析】(1)观察图形,AE、CG的位置关系可能是垂直,下面着手证明.由于四边形ABCD、DEFG都是正方形,易证得△ADE≌△CDG,则∠1=∠2,由于∠2、∠3互余,所以∠1、∠3互余,由此可得AE⊥GC.(2)题(1)的结论仍然成立,参照(1)题的解题方法,可证△ADE≌△CDG,得∠5=∠4,由于∠4、∠7互余,而∠5、∠6互余,那么∠6=∠7;由图知∠AEB=∠CEH=90°﹣∠6,即∠7+∠CEH=90°,由此得证.(3)如图3中,作CM⊥DG于G,GN⊥CD于N,CH⊥FG于H,则四边形CMGH是矩形,可得CM=GH,CH=GM.想办法求出CH,HF,再利用勾股定理即可解决问题.【详解】(1)AE=CG,AE⊥GC;证明:延长GC交AE于点H,在正方形ABCD与正方形DEFG中,AD=DC,∠ADE=∠CDG=90°,DE=DG,∴△ADE≌△CDG(SAS),∴AE,CG,∠1=∠2∵∠2+∠3=90°,∴∠1+∠3=90°,∴∠AHG=180°﹣(∠1+∠3)=180°﹣90°=90°,∴AE⊥GC.(2)答:成立;证明:延长AE和GC相交于点H,在正方形ABCD和正方形DEFG中,AD=DC,DE=DG,∠ADC=∠DCB=∠B=∠BAD=∠EDG=90°,∴∠1=∠2=90°﹣∠3;∴△ADE≌△CDG(SAS),∴AE=CG,∠5=∠4;又∵∠5+∠6=90°,∠4+∠7=180°﹣∠DCE=180°﹣90°=90°,∴∠6=∠7,又∵∠6+∠AEB=90°,∠AEB=∠CEH,∴∠CEH+∠7=90°,∴∠EHC=90°,∴AE⊥GC.(3)如图3中,作CM⊥DG于G,GN⊥CD于N,CH⊥FG于H,则四边形CMGH是矩形,可得CM=GH,CH=GM.∵BE =CE =1,AB =CD =2,∴AE =DE =CG ═DG =FG 5∵DE =DG ,∠DCE =∠GND ,∠EDC =∠DGN ,∴△DCE ≌△GND(AAS),∴GCD =2,∵S △DCG =12•CD•NG =12•DG•CM , ∴2×25, ∴CM =GH 45, ∴MG =CH 22CG CM -355, ∴FH =FG ﹣FG 5, ∴CF 22FH CH +22535()()55+2. 2.【点睛】 本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.6.(1)(问题发现)如图1,在Rt △ABC 中,AB =AC =2,∠BAC =90°,点D 为BC 的中点,以CD 为一边作正方形CDEF ,点E 恰好与点A 重合,则线段BE 与AF 的数量关系为(2)(拓展研究)在(1)的条件下,如果正方形CDEF 绕点C 旋转,连接BE ,CE ,AF ,线段BE 与AF 的数量关系有无变化?请仅就图2的情形给出证明;(3)(问题发现)当正方形CDEF 旋转到B ,E ,F 三点共线时候,直接写出线段AF 的长.【答案】(1)2AF ;(2)无变化;(3)AF 313.【解析】试题分析:(1)先利用等腰直角三角形的性质得出2 ,再得出BE=AB=2,即可得出结论;(2)先利用三角函数得出22CA CB =,同理得出22CF CE =,夹角相等即可得出△ACF ∽△BCE ,进而得出结论;(3)分两种情况计算,当点E 在线段BF 上时,如图2,先利用勾股定理求出2,6,即可得出62,借助(2)得出的结论,当点E 在线段BF 的延长线上,同前一种情况一样即可得出结论.试题解析:(1)在Rt △ABC 中,AB=AC=2,根据勾股定理得,22,点D 为BC 的中点,∴AD=122, ∵四边形CDEF 是正方形,∴2,∵BE=AB=2,∴2AF ,故答案为2AF ;(2)无变化;如图2,在Rt △ABC 中,AB=AC=2,∴∠ABC=∠ACB=45°,∴sin ∠ABC=2CA CB = 在正方形CDEF 中,∠FEC=12∠FED=45°, 在Rt △CEF 中,sin ∠FEC=2CF CE = ∴CF CA CE CB=, ∵∠FCE=∠ACB=45°,∴∠FCE ﹣∠ACE=∠ACB ﹣∠ACE ,∴∠FCA=∠ECB ,∴△ACF ∽△BCE ,∴BE CB AF CA=2∴2AF , ∴线段BE 与AF 的数量关系无变化;(3)当点E 在线段AF 上时,如图2,由(1)知,CF=EF=CD=2, 在Rt △BCF 中,CF=2,BC=22, 根据勾股定理得,BF=6,∴BE=BF ﹣EF=6﹣2,由(2)知,BE=2AF ,∴AF=3﹣1,当点E 在线段BF 的延长线上时,如图3,在Rt △ABC 中,AB=AC=2,∴∠ABC=∠ACB=45°,∴sin ∠ABC=2CA CB =, 在正方形CDEF 中,∠FEC=12∠FED=45°, 在Rt △CEF 中,sin ∠FEC=2CF CE = ,∴CF CA CE CB = , ∵∠FCE=∠ACB=45°,∴∠FCB+∠ACB=∠FCB+∠FCE ,∴∠FCA=∠ECB ,∴△ACF ∽△BCE ,∴BE CB AF CA= =2,∴BE=2AF , 由(1)知,CF=EF=CD=2,在Rt △BCF 中,CF=2,BC=22,根据勾股定理得,BF=6,∴BE=BF+EF=6+2,由(2)知,BE=2AF ,∴AF=3+1.即:当正方形CDEF 旋转到B ,E ,F 三点共线时候,线段AF 的长为3﹣1或3+1.7.已知90AOB ∠=︒,点C 是AOB ∠的角平分线OP 上的任意一点,现有一个直角MCN ∠绕点C 旋转,两直角边CM ,CN 分别与直线OA ,OB 相交于点D ,点E .(1)如图1,若CD OA ⊥,猜想线段OD ,OE ,OC 之间的数量关系,并说明理由. (2)如图2,若点D 在射线OA 上,且CD 与OA 不垂直,则(1)中的数量关系是否仍成立?如成立,请说明理由;如不成立,请写出线段OD ,OE ,OC 之间的数量关系,并加以证明.(3)如图3,若点D 在射线OA 的反向延长线上,且2OD =,8OE =,请直接写出线段CE 的长度.【答案】(1)详见解析;(2)详见解析;(334【解析】【分析】(1)先证四边形ODCE 为矩形,再证矩形ODCE 为正方形,由正方形性质可得;(2)过点C 作CG OA ⊥于点G ,CH OB ⊥于点H ,证四边形OGCH 为正方形,再证()CGD CHE ASA ∆≅∆,可得;(3)根据()CGD CHE ASA ∆≅∆,可得2OE OD OH OG OC -=+=.【详解】解:(1)∵90AOB ∠=︒,90MCN ∠=︒,CD OA ⊥,∴四边形ODCE 为矩形.∵OP 是AOB ∠的角平分线,∴45DOC EOC ∠=∠=︒,∴OD CD =,∴矩形ODCE 为正方形, ∴2OC OD =,2OC OE =.∴2OD OE OC +=.(2)如图,过点C 作CG OA ⊥于点G ,CH OB ⊥于点H ,∵OP 平分AOB ∠,90AOB ∠=︒,∴四边形OGCH 为正方形,由(1)得:2OG OH OC +=,在CGD ∆和CHE ∆中, 90CGD CHE CG CHDCG ECH ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩, ∴()CGD CHE ASA ∆≅∆,∴GD HE =,∴2OD OE OC +=.(3)2OG OH OC +=, ()CGD CHE ASA ∆≅∆,∴GD HE =. ∵OD GD OG =-,OE OH EH =+,∴2OE OD OH OG OC -=+=, ∴32OC =,∴34CE =,CE 的长度为34.【点睛】考核知识点:矩形,正方形的判定和性质.熟练运用特殊四边形的性质和判定是关键.8.如图,在平面直角坐标系xOy 中,四边形OABC 的顶点A 在x 轴的正半轴上,OA=4,OC=2,点D 、E 、F 、G 分别为边OA 、AB 、BC 、CO 的中点,连结DE 、EF 、FG 、GD .(1)若点C 在y 轴的正半轴上,当点B 的坐标为(2,4)时,判断四边形DEFG 的形状,并说明理由.(2)若点C 在第二象限运动,且四边形DEFG 为菱形时,求点四边形OABC 对角线OB 长度的取值范围.(3)若在点C 的运动过程中,四边形DEFG 始终为正方形,当点C 从X 轴负半轴经过Y 轴正半轴,运动至X 轴正半轴时,直接写出点B 的运动路径长.【答案】(1)正方形(2)256OB <<(3)2π【解析】分析:(1)连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25,当点C 在x 轴上时,AC=6, 故可得结论;(3)根据题意计算弧长即可.详解:(1)正方形,如图1,证明连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)256OB <<如图2,由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25,当点C 在x 轴上时,AC=6, ∴256OB << ;(3)2π.如图3,当四边形DEFG 是正方形时,OB ⊥AC ,且OB=AC ,构造△OBE ≌△ACO ,可得B 点在以E (0,4)为圆心,2为半径的圆上运动.所以当C 点从x 轴负半轴到正半轴运动时,B 点的运动路径为2π .图1 图2 图3点睛:本题主要考查了正方形的判定,菱形的性质以及弧长的计算.灵活运用正方形的判定定理和菱形的性质运用是解题的关键.9.已知:如图,四边形ABCD 和四边形AECF 都是矩形,AE 与BC 交于点M ,CF 与AD 交于点N .(1)求证:△ABM≌△CDN;(2)矩形ABCD和矩形AECF满足何种关系时,四边形 AMCN是菱形,证明你的结论.【答案】(1)证明见解析;(2)当AB=AF时,四边形AMCN是菱形.证明见解析;【解析】试题分析:(1)由已知条件可得四边形AMCN是平行四边形,从而可得AM=CN,再由AB=CD,∠B=∠D=90°,利用HL即可证明;(2)若四边形AMCN为菱形,则有AM=AN,从已知可得∠BAM=∠FAN,又∠B=∠F=90°,所以有△ABM≌△AFN,从而得AB=AF,因此当AB=AF时,四边形AMCN是菱形.试题解析:(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD∥BC.∵四边形AECF是矩形,∴AE∥CF.∴四边形AMCN是平行四边形.∴AM=CN.在Rt△ABM和Rt△CDN中,AB=CD,AM=CN,∴Rt△ABM≌Rt△CDN.(2)当AB=AF时,四边形AMCN是菱形.∵四边形ABCD、AECF是矩形,∴∠B=∠BAD=∠EAF=∠F=90°.∴∠BAD-∠NAM=∠EAF-∠NAM,即∠BAM=∠FAN.又∵AB=AF,∴△ABM≌△AFN.∴AM=AN.由(1)知四边形AMCN是平行四边形,∴平行四边形AMCN是菱形.考点:1.矩形的性质;2.三角形全等的判定与性质;3.菱形的判定.10.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO 绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式;(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.【答案】(1)见解析(2)∠PAG =45°,PG=OG+BP.理由见解析(3)y=x﹣3.(4)、.【解析】试题分析:(1)由AO=AD,AG=AG,根据斜边和一条直角边对应相等的两个直角三角形全等,判断出△AOG≌△ADG即可.(2)首先根据三角形全等的判定方法,判断出△ADP≌△ABP,再结合△AOG≌△ADG,可得∠DAP=∠BAP,∠1=∠DAG;然后根据∠1+∠DAG+∠DAP+∠BAP=90°,求出∠PAG的度数;最后判断出线段OG、PG、BP之间的数量关系即可.(3)首先根据△AOG≌△ADG,判断出∠AGO=∠AGD;然后根据∠1+∠AGO=90°,∠2+∠PGC=90°,判断出当∠1=∠2时,∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,求出∠1=∠2=30°;最后确定出P、G两点坐标,即可判断出直线PE的解析式.(4)根据题意,分两种情况:①当点M在x轴的负半轴上时;②当点M在EP的延长线上时;根据以M、A、G为顶点的三角形是等腰三角形,求出M点坐标是多少即可.试题解析:(1)在Rt△AOG和Rt△ADG中,(HL)∴△AOG≌△ADG.(2)在Rt△ADP和Rt△ABP中,∴△ADP≌△ABP,则∠DAP=∠BAP;∵△AOG≌△ADG,∴∠1=∠DAG;又∵∠1+∠DAG+∠DAP+∠BAP=90°,∴2∠DAG+2∠DAP=90°,∴∠DAG+∠DAP=45°,∵∠PAG=∠DAG+∠DAP,∴∠PAG=45°;∵△AOG≌△ADG,∴DG=OG,∵△ADP≌△ABP,∴DP=BP,∴PG=DG+DP=OG+BP.(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠PGC,又∵∠AGO=∠AGD,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=180°÷3=60°,∴∠1=∠2=90°﹣60°=30°;在Rt△AOG中,∵AO=3,∴OG=AOtan30°=3×=,∴G点坐标为(,0),CG=3﹣,在Rt△PCG中,PC===3(﹣1),∴P点坐标为:(3,3﹣3 ),设直线PE的解析式为:y=kx+b,则,解得:,∴直线PE的解析式为y=x﹣3.(4)①如图1,当点M在x轴的负半轴上时,,∵AG=MG,点A坐标为(0,3),∴点M坐标为(0,﹣3).②如图2,当点M在EP的延长线上时,,由(3),可得∠AGO=∠PGC=60°,∴EP与AB的交点M,满足AG=MG,∵A点的横坐标是0,G点横坐标为,∴M的横坐标是2,纵坐标是3,∴点M坐标为(2,3).综上,可得点M坐标为(0,﹣3)或(2,3).考点:几何变换综合题.。
2024中考数学全国真题分类卷 第十七讲 平行四边形与多变形(含答案)

2024中考数学全国真题分类卷第十七讲平行四边形与多变形命题点1平行四边形的判定1.(2023河北)依据所标数据,下列一定为平行四边形的是()2.(2023达州)如图,在△ABC 中,点D ,E 分别是AB ,BC 边的中点,点F 在DE 的延长线上.添加一个条件,使得四边形ADFC 为平行四边形,则这个条件可以是()第2题图A.∠B =∠FB.DE =EFC.AC =CFD.AD =CF3.(新趋势)·注重学习过程(2023永州)如图,BD 是平行四边形ABCD 的对角线,BF 平分∠DBC ,交CD 于点F .(1)请用尺规作∠ADB 的角平分线DE ,交AB 于点E (要求保留作图痕迹,不写作法);第3题图(2)根据图形猜想四边形DEBF 为平行四边形,请将下面的证明过程补充完整.证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠ADB =∠________(两直线平行,内错角相等).又∵DE 平分∠ADB ,BF 平分∠DBC ,∴∠EDB =12∠ADB ,∠DBF =12∠DBC ,∴∠EDB =∠DBF .∴DE ∥__________(______________________)(填推理的依据).又∵四边形ABCD 是平行四边形,∴BE ∥DF .∴四边形DEBF为平行四边形(________________________)(填推理的依据).4.(2023贺州)如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且ED=BF,连接AF,CE,AC,EF,且AC与EF相交于点O.(1)求证:四边形AFCE是平行四边形;(2)若AC平分∠FAE,AC=8,tan∠DAC=34,求四边形AFCE的面积.第4题图5.(2023毕节)如图①,在四边形ABCD中,AC和BD相交于点O,AO=CO,∠BCA=∠CA D.(1)求证:四边形ABCD是平行四边形;(2)如图②,E,F,G分别是BO,CO,AD的中点,连接EF,GE,GF,若BD=2AB,BC =15,AC=16,求△EFG的周长.第5题图命题点2平行四边形性质的相关证明与计算6.(2023广东省卷)如图,在▱ABCD中,一定正确的是()第6题图A.AD=CDB.AC=BDC.AB=CDD.CD=BC7.(2023湘潭)如图,在▱ABCD 中,连接AC ,已知∠BAC =40°,∠ACB =80°,则∠BCD =()第7题图A.80°B.100°C.120°D.140°8.(2023内江)如图,在▱ABCD 中,已知AB =12,AD =8,∠ABC 的平分线BM 交CD 边于点M ,则DM 的长为()第8题图A.2B.4C.6D.89.(2023赤峰)如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD ,其中一张纸条在转动过程中,下列结论一定成立的是()第9题图A.四边形ABCD 周长不变B.AD =CDC.四边形ABCD 面积不变D.AD =BC源自人教八下P 43第2题10.(2023无锡)如图,在▱ABCD 中,AD =BD ,∠ADC =105°,点E 在AD 上,∠EBA =60°,则ED CD 的值是()第10题图A.23B.12C.32D.2211.(2023泰安)如图,四边形ABCD为平行四边形,则点B的坐标为________.第11题图12.(2023邵阳)如图,在等腰△ABC中,∠A=120°,顶点B在▱ODEF的边DE上,已知∠1=40°,则∠2=________.第12题图13.(2022青海省卷)如图,在▱ABCD中,对角线BD=8cm,AE⊥BD,垂足为E,且AE=3cm,BC=4cm.则AD与BC之间的距离为________.第13题图14.(2022嘉兴)如图,在▱ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=23,则AH的长为________.第14题图15.(2022哈尔滨)四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E,若CE=2,则▱ABCD的周长为________.16.(2023烟台)如图,在▱ABCD中,DF平分∠ADC,交AB于点F,BE∥DF,交AD的延长线于点E.若∠A=40°,求∠ABE的度数.第16题图17.(2023扬州)如图,在▱ABCD中,BE,DG分别平分∠ABC,∠ADC,交AC于点E,G.(1)求证:BE∥DG,BE=DG;(2)过点E作EF⊥AB,垂足为F.若▱ABCD的周长为56,EF=6,求△ABC的面积.第17题图18.(挑战题)(2023包头)如图,在▱ABCD中,AC是一条对角线,且AB=AC=5,BC=6,E,F是AD边上两点,点F在点E的右侧,AE=DF,连接CE,CE的延长线与BA的延长线相交于点G.(1)如图①,M是BC边上一点,连接AM,MF,MF与CE相交于点N.①若AE =32,求AG 的长;②在满足①的条件下,若EN =NC ,求证:AM ⊥BC ;(2)如图②,连接GF ,H 是GF 上一点,连接EH .若∠EHG =∠EFG +∠CEF ,且HF =2GH ,求EF 的长.第18题图命题点3多边形及其性质类型一多边形的计算19.(2023柳州)如图,四边形ABCD 的内角和等于()第19题图A.180°B.270°C.360°D.540°20.(2022扬州)如图,点A ,B ,C ,D ,E 在同一平面内,连接AB ,BC ,CD ,DE ,EA ,若∠BCD =100°,则∠A +∠B +∠D +∠E =()第20题图A.220°B.240°C.260°D.280°21.(2023河北)如图,将三角形纸片剪掉一角得四边形,设△ABC与四边形BCDE的外角和的度数分别为α,β,,则正确的是()第21题图A.α-β=0B.α-β<0C.α-β>0D.无法比较α与β的大小22.(2023眉山)一个多边形外角和是内角和的29,则这个多边形的边数为______.类型二正多边形的性质及计算23.(2023烟台)一个正多边形每个内角与它相邻外角的度数比为3∶1,则这个正多边形是()A.正方形B.正六边形C.正八边形D.正十边形24.(2023甘肃省卷)大自然中有许多小动物都是“小数学家”,如图①,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图②,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为()第24题图A.2mmB.22mmC.23mmD.4mm25.(2023舟山)正八边形一个内角的度数是________.26.(2023株洲)如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO=________度.第26题图27.(2022上海)六个带30度角的直角三角板拼成一个正六边形,直角三角板的最短边为1,中间正六边形的面积为________.第27题图28.(2023宿迁)如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形面积平分,则直线l被正六边形所截的线段长是________.第28题图类型三平面镶嵌29.(2023青岛)图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果.图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图③镶嵌得到图④,将图④着色后,再次镶嵌便得到图①,则图④中∠ABC的度数是________°.第29题图参考答案与解析1.D【解析】A选项只能得到上下一组对边平行,不能判定为平行四边形;B选项只能得到左右一组对边平行,不能判定为平行四边形;C选项只能得到左右一组对边相等,不能判定为平行四边形;D选项可以得到上下一组对边平行且相等,可以判定为平行四边形.2.B【解析】∵在△ABC中,D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE∥AC且DE=12AC.当∠B=∠F时,不能判定CF∥AD,即不能判定四边形ADFC为平行四边形,故选项A不符合题意,当DE=EF时,DF=AC,∴四边形ADFC为平行四边形,故选项B符合题意;当AC=CF时,不能判定CF∥AD,即不能判定四边形ADFC为平行四边形,故选项C不符合题意;根据AD=CF,DF∥AC不能判定四边形ADFC为平行四边形,故选项D不符合题意.3.解:(1)如解图,DE即为所求作的角平分线;第3题解图(2)DBC;BF;内错角相等,两直线平行;两组对边分别平行的四边形是平行四边形.4.(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AE∥FC.∵ED=BF,∴AD-ED=BC-BF,即AE=FC,∴四边形AFCE是平行四边形;(2)解:∵AE∥FC,∴∠EAC=∠ACF.∵AC平分∠FAE,∴∠EAC=∠FAC,∴∠ACF=∠FAC,∴AF=FC,由(1)知四边形AFCE是平行四边形,∴平行四边形AFCE是菱形,∴AO =12AC =4,AC ⊥EF ,在Rt △AOE 中,AO =4,tan ∠DAC =34,∴EO =3,∴S △AOE =12AO ·EO =12×4×3=6,∴S 菱形AFCE =4S △AOE =24.5.(1)证明:在△AOD 和△COB 中,DAO =∠BCO ,=CO ,AOD =∠COB ,∴△AOD ≌△COB ,∴DO =BO ,∴四边形ABCD 是平行四边形;(2)解:如解图,连接DF .∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB =DC .∵BD =2AB ,∴DO =DC .∵E ,F 分别是BO ,CO 的中点,∴DF ⊥OC ,EF ∥12BC ,EF ∥12AD ,∴∠DFA =90°.∵G 是AD 的中点,∴GF =12AD =EF =GD ,∴四边形EFDG 是平行四边形,∴GE =DF .∵AC =16,∴AF =12,∵BC =15,∴EF =GF =7.5,∴在Rt △ADF 中,DF =AD 2-AF 2=152-122=9,∴△EFG 的周长为EF +GF +GE =7.5+7.5+9=24.第5题解图6.C7.C 【解析】∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠ACD =∠BAC =40°,∴∠BCD =∠ACB +∠ACD =80°+40°=120°.8.B 【解析】∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB =CD =12,AD =BC =8,∴∠CMB =∠ABM ,∵BM 平分∠ABC ,∴∠ABM =∠CBM ,∴∠CMB =∠CBM ,∴CM =CB =8,∴DM =CD -CM =12-8=4.9.D 【解析】∵两张纸条对边平行,∴四边形ABCD 是平行四边形,∴AB =CD ,AD =BC ,但长度在改变,∴周长、面积都会改变.10.D 【解析】如解图,过点B 作BF ⊥AD 于点F ,则∠BFD =∠BFA =90°,∵四边形ABCD 是平行四边形,∴∠A +∠ADC =180°,AB =CD ,∵∠ADC =105°,∴∠A =75°,∵AD =BD ,∴∠ABD =∠A =75°,∴∠ADB =30°,设BF =x ,则BD =2x ,DF =3x ,∴AF =AD -DF =BD -DF =2x -3x ,∴AB =BF 2+AF 2=x 2+(2x -3x )2=(6-2)x ,即CD =(6-2)x ,∵∠EBA =60°,∠A =75°,∴∠BEF =45°,∴∠EBF =90°-45°=45°,∴∠BEF =∠EBF ,∴EF =BF =x ,∴ED =DF -EF =3x -x =(3-1)x ,∴ED CD=(3-1)x(6-2)x =22.第10题解图11.(-2,-1)【解析】∵A (-1,2),D (3,2),∴AD ∥x 轴,AD =4.∵四边形ABCD 为平行四边形,∴AD ∥BC ,BC =AD ,∴BC ∥x 轴,BC =4,∵C (2,-1),点C 在点B 右边,∴点B 的坐标为(-2,-1).12.110°【解析】∵在等腰△ABC 中,∠A =120°,∴∠ABC =∠C =30°,∵∠1=40°,∴∠ABE =70°,∵四边形ODEF 是平行四边形,∴OF ∥DE ,∴∠2+∠ABE =180°,∴∠2=110°.13.6cm【解析】设AD 与BC 之间的距离为h cm ,∵BD =8cm ,AE =3cm ,AE ⊥BD ,∴S △ABD =12BD ·AE =12×8×3=12(cm 2),∴S ▱ABCD =2S △ABD =24(cm 2),又∵S ▱ABCD =BC ·h =24,BC =4cm ,∴h =244=6(cm).14.233【解析】∵AB ⊥AC ,BC =23,AB =2,∴在Rt △ABC 中,AC =BC 2-AB 2=22,∴在▱ABCD 中,AO =12AC =2.在Rt △ABO 中,BO =AO 2+AB 2=6,∵AB ⊥AC ,AH ⊥BD ,∴∠OAB =∠AHB =90°.又∵∠ABO =∠HBA ,∴△ABO ∽△HBA ,∴AH AO =AB BO ,即AH 2=26,解得AH =233.15.20或28【解析】如解图①,当点E 在线段BC 上时,∵四边形ABCD 为平行四边形,∴BC ∥AD ,∴∠BEA =∠EAD .∵AE 平分∠BAD ,∴∠BAE =∠EAD ,∴∠BEA =∠BAE ,∴BE =AB =6,∵CE =2,∴BC =BE +CE =6+2=8,∴▱ABCD 的周长为2×(6+8)=28;如解图②,当点E 在线段BC 延长线上时,∵四边形ABCD 为平行四边形,∴BC ∥AD ,∴∠BEA =∠EAD .∵AE 平分∠BAD ,∴∠BAE =∠EAD ,∴∠BEA =∠BAE ,∴BE =AB =6,∵CE =2,∴BC =BE -CE =6-2=4,∴▱ABCD 的周长为2×(6+4)=20,∴▱ABCD 的周长为20或28.第15题解图16.解:如解图,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠1=∠2.又∵DF 平分∠ADC ,第16题解图∴∠1=∠3,∴∠2=∠3.∵∠A =40°,∴∠2=∠3=70°.又∵BE ∥DF ,∴∠ABE =∠2=70°.17.(1)证明:∵四边形ABCD 是平行四边形,∴∠ABC =∠ADC ,AD =BC ,AD ∥BC ,∵BE ,DG 分别平分∠ABC ,∠ADC ,∴∠CBE =12∠ABC ,∠ADG =12∠ADC ,∴∠CBE =∠ADG ,∵AD ∥BC ,∴∠DAG =∠BCE ,∴△ADG ≌△CBE ,∴∠AGD =∠BEC ,BE =DG ,∴∠CGD =∠AEB ,∴BE ∥DG ;(2)解:如解图,过点E 作EM ⊥BC 于点M ,第17题解图∵▱ABCD 的周长为56,∴AB +BC =28,∵BE 为∠ABC 的平分线,∴EF =EM =6,∴S △ABC =S △ABE +S △BCE =12AB ·EF +12BC ·EM =12×6(AB +BC )=84.18.(1)①解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,DC =AB =5,AD =BC =6,∴∠GAE =∠CDE ,∠AGE =∠DCE ,∴△AGE ∽△DCE ,∴AG DC =AE DE,∴AG ·DE =DC ·AE .∵AE =32,∴DE =AD -AE =6-32=92,∴92AG =5×32,∴AG =53;②证明:∵AD ∥BC ,∴∠EFN =∠CMN ,∵EN =NC ,∠ENF =∠CNM ,∴△ENF ≌△CNM ,∴EF =CM ,∵AE =32,AE =DF ,∴EF =AD -AE -DF =3,∴CM =3,∴BM =BC -CM =3,∴BM =CM ,∵AB =AC ,∴AM ⊥BC ;(2)解:如解图,连接CF ,第18题解图∵AB =AC ,AB =DC ,∴AC =DC ,∴∠CAD =∠CDA ,∵AE =DF ,∴△AEC ≌△DFC ,∴CE =CF ,∴∠CEF =∠CFE .∵∠EHG =∠EFG +∠CEF ,∴∠EHG =∠EFG +∠CFE =∠CFG ,∴EH ∥CF ,∴GH HF =GE EC,∵HF =2GH ,∴GE EC =12.由(1)①知△AGE ∽△DCE ,∴AE DE =GE CE =12,∴DE =2AE .∵AD =6,∴AE =2,∴DF =2,∴EF =AD -AE -DF =2.19.C20.D 【解析】如解图,连接BD ,∵∠BCD =100°,∴∠CBD +∠CDB =180°-100°=80°,∴∠A +∠ABC +∠CDE +∠E =360°-(∠CBD +∠CDB )=360°-80°=280°.第20题解图21.A 【解析】任意多边形外角和度数均为360°,∴△ABC 与四边形BCDE 的外角和度数都为360°,∴α=β=360°,∴α-β=0.22.11【解析】∵外角和等于内角和的29,多边形的外角和为360°,∴内角和等于360°÷29=1620°,设多边形的边数为n ,由题意得(n -2)×180°=1620°,解得n =11,故该多边形的边数是11.23.C 【解析】∵该正多边形每个内角与它相邻的外角的度数比为3∶1,∴可设该正多边形每个内角与它相邻的外角的度数分别为3x ,x ,∴x +3x =180°,解得x =45°.∵正多边形的外角和为360°,∴该多边形的边数为360°÷45°=8,∴这个正多边形是正八边形.24.D 【解析】如解图,分别过点B ,C 作BM ⊥AD ,CN ⊥AD 于点M ,N ,∵六边形ABCDEF是正六边形,∴∠BAM =60°,∠ABM =30°,∴AM =12AB ,同理DN =12AB ,由作图可知四边形BCNM 是矩形,∴MN =BC =AB ,∴AD =AM +MN +DN =2AB =8,∴AB =4.第24题解图【一题多解】取AD 的中点O ,构造出△ABO ,△CBO ,△CDO ,易得均为等边三角形,即可求解.25.135°【解析】正八边形的内角和为(8-2)×180°=1080°,所以它的一个内角的度数是1080°÷8=135°.26.48【解析】由正多边形内角和定理可知,∠EAB =(5-2)×180°5=108°,又∵∠EAB =∠MON +∠AEO ,∠MON =60°,∴∠AEO =48°.27.332【解析】由对称性及直角三角形的性质可知,中间小正六边形的边长为1.根据正六边形的面积公式可得,S =6×34×12=332.28.47【解析】如解图,设正六边形ABCDEF 的中心为O ,连接MO 并延长交边CD 于点N ,∵正六边形是中心对称图形,∴MN 将正六边形ABCDEF 的面积平分,点M 和点N 关于点O 对称,∴OM =ON ,即MN =2OM ,连接OA ,OF ,过点O 作OP ⊥AF 于点P ,∵六边形ABCDEF 是正六边形,AB =6,∴AB =AF =6,OA =OF ,∠AOF =60°,∴△OAF是等边三角形,∴OA =6,∵OP ⊥AF ,∴PA =PF =12AF =3,∴OP =OA 2-PA 2=33,∵AM =2,∴PM =PA -AM =3-2=1,∴OM =OP 2+PM 2=27,∴MN =2OM =47,即直线l 被正六边形所截的线段长是47.第28题解图29.60【解析】如解图,∵BC ∥AE ,∴∠ABC +∠BAE =180°,∴∠BAE =180°-∠ABC .∵图④是由有3个大小相同的图③镶嵌得到的,∴∠BAF =∠EAF =∠BAE ,∵∠BAF +∠EAF+∠BAE=360°,∴∠BAE=120°,∴∠ABC=60°.第29题解图。
九年级中考数学平行四边形专题复习(含答案)

九年级中考数学平行四边形专题复习一、选择题:1.已知四边形ABCD是平行四边形,再从①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ) A.选①② B.选②③ C.选①③ D.选②④2.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )A.△EBD是等腰三角形,EB=ED B.折叠后∠ABE和∠CBD一定相等C.折叠后得到的图形是轴对称图形 D.△EBA和△EDC一定是全等三角形3.有下列说法:①由许多条线段连接而成的图形叫做多边形;②多边形的边数是不小于4的自然数;③从一个多边形(边数为n)的同一个顶点出发,分别连接这个顶点与其余与之不相邻的各顶点,可以把这个多边形分割成(n-2)个三角形;④半圆是扇形.其中正确的结论有( )A.1个 B.2个 C.3个 D.4个4.如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )95°D D.85°105°C C.95°A.115°115°B B.105°5.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )A.1.8B.2.4C.3.2D.3.66.现有纸片:4张边长为a的正方形,3张边长为b的正方形,8张宽为a、长为b的长方形,用这15张纸片重新拼出一个长方形,那么该长方形的长为( )A.2a+3b B.2a+b C.a+3b D.无法确定7.如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形 ENCM 的面积之比为( )A.9:4 B.12:5 C.3:1 D.5:28.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )A. B.2 C. +1 D.2+19.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )A.1 B.2 C.3 D.410.如图,已知矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )A.6cm2 B.8cm2 C.10cm2 D.12cm2二、填空题:11.如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形______.12.如图,在▱ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD度数为 .13.如图,为一块面积为1.5m2的直角三角形模板,其中∠B=90°,AB=1.5m,现要把它加工成正方形DEFG 木板(EF在AC上,点D和点G分别在AB和BC上),则该正方形木板的边长为______m.14.如图,正方形ABCD的长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH,则四边形EFGH面积的最小值是 cm2.15.在中,,其面积为,则的最大值是.16.已知平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+0.5m-0.25=0的两个实数根.当m= 时,四边形ABCD是菱形.三、解答题:17.如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.求平行四边形ABCD的周长.18.如图,已知在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.19.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上, 顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.(1)求证:△AEH∽△ABC;(2)求这个正方形的边长与面积.20.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的九分之一?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.21.下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长为 ;(2)在图中画出两条裁剪线,并画出将此六边形剪拼成的正方形.22.如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45°,交直线BC边于点F,连结EF.探究:当点E在边AB上,求证:EF=AE+CF.应用:(1)当点E在边AB上,且AD=2时,则△BEF的周长是 .(2)当点E不在边AB上时,EF,AE,CF三者的数量关系是 .参考答案1.B2.B3.B4.C5.D6.A7.D8.B9.C10.A11.答案为:△AFE(答案不唯一).12.答案为:120°.13.答案为:.14.答案为:32.15.答案为:16.答案为:1.17.解:在平行四边形ABCD中,∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABE=∠EBC,∠BCE=∠ECD.,∴∠EBC+∠BCE=90°,∴∠BEC=90°, ∴BC22=BE22+CE22=1222+522=1322∴BC=13cm,∵AD∥BC,∴∠AEB=∠EBC,∴∠AEB=∠ABE,∴AB=AE,同理CD=ED,∵AB=CD,∴AB=AE=CD=ED=0.5BC=6.5cm,∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm18.提示:取BE的中点P,证明四边形EFPC是平行四边形.19.(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC.(2)解:如图设AD与EH交于点M.∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM,设正方形EFGH的边长为x,∵△AEH∽△ABC,∴=,∴=,∴x=,∴正方形EFGH的边长为cm,面积为cm2.20.21.答案为:(1);(2)如图:22.探究:证明:如图,延长BA到G,使AG=CF,连接DG,∵四边形ABCD 是正方形,∴DA=DC ,∠DAG=∠DCF=90°, ∴△DAG ≌△DCF (SAS ),∴∠1=∠3,DG=DF ,∵∠ADC=90°,∠EDF=45°,∴∠EDG=∠1+∠2=∠3+∠2=45°2=45°==∠EDF , ∵DE=DE ,∴△GDE ≌△FDE (SAS ),∴EF=EG=AE+AG=AE+CF ; 应用:解:(1)△BEF 的周长=BE+BF+EF ,由探究得:EF=AE+CF , ∴△BEF 的周长=BE+BF+AE+CF=AB+BC=2+2=4,故答案为:4; (2)当点E 不在边AB 上时,分两种情况:①点E 在BA 的延长线上时,如图2,EF=CF ﹣AE ,理由是:在CB 上取CG=AE ,连接DG , ∵∠DAE=∠DCG=90°,AD=DC ,∴△DAE ≌△DCG (SAS )∴DE=DG ,∠EDA=∠GDC ∵∠ADC=90°,∴∠EDG=90°∴∠EDF+∠FDG=90°,∵∠EDF=45°,∴∠FDG=90°﹣45°45°=45°=45°,∴∠EDF=∠FDG=45°, 在△EDF 和△GDF 中,∵,∴△EDF ≌△GDF (SAS ),∴EF=FG ,∴EF=CF ﹣CG=CF ﹣AE ;②当点E 在AB 的延长线上时,如图3,EF=AE ﹣CF ,理由是:把△DAE 绕点D 逆时针旋转90°至△DCG ,可使AD 与DC 重合,连接DG , 由旋转得:DE=DG ,∠EDG=90°,AE=CG ,∵∠EDF=45°,∴∠GDF=90°﹣45°45°=45°=45°,∴∠EDF=∠GDF , ∵DF=DF ,∴△EDF ≌△GDF ,∴EF=GF ,∴EF=CG ﹣CF=AE ﹣CF ;综上所述,当点E 不在边AB 上时,EF ,AE ,CF 三者的数量关系是:EF=CF ﹣AE 或EF=AE ﹣CF ;故答案为:EF=CF ﹣AE 或EF=AE ﹣CF .。
人教备战中考数学平行四边形综合经典题及详细答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,矩形ABCD 中,AB =6,BC =4,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F .(1)求证:四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,求EF 的长.【答案】(1)证明见解析;(2)133. 【解析】 分析:(1)根据平行四边形ABCD 的性质,判定△BOE ≌△DOF (ASA ),得出四边形BEDF 的对角线互相平分,进而得出结论;(2)在Rt △ADE 中,由勾股定理得出方程,解方程求出BE ,由勾股定理求出BD ,得出OB ,再由勾股定理求出EO ,即可得出EF 的长.详解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A=90°,AD=BC=4,AB ∥DC ,OB=OD ,∴∠OBE=∠ODF ,在△BOE 和△DOF 中,OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF (ASA ),∴EO=FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF ,设BE=x ,则 DE=x ,AE=6-x ,在Rt △ADE 中,DE 2=AD 2+AE 2,∴x 2=42+(6-x )2,解得:x=133, ∵22AD AB +13 ∴OB=1213 ∵BD ⊥EF ,∴EO=22BE OB -=2133, ∴EF=2EO=4133. 点睛:本题主要考查了矩形的性质,菱形的性质、勾股定理、全等三角形的判定与性质,熟练掌握矩形的性质和勾股定理,证明三角形全等是解决问的关键 2.已知矩形纸片OBCD 的边OB 在x 轴上,OD 在y 轴上,点C 在第一象限,且86OB OD ==,.现将纸片折叠,折痕为EF (点E ,F 是折痕与矩形的边的交点),点P 为点D 的对应点,再将纸片还原。
(I )若点P 落在矩形OBCD 的边OB 上,①如图①,当点E 与点O 重合时,求点F 的坐标;②如图②,当点E 在OB 上,点F 在DC 上时,EF 与DP 交于点G ,若7OP =,求点F 的坐标:(Ⅱ)若点P 落在矩形OBCD 的内部,且点E ,F 分别在边OD ,边DC 上,当OP 取最小值时,求点P 的坐标(直接写出结果即可)。
平行四边形中考真题精选含答案
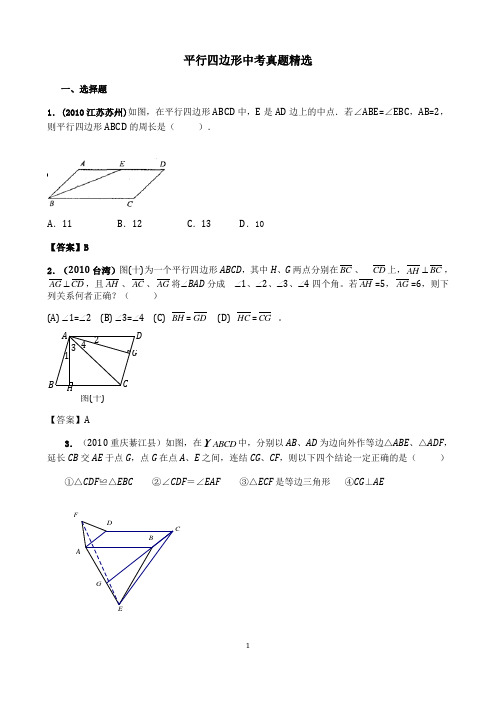
平行四边形中考真题精选一、选择题1.(2010江苏苏州)如图,在平行四边形ABCD 中,E 是AD 边上的中点.若∠ABE=∠EBC ,AB=2,则平行四边形ABCD 的周长是( ).A .11B .12C .13D .10【答案】B2.(2010台湾)图(十)为一个平行四边形ABCD ,其中H 、G 两点分别在BC 、 CD 上,AH ⊥BC ,AG ⊥CD ,且AH 、AC 、AG 将∠BAD 分成 ∠1、∠2、∠3、∠4四个角。
若AH =5,AG =6,则下列关系何者正确?( )(A) ∠1=∠2 (B) ∠3=∠4 (C) BH =GD (D) HC =CG 。
【答案】A3.(2010重庆綦江县)如图,在ABCD 中,分别以AB 、AD 为边向外作等边△ABE 、△ADF ,延长CB 交AE 于点G ,点G 在点A 、E 之间,连结CG 、CF ,则以下四个结论一定正确的是( )①△CDF ≌△EBC②∠CDF =∠EAF③△ECF 是等边三角形④CG ⊥AEGFEDCBAA BCD G H 1 23 4 图(十)A .只有①②B .只有①②③C .只有③④D .①②③④【答案】B4.(2010山东临沂)如图,在ABCD 中,AC 与BD 相交于点O ,点E 是边BC 的中点,4AB ,则OE 的长是( )(A )2 (B(C )1 (D )12【答案】A5.(2010湖南衡阳)如图,在□ABCD 中,AB=6,AD=9,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE ,垂足为G ,BG=24,则ΔCEF 的周长为( ) A.8 B.9.5 C.10D.11.5【答案】A6.(2010 河北)如图 ,在□ABCD 中,AC 平分∠DAB ,AB = 3, 则□ABCD 的周长为( )A .6B .9C .12D .15 【答案】CABCD第6题EODCBA7.(2010浙江湖州)如图在ABCD 中,AD =3cm ,AB =2cm ,则ABCD 的周长等于( )A .10cmB .6cmC .5cmD .4cm【答案】A .8.(2010 四川成都)已知四边形ABCD ,有以下四个条件:①//AB CD ;②A B C D=;③//BC AD ;④BC AD =.从这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法种数共有( ) (A )6种 (B )5种 (C )4种 (D )3种 【答案】C9.(2010山东泰安)如图,E 是□ABCD 的边AD 的中点,CE 与BA 的延长线交于点F ,若∠FCD=∠D ,则下列结论不成立的是( )A 、AD=CFB 、BF=CFC 、AF=CD D 、DE=EF【答案】C10.(2010 内蒙古包头)已知下列命题:①若00a b >>,,则0a b +>; ②若a b ≠,则22a b ≠;③角的平分线上的点到角的两边的距离相等; ④平行四边形的对角线互相平分.其中原命题与逆命题均为真命题的个数是( ) A .1个 B .2个 C .3个 D .4个【答案】BA DCB11.(2010 重庆江津)如图,四边形ABCD 的对角线互相平分,要使它成为矩形, 那么需要添加的条件是( ) A .AB CD =B .AD BC = C .AB BC =D .AC BD =【答案】D12.(2010宁夏回族自治区)点A 、B 、C 是平面内不在同一条直线上的三点,点D 是平面内任意一点,若A 、B 、C 、D 四点恰能构成一个平行四边形,则在平面内符合这样条件的点D 有 ( ) A .1个 B .2个 C .3个 D .4个 【答案】C13.(2010鄂尔多斯)如图,在□ABCD 中,E 是BC 的中点,且∠AEC=∠DCE ,则下列结论不正确...的是( )A .S △ADF=2S △EBFB .BF=21DF C .四边形AECD 是等腰梯形 D . ∠AEC=∠ADC【答案】A14.(2010广东清远)如图 ,在ABCD 中,已知∠ODA =90°,AC =10cm ,BD =6cm ,则AD 的长为( ) A .4cmB .5cmC .6cmD .8cm【答案】A 二、填空题1.(2010福建福州)如图,在ABCD 中,对角线AC 、BD 相交于点O ,若AC =14,BD =8,AB =10,则△OAB 的周长为_______.(第1题)【答案】212.(2010福建宁德)如图,在□ABCD 中,AE =EB ,AF =2,则FC 等于_____.【答案】43.(2010 山东滨州)如图,平行四边形ABCD 中, ∠ABC=60°,E 、F 分别在CD 、BC 的延长线上,AE∥BD,EF ⊥BC,DF=2,则EF 的长为 .【答案】4.(2010山东潍坊)如图,在△ABC 中,AB =BC ,AB =12cm ,F 是AB 边上的一点,过点F 作FE∥BC 交CA 于点E ,过点E 作ED ∥AB 交于BC 于点D ,则四边形BDEF 的周长是 .第2题图FA E BCD【答案】24cm5.(2010湖南常德)如图 ,四边形ABCD 中,AB//CD ,要使四边形ABCD 为平行四边形,则可添加的条件为 .(填一个即可).【答案】AB CD A C AD =∠=∠或或∥BC 等6.(2010湖南郴州)如图,已知平行四边形ABCD ,E 是AB 延长线上一点,连结DE 交BC 于点F ,在不添加任何辅助线的情况下,请补充一个条件,使CDF BEF △≌△,这个条件是.(只要填一个)【答案】DC EB =或CF BF =或DF EF = 或F 为DE 的中点或F 为BC 的中点或AB BE =或B 为AE 的中点7.(2010湖北荆州)如图,在平行四边形ABCD 中,∠A=130°,在AD 上取DE=DC ,则∠ECB 的度数是.【答案】65°8.(2010湖北恩施自治州)如图,在ABCD 中,已知AB =9㎝,AD =6㎝,BE 平分∠ABC 交DC 边于点E ,则DE 等于 ㎝.ABEFDC第6题D BCA5题【答案】39.(2010云南红河哈尼族彝族自治州) 如图,在图(1)中,A 1、B 1、C 1分别是△ABC 的边BC 、CA 、AB 的中点,在图(2)中,A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 1、C 1 A 1、 A 1B 1的中点,…,按此规律,则第n 个图形中平行四边形的个数共有 个.【答案】3n10.(2010 江苏镇江)如图,在平行四边形ABCD 中,CD=10,F 是AB 边上一点,DF 交AC 于点E ,且的面积的面积则CDE AEF EC AE ∆∆=,52= ,BF=.【答案】6,25411.(2010 广西钦州市)如图,□ABCD 的对角线AC 、BD 相交于点O ,点E 是CD 的中点, 若AD =4cm ,则OE 的长为 cm .【答案】212.(2010青海西宁)如图,在□ABCD 中,对角线AC 、BD 相交于点O ,如果AC=14,BD=8,AB=x ,那么x 的取值范围是 .D11题ECBAO(3)(2)(1)C 3B 3A 3A 2C 1B 11CBAC 2B 2B 2C 2ABC1B 1C 1A 2C 1B 11CBA…第9题12题 【答案】3﹤x ﹤11.13.(2010广西梧州)如图 ,在□ABCD 中,E 是对角线BD 上的点,且E F ∥AB ,DE :EB =2:3,E F =4,则CD =的长为________【答案】1014.(2010广东深圳)如图 ,在□ABCD 中,AB=5,AD=8,DE 平分∠ADC ,则BE=【答案】315.(2010辽宁本溪)过□ABCD 对角线交点O 作直线m ,分别交直线AB 于点E ,交直线CD 于点F ,若AB =4,AE =6,则DF 的长是 . 【答案】2或1016.(2010广西河池)如图 ,在□ABCD 中,∠A =120°,则∠D = °.【答案】60 三、解答题BD1613题ABCD F E1. (2010浙江嘉兴)如图,在□ABCD 中,已知点E 在AB 上,点F 在CD 上,且CF AE =. (1)求证:BF DE =;(2)连结BD ,并写出图中所有的全等三角形.(不要求证明)【答案】(1)在□ABCD 中,AB //CD ,AB =CD .∵AE =CF ,∴BE =DF ,且BE //DF . ∴四边形BFDE 是平行四边形. ∴BF DE =. …5分(2)连结BD ,如图,图中有三对全等三角形: △ADE ≌△CBF , △BDE ≌△DBF , △ABD ≌△CDB . …3分2.(2010 嵊州市)(10分)已知:在四边形ABCD 中,A D ∥BC ,∠BAC =∠D ,点E 、F 分别在BC 、CD 上,且∠AEF =∠ACD ,试探究AE 与EF 之间的数量关系。
中考数学平行四边形综合经典题含答案

中考数学平行四边形综合经典题含答案一、平行四边形1.(1)、动手操作:如图①:将矩形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=20°,那么的度数为 .(2)、观察发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由.(3)、实践与运用:将矩形纸片ABCD按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC 边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F 重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.【答案】(1)125°;(2)同意;(3)60°【解析】试题分析:(1)根据直角三角形的两个锐角互余求得∠AEB=70°,根据折叠重合的角相等,得∠BEF=∠DEF=55°,根据平行线的性质得到∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°;(2)根据第一次折叠,得∠BAD=∠CAD;根据第二次折叠,得EF垂直平分AD,根据等角的余角相等,得∠AEG=∠AFG,则△AEF是等腰三角形;(3)由题意得出:∠NMF=∠AMN=∠MNF,MF=NF,由对称性可知,MF=PF,进而得出△MNF≌△MPF,得出3∠MNF=180°求出即可.试题解析:(1)、∵在直角三角形ABE中,∠ABE=20°,∴∠AEB=70°,∴∠BED=110°,根据折叠重合的角相等,得∠BEF=∠DEF=55°.∵AD∥BC,∴∠EFC=125°,再根据折叠的性质得到∠EFC′=∠EFC=125°.;(2)、同意,如图,设AD与EF交于点G由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.由折叠知,∠AGE=∠DGE=90°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE.所以AE=AF,即△AEF为等腰三角形.(3)、由题意得出:∠NMF=∠AMN=∠MNF,∴MF=NF,由折叠可知,MF=PF,∴NF=PF,而由题意得出:MP=MN,又∵MF=MF,∴△MNF≌△MPF,∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,即3∠MNF=180°,∴∠MNF=60°.考点:1.折叠的性质;2.等边三角形的性质;3.全等三角形的判定和性质;4.等腰三角形的判定2.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到到B′的位置,AB′与CD交于点E.(1)求证:△AED≌△CEB′(2)若AB = 8,DE = 3,点P为线段AC上任意一点,PG⊥AE于G,PH⊥BC于H.求PG + PH的值.【答案】(1)证明见解析;(2).【解析】【分析】(1)由折叠的性质知,,,,则由得到;(2)由,可得,又由,即可求得的长,然后在中,利用勾股定理即可求得的长,再过点作于,由角平分线的性质,可得,易证得四边形是矩形,继而可求得答案.【详解】(1)四边形为矩形,,,又,;(2),,,,在中,,过点作于,,,,,,,、、共线,,四边形是矩形,,.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作法,注意数形结合思想的应用.3.操作:如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.探究:(1)如图1,当点P在线段BC上时,①若∠BAP=30°,求∠AFE的度数;②若点E 恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?并求出此时∠AFD 的度数.归纳:(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;猜想:(3)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论.【答案】(1)①45°;②BC的中点,45°;(2)不会发生变化,证明参见解析;(3)不会发生变化,作图参见解析.【解析】试题分析:(1)当点P在线段BC上时,①由折叠得到一对角相等,再利用正方形性质求出∠DAE度数,在三角形AFD中,利用内角和定理求出所求角度数即可;②由E为DF中点,得到P为BC中点,如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,得到AF 垂直平分BE,进而得到三角形BOP与三角形EOG全等,利用全等三角形对应边相等得到BP=EG=1,得到P为BC中点,进而求出所求角度数即可;(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数不会发生变化,作AG⊥DF于点G,如图1(a)所示,利用折叠的性质及三线合一性质,根据等式的性质求出∠1+∠2的度数,即为∠FAG 度数,即可求出∠F度数;(3)作出相应图形,如图2所示,若点P在BC边的延长线上时,∠AFD的度数不会发生变化,理由为:作AG⊥DE于G,得∠DAG=∠EAG,设∠DAG=∠EAG=α,根据∠FAE为∠BAE一半求出所求角度数即可.试题解析:(1)①当点P在线段BC上时,∵∠EAP=∠BAP=30°,∴∠DAE=90°﹣30°×2=30°,在△ADE中,AD=AE,∠DAE=30°,∴∠ADE=∠AED=(180°﹣30°)÷2=75°,在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,∴∠AFE=180°﹣60°﹣75°=45°;②点E为DF 的中点时,P也为BC的中点,理由如下:如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,∵EG∥AD,DE=EF,∴EG=AD=1,∵AB=AE,∴点A在线段BE的垂直平分线上,同理可得点P在线段BE的垂直平分线上,∴AF垂直平分线段BE,∴OB=OE,∵GE∥BP,∴∠OBP=∠OEG,∠OPB=∠OGE,∴△BOP≌△EOG,∴BP=EG=1,即P为BC的中点,∴∠DAF=90°﹣∠BAF,∠ADF=45°+∠BAF,∴∠AFD=180°﹣∠DAF﹣∠ADF=45°;(2)∠AFD的度数不会发生变化,作AG⊥DF于点G,如图1(a)所示,在△ADE中,AD=AE,AG⊥DE,∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,∴∠1+∠2=×90°=45°,即∠FAG=45°,则∠AFD=90°﹣45°=45°;(3)如图2所示,∠AFE的大小不会发生变化,∠AFE=45°,作AG⊥DE于G,得∠DAG=∠EAG,设∠DAG=∠EAG=α,∴∠BAE=90°+2α,∴∠FAE=∠BAE=45°+α,∴∠FAG=∠FAE﹣∠EAG=45°,在Rt△AFG中,∠AFE=90°﹣45°=45°.考点:1.正方形的性质;2.折叠性质;3.全等三角形的判定与性质.4.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长.【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP62 23.【解析】【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】(1)如图1中,延长EO交CF于K,∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,∵△EFK是直角三角形,∴OF=12EK=OE;(2)如图2中,延长EO交CF于K,∵∠ABC=∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,∵|CF ﹣AE|=2,EF=23,AE=CK ,∴FK=2, 在Rt △EFK 中,tan ∠FEK=33,∴∠FEK=30°,∠EKF=60°, ∴EK=2FK=4,OF=12EK=2, ∵△OPF 是等腰三角形,观察图形可知,只有OF=FP=2, 在Rt △PHF 中,PH=12PF=1,HF=3,OH=2﹣3, ∴OP=()2212362+-=-.如图4中,点P 在线段OC 上,当PO=PF 时,∠POF=∠PFO=30°,∴∠BOP=90°,∴OP=33OE=33, 综上所述:OP 6223. 【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等,综合性较强,正确添加辅助线是解题的关键.5.如图①,在等腰Rt ABC V 中,90BAC ∠=o ,点E 在AC 上(且不与点A 、C 重合),在ABC △的外部作等腰Rt CED △,使90CED ∠=o ,连接AD ,分别以AB ,AD 为邻边作平行四边形ABFD ,连接AF .()1请直接写出线段AF ,AE 的数量关系;()2①将CED V 绕点C 逆时针旋转,当点E 在线段BC 上时,如图②,连接AE ,请判断线段AF ,AE 的数量关系,并证明你的结论;②若25AB =,2CE =,在图②的基础上将CED V 绕点C 继续逆时针旋转一周的过程中,当平行四边形ABFD 为菱形时,直接写出线段AE 的长度.【答案】(1)证明见解析;(2)①AF 2AE =②42或22.【解析】【分析】 ()1如图①中,结论:AF 2AE =,只要证明AEF V 是等腰直角三角形即可; ()2①如图②中,结论:AF 2AE =,连接EF ,DF 交BC 于K ,先证明EKF V ≌EDA V 再证明AEF V 是等腰直角三角形即可;②分两种情形a 、如图③中,当AD AC =时,四边形ABFD 是菱形.b 、如图④中当AD AC =时,四边形ABFD 是菱形.分别求解即可.【详解】()1如图①中,结论:AF 2AE =.理由:Q 四边形ABFD 是平行四边形,AB DF ∴=,AB AC =Q ,AC DF ∴=,DE EC =Q ,AE EF ∴=,DEC AEF 90∠∠==o Q ,AEF ∴V 是等腰直角三角形,AF 2AE ∴=.故答案为AF 2AE =.()2①如图②中,结论:AF 2AE =.理由:连接EF ,DF 交BC 于K .Q 四边形ABFD 是平行四边形,AB//DF ∴,DKE ABC 45∠∠∴==o ,EKF 180DKE 135∠∠∴=-=o o ,EK ED =,ADE 180EDC 18045135∠∠=-=-=o o o o Q ,EKF ADE ∠∠∴=,DKC C ∠∠=Q ,DK DC ∴=,DF AB AC ==Q ,KF AD ∴=,在EKF V 和EDA V 中,EK ED EKF ADE KF AD =⎧⎪∠=∠⎨⎪=⎩,EKF ∴V ≌EDA V ,EF EA ∴=,KEF AED ∠∠=,FEA BED 90∠∠∴==o ,AEF ∴V 是等腰直角三角形,AF 2AE ∴=.②如图③中,当AD AC =时,四边形ABFD 是菱形,设AE 交CD 于H ,易知EH DH CH 2===22AH (25)(2)32=-=,AE AH EH 42=+=,=时,四边形ABFD是菱形,易知如图④中当AD AC=-=-=,AE AH EH32222综上所述,满足条件的AE的长为42或22.【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质、勾股定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,寻找全等的条件是解题的难点,属于中考常考题型.6.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD 的延长线于点F,连接CF.(1)求证:四边形BCFD是菱形;(2)若AD=1,BC=2,求BF的长.【答案】(1)证明见解析(2)23【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB=223BD AD-=,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF=22AB AF+=23.7.已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且86OB OD==,.现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P 为点D的对应点,再将纸片还原。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
欢迎阅读平行四边形经典考点1 特殊的平行四边形的性质与判定1.矩形的定义、性质与判定(1)矩形的定义:有一个角是直角的平行四边形是矩形。
(2)矩形的性质:矩形的对角线_________;矩形的四个角都是________角。
矩形具有________的一切性质。
矩形是轴对称图形,对称轴有_____________条,矩形也是中心对称图形,对称中心为_____________的交点。
矩形被对角线分成了____________个等腰三角形。
(32(1(2菱形的(3(4_______3.正方形的性质及判定方法(1)正方形的性质:正方形的四个角都是_____________,四条边都_____________;正方形的两条对角线____________,并且互相垂直平分,每条对角线平分一组对角;正方形即是轴对称图形也是中心对称图形。
正方形具有平行四边形、矩形、菱形的一切性质。
(2)正方形的判定方法:有一组邻边相等的__ __是正方形;对角线互相____的矩形是正方形;有一个角是直角的菱形是正方形;对角线________的菱形是正方形。
温馨提示:无论是正方形的性质还是正方形的判定,它的中心思想就是正方形即是矩形,又是菱形,如果都从这个出发,则一切的性质与判定就都有了。
但要注意在利用对角线判定正方形时,“平分”这个前提,因为只有对角线平分了,此四边形才是平行四边形了,然后再证明是矩形又是菱形。
考点2 梯形的概念及判定方法1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形。
(1)等腰梯形:两腰相等的梯形叫做等腰梯形;(2)直角梯形:一腰垂直于底的梯形叫做直角梯形。
在初中阶段重点研究等腰梯形。
2.等腰梯形的性质与判定性质:(1)等腰梯形中,同一底上的两个角相等;(2)等腰梯形的对角线相等;判定:(1)同一底上的两个角相等的梯形是等腰梯形;(2)对角线相等的梯形是等腰梯形;(3)有两个腰相等的梯形是等腰梯形。
则△AEF 的周长为( ) A .32B .33C .34D .3例2:如图,把矩形ABCD 沿EF 对折后使两部分重合,若150∠=,则AEF ∠=( ) A .110° B .115° C .120° D .130° 一、选择题(每题3分,共30分)1.(09年河北)如图,在菱形ABCD 中,AB = 5,∠BCD =?120°,则对角线AC 等于( )BACD第1题图例1题图例2题图A .20B .15C . 10D .52.(09年广西南宁)如图,将一个长为10cm ,宽为8cm 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( ) A .210cmB .220cmC .240cmD .280cm3.(09年宁波市)如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙述正确的是( ) A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形AMON 与四边形ABCD 是位似图形D .四边形MBCO 和四边形NDCO 都是等腰梯形4.() A 5. 6.(A C 78 A .11 B .16 C .17 D .229.如图,□ABCD 的周长是28㎝, △ABC 的周长是22㎝,则AC 的长为 ( )A .6㎝B . 12㎝C .4㎝D . 8㎝10.(’09年孝感)如图,正方形ABCD 内有两条相交线段MN 、EF ,M 、N 、E 、F 分别在边AB 、CD 、AD 、BC 上.小明认为:若MN = EF ,则MN ⊥EF ;小亮认为: 若MN ⊥EF ,则MN = EF .你认为 A .仅小明对B .仅小亮对C .两人都对D .两人都不对第10题图A BD第8题图第9题图 题图11.(09年甘肃庆阳)如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5A =,则这个菱形的面积= cm 2.12.(09年南充)如图,等腰梯形ABCD 中,AD BC ∥,6047B AD BC ∠===°,,则梯形ABCD 的周长是 .13.(09白银市)如图,四边形ABCD 是平行四边形,使它为矩形的条件可以是 . 14.(09年济宁市)在等腰梯形ABCD 中,AD ∥BC , AD =3cm , AB =4cm , ∠B =60°, 则下底BC 的长为 cm . 15.(09江西)如图,一活动菱形衣架中,菱形的边长均为16cm ,若墙上钉子间的距离16cm AB BC ==,则1=∠ 度.年天津市)我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.若一个四边形18192021交CD 的延长线于点F . (1)求证:AM =DM ;(2)若DF =2,求菱形ABCD 的周长.23.(本题6分)(09襄樊市)如图所示,在Rt ABC △中,90ABC=︒∠.将Rt ABC △绕点C 顺时针方向旋转60︒得到DEC △,点E 在AC 上,再将Rt ABC △沿着AB 所在直线翻转180︒得到ABF △.连接AD . (1)求证:四边形AFCD 是菱形; (2)连接BE 并延长交AD 于G ,连接CG ,DCAB第12题图 第13题图第20题图A DFCEG 第11题图BA C D F M第22题图 E请问:四边形ABCG 是什么特殊平行四边形?为什么?24.(本题6分) (09年湖州)如图:已知在ABC △中,AB AC =,D 为BC 边的中点,过点D 作DE AB DF AC ⊥,⊥,垂足分别为E F ,.(1) 求证:BED CFD △≌△;(2)若90A ∠=°,求证:四边形DFAE 是正方形.25.(本题8分)(09年杭州市)如图,在等腰梯形ABCD 中,∠C =60°,AD ∥BC ,且AD =DC ,E 、F 分别在AD 、DC 的延长线上,且DE =CF ,AF 、BE 交于点P . (1(226.(本题(2)求下底27.(本题作BE (1(2)∠(3)∠28.(2010角线⑴ ⑵ ⑶ 当28.(本题且EF 交正方形外角的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.第24题图DC BE AF参考答案基础知识回放答案:①相等 ②直 ③平行四边形 ④2 ⑤对角线 ⑥4 ⑦直角 ⑧相等 ⑨四条边 ⑩垂直平分 ○11平分 ○122 ○13四条边 ○14互相垂直 ○15直角 ○16相等○17相等 ○18矩形 ○19垂直 ○20相等 中考效能测试 一、选择题1.D 【解析】本题考查了菱形的性质和等边三角形的判定。
根据菱形的性质知:AB=BC,∠B+∠BCD=180°,又有∠BCD=120°,∴∠B=60°,2.A 3.C 得,OM和NDCO 4.C5.D.由题意得∠即3x=36.C7.D 置,此时有最小值,BM 的长度就是DN+MN 的最小值.根据勾股定理BM=BC 2+CM 2=10,故答案为D.8.D 【解析】过点D 作D E ∥AC ,交AC 的延长线于点C 。
则此等腰梯形的周长就为三角形DBE 的周长,即等于此梯形的中位线的2倍加上腰长的2倍即可。
9.D 10.D 【解析】本题综合考查了菱形的性质、等腰三角形的性质、三角形全等、 直角三角形斜边上的中线的性质、三角形的内角和等知识点,是一道综合性很强的题目。
解答本题应首先延长PF 交AB 的延长线于点G ,根据题意,利用角角边可证明BGF ∆≌CPF ∆,于是得到G FPC ∠=∠,PF=FG ,所以在EGP Rt ∆中,EF 是斜边上的中线,于是得到FE=FG ,所以FEG G ∠=∠,又因为E 、F 分别为中点,所以EB=FB ,ADFC G E B图1 ADFC G E B 图2 A DFC E B 图3CD所以,FE=FG=BF ,所以B F E B E F G F PC ∠=∠=∠=∠,又因为∠A=110°,所以070=∠EBF ,因此,00180702=+∠FPC ,解得055=∠FPC 。
11.60 12.1713.答案不唯一,如AC =BD ,∠BAD =90o ,等 14.715.120 【解析】本题考查了菱形和等边三角形的性质。
如图,连接AB ,由题意可知AB=AC=BC=16cm ,∴△ABC 是等边三角形,所以∠ACB=60°,∴∠2=180°-60°=120°,由菱形的性质可得∠1=∠2=120°。
1617.AC =是平行四边形.条件“∠18.14或1912-。
所以,S 20.42 CDEF ,△ADE ≌△因为所以DE=6三、解答题21.(1)证明:∵AC 是菱形ABCD 的对角线, ∴AC 平分∠BCD . 又∠ACD=30°,∴∠BCD =60°. ∵∠BAD 与∠BCD 是菱形的一组对角, ∴∠BAD =∠BCD =60°. ∵AB 、AD 是菱形的两条边,∴AB AD =. ∴△ABD 是正三角形.(2)解:∵O 为菱形对角线的交点, ∴123902AC OC OD BD COD ===∠=,,°.在Rt COD △中,tan tan 30ODOCD OC=∠=°,∴tan30ODOC===°∴2AC OC==AC的长为22.(1)略证:∵四边形ABCD是菱形,∴AB∥CD,AB=AD. ∵AC⊥EF,∴AM=AE. ∵AE=21AB, ∴AM=21AD.∴AM=DM.(2)提示:证明△AME≌△DMF.DF=AE=2.菱形ABCD的周长为16.23.(1)证明:Rt DEC△是由Rt ABC△绕C点旋转60︒得到,∴60AC DC ACB ACD===︒,∠∠∴ACD△是等边三角形,∴AD又∵Rt∴∠∴AF(2∴AE∴∠∴AG24.(1BED CFD∴∠=∠,AB AC=B C∴∠=∠,D是BC的中点,BD∴(2)AB DF AC,⊥,90AFD∴∠=°,90A∠=∴BED△≌△25.(1)∵∠ADF,AE=DF,∴△(2)猜想∠BPF=120° .∵由(1)知△BAE≌△ADF,∴∠ABE=∠DAF .∴∠BPF=∠ABE+∠BAP=∠BAE,而AD∥BC,∠C=∠ABC=60°,∴∠BPF=120° .26.解:(1)∵∠A=60°,BD⊥AD∴∠ABD=30°.又∵AB∥CD∴∠CDB=∠ABD=30°.∵BC=CD∴∠CBD=∠CDB=30°.(2)∵∠ABD=∠CBD=30°∴∠ABC=60°=∠A.∴AD=BC=CD=2cm在Rt△ABD中,∴AB=2AD=4cm27.(1)在Rt AEB△中,AC BC=,12CE AB∴=,A DF CEGBABCDFEMGCB CE ∴=,CEB CBE ∴∠=∠.90CEF CBF ∠=∠=,BEF EBF ∴∠=∠,EF BF ∴=.90BEF FED ∠+∠=,90EBD EDB ∠+∠=,FED EDF ∴∠=∠.EF FD =.BF FD ∴=.(2)由(1)BFFD =,而BC CA =,CF AD ∴∥,即AE CF ∥.若AC EF ∥,则AC EF =,BC BF ∴=.BA BD ∴=,45A ∠=.∴当045A <∠<或4590A <∠<时,四边形ACFE 为梯形.(3)作GHBD ⊥,垂足为H ,则GH AB ∥.4DG =∴∠点180,∴∠60EDF ∴∠≤.又A ∠+∴当28.解:∴∴∠.AEB ∠+∴∠AME ∴△≌△(2证明:在BA 的延长线上取一点N . 使AN CE =,连接NE .BN BE ∴=.45N PCE ∴∠=∠=°.四边形ABCD 是正方形,AD BE ∴∥.DAE BEA ∴∠=∠. NAE CEF ∴∠=∠.ANE ECF ∴△≌△(ASA ). AE EF ∴=.7.(2010年宁德市)(本题满分13分)如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM. ⑴ 求证:△AMB ≌△ENB ;⑵ ①当M 点在何处时,AM +CM 的值最小;⑶ 当∴BA ∵∠∴∠即∠又∵∴△⑵①当AM +∴AM ∵∠∴△∴BM ∴AM ∴当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小,即等于EC 的长. ⑶过E 点作EF ⊥BC 交CB 的延长线于F , ∴∠EBF =90°-60°=30°. 设正方形的边长为x ,则BF =23x ,EF =2x . 在Rt △EFC 中, ∵EF 2+FC 2=EC 2,∴(2x )2+(23x +x )2=()213+. 解得,x =2(舍去负值).∴正方形的边长为2.。
