运筹学自测试题及答案word精品
最新运筹学试题及答案4套
《运筹学》试卷 、（15分）用图解法求解下列线性规划问题 max £ = 3歼 + 4X 2一兀］+ 2兀2 — 8X, + 2花 < 12 2眄 + r 2 <16 > 0 , x 2 > 0二、（20 分）下表为某求极大值线性规划问题的初始单纯形表及迭代后的表, 〔为松弛变量，试求表中」至匚的值及各变量下标匸至L 的值。
x 斗花hC1 0 6-1 3i11a1 -20 02-1 1/2 0 /hi 1 1/2 147JitZ、（15分）用图解法求解矩阵对策四、（20分）（1）某项工程由8个工序组成，各工序之间的关系为工序 a b c d e f g h紧前工序————aa b,c b,c,d b,c,d e试画出该工程的网络图。
（2）试计算下面工程网络图中各事项发生的最早、最迟时间及关键 精品文档其中 3 -24 1 3线路（箭线下的数字是完成该工序的所需时间，单位：天）五、（15分）已知线性规划问题max ? = ltbq + 24x a + 20x3+ 20JC4+2Sx5pq +羽+2X3 +3x t+ 5x s<19st/ 2Xj + 4x a + 3X3 + 2工4 +Xj <575 >o 0=12阳①其对偶问题最优解为匚；二'，试根据对偶理论求原问题的最优解六、（15分）用动态规划法求解下面问题：MAX Z = x}Xj + x2 + x3 = c（亏>0, ； = 1, 2,3七、（30分）已知线性规划问题MAX Z = 2^-+P 1Xj + x 2 + < 6 x ； +2^2<4用单纯形法求得最优单纯形表如下， 试分析在下列各种条件单独变化的情况下，最优解将如（1）目标函数变为''；；~6~丁 （2）约束条件右端项由4 变为 4（3）增加一个新的约束:I 十八、（20分）某地区有A 、B 、C 三个化肥厂向甲、乙、丙、丁四个销地供应同一 种化肥，已知产地产量、销地需求量和各产地运往不同销地单位运价如下表，试 用最小元素法确定初始调运方案，并调整求最优运输方案《运筹学》试卷二、（20分）已知线性规划问题：min z -2^ +5x3 +6x4x L+2X3+3X5+ > 2就,一2旺 +阳-+3X4 <-3x ■> 0 （j = 1^3,4）（a）写出其对偶问题；（b）用图解法求对偶问题的解；（c）利用（b）的结果及对偶性质求原问题的解。
《运筹学》试题及答案大全
《运筹学》试题及参考答案一、填空题（每空2分，共10分）1、在线性规划问题中，称满足所有约束条件方程和非负限制的解为可行解。
2、在线性规划问题中，图解法适合用于处理变量为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是设立虚供地或虚需求点，化为供求平衡的标准形式。
4、在图论中，称无圈的连通图为树。
5、运输问题中求初始基本可行解的方法通常有最小费用法、西北角法两种方法。
二、（每小题5分，共10分）用图解法求解下列线性规划问题：1）max z =6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x ，解：此题在“《运筹学》复习参考资料.doc ”中已有，不再重复。
2）min z =－3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解：可行解域为abcda ，最优解为b 点。
⑴⑵⑶⑷⑸⑹、⑺由方程组⎩⎨⎧==+02242221x x x 解出x 1=11，x 2=0∴X *=⎪⎪⎭⎫⎝⎛21x x =（11，0）T∴min z =－3×11+2×0=－33三、（15分）某厂生产甲、乙两种产品，这两种产品均需要A 、B 、C 三种资源，每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示：AB C 甲94370乙46101203602003001）建立使得该厂能获得最大利润的生产计划的线性规划模型；（5分）2）用单纯形法求该问题的最优解。
（10分）解：1）建立线性规划数学模型：设甲、乙产品的生产数量应为x 1、x 2，则x 1、x 2≥0，设z 是产品售后的总利润，则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x ，2）用单纯形法求最优解：加入松弛变量x 3，x 4，x 5，得到等效的标准模型：max z =70x 1+120x 2+0x 3+0x 4+0x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下：四、（10分）用大M 法或对偶单纯形法求解如下线性规划模型：min z =5x 1＋2x 2＋4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x 解：用大M 法，先化为等效的标准模型：max z /=－5x 1－2x 2－4x 3s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7，得到：max z /=－5x 1－2x 2－4x 3－M x 6－M x 7s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下：五、（15分）给定下列运输问题：（表中数据为产地A i 到销地B j 的单位运费）B 1B 2B 3B 4s iA 1A 2A 312348765910119108015d j82212181）用最小费用法求初始运输方案，并写出相应的总运费；（5分）2）用1）得到的基本可行解，继续迭代求该问题的最优解。
运筹学试题及详细答案
运筹学试题及详细答案
一、选择题
1、Nash均衡的定义是：
A、每位参与者的行为均达到最佳利益的状态
B、每位参与者的行为均达到得到最大胜利的状态
C、每位参与者的行为均达到合作的最佳状态
D、每位参与者的行为均达到合作的最大胜利的状态
答案：A
2、决策就是参与者用来实现选择的：
A、计划
B、机构
C、程序
D、工具
答案：D
3、运筹学可以分为：
A、组合数学
B、运动学
C、博弈论
D、概率论
答案：A、B、C、D
4、非线性规划有：
A、分支定界法
B、梯度下降法
C、基于格法的解法
D、对偶法
答案：A、B、C、D
5、关于迭代法,下列表述正确的有：
A、可以求解非凸优化问题
B、单次迭代过程简单
C、收敛性较好
D、用于非线性规划
答案：A、B、C
二、填空题：
1、博弈论是研究__参与者之间的__的科学。
答案：多，竞争。
(完整word版)最全的运筹学复习题及答案
5、线性规划数学模型具备哪几个要素？答：（1）.求一组决策变量x i或x ij的值（i =1，2，…m j=1，2…n）使目标函数达到极大或极小；（2）。
表示约束条件的数学式都是线性等式或不等式；(3）。
表示问题最优化指标的目标函数都是决策变量的线性函数第二章线性规划的基本概念一、填空题1．线性规划问题是求一个线性目标函数_在一组线性约束条件下的极值问题。
2．图解法适用于含有两个变量的线性规划问题.3．线性规划问题的可行解是指满足所有约束条件的解。
4．在线性规划问题的基本解中，所有的非基变量等于零.5．在线性规划问题中,基可行解的非零分量所对应的列向量线性无关6．若线性规划问题有最优解，则最优解一定可以在可行域的顶点（极点）达到。
7．线性规划问题有可行解，则必有基可行解。
8．如果线性规划问题存在目标函数为有限值的最优解，求解时只需在其基可行解_的集合中进行搜索即可得到最优解.9．满足非负条件的基本解称为基本可行解。
10．在将线性规划问题的一般形式转化为标准形式时,引入的松驰数量在目标函数中的系数为零。
11．将线性规划模型化成标准形式时，“≤”的约束条件要在不等式左_端加入松弛变量。
12．线性规划模型包括决策（可控）变量，约束条件，目标函数三个要素。
13．线性规划问题可分为目标函数求极大值和极小_值两类。
14．线性规划问题的标准形式中，约束条件取等式,目标函数求极大值,而所有变量必须非负。
15．线性规划问题的基可行解与可行域顶点的关系是顶点多于基可行解16．在用图解法求解线性规划问题时,如果取得极值的等值线与可行域的一段边界重合，则这段边界上的一切点都是最优解. 17．求解线性规划问题可能的结果有无解，有唯一最优解，有无穷多个最优解。
18。
如果某个约束条件是“≤"情形,若化为标准形式，需要引入一松弛变量。
19。
如果某个变量X j 为自由变量，则应引进两个非负变量X j ′ ， X j 〞， 同时令X j ＝X j ′－ X j 。
运筹学考试练习题精选全文完整版
可编辑修改精选全文完整版运筹学自测题第一套题一、判断题（T－正确，F－错误）1．图解法同单纯形法虽然求解的形式不同，但从几何上理解，两者是一致的。
2．若线性规划问题存在最优解，则最优解一定对应可行域边界上的一个点。
3．一旦一个人工变量在迭代中变为非基变量后，该变量及相应列的数字可以从单纯形表中删除，而不影响计算结果。
4．线性规划问题的可行解如为最优解，则该可行解一定是基可行解。
5．任何线性规划问题存在并具有唯一的对偶问题。
6．运输问题是一种特殊的线性规划模型，因而求解结果也可能出现下列四种情况之一：有唯一最优解，有无穷多最优解，无界解，无可行解。
7．整数规划的目标函数值一般优于其相应的线性规划问题的解的目标函数值。
8．分枝定界法在需要分枝时必须满足：分枝后的各子问题必须容易求解；各子问题解的集合必须包含原问题的解。
9．整数割平面法每次只割去问题的部分非整数解。
10．线性规划问题是目标规划问题的一种特殊形式。
11．目标规划模型中，应同时包含系统约束（绝对约束）与目标约束。
12．图论中的图不仅反映了研究对象之间的关系，而且是真实图形的写照，因而对图中点与点的相对位置、点与点连线的长短曲直等都要严格注意。
13．网络图中代表两点之间的距离长短的数字，其含义也可以是时间或费用。
14．在制定网络计划时，将一个任务分解成若干个独立的工作单元，称为任务的分解。
二、选择题1．线性规划数学模型的特征是：________都是线性的。
A. 目标函数和决策变量B. 决策变量和约束条件C. 目标函数和约束条件D. 目标函数、约束条件及决策变量2．关于剩余变量，下列说法错误的是：A. 为将某个大于等于约束化为等式约束，在该约束中减去一个剩余变量B. 剩余变量在实际问题中表示超过收益的部分C. 剩余变量在目标函数中的系数为零D. 在用单纯形法求解线性规划问题时，剩余变量一般作为初始基变量。
A. 任意m 个列向量组成的矩阵B. 任意m 阶子矩阵C. 前m 个列向量组成的矩阵D. 任意m 个线性无关的列向量组成的矩阵A. mB. n-mC. 至少mD. 至少n-m5．如果是求极大值的线性规划问题，单纯形法的每次迭代意味着其目标函数值将（ A）必然增加；（B）必然减少；（C）可能增加；（D）可能减少6．单纯形法求解线性规划问题时，如何判断问题存在无界解？（A）全部变量的检验数非负；（B）某个检验数为正的非基变量，其系数列向量不存在正分量；（C）最终的单纯形表中含有人工变量，且其取值不为零；（D）非基变量全部非正，且某个非基变量的检验数为零。
(完整word版)运筹学》习题答案 运筹学答案汇总
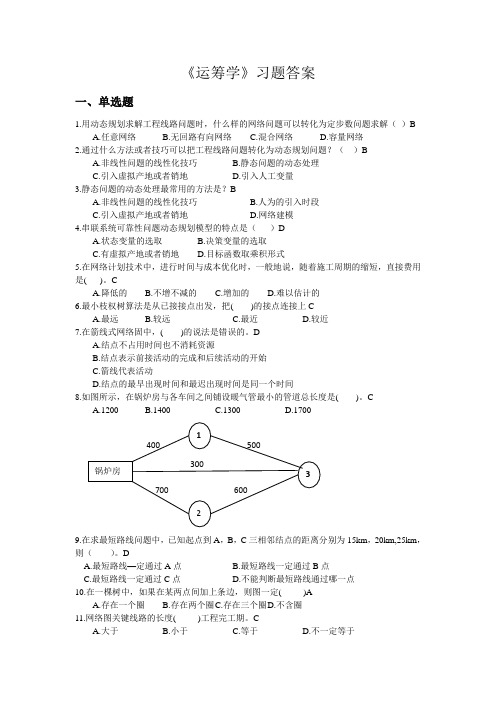
《运筹学》习题答案一、单选题1.用动态规划求解工程线路问题时，什么样的网络问题可以转化为定步数问题求解（ ）BA.任意网络B.无回路有向网络C.混合网络D.容量网络2.通过什么方法或者技巧可以把工程线路问题转化为动态规划问题？（ ）BA.非线性问题的线性化技巧B.静态问题的动态处理C.引入虚拟产地或者销地D.引入人工变量3.静态问题的动态处理最常用的方法是？BA.非线性问题的线性化技巧B.人为的引入时段C.引入虚拟产地或者销地D.网络建模4.串联系统可靠性问题动态规划模型的特点是（ ）DA.状态变量的选取B.决策变量的选取C.有虚拟产地或者销地D.目标函数取乘积形式5.在网络计划技术中，进行时间与成本优化时，一般地说，随着施工周期的缩短，直接费用是( )。
CA.降低的 B .不增不减的 C .增加的 D .难以估计的6.最小枝权树算法是从已接接点出发，把( )的接点连接上CA.最远B.较远C.最近D.较近7.在箭线式网络固中，( )的说法是错误的。
DA.结点不占用时间也不消耗资源B.结点表示前接活动的完成和后续活动的开始C.箭线代表活动D.结点的最早出现时间和最迟出现时间是同一个时间8.如图所示，在锅炉房与各车间之间铺设暖气管最小的管道总长度是( )。
CA.1200B.1400C.1300D.17009.在求最短路线问题中，已知起点到A ，B ，C 三相邻结点的距离分别为15km ，20km,25km ，则（ ）。
DA.最短路线—定通过A 点B.最短路线一定通过B 点C.最短路线一定通过C 点D.不能判断最短路线通过哪一点10.在一棵树中，如果在某两点间加上条边，则图一定( )AA.存在一个圈B.存在两个圈 C .存在三个圈 D .不含圈11.网络图关键线路的长度( )工程完工期。
CA.大于B.小于C.等于D.不一定等于 600 700300 500 400锅炉房12312.在计算最大流量时，我们选中的每一条路线( )。
运筹学考试试卷及答案
运筹学考试试卷及答案一、选择题（每题2分，共20分）1. 线性规划问题的标准形式是：A. 所有变量都非负B. 目标函数是最大化C. 所有约束条件都是等式D. 所有约束条件都是不等式答案：A2. 单纯形法中，如果某个变量的检验数为负数，那么：A. 该变量可以增大B. 该变量可以减小C. 该变量保持不变D. 该变量不能进入基答案：A3. 在运输问题中，如果某种资源的供应量大于需求量，那么应该：A. 增加供应量B. 减少需求量C. 增加需求量D. 减少供应量答案：C4. 动态规划的基本原理是：A. 递归B. 迭代C. 回溯D. 分解答案：D5. 决策树中，每个节点代表：A. 一个决策B. 一个状态C. 一个结果D. 一个概率答案：A6. 排队论中，M/M/1队列的特点是：A. 到达时间服从泊松分布，服务时间服从指数分布，且只有一个服务台B. 到达时间服从指数分布，服务时间服从泊松分布，且只有一个服务台C. 到达时间服从泊松分布，服务时间服从指数分布，且有两个服务台D. 到达时间服从指数分布，服务时间服从泊松分布，且有两个服务台答案：A7. 网络流问题中，最大流最小割定理说明：A. 最大流等于最小割B. 最大流小于最小割C. 最大流大于最小割D. 最大流与最小割无关答案：A8. 整数规划问题中，分支定界法的基本思想是：A. 将问题分解为多个子问题B. 将问题转化为线性规划问题C. 将问题转化为非线性规划问题D. 将问题转化为动态规划问题答案：A9. 在多目标决策中，如果目标之间存在冲突，通常采用的方法是：A. 目标排序B. 目标加权C. 目标合并D. 目标替换答案：B10. 敏感性分析的目的是：A. 确定最优解的稳定性B. 确定最优解的唯一性C. 确定最优解的可行性D. 确定最优解的最优性答案：A二、填空题（每题2分，共20分）1. 线性规划问题的可行域是由所有_________约束条件构成的集合。
答案：可行2. 在单纯形法中，如果目标函数的系数都是正数，则该问题为_________问题。
运筹学试题及答案
运筹学试题及答案考试时间：120分钟命题人：XXX一、选择题（共60分）1. 运筹学的核心思想是：A. 尽可能地满足需求B. 确定最优决策C. 提高运营效率D. 预测未来趋势答案：B2. 下列哪个不是运筹学的应用领域？A. 生产调度B. 金融风险管理C. 市场营销D. 交通规划答案：C3. 线性规划是研究下列问题的数学方法：A. 最大化目标函数B. 最小化目标函数C. 求解等式系统D. 优化约束条件答案：D4. 整数规划是线性规划的扩展，其特点是：A. 变量只能取整数值B. 变量可以取任意实数值C. 目标函数必须是整数D. 约束条件必须是整数答案：A5. 运筹学中的最短路径问题是指：A. 在有向图中找到从起点到终点的最短路径B. 在无向图中找到连接所有节点的最短路径C. 在网络中找到连接所有节点的最短路径D. 在带权图中找到权值最小的路径答案：A二、计算题（共40分）1. 某工厂有3个生产车间，分别需要完成4个任务。
完成每个任务所需时间如下：车间1：10小时车间2：8小时车间3：6小时为了提高效率，每个车间只能同时进行一个任务。
请问应如何分配任务，才能使得所有任务完成的时间最短？答案：将任务按照时间从大到小排序分配，先将任务分配给车间1和车间2，然后再将任务分配给车间3。
具体分配如下：车间1：10小时（任务1）车间2：8小时（任务2）车间3：6小时（任务3）车间1：18小时（任务1+任务4）车间2：16小时（任务2+任务4）车间3：12小时（任务3）总时间为18小时。
2. 某物流公司需要将货物从发货仓库A送至目的地仓库B。
货物可通过3条不同的路径运送，分别需要的运输时间为：路径1：6小时路径2：8小时路径3：10小时若考虑各路径的运输成本，路径1的运输成本为100元/小时，路径2的运输成本为150元/小时，路径3的运输成本为120元/小时。
请问应如何选择路径，使得运输成本最低？答案：计算各路径的单位成本，并选择单位成本最低的路径。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
运筹学试题（代码：8054）一、填空题（本大题共8小题，每空2分，共20分）1 •线性规划闯题中，如果在约束条件中出现等式约束，我们通常用增加_人工变量—的方法来产生初始可行基。
2 •线性规划模型有三种参数，其名称分别为价值系数、_技术系数—和_限定系数__。
3•原问题的第1个约束方程是“=”型，则对偶问题相应的变量是—无非负约束（或无约束、或自由__变量。
4 •求最小生成树问题，常用的方法有：避圈法和_破圈法5 •排队模型M T M T2中的M M 2分别表示到达时间为—负指数—分布，服务时间服从负指数分布和服务台数为2。
6.如果有两个以上的决策自然条件，但决策人无法估计各自然状态出现的概率，那么这种决策类型称为—不确定__型决策。
7 •在风险型决策问题中，我们一般采用—效用曲线__来反映每个人对待风险的态度。
&目标规划总是求目标函数的最小信,且目标函数中没有线性规划中的价值系数，而是在各偏差变量前加上级别不同的_优先因子（或权重）。
二、单项选择题（本大题共10小题，每小题3分，共30分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
多选无分。
9•使用人工变量法求解极大化线性规划问题时，当所有的检验数。
在基变量中仍含有非零的人工变量，表明该线性规划问题【D】A .有唯一的最优解B .有无穷多最优解C •为无界解D •无可行解10 •对偶单纯形法解最大化线性规划问题时，每次迭代要求单纯形表中【D】A • b列元素不小于零B .检验数都大于零C .检验数都不小于零D .检验数都不大于零11.已知某个含10个结点的树图，其中9个结点的次为1，1，3，1，1，1，3，1，3，贝U 另一个结点的次为【A 】A . 3B . 2C . 1D .以上三种情况均有可能12•如果要使目标规划实际实现值不超过目标值。
则相应的偏离变量应满足【B】A, d +>0 c. r=oD. LXh d +>013 •在运输方案中出现退化现象，是指数字格的数目 【C 】A .等于 m+nB .等于 m+n-1C .小于 m+n-1D .大于 m+n-1 14.关于矩阵对策，下列说法错误的是 【D 】A .矩阵对策的解可以不是唯一的B.对任一矩阵对策G = {S H S 1； A}, —定存在混合策略意义下的解c.矩阵对策中，当局势达到均衡时，任何一方单方面改变自己的策略，都将意味着自己更少的赢得和更大的损失D.矩阵对策的对策值，相当于进行若干次对策后，局中人I 的平均赢得或局中人n 的平均损失值-6 3 15.若某一矩阵对策之对策矩阵A =；-3 A . 2 8. — I C . — 3 D . 116.关于线性规划的原问题和对偶问题，下列说法正确的是【B 】A .若原问题为元界解，则对偶问题也为无界解B .若原问题无可行解，其对偶问题具有无界解或无可行解 c .若原问题存在可行解，其对偶问题必存在可行解 D .若原问题存在可行解，其对偶问题无可行解 17.下列叙述不属于解决风险决策问题的基本原则的是【C 】A .最大可能原则B .渴望水平原则C .最大最小原则D .期望值最大原则 18.下列说法正确的是 【D 】1 ~82 4■1 -10 0 6则对策值为A .线性规划问题的基本解对应可行域的顶点B若X?是某线性规划问题的可行解，则〔其中九+花=1）也必是该问题的可行解c单纯形法解标准的线性规划问题时卜当所有检验数q-z^o时，即可判定表中解为最优解D.单纯形法解标准的线性规划问题时，按最小比值原则确定换出基变量是为了保证迭代计算后的解仍为基本可行解三、多项选择题（本大题共5小题，每小题2分，共10分）在每小题列出的四个备选项中至少有两个是符合题目要求的，请将其代码填写在题后的括号内。
多选、少选均无分。
19 •线性规划问题的标准型最本质的特点是【CD 】A •目标要求是极小化B •变量可以取任意值C •变量和右端常数要求非负D •约束条件一定是等式形式20 •下列方法中属于解决确定型决策方法的有【ABCD】A •线性规划B •动态规划C •盈亏分析D •企业作业计划21. 关于矩阵对策，下列说法正确的是【BCD :A •矩阵对策中，如果最优解要求一个局中人采取纯策略，则另一局中人也必须采取纯策略B •在二人有限零和对策的任一局势中，两个局中人的得失之和为零C .矩阵对策的对策值是唯一的D •如果矩阵对策存在最优纯策略意义下的解，则决策问题中必存在一个鞍点22. 关于运输问题，下列说法正确的是【BCD :A •在其数学模型中，有m+—1个约束方程B •用最小费用法求得的初始解比用西北角法得到的初始解在一般情况下更靠近最优解C .对任何一个运输问题，一定存在最优解D •对于产销不平衡的运输问题。
同样也可以用表上作业法求解23 •关于网络图，下列说法错误的是【CD 】A •总时差为0的各项作业所组成的路线即为关键路线B •以同一结点为结束事件的各项作业的最迟结束时间相同C •以同一结点为开始事件的各项作业的最早开始时间相同D •网络图中的任一结点都具有某项作业的开始和他项作业结束的双重标志属性四、计算题（本大题共5小题，每小题8分，共40分）24. 已知线性觀划冋题max乞=3x：i+4天2 + 心-Xi +2X3 +3勒W6--3XI + X2-4X3 W7L X H x2t x3 >0利用对偶理论证明其目标函数值无界。
24.证明：原问题的对偶问题是minw = 6y1+7y z一y 广3^23" ••①2儿卡兀>4—②妙-4力勿……③$小川NQ由于①不成立，所以对偶问题无可行解，由此可知原问题无最优解。
又容易知x=[0 , 1, 0]是原问题的可行解，所以原问题具有无界解，即目标值无界。
25.试用大M法解下列线性规划问题。
max z = 3x t+ 5x3「小W 4j2xy^ 123小+2X3= 18Xi, x2三O加入人工变量，化原问题为标准形maxz = 3x)+ 5x2 + 0x3 + 0x4一Mx5 r百+x3=4 2X2 +x4 =123xi + 2X2 +x5 = 18Xi ^03 = 1,2,3,4,5最优单纯形表如下:店熄兰］所以最优解为X = (262,O,0> , Z* 36 ,26.福安商场是个中型的百货商场， 它对售货人员的需求经过统计分析如下表所示，证售货人员充分休息，售货人员每周工作五天，休息两天，并要求休息的两天是连续的，问 该如何安排售货人员的休息， 既满足了工作需要， 又使配备的售货人员的人数最少，此问题的数学模型。
为了保请列出26.解：设出为从星期i(i=】,23……,7)开始休息的人数。
7则minz^^Xii=lf 5£2 28 1=1£论M151=2i±3x4 + x5 + x6 + x7 + X! > 25x5 + + x7 + X| + x2 > 19x6+ x7 + Xi + x2 + x3 > 31x7+旳+x2 + x3 + x^ + x5 28>O t(i-lA (7)Xi27.某公司拟定扩大再生产的三种方案，给出四种自然状态和益损矩阵(单位：万元)。
试根据以下决策准则选择方案。
①悲观准则；②等概率准则；⑨后悔值准则$£Ai13065*70*160扎2405-45-100Aj9550' -60-120"min{ 130,65,-70,“ 60}]27.①max« min{40, 5 ,-45,-100} *--100 min{95,50, - 60, 120}；选择方案A2②扌若=-8.75选择Ai或A3③后悔值矩阵1002560B =906000_35151520r max(0,0,25,60) = 60 I'min」max(90,60,0,0) = 90 > = 35max(35,15,15,20)；35：・；选择A328. A B两人分别有10分(1角)、5分、1分的硬币各一枚，双方都不知道的情况下各出一枚，规定和为偶数，A赢得8所出硬币，和为奇数，8赢得A所出硬币，试据此列出二人零和对策模型，并说明此游戏对双方是否公平。
28. G={S B S2;A}S严S2 ={1,5,10}I 1 5 -fA的赢得矩阵A= 1 5 -5士i-10 -10 10»V G=0,故游戏公平。
参考答案、填空题(本大题共8小题，每空2分，共20分)1 .人工变量2 •技术系数限定系数3 .无非负约束（或无约束、或自由）4 .破圈法5 .负指数6 .不确定7 .效用曲线8 .最小优先因子（或权重）二、单项选择题（本大题共10小题，每小题3分，共30分）9. D 10 . D 11 . A 12 . B 13 . C 14 . D 15 . A 16 . B 17 . C 18 . D三、多项选择题（本大题共5小题，每小题2分，共10分）19 . CD 20 . ABCD 21 . BCD 22 . BCD 23 . CD四、计算题（本大题共5小题，每小题8分，共40分）24.证明：原问题的对偶问题是讪11训=6划+7力L yi-3y：＞3—■©2沪巾＞4…②3丫|・4力勿一③由于①不成立，所以对偶问题无可行解，由此可知原问题无最优解。
又容易知x=[0 , 1, 0]是原问题的可行解，所以原问题具有无界解，即目标值无界。
25 .加入人工变量，化原问题为标准形maxz = 3x）+ 5x2+ 0x3+ 0x4一Mx5'百+x3=42X2 +x4=123x, + 2X2 +x5= 18Xi ^03 = 1,2,3,4,5最优单纯形表如下:所以最优解为X = (2,6,2,0,0” Z* = 36 o26.解：设Xi为从星期i(i-l,2,3,•・•••・,7)开始休息的人数。
7则minz =》Xi1=1fx&28i=l6£X&15i=2£X&24i=3X4 + X5 + *6 + x? + Xi N 25X5 + 心十X7 + X] + X2 M19X6 + X7 + X] + X2 + X3 M 31X? + Xi + X2 + X3 + X4 + X5 N 28xK(i=l,2, (7)min{130,65,-70,-160y127.①max« min{40, 5 ,-45,-100}》= -100 min{95,50,-60, 120}••・选择方案A2Gjj — *-8*75选择Ai或A3③后悔值矩阵0 0 25 60B= 90 60 0 035 15 15 20 max(0,0,25,60) = 60min* max(90,60,0,0) = 90 =35max(35,15,15,20)；35・•・选择A328. G = {S1,S2;A} ={1,5,10}_ 1 5-1A的贏得矩阵A = 1 5 -5• ••一10 -10 10解故游戏公平。