第七章 平行线的证明单元检测
第七章 平行线的证明单元测试卷(含解析)

第七章平行线的证明单元测试卷一.选择题(共10小题,满分30分,每小题3分)1.下列命题:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程=1.2中的分母化为整数,得=12;④平面内有4个点,过每两点画直线,可画6条.其中正确的有()A.1个B.2个C.3个D.4个2.如图,AO平分∠BAC,AO⊥BC,DE⊥BC,GH⊥BC,垂足分别为O、E、H,且DO∥AC,∠B=43°,则图中角的度数为47°的角的个数是()A.5 B.6 C.7 D.83.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=()A.75°B.80°C.85°D.90°4.如图,在△ABC中,∠ABC=40°,∠ACD=76°,BE平分∠ABC,CE平分△ABC的外角∠ACD,则∠E=()A.40°B.36°C.20°D.18°5.如图,AB∥CD,MP∥AB,MN平分∠AMD,∠A=40°,∠D=30°,则∠NMP等于()A.10°B.15°C.5°D.7.5°6.如图,△ABC中,∠B,∠C的平分线相交于点O,过O作DE∥BC,若BD+EC=5,则DE等于()A.7 B.6 C.5 D.47.如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=()A.76°B.78°C.80°D.82°8.如图,△ABC中,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=120°,∠BGC=102°,则∠A的度数为()A.34°B.40°C.42°D.46°9.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是()A.∠A=∠1+∠2 B.2∠A=∠1+∠2 C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)10.已知,如图AB∥CD,∠1=∠2,EP⊥FP,则以下错误的是()A.∠3=∠4 B.∠2+∠4=90°C.∠1与∠3互余D.∠1=∠3二.填空题(共8小题,满分24分,每小题3分)11.用推理的方法判断为正确的命题叫做.12.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,和∠DCE n﹣1的平分线,交点为E n.第n次操作,分别作∠ABE n﹣1若∠E n=1度,那∠BEC等于度13.将一副直角三角尺如图放置(其中∠A=60°,∠F=45°),点E在AC上,ED∥BC,则∠AEF的度数是.14.如图,∠1=52°,∠2=128°,∠C=∠D.探索∠A与∠F的数量关系为.15.说理解答题在空白处填上适当的内容(理由或数学式)解:在ABC中∠B+∠ACB+∠BAC=180°∴∠BAC=180°﹣∠B﹣(等式的性质)=180°﹣36°﹣110°=∵AE是∠BAC的平分线(已知)∴∠CAE=∠BAC=17°∵AD是BC边上的高即AD⊥BC (已知)∴∠D=∵∠AC E是△ACD的外角(已知)∴∠ACE=∠CAD+∠D∴∠CAD=∠ACE﹣∠D (等式的性质)=110°﹣90°═20°∴∠DAE=∠CAD+=20°+17°=.16.如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1,若BC=,,则BB1=.17.一个三角形有一内角为48°,如果经过其一个顶点作直线能把其分成两个等腰三角形,那么它的最大内角可能是.18.如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为°.三.解答题(共7小题,满分66分)19.(8分)如图,∠ACD=2∠B,CE平分∠ACD,求证:CE∥AB.20.(8分)补全解题过程.如图,在△ABC中∠ABC平分线BP和外角平分线CP交于点P,试猜想∠A与∠P之间的关系,并说明理由.解:∠A=2∠P理由:∵BP、CP分别平分∠ABC、∠ACD(已知)∴∠ABC=∠1,∠ACD=2∠2 ()∵∠ACD为△ABC的外角∴∠ACD=∠A+∠=∠A+2∠1(三角形外角的性质)即:2∠2=∠A+2∠1同理:∠2=∠P+∴∠A=2∠P.21.(8分)如图:在△ABC中,∠C=90°,点D是AB边上一点,DM⊥AB且DE=BC,过点M作ME∥BC交AB于点E.求证:ME=AB.22.(10分)已知:如图,在Rt△ABC中,∠A=90°,AB=AC=1,P是AB边上不与A点、B点重合的任意一个动点,PQ⊥BC于点Q,QR⊥AC于点R.(1)求证:PQ=BQ;(2)设BP=x,CR=y,求y关于x的函数解析式,并写出定义域;(3)当x为何值时,PR∥BC.23.(10分)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.(1)如图,一束光线m射到平面镜上,被a反射到平面镜b上,又被b镜反射,若被b 反射出的光线n与光线m平行,且∠1=50°,则∠2=°,∠3=°;(2)在(1)中,若∠1=55°,则∠3=°,若∠1=40°,则∠3=°;(3)由(1)、(2)请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n 平行,请说明理由.24.(10分)如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.25.(12分)如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=82°,则∠BEC=;若∠A=a°,则∠BEC=.【探究】(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=a°,则∠BEC=;(2)如图3,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A 有怎样的关系?请说明理由;(3)如图4,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A 有怎样的关系?请说明理由.参考答案与试题解析1.解:①错误,﹣1的平方是1;②正确;③错误,方程右应还为1.2;④错误,只有每任意三点不在同一直线上的四个点才能画6条直线,若四点在同一直线上,则只有画一条直线了.故选:A.2.解:∵AO平分∠BAC,AO⊥BC,∴∠BAO=∠CAO,∠AOB=∠AOC=90°,∴∠B=∠C,∵DO∥AC,∴∠BOD=∠C,∴∠B=∠BOD,∴DB=DO,又∵DE⊥BO,∴ED平分∠BDO,∵∠B=43°,∴∠BDE=47°,∴∠BAO=∠EDO=∠AOD=∠CAO=∠CGH=47°,故选:A.3.解:∵AD是BC边上的高,∠ABC=60°,∴∠BAD=30°,∵∠BAC=50°,AE平分∠BAC,∴∠BAE=25°,∴∠DAE=30°﹣25°=5°,∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,∴∠EAD+∠ACD=5°+70°=75°,故选:A.4.解:∵∠ACD是△ABC的一个外角,∴∠ACD=∠A+∠ABC,∴∠A=∠ACD﹣∠ABC,∵∠ABC=40°,∠ACD=76°,∴∠ACD﹣∠ABC=36°,∵BE平分∠ABC,CE平分∠ACD,∴∠ECD=∠ACD,∠EBC=∠ABC,∵∠ECD是△BCE的一个外角,∴∠ECD=∠EBC+∠E,∴∠E=∠ECD﹣∠EBC=∠ACD﹣∠ABC=18°.故选:D.5.解:∵AB∥CD,MP∥AB,∴AB∥CD∥MP,∵∠A=40°,∠D=30°,∴∠AMP=∠A=40°,∠DMP=∠D=30°,∴∠AMD=40°+30°=70°,∵MN平分∠AMD,∴∠AMN=∠AMD=×70°=35°,∴∠NMP=∠AMP﹣∠AMN=40°﹣35°=5°.故选:C.6.解:∵DE∥BC,∴∠DOB=∠OBC,∠EOC=∠OCB.又∵∠B,∠C的平分线相交于点O,∴∠DBO=∠DOB,∠EOC=∠ECO.∴DB=DO,EC=EO,又∵BD+EC=5,DO+EO=DE,∴DE=5.故选:C.7.解:如图,分别过K、H作AB的平行线MN和RS,∵AB∥CD,∴AB∥CD∥RS∥MN,∴∠RHB=∠ABE=∠ABK,∠SHC=∠DCF=∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,∴∠BHC=180°﹣∠RHB﹣∠SHC=180°﹣(∠ABK+∠DCK),∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK ﹣180°,∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC,又∠BKC﹣∠BHC=27°,∴∠BHC=∠BKC﹣27°,∴∠BKC=180°﹣2(∠BKC﹣27°),∴∠BKC=78°,故选:B.8.解:设∠GBC=x,∠DCB=y,在△BFC中,2x+y=180°﹣120°=60°①,在△BGC中,x+2y=180°﹣102°=78°②,解得:①+②:3x+3y=138°,∴∠A=180°﹣(3x+3y)=180°﹣138°=42°,故选:C.9.解:2∠A=∠1+∠2,理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,则2∠A+180°﹣∠2+180°﹣∠1=360°,∴可得2∠A=∠1+∠2.故选:B.10.解:过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠1=∠EPH,∠3=∠HPF,∵EP⊥FP,∴∠2+∠4=90°,∠HPF+∠EPH=90°,∴∠3=∠4,故A正确;∵EP⊥FP,∴∠2+∠4=90°,故B正确;∵∠1=∠2,∠3=∠4,∠2+∠4=90°,∴∠1+∠3=90°,∠1与∠3互余,故C正确;故选:D.11.解:定理是用推理的方法判断为正确的命题,故用推理的方法判断为正确的命题叫做定理.12.解:如图①,过E作EF∥AB,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE;如图②,∵∠ABE和∠DCE的平分线交点为E1,∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC.∵∠ABE1和∠DCE1的平分线交点为E2,∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;…以此类推,∠E n=∠BEC.∴当∠E n=1度时,∠BEC等于2n度.故答案为:2n .13.解:∵ED∥BC,∴∠DEC=∠C=30°,∴∠FEC=15°,∴∠AEF=180°﹣15°=165°,故答案为:165°.14.解:∵∠1=52°,∠2=128°,∴∠1+∠2=180°,∵∠C=∠D,∴∠D=∠ABD,∴AC∥DF,∴∠A=∠F.15.解:在ABC中,∵∠B+∠ACB+∠BAC=180°(三角形内角和定理)∴∠BAC=180°﹣∠B﹣∠BCA(等式的性质)=180°﹣36°﹣110°=34°∵AE是∠BAC的平分线(已知)∴∠CAE=∠BAC=17°∵AD是BC边上的高即AD⊥BC (已知)∴∠D=90°,∵∠AC E是△ACD的外角(已知)∴∠ACE=∠CAD+∠D(三角形外角的性质)∴∠CAD=∠ACE﹣∠D (等式的性质)=110°﹣90°=20°∴∠DAE=∠CAD+∠CAE=20°+17°=37°.故答案为:三角形内角和定理;∠BAC;34°;;90°;三角形外角的性质;∠CAE;37°.16.解:∵△ABC是等腰直角三角形,∴平移后∠PB1C=∠CB=45°,∴△PB1C是等腰直角三角形,∴S=B1C•(B1C)=2,△PB1C解得B1C=2,∴BB1=BC﹣B1C=3﹣2=.故答案为:.17.解:如图①所示,当∠BAC=48°时,那么它的最大内角是90°当∠ACB=48°时,有以下4种情况,故答案为:88°,90°,99°,108°,116°18.解:如图所示,作DE∥AC,则有∠1=∠A=α,则上下最大可以转动的角度为2α.故答案为:2α.19.证明:∵CE平分∠ACD,∴∠ACD=2∠DCE,∵∠ACD=2∠B,∴∠DCE=∠B,∴AB∥CE.20.解:∠A=2∠P理由:∵BP、CP分别平分∠ABC、∠ACD(已知)∴∠ABC=2∠1,∠ACD=2∠2 (角平分线的定义)∵∠ACD为△ABC的外角∴∠ACD=∠A+∠ABC=∠A+2∠1(三角形外角的性质)即:2∠2=∠A+2∠1,∴∠A=2∠P.故答案为:2,角平分线的定义,ABC,∠1.21.证明:∵ME∥BC,∴∠B=∠MED,∵DM⊥AB,∴∠MDE=90°,∴∠MDE=∠C=90°,在△ABC和△MED中,,∴△ABC≌△MED(ASA),∴ME=AB.22.(1)证明:∵∠A=90°,AB=AC=1∴∠B=∠C=45°又∵PQ⊥BQ∴∠BPQ=45°∴△BPQ是等腰三角形∴PQ=BQ.(2)解:在等腰直角△BPQ中,∵BP=x∴BQ=在Rt△ABC中,BC==在等腰直角三角形CQR中,CR=y∴CQ=y∵CQ=BC﹣BQ即y=﹣所以y=﹣x+1.又∵△BPQ为等腰三角形,∴PQ=∵PR∥BC∴∠PRQ=∠RQC=45°∴PR=∠A=∠A,∠APR=∠B,∠ARP=∠C∴△APR∽△ABC∴即解得:x=.23.解:(1)100°,90°.∵入射角与反射角相等,即∠1=∠4,∠5=∠6,根据邻补角的定义可得∠7=180°﹣∠1﹣∠4=80°,根据m∥n,所以∠2=180°﹣∠7=100°,所以∠5=∠6=(180°﹣100°)÷2=40°,根据三角形内角和为180°,所以∠3=180°﹣∠4﹣∠5=90°;(2)90°,90°.由(1)可得∠3的度数都是90°;(3)90°(2分)理由:因为∠3=90°,所以∠4+∠5=90°,=360°﹣2∠4﹣2∠5,=360°﹣2(∠4+∠5),=180°.由同旁内角互补,两直线平行,可知:m∥n.24.解:∠AED=∠ACB.理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知).∴∠2=∠4.∴EF∥AB(内错角相等,两直线平行).∴∠3=∠ADE(两直线平行,内错角相等).∵∠3=∠B(已知),∴∠B=∠ADE(等量代换).∴DE∥BC(同位角相等,两直线平行).∴∠AED=∠ACB(两直线平行,同位角相等).25.解:∵∠A=82°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣82°=98°,∵BE平分∠ABC,CE平分∠ACB,∴∠EBC=∠ABC,∠ECB=∠ACB,∴∠EBC+∠ECB=(∠ABC+∠ACB)=×98°=49°,∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣49°=131°;由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A=180°﹣a°,∵BE平分∠ABC,CE平分∠ACB,∴∠EBC=∠ABC,∠ECB=∠ACB,∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°﹣a°)=90°﹣a°,故答案为:131°,90°+a°;探究:(1)由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A=180°﹣a°,∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,∴∠EBC=∠ABC,∠ECB=∠ACB,∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°﹣a°)=120°﹣a°,∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(120°﹣a°)=60°+a°;故答案为:60°+a°;(2)∠BOC=∠A.理由如下:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠OCD=∠BOC+∠OBC,∵O是∠ABC与外角∠ACD的平分线BO和CO的交点,∴∠ABC=2∠OBC,∠ACD=2∠OCD,∴∠A+∠ABC=2(∠BOC+∠OBC),∴∠A=2∠BOC,∴∠BOC=∠A;(3)∠BOC=90°﹣∠A.理由如下:∵O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,∴∠OBC=(180°﹣∠ABC)=90°﹣∠ABC,∠OCB=(180°﹣∠ACB)=90°﹣∠ACB,在△OBC中,∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(90°﹣∠ABC)﹣(90°﹣∠ACB)=(∠ABC+∠ACB),由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A,∴∠BOC=(180°﹣∠A)=90°﹣∠A.。
第七章 平行线的证明 单元测试 2022-2023学年北师大版数学八年级上册
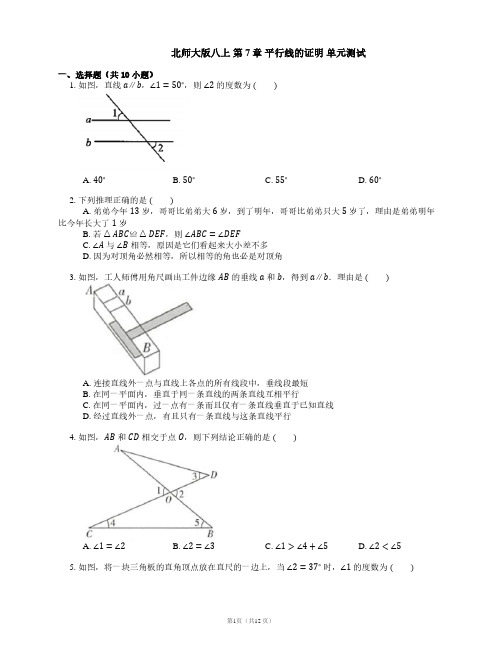
北师大版八上第7章平行线的证明单元测试一、选择题(共10小题)1. 如图,直线a∥b,∠1=50∘,则∠2的度数为( )A. 40∘B. 50∘C. 55∘D. 60∘2. 下列推理正确的是( )A. 弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,理由是弟弟明年比今年长大了1岁B. 若△ABC≌△DEF,则∠ABC=∠DEFC. ∠A与∠B相等,原因是它们看起来大小差不多D. 因为对顶角必然相等,所以相等的角也必是对顶角3. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )A. 连接直线外一点与直线上各点的所有线段中,垂线段最短B. 在同一平面内,垂直于同一条直线的两条直线互相平行C. 在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D. 经过直线外一点,有且只有一条直线与这条直线平行4. 如图,AB和CD相交于点O,则下列结论正确的是( )A. ∠1=∠2B. ∠2=∠3C. ∠1>∠4+∠5D. ∠2<∠55. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37∘时,∠1的度数为( )A. 37∘B. 43∘C. 53∘D. 54∘6. 下列命题中,是真命题的是( )A. √9的算术平方根是3B. 数据−2,1,0,2,2,3的方差是83C. y=kx+b(k,b为常数)是一次函数D. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等7. 如图,在△ABC中,点D在AC上,延长BC至E,连接DE,则下列结论不成立的是( )A. ∠DCE>∠ADBB. ∠ADB>∠DBCC. ∠ADB>∠ACBD. ∠ADB>∠DEC8. 如图是汽车灯的剖面图,从位于O点的灯发出光照射到凹面镜上反射出的光线BA,CD都是水平线,若∠ABO=α,∠DCO=60∘,则∠BOC的度数为( )A. 180∘−αB. 120∘−αC. 60∘+αD. 60∘−α9. 如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )A. 180∘B. 360∘C. 270∘D. 540∘10. 如图,△ABC中,将∠A沿DE翻折,点A落在Aʹ处,∠CEAʹ,∠BDAʹ,∠A三者之间的关系是( )A. ∠CEAʹ=∠BDAʹ+∠AB. ∠CEAʹ−3∠A=∠BDAʹC. ∠CEAʹ=2(∠BDAʹ+∠A)D. ∠CEAʹ−∠BDAʹ=2∠A二、填空题(共6小题)11. 命题“没有公共点的两条直线是平行的”的条件是,结论是,这个命题是命题.12. 如图,若AB∥CD,∠A=110∘,则∠1=∘.13. 如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30∘,∠EFC=130∘,则∠A=.14. 如图,将分别含有30∘,45∘角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65∘,则图中角α的度数为.15. 如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为.(任意添加一个符合题意的条件即可)16. 一个大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150∘,则∠ABC=∘.三、解答题(共5小题)17. 补全证明过程:(括号内填写理由)如图,一条直线分别与直线BE,直线CE,直线BF,直线CF相交于A,G,H,D,如果∠1=∠2,∠A=∠D,求证:∠B=∠C.证明:∵∠1=∠2,(已知)∠1=∠3,()∴∠2=∠3()∴CE∥BF,()∴∠C=∠4,()又∵∠A=∠D,()∴AB∥,()∴∠B=∠4,()∴∠B=∠C.(等量代换)18. 如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在Dʹ,Cʹ的位置上,EDʹ与BC的交点为G,若∠EFG=55∘,求∠1,∠2的度数.19. 如图①,在三角形ABC中,∠BAE=1∠BAC,∠C>∠B,且FD⊥BC于点D.2(1)试推出∠EFD,∠B,∠C之间的关系;(2)如图②,当点F在AE的延长线上时,其他条件不变,(1)中推导的结论还成立吗?请直接写出结论.20. 如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.21. 如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.(1)求证:∠OAC=∠OCA;(2)如图②,若分别作∠AOC的三等分线及∠OCA的邻补角的三等分线交于点P,即∠POC=1 3∠AOC,∠PCE=13∠ACE,求∠P的大小;(3)如图③,若∠POC=1n ∠AOC,∠PCE=1n∠ACE,猜想∠OPC的大小.(用含n的式子表示)答案1. B2. B【解析】由全等三角形的性质可知,B 正确.3. B 【解析】由题意得 a ⊥AB ,b ⊥AB ,∴a ∥b (在同一平面内,垂直于同一条直线的两条直线平行).4. A【解析】∵∠1 和 ∠2 是对顶角,∴∠1=∠2,故A 正确;∵∠2=∠A +∠3,∴∠2>∠3,故B 错误;∵∠1=∠4+∠5,故③错误;∵∠2=∠4+∠5,∴∠2>∠5,故D 错误.故选A .5. C【解析】如图,∵AB ∥CD ,∠2=37∘,∴∠2=∠3=37∘,∵∠1+∠3=90∘,∴∠1=53∘.6. B【解析】A .√9=3,3 的算术平方根是 √3,原命题是假命题,不符合题意;B .数据 −2,1,0,2,2,3 的平均数是 1,方差=16×[(−2−1)2+(1−1)2+(0−1)2+(2−1)2×2+(3−1)2]=83,原命题是真命题,符合题意;C .y =kx +b (k ,b 为常数,且 k ≠0)是一次函数,原命题是假命题,不符合题意;D .如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,原命题是假命题,不符合题意.故选B .7. A【解析】A 选项无法判断;∵∠ADB 是 △BCD 的一个外角,∴∠ADB >∠DBC ,∠ADB >∠ACB ,故选项B ,C 均成立;∵∠ACB 是 △CDE 的一个外角,∴∠ACB >∠DEC ,∴∠ADB >∠DEC ,故选项D 成立.8. C【解析】连接 BC ,∵AB∥CD,∴∠ABO+∠CBO+∠BCO+∠OCD=180∘,又∠CBO+∠BCO+∠BOC=180∘,∴∠BOC=∠ABO+∠DCO=α+60∘.9. B 【解析】过点P作PA∥a,∵a∥b,PA∥a,∴a∥b∥PA,∴∠1+∠MPA=180∘,∠3+∠APN=180∘,∴∠1+∠MPA+∠3+∠APN=180∘+180∘=360∘,∴∠1+∠2+∠3=360∘.10. D【解析】如图,由折叠得∠A=∠Aʹ,∵∠CEAʹ=∠A+∠1,∠1=∠Aʹ+∠BDAʹ,∴∠CEAʹ=∠A+∠Aʹ+∠BDAʹ=2∠A+∠BDAʹ,∴∠CEAʹ−∠BDAʹ=2∠A.故选D.11. 两条直线没有公共点,这两条直线互相平行,假12. 70【解析】如图,∵AB∥CD,∴∠2=∠A=110∘.又∵∠1+∠2=180∘,∴∠1=180∘−∠2=180∘−110∘=70∘.13. 20∘【解析】∵AB∥CD,∴∠ABF+∠EFC=180∘,∵∠EFC=130∘,∴∠ABF=50∘,∵∠A+∠E=∠ABF=50∘,∠E=30∘,∴∠A=20∘.14. 140∘【解析】如图,∵∠ACB=90∘,∠DCB=65∘,∴∠ACD=∠ACB−∠BCD=90∘−65∘=25∘,∵∠A=60∘,∴∠DFB=∠AFC=180∘−∠ACD−∠A=180∘−25∘−60∘=95∘,∵∠D=45∘,∴∠α=∠D+∠DFB=45∘+95∘=140∘.15. ∠A+∠ABC=180∘或∠C+∠ADC=180∘或∠CBD=∠ADB或∠C=∠CDE(答案不唯一)【解析】若∠A+∠ABC=180∘,则BC∥AD;若∠C+∠ADC=180∘,则BC∥AD;若∠CBD=∠ADB,则BC∥AD;若∠C=∠CDE,则BC∥AD,故答案为∠A+∠ABC=180∘或∠C+∠ADC=180∘或∠CBD=∠ADB或∠C=∠CDE(答案不唯一).16. 120【解析】如图,过点B作BG∥CD.∵CD∥AE,CD∥BG,∴∠C+∠CBG=180∘,BG∥AE,∴∠BAE+∠ABG=180∘,又易知∠BAE=90∘,∴∠ABG=90∘,∵∠C=150∘,∴∠CBG=30∘,∴∠ABC=∠ABG+∠CBG=90∘+30∘=120∘.17. 对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;CD;内错角相等,两直线平行;两直线平行,内错角相等18. ∵AD∥BC,∠EFG=55∘,∴∠2=∠GED,∠DEF=∠EFG=55∘,由折叠知∠GEF=∠DEF=55∘,∴∠GED=110∘,∴∠1=180∘−∠GED=70∘,∠2=110∘.19. (1)∠EFD=90∘−∠FED=90∘−(∠B+∠BAE)=90∘−∠B−12∠BAC=90∘−∠B−12(180∘−∠B−∠C)=90∘−∠B−90∘+12∠B+12∠C=12(∠C−∠B).(2)(1)中推导的结论仍成立,∠EFD=12(∠C−∠B).20. ∵AD是△ABC的角平分线,∴∠BAC=2∠BAD,∵∠1=∠B+∠BAC,∠2=∠B+∠BAD,∴∠B+∠1=∠B+∠B+∠BAC=2∠B+2∠BAD=2∠2.21. (1)∵A,B的纵坐标相等,所以AB∥OC,∴∠BAC=∠OCA,又AC平分∠OAB,∴∠OAC=∠BAC,∴∠OAC=∠OCA.(2)由(1)得∠OAC=∠OCA,∴OA=OC,∴∠OAC=∠OCA=45∘,∴∠ACE=135∘,∵∠POC=13∠AOC,∠PCE=13∠ACE,∴∠P=∠PCE−∠POC=13∠ACE−13∠AOC=13×(∠ACE−∠AOC)=13×(135∘−90∘)=15∘.(3)∠OPC=45∘n .证明:∠OPC=∠PCE−∠POC(∠ACE−∠AOC)=1n(135∘−90∘)=1n=45∘.n第11页(共12 页)第12页(共12 页)。
北师大版八年级数学上《第7章平行线的证明》单元测试

《第7章平行线的证明》一、选择题(本题共10小题,每小题3分,共30分)A.延长线段AB到C B.垂线段最短C.过点O作直线a∥b D.锐角都相等吗A.两个锐角之和为钝角B.两个锐角之和为锐角C.钝角大于它的补角 D.锐角小于它的余角3.“两条直线相交,有且只有一个交点”的题设是()A.两条直线 B.交点 C.两条直线相交 D.只有一个交点4.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是()A.相等 B.互余或互补C.互补 D.相等或互补5.三角形的一个外角等于与它不相邻的内角的4倍,等于与它相邻的一个内角的2倍,则三角形各角的度数为()A.45°,45°,90° B.30°,60°,90° C.25°,25°,130°D.36°,72°,72°6.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=30°,那么与∠FCD相等的角有()A.1个B.2个C.3个D.4个(1)两条直线被第三条直线所截,内错角相等(2)如果∠1和∠2是对顶角,那么∠1=∠2(3)一个角的余角一定小于这个角的补角(4)如果∠1和∠3互余,∠2与∠3的余角互补,那么∠1和∠2互补.A.1个B.2个C.3个D.4个8.如图,∠B=∠C,则∠ADC和∠AEB的大小关系是()A.∠ADC>∠AEB B.∠ADC=∠AEBC.∠ADC<∠AEB D.大小关系不能确定9.如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于()A.50° B.65° C.80° D.95°10.如图AB∥CD,AD、BC交于点O,∠A=42°,∠C=58°,则∠AOB=()A.42° B.58° C.80° D.100°二、填空题(本大题共10小题,每小题4分,共40分)11.如图所示,∠1=∠2,∠3=80°,那么∠4= .12.如图所示,∠ABC=36°40′,DE∥BC,DF⊥AB于F,则∠D= .13.如图所示,AB∥CD,∠1=115°,∠3=140°,∠2= °.14.如果一个三角形三个内角的比是1:2:3,那么这个三角形是三角形.15.一个三角形的三个外角的度数比为2:3:4,则与此对应的三个内角的比为.16.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°,则∠BEC= 度.18.如图所示,AB∥EF∥CD,且∠B=∠1,∠D=∠2,则∠BED的度数为°.19.如果等腰三角形底边上的高等于底边的一半,那么这个等腰三角形的顶角等于度.20.过△ABC的顶点C作边AB的垂线,如果这垂线将∠ACB分为40°和20°的两个角,那么∠A、∠B中较大的角的度数是.三、解答题(本大题共5小题,共30分)21.如图所示,∠1=∠2,AE∥BC,求证:△ABC是等腰三角形.22.如图所示,BF∥DE,∠1=∠2,求证:GF∥BC.23.如图所示,已知AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,求∠GFC的度数.24.已知,如图所示,直线AB∥CD,∠AEP=∠CFQ.求证:∠EPM=∠FQM.25.△ABC中,BE平分∠ABC,AD为BC上的高,且∠ABC=60°,∠BEC=75°,求∠DAC的度数.《第7章平行线的证明》参考答案与试题解析一、选择题(本题共10小题,每小题3分,共30分)A.延长线段AB到C B.垂线段最短C.过点O作直线a∥b D.锐角都相等吗故选B.A.两个锐角之和为钝角B.两个锐角之和为锐角C.钝角大于它的补角 D.锐角小于它的余角【分析】根据补角、余角的定义结合反例即可作出判断.【解答】解:A、两个30°角的和是60°,是锐角,不正确;B、两个80°的角之和是160°,是钝角,不正确;C、钝角大于90°,它的补角小于90°,正确;D、80°锐角的余角是10°,不正确.故选C.【点评】可以举具体角的度数来证明.3.“两条直线相交,有且只有一个交点”的题设是()A.两条直线 B.交点 C.两条直线相交 D.只有一个交点【考点】直线、射线、线段.故选C.【点评】本题主要考查直线、线段、射线的知识点,不是很难,不过做题要仔细.4.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是()A.相等 B.互余或互补C.互补 D.相等或互补【考点】平行线的性质.【分析】本题主要利用两直线平行,同位角相等以及同旁内角互补作答.【解答】解:如图知∠A和∠B的关系是相等或互补.故选D.【点评】如果两个的两条边分别平行,那么这两个角的关系是相等或互补.5.三角形的一个外角等于与它不相邻的内角的4倍,等于与它相邻的一个内角的2倍,则三角形各角的度数为()A.45°,45°,90° B.30°,60°,90° C.25°,25°,130°D.36°,72°,72°【考点】三角形的外角性质.【专题】探究型.【分析】设这个外角为4x,则与它不相邻的内角的度数为x,则与它相邻的一个内角为2x,再由2x+4x=180°即可求出x的值,故可得出各内角的度数.【解答】解:设这个外角为4x,则与它不相邻的内角的度数为x,则与它相邻的一个内角为2x,另一个内角为4x﹣x=3x,∵2x+4x=180°,∴x=30°,∴2x=60°,4×30°﹣30°=90°,∴三角形各角的度数为30°,60°,90°.故选B.【点评】本题主要考查了三角形的外角性质及三角形的内角和定理,解题的关键是熟练掌握三角形的外角性质定理,即三角形的一个外角等于与它不相邻的两个内角之和,难度适中.6.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=30°,那么与∠FCD相等的角有()A.1个B.2个C.3个D.4个【考点】平行线的判定与性质.【分析】利用平行线的性质进行求解.【解答】解:∵AB⊥EF,CD⊥EF,∴AB∥CD,∴∠FCD=∠A,∵∠1=∠F=30°,∴BG∥AF,∴∠A=∠ABG;故选B.【点评】考查了平行线的判定以及平行线的性质,需要熟练掌握.(1)两条直线被第三条直线所截,内错角相等(2)如果∠1和∠2是对顶角,那么∠1=∠2(3)一个角的余角一定小于这个角的补角(4)如果∠1和∠3互余,∠2与∠3的余角互补,那么∠1和∠2互补.A.1个B.2个C.3个D.4个【解答】解:(1)不正确,应该是两条平行线被第三条直线所截,内错角相等;(2)正确,因为对顶角相等;(3)正确,因为一个角的补角比它的余角大90°;(4)正确,因为∠3的余角即∠1,则∠1与∠2互补.所以正确有的三个,故选:C.8.如图,∠B=∠C,则∠ADC和∠AEB的大小关系是()A.∠ADC>∠AEB B.∠ADC=∠AEBC.∠ADC<∠AEB D.大小关系不能确定【考点】三角形的外角性质.【分析】利用三角形的内角和为180度计算.【解答】解:在△ADC中有∠A+∠C+∠ADC=180°,在△AEB有∠AEB+∠A+∠B=180°,∵∠B=∠C,∴等量代换后有∠ADC=∠AEB.故选B.【点评】本题利用了三角形内角和为180度.9.如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于()A.50° B.65° C.80° D.95°【考点】三角形的外角性质;角平分线的定义;三角形内角和定理.【分析】利用平分线的性质,三角形的内角和定理以及外角的性质计算.【解答】解:由题意可得,∠CAE=130°,∴∠BAC=50°,∴∠ACD=∠B+∠BAC=30°+50°=80°.故选C.【点评】此题主要考查角平分线的性质,三角形的内角和定理以及外角的性质.10.如图AB∥CD,AD、BC交于点O,∠A=42°,∠C=58°,则∠AOB=()A.42° B.58° C.80° D.100°【考点】平行线的性质;三角形内角和定理.【专题】计算题.【分析】由AB∥CD,可得∠B=∠C=58°,根据三角形的内角和为180°即可求得∠AOB的值.【解答】解:∵AB∥CD,∴∠B=∠C=58°;∵∠A+∠B+∠AOB=180°,∠A=42°,∴∠AOB=80°.故选C.【点评】此题考查了平行线的性质:两直线平行,内错角相等.还考查了三角形的内角和为180°.二、填空题(本大题共10小题,每小题4分,共40分)11.如图所示,∠1=∠2,∠3=80°,那么∠4= 80°.【考点】平行线的判定与性质.【专题】计算题.【分析】由∠1=∠2,根据同位角相等,两直线平行得到a∥b,然后根据平行线的性质得∠4=∠3=80°.【解答】解:∵∠1=∠2,∴a∥b,∴∠4=∠3=80°.故答案为80°.【点评】本题考查了平行线的判定与性质:同位角相等,两直线平行;两直线平行,内错角相等.12.如图所示,∠ABC=36°40′,DE∥BC,DF⊥AB于F,则∠D= 53°20′.【考点】平行线的性质;垂线.【专题】计算题.【分析】由平行线的性质可得出∠ABC=∠DAF=36°40′,再由DF⊥AB于F,可得出∠D的值.【解答】解:∵DE∥BC,∴∠ABC=∠DAF=36°40′,又∵DF⊥AB,∴∠D=90°﹣∠DAF=53°20′.【点评】本题考查平行线的性质,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补.13.如图所示,AB∥CD,∠1=115°,∠3=140°,∠2= 75 °.【考点】平行线的性质.【专题】计算题.【分析】根据两直线平行,同旁内角互补求出∠4的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和即可求出∠2的度数.【解答】解:如图,∵AB∥CD,∠3=140°,∴∠4=180°﹣140°=40°,∵∠1=115°,∴∠2=∠1﹣∠4=115°﹣40°=75°.【点评】本题主要利用两直线平行,同旁内角互补的性质和三角形的一个外角等于和它不相邻的两个内角的和求解.14.如果一个三角形三个内角的比是1:2:3,那么这个三角形是直角三角形.【考点】三角形内角和定理.【分析】根据三角形的内角和等于180°和已知求出三角形的最大角的度数,即可得出答案.【解答】解:∵一个三角形三个内角的比是1:2:3,∴这个三角形的最大内角的度数是:180°×=90°,∴这个三角形是直角三角形,故答案为:直角.【点评】本题考查了三角形内角和定理的应用,能求出这个三角形的最大内角是解此题的关键,注意:三角形的内角和等于180°.15.一个三角形的三个外角的度数比为2:3:4,则与此对应的三个内角的比为5:3:1 .【考点】三角形的外角性质.【分析】设设三个外角的度数分别为2x、3x、4x,根据三角形的外角和等于360°列出方程,解方程即可求出三个外角的度数,得到与此对应的三个内角的度数,计算即可.【解答】解:设三个外角的度数分别为2x、3x、4x,由题意得,2x+3x+4x=360°,解得,x=40°,则三个外角分别为80°、120°、160°则对应的三个内角分别为:100°、60°、20°,∴与此对应的三个内角的比为5:3:1.故答案为:5:3:1.【点评】本题考查的是三角形的外角的性质,掌握三角形的外角和等于360°是解题的关键.16.如图,在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°,则∠BEC= 122.5 度.【考点】三角形内角和定理;角平分线的定义.【分析】根据三角形的内角和定理和角平分线的定义求得.【解答】解:∵在△ABC中,BE平分∠ABC,CE平分∠ACB,∠A=65°.∴∠EBC+∠ECB==57.5°,∴∠BEC=180°﹣57.5°=122.5°.【点评】此题考查了三角形内角和定理,属简单题目.【专题】计算题.【解答】解:“同角的余角相等”可写成是“如果是同角的余角,那么这两个角相等”.故答案为:如果是同角的余角;那么这两个角相等.18.如图所示,AB∥EF∥CD,且∠B=∠1,∠D=∠2,则∠BED的度数为90 °.【考点】平行线的性质.【专题】计算题.【分析】根据两直线平行,内错角相等可得∠B=∠BEF,∠D=∠DEF,又知∠B=∠1,∠D=∠2,可得出∠1+∠2=∠DEF+∠DEF,由平角的定义,求出∠BED的值即可.【解答】解:∵AB∥EF∥CD,∴∠B=∠BEF,∠D=∠DEF,又∵∠B=∠1,∠D=∠2,∴∠1=∠BEF,∠2=∠DEF,又∵∠1+∠BEF+∠2+∠DEF=180°,∴∠BED=×180°=90°.【点评】本题主要考查运用平行线的性质的能力,主要考查平行线的性质(两直线平行,内错角相等)以及等量代换等知识点.19.如果等腰三角形底边上的高等于底边的一半,那么这个等腰三角形的顶角等于90 度.【考点】等腰直角三角形.【分析】根据等腰直角三角形底边上的“三线合一”的性质,判定等腰直角三角形.【解答】解:根据等腰三角形底边上的高也是底边上的中线和顶角的角平分线可知,高把原等腰直角三角形分成两个等腰直角三角形,顶角也就平分成两个45°,故顶角是90°,故填90.【点评】本题充分运用等腰直角三角形底边上的“三线合一”的性质解题.20.过△ABC的顶点C作边AB的垂线,如果这垂线将∠ACB分为40°和20°的两个角,那么∠A、∠B中较大的角的度数是70°.【考点】直角三角形的性质.【分析】根据直角三角形两锐角互余可以得到,∠A、∠B中有一个是70°,另一个是50°,因而∠A、∠B中较大的角的度数是70°.【解答】解:如图,依题意得∠ACD=40°,∠DCB=20°,而CD⊥AB于D,∴∠A=50°,∠B=70°,因而∠A、∠B中较大的角的度数是70°.故填空答案:70°.【点评】本题主要考查的是直角三角形两锐角互余的性质,比较简单.三、解答题(本大题共5小题,共30分)21.如图所示,∠1=∠2,AE∥BC,求证:△ABC是等腰三角形.【考点】等腰三角形的判定.【专题】证明题.【分析】由平行线的性质可得∠2=∠C,∠1=∠B,已知∠1=∠2,从而推出∠B=∠C,根据等角对等边可得到AB=AC,即△ABC是等腰三角形.【解答】证明:∵AE∥BC(已知),∴∠2=∠C(两直线平行,内错角相等).∠1=∠B(两直线平行,同位角相等).∵∠1=∠2(已知),∴∠B=∠C(等量代换).∴AB=AC.∴△ABC是等腰三角形(等角对等边).【点评】此题主要考查平行线的性质及等腰三角形的判定;进行角的等量代换是正确解答本题的关键.22.如图所示,BF∥DE,∠1=∠2,求证:GF∥BC.【考点】平行线的判定与性质.【专题】证明题.【分析】先根据两直线平行,同位角相等,得∠2=∠FBC,再结合已知条件和等量代换证得内错角∠FBC=∠1,从而得GF∥BC.【解答】解:∵BF∥DE(已知),∴∠2=∠FBC(两直线平行,同位角相等),∵∠2=∠1(已知),∴∠FBC=∠1(等量代换),∴GF∥BC(内错角相等,两直线平行).【点评】本题主要考查平行线的性质及判定,熟练记忆公理和定义是学好数学的关键.23.如图所示,已知AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,求∠GFC的度数.【考点】平行线的性质;角平分线的定义;垂线.【专题】计算题.【分析】根据平行线的性质,结合角平分线的定义和垂线的定义求解.【解答】解:∵AB∥CD,∠AEF=62°,∴∠EFD=∠A EF=62°,∠CFE=180°﹣∠AEF=180°﹣62°=118°;∵FH平分∠EFD,∴∠EFH=∠EFD=×62°=31°;又∵FG⊥FH,∴∠GFE=90°﹣∠EFH=90°﹣31°=59°,∴∠GFC=∠CFE﹣∠GFE=118°﹣59°=59°.【点评】此题考查的是平行线的性质,即两直线平行内错角相等,同旁内角互补.24.已知,如图所示,直线AB∥CD,∠AEP=∠CFQ.求证:∠EPM=∠FQM.【考点】平行线的判定与性质.【专题】证明题.【分析】根据题意证得∠AEF=∠CFM,再由∠AEP=∠CFQ,可得出∠PEM=∠QFM,PE∥QF,即能得出∠EPM=∠FQM.【解答】证明:∵AB∥CD(已知),∴∠AEF=∠CFM(两直线平行,同位角相等).又∵∠PEA=∠QFC(已知),∴∠AEF+∠PEA=∠CFM+∠QFC(等式性质).即∠PEM=∠QFM.∴PE∥QF(同位角相等,两直线平行).∴∠EPM=∠FQM(两直线平行,同位角相等).【点评】本题考查平行线的判定与性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.25.△ABC中,BE平分∠ABC,AD为BC上的高,且∠ABC=60°,∠BEC=75°,求∠DAC的度数.【考点】三角形内角和定理;角平分线的定义.【分析】要求∠DAC的度数,只要求出∠C的度数即可.先根据角平分线的定义,可得∠EBC的度数,在△BEC中利用三角形的内角和可得∠C的度数.因AD为BC上的高,所以∠ADC=90°,在△ADC中,再运用三角形的内角和可求∠DAC的度数.【解答】解:∵BE平分∠ABC,且∠ABC=60°,∴∠ABE=∠EBC=30°,∴∠C=180°﹣∠EBC﹣∠BEC=180°﹣30°﹣75°=75°.又∵∠C+∠DAC=90°,∴∠DAC=90°﹣∠C=90°﹣75°=15°.【点评】灵活运用垂直的定义和角平分线的定义,结合三角形的内角和定理是解决本题的关键.特别注意“三角形的内角和是180°”这一隐含的条件.。
第7章 平行线的证明单元测试卷(解析卷)

第7章平行线的证明单元测试卷参考答案与试题解析一.选择题(共12小题,满分36分,每小题3分)1.下列命题是真命题的是()A.有两边及一角对应相等的两个三角形全等B.底角相等的两个等腰三角形全等C.若a+b=0,则|a|=|b|D.角不是轴对称图形解:A、有两边及一角对应相等的两个三角形不一定全等,错误,是假命题;B、底角相等的两个等腰三角形不一定全等,错误,是假命题;C、若a+b=0,则|a|=|b|,正确,是真命题;D、角是轴对称图形,错误,是假命题,故选:C.2.在同一平面内,两直线的位置关系必是()A.相交B.平行C.相交或平行D.垂直解:在同一个平面内,两条直线只有两种位置关系,即平行或相交.故选:C.3.已知在同一平面内有三条不同的直线a,b,c,下列说法错误的是()A.如果a∥b,a⊥c,那么b⊥c B.如果b∥a,c∥a,那么b∥c C.如果b⊥a,c⊥a,那么b⊥c D.如果b⊥a,c⊥a,那么b∥c 解:A、如果a∥b,a⊥c,那么b⊥c,说法正确;B、如果b∥a,c∥a,那么b∥c,说法正确;C、如果b⊥a,c⊥a,那么b⊥c,说法错误;D、如果b⊥a,c⊥a,那么b∥c,说法正确;故选:C.4.如图,点在延长线上,下列条件中不能判定BD∥AC的是()A.∠1=∠2B.∠3=∠4C.∠5=∠C D.∠C+∠BDC=180°解:选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,故A选项不合题意.选项B中,∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),不能判定BD∥AC,所以B选项符合题意;选项C中,∵∠5=∠C,∴BD∥AC (内错角相等,两直线平行),所以C选项不合题意;选项D中,∵∠C+∠BDC=180°,∴BD∥AC(同旁内角互补,两直线平行),所以D 选项不合题意;故选:B.5.甲、乙、丙、丁4人进行乒乓球单循环比赛(每两个人都要比赛一场),结果甲胜了丁,并且甲、乙、丙胜的场数相同,则丁胜的场数是()A.3B.2C.1D.0解:四个人共有6场比赛,由于甲、乙、丙三人胜的场数相同,所以只有两种可能性:甲胜1场或甲胜2场;若甲只胜一场,这时乙、丙各胜一场,说明丁胜三场,这与甲胜丁矛盾,所以甲只能是胜两场,即:甲、乙、丙各胜2场,此时丁三场全败,也就是胜0场.答:甲、乙、丙各胜2场,此时丁三场全败,丁胜0场.故选:D.6.如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD 于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有()A.6个B.5个C.4个D.3个证明:∵∠EOD=∠BOC,∠EOD+∠OBF=180°,∴∠BOC+∠OBF=180°,∴EC∥BF,∴∠ECD=∠F,∠ECB=∠CBF,又∵CE平分∠ACB,∴∠ECD=∠ECB.又∵∠F=∠G,∴∠G=∠ECB.∴DG∥CE,∴∠CDG=∠DCE,∴∠CDG=∠G=∠F=DCE=∠CBF=∠ECB,故选:B.7.在△ABC中,∠A:∠B:∠C=3:4:8,则这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形解:∵∠A:∠B:∠C=3:4:8,∴设∠A=3α,∠B=4α,∠C=8α,∵∠A+∠B+∠C=180°,∴3α+4α+8α=180°,∴α=12°,∴∠C=8α=96°,∴这个三角形一定是钝角三角形,故选:D.8.如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是()A.∠BEF=∠EGH B.∠AEF=∠EFD C.AB∥CH D.GH∥CD 解:∵∠AEF=∠EGH,∴AB∥GH,∵AB∥CD,∴AB∥GH∥CD,故C、D正确;∴∠AEF=∠EFD,故B正确;故选:A.9.下列结论正确的是()A.不相交的两条直线叫做平行线B.两条直线被第三条直线所截,同位角相等C.垂直于同一条直线的两条直线互相平行D.平行于同一条直线的两条直线互相平行解:A、在同一个平面内不相交的两条直线叫做平行线,故A不符合题意;B、两条平行线被第三条直线所截,同位角相等,故B不符合题意;C、在同一平面内垂直于同一条直线的两条直线互相平行,故C不符合题意;D、平行于同一条直线的两条直线互相平行,故D符合题意;故选:D.10.在下面的四个图形中,已知∠1=∠2,那么能判定AB∥CD的是()A.B.C.D.解:A.由∠1=∠2,能判定AB∥CD,故本选项正确;B.由∠1=∠2,不能判定AB∥CD,故本选项错误;C.由∠1=∠2,不能判定AB∥CD,故本选项错误;D.由∠1=∠2,只能判定AD∥CB,故本选项错误;故选:A.11.如图△ABC中,∠C=∠ABC=2∠A,BD是边AC上的高,则∠DBC的度数是()A.36°B.26°C.18°D.16°解:∵∠A+∠C+∠ABC=180°,∠C=∠ABC=2∠A,∴2∠A+2∠A+∠A=180°,解得,∠A=36°,则∠C=72°,∵BD是边AC上的高,∴∠BDC=90°,∴∠DBC=90°﹣∠C=18°,故选:C.12.如图,将△ADE沿DE折叠,折痕为DE,则图中∠1,∠2,∠3之间的关系中,下列式子中正确的是()A.∠3=2∠1+∠2B.∠3=∠1+2∠2C.∠3=∠1+∠2D.∠3=180°﹣∠1﹣∠2解:∵将△ADE沿DE折叠,∴∠A=∠A′,即∠1=∠A′,∵∠4=180°﹣∠2﹣∠A′=180°﹣∠2﹣∠1,又∵∠B+∠C=180﹣∠1,∠3+∠4+∠B+∠C=360°∴∠3+180°﹣∠2﹣∠1+180°﹣∠1=360°∴∠3=2∠1+∠2,故选:A.二.填空题(共4小题,满分12分,每小题3分)13.如图,∠1=∠2,∠3=125°,则∠4等于55°.解:如图,∵∠1=∠2,∠2=∠6,∴∠1=∠6,∴a∥b,∴∠3=∠5=125°,∴∠4=180°﹣125°=55°,故答案为:55°.14.已知:a∥b,b∥c,则a∥c.理由是平行于同一直线的两条直线平行.解:∵a∥b,a∥c(已知),∴b∥c(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).故答案为平行于同一直线的两条直线平行15.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC、点G在DE的延长线上,∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为70°.解:∵∠DCE=∠DEC,∠DFG=∠DGF,∴设∠DCE=∠DEC=x°,∠DFG=∠DGF=y°,则∠FEG=∠DEC=x°,∵在△GFE中,∠EFG=35°,∴∠FEG+∠DGF=x°+y°=180°﹣35°=145°,即x+y=145,在△FDC中,∠CDF=180°﹣∠DCE﹣∠DFC=180°﹣x°﹣(y°﹣35°)=215°﹣(x°+y°)=70°,故答案为:70°.16.如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°;⑤∠6=∠8,其中能判断a∥b的是①③④⑤(填序号)解:①∵∠1=∠2,∴a∥b,故此选项正确;②∠3=∠6无法得出a∥b,故此选项错误;③∵∠4+∠7=180°,∴a∥b,故此选项正确;④∵∠5+∠3=180°,∴∠2+∠5=180°,∴a∥b,故此选项正确;⑤∵∠7=∠8,∠6=∠8,∴∠6=∠7,∴a∥b,故此选项正确;综上所述,正确的有①③④⑤.故答案为:①③④⑤.三.解答题(共8小题,满分52分)17.(6分)如图所示,∠B=25°,∠D=42°,∠BCD=67°,试判断AB和ED的位置关系,并说明理由.解:AB∥ED,理由:如图,过C作CF∥AB,∵∠B=25°,∴∠BCF=∠B=25°,∴∠DCF=∠BCD﹣∠BCF=42°,又∵∠D=42°,∴∠DCF=∠D,∴CF∥ED,∴AB∥ED.18.(6分)先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例(1)同旁内角互补,两直线平行;(2)一个角的补角一定是钝角.解:(1)如果两条直线被第三条直线所截得的同旁内角互补,那么这两条直线平行.是真命题.(2)如果一个角是另一个角的补角,那么这个角一定是钝角.是假命题;如:设∠1=60°,∠2=120°,∠1是∠2的补角,但∠1不是钝角.19.(6分)已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.解:过P点作PM∥AB交AC于点M.∵AB∥CD,(已知)∴∠BAC+∠ACD=180°.(两直线平行,同旁内角互补)∵PM∥AB,∴∠1=∠2,(两直线平行,内错角相等)且PM∥DC.(平行于同一直线的两直线也互相平行)∴∠3=∠4.(两直线平行,内错角相等)∵AP平分∠BAC,CP平分∠ACD,(已知)∴∠1=∠BAC,∠4=ACD.∴∠1+∠4=∠BAC+∠ACD=90°.∴∠APC=∠2+∠3=∠1+∠4=90°.总结:两直线平行时,同旁内角的角平分线互相垂直.解:过P点作PM∥AB交AC于点M.∵AB∥CD,(已知)∴∠BAC+∠ACD=180°.(两直线平行,同旁内角互补)∵PM∥AB,∴∠1=∠2,(两直线平行,内错角相等)且PM∥DC.(平行于同一直线的两直线也互相平行)∴∠3=∠4.(两直线平行,内错角相等)∵AP平分∠BAC,CP平分∠ACD,(已知)∴∠1=∠BAC,∠4=ACD.∴∠1+∠4=∠BAC+∠ACD=90°.∴∠APC=∠2+∠3=∠1+∠4=90°.总结:两直线平行时,同旁内角的角平分线互相垂直.故答案为:已知;两直线平行,同旁内角互补;2;两直线平行,内错角相等,DC;4;两直线平行,内错角相等;已知;互相垂直.20.(6分)如图,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.证明:∵∠ABC+∠ECB=180°,∴AB∥DE,∴∠ABC=∠BCD,∵∠P=∠Q,∴PB∥CQ,∴∠PBC=∠BCQ,∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,∴∠1=∠2.21.(6分)四个足球队进行单循环比赛,规定胜一场得3分,平一场得1分,负一场得0分,有一个队一场都没输过,排名却倒数第一,你觉得可能吗?如果可能,请举出这情况何时出现;如果不可能,请说明理由.解:某队全平的情况下会排名倒数第一,如:甲队:全平⇒1+1+1=3(分),乙队:平1场,胜1场(乙胜丙),输1场⇒1+3+0=4(分),丙队:平1场,胜1场(丙胜丁),输1场⇒1+3+0=4(分),丁队:平1场,胜1场(丁胜乙),输1场⇒1+3+0=4(分),当然还有其它情况出现.22.(6分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=10°,∠B=50°,求∠C的度数.解:∵AD是BC边上的高,∠EAD=10°,∴∠AED=80°,∵∠B=50°,∴∠BAE=∠AED﹣∠B=80°﹣50°=30°,∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=60°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣60°=70°.23.(8分)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+D;(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.①以线段AC为边的“8字型”有3个,以点O为交点的“8字型”有4个;②若∠B=100°,∠C=120°,求∠P的度数;③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;(2)解:①3;4;故答案为:3,4;②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,∵AP、DP分别平分∠CAB和∠BDC,∴∠BAP=∠CAP,∠CDP=∠BDP,∴2∠P=∠B+∠C,∵∠B=100°,∠C=120°,∴∠P=(∠B+∠C)=(100°+120°)=110°;③3∠P=∠B+2∠C,其理由是:∵∠CAP=∠CAB,∠CDP=∠CDB,∴∠BAP=∠CAB,∠BDP=∠CDB,以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).∴2(∠C﹣∠P)=∠P﹣∠B,∴3∠P=∠B+2∠C.24.(8分)如图1,点E在直线AB上,点F在直线CD上,EG⊥FG.(1)若∠BEG+∠DFG=90°,请判断AB与CD的位置关系,并说明理由;(2)如图2,在(1)的结论下,当EG⊥FG保持不变,EG上有一点M,使∠MFG=2∠DFG,则∠BEG与∠MFD存在怎样的数量关系?并说明理由.(3)如图2,若移动点M,使∠MFG=n∠DFG,请直接写出∠BEG与∠MFD的数量关系.解:(1)AB∥CD,理由:延长EG交CD于H,∴∠HGF=∠EGF=90°,∴∠GHF+∠GFH=90°,∵∠BEG+∠DFG=90°,∴∠BEG=∠GHF,∴AB∥CD;(3)∠BEG+∠MFD=90°,理由:∵AB∥CD,∴∠BEG=∠GHF,∵EG⊥FG,∴∠GHF+∠GFH=90°,∵∠MFG=n∠DFG,∴∠BEG+∠MFG=90°.。
北师版八年级数学上册 第七章 平行线的证明(单元综合测试卷)

第七章平行线的证明(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围:全章的内容;考试时间:120分钟;总分:120分一、单选题(本大题共10小题,每小题3分,共30分)1.下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB 到C ,使BC=AB ,其中是命题的有()A .①②B .②③C .①④D .①③2.如图,下列说法不正确的是()A .∠1和∠2互为邻补角B .∠1和∠4是内错角C .∠2和∠3是同旁内角D .∠1和∠3是同位角3.如图,点E 在AC 的延长线上,下列条件不能判定AB CD ∥的是()A .12∠=∠B .3=4∠∠C .A DCE ∠=∠D .24180A ∠+∠+∠=︒4.如图,在ABC V 中,外角105,58ACD B ∠=︒∠=︒,则A ∠的度数是()A .43︒B .47︒C .53︒D .57︒5.一条杆秤在称物时的状态如图所示,秤上的线在称东西时都平行,当1105∠=︒时,2∠的度数是()A .35︒B .75︒C .85︒D .105︒6.设a 、b 、c 为同一平面内的三条直线,下列判断不正确的是()A .若a //b ,b //c ,则a //cB .若a ⊥b ,b ⊥c ,则a ⊥cC .若a ⊥b ,b ⊥c ,则a //cD .若a //b ,b ⊥c ,则a ⊥c7.一副三角尺如图放置,45A ∠=︒,30E ∠=︒,∥DE AC ,则1∠的度数为()A .95︒B .100︒C .105︒D .120︒8.如图,在ABC V 中,:1:2A B ∠∠=,D 是BC 延长线上一点,过点D 作DE AB ⊥于点E ,若75FCD ∠=︒,则D ∠=()A .40︒B .30︒C .45︒D .50︒9.如图所示,在四边形ABCD 中,B 是它的一条对角线,若12∠=∠,5516A '∠=︒,则ADC ∠=()A .12444'︒B .3444'︒C .14444︒'D .11444'︒10.如图,AB CD ∥,用含1∠,2∠,3∠的式子表示4∠,则4∠的值为()A .123∠+∠-∠B .132∠+∠-∠C .180312︒+∠-∠-∠D .231180∠+∠-∠-︒二、填空题(本大题共8小题,每小题3分,共24分)11.将命题“两直线平行,同位角相等”写成“如果……那么……”的形式是.12.如图,1108∠=︒,230∠=︒,若使b c ∥,则可将直线b 绕点A 逆时针旋转度.13.如图所示,下列结论:①1∠和2∠是同旁内角;②3∠和4∠是对顶角;③2∠和5∠是内错角;④4∠和5∠是同位角.其中正确的是.(把正确结论的序号都填上)14.三角形三个内角度数的比为2:3:4,则这个三角形最大的外角是度.15.已知:如图,OAD OBC △≌△,且8025O C ∠=︒∠=︒,,则AEB ∠=度.16.平行线在生活中应用很广泛,人们为了准确地画出平行线,往往利用三角尺和直尺按照下面的方法去做:第一步:作直线AB ,并用三角尺的一条边贴住直线AB ;第二步:用直尺紧靠三角尺的另一条边;第三步:沿直尺下移三角尺;第四步:沿三角尺的边作出直线CD .这样,就得到AB CD ∥.请写出其中的道理:.17.如图,在ABC V 中,50A ∠=︒,内角ABC ∠和外角ACD ∠的平分线BE ,CE 相交于点E ,则E ∠的度数为.18.如图,在ABC V 中,5490A B ∠=︒∠=︒,,D 是AC 边上的定点,E 是CB 上的动点,沿DE 折叠CDE ,点C 落在点F 处.当EF 与ABC V 的一边平行时,DEB ∠的度数是.三、解答题(本大题共9小题,共66分)19.如图,,12,55AD BC C ⊥∠=∠∠=︒.求BAC ∠的度数.20.已知:如图12,C D ∠=∠∠=∠,证明:DF AC ∥.21.如图,在ABC V 中,AC AB >.尺规作图(保留作图痕迹,不写作法):(1)在AC 上截取AD AB =,连接BD ;(2)过D 作BC 的平行线交AB 于点E .22.按下列要求画图并填空:如图,直线AB 与CD 相交于点O ,P 是CD 上的一点.(1)过点P 画出CD 的垂线,交直线AB 于点E ;(2)过点P 画PF ⊥AB ,垂足为点F ;(3)点O 到直线PE 的距离是线段的长;(4)点P 到直线CD 的距离为.23.如图,点G 在CD 上,已知180BAG AGD ∠+∠=︒,EA 平分BAG ∠,FG 平分AGC ∠.请说明AE GF ∥的理由.解:因为180BAG AGD ∠+∠=︒(已知),180AGC AGD ∠+∠=︒(______),所以BAG AGC ∠=∠(______).因为EA 平分BAG ∠,所以112BAG ∠=∠(______).因为FG 平分AGC ∠,所以122∠=______,得12∠=∠(等量代换),所以______(______).24.如图,在ABC V 中,D 为AB 上一点,E 为AC 中点,连接DE 并延长至点F ,使得EF ED =,连CF .(1)求证:CF AB∥(2)若7035A F BE AC ∠=︒∠=︒⊥,,,求BED ∠的度数.25.如图,在ABC V 中,AD 是高,AE 是角平分线.(1)若70,40B C ∠=︒∠=︒,求DAE ∠的度数.(2)若30B C ∠-∠= ,则DAE ∠=_______︒.(3)若B C α∠-∠=.则DAE ∠的度数_______(结果用含α的代数式表示).26.如图,AB CD ∥.(1)如图1,请探索A ∠,E ∠,C ∠三个角之间的数量关系,并说明理由;(2)已知24A ∠=︒.①如图2,若100F ∠=︒,求C E ∠+∠的度数;②如图3,若AEF ∠和DCF ∠的平分线交于点G ,请直接写出EGC ∠与F ∠的数量关系.27.已知:在ABC V 中,90ABC ACB ∠-∠=︒,点D 在BC 上,连接AD ,且45ADB ∠=︒(1)如图1,求证:BAD CAD ∠=∠;(2)如图2,点E 为BC 的中点,过点E 作AD 的垂线分别交AD 的延长线,AB 的延长线,AC 于点F ,G ,H ,求证:BG CH =;(3)如图3,在(2)的条件下,过点E 分别作EM AG ⊥于点M ,EN AC ⊥于点N ,若1401326AB AC EM EN +=+=,,求AFG 的面积.第七章平行线的证明(单元重点综合测试)班级___________姓名___________学号____________分数____________考试范围:全章的内容;考试时间:120分钟;总分:120分一、单选题1.下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有()A.①②B.②③C.①④D.①③【答案】D【解析】①三角形的内角和是180°,是命题;②作一个角等于一个已知角,不是命题;③两条直线被第三条直线所截,同位角相等,是命题;④延长线段AB到C,使BC=AB,不是命题,故选D.2.如图,下列说法不正确的是()A.∠1和∠2互为邻补角B.∠1和∠4是内错角C.∠2和∠3是同旁内角D.∠1和∠3是同位角【答案】B【分析】根据同位角、同旁内角、内错角和邻补角的概念解答即可.【详解】解:A、∠1和∠2互为邻补角,正确,不符合题意;B、∠1和∠4不是内错角,错误,符合题意;C、∠2和∠3是同旁内角,正确,不符合题意;D、∠1和∠3是同位角,正确,不符合题意;故选:B.【点睛】此题考查同位角、同旁内角、内错角和邻补角,熟练掌握同位角、内错角相等,同旁内角的定义是解题的关键.3.如图,点E 在AC 的延长线上,下列条件不能判定AB CD ∥的是()A .12∠=∠B .3=4∠∠C .A DCE ∠=∠D .24180A ∠+∠+∠=︒【答案】B 【分析】根据平行线判定定理逐个判断即可得到答案.【详解】解:∵12∠=∠,∴AB CD ∥,故A 不符合题意;∵3=4∠∠,∴BD AC ∥,故B 符合题意;∵A DCE ∠=∠,∴AB CD ∥,故C 不符合题意;∵24180A ∠+∠+∠=︒,∴AB CD ∥,故D 不符合题意;故选B .【点睛】本题考查平行线的判定:内错角相等两直线平行,同位角相等两直线平行,同旁内角互补两线平行.4.如图,在ABC V 中,外角105,58ACD B ∠=︒∠=︒,则A ∠的度数是()A .43︒B .47︒C .53︒D .57︒【答案】B 【分析】此题考查了三角形外角的性质,三角形的外角等于与它不相邻的两个内角的和,据此进行解答即可.【详解】解:在ABC V 中,外角105,58ACD B ∠=︒∠=︒,∴1055847A ACD B ∠=∠-∠=︒-︒=︒,故选:B .5.一条杆秤在称物时的状态如图所示,秤上的线在称东西时都平行,当1105∠=︒时,2∠的度数是()A .35︒B .75︒C .85︒D .105︒【答案】B 【分析】本题考查平行线的知识,解题的关键根据平角的性质,求出3∠,根据平行线的性质,两直线平行,内错角相等,即可.【详解】∵13180∠+∠=︒,1105∠=︒,∴375∠=︒,∵秤上的线在称东西时都平行,即AB CD ∥,∴2375∠=∠=︒,故选:B .6.设a 、b 、c 为同一平面内的三条直线,下列判断不正确的是()A .若a //b ,b //c ,则a //cB .若a ⊥b ,b ⊥c ,则a ⊥cC .若a ⊥b ,b ⊥c ,则a //cD .若a //b ,b ⊥c ,则a ⊥c【答案】B 【详解】根据平行线的判定定理及垂直的性质逐项进行分析即可解答.【解答】解:A .根据平行于同一直线的两直线平行,即可推出a //c ,则本选项正确,不合题意,B .根据垂直于同一直线的两直线平行,即可推出a ∥c ,故本选项错误,符合题意,C .根据垂直于同一直线的两直线平行,即可推出a ∥c ,本选项正确,不合题意,D .根据平行线的性质,即可推出a ⊥c ,本选项正确,不合题意.故选:B .【点睛】本题主要考查平行线的判定定理及性质、垂直的性质等知识点,灵活运用相关的性质定理并是解答本题的关键.7.一副三角尺如图放置,45A ∠=︒,30E ∠=︒,∥DE AC ,则1∠的度数为()A .95︒B .100︒C .105︒D .120︒【答案】C 【分析】本题考查平行线的性质、邻补角,三角形的内角和定理,熟练运用平行线的性质是关键.利用平行线的性质求出245A ∠=∠=︒,根据三角形内角和求出DGB ∠,进一步求出1∠.【详解】解:如图,∵∥DE AC ,∴245A ∠=∠=︒.∵90F ∠=︒,∴180903060D ∠=︒-︒-︒=︒,∴180456075DGB ∠=︒-︒-︒=︒.∵1180DGB ∠+∠=︒,∴118075105∠=︒-︒=︒.故选:C .8.如图,在ABC V 中,:1:2A B ∠∠=,D 是BC 延长线上一点,过点D 作DE AB ⊥于点E ,若75FCD ∠=︒,则D ∠=()A .40︒B .30︒C .45︒D .50︒【答案】A 【分析】本题考查了三角形的内角和定理,外角性质,掌握三角形的外角性质是解题的关键.根据三角形的外角性质可得A B FCD ∠+∠=∠,由此解答即可.【详解】解:DE AB ∵⊥,90BED ∴∠=︒,:1:2A B ∠∠= ,75FCD ∠=︒,A B FCD ∠+∠=∠ ,∴3752B ∠=︒.50B ∴∠=︒,180B BED D ∠+∠+∠=︒ ,180509040D ∴∠=︒-︒-︒=︒.故选:A .9.如图所示,在四边形ABCD 中,B 是它的一条对角线,若12∠=∠,5516A '∠=︒,则ADC ∠=()A .12444'︒B .3444'︒C .14444︒'D .11444'︒【答案】A 【分析】本题考查了平行线的判定和性质,由12∠=∠可得AB CD ∥,即得180A ADC ∠+∠=︒,据此即可求解,掌握平行线的判定和性质是解题的关键.【详解】解:∵12∠=∠,∴AB CD ∥,∴180A ADC ∠+∠=︒,∵5516A '∠=︒,∴180551612444ADC ∠=︒-︒=︒'',故选:A .10.如图,AB CD ∥,用含1∠,2∠,3∠的式子表示4∠,则4∠的值为()A .123∠+∠-∠B .132∠+∠-∠C .180312︒+∠-∠-∠D .231180∠+∠-∠-︒【答案】D 【分析】本题考查了平行的性质,作出相应的辅助线是解题的关键.过点E 作EG AB ∥,过点F 作FH CD ∥,可得AB CD EG FH ∥∥∥,从而推出21GEF ∠=∠-∠,180EFH GEF ∠=︒-∠,43CFH EFH ∠=∠=∠-∠即可得到答案.【详解】解:过点E 作EG AB ∥,过点F 作FH CD ∥,AB CDAB CD EG FH∴∥∥∥1AEG∴∠=∠21GEF ∴∠=∠-∠EG FH∥180180(21)18021EFH GEF ∴∠=︒-∠=︒-∠-∠=︒-∠+∠33(18021)321180CFH EFH ∴∠=∠-∠=∠-︒-∠+∠=∠+∠-∠-︒FH CD∥4321180CFH ∴∠=∠=∠+∠-∠-︒故选:D .二、填空题11.将命题“两直线平行,同位角相等”写成“如果……那么……”的形式是.【答案】如果两直线平行,那么同位角相等【分析】一个命题都能写成“如果…那么…”的形式,如果后面是题设,那么后面是结论.【详解】解:命题“两直线平行,同位角相等”的条件是:“两直线平行”,结论为:“同位角相等”,所以写成“如果…,那么…”的形式为:“如果两直线平行,那么同位角相等”,故答案为:如果两直线平行,那么同位角相等.【点睛】本题考查了命题的叙述形式,比较简单.12.如图,1108∠=︒,230∠=︒,若使b c ∥,则可将直线b 绕点A 逆时针旋转度.【答案】42【分析】先根据邻补角进行计算得到372∠=︒,根据平行线的判定当b 与a 的夹角为72︒时,b c ∥,由此得到直线b 绕点A 逆时针旋转723042︒-︒=︒.【详解】解:如图:∵1108∠=︒,∴372∠=︒,∵230∠=︒,∴当3230∠=∠=︒时,b c ∥,∴直线b 绕点A 逆时针旋转723042︒-︒=︒.故答案为:42.【点睛】本题考查的是平行线的判定定理,熟知同位角相等,两直线平行是解答此题的关键.13.如图所示,下列结论:①1∠和2∠是同旁内角;②3∠和4∠是对顶角;③2∠和5∠是内错角;④4∠和5∠是同位角.其中正确的是.(把正确结论的序号都填上)【答案】①③【分析】根据同位角,对顶角,同旁内角,内错角的定义进行判断即可得到答案.【详解】解:①∠1和∠2是同旁内角,故此说法正确;②∠3和∠4不是对顶角,故此说法错误;③∠2和∠5是内错角,故此说法正确;④∠4和∠5不是同位角。
第七章 平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)

第七章平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如图,已知,,,则的度数是()A. B. C. D.2、如图,是一块三角形木板的残余部分,量得,,这块三角形木板缺少的角是( )A. B. C. D.3、如图,Rt△ABC中,∠C=900, AB的垂直平分线DE交AC于点E,连接BE,若∠A=40°,则∠CBE的度数为()A.10°B.15°C.20°D.25°4、如图,AE‖BD,∠1=120°,∠2=40°,则∠C的度数是()A.10°B.20°C.30°D.40°5、已知,如图:AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD为()度.A.40°B.50°C.60°D.70°6、下列语句中正确的是()A.三角形的一个外角等于两个内角的和B.有两边和一角对应相等的两个三角形一定全等C.有两边分别相等的两个直角三角形全等D.到角的两边距离相等的点在这个角的平分线上7、若,,为的三边长,则下列条件中不能判定是直角三角形的是()A. ,,B.C.D.8、如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,BD,OD,OC,若∠ABD=15°,且AD∥OC,则∠BOC的度数为()A.120°B.105°C.100°D.110°9、若一个三角形三个内角的度数之比是,则这个三角形一定是()A.直角三角形B.锐角三角形C.钝角三角形D.不能确定10、如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为()A.30°B.40°C.50°D.70°11、将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( )A.45°B.60°C.75°D.90°12、如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=20°,则∠CEF等于()A.110°B.100°C.80°D.70°13、如图,△APB与△CDP均为等边三角形,且PA⊥PD,PA=PD.有下列三个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直.其中正确的有( )A.0个B.1个C.2个D.3个14、如图,PA是⊙O的切线,A为切点,PO的延长线交⊙O于点B,若∠B=32°,则∠P 的度数为()A.24ºB.26ºC.28ºD.32º15、如图,ΔABC与关于直线l对称,则∠B的度数为()A.30°B.50°C.90°D.100°二、填空题(共10题,共计30分)16、按一定规律排列的一列数:,,,,,,…,若、、表示这列数中依次排列的连续的三个数,猜想、、满足的关系式是________.17、探究一列数的规律,写出最后一个数,(________)18、观察下列各式数:0,3,8,15,24,……试按此规律写出第n个数是________ 。
北师大版八年级数学上册 第七章 平行线的证明单元检测题(含答案解析)

第七章平行线的证明检测题(本检测题满分:100分,时间:90分钟)一、选择题(每小题3分,共30分)1.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有()A.1个B.2个C.3个D.4个2.点P是直线l外一点,,A为垂足,且PA=4 cm,则点P到直线l的距离()A.小于4 cm B.等于4 cm C.大于4 cm D.不确定3.如图,点在的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2 B.∠3=∠4C.∠5=∠D.∠+∠BDC=180°第3题图第4题图第5题图4.如图,a∥b,∠3=108°,则∠1的度数是()A.72°B.80°C.82°D.108°5.如图,BE平分∠ABC,DE∥BC,图中相等的角共有()A.3对B.4对C.5对D.6对6.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有()A.1个B.2个C.3个D.4个第6题第7题图第8题图7.(2013•安徽中考)如图,AB∥CD,∠A+∠E=75°,则∠C为()A.60°B.65°C.75°D.80°8.如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为()A.2个B.3个C.4个D.5个9、下列条件中能得到平行线的是()①邻补角的角平分线;②平行线内错角的角平分线;③平行线同旁内角的角平分线.A.①②B.②③C.②D.③10、两条平行直线被第三条直线所截,同位角的平分线()A.互相重合B.互相平行C.互相垂直D.相交二、填空题(共8小题,每小题3分,满分24分)11.命题“对顶角相等”的题设是,结论是.12.一个三角形的两个内角是35°和110°,则另一个内角是.第13题图第14题图第15题图13.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是.14.如图,D是AB上一点,CE∥BD,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED= .15.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= .16.如图,直线a∥b,则∠ACB= .第16题图第17题图第19题图17.一个宽度相等的纸条按如图所示方法折叠一下,则∠1= .18、三角形的外角和等于它的内角和的倍.三、解答题(共6小题,满分46分)19.(6分)读句画图:如图,直线CD与直线AB相交于点C,根据下列语句画图:(1)过点P作PQ∥CD,交AB于点Q;(2)过点P作PR⊥CD,垂足为R;(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.20.(6分)我们知道,三角形一个外角等于与它不相邻的两个内角的和.请利用这条定理解决下列问题:如图,∠1=∠2=∠3.(1)试说明∠BAC=∠DEF.(2)∠BAC=70°,∠DFE =50°,求∠ABC的度数.21.(6分)已知:如图,∠BAP +∠APD =,∠1 =∠2、求证:∠E =∠F.22.(7分)已知:如图,∠1 =∠2,∠3 =∠4,∠5 =∠6、求证:ED∥FB.23.(7分)如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.24.(7分)如图,已知AB∥ED,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.25、(7分) 在“三角形内角和”的探究中课本中给了我们这样一种折叠方法,把三角形按如图的虚线折叠,可以得到三角形的内角和等于180°,请你根据折叠过程证明这个结论.参考答案一、选择题1、B 解析:①是正确的,对顶角相等;②正确,在同一平面内,垂直于同一条直线的两直线平行;③错误,角平分线分成的两个角相等但不是对顶角;④错误,同位角只有在两直线平行的情况下才相等.故①②正确,③④错误,所以错误的有两个,故选B.2、B 解析:因为点到直线的距离为点到直线的垂线段的长度(垂线段最短),所以点P到直线l的距离等于4 cm,故选B.3、A 解析:选项B中,∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),故正确;选项C中,∵∠5=∠B,∴AB∥CD(内错角相等,两直线平行),故正确;选项D中,∵∠B+∠BDC=180°,∴AB∥CD(同旁内角互补,两直线平行),故正确;而选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,∵∠1=∠2,∴AC∥BD,故选项A错误.选A.4、A 解析:∵a∥b,∠3=108°,∴∠1=∠2=180°∠3=72°.故选A.5、C 解析:∵ DE∥BC,∴∠DEB=∠EBC,∠ADE=∠ABC,∠AED=∠ACB、又∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠DEB(等量代换).∴图中相等的角共有5对.故选C.6、C 解析:∵AB∥CD,∴∠ABC=∠BCD、设∠ABC的对顶角为∠1,则∠ABC=∠1、又∵AC⊥BC,∴∠ACB=90°,∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°,因此与∠CAB互余的角为∠ABC,∠BCD,∠1.故选C.7、C 解析:∵∠A+∠E=75°,∴∠EOB=∠A+∠E=75°、∵AB∥CD,∴∠C=∠EOB=75°,故选C.8、D 解析:如题图,∵ DC∥EF,∴∠DCB=∠EFB、∵DH∥EG∥BC,∴∠GEF=∠EFB,∴∠DCB =∠GEF、∠DCB=∠HDC,∠DCB=∠CMG=∠DME,故与∠DCB相等的角共有5个.故选D.9、C 解析:结合已知条件,利用平行线的判定定理依次推理判断.10、B 解析:∵两条平行直线被第三条直线所截,同位角相等,∴它们角的平分线形成的同位角相等,∴同位角相等的平分线平行.故选B.二、填空题11、两个角是对顶角这两个角相等解析:命题“对顶角相等”可写成:如果两个角是对顶角,那么这两个角相等.故命题“对顶角相等”的题设是“两个角是对顶角”,结论是“这两个角相等”.12、35°解析:因为三角形的内角度数和是180°,所以另一个内角的度数为180°-110°-35°=35°、13、∠1+∠2=90°(互为余角)解析:∵直线AB、EF相交于O点,∴∠1=∠DOF、又∵ AB⊥CD,∴∠2+∠DOF=90°,∴∠1+∠2=90°.14、52°解析:∵ EA⊥BA,∴∠EAD=90°、∵CB∥ED,∠ABC=38°,∴∠EDA=∠ABC=38°,∴∠AED=180°∠EAD∠EDA=52°.15、54°解析:∵AB∥CD,∴∠BEF=180°∠1=180°72°=108°,∠2=∠BEG、又∵EG平分∠BEF,∴∠BEG=∠BEF=×108°=54°,故∠2=∠BEG=54°.16、78°解析:延长BC与直线a相交于点D,∵a∥b,∴∠ADC=∠CBE=50°、∴∠ACB=∠ADC +28°=50°+28°=78°、故应填78°、17、65°解析:根据题意,得2∠1与130°角相等,即2∠1=130°,解得∠1=65°.故填65°.18、2 解析:∵ 三角形内角和为180°,任意多边形外角和等于360°,∴ 三角形的外角和等于它的内角和的360÷180=2(倍)、 三、解答题19.解:(1)(2)如图所示、第19题答图 (3)∠PQC =60°、理由:∵ PQ ∥CD ,∴ ∠DCB +∠PQC =180°、 ∵ ∠DCB =120°,∴ ∠PQC =180°120°=60°. 20、(1)证明:∠DEF =∠3+∠CAE ,∵ ∠1=∠3,∴ ∠DEF =∠1+∠CAE =∠BAC , 即∠BAC =∠DEF 、(2)解:∠DFE =∠2+∠BCF ,∵ ∠2=∠3,∴ ∠DFE =∠3+∠BCF , 即∠DFE =∠ACB 、 ∵ ∠BAC =70°,∠DFE =50°、 ∴ 在△ABC 中,∠ABC =180°-∠BAC -∠ACB =180°-70°-50°=60°. 21、证明:∵ ∠BAP +∠APD = 180°,∴ AB ∥CD 、∴ ∠BAP =∠APC 、 又∵ ∠1 =∠2,∴ ∠BAP −∠1 =∠APC −∠2、即∠EAP =∠APF 、 ∴ AE ∥FP 、∴ ∠E =∠F 、22.证明:∵ ∠3 =∠4,∴ AC ∥BD 、∴ ∠6+∠2+∠3 = 180°、 ∵ ∠6 =∠5,∠2 =∠1,∴ ∠5+∠1+∠3 = 180°、∴ ED ∥FB 、 23、 解:∵ DE ∥BC ,∠AED =80°,∴ ∠EDC =∠BCD ,∠ACB =∠AED =80°、 ∵ CD 平分∠ACB ,∴ ∠BCD = 21∠ACB =40°, ∴ ∠EDC =∠BCD =40°.24、 解:∵ AB ∥ED ,∴ ∠B +∠BCE =180°(两直线平行,同旁内角互补)、∵ ∠B =65°,∴ ∠BCE =115°、 ∵ CM 平分∠BCE ,∴ ∠ECM =21∠BCE =57、5°、 ∵ ∠ECM +∠MCN +∠NCD =180°,∠MCN =90°, ∴ ∠NCD =180°-∠ECM -∠MCN =180°-57、5°-90°=32、5°. 25、 证明:∵△DEF 由△AEF 折叠而得,∴ ∠EDF =∠EAF , 同理∠EDB =∠B ,∠FDC =∠C 、 ∵ ∠BDE +∠EDF +∠FDC =180°,∴ ∠B +∠BAC +∠C =180°, ∴ 三角形内角和等于180°、。
(好题)初中数学八年级数学上册第七单元《平行线的证明》检测(包含答案解析)

一、选择题1.下列命题中,为真命题的是( )A .13是13的算术平方根B .三角形的一个外角大于任何一个内角C .13是最简二次根式 D .两条直线被第三条直线所截,内错角相等 2.如图,将ABC 绕点C 顺时针旋转90︒得到EDC △,点A 、D 、E 在同一条直线上.若20ACB ∠=︒,则ADC ∠的度数是( )A .60︒B .65︒C .70︒D .75︒3.如图,有下列说法:①若13∠=∠,//AD BC ,则BD 是ABC ∠的平分线;②若//AD BC ,则123∠=∠=∠;③若13∠=∠,则//AD BC ;④若34180C ∠+∠+∠=,则//AD BC .其中正确的有( ).A .1个B .2个C .3个D .44.下列命题是假命题的是( )A .三角形的内角和是180°B .两直线平行,内错角相等C .三角形的外角大于任何一个内角D .同旁内角互补,两直线平行 5.如图,在ABC 中,AD 是角平分线,AE 是高,已知2BAC B ∠=∠,2B DAE ∠=∠,那么C ∠的度数为( )A .72°B .75°C .70°D .60° 6.一副透明的三角板,如图叠放,直角三角板的斜边AB 、CE 相交于点D ,则BDC∠的度数是( )A .65︒B .75︒C .85︒D .105︒ 7.如图,AD 平分∠BAC ,AE ⊥BC ,∠B=45°,∠C=73°,则∠DAE 的度数是( ).A .22°B .16°C .14°D .23°8.如图,Rt △ABC 中,∠ACB=90°,∠A=50°,将其折叠,使点A 落在边CB 上A′处,折痕为CD ,则∠A′DB=( )A .15°B .30°C .10°D .20° 9.如图,△CEF 中,∠E=70°,∠F=50°,且AB ∥CF ,AD ∥CE ,连接BC ,CD ,则∠A 的度数是( )A .40°B .45°C .50°D .60° 10.在△ABC 中,∠A =80°,∠B =50°,则∠C =( )A .130°B .50°C .40°D .20° 11.如图,已知四边形ABCD 中,98B ∠=︒,62D ∠=︒,点E 、F 分别在边BC 、CD 上.将CEF △沿EF 翻折得到GEF △,若GE AB ∥,GF AD ∥,则C ∠的度数为( )A .80︒B .90︒C .100︒D .110︒12.下列命题中,假命题是( )A .负数没有平方根B .两条平行直线被第三条直线所截,同位角相等C .对顶角相等D .内错角相等 二、填空题13.在一个三角形中,若其中一个内角的度数是另一个内角的2倍,则我们称这个三角形为“倍角三角形”.已知某“倍角三角形”的一个内角的度数为60°,则其它两个内角的度数分别是_______.14.如图,A α∠=,,ABC ACD ∠∠的平分线相交于点1P ,11,PBC PCD ∠∠的平分线相交于点2P ,2P BC ∠,2P CD ∠的平分线相交于点3P ……以此类推,则n P ∠的度数是___________(用含n 与α的代数式表示).15.请写出命题“直角三角形的两个锐角互余”的逆命题:__________.16.如图,已知AD BC ⊥,EF BC ⊥,3C ∠∠=,试说明:12∠∠=.请将以下不完整的推理过程补充完整:解:因为AD BC ⊥,EF BC ⊥,所以90ADC EFC ∠∠︒==,根据“同位角相等,两直线平行”,所以//AD EF , 根据“ ”,所以1CAD ∠∠=.因为3C ∠∠=,根据“ ”,所以//DG ,根据“ ”,所以2CAD ∠∠=.所以12∠∠=.17.已知直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为___________.18.下列命题中,其逆命题成立的是_____.(填上正确的序号)①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④在角的内部,到角的两边距离相等的点在角的平分线上;⑤等边三角形是锐角三角形.19.如图,12∠=∠,4120︒∠=,则3∠=____.20.在△ABC 中,BO 平分∠ABC ,CO 平分∠ACB ,若∠O =120°,则∠A =_____.三、解答题21.如图,178∠=︒,2102∠=︒,C D ∠=∠.求证://AC DF .22.定义:一个三位数,如果它的各个数位上的数字互不相等且都不为0,同时满足十位上的数字为百位与个位数字之和,则称这个三位数为“西西数”.A 是一个“西西数”,从A 各数位上的数字中任选两个组成一个两位数,由此我们可以得到6个不同的两位数.我们把这6个数之和与44的商记为()h A ,如:132A =,133112212332(132)344h +++++==. (1)求()187h ,()693h 的值. (2)若A ,B 为两个“西西数”,且()()35h A h B =,求B A 的最大值. 23.在ABC 中,AB AC =,直线l 经过点A ,且与BC 平行.仅用圆规完成下列画图.(保留画图痕迹,不写作法)(1)如图①,在直线l 上画出一点P ,使得APC ACB ∠=∠;(2)如图②,在直线l 上画出所有的点Q ,使得12AQC ACB ∠=∠.24.如图,已知:∠DGA=∠FHC ,∠A=∠F .求证:DF ∥AC .(注:证明时要求写出每一步的依据)25.如图,在ABC 中,EF AB ⊥,CD AB ⊥,G 在AC 边上,AGD ACB ∠=∠.求证:(1)12∠=∠;(2)90BCD ADG ∠+∠=︒.26.数学课上,张老师给出这样一个问题——已知:如图,直线//a b ,//a c ,请说明://b c .请你把小明的说明过程补充完整: 说明:作直线l 分别和a ,b ,c 相交(如图)//a b (已知)1∴∠=______,(______)又//a c (已知)1∴∠=______,(两直线平行,内错角相等)∴______,//b c ∴,(______)由此我们可以得到一个基本事实:平行于同一条直线的两条直线互相______.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据算术平方根、三角形外角定理、最简二次根式定义、平行线性质逐项判断即可求解.【详解】解:13的算术平方根”,判断正确,符合题意;B. “三角形的一个外角大于任何一个内角”,应为“三角形的一个外角大于和它不相邻的任意一个内角”,判断错误,不合题意;”,不是最简二次根式,判断错误,不合题意;D. “两条直线被第三条直线所截,内错角相等”,两条直线不一定平行,判断错误,不合题意.故选:A【点睛】本题考查了命题、算术平方根、三角形外角定理、最简二次根式定义、平行线性质等知识,熟练掌握相关知识是解题的关键,注意:题设成立,结论一定成立的命题是真命题;题设成立,结论不一定成立的命题是假命题.2.B解析:B【分析】根据全等三角形的性质和三角形内角和定理解答即可;【详解】∵将ABC 绕点C 顺时针旋转90︒得到EDC △,∴ABC EDC ≅△△,∴20DCE ACB ∠=∠=︒,90BCD ACE ∠=∠=︒,AC CE =,∴902070ACD ∠=︒-︒=︒,∵点A 、D 、E 在同一条直线上,∴180ADC EDC ∠+∠=︒,∵180EDC E DCE ∠+∠+∠=︒,∴20ADC E ∠=∠+︒,∵90ACE ∠=︒,AC CE =,∴90DAC E ∠+∠=︒,45E DAC ∠=∠=︒,∴65ADC ∠=︒; 故选:B .【点睛】本题主要考查了全等三角形的性质,三角形的外角性质,准确计算是解题的关键. 3.B解析:B【分析】根据平行线的性质和角平分线的定义,对各个选项逐个分析,即可得到答案.【详解】13∠=∠,//AD BC∴23∠∠=∴123∠=∠=∠∴BD 是ABC ∠的平分线,即①正确;若//AD BC ,得23∠∠=,14∠=∠,不构成123∠=∠=∠成立的条件,故②错误; 若13∠=∠,不构成//AD BC 成立的条件,故③错误;若34180C ∠+∠+∠=,且34ADC ∠+∠=∠∴180C ADC ∠+∠=∴//AD BC ,即④正确;故选:B .【点睛】本题考查了平行线和角平分线的知识,解题的关键是熟练掌握平行线的性质和角平分线的定义.4.C解析:C【分析】根据三角形内角和定理、外角性质、平行线的性质与判定进行判断即可.【详解】解:A 选项,三角形的内角和是180°,是真命题,不符合题意;B 选项,两直线平行,内错角相等,是真命题,不符合题意;C 选项,三角形的外角大于任何一个内角,是假命题,符合题意;D 选项,同旁内角互补,两直线平行,是真命题,不符合题意;故选:C .【点睛】本题考查了三角形内角和定理和外角的性质,平行的性质与判定,解题关键是熟练准确掌握基础知识.5.A解析:A【分析】利用角平分线的定义和三角形内角和定理,余角即可计算.【详解】由图可知DAE DAC EAC ∠=∠-∠,∵AD 是角平分线. ∴12DAC BAC ∠=∠, ∴12DAE BAC EAC ∠=∠-∠, ∵90EAC C ∠=︒-∠, ∴1(90)2DAE BAC C ∠=∠-︒-∠∵2BAC B ∠=∠,2B DAE ∠=∠, ∴14(90)2DAE DAE C ∠=⨯∠-︒-∠, ∴90DAE C ∠=︒-∠∵180C B BAC ∠=︒-∠-∠, ∴18024C DAE DAE ∠=︒-∠-∠,∴1802(90)4(90)C C C ∠=︒-︒-∠-︒-∠,∴72C ∠=︒.故选:A .【点睛】本题主要考查了角平分线的定义和三角形的内角和定理以及余角.根据题意找到角之间的数量关系是解答本题的关键.6.B解析:B【分析】根据三角板的性质以及三角形内角和定理计算即可.【详解】解:∵∠CEA =60︒,∠BAE =45︒,∴∠ADE = 180︒−∠CEA −∠BAE =75︒,∴∠BDC =∠ADE =75︒,故选:B【点睛】本题考查三角板的性质,三角形内角和定理等知识,对顶角相等,解题的关键是熟练掌握基本知识,属于中考基础题.7.C解析:C【分析】根据∠DAE=∠DAC-∠CAE ,只要求出∠DAC ,∠CAE 即可.【详解】解:∵∠BAC=180°-∠B-∠C ,∠B=45°,∠C=73°,∴∠BAC=62°,∵AD 平分∠BAC ,∴∠DAC=12∠BAC=31°, ∵AE ⊥BC ,∴∠AEC=90°,∴∠CAE=90°-73°=17°,∴∠DAE=31°-17°=14°,故选:C .【点睛】本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识. 8.C解析:C【分析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠A′DB=∠CA'D-∠B ,又由于折叠前后图形的形状和大小不变,∠CA'D=∠A=50°,易求∠B=90°-∠A=40°,从而求出∠A′DB 的度数.【详解】解:∵Rt △ABC 中,∠ACB=90°,∠A=50°,∴∠B=90°-50°=40°,∵将其折叠,使点A 落在边CB 上A′处,折痕为CD ,则∠CA'D=∠A ,∵∠CA'D 是△A'BD 的外角,∴∠A′DB=∠CA'D-∠B=50°-40°=10°.故选:C .【点睛】本题考查图形的折叠变化及三角形的外角性质.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.解答此题的关键是要明白图形折叠后与折叠前所对应的角相等.9.D解析:D【分析】连接AC 并延长交EF 于点M .由平行线的性质得31∠=∠,24∠∠=,再由等量代换得3412BAD FCE ∠=∠+∠=∠+∠=∠,先求出FCE ∠即可求出A ∠.【详解】连接AC 并延长交EF 于点M .∵AB CF , ∴31∠=∠, ∵AD CE , ∴24∠∠=,∴3412BAD FCE ∠=∠+∠=∠+∠=∠,∵180180705060FCE E F ∠=︒-∠-∠=︒-︒-︒=︒,∴60BAD FCE ∠=∠=︒,故选D .【点睛】本题主要考查了平行线的性质以及三角形的内角和定理,属于基础题型.10.B解析:B【分析】直接利用三角形内角和定理得到∠C 的度数即可.【详解】解:∵在△ABC 中,∠A=80°,∠B=50°,∴∠C=180°-80°-50°=50°,故选:B .【点睛】本题考查了三角形内角和定理,正确把握定义是解题的关键.11.C解析:C【分析】已知GE AB ∥,GF AD ∥,98B ∠=︒,62D ∠=︒,根据平行线的性质可得98B GEC ∠=∠=︒,62D GFC ∠=∠=︒;因CEF △沿EF 翻折得到GEF △,由折叠的性质可得1492GEF CEF GEC ∠=∠=∠=︒,1312GFE CFE GFC ∠=∠=∠=︒;在△EFC 中,由三角形的内角和定理即可求得∠C=00°.【详解】∵GE AB ∥,GF AD ∥,98B ∠=︒,62D ∠=︒,∴98B GEC ∠=∠=︒,62D GFC ∠=∠=︒,∵CEF △沿EF 翻折得到GEF △, ∴1492GEF CEF GEC ∠=∠=∠=︒,1312GFE CFE GFC ∠=∠=∠=︒, 在△EFC 中,由三角形的内角和定理可得,∠C=180°-∠FEC-∠CFE=180°-49°-31°=100°.故选C.【点睛】本题考查了平行线的性质、折叠的性质及三角形的内角和定理,熟练运用相关知识是解决问题的关键.12.D解析:D【分析】根据平方根的概念、平行线的性质、对顶角相等判断即可.【详解】A 、负数没有平方根,本选项说法是真命题;B、两条平行直线被第三条直线所截,同位角相等,本选项说法是真命题;C、对顶角相等,本选项说法是真命题;D、两直线平行,内错角相等,本选项说法是假命题;故选:D.【点睛】本题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.二、填空题13.30°90°或40°80°【分析】根据倍角三角形的定义结合三角形的内角和定理分三种情况即可得出结论【详解】在△ABC中不妨设∠A=60①若∠A=2∠C则∠C=30∴∠B=;②若∠C=2∠A则∠C=1解析:30°,90°或40°,80°【分析】根据“倍角三角形”的定义结合三角形的内角和定理分三种情况即可得出结论.【详解】在△ABC中,不妨设∠A=60︒,①若∠A=2∠C,则∠C=30︒,∴∠B=180603090︒-︒-︒=︒;②若∠C=2∠A,则∠C=120︒,∴∠B=180601200︒-︒-︒=︒(不合题意,舍去);③若∠B=2∠C,则3∠C18060=︒-︒=120︒,∴∠C4=0︒,∠B=180604080︒-︒-︒=︒;综上所述,其它两个内角的度数分别是:30︒,90︒或40︒,80︒.【点睛】本题考查了“倍角三角形”的定义以及三角形的内角和等知识,解题的关键是学会用分类讨论的思想解决问题.14.【分析】由∠P1CD=∠P1+∠P1BC∠ACD=∠ABC+∠A而P1BP1C分别平分∠ABC和∠ACD得到∠ACD=2∠P1CD∠ABC=2∠P1BC于是有∠A=2∠P1同理可得∠P1=2∠P2即解析:12nα⎛⎫ ⎪⎝⎭【分析】由∠P1CD=∠P1+∠P1BC,∠ACD=∠ABC+∠A,而P1B、P1C分别平分∠ABC和∠ACD,得到∠ACD=2∠P1CD,∠ABC=2∠P1BC,于是有∠A=2∠P1,同理可得∠P1=2∠P2,即∠A=22∠P2,因此找出规律.【详解】∵P1B、P1C分别平分∠ABC和∠ACD,∴∠ACD=2∠P1CD,∠ABC=2∠P1BC,而∠P1CD=∠P1+∠P1BC,∠ACD=∠ABC+∠A,∴∠A=2∠P1,∴∠P1=12∠A,同理可得∠P1=2∠P2,即∠A=22∠P2,∴∠A=2n∠P n,∴∠P n=12n α⎛⎫⎪⎝⎭.故答案为:12nα⎛⎫⎪⎝⎭.【点睛】本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质,难度适中.15.两个锐角互余的三角形是直角三角形【分析】把原命题的题设与结论部分交换即可得到其逆命题【详解】解:命题直角三角形的两个锐角互余的逆命题为两个锐角互余的三角形是直角三角形故答案为:两个锐角互余的三角形是解析:两个锐角互余的三角形是直角三角形【分析】把原命题的题设与结论部分交换即可得到其逆命题.【详解】解:命题“直角三角形的两个锐角互余”的逆命题为“两个锐角互余的三角形是直角三角形”.故答案为:两个锐角互余的三角形是直角三角形.【点睛】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.16.两直线平行同位角相等;同位角相等两直线平行;AC;两直线平行内错角相等【分析】根据平行线的判定和性质解题【详解】解:因为AD⊥BCEF⊥BC 所以∠ADC=∠EFC=90°根据同位角相等两直线平行所以解析:两直线平行,同位角相等;同位角相等,两直线平行;AC;两直线平行,内错角相等.【分析】根据平行线的判定和性质解题.【详解】解:因为AD⊥BC,EF⊥BC,所以∠ADC=∠EFC=90°,根据“同位角相等,两直线平行”,所以AD//EF,根据“两直线平行,同位角相等”,所以∠1=∠CAD.因为∠3=∠C,根据“同位角相等,两直线平行”,所以DG//AC,根据“两直线平行,内错角相等”,所以∠2=∠CAD.所以∠1=∠2.故答案为:两直线平行,同位角相等;同位角相等,两直线平行;AC;两直线平行,内错角相等.【点睛】本题考查平行线的判定和性质,根据题目已知条件灵活运用平行线的判定和性质求解是解题关键.17.40°【分析】如图过E作EF∥AB则AB∥EF∥CD根据平行线的性质和三角形的内角和定理即可求得答案【详解】解:如图过E作EF∥AB则AB∥EF∥CD∴∠1=∠3∠2=∠4∵∠3+∠4=180°-9解析:40°【分析】如图,过E作EF∥AB,则AB∥EF∥CD,根据平行线的性质和三角形的内角和定理即可求得答案.【详解】解:如图,过E作EF∥AB,则AB∥EF∥CD,∴∠1=∠3,∠2=∠4,∵∠3+∠4=180°-90°-30°=60°,∴∠1+∠2=60°,∵∠1=20°,∴∠2=40°.故答案为:40°.【点睛】本题以三角板为载体,主要考查了平行线的性质和三角形的内角和定理,正确添加辅助线、熟练掌握平行线的性质是解题的关键.18.①④【分析】分别写出原命题的逆命题然后判断正误即可【详解】①同旁内角互补两直线平行的逆命题是两直线平行同旁内角互补成立符合题意;②如果两个角是直角那么它们相等的逆命题为相等的两个角都是直角不成立不符解析:①④【分析】分别写出原命题的逆命题,然后判断正误即可.【详解】①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立,符合题意;②如果两个角是直角,那么它们相等的逆命题为相等的两个角都是直角,不成立,不符合题意;③如果两个实数相等,那么它们的平方相等的逆命题为平方相等的两个实数相等,不成立,不符合题意;④在角的内部,到角的两边距离相等的点在角的平分线上的逆命题为角平分线上的点到角的两边的距离相等,成立,符合题意;⑤等边三角形是锐角三角形的逆命题为锐角三角形是等边三角形,不成立,不符合题意;成立的有①④,故答案为:①④.【点睛】本题考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题,难度不大.19.60°【分析】本题首先利用证明直线与平行继而利用对顶角性质以及两直线平行同旁内角互补求解【详解】如下图所示:∵∠1=∠5∠2=∠6又∵∠1=∠2∴∠5=∠6∴∥∵∠4=120°∴∠7=∠4=120°解析:60°【分析】∠=∠证明直线1l与2l平行,继而利用对顶角性质以及两直线平行,同旁本题首先利用12∠.内角互补求解3【详解】如下图所示:∵∠1=∠5,∠2=∠6,又∵∠1=∠2,∴∠5=∠6,∴1l ∥2l .∵∠4=120°,∴∠7=∠4=120°,又∵∠3+∠7=180°,∴∠3=60°.故填:60°.【点睛】本题考查平行线的判定与性质,需要灵活运用两直线平行,内错角、同位角相等、同旁内角互补.20.60°【分析】根据三角形的内角和等于180°求出∠ABC+∠ACB 的度数再根据角平分线的定义求出∠OBC+∠OCB 的度数然后利用三角形的内角和等于180°列式计算即可得解【详解】解:∵∠ABC+∠A解析:60°.【分析】根据三角形的内角和等于180°求出∠ABC +∠ACB 的度数,再根据角平分线的定义求出∠OBC +∠OCB 的度数,然后利用三角形的内角和等于180°列式计算即可得解.【详解】解:∵∠ABC +∠ACB =180°﹣∠A ,BO 平分∠ABC ,CO 平分∠ACB ,∴∠OBC =12∠ABC ,∠OCB =12∠ACB , ∴∠OBC +∠OCB =12(∠ABC +∠ACB ) =12(180°﹣∠A ) =90°﹣12∠A , ∴在△OBC 中,∠BOC =180°﹣(∠OBC +∠OCB )=90°+12∠A =120°, ∴∠A =60°,故答案为:60°.【点睛】本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.三、解答题21.证明见解析【分析】先根据已给的角度判断BD//CE ,从而可得∠ABD=∠C ,再根据等量代换可得∠ABD=∠D ,从而可证//AC DF .【详解】证明:∵178∠=︒,2102∠=︒,∴∠1+∠2=78°+102°=180°,∴BD//CE ,∴∠ABD=∠C ,∵C D ∠=∠,∴∠ABD=∠D ,∴//AC DF .【点睛】本题考查平行线的性质和判定.熟练掌握平行线的性质和判定定理,并能正确识别同位角、同旁内角是解题关键.22.(1)8,9;(2)671.154B A 【分析】(1)根据新定义的法则进行运算即可得到答案;(2)先由(1)的运算发现并总结规律,可得()h A 的值等于A 的十位数字,再运用规律结合()()35h A h B =进行合理的分类讨论,分4种情况:()()5,7h A h B ==或()()7,5,h A h B == ()()35,1h A h B ==或()()1,35h A h B ==,再根据新定义可得答案.【详解】解:(1)由定义可得:()18+81+17+71+78+87352===84417448h , ()699663369339396=9.4444693h +++++== (2)探究: 133112212332(132)344h +++++==, ()18+81+17+71+78+87352===84417448h , ()699663369339396=9.4444693h +++++==发现并总结规律:()h A 的值等于A 的十位数字,A ,B 为两个“西西数”,且()()35h A h B =,()()5,7h A h B ∴==或()()7,5,h A h B ==而()()35,1h A h B ==或()()1,35h A h B ==不合题意舍去, BA 的值最大,则B 最大,A 最小, ()()5,7,h A h B ∴==当()5h A =时,154A =或451A =或253A =或352A =,当()7h B =时,671B =或176B =或572B =或275B =或374B =或473.B =A ∴最小为154,B 最大为671, 此时B A 的值最大为 671.154B A 【点睛】本题考查的是新定义运算,同时考查了规律探究,弄懂新定义的运算法则,理解并运用规律,掌握合理的分类讨论是解题的关键.23.(1)见解析;(2)见解析【分析】(1)以C 为圆心,以CA 为半径画弧,交点即为所求;(2)以A 为圆心,以AC 为半径画弧,交点即为所求.【详解】(1)如图所示,点P 即为所求,理由如下:CP CA =,//l BC ,则APC CAP ACB ∠=∠=∠.(2)如图所示,点12Q Q 、即为所求,理由如下:1AC AQ =,//l BC ,则11112AQ C ACQ BCQ ACB ∠=∠=∠=∠; 12CQ CQ =,则1221CQ Q CQ Q ∠=∠.【点睛】本题考查了基本作图,熟记等腰三角形的性质,平行线的性质是解题的关键.24.见解析.【分析】先根据∠DGA=∠EGC 证出AE ∥BF ,再根据平行证明出∠F=∠FBC 即可求证出结论.【详解】证明:∵∠DGA=∠EGC(对顶角相等)又∵∠DGA=∠FHC (已知)∴∠EGC=∠FHC (等量代换)∴AE ∥BF (同位角相等,两直线平行)∴∠A=∠FBC (两直线平行,同位角相等)又∵∠A=∠F (已知)∴∠F=∠FBC (等量代换)∴DF ∥AC (内错角相等,两直线平行).【点睛】此题考查平行线的判定与性质:同位角相等,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行.25.(1)见解析;(2)见解析【分析】(1)根据同位角相等证得//DG BC ,根据垂直得到同位角相等进而得到//FE DC ,然后根据平行线的性质,利用等量代换即可证明;(2)根据90CDB ∠=︒,得到190ADG ∠+∠=︒,结合(1)中结论12∠=∠和1DCB ∠=∠,利用等量代换即可证明.【详解】(1)∵AGD ACB ∠=∠∴//DG BC∴1DCB ∠=∠∵EF AB ⊥,CD AB ⊥∴//FE DC∴2DCB =∠∠∴12∠=∠(2)由(1)得1DCB ∠=∠∵CD AB ⊥∴90CDB ∠=︒∴190ADG ∠+∠=︒又∵1DCB ∠=∠∴90BCD ADG ∠+∠=︒【点睛】本题考查了平行的判定和性质,等量代换,熟练掌握平行线的判定和性质是本题的关键. 26.∠2;两直线平行,同位角相等;∠3;∠2=∠3;内错角相等,两直线平行;平行【分析】根据平行线的判定和性质解答即可.【详解】解:∵a ∥b (已知)∴∠1=∠2,( 两直线平行,同位角相等)又∵a ∥c (已知)∴∠1=∠3,( 两直线平行,内错角相等 )∴∠2=∠3,∴b ∥c ,(内错角相等,两直线平行);得出:平行于同一条直线的两条直线互相平行;故答案为:∠2,两直线平行,同位角相等,∠3,∠2=∠3,内错角相等,两直线平行,平行.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级第七章 平行线的证明单元测试卷
一、填空题(每空3分,共 30分)
1、“两直线平行,同位角互补”是 命题(填真、假)
2、把命题“对顶角相等”改写成“如果…那么…”的形式
3、如图所示,∠1+ ∠2=180°,若∠3=50°,则∠4=
4、如图所示,△ABC 中,∠ACD=115°,∠B=55°,则∠A= , ∠ACB=
5、如图,一张宽度相等的纸条,折叠后,若∠ABC =120°,则∠1的度数为_____。
6、在△ABC 中,∠B —∠C=40°,则∠C= ,∠B=
7、在三角形中,最多有 个锐角,至少有 个锐角,最多有 个钝角(或直角)
8、△ABC 的三个外角度数比为3∶4∶5,则它的三个外角度数分别为 9、在△ABC 中,∠ABC 和∠ACB 的平分线交于点I, 若∠A=60°,则∠BIC= 10、已知如图,平行四边形ABCD 中,E 为AB 上一点,DE 与AC 交于点F ,AF ∶FC=3∶7,则AE ∶EB= 二、选择题(每小题3分,共30分) 11、下列命题是真命题的是( )
A 、同旁内角互补
B 、直角三角形的两锐角互余
C 、 三角形的一个外角等于它的两个内角之和
D 、三角形的一个外角大于内角 12、下列语句为命题的是( )
A 、你吃过午饭了吗?
B 、过点A 作直线MN
C 、同角的余角相等
D 、红扑扑的脸蛋
13、命题“垂直与同一条直线的两条直线互相平行”的题设是( ) A 、垂直 B 、两条直线 C 、同一条直线 D 、两条直线垂直于同一条直线
14、已知△ABC 的三个内角度数比为2∶3∶4,则个三角形是( )
A 、锐角三角形
B 、直角三角形
C 、钝角三角形
D 、等腰三角形
15、如图,一个任意的五角星,它的五个内角的度数和为( )
A 、90°
B 、180°
C 、360°
D 、120°
18题图
16、如图,AB ∥EF , ∠C=90°,则α、β、γ的关系为( )
A 、β=α+γ
B 、α+β+γ=180°
C 、β+γ-α=90°
D 、α+β-γ=90° 17、如果∠A 和∠B 的两边分别平行,那么∠A 和∠B 的关系是( ). A.相等
B.互余或互补
C.互补
D.相等或互补
18如图,点E 在BC 的延长线上,下列条件中不能判定AB ∥CD 的是( ).
A.∠3=∠4
B.∠1=∠2
C.∠B=∠DCE
D.∠D+∠DAB=180°
19、某人从A 点出发向北偏东60°方向速到B 点,再从B 点出发向南偏西15°方向速到C 点,
则∠ABC 等于( )度
A. 45
B.75
C. 105
D.45或
135
20、满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A :∠B :∠C =1:2:3
B. ∠A -∠B =∠C
C. ∠A和它的外角相等
D. ∠A =2∠B =3∠C
三解答题与证明(40分)
17、已知如图,在△ABC中,CH是外角∠ACD的平分线,BH是∠ABC的平分线。
求证:∠A= 2∠H
18已知:如图,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
19、求证:两条直线平行,同旁内角的角平分线互相垂直。
(提示:先画图,写出已知,求证,然后进行证明)
20、已知如图,O是四边形ABCD的两条对角线的交点,过点O作OE∥CD,交
AD于E,作OF∥BC,交AB于F,连接EF。
求证:EF∥BD。
