数字逻辑第七章
合集下载
《数字电路与数字逻辑》第七章
u C 3 2 V C， CR 则 1 ， S 0 ， u o 0 ；第二暂稳态
ppt课件
15
③放电阶段：
u C 1 3 V C ， CR 0 则 (或 1 ) ， S 0 ， u o 0 ；第二暂稳态
u C 1 3 V C， CR 则 0 ， S 1 ， u o 1 ；第一暂稳态
ppt课件
ppt课件
8
(3) 3脚—输出端
(4) 4脚—直接置0端
(5) 5脚—电压控制端UIC ①接UREF ，则高触发电平、低触发电平分别为
UREF 、12UREF ②不接UREF ，则高、低触发电平分别为
32VCC 、13VCC
ppt课件
9
(6) 6脚—高触发输入端（阈值输入端） (7) 7脚—放电端 (8) 8脚—电源端
当ui为高电平时，uo为低电平； 当ui变为低电平时，uo变为高电平；
tr
tf
Um
tW
T
ppt课件
4
P1
△U
P2
图 7.1.2Βιβλιοθήκη 矩形脉冲的参数ppt课件5
第二节 集成定时器
一、555定时器的结构
1.组成 分压器，电压比较器，基本SREF，集电极开 路输出的放电三极管。
2.各引脚功能 (1) 1脚—接地端 (2) 2脚—低触发输入端（触发输入端）
ppt课件
6
V CC
16
3.矩形波参数
T P H 0 .7 (R A R B )C ;H (R A R B )C
T PL 0.7R BC
;LRBC
T T P T H P 0 L . 7 ( R A 2 R B ) C
qtW T PH R AR B T T PH T PLR A2R B
ppt课件
15
③放电阶段：
u C 1 3 V C ， CR 0 则 (或 1 ) ， S 0 ， u o 0 ；第二暂稳态
u C 1 3 V C， CR 则 0 ， S 1 ， u o 1 ；第一暂稳态
ppt课件
ppt课件
8
(3) 3脚—输出端
(4) 4脚—直接置0端
(5) 5脚—电压控制端UIC ①接UREF ，则高触发电平、低触发电平分别为
UREF 、12UREF ②不接UREF ，则高、低触发电平分别为
32VCC 、13VCC
ppt课件
9
(6) 6脚—高触发输入端（阈值输入端） (7) 7脚—放电端 (8) 8脚—电源端
当ui为高电平时，uo为低电平； 当ui变为低电平时，uo变为高电平；
tr
tf
Um
tW
T
ppt课件
4
P1
△U
P2
图 7.1.2Βιβλιοθήκη 矩形脉冲的参数ppt课件5
第二节 集成定时器
一、555定时器的结构
1.组成 分压器，电压比较器，基本SREF，集电极开 路输出的放电三极管。
2.各引脚功能 (1) 1脚—接地端 (2) 2脚—低触发输入端（触发输入端）
ppt课件
6
V CC
16
3.矩形波参数
T P H 0 .7 (R A R B )C ;H (R A R B )C
T PL 0.7R BC
;LRBC
T T P T H P 0 L . 7 ( R A 2 R B ) C
qtW T PH R AR B T T PH T PLR A2R B
(整理)《数字逻辑电路》试题2.
一、选择题（每小题1.5分）第一章：1. 带符号位二进制数10011010的反码是（ ）。
A. 11100101B. 10011010C. 10011011D. 111001102. 十进制数5对应的余3码是（ ）。
A. 0101B. 1000C. 1010D. 11003. 二进制代码1011对应的格雷码是（ ）。
A. 1011B. 1010C. 1110D. 0001第二章：1. 下列公式中哪一个是错误的？ （ ）A. A A 0=+B. A A A =+C. B A )B A ('+'='+D. )C A )(B A (BC A ++=+2. 下列各式中哪个是三变量A 、B 、C 的最小项？ （ ）A. B A ''B. C B A +'+'C.ABCD. C B '+'3. 下列函数中不等于A 的是（ ）。
A. A ＋1B. A ＋AC. A ＋ABD. A （A ＋B ）4. 在逻辑代数的加法运算中，1＋1＝（ ）。
A. 2B. 1C. 10D. 05. A ⊕1＝（ ）。
A. AB. 1C. A 'D. 06. 含有A 、B 、C 、D 四个逻辑变量的函数Y=A+B+D 中所含最小项的个数是（）。
A. 3 B. 8 C. 14 D. 167. 下列函数中等于AB 的是（ ）。
A. （A ＋1）BB. （A ＋B ）BC. A ＋ABD. A （AB ）8. 为了将600份文件顺序编码，如果采用二进制代码，最少需要用（ ）位。
A. 3B. 10C. 1024D. 6009. 为了将600个运动员顺序编码，如果采用八进制代码，最少需要用（ ）位。
A. 3B. 4C. 10D. 75第三章：1. 采用漏极开路输出门电路（OD 门）主要解决了（ ）。
A. CMOS 门不能相“与”的问题B. CMOS 门的输出端不能“线与”的问题C. CMOS 门的输出端不能相“或”的问题2. 下列哪个特点不属于CMOS 传输门？（ ）A. CMOS 传输门属于双向器件。
精品课件-数字电子技术-第7章
第7章 集成逻辑门电路简介
7.4 已知电路和输入信号的波形如图7.12所示，信号 的重复频率为1 MHz，每个门的平均延迟时间tpd=20 ns，试 画出：（1） 不考虑tpd影响时的波形；（2） 考虑tpd影响
第7章 集成逻辑门电路简介
图7.12 题7.4图
第7章 集成逻辑门电路简介
7.5 电路如图7.13所示。（1） 分别写出Y1、Y2、Y3、 Y4的逻辑函数表达式；（2） 若已知A、B、C的波形，试分别 画出Y1、Y2、Y3、Y4
(4) DE段。当UI≥1.4 V时，V2、V5饱和，V4截止，输 出为低电平, 与非门处于饱和状态, 所以把DE段称为饱和
第7章 集成逻辑门电路简介
4. （1） 输出高电平UOH和输出低电平UOL。电压传输特性 曲线截止区的输出电压为UOH，饱和区的输出电压为UOL。 一般产品规定UOH≥2.4 V，UOL＜0.4 V （2） 阈值电压Uth。电压传输特性曲线转折区中点所 对应的输入电压为Uth，也称门槛电压。一般TTL与非门的 Uth≈1.4 V
Y=Y1·Y2
第7章 集成逻辑门电路简介
图7.4 实现“线与”功能的电路
第7章 集成逻辑门电路简介
但是普通TTL逻辑门的输出端是不允许直接相连的，如 图7.5所示电路：设门1的输出为高电平（Y1=1）， 门2的输 出为低电平（Y2=0），此时门1的V4管和门2的V5管均饱和导通， 这样在电源UCC的作用下将产生很大的电流流过V4、V5管使V4、 V5
第7章 集成逻辑门电路简介
（3） 关门电平UOFF和开门电平UON。保证输出电平为 额定高电平（2.7 V左右）时，允许输入低电平的最大值， 称为关门电平UOFF。通常UOFF≈1 V ， 一般产品要求 UOFF≥0.8 V。 保证输出电平达到额定低电平（0.3 V）时， 允许输入高电平的最小值，称为开门电平UON。通常 UON≈1.4 V，一般产品要求UON≤1.8 V
数字逻辑欧阳星明第四版华科出版1~7全答案ppt课件
Y＝ XYXY＝ XYXY＝ XY ，
所以，X＝Y。
.
18
习题课
2.6 用逻辑代数的公理、定理和规则将下列逻辑函数化简为 最简“与－或”表达式 。
（1） FAB ABCBC
（2） FABBBCD
（3） F (A B C )A ( B )A ( B C )
（4） FB C D D (B C )A ( C B )
.
2
习题课
1.3 数字逻辑电路可分为哪两种类型？主要区别是什么？
解答： 根据一个电路有无记忆功能，可将数字逻辑电路分为组
合逻辑电路和时序逻辑电路。如果一个逻辑电路在任何时刻 的稳定输出仅取决于该时刻的输入，而与电路过去的输入无 关，则称为组合逻辑电路。由于这类电路的输出与过去的输 入信号无关，所以不需要有记忆功能。如果一个逻辑电路在 任何时刻的稳定输出不仅取决于该时刻的输入，而与电路过 去的输入相关，则称为时序逻辑电路。由于这类电路的输出 与过去的输入信号相关，所以要有记忆功能，要用电路中的 记忆元件的状态来反映过去的输入信号。
解答：
8421码： 十进制： 2421码：
0110 1000 0011 0011 0101 0000 350 0011 1011 0000
0100 0101.1001 0001 0010.0110 12.6 0001 0010.1100
.
10
习题课
1.12 试用8421码和Gray码分别表示下列各数。
4×8-3
（4）(785.4AF)16＝7×162＋8×161＋5×160＋4×16-1＋
10×8-2
＋15×16-3
.
5
习题课
1.6 将下列二进制数转换成十进制数、八进制数和十六进制 数。
数字逻辑课后答案第七章
D80 D20
D20 D4
D10 D10
D8 D2
D1
图2
3. 用4位二进制并行加法器设计一个用8421码表示的1位十进制加法
器。
解答
分析：由于十进制数采用8421码，因此，二进制并行加法器输入被加数和 加数的取值范围为0000～1001（0～9），输出端输出的和是一个二进制数，数的 范围为0000～10011(0～19,19=9+9+最低位的进位)。因为题目要求运算的结果也
0
0000000000
0
1
0000100001
0
2
0001000010
0
3
0001100011
0
4
0010000100
0
5
0010100101
0
6
0011000110
0
7
0011100111
0
8
0100001000
0
9
0100101001
0
10
0101010000
1
11
0101110001
1
12
0110010010
设计出该序列发生器的逻辑电路图如图8所示。
图8
11. 在图9所示电路中，若取R1=2R2 ,请问输出矩形波的占空比为多 少?
图9 解答
2R2 + R2 = 3R2 = 3 2R2 + 2R2 4R2 4
12. 分析图10所示由定时器5G555构成的多谐振荡器。
图10
（1）计算其振荡周期；
（2）若要产生占空比为50%的方波，R1和R2的取值关系如何?
路较复杂，一般分辨率较低；逐次比较型速度较快，精度高；双积 分型精度高、抗干扰能力强，但速度较慢。 18. ADC0809如何实现对8路模拟量输入的选择?当它与微机连接时是
数字逻辑第七章作业答案
H’·L’·R’
1
IDLE
R R·H’ 1 H’
R1
H
R2
L2
H’(L’+R’) 1
L3 1 H+LR L L·H’·R’ IDLE 1 R3 1 H’(L’+R’) R R·H’·L’ H+LR
H’(L’+R’) 1 L1 H+LR 1 H+L·R H H+LR R1 1H’(L’+R’) LR3
R
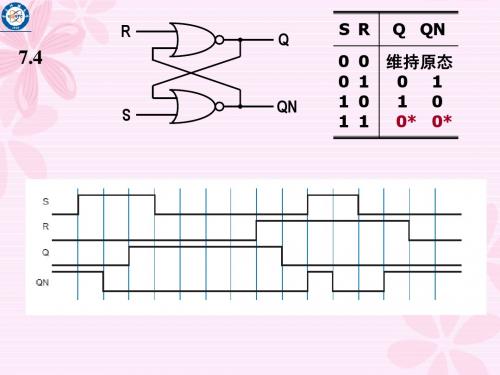
7.4
S
Q
S R 0 0 1 1 0 1 0 1
Q QN 维持原态 0 1 1 0 0* 0*
QN
R
Q
7.5
S QN
7.6 利用带有使能端的T触发器和组合逻辑构造D触发 器
D触发器：Q* = D （转移方程） T触发器的特征方程：Q*= EN·Q’ + EN’·Q=ENQ 所以，激励方程：EN = DQ
W’Y’
X’YZ
X’Z’
对A状态，不满足完备性，少了(X+YZ)’ 对B状态，不满足互斥性，多了W’Y’ 对C状态，满足二义性 对D状态，不满足互斥性，多了XY，并且不满足完备性， 少了(X+Y’)’
L2
7.24修改状态图
L3
H’ 1
H’ 1
H
L1
1 L L·H’·R’ H 1 H+L·R H H
H’·L’·R’
R2
Transition list
Q2Q1Q0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 S 转移表达式 S* Q2*Q1*Q0* 0 0 1 1 0 0 0 0 0 0 1 0 0 1 1 0 1 0 H’·L’·R’ IDLE L1 IDLE L·H’·R’ R·H’·L’ R1 H+L·R LR3 H’·(L’+R’) L2 L1 H+LR LR3
第7章数字逻辑基础
AB Y 00 1 01 0 10 0 11 1
三、逻辑函数及其表示方法
1.逻辑变量和逻辑函数 在数字系统中，开关的接通与断开，电压的高和低 ，信号的有和无，晶体管的导通与截止等两种稳定的物理 状态，均可用1和0这两种不同的逻辑值来表征，这种仅有 两个取值的自变量称为逻辑变量，通常用字母A、B、 C…来表示。 如果对应于输入逻辑变量A、B、C、…的每一组确 定值，输出逻辑变量Y就有唯一确定的值，则称Y是A、B 、C、…的逻辑函数。记为：
YA BA BA B
异或运算
AB Y 00 0 01 1 10 1 11 0
异或逻辑运算的规则：相同为0，相异为1。
5.同或运算
所谓同或运算，是指两个输入变量取值相同时输出为1， 取值不相同时输出为0。 逻辑表达式：
式中，符号“⊙”表示同或运算，读作“同或”。 同或运算
同或逻辑运算的规则：相同 为1，相异为0
起来的逻辑代数式。它是数字电路输入量与输出量 之间逻辑函数关系的表达式，也称函数式或代数式。 优点：形式简洁，书写方便，直接反映了变量间 的运算关系，便于用逻辑图实现该函数。
例7-4 写出如图所示逻辑图的函数表达式。
解：根据门电路的逻辑符号和对应的逻辑运算， 由前向后逐级推算，即可写出输出函数Y的表达式
（128）8=（1×82+2×81+8×80）10 =（64+16+8）10 =（88）10
（5D）16=（5×161+13×160）10 =（80+13）10 =（93）10
2.十进制数转换二进制
例7-2 求[29]10=[
]2。“除2取余法”
2
29
…余1
底位
2
14
数字逻辑第7章
1
Digital Logic Design and Application (数字逻辑设计及应用)
Review of Last Class (内容回顾)
锁存器与触发器
R Q
S-R锁存器 S-R锁存器
具有使能端的S-R锁存器
有约束条件
S S_L
QL
D
C C
S
Q
D锁存器
2
QL
R R_L
Digital Logic Design and Application (数字逻辑设计及应用)
6
Digital Logic Design and Application (数字逻辑设计及应用)
Scan Flip-Flop (扫描触发器)
Logic Symbol (逻辑符号)
TE = 0 正常操作 Q=D TE = 1 进入测试模式
D 测试使能端 TE 测试输入端 TI CLK
思考：同样是主从结构， 为什么由D锁存器构成的可以称为边沿D触发器， 而由S-R锁存器构成的不能称为边沿S-R触发器？
D D Q C Q D Q C Q
Dynamic-Input Indicator Q (动态输入指示 D Q QN 边沿触发) CLK Q S C R
CLK S S C R Q S C R Q Q Q Q Postponed-Output
D Flip-Flops (D触发器)
—— 主从结构
D
Master(主) Slave (从) Qm Q D Q D Q C Q QL C Q
CLK
CLK=0时， 主锁存器工作，接收输入信号 Qm = D
从锁存器不工作，输出 Q 保持不变 CLK=1时， 主锁存器不工作，Qm 保持不变
Digital Logic Design and Application (数字逻辑设计及应用)
Review of Last Class (内容回顾)
锁存器与触发器
R Q
S-R锁存器 S-R锁存器
具有使能端的S-R锁存器
有约束条件
S S_L
QL
D
C C
S
Q
D锁存器
2
QL
R R_L
Digital Logic Design and Application (数字逻辑设计及应用)
6
Digital Logic Design and Application (数字逻辑设计及应用)
Scan Flip-Flop (扫描触发器)
Logic Symbol (逻辑符号)
TE = 0 正常操作 Q=D TE = 1 进入测试模式
D 测试使能端 TE 测试输入端 TI CLK
思考：同样是主从结构， 为什么由D锁存器构成的可以称为边沿D触发器， 而由S-R锁存器构成的不能称为边沿S-R触发器？
D D Q C Q D Q C Q
Dynamic-Input Indicator Q (动态输入指示 D Q QN 边沿触发) CLK Q S C R
CLK S S C R Q S C R Q Q Q Q Postponed-Output
D Flip-Flops (D触发器)
—— 主从结构
D
Master(主) Slave (从) Qm Q D Q D Q C Q QL C Q
CLK
CLK=0时， 主锁存器工作，接收输入信号 Qm = D
从锁存器不工作，输出 Q 保持不变 CLK=1时， 主锁存器不工作，Qm 保持不变
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
J Q1 K Q1 J Q2 K Q2 J Q3 K Q3
“1” CP J Q1 J Q2 J Q3
K Q1
CP 时钟方程： 1 CP
K Q2
K Q3
CP2 Q1 CP3 Q2
激励方程： J 3 K 3 J 2 K 2 J 1 K1 1
Q 状态方程：
n 1 3
X1 XK
Z1 组合 逻辑 Zm
Q1
Qr 触发器
w1 wr
脉冲型异步时序电路框图
X1
XK 组合 逻辑
Z1 Zm
y1
yr
延迟线τ 延迟线τ
Y1 Yr
电平型异步时序电路框图
7.2 脉冲异步时序电路 7.2.1 脉冲异步时序电路分析
其的分析方法和同步时序电路类似,但还需考虑一个 时钟方程. 例1: 试分析下列电路 “1” CP
CP3 Q1
J 3 Q2
K3 1
CP2 Q nQ n 2 1 Q3n 00 01 11 10 0 0 1 1 0 1 0 d* d d
CP2 Q1
J2 Q2nQ1n Q3n 00 01 11 10 0 d 1 d d 1 d 0* d d
J 2 Q3
K2 1
CP1 Q2nQ1n Q3n 00 01 11 10 0 1 1 1 1 1 1 1 d d
状态方程: Q3n1 Q3n Q2n1 Q2n Q1n1 Q1n
时钟方程：CP1 CP
CP2 Q1 CP3 Q2
状态方程: Q3n1 Q3n Q2n1 Q2n Q1n1 Q1n Q3n Q2n Q1n 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Q3n+1 1 0 0 0 0 1 1 1 Q2n+1 1 0 0 1 1 0 0 1 Q1n+1 1 0 1 0 1 0 1 0 CP3 CP2 CP1
/0 /0
010 /0 011 0 d 0 1 0 1 d d 0 1 0 1 0 d d d 1 1 1 1 1 1 d d 0 0 0 0 0 1 d d
Q3n Q2n Q1n Q3n+1 Q2n+1 Q1n+1 CP3 CP2 CP1 Z 1 0 1 0 1 0 d d
Q3nQ2nQ1n Q3n+1 Q2n+1 Q1n+1 CP3 J3 K3 CP2 J2 K2 CP1 J1 K1
CP 1 1 J1 K1 1
Q1n1 Q1n
n Q 2n 1 Q3n Q2
n n Q3n 1 Q2 Q3
Z Q3 Q2 Q1
检查能否自启动: CP1 1 CP2 Q1 CP3 Q1 Q3n Q2n Q1n 1 1 0 1 1 1 Q3n+1 Q2n+1 Q1n+1 1 1 1 0 0 0 CP3 CP2 CP1 Z 0 0
CP
Q1n
Q2n Q3n
例4 : 试分析下列电路 & D Q1 D Q2 & Q1
CP 1 CP
Q
n 1 1
Z
CP
Q2
D1 Q2 D2 Q2
CP2 Q1CP
n 1 n Q2 Q2
Q
n 2
Z Q1Q2 CP
CP 1 CP
Q
n 1 1
CP2 Q1CP
n 1 n Q2 Q2
Q
n 1
脉冲异步时序逻辑电路的设计方法与同步时序逻
( J Q KQ )CP
n n
即将时钟控制端当作激励端来看.故可得以下J-K 触发器的激励表:
Qn
0 0 1 1
Qn+1 CP
0 1 0 1
J K
0 d d 1 1 d 1 d 1 0 d d
Qn 0 0 1 1
Qn+1 0 1 0 1
CP J d 0 1 1 1 d d d
Q
n 2
Z Q1Q2 CP
Q 2n 0 0 1 1
Q 1n 0 1 0 1
Q2n+1 0 1 1 0
Q1n+1 1 1 0 0
Z CP2 CP1 0 0 0 1
Q 2n 0 0 1 1
Q1n 0 1 0 1 ／0
Q2n+1 0 1 1 0
Q1n+1 1 1 0 0
Z CP2 CP1 0 0 0 1
状态图 Q3n Q2n Q1n
000 001 010 011
111
110
101
100
时序图
1 2 3 4 5 6 7 8 CP Q1n
Q2n
Q3n
例3: 试分析下列电路 D Q1 Q1 时钟方程: CP1 CP 激励方程: D1 Q1 D Q2 Q2 D Q3 Q3
CP2 Q1 CP3 Q2
输出方程 : Zi=fi (Xk , yr)
激励方程 :Yj=fj (Xk , yr)
二次状态方程 : yjt+τ= Yjt ( j=1,2 r )
电路中，Z和Y是随X的变化而变化的。Y变化后经 过τ的延迟形成二次状态y反馈到输入端，从而引 起电路状态的进一步变化，直到Y=y，电路才进入 稳定状态。 电路的二次状态和激励状态仅仅相差一个时间延 迟。即二次状态y是激励状态Y经过△t延迟后的“重
状态图 Q3n Q2n Q1n
000 001 010 011
111
110
101
100
时序图
1 2 3 4 5 6 7 8 CP Q1n
Q2n
Q3n
例2 试分析下列电路 “1 ” CP
J Q1
K Q
1
J Q2
K Q2
CP2 Q1
J Q3
K Q3
CP3 Q2
时钟方程： CP 1 CP
激励方程: J 3 K 3 J 2 K 2 J 1 K1 1
D1 Q1
D0 n n Q1 Q0 Q2n 00 01 11 10 0 1 0 0 1 1 0 d d d
D0 Q2 Q1
D2 Q1Q0
Z Q2
D Q0 Q0 CP
D Q1 Q1
D Q2 Q2
Z
7.3 电平异步时序逻辑电路 7.3.1电平异步时序电路的定义
X1 XK
y1 yr
1 d 1
0
d
d d 1 1 d
0 d 1 d 1
d
d
d
d
d
d
d d d
d d d
d
d
d d d d d
d d d d d
CP3 Q nQ n 2 1 Q3n 00 01 11 10 0 0 d* 1 0 1 0 1 d d
J3 Q nQ n 2 1 Q3n 00 01 11 10 0 d 0* 1 d 1 d d d d
故电平异步时序电路是时序逻辑电路中更具一般
性的形式。
X1 XK y1 yr
组合 逻辑 Y1 Yr
Z1 Zm
延迟线 τ 延迟线 τ
X=X1～ XK :输入状态 Y=Y1～Yr :激励状态
y=y1～yr :二次状态 Z=Z1～Zm :输出状态
(X，y) :总态(全状态) τ:延迟元件的延迟时间
对上图的异步时序逻辑电路框图可用一组方程 对其描述：
Q3n+1 Q2n+1 Q1n+1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 001 110 1 0 1 0 1 0 1 0 010 101
CP3 CP2 CP1
000
011 100
000 111 时序图
001 110
010 101
011 100
1 2 3 4 5 6 7 8
组合 逻辑 Y1
Z1 Zm
延迟线 τ 延迟线 τ
Yr
电平型异步时序电路框图
事实上，脉冲信号只不过是电平信号的一种特殊 形式。所谓电平信号是指信号的“0”值和“1”的持续 时间是随意的，它以电位的变化作为信号的变化。 而脉冲信号的“1”值仅仅维持一个固定的短暂时刻， 它以脉冲信号的有、无标志信号的变化。显然，电 平信号在短时间内的两次变化便形成了脉冲。 至于时序电路中的触发器，都是由逻辑门加反馈 回路构成的。
0 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 0 1 0 1 0 0 d d d 0 d 0 d d 1 1 d 0 1 0 1 d d 1 1 d
1 d 1 d 1 d d 1 1 d d 1 1 d 1
1 0 0 1 1 0
1
0
0
0
1
0
0 d d
CP 1 Q0
n 1 Q2 Q1n 1 Q0n 1 D2 D1 D0 Z 0 0 1 0 d 1 0
0 0 0
0 0 1
0 1 0
0 0
1 1
0 1
0 0
1 d
0 1
0 0
0 1 1 1 1
1 0 0 1 1
1 0 1 0 1
1 0 d d d
0 0 d d d
0 0 d d d
1 0 d d d
CP2 Q1 CP3 Q2
Q
n 1 2
Q
n 1
Q
n 2
Q
n 1 3
Q
n 3
Q3n+1 Q2n+1 Q1n+1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0
CP3 CP2 CP1
Q3n Q2n Q1n 0 0 0 0 1 1 1 1 状态图 111 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1
“1” CP J Q1 J Q2 J Q3
K Q1
CP 时钟方程： 1 CP
K Q2
K Q3
CP2 Q1 CP3 Q2
激励方程： J 3 K 3 J 2 K 2 J 1 K1 1
Q 状态方程：
n 1 3
X1 XK
Z1 组合 逻辑 Zm
Q1
Qr 触发器
w1 wr
脉冲型异步时序电路框图
X1
XK 组合 逻辑
Z1 Zm
y1
yr
延迟线τ 延迟线τ
Y1 Yr
电平型异步时序电路框图
7.2 脉冲异步时序电路 7.2.1 脉冲异步时序电路分析
其的分析方法和同步时序电路类似,但还需考虑一个 时钟方程. 例1: 试分析下列电路 “1” CP
CP3 Q1
J 3 Q2
K3 1
CP2 Q nQ n 2 1 Q3n 00 01 11 10 0 0 1 1 0 1 0 d* d d
CP2 Q1
J2 Q2nQ1n Q3n 00 01 11 10 0 d 1 d d 1 d 0* d d
J 2 Q3
K2 1
CP1 Q2nQ1n Q3n 00 01 11 10 0 1 1 1 1 1 1 1 d d
状态方程: Q3n1 Q3n Q2n1 Q2n Q1n1 Q1n
时钟方程：CP1 CP
CP2 Q1 CP3 Q2
状态方程: Q3n1 Q3n Q2n1 Q2n Q1n1 Q1n Q3n Q2n Q1n 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Q3n+1 1 0 0 0 0 1 1 1 Q2n+1 1 0 0 1 1 0 0 1 Q1n+1 1 0 1 0 1 0 1 0 CP3 CP2 CP1
/0 /0
010 /0 011 0 d 0 1 0 1 d d 0 1 0 1 0 d d d 1 1 1 1 1 1 d d 0 0 0 0 0 1 d d
Q3n Q2n Q1n Q3n+1 Q2n+1 Q1n+1 CP3 CP2 CP1 Z 1 0 1 0 1 0 d d
Q3nQ2nQ1n Q3n+1 Q2n+1 Q1n+1 CP3 J3 K3 CP2 J2 K2 CP1 J1 K1
CP 1 1 J1 K1 1
Q1n1 Q1n
n Q 2n 1 Q3n Q2
n n Q3n 1 Q2 Q3
Z Q3 Q2 Q1
检查能否自启动: CP1 1 CP2 Q1 CP3 Q1 Q3n Q2n Q1n 1 1 0 1 1 1 Q3n+1 Q2n+1 Q1n+1 1 1 1 0 0 0 CP3 CP2 CP1 Z 0 0
CP
Q1n
Q2n Q3n
例4 : 试分析下列电路 & D Q1 D Q2 & Q1
CP 1 CP
Q
n 1 1
Z
CP
Q2
D1 Q2 D2 Q2
CP2 Q1CP
n 1 n Q2 Q2
Q
n 2
Z Q1Q2 CP
CP 1 CP
Q
n 1 1
CP2 Q1CP
n 1 n Q2 Q2
Q
n 1
脉冲异步时序逻辑电路的设计方法与同步时序逻
( J Q KQ )CP
n n
即将时钟控制端当作激励端来看.故可得以下J-K 触发器的激励表:
Qn
0 0 1 1
Qn+1 CP
0 1 0 1
J K
0 d d 1 1 d 1 d 1 0 d d
Qn 0 0 1 1
Qn+1 0 1 0 1
CP J d 0 1 1 1 d d d
Q
n 2
Z Q1Q2 CP
Q 2n 0 0 1 1
Q 1n 0 1 0 1
Q2n+1 0 1 1 0
Q1n+1 1 1 0 0
Z CP2 CP1 0 0 0 1
Q 2n 0 0 1 1
Q1n 0 1 0 1 ／0
Q2n+1 0 1 1 0
Q1n+1 1 1 0 0
Z CP2 CP1 0 0 0 1
状态图 Q3n Q2n Q1n
000 001 010 011
111
110
101
100
时序图
1 2 3 4 5 6 7 8 CP Q1n
Q2n
Q3n
例3: 试分析下列电路 D Q1 Q1 时钟方程: CP1 CP 激励方程: D1 Q1 D Q2 Q2 D Q3 Q3
CP2 Q1 CP3 Q2
输出方程 : Zi=fi (Xk , yr)
激励方程 :Yj=fj (Xk , yr)
二次状态方程 : yjt+τ= Yjt ( j=1,2 r )
电路中，Z和Y是随X的变化而变化的。Y变化后经 过τ的延迟形成二次状态y反馈到输入端，从而引 起电路状态的进一步变化，直到Y=y，电路才进入 稳定状态。 电路的二次状态和激励状态仅仅相差一个时间延 迟。即二次状态y是激励状态Y经过△t延迟后的“重
状态图 Q3n Q2n Q1n
000 001 010 011
111
110
101
100
时序图
1 2 3 4 5 6 7 8 CP Q1n
Q2n
Q3n
例2 试分析下列电路 “1 ” CP
J Q1
K Q
1
J Q2
K Q2
CP2 Q1
J Q3
K Q3
CP3 Q2
时钟方程： CP 1 CP
激励方程: J 3 K 3 J 2 K 2 J 1 K1 1
D1 Q1
D0 n n Q1 Q0 Q2n 00 01 11 10 0 1 0 0 1 1 0 d d d
D0 Q2 Q1
D2 Q1Q0
Z Q2
D Q0 Q0 CP
D Q1 Q1
D Q2 Q2
Z
7.3 电平异步时序逻辑电路 7.3.1电平异步时序电路的定义
X1 XK
y1 yr
1 d 1
0
d
d d 1 1 d
0 d 1 d 1
d
d
d
d
d
d
d d d
d d d
d
d
d d d d d
d d d d d
CP3 Q nQ n 2 1 Q3n 00 01 11 10 0 0 d* 1 0 1 0 1 d d
J3 Q nQ n 2 1 Q3n 00 01 11 10 0 d 0* 1 d 1 d d d d
故电平异步时序电路是时序逻辑电路中更具一般
性的形式。
X1 XK y1 yr
组合 逻辑 Y1 Yr
Z1 Zm
延迟线 τ 延迟线 τ
X=X1～ XK :输入状态 Y=Y1～Yr :激励状态
y=y1～yr :二次状态 Z=Z1～Zm :输出状态
(X，y) :总态(全状态) τ:延迟元件的延迟时间
对上图的异步时序逻辑电路框图可用一组方程 对其描述：
Q3n+1 Q2n+1 Q1n+1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 001 110 1 0 1 0 1 0 1 0 010 101
CP3 CP2 CP1
000
011 100
000 111 时序图
001 110
010 101
011 100
1 2 3 4 5 6 7 8
组合 逻辑 Y1
Z1 Zm
延迟线 τ 延迟线 τ
Yr
电平型异步时序电路框图
事实上，脉冲信号只不过是电平信号的一种特殊 形式。所谓电平信号是指信号的“0”值和“1”的持续 时间是随意的，它以电位的变化作为信号的变化。 而脉冲信号的“1”值仅仅维持一个固定的短暂时刻， 它以脉冲信号的有、无标志信号的变化。显然，电 平信号在短时间内的两次变化便形成了脉冲。 至于时序电路中的触发器，都是由逻辑门加反馈 回路构成的。
0 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 0 1 0 1 0 0 d d d 0 d 0 d d 1 1 d 0 1 0 1 d d 1 1 d
1 d 1 d 1 d d 1 1 d d 1 1 d 1
1 0 0 1 1 0
1
0
0
0
1
0
0 d d
CP 1 Q0
n 1 Q2 Q1n 1 Q0n 1 D2 D1 D0 Z 0 0 1 0 d 1 0
0 0 0
0 0 1
0 1 0
0 0
1 1
0 1
0 0
1 d
0 1
0 0
0 1 1 1 1
1 0 0 1 1
1 0 1 0 1
1 0 d d d
0 0 d d d
0 0 d d d
1 0 d d d
CP2 Q1 CP3 Q2
Q
n 1 2
Q
n 1
Q
n 2
Q
n 1 3
Q
n 3
Q3n+1 Q2n+1 Q1n+1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0
CP3 CP2 CP1
Q3n Q2n Q1n 0 0 0 0 1 1 1 1 状态图 111 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1