《电路分析》第九章 正弦稳态功率和能量 三相电路解析
合集下载
正弦稳态电路分析和功率计算
2
Y = 0.1 + j0.2S
0.025F 0.1S
0.02F
十、利用相量图求解电路
例 如图所示电路，uS 2US cost ，求输出电压 uO(t) 对 uS(t) 的相位关系。
C
解：（一）解析法
+
+
1
uS
R uO
–
–
（二）相量图法
U O②
I jC
+ US
U C
R
+ UO
–
–
I ①
③ U C
直流电阻电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
R11Im1 R12Im2 R1mImm uS11
R
21I
m1
R
22I
m2
R 2mImm
uS22
R m1Im1 R m2Im2 R mm Imm uSmm
正弦稳态电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
ZZ1211IImm11
Z12I m 2 Z 22I m 2
Z1m I mm Z 2 m I mm
U S11 U S22
Zm1Im1 Zm2Im2 Zmm Imm U Smm
例 uS = 6cos3000t V，求正弦稳态时的 i1 , i2 。
i1 1k
+2000–i1 i2
uS
(3)
Z
U I
U I
u i
= R + jX = |Z| Z
Z R2 X2
Z
arctg
X R
ZU I
Z = u – i
(4) 阻抗的性质
电路分析基础课件10正弦稳态功率和能量、三相电路
U
m
I
m
UI
单位为VA（伏安），不用W（平均功率用）
在正弦交流电路中，平均功率P不等于S，而一般是 P<S，只有在纯电阻情况下，P=S.
31
3、功率因数
定义：功率因数
P cos
S
式中，φ是单口网络N的端口电压与端口电流的相位差角，
也称作功率因数角。
讨论：不含独立源时， φ= φZ, 当φZ>0时，阻抗呈感性 当φZ<0时，阻抗呈容性
不断往返。（这是由电感的贮能本质决定的。）
14
2、电容的平均贮能
设：电容的电流为： i(t) Im sin t
则，电容电压为：
u(t)
Im
C
cost
U
m
cost
瞬时功率为：
p(t)
ui
U m Im
cost
sin
t
U m Im
1 2
sin
2t
UI sin 2t
电容吸收的平均功率为:
P
1 T
T
0
p(t )d t
u, i, p u
能量流入电感
p i
2
ωt
能量流出电感
wL
wL
1 2
Li 2
WL
1 2
LI 2
2
ωt
☺12
u, i, p u
能量流入电感
p i
2
ωt
能量流出电感
wL
wL
1 2
Li 2
WL
1 2
LI 2
2
ωt
☺13
说明： 1）由图9-3可知，当P>0时，能量流入电感，电感贮能增
电路第9章 正弦稳态电路的分析
I 1 Y G jC j G jB Y y U L
§9-1
阻抗和导纳
Y—复导纳；|Y| —复导纳的模；y—
导纳角； G —电导(导纳的实部)；
B —电纳(导纳的虚部)；
| Y | G 2 B 2 转换关系： 或 B y arctan G
I
相量图：选电压为参考向量，
u 0
y
IG
.
IB U
I I G2 I B2 I G2 (I C I L )2
注意
RLC并联电路会出现分电流大于总电流的现象
§9-1
阻抗和导纳
+ I R U -
等效电路
IR
1 jC eq
I B
（3）wC<1/wL，B<0，y<0，电路为感性，电流落后电压；
1 Y 0.0128 50.20 Z 78.150.20 0.0082 j0.0098 S 1
R’
L’
1 1 1 0.102mH R 122 L 0.0098 G 0.0082
§9-1
阻抗和导纳
① 一端口N0的阻抗或导纳是由其内部的参数、
y
IG
I
.
U
.
I I I I (I L IC )
2 G 2 B 2 G
2
IC .
IL
§9-1
阻抗和导纳
I
+
IR
R
j Leg
等效电路
I B
U -
（4）wC=1/wL，B=0，j y =0，电路为电阻性， 电流与电压同相。
I
C
IL
I IG
最全第九章(正弦稳态电路分析)习题解答打印版.doc
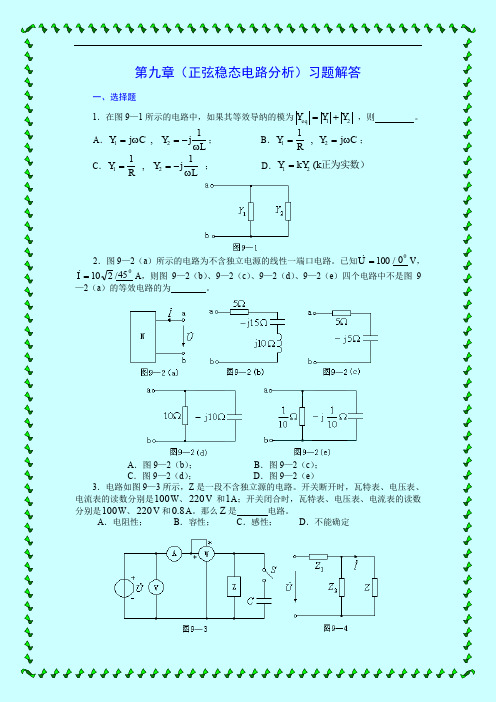
第九章（正弦稳态电路分析）习题解答一、选择题1．在图9—1所示的电路中，如果其等效导纳的模为21Y Y Y eq += ，则 。
A ．L Y C Y ω-=ω=1j, j 21； B ．C Y RY ω==j , 121；C ．L Y R Y ω-==1j , 121 ；D ．正为实数）k kY Y ( 21=2．图9—2（a ）所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ，045 /210=I A ，则图9—2（b ）、9—2（c ）、9—2（d ）、9—2（e ）四个电路中不是图9—2（a ）的等效电路的为 。
A ．图9—2（b ）；B ．图9—2（c ）；C ．图9—2（d ）；D ．图9—2（e ）3．电路如图9—3所示，Z 是一段不含独立源的电路。
开关断开时，瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ；开关闭合时，瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A ．电阻性；B ．容性；C ．感性；D ．不能确定4．电路如图9—4所示，U固定不变。
如果 ，则改变Z （Z 不等于无限大）时，I不变。
A ．21Z Z =； B ．21Z Z -=； C ．21Z Z =； D ．)Arg()Arg(21Z Z =5．Ω=10R 的电阻，F 1μ=C 的电容与电感L 串联，接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高，电感应取 。
A ．1H ；B ．π21Ｈ； C ．21H ； D ．241πＨ二、填空题1．若Ω=3R ，Ω=ω6L ，Ω=ω2011C ，Ω=ω2012C ，则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2．线性一端口电路如图9—6所示，A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率，有功功率、无功功率分别为V A 30/1000、W 350、50Var 。
第九章(2) 正弦稳态电路的功率
由 P = U I cos ϕ , Q = U I sin ϕ 得
S =U I =
P2 + Q2
P λ = cos ϕ = = S
P P +Q
2 2
并电容前，Q＝Q L 并电容后，Q′＝Q L+ Q C 由于 Q C 为负值，故 Q′< Q ；而并电容前后的平均 功率 P 未变，因此并电容后功率因数 λ 得到提高。
定义网络 N 的无功功率 Q 为：
Q = U I sin ϕ
Q 的单位：无功伏安，简称为：乏 (var)、千乏(kvar)
当
ϕ >0
（感性电路），
Q > 0;
当 ϕ<0
（容性电路）， Q < 0 .
R、L、C 元件的无功功率
电阻 R：ϕ = 0，
Q R = U I sin ϕ = 0
电感 L：ϕ = π/2 ，
T
可求得
P = U I cos ϕ = U I λ
其中 λ=cosϕ 。P的单位：瓦特 (W) 网络 N 的平均功率与其端电压和端电流的有 效值成正比，还与电压、电流相位差的余弦 函数成正比。
R、L、C 元件的平均功率
电阻 R：ϕ = 0，
PR =U I cos ϕ = U I = I 2 R = U 2 R
‘’例：电路如图，已知 U＝100V，求 该单口网络吸收 的总无功功率 Q 及 Q L、Q C 。
+ U
I
-j5Ω
R1 10Ω j30Ω
解：
R2 15Ω
Z = (10 + 15 ) + j ( 30 − 5 ) = 25 ×
2 45 o ( Ω )
I =U
正弦交流电路的稳态分析(课件)
02
正弦交流电的基本概念
正弦交流电的定义
正弦交流电
正弦交流电的产生
大小和方向随时间作正弦函数周期性 变化的电流。
通过交流发电机产生，当磁场和导体 线圈发生相对运动时，导体线圈中就 会产生正弦交流电。
正弦交流电的波形图
正弦交流电的波形图呈现正弦函数的 形状，随着时间的推移，电流值在正 弦波的最高点和最低点之间变化。
线性时不变正弦交流电路具有 叠加性、比例性和线性特性。
相量法分析正弦交流电路
相量法是一种分析正弦交流电 路的方法，通过引入复数和相 量，将时域的电压和电流表示
为复数形式的相量。
相量法的优点在于可以将正 弦交流电路中的复杂数学问 题简化为复数代数问题，从
而方便求解。
通过相量法，可以得出正弦交 流电路的阻抗、功率和相位等
未来研究的方向和展望
研究方向一
研究方向二
针对复杂正弦交流电路的稳态分析，深入 研究不同元件之间的相互影响，提高分析 精度。
结合新型材料在正弦交流电路中的应用， 研究其对电路性能的影响，探索新型材料 在优化电路性能方面的潜力。
研究方向三
研究方向四
结合现代计算技术和仿真软件，开发高效 、精确的正弦交流电路稳态分析方法和工 具。
正弦交流电路的稳态分析 (课件)
• 引言 • 正弦交流电的基本概念 • 正弦交流电路的稳态分析 • 实例分析 • 总结与展望
01
引言
主题简介
正弦交流电路
正弦交流电路是指电流和电压随时间按正弦规律变化的电路 。在日常生活和工业生产中，许多电源和负荷都是以正弦交 流电的形式存在。
稳态分析
稳态分析是电路分析的一个重要方面，主要研究电路在稳定 状态下各元件的电压、电流和功率等参数。对于正弦交流电 路，稳态分析涉及对电路中各元件的电压和电流进行傅里叶 变换，以得到各次谐波的幅值和相位。
第九章-正弦稳态电路的分析
（举例略）
例：9-4-2如图，列出节点电压相量方程
33
-j5Ω
1
2
5Ω 10o A
j12Ω
j5Ω -j10Ω
10Ω -j0.5A
设节点与参考节 点如图
(1 5
1 j10
1 j12
1 )U j5 1
(
1 - j5
1 )U j12 2
00
A
I 2
3
.
1
4
-
300
A
I 3.14300 A
R jωL IU2S（略）
练习9-7
习题：9-1 （b）、（e）
23
9-3 （4）
9-7 9-11
说明：9-7 求R、L时，习题解答单纯根据相量电 路列方程求解较麻烦，借助相量图分析得 到电流电压相量，然后，由
Z
R
jωL
U I
部分答案参考：
9 （1 b)Zin 2 j, Yin 0.4 j0.2
=2A。求电流表 A 读数
1
I
解：利用KCL建立电路方程
+
U
-
A
R1
-j 1
A1 I1
I2 A2
R2
1、设I2 20O
I 1
R1
U
j1 ωC
U00
1 ωC
j1 ωC
I1 1A
I1 14 5O
I14 5O
ωC
2 、I I1 I2 0 . 7 0 7 j 0 . 7 0 7 2 I 2 . 7 0 72 0 . 7 0 72 2.8( A )
Yeq Y1 Y2 Yn — 端口等效导纳
两个阻抗并联，则等效导纳：
Y
Y 1
例：9-4-2如图，列出节点电压相量方程
33
-j5Ω
1
2
5Ω 10o A
j12Ω
j5Ω -j10Ω
10Ω -j0.5A
设节点与参考节 点如图
(1 5
1 j10
1 j12
1 )U j5 1
(
1 - j5
1 )U j12 2
00
A
I 2
3
.
1
4
-
300
A
I 3.14300 A
R jωL IU2S（略）
练习9-7
习题：9-1 （b）、（e）
23
9-3 （4）
9-7 9-11
说明：9-7 求R、L时，习题解答单纯根据相量电 路列方程求解较麻烦，借助相量图分析得 到电流电压相量，然后，由
Z
R
jωL
U I
部分答案参考：
9 （1 b)Zin 2 j, Yin 0.4 j0.2
=2A。求电流表 A 读数
1
I
解：利用KCL建立电路方程
+
U
-
A
R1
-j 1
A1 I1
I2 A2
R2
1、设I2 20O
I 1
R1
U
j1 ωC
U00
1 ωC
j1 ωC
I1 1A
I1 14 5O
I14 5O
ωC
2 、I I1 I2 0 . 7 0 7 j 0 . 7 0 7 2 I 2 . 7 0 72 0 . 7 0 72 2.8( A )
Yeq Y1 Y2 Yn — 端口等效导纳
两个阻抗并联，则等效导纳：
Y
Y 1
《电路》课件：第九章 正弦稳态电路的分析1-3
(4) 当 z 90 ~ 0或Y 0 ~ 90 时为容性
§9-2 阻抗(导纳)的串联和并联
1．串联：
Z Z1Z 2Z n
分压：
U k
Zk Z
U
2．并联：
1 1 1 1
Z Z1 Z2
Zn
Y Y1 Y2 Yn
分流：
Ik
Yk Y
I
例5-4-2 如图RLC串联电路。R= 2105 ，L= 152 mH，C= 150 F，
（2〕当ω =1 rad/s
Zac
1.5
1 2
j(2
1) 2
2
j1.5
（Ω
）
等效相量电路如图
ch9s1-7 例5-4-2 求如图RLC串联电路的阻抗
解：
Zi
R
j(L 1 ) C
X L 1 C
R jX
Zi R2 X2
Zi z
当
z
tg 1
X R
(1)L 1 C
即
＝
1 LC
时，Zi
端电压 u=141.4cos(5000t)V。
求：i、元件的电压相量。
解： 用相量法。
U 1000 (V ) 5000(rad / s)
Z R j L 1
1250
j(5000
j
1125
C
10 3
5000
1 15 0
10 6
)
I
U R
1250 U Z
IR
j2505 2558.52 5730.1.03 ()
R
(2)L 1 C
即
1 LC
时，感性Zi
(3)L 1 C
即
1 LC
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
网络 N 吸收的瞬时功率为：
p(t) u i 2U cos(t ) 2I cost
U I[cos cos(2t )]
cosx cos y cos(x y) cos(x y) 2
网络 N 的瞬时功率随时间而变化。若 0 且 ，则 p(t) 的正负也随时间变化，说明网 络 N 与外电路之间有能量往返，这是由于电路 中存在储能元件的缘故。
第九章 正弦稳态功率和能量 三相电路
❖ §9-1 元件的功率和能量关系 ❖ §9-2 单口网络的平均功率 ❖ §9-3 单口网络的无功功率 ❖ §9-4 复功率 复功率守恒 ❖ §9-5 最大功率传输定理 ❖ §9-6 三相电路
郑州大学信息工程学院
返回目录
本章学习目的及要求
本章重点： 1、掌握有功功率、无功功率、视在功
1、瞬时功率：
pC(t)＝-UCmICmcosωtsinωt=－UCICsin2ωt
2、电容元件的平均功率 ：
PC＝0
3、电容元件的平均贮能：
WC
1 4
CU
Cm
2
1 2
CU
C
2
结论
只有电阻的平均功率大于零，而电感 和电容的平均功率等于零。以后提到的功 率就是指平均功率，是电路中电阻消耗的 功率，或指电源提供的功率，也称为有功 功率。
+ uU22
－
I1 0.563 50.70 A，I2 0.2147 .30 A
解法二：
I1 1 j2 I2 j2
+
U S
－
I3
j0.5
+ 1 U1 － j0.5
+ U 2 －
1 *(2 j 1 1)
总阻抗为 Z 1 2 j j2
j2 9 11 j
1 2 j 1 1
8
j2
j2
I1
Us Z
8 9 11 j
36 44 j 101
0.563129.3o
I1 1 j2 I2 j2
+
U S
－
I3
j0.5
+ 1
U1
－ j0.5
+
U 2
－
1 *(2 j 1 1)
U1 I1
j2 1
j2 2 j 1 1
23 28 j 0.359 50.60o 101
j2
j2
WC1 0.5*1*U12 0.064J
率、功率因数的概念和求法； 2、掌握正弦交流稳态下最大功率传输
定理； 3、对称三相电路的计算。
§9-1 元件的功率和能量关系
一、基本关系式：
VAR: uR RiR
uL
(t
)
L
diL dt
iC
(t)
C
duC dt
p(t) u(t)i(t) dw(t) dt
p>0，元件吸收功率，能量增加，有能量流入元件. p<0，元件提供功率，能量减少，元件放出能量。
返回 上页பைடு நூலகம்下页
二、平均功率（有功功率）
平均功率--指瞬时功率在一周期内的平均值，又 称为有功功率，简称为功率。平均功率表示电路 吸收或产生电功率的平均速率。
P 1
T p(t)dt 1
T
[UI cos
UI cos(2t )]dt
T0
T0
可求得
P U I cos
网络 N 的平均功率与其端电压和端电流的有效 值成正比，还与电压、电流相位差的余弦函数 成正比。
1、瞬时功率： pL (t) U Lm ILm cost sin t
sin 2t 2sint cost
pL (t) ULIL sin 2t
p(t) u(t) i(t)
uL (t) U Lm cost iL (t) I Lm sin t
ωt
pL (t) ULIL sin 2t
2.电感元件的平均功率： PL 0
w(t)
t
p(t)dt
t
uidt
1 L i2 (t) 2 1 C u2 (t) 2
(L) (C )
二、周期信号的平均值
f (t) 1
T
f (t)dt
T0
正弦函数在一个周期内的平均值为0。
三、电阻元件上的功率
+ i(t)
u(t)
u(t)=Umcos(ωt＋u） i(t)=Imcos(ωt＋i） －
1
U2 2 j 2 j 1
1
U1
1 10 101
j
0.099584.29o
2j
WC 2
0.5
*1*U
2 2
0.00495J
§9-2 单口网络的平均功率
❖ 一. 瞬时功率
正弦稳态电路中，电流 + i
和电压是同频率的正弦量。 u
N
-
不妨设
i 2 I cost
u 2 U cos(t )
其中 是电压与电流的相位差。
T0 电阻元件的平均功率为：
P
UI
U2 R
I 2R
1 2
U
m
I
m
平均功率(average power)也称为有功功率(active
power)，简称为功率。
电阻的平均功率的求法与直流电阻相同。
四、电感元件的功率和平均贮能
iL
uL (t) U Lm cost
+ uL -
iL (t) I Lm cos(t 90 0 ) I Lm sin t
瞬时功率为：
p(t) ui UmIm cos2 (t u )
1 2
UmIm1 cos2( t u ) UI1 cos2( t u )
P(t)0，所以电阻只消耗能量。
p(t) Uu(It恒) 定分量 i(t)
ωt
p(t) UI 1 cos 2( t u )
p(t) 1
T
p(t)dt P
p(t) UI[cos φ cos(2t φ)]
p
UIcos 恒定分量
o
• p 有时为正, 有时为负； • p>0, 电路吸收功率； • p<0，电路发出功率；
u i
t
UIcos (2 t+)为
正弦分量
这表明电路中的动态元件与外电路或电源进行能量交 换。对无源网络，在一周期内电路吸收的功率大于供给的 功率（有源网络则相反），电路的平均功率不为零。
电容和电感不消耗也不再生能量，它 只是从电源处吸收能量，贮存起来，在下 一个时间段再向外放出，说明它与电源之 间进行能量的交换。
P73例9-4：已知us = 2cos2t v ,求电阻的平 均功率、电感和电容的平均贮能。
1 j12H
1j2H
+
UusS －
I1 j01.5F
－+uU11Ij2110.F5
3.电感元件的瞬时贮能为：
wL (t)
1 2
LiL2 (t)
1 2
LI
2 Lm
sin 2
t
1 2
LI
2 L
(1
c os 2t )
4.电感元件的平均贮能为：
WL
1 4
LILm 2
1 2
LIL2
五、电容元件的功率和平均贮能
ic + uc -
uC(t)=UCmcosωt , iC(t)=ICmcos(ωt +900)＝－ICmsinωt